JAC Class 10 Maths Important Questions Chapter 11 रचनाएँ

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 11 रचनाएँ Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 11 रचनाएँ

प्रश्न 1.
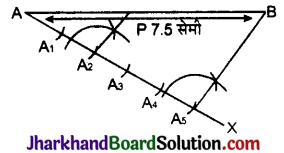
7.5 सेमी. रेखाखण्ड को 2 : 3 के अनुपात में विभाजित कीजिए। केवल चित्र बनाइए।
हल:
AP : PB = 2 : 3 होगा।

प्रश्न 2.
एक समकोण त्रिभुज ABC खींचिए, जिसमें BC = 12 सेमी., AB = 5 सेमी. और ∠B = 90° है। इस त्रिभुज के समरूप एक त्रिभुज की रचना कीजिए, जिसका स्केल गुणक \(\frac{2}{3}\) हो। क्या नया त्रिभुज भी क त्रिभुज है।
हल:
रचना के चरण :

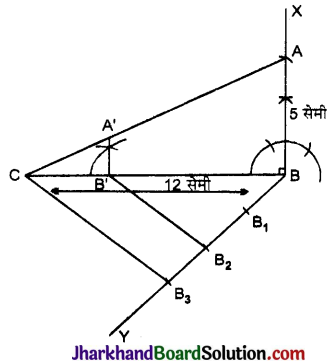
• BC = 12 सेमी. की एक रेखा खींची।
• BC के बिन्दु B से 90° का कोण बनाती हुई BX रेखाखण्ड खींची।
• रेखाखण्ड BX से AB = 5 सेमी. काटा तथा AC को मिलाया। इस प्रकार ABC प्राप्त हुआ।
• रेखाखण्ड BC के नीचे की ओर B बिन्दु से न्यून कोण बनाती हुई BY किरण खींची।
• किरण BY के तीन बराबर भाग इस प्रकार किए कि BB₁ = B₁B₂ = B₂B₃।
• B₃ को C से मिलाया।
• B₂ से B₃C के समान्तर रेखा B₂B’ खींची जो BC को B’ पर मिलती है।
• B’ से AB के समान्तर रेखा A’B’ खींची जो AC से A’ पर मिलती है।

इस प्रकार ΔA’B’C, अभीष्ट समरूप त्रिभुज है।

औचित्य (उपपत्ति) : ΔBB’B₂ तथा ΔBCB₃ में
∠B = ∠B (उभयनिष्ठ)
∠BB₂B’ = ∠BB₃C (रचना से)
ΔBB’B₂ ~ ΔBCB₃ (AA समरूपता कसौटी से)
\(\frac{B B^{\prime}}{B C}=\frac{B B_2}{B B_3}\)
(समरूप त्रिभुज की संगत भुजाएँ समानुपाती होती है)

∠A’BC = ∠ABC = 90° (रचना से)
अतः ΔA’B’C की भुजाएँ ΔABC की संगत भुजाओं \(\frac{2}{3}\) गुनी होंगी तथा ΔA’B’ C समकोण Δ होगी।

प्रश्न 3.
3 सेमी त्रिज्या के एक वृत्त पर 5 सेमी. त्रिज्या के एक संकेन्द्रीय वृत्त के किसी विन्दु से एक स्पर्श रेखा की रचना कीजिए और उसकी लम्बाई मापिए।
हल:
दिया है : 3 सेमी त्रिज्या का एक वृत्त और 6 सेमी त्रिज्या का एक संकेन्द्रीय वृत्त जिस पर एक बिन्दु माना P दिया गया है।

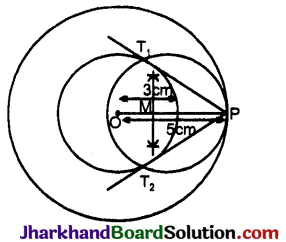
रचना के चरण :

• 3 सेमी त्रिज्या लेकर केन्द्र O वाला एक वृत्त खींचा।
• केन्द्र O से 5 सेमी त्रिज्या का एक संकेन्द्रीय वृत्त खींचा और इस पर एक बिन्दु P लिया।
• रेखाखण्ड OP खींचा और इसका लम्ब समद्विभाजक खींचा जो OP को बिन्दु M पर काटता है।
• बिन्दु M को लेकर MP त्रिज्या का एक वृत खींचा जो केन्द्र O के 3 सेमी त्रिज्या वाले वृत्त को T₁ और T₂ बिन्दुओं पर काटता है।
• PT₁ और PT₂ को मिलाया जो वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।

उपपत्ति: हम जानते हैं स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∠OT₁P = ∠OT₂P = 90°
OT₁ तथा OT₂ को मिलाया, OP वृत्त का व्यास है।
∠OT₁P तथा ∠OT₂P अर्द्धवृत्त के कोण हैं।
∠OT₁P = 90° तथा ∠OT₂P = 90°
OT1 ⊥ PT1 तथा OT2 ⊥ PT2
अत: PT₁ तथा PT₂ अभीष्ट स्पर्श रेखाएँ हैं।
लम्बाई मापने पर-
परिकलन : स्पर्श रेखा

प्रश्न 4.
8 सेमी. लम्बी एक रेखाखण्ड AB खींचिए। A को केन्द्र मानकर 4 सेमी त्रिज्या पर एक वृत्त बनाइये तथा बिन्दु B से इस वृत्त पर स्पर्श रेखा युग्मों की रचना कीजिए एवम् उनकी लम्बाइयाँ मापिए।
हल:
रचना के चरण :

• 8 सेमी. लम्बाई का AB रेखाखण्ड खींचा।
• AB के A बिन्दु से 4 सेमी. त्रिज्या का एक वृत्त खींचा।
• AB का समद्विभाजक खींचा तथा समद्विभाजक बिन्दु को M अंकित किया।
• M को केन्द्र मानकर MA त्रिज्या का वृत्त खींचा जो A केन्द्र वाले वृत्त को T₁ तथा T₂ पर काटता है।
• BT₁ तथा BT₂ को मिलाया BT₁ तथा BT₂ अभीष्ट रेखाएँ हैं। नापने पर स्पर्श रेखाओं की लम्बाई = 6.93 सेमी।

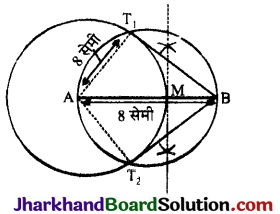
औचित्य (उपपत्ति) : AT₁ तथा AT₂ को मिलाया।
∵ हम जानते हैं कि स्पर्श रेखा स्पर्श बिन्दु से होकर जाने वाली त्रिज्या पर लम्ब होती है।
अत: ∠AT₁B = ∠AT₂B = 90°
AB, M केन्द्र वाले वृत्त का व्यास है।
∠AT₁B = ∠AT₂B = 90°
(अर्द्धवृत्त में बनी कोण समकोण होता है)
अत: BT₁ तथा BT₂ अभीष्ट स्पर्श रेखाएँ हैं।

प्रश्न 5.
4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिये गये त्रिभुज की संगत भुजा की \(\frac{3}{5}\) गुनी हो।
हल:
माना ΔABC है जिसमें AB = 5 सेमी, AC = 4 सेमी, BC = 6 सेमी।

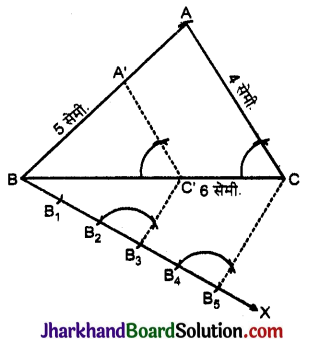
रचना के चरण :

• एक रेखाखण्ड BC 6 सेमी खींचा।
• B को केन्द्र मानकर 5 सेमी त्रिज्या का चाप लगाया।
• C को केन्द्र मानकर 4 सेमी. त्रिज्या लेकर एक चाप लगाया जो पहले चाप को A बिन्दु पर काटता है।
• AB और AC को मिलाया ΔABC वांछित त्रिभुज है।
• आधार BC के नीचे की ओर कोई न्यून कोण बनाती BX किरण खींची।
• BX किरण के पाँच बराबर भाग इस प्रकार किए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
• B₅C को मिलाया। B₃ से B5C के समान्तर B₃C’ रेखा खींची जो B₃ से C’ पर मिलती है।
• C’ से AC के समान्तर A’C’ रेखा खींची जो AB को A’ पर मिलती है।

अतः A’BC’ अभीष्ट समरूप त्रिभुज होगा।

औचित्य (उपपत्ति) : ΔBB₃C तथा BB₅C में
∠B = ∠B (उभयनिष्ठ)
∠BB₃C’ = ∠BB₅C (रचना से)
ΔBB₃C’ ~ ΔBB₅C (AA समरूपता कसौटी से)
\(\frac{B C^{\prime}}{B C}=\frac{B B_3}{B B_5}\)
[समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं]

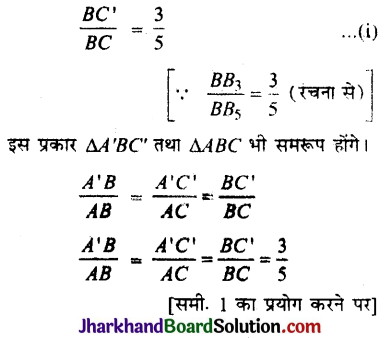
A’B = \(\frac{3}{5}\)AB, A’C’ = \(\frac{3}{5}\)AC तथा BC’ = \(\frac{3}{5}\)BC
अत: ΔA’BC’ की भुजाएँ ABC की संगत भुजाओं \(\frac{3}{5}\) की हुँ गुनी होंगी।

प्रश्न 6.
त्रिज्या 5 सेमी का वृत्त खींचिए। वृत्त के केन्द्र से 13 सेमी दूरी पर स्थित किसी बिन्दु से वृत्त की स्पर्श रेखाएं खींचिए। स्पर्श रेखाओं की लम्बाई नापिए तथा गणना करो व औचित्य भी दीजिए।
हल:
रचना के चरण :

• सर्वप्रथम 5 सेमी का वृत्त खींचा जिसका केन्द्र O है।
• बिन्दु ‘O’ से 13 सेमी दूरी पर बिन्दु P लिया, OP को मिलाया।
• PO को सम द्विभाजित किया सम द्विभाजक को M अंकित है।
• M केन्द्र मानकर PM त्रिज्या का एक वृत्त खींचा जो O केन्द्र वाले वृत्त को A और B बिन्दुओं पर काटता है।
• PA और PB को मिलाया अतः PA और PB अभीष्ट स्पर्श रेखाएँ हैं। स्पर्श रेखा को नापने पर लम्बाई = 12 सेमी हैं।

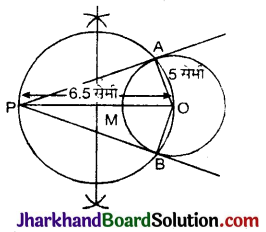
गणना द्वारा लम्बाई ज्ञात करना : ΔPOA में,
∠PAO = 90° (प्रमेय 10.1 से)
अत: ΔPOA एक समकोण त्रिभुज है, अत: पाइथागोरस प्रमेय के अनुसार,
PO² = AO² + PA²
PA² = PO² + AO²
= (13)² – (5)²
= 169 – 25
PA = 144
PA = \(\sqrt{144}\)
= 12 सेमी
अतः नापने और गणना द्वारा स्पर्श रेखाओं की लम्बाई 12 सेमी।

औचित्य (उपपत्ति) :
∵ हम जानते हैं कि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती हैं।
अतः ∠PAO = 90° तथा ∠PBO = 90°
∵ OA, OB की मिलाया, OP वृत्त का व्यास हैं।
∠PAO व ∠PBO अर्द्धवृत्त में बने कोण हैं।
∴ ∠PAO = 90°, ∠PBO = 90°
अत: PA व PB अभीष्ट स्पर्श रेखाएँ हैं।

प्रश्न 7.
4 सेमी. त्रिज्या का एक वृत्त खींचिए। इस पर स्पर्श रेखाओं के ऐसे युग्म की रचना कीजिए कि इनके बीच का कोण 60° हो। रचना का औचित्य भी दीजिए। वृत्त के केन्द्र और स्पर्श रेखाओं के प्रतिच्छेद बिन्दु के बीच की दूरी को मापिये।
हल:
रचना के चरण :

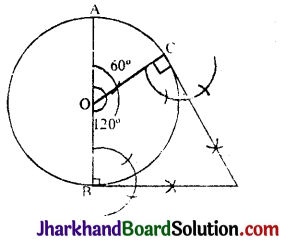
• O को केन्द्र मानकर 4 सेमी. त्रिज्या वाला वृत्त खींचा।
• वृत्त का व्यास AB खींचा।
• त्रिज्या AO के बिन्दु O पर 60° का कोण बनाती हुई एक रेखा OC खींची जो वृत्त को C बिन्दु पर काटती है।
• OC रेखाखण्ड के बिन्दु C से 90° का कोण बनाती हुई स्पर्श रेखा खींची।
• OB के बिन्दु B से 90° का कोण बनाती हुई दूसरी स्पर्श रेखा खींची जो पहली स्पर्श रेखा को D बिन्दु पर मिलती है।

अत: CD तथा BD वृत्त की स्पर्श रेखाएँ हैं जो एक दूसरे के साथ 60″ का कोण बनाती है। मापने पर केन्द्र और स्पर्श रेखाओं के प्रतिच्छेद बिन्दु के बीच की दूरी = 8 सेमी.।
औचित्य (उपपत्ति) :
∠AOC + ∠BOC = 180° (रैखिक समीकरण युग्म)
⇒ 60° + ∠BOC = 180°
⇒ ∠BOC = 180° – 60° = 120°
∵ OB तथा OC वृत्त की त्रिज्याएँ हैं तथा CD व BD वृत्त पर स्पर्श रेखाएँ हैं।
∴ ∠OCD = ∠OBD = 90° (प्रमेय 10.1 से)
अब ∠BOC + ∠OCD + ∠BDC + ∠OBD = 360°
⇒ 120° + 90° + ∠BDC + 90° = 360°
⇒ 300° + ∠BDC = 360°
⇒ ∠BDC = 360° – 300°
= 60°
अंतः CD व BD वृत्त की स्पर्श रेखाएँ हैं।

प्रश्न 8.
5 सेमी त्रिज्या के एक वृत्त की रचना कीजिए। वृत्त के बाहर स्थित बिन्दु P से केन्द्र का उपयोग किए बिना वृत्त की स्पर्श रेखाओं की रचना कीजिए तथा औचित्य भी दीजिए।
हल:
दिया है : एक वृत्त और इसका बाह्य बिन्द P हैं। वृत का केन्द्र अज्ञात है।
रचना के चरण :

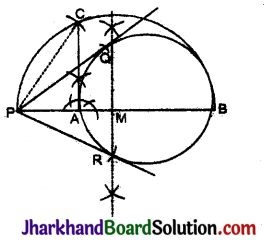
•  वृत्त की छेदक रेखा PAB खींची।
• PB को समद्विभाजित किया और इसके मध्य-बिन्दु M से MP = MB त्रिज्या का अर्द्धवृत खींचा।
• बिन्दु A पर लम्ब AC खींचा जो अर्द्ध वृत्त को C बिन्दु पर मिलता है।
• P को केन्द्र मानकर PC त्रिज्या के चाप खींचे जो वृत्त को Q और R पर प्रतिच्छेद करते हैं।
• PR और PQ को मिलाया। अब PQ और PR अभीष्ट स्पर्श रेखाएँ हैं।

औचित्य (उपपत्ति) : PB को व्यास मानकर अर्द्धवृत PCB खींचा और PB के बिन्दु A पर AC ⊥ PB पर,
PC² = PA.PB
(∵ PC त्रिज्या के चाप R व Q हैं)
∴ PR² = PA.PB (PC = PR = PQ)
PQ² = PA.PB
अत: PR और PQ अभीष्ट स्पर्श रेखाएँ हैं।

प्रश्न 9.
4.5 सेमी त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएं खींचिए जो परस्पर 45° का कोण बनाती हों। औचित्य भी दीजिए।
हल:
रचना के चरण :

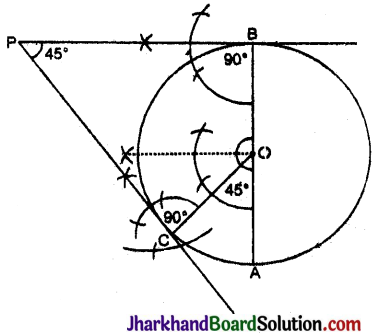
• O को केन्द्र मानकर 4.5 सेमी त्रिज्या का वृत्त खींचा।
• वृत्त का व्यास AB खींचा।
• बिन्दु O पर OA से 45° का कोण बनाती हुई एक रेखा OC खींची जो वृत्त को C बिन्दु पर काटती है।
• बिन्दु B पर OB के लम्बवत् रेखा खींची तथा विन्दु C पर OC के लम्बवत् एक रेखा खींची। दोनों रेखाएँ एक-दूसरे को P बिन्दु पर काटती हैं।

अत: PB और PC वृत्त की दो अभीष्ट स्पर्श रेखाएँ हैं जो एक-दूसरे से 45° का कोण बनाती हैं।
औचित्य (उपपत्ति) : माना वृत्त का केन्द्र O है। PB व PC स्पर्श रेखाएँ हैं।
इनके बीच का कोण BPC = 45° है।
∠BOC = 180° – 45° = 135°
∠AOC = 180° – ∠BOC (रैखिक समीकरण युग्म से)
= 180° – 135°
= 45°.

प्रश्न 10.
8.5 सेमी लम्बा एक रेखाखण्ड AB खींचिए। A को केन्द्र मानकर 5 सेमी त्रिज्या का एक वृत्त तथा B को केन्द्र मानकर 2 सेमी त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखाओं की रचना कीजिए।
हल:
केन्द्र A से 5 सेमी त्रिज्या का वृत्त खींचा गया है तथा B को केन्द्र मानकर 2 सेमी त्रिज्या का वृत्त खींचा गया है।
रचना के चरण :

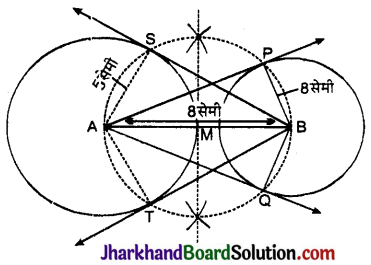
• सर्वप्रथम AB रेखाखण्ड 8.5 सेमी खींचा।
• A को केन्द्र मानकर 5 सेमी त्रिज्या का एक वृत्त खींचा और केन्द्र B से 2 सेमी त्रिज्या का वृत्त खींचा।
• रेखाखण्ड AB का समद्विभाजक किया जो कि AB को M बिन्दु पर काटता है।
• बिन्दु M को केन्द्र मानकर MA त्रिज्या का एक वृत्त खींचा जो 4 केन्द्र वाले वृत्त को S वT बिन्दुओं पर तथा B केन्द्र वाले वृत्त को P और Q बिन्दुओं पर काटता है।
• SB, TB, PA व QA को मिलाया।

अत: SB और TB केन्द्र A वाले वृत्त की स्पर्श रेखाएँ हैं तथा PA और QA केन्द्र B वाले वृत्त की स्पर्श रेखाएँ हैं।
औचित्य (उपपत्ति) : ∵ हम जानते हैं कि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∠ASB = ∠ATB = 90°
और ∠APB = ∠AQB = 90°
M केन्द्र वाले वृत्त का व्यास AB है।
∠ASB, ∠ATB अर्द्धवृत्त में बने कोण हैं।
∴ ∠ASB = 90°, ∠ATB = 90°.
∴ SB और TB केन्द्र A वाले वृत्त की स्पर्श रेखाएँ हैं।
इसी प्रकार ∠APB और ∠AQB अर्द्धवृत्त में बने कोण हैं।
∴ ∠APB = 90°, ∠AQB = 90°,
∴ PA और QA केन्द्र B वाले वृत्त की स्पर्श रेखाएँ हैं।

प्रश्न 11.
5 सेमी भुजा वाले समबाहु त्रिभुज ABC की रचना कीजिए। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज ABC की संगत भुजाओं \(\frac{2}{3}\) की गुनी हों।
हल:
रचना के चरण :

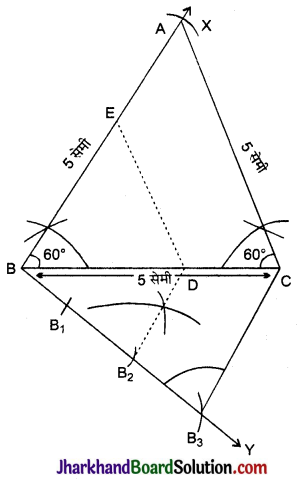
• एक रेखाखण्ड BC = 5 सेमी खींचिए।
• बिन्दु B को केन्द्र मनाकर 5 सेमी त्रिज्या लेकर लगाइए।
• इसी प्रकार, बिन्दु C को केन्द्र मनाकर 5 सेमी त्रिज्या एक अन्य चाप लगाइए, जो बिन्दु B से लगे चाप के है। यह प्रतिच्छेदित बिन्दु A है।
• A से C को मिलाइये। अतः एक समबाहु त्रिभुज BC रचना हो गई।
• BC से शीर्ष A के दूसरी ओर न्यूनकोण बनाती किरण XY खींचिए।
• 3 बिन्दु B₁, B₂, B₃ किरण BY पर इस प्रकार कीजिए कि BB₁ = BB₂ = B₂B₃ है।
• B₃ को C से मिलाइए।
• बिन्दु B₂ से, B₂D || B₃C खींचिए।
• बिन्दु D से, DE || CA खींचिए।
  तब ΔEBD अभीष्ट त्रिभुज है, जिसकी भुजाएँ त्रिभुज की संगत भुजाओं \(\frac{2}{3}\) की गुनी है।

प्रश्न 12.
2 सेमी त्रिज्या के वृत्त पर 5 सेमी त्रिज्या का एक संकेन्द्री वृत्त खींचिए। बाह्य वृत्त पर लिए गए एक बिन्दु P में छोटे वृत्त पर दो स्पर्श रेखाओं PA तथा PB की रचना कीजिए। PA की लम्बाई मापिए।
हल:
रचना के चरण :

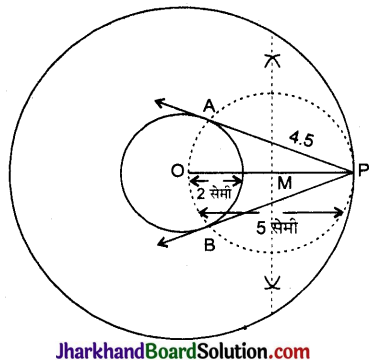
• एक 2 सेमी त्रिज्या का वृत्त खींचिए। अब इस O से एक 5 सेमी त्रिज्या का वृत्त खींचिए।
• बाह्य वृत्त पर बिन्दु P लेकर उसे केन्द्र O से मिलाइये।
• अब OP का लम्ब अर्द्धक खींचिए, जो OP को M पर काटता है।
• बिन्दु M को केन्द्र मानकर तथा OM त्रिज्या से वृत्त खींचिए जो अंतः वृत्त को बिन्दु A व B परकाटता है।
• बिन्दु A व B को बिन्दु P से मिलाइए। PA तथा PB अभीष्ट स्पर्श रेखाएँ हैं। PA = 4.5 सेमी।

प्रश्न 13.
एक त्रिभुज ABC की रचना कीजिए, जिसमें भुजा BC = 6 सेमी ∠B = 45° तथा ∠A = 105° हो, तब एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हों।
हल:
रचना के चरण :
(1) एक रेखाखण्ड BC = 6 सेमी खींचिए।
(2) बिन्दु B पर ∠B 45° बनाया।
∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C = 180° – 150°
∠C = 30°
(3) बिन्दु C पर ∠C = 30° बनाया। दोनों किरणें 4 पर काटती हैं। इस प्रकार ΔABC प्राप्त होता है।
(4) BC पर न्यून कोण बनाती एक किरण BX खींचिए।
(5) बिन्दुओं B₁, B₂, B₃ और B₄ को इस प्रकार अंकित कीजिए कि BB₁ = BB₂ = B₂B₃ = B₃B₄

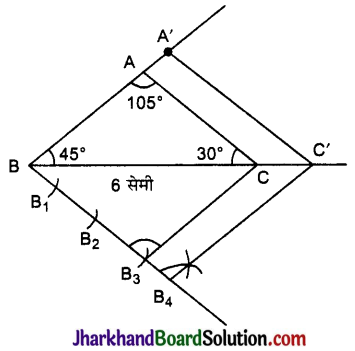
(6) B₂C को मिलाइए।
(7) B₄ में होती हुई रेखा B₄C || B₃ खींचिए।
(∠BB₃C = ∠BB₄C
(8) C में होती हुई रेखा C₄‘A’ || AC खींचिए।
(∠BCA = ∠BC’A)
अत: ΔA’BC’ एक अभीष्ट त्रिभुज हैं।

प्रश्न 14.
एक त्रिभुज ABC की रचना कीजिए जिसमें भूजा BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। तब एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हों।
हल:
BC = 7 सेमी, ∠B = 45°, ∠A = 105°
∠C = 180° – ( ∠B + ∠A)
= 180° – (45° + 105°)
= 180° – 150°
= 30°
रचना के चरण :

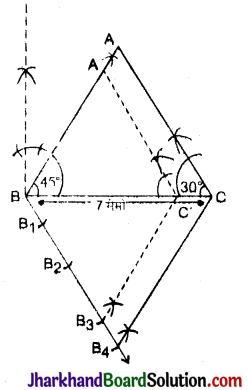
• BC = 7 सेमी की रेखा खींचे।
• बिंदु B पर 45° तथा बिंदु C पर 30° का कोण बनाएँ। यह एक दूसरे को पर काटते हैं।
• बिंदु B पर एक न्यून कोण बनाएँ।
• कोण किरण को चार सामान भागों B₁, B₂, B₃ और B₄ पर विभाजित किया।
• B₄ को C पर मिलाएँ।
• बिंदु B₃ मैं रेखा B₄C के समानान्तर रेखा बनाये जो BC को C’ पर काटती है।
• C से AC के समानान्तर CA’ रेखा खींची जो AB को A’ पर काटती है।
• ΔA’BC’ अभीष्ट त्रिभुज है। जिसमें A’B = \(\frac{3}{4}\)AB.

प्रश्न 15.
आधार 5 सेमी और ऊँचाई 4 सेमी वाले एक समद्विबाहु त्रिभुज की रचना कीजिए। एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ समद्विबाहु त्रिभुज की संगत भुजाओं का \(\frac{2}{3}\) गुना हो।
हल:
रचना के चरण :

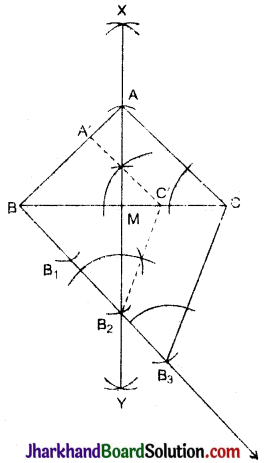
• BC = 8 सेमी खींचें।
• BC रेखा का लम्ब समद्विभाजक XY खींचा जां BC को M पर काटता है।
• XM पर MA = 4 सेमी काटा, तब BA और CA को मिलाया जिसमें ΔABC प्राप्त हुआ।
• बिन्दु B पर एक न्यूनकोण बनाया तथा उस पर तीन चाप B₁, B₂ और B₃ बनाए।
• B₃C मिलाया और B₂ से B₃C के समान्तर रेखा खींची जी BC को C’ पर काटती है।
• C’ से A’C’ || AC खींची।
• अत: A’C’B अभीष्ट त्रिभुज है।