JAC Class 10 Maths Important Questions Chapter 2 बहुपद

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 2 बहुपद Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 2 बहुपद

लयूत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
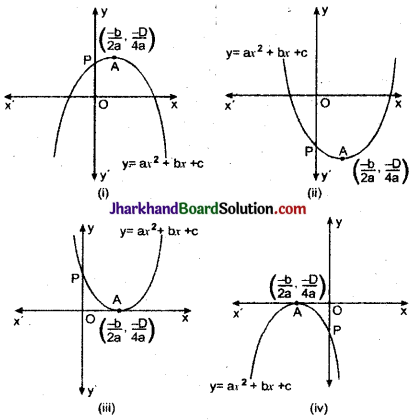
बहुपद ax² + bx + c के आलेखों की आकृतियाँ, चित्र में दी गयी हैं। प्रत्येक आकृति में a, b और c के चिह्न ज्ञात कीजिए:

हल :
(i) बहुपद y = ax² + bx + c का परवलय नीचे की ओर खुलता है।
∴ a < 0 होगा तथा परवलय का शीर्ष प्रथम चतुर्थांश में है। –\(\frac{b}{2a}\) > 0 ⇒ – b < 0 ⇒ b > 0
परलवय y-अक्ष को बिन्दु P पर प्रतिच्छेद करता है। y-अक्ष पर x = 0 होता हैं। x = 0 का मान समीकरण y = ax² + bx + c में रखने पर हम y = c प्राप्त करते हैं। अतः P के निर्देशांक (o, c) हैं। ∵ P, y- अक्ष की धनात्मक दिशा में है । अतः
∴ c > 0.
∴ a < 0, b > 0 तथा c > 0

(ii) दिशा है : y = ax² + bx + c परवलय ऊपर की ओर खुलता है। अत: a > 0 हैं। परवलय के शीर्ष चौथे चतुर्थाश में हैं।
∴ – \(\frac{b}{2a}\) > 0 ⇒ b < 0 ⇒ b < 0
परवलय y-अक्ष को बिन्दु p पर प्रतिच्छेद करता है। x = 0, अत: y = ax 2 + bx + c में x = 0 रखने पर y = c प्राप्त होता हैं।
∴ p के निर्देशांक (0, c) हैं।
∵ बिन्दु P, OY’ पर स्थित है। अतः c < 0 होगा। a > 0, b < 0 ओर c <0

(iii) बहुपद y = ax² + bx + c का परवलय ऊपर की ओर खुलता है। अतः a > 0 है।
परवलय का शीर्ष OX पर स्थित है।
∴ – \(\frac{b}{2a}\) > 0 ⇒ – b > 0 ⇒ b < 0 परवलय y = ax² + bx + c Y-अक्ष को बिन्दु P पर प्रतिच्छेद करता है जो OY पर स्थित है। समीकरण y = ax² + bx + c में x = 0 रखने पर, y = c प्राप्त होता है। अत: बिन्दु P के निर्देशांक (0, c) हैं। ∵ P, OY अक्ष पर स्थित है। ∴ c > 0 होगा।
∴ a > 0, b < 0 और c > 0.

(iv) परवलय y = ax² + bx + c नीचे की ओर खुलता है। अत: a < 0 है।
परवलय का शीर्ष (\(\frac{-b}{2a}\), \(\frac{-D}{4a}\))OX’ पर स्थित है।
∴ – \(\frac{b}{2a}\) < 0 ⇒ b > 0
परवलय y = ax² + bx + c, Y-अक्ष को P(0, c) पर प्रतिच्छेद करता है जो OY’ पर है। अतः c < 0 होगा।
∴ a < 0, b > 0 तथा c < 0.

प्रश्न 2.
यदि बहुपद p(x) = 2x² + 5x + k के शून्यक α तथा β, सम्बन्ध α² + β² + αβ = \(\frac{21}{4}\) को सन्तुष्ट करते हैं, तो k का मान ज्ञात कीजिए।
हल :
∵ αβ बहुपद p(x) = 2x² + 5x + k के शून्यक हैं।
∴ α + β = \(\frac{-5}{2}\)
तथा α × β = \(\frac{k}{2}\) ………(1)
α² + β² + αβ = \(\frac{21}{4}\) (दिया है)
⇒ α² + β² + 2αβ – αβ = \(\frac{21}{4}\) (αβ जोड़ने तथा घटाने पर)
⇒ (α + β)² – αβ = \(\frac{21}{4}\)
⇒ (\(\frac{-5}{2}\))² – \(\frac{k}{2}\) = \(\frac{21}{4}\)
[समी. (1) का प्रयोग करने पर]
⇒ \(\frac{25}{4}-\frac{k}{2}\) = \(\frac{21}{4}\)
\(\frac{25}{4}-\frac{21}{4}\) = \(\frac{k}{2}\)
\(\frac{4}{4}\) = \(\frac{k}{2}\)
\(\frac{k}{2}\) = 1
⇒ k = 2
अतः k = 2

प्रश्न 3.
यदि α और β द्विघात बहुपद f(x) = x² – px + g के शून्यक हैं तो निम्न के मान ज्ञात कीजिए :
(i) α² + β²
(ii) \(\frac{1}{α}=\frac{1}{β}\)
हल :
∵ α और β बहुपद f(x) = x² – px + q के शून्यक हैं।
∴ शून्यकों का योग (α + β) = – (\(\frac{-p}{1}\)) = p
शून्यकों का गुणनफल (αβ) = \(\frac{q}{1}\) = q

(i) α² + β² = (α + β)² – 2αβ
= p² – 2q

(ii) \(\frac{1}{α}=\frac{1}{β}\) = \(\frac{\alpha+\beta}{\alpha \beta}\) = \(\frac{p}{q}\)

प्रश्न 4.
यदि α, β द्विघात बहुपद f(x)= 2x² – 5x + 7 के शून्यक हों तो एक बहुपद ज्ञात कीजिए जिसके शून्यक 2α + 3β और 3α + 2β हों।
हल
∵ α और β द्विघात बहुपद f(x) = 2x² – 5x + 7 के शून्यक हैं।
∴ α + β = -(\(\frac{-5}{2}\)) = \(\frac{5}{2}\) और αβ = \(\frac{7}{2}\)
माना अभीष्ट बहुपद के शून्यकों के योग व गुणनफल को S व P से व्यक्त करें तो :
S = (2α + 3β) + (3α + 2β)
= 5(α + β) = 5 × \(\frac{5}{2}=\frac{25}{2}\)
या P = (2α + 3β) × (3α + 2β)
या P = 6(α² + β²) + 13αβ
या P = 6α² + 6β² + 12αβ + αβ
या P = 6 (α + β)² + αβ
या P = 6(\(\frac{5}{2}\))² + \(\frac{7}{2}\)
या P = 6 × \(\frac{25}{4}+\frac{7}{2}=\frac{75}{2}+\frac{7}{2}\)
∴ P = \(\frac{75+7}{2}=\frac{82}{2}\) = 41
अत: अभीष्ट बहुपद g(x) निम्न होगा :
g(x) = k(x² – Sx + P)
⇒ g (x) = k(x² – \(\frac{25}{2}\)x + 41)
जहाँ k एक अशून्य वास्तविक संख्या है।

प्रश्न 5.
बहुपद f(x) = 3x³ + ax² + 4x + b का एक गुणनखण्ड (x + 2) है। यदि इसमें (x – 3) का भाग दिया जाये तो शेषफल – 5 बचता है। a तथा b के मान ज्ञात कीजिए।
हल :
यहाँ f(x) = 3x³ + ax² + 4x + b का एक गुणनखण्ड (x + 2) है।
अत: x + 2 = 0
⇒ x = – 2 रखने पर
f(-2) = 0 होगा।
यहाँ f(x) = 3x³ + ax² + 4x + b
∴ f(-2) = 3(-2)³ + a(-2)² + 4(-2) + b
⇒ 0 = 3(-8) + a(4) – 8 + b
⇒ 0 = – 24 + 4a – 8 + b
⇒ 0 = 4a + b – 32
⇒ 4a + b = 32 ……..(i)
पुन: (x – 3) से भाग देने पर शेषफल – 5 बचता है।
अत: f(3) = – 5.
∵ f(x) = 3x³ + ax² + 4x + b
∴ f(3) = 3(3)³ + a(3)² + 4(3) + b
⇒ – 5 = 3 × 27 + a(9) + 12 + b
⇒ – 5 = 81 + 9a + 12 + b
⇒ – 5 = 93 + 9a + b
⇒ 9a + b = – 5 – 93
⇒ 9a + b = – 98 ….(ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर,

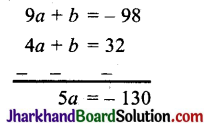
∴ a = \(\frac{-130}{5}\) = – 26
a का मान समीकरण (i) में रखने पर,
⇒ 4(-26) + b = 32
⇒ – 104 + b = 32
∴ b = 32 + 104 = 136
अतः a = – 26 और b = 136 होगा।

प्रश्न 6.
3x³ + x² + 2x + 5 को 1 + 2x + x² से भाग दीजिए।
हल :
3x³ + x² + 2x + 5 ÷ 1 + 2x + x²
1 + 2x + x² को x² + 2x + 1 लिख सकते है

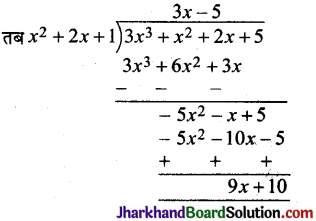
जाँच-
(3x – 5) (1 + 2x + x²) + 9x + 10
= 3x + 6x² + 3x² – 5 – 10x – 5x² + 9x + 10
= 3x³ + x² – 7x – 5 + 9x + 10
= 3x³ + x² + 2x + 5

प्रश्न 7.
x³ – 3x² + 3x – 5 को x – 1 – x² से भाग दीजिए और विभाजन एल्गोरिथ्म की सत्यता की जाँच कीजिए।
हल :
माना कि
f(x) = x³ – 3x² + 3x – 5
तथा g(x) = x – 1 – x² = – x² + x + 1
अब f(x) को g(x) से विभाजित करेंगे।

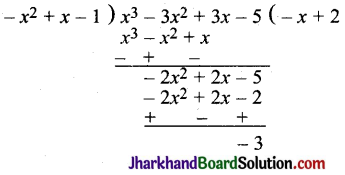
अत: भागफल q(x) = – x + 2
तथा शेषफल (x) = – 3
विभाजन एल्गोरिथ्म के प्रयोग से भाग्य = भाजक × भागफल + शेषफल
⇒ x³ – 3x² + 3x – 5 = (- x² + x – 1) (- x + 2) – 3
⇒ x³ – 3x² + 3x – 5 = (x³ – 2x² – x² + 2x + x – 2) – 3
⇒ x³ – 3x² + 3x – 5 = x³ – 3x² + 3x – 2 – 3
⇒ x³ – 3x² + 3x – 5 = x³ – 3x² + 3x – 5
चूँकि बायाँ पक्ष = दायाँ पक्ष
अतः विभाजन एल्गोरिथ्म सत्यापित होता है।

प्रश्न 8.
वह प्रतिबन्ध ज्ञात कीजिए कि बहुपद p(x) = ax² + bx + c के शून्यक एक दूसरे के व्युत्क्रम हैं।
हल :
माना कि α बहुपद p(x) = ax² + bx + c का प्रथम शून्यक है।
प्रश्नानुसार बहुपद p(x) का दूसरा शून्यक (β) = \(\frac{1}{α}\)
α × β = \(\frac{c}{a}\)
⇒ α × \(\frac{1}{α}\) = \(\frac{c}{a}\)
⇒ 1 = \(\frac{c}{a}\)
⇒ c = a
अतः प्रतिबन्ध c = a है ।

प्रश्न 9.
x³ – 6x² + 11x – 6 को x – 2 से भाग दीजिए और विभाजन एल्गोरिथ्म की सत्यता की जाँच कीजिए ।
हल :

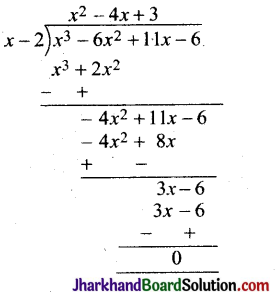
अतः भागफल = x² – 4x + 3 तथा शेषफल = 0
विभाजन एल्गोरिथ्य की सत्यता
भागफल भाजक + शेषफल
= (x² – 4x + 3) × (x – 2) + 0
= x³ – 4x² + 3x – 2x² + 8x – 6
= x³ – 6x² + 11x – 6
= भाज्य
अतः भागफल × भाजक + शेपफल = भाज्य
इति सिद्धम्

प्रश्न 10.
यदि त्रिघातीय बहुपद x³ – 3x² – 10x + 24 का एक शून्यक 4 है, तो इसके अन्य दो शून्यक ज्ञात कीजिए।
हल :
माना p(x) = x³ – 3x² – 10x + 24
दिया है, 4, p(x) का एक शून्यक है।
∴ (x – 4), p(x) का एक गुणनखंड होगा।

भागफल = x² + x – 6 तथा शेषफल = 0
∴ x³ – 3x² – 10x + 24 = (x – 4)(x² + x – 6).
अब p(x) के अन्य शून्यक ज्ञात करने के लिए भागफल (x² + x – 6) = 0 रखकर गुणनखंड करने पर,
x² + x – 6 = 0
⇒ x² + 3x – 2x – 6 = 0
⇒ x(x + 3) – 2(x + 3) = 0
⇒ (x + 3) (x – 2) = 0
यदि x + 3 = 0, तो x = – 3
और यदि x – 2 = 0, तो x = 2
अत: – 3 और 2 बहुपद x³ – 3x² – 10x + 24 के अन्य दो गुणनखंड है।

प्रश्न 11.
एक अध्यापक ने अपने 10 विद्यार्थियों में से प्रत्येक को एक कागज पर एक चर वाला एक बहुपद लिखकर देने को कहा। विद्यार्थियों के उत्तर निम्न थे :
2x + 3, 3x² + 7x + 2, 4x² + 3x² + 2,
x² + \(\sqrt{3}\)x + 7, 5x³ – 7x + 2,
2x² + 3 – \(\frac{5}{x}\), 5x – \(\frac{1}{2}\),
ax³ + bx³ + cx + d, x + \(\frac{1}{x}\), x³ – 3
निम्न प्रश्नों के उत्तर दीजिए:
(i) उपरोक्त दस में कितने बहुपद नहीं हैं?
(ii) उपरोक्त दस में कितने द्विघात बहुपद हैं?
हल :
(i) तीन, x² + \(\sqrt{3x}\) + 7, 2x² + 3 – \(\frac{5}{x}\), x + \(\frac{1}{x}\) बहुपद नहीं है।
(ii) एक 3x² + 7x + 2 एक द्विघातीय बहुपद है।

प्रश्न 12.
यदि बहुपद f(x) = x² – 8x + k के शून्यकों के वर्गों का योग 40 है, तो का मान ज्ञात कीजिए।
हल :
दिया है, f(x) = x² – 8x + k
माना f(x) के शून्यक α और β हैं।
∴ शून्यकों का योग = – \(\frac{b}{a}\)
α + β = \(\frac{-(-8)}{1}\)
और शून्यकों का गुणन = \(\frac{c}{a}\)
αβ = \(\frac{k}{1}\)
प्रश्नानुसार, α² + β² = 40
हम जानते हैं कि
(α + β)² = α² + β² + 2αβ
⇒ (8)² = 40 + 2k
⇒ 64 – 40 = 2k
⇒ 24 = 2k
⇒ k = \(\frac{24}{2}\) = 12

प्रश्न 13.
बहुपद p(x) = 2x⁴ – x³ – 11x² + 5x + 5 के दो शून्यक \(\sqrt{5}\) और – \(\sqrt{5}\) है। इस बहुपद के अन्य दो शून्यक ज्ञात कीजिए।
हल :
\(\sqrt{5}\) और – \(\sqrt{5}\) दिए गए बहुपद के शून्यक है।
∴ (x – \(\sqrt{5}\))(x + \(\sqrt{5}\)) = x² – 5, दिए गए बहुपद का एक गुणनखंड होगा।

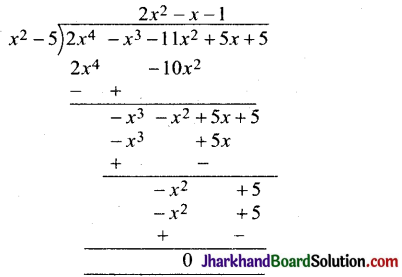
विभाजन एल्गोरिथ्य प्रमेय से
2x⁴ – x³ – 11x² + 5x + 5 = (2x² – x – 1)(x² – 5)
अब p(x) के अन्य दो शून्यक ज्ञात करने के लिए भागफल (2x² – x – 1) = 0 रखकर गुणनखंड करने पर
2x² – x – 1 = 0
⇒ 2x² – 2x + x – 1 = 0
⇒ 2x(x – 1) + 1 (x – 1) = 0
⇒ (x – 1) (2x + 1) = 0
यदि x – 1 = 0, तो x = 1
और यदि 2x + 1 = 0, तो x = – \(\frac{1}{2}\)
अतः 1 और – \(\frac{1}{2}\) व्यंजक p(x) के अन्य दो गुणनखंड है।

प्रश्न 14.
बहुपद 2x³ – 3x² + 6x + 7 में कम-से-कम क्या जोड़ा जाए कि प्राप्त बहुपद x² – 4x + 8 से पूर्णतया विभाजित हो जाए?
हल :
माना p(x) = 2x³ – 3x² + 6x + 7
और q(x) = x² – 4x + 8
अब p(x) को q(x) से भाग देने पर

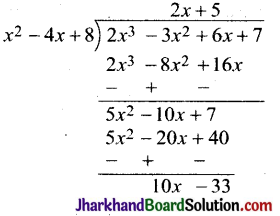
यहाँ शेषफल 10x – 33 प्राप्त होता है। यदि 2x³ – 3x² + 6x +7 में 10x – 33 घटा दिया जाए तो जो बहुपद प्राप्त होगा वह q(x) से पूर्णतया विभाजित हो जाएगा।

प्रश्न 15.
यदि α तथा β बहुपद f(x) = 5x² – 7x + 1 के शून्यक है, तो (\(\frac{α}{β}=\frac{β}{α}\)) का मान ज्ञात कीजिए।
हल :
दिया, f (x)= 5x² – 7x + 1

प्रश्न 16.
k के किस मान के लिए, बहुपद
f(x) = 3x⁴ – 9x³ + x² + 15x + k,
माना, g(x) = 3x² – 5
g(x) से f(x) को भाग करने पर,

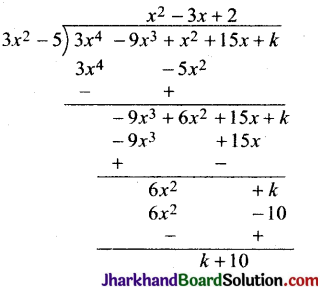
∵ f(x), g(x) से पूर्णतया विभाजित होता है, इसलिए शेषफल को शून्य के बराबर रखने पर,
k + 10 = 0
k = – 10

प्रश्न 17.
3x³ + 10x² – 9x – 4 के सभी शून्यक ज्ञात कीजिए यदि इसका एक शून्य 1 है।
हल :
दिया गया बहुपद है –
3x³ + 10x² – 9x – 4
माना, इस बहुपद के शून्यक α, β तथा γ है तथा α = 1 है।
दिए गए समीकरण को, ax³ + bx² + cx + d = 0 से तुलना करने पर प्राप्त होता है,
a = 3 b = 10, c = – 9 तथा d = – 4

⇒ 3β² + 4 = – 13β
⇒ 3β² + 13β + 4 = 0
⇒ 3β² + 12β + β + 4 = 0
⇒ 3β(β + 4) + 1(β + 4) = 0
⇒ (β + 4) (3β + 1) = 0
β = – 4 या β = \(\frac{-1}{3}\)
तब समीकरण (ii) से,
βγ = \(\frac{4}{3}\)
– 4 × γ = \(\frac{4}{3}\) या – \(\frac{1}{3}\) × γ = \(\frac{4}{3}\)
γ = –\(\frac{1}{3}\)
γ = – 4
अतः इसके शून्यक 1, – 4, – \(\frac{1}{3}\) या 1, – \(\frac{1}{3}\), – 4 होंगे।

प्रश्न 18.
p का यह मान ज्ञात कीजिए जिसके लिए बहुपद px² – 14x + 8 = 0 का एक शून्यक दूसरे का 6 गुना है।
हल :
दिया गया समीकरण है
px² – 14x + 8 = 0
माना, एक मूल = α
दूसरा मूल = 6α
मूलों का योग = – \(\frac{b}{a}\)
α + 6α = \(\frac{-(-14)}{p}\)
7α = \(\frac{14}{p}\)
α = \(\frac{14}{p \times 7}\)
α = \(\frac{2}{p}\) ……(i)
मूलों का गुणनफल = \(\frac{c}{a}\)
(α) (6α) = \(\frac{8}{p}\)
6α² = \(\frac{8}{p}\) ……(ii)
α का मान समीकरण (ii) में रखने पर,
6(\(\frac{2}{p}\))² = \(\frac{8}{p}\)
⇒ 6 × \(\frac{4}{p^2}\) = \(\frac{8}{p}\)
⇒ 24p = 8p²
⇒ 8p² – 24p = 0
⇒ 8p (p – 3) = 0
⇒ 8p = 0 ⇒ p = 0
या p – 3 = 0 ⇒ p = 3
p = 0 दिए द्विघात समीकरण px² – 14x + 8 = 0 की सन्तुष्ट नहीं करती है।
अत: p = 3

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. बहुपद में चर राशि की उच्चतम घात वाले पद के घातांक को बहुपद की …………… कहते हैं।
2. …………… बहुपद की कोई घात नहीं होती है।
3. यदि ग्राफ x-अक्ष के दो भिन्न बिन्दुओं पर काटता है, तो बहुपद के ……………. शून्यक होते हैं।
4. 1 घात के बहुपद के अधिकतम …………………. वास्तविक शून्यक हो सकते हैं।
5. ऐसे बहुपद जिसमें चर राशि की उच्चतम घात 1 हो, …………….. बहुपद कहलाते हैं।

हल:

1. घात,
2. शून्य,
3. दो,
4. 1,
5. रैखिक ।

निम्न में सत्य / असत्य बताइए :

प्रश्न (ख)

1. ऐसे बीजीय व्यजंक जिनमें चर राशियों की घात धनात्मक, ऋणात्मक अथवा शून्य हो, बहुपद कहलाते हैं।
2. बहुपद 5y³ + 2y² + 4y⁵ + y + 7 की घात 3 है।
3. बीजीय व्यंजक \(\frac{3}{4}\)x³ – \(\frac{5}{4}\)x² + 2x – 5 चर x का परिमेय संख्याओं पर बहुपद है।
4. ऐसे बहुपद को, जिसमें चर राशि की उच्चतम घात 2 हो विघातीय बहुपद कहलाता है।
5. यदि कोई व्यजंक f(x), x में बहुपद है, तब एक वास्तविक संख्या, बहुपद (x) का शून्यक कहलाती है, यदि और केवल यदि (k) = 0 हो ।

हल :

1. असत्य,
2. असत्य,
3. सत्य,
4. असत्य,
5. सत्य ।

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
यदि द्विघात बहुपद x² + 3x + k का एक शून्यक 2 है, तो k का मान है:
(A) 10
(B) – 10
(C) – 7
(D) – 2
हल :
माना p(x) = x² + 3x + k
∵ 2, p(x) का एक शून्यक है।
∴ p(2) = 0
⇒ (2)² + 3(2) + k = 0
⇒ 4 + 6 + k = 0
⇒ k = – 10
अत: सही विकल्प (B) है।

प्रश्न 2.
वह द्विघात बहुपद जिसके तथा गुणनफल 6 है, है :
(A) x² + 5x + 6
(B) x² – 5x + 6
(C) x² – 5x – 6
(D) – x² + 5x + 6
हल :
बहुपद = x² – (शून्यकों का योग)x + शून्यकों का गुणनफल
= x² – (- 5)x + 6
= x² + 5x + 6
अत: सही विकल्प (A) है।

प्रश्न 3.
निम्न आकृति में, बहुपद p(x) का आलेख दिया है। बहुपद के शून्यकों की संख्या है।

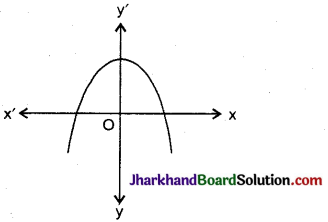
(A) 1
(B) 2
(C) 3
(D) 0
हल :
∵ बहुपद का आलेख x अक्ष को दो बिन्दुओं पर काटता है।
∴ बहुपद के दो शून्यक हैं।
अतः सही विकल्प (B) है।

प्रश्न 4.
बहुपद p(x) को x² – 4 से विभाजित करने पर भागफल तथा शेषफल क्रमशः x तथा 3 पाए गए। बहुपद p(x) है:
(A) 3x² + x – 12
(B) x³ – 4x + 3
(C) x² + 3x – 4
(D) x³ – 4x – 3
हल :
∵ भाज्य = भागफल × भाजक + शेषफल
p(x) = x × (x² – 4) + 3
= x³ – 4x + 3
अत: सही विकल्प (D) है।

प्रश्न 5.
ऐसे बहुपद जिनके शून्यक केवल 3 तथा 4 हैं, की घात है :
(A) 2
(B) 1
(C) 3 से अधिक
(D) 3
हल :
ऐसा बहुपद जिसके दो शून्यक होते हैं, द्विघातीय बहुपद होता है।
अत: सही विकल्प (A) है।

प्रश्न 6.
यदि α और β बहुपद x² + 2x + 1 के शून्यक हैं, तो \(\frac{1}{\alpha}+\frac{1}{\beta}\) बराबर है।
(A) – 2
(B) 2
(C) 0
(D) 1
हल :
दिया है, बहुपद = x² + 2x + 1
∴ α + β = \(\frac{-b}{a}=\frac{-2}{1}\) = – 2
और αβ = \(\frac{c}{a}=\frac{c}{a}=\frac{1}{1}\) = 1
अब \(\frac{1}{\alpha}+\frac{1}{\beta}\) = \(\frac{\beta+\alpha}{\alpha \beta}\) = \(\frac{-2}{1}\) = – 2
अत: सही विकल्प (A) है।

प्रश्न 7.
यदि बहुपद (3x² + 8x + k) का एक शून्यक दूसरे का व्युत्क्रम है, तो k का मान है :
(A) 3
(B) – 3
(C) \(\frac{1}{3}\)
(D) \(\frac{-1}{3}\)
हल :
दिया है,
बहुपद = 3x² + 8x + k
माना एक शून्यक α है, तब दूसरा शून्यक α होगा।
शून्यकों का गुणनफल = \(\frac{c}{a}\)
⇒ α × \(\frac{1}{α}\) = \(\frac{k}{3}\)
⇒ 1 = \(\frac{k}{3}\)
⇒ k = 3
अत: सही विकल्प (A) है।

प्रश्न 8.
एक तीन घात वाले बहुपद के शून्यकों की अधिकतम संख्या है :
(A) 1
(B) 4
(C) 2
(D) 3
हल :
किसी बहुपद के शून्यकों की अधिकतम संख्या उसके घात के बराबर होती है।
अत: सही विकल्प (D) है।

प्रश्न 9.
यदि बहुपद kx² + 2x + 3 के शून्यकों का योग उनके गुणनफल के बराबर है, तो k बराबर है:
(A) \(\frac{1}{3}\)
(B) \(\frac{-1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{-2}{3}\)
हल :
शून्यकों का योग = \(\frac{-b}{a}=\frac{-2}{k}\)
शून्यकों का गुणनफल = \(\frac{c}{a}=\frac{3 k}{k}\) = 3
प्रश्नानुसार,
शून्यकों का योग = शून्यकों का गुणनफल
⇒ \(\frac{-2}{k}\) = 3
⇒ k = \(\frac{-2}{3}\)
अत: सही विकल्प (D) है।

प्रश्न 10.
द्विघात समीकरण x² + 99x + 127 के शून्यक होंगे:
(A) दोनों धनात्मक
(B) दोनों ऋणात्मक
(C) एक धनात्मक और एक ऋणात्मक
(D) दोनों समान।
हल :
∵ a > 0, b > 0 तथा c > 0 तब दोनों शून्यक ऋणात्मक होते हैं। अतः विकल्प (B) सही है।

प्रश्न 11.
चित्र में बहुपद f(x) = ax² + bx + c का आलेख दर्शाया गया हो तो :

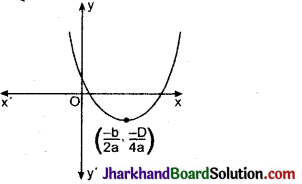
(A) a > 0, b > 0 तथा c > 0
(B) a > 0 b < 0 तथा c < 0
(C) a > 0, b < 0 तथा c > 0
(D) a > 0, b > 0 तथा c < 0.
हल :
विकल्प (B) सही है।

प्रश्न 12.
चित्र में बहुपद f (x) = ax² + bx + c का आलेख दर्शाया गया हो तो :

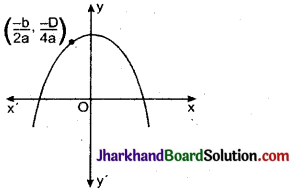
(A) a < 0, b < 0 तथा c > 0
(B) a < 0, b < 0 तथा c < 0
(C) a < 0, b > 0 तथा c > 0
(D) a < 0, b > 0 तथा c < 0.
हल :
विकल्प (A) सही है।

प्रश्न 13.
त्रिघात बहुपद ax³ + bx² + cx+ d के दो शून्यक 0 दिए हैं। तीसरा शून्यक है:
(A) \(\frac{-b}{a}\)
(B) \(\frac{b}{a}\)
(C) \(\frac{c}{a}\)
(D) \(\frac{-d}{a}\)
हल :
बहुपद ax³ + bx² + cx + d के दो शून्यक 0 हैं। माना कि तीसरा शून्यक α है।
अतः शून्यकों का योग = α + 0 + 0 = \(\frac{-b}{a}\)
= α = \(\frac{-b}{a}\)
अंत: विकल्प (A) सही है।

प्रश्न 14.
यदि a – b, a तथा a + b बहुपद x³ – 3x² + x + 1 के शून्यक हैं तो (a + b) का मान होगा :
(A) 1 ± \(\sqrt{2}\)
(B) – 1 ± \(\sqrt{2}\)
(C) – 1 – \(\sqrt{2}\)
(D) 3
हल :
शून्यकों का योगफल = – \(\frac{b}{a}\)
⇒ a – b + a + a + b = \(\frac{-(-3)}{1}\)
⇒ 3a = 3
⇒ a = 1
तथा (a – b)a + a(a + b) + (a + b) (a – b) = \(\frac{c}{a}\)
⇒ (1 – b) × 1 + 1(1 + b) + (1 + b) (1 – b) = \(\frac{1}{1}\)
⇒ 1 – b + 1 + b + 1 – b² = 1
⇒ 3 – b² = 1
⇒ b² = 2
⇒ b = ± \(\sqrt{2}\)
अब a + b = 1 ± \(\sqrt{2}\)
अतः सही विकल्प (A) है।

प्रश्न 15.
यदि बहुपद f(x) = x² – 5x + k के शून्यक α तथा β इस प्रकार हों कि α – β = 1 तो k की मान होगा:
(A) 6
(B) 4
(C) 3
(D) शून्य।
हल :
बहुपद x² – 5x + k के शून्यक α, β हों तो
α + β = – (\(\frac{-5}{1}\)) = 5
αβ = \(\frac{k}{1}\) = k
अब α – β = 1
या (α – β)² = 1
या (α + β)² – 4αβ = 1
या 25 – 4k = 1
या 24 = 4k
∴ k = 6
अत: विकल्प (A) सही है।