JAC Class 10 Maths Important Questions Chapter 4 द्विघात समीकरण

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 4 द्विघात समीकरण Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 4 द्विघात समीकरण

लयूत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
एक मोटर बोट जिसकी स्थिर जल में चाल 18 किमी / घण्टा है। वह वोट 12 किमी धारा के प्रतिकूल जाने में समय धारा के अनुकूल जाने की अपेक्षा अधिक लेती है। धारा की चाल ज्ञात कीजिए।
हल :
माना कि धारा की चाल x किमी / घण्टा है।
धारा की अनुकूल में मोटर बोट की चाल = (18 + x) किमी / घण्टा
धारा की प्रतिकूल जाने में मोटर बोट की चाल = (18 – x) किमी / घण्टा
धारा की प्रतिकूल में जाने में लगा समय = \(\frac{12}{18-x}\) घण्टे
[∵ समय = दूरी / चाल]
इसी प्रकार अनुकूल जाने में लगा समय = \(\frac{12}{18+x}\) घण्टे
प्रश्नानुसार,
\(\frac{12}{18-x}-\frac{12}{18+x}\) = \(\frac{1}{2}\)
2 × 12 [(18 + x) – (18 – x)] = (18 + x) (18 – x)
24 [18 + x – 18 + x] = 324 – x²
24 × 2x = 324 – x²
48x + x² – 324 = 0
⇒ x² + 48x – 324 = 0
श्रीधराचार्य सूत्र से :
x = \(\frac{-48 \pm \sqrt{48^2+1296}}{2}\)
= \(\frac{-48 \pm \sqrt{3600}}{2}\)
= \(\frac{-48 \pm 60}{2}\)
= 6 या – 54
∵ x धारा की चाल है और यह ऋणात्मक नहीं हो सकती है। इसलिए हम – 54 को छोड़ देते है।
∴ धारा की चाल x = 6 किमी / घण्टा है।

प्रश्न 2.
एक रेलगाड़ी 63 किमी दूरी सामान्य चाल से तथा 72 किमी दूरी सामान्य चाल से 6 किमी / घण्टा ज्यादा चाल से तय करती है। यदि रेलगाड़ी यात्रा को पूरा करने में 3 घण्टे का समय लेती है, तो उसकी सामान्य चाल क्या है ?
हल :
माना कि रेलगाड़ी की चाल x किमी / घण्टा है। तब रेलगाड़ी की बढ़ी हुई चाल = (x + 6) किमी / घण्टा ।

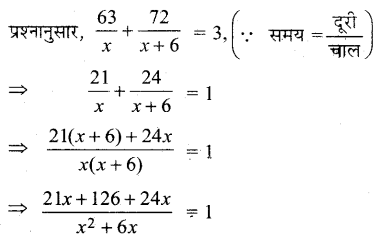
⇒ 45x + 126 = x² + 6x
⇒ x² + 6x – 45x – 126 = 0
⇒ x² – 39x – 126 = 0
⇒ x² – (42 – 3)x – 126 = 0
⇒ x² – 42x + 3x – 126 = 0
⇒ x (x – 42) + 3 (x – 42) = 0
⇒ (x – 42) (x + 3) = 0
यदि x – 42 = 0 हो, तो x = 42
या x + 3 = 0 हो, तो x = – 3
∵ x रेलगाड़ी की सामान्य चाल है तथा यह कभी भी ऋणात्मक नहीं हो सकती है।
∴ x = – 3 को छोड़ देते हैं।
अत: x = 42
इसलिए रेलगाड़ी की सामान्य चाल = 42 किमी/ घण्टा ।

प्रश्न 3.
9000 रुपये को समान रूप से कुछ लोगों में बाँटा गया। यदि 20 व्यक्ति और होते तो प्रत्येक व्यक्ति को 160 रुपये कम मिलते। व्यक्तियों की वास्तविक संख्या कितनी है?
हल :
माना व्यक्तियों की वास्तविक संख्या है।
∴ प्रत्येक व्यक्ति का हिस्सा = \(\frac{9000}{x}\)
यदि व्यक्तियों की संख्या 20 और बढ़ायी जाए तो प्रति व्यक्ति का हिस्सा = \(\frac{9000}{x+20}\)
चूँकि 20 व्यक्ति बढ़ने पर प्रति व्यक्ति का हिस्सा 160 रुपये कम हो जाता हैं ।

⇒ 9000 × 20 = 160x (x + 20)
⇒ x² + 20x – 1125 = 0
⇒ x² + 45x – 25x – 1125 = 0
⇒ x(x + 45) – 25(x + 45) = 0
⇒ (x + 45)(x – 25) = 0
अर्थात् x + 45 = 0 या फिर x – 25 = 0
x = – 45 या x = 25
∵ व्यक्तियों की संख्या ऋणात्मक नहीं हो सकती है।
अतः व्यक्तियों की वास्तविक संख्या = 25 है।

प्रश्न 4.
17 मीटर व्यास वाले एक वृत्ताकार पार्क की परिसीमा के एक बिन्दु पर एक खम्भा इस प्रकार गाड़ना है कि इस पार्क के एक व्यास के दोनों अन्त बिन्दुओं पर बने फाटकों A और B से खम्भे की दूरियों का अन्तर 7 मीटर हो क्या ऐसा करना सम्भव है ? यदि है, तो दोनों फाटकों से कितनी दूरियों पर खम्भा गाड़ना है ?
हल :
माना कि बिन्दु C पर खम्भा गाड़ा गया है तथा फाटक B से बिन्दु C की दूरी = x मीटर

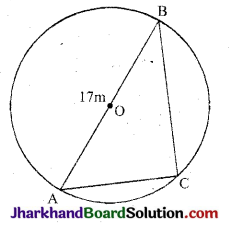
प्रश्नानुसार, फाटक B और A से खम्भे की दूरियों का अन्तर 7 मी. है।
∴ AC = (x + 7) मी.
चूँकि AB व्यास है।
अतः ∠ACB = 90°
(∵ अर्द्धवृत्त में बना कोण समकोण होता है)
अब समकोण त्रिभुज ACB में,
AB² = AC² + BC²
(पाइथागोरस प्रमेय से)
⇒ (17)² = (x + 7)² + x²
⇒ 289 = x² + 49 + 14x + x²
⇒ 289 = 2x² + 14x + 49
⇒ 2x² + 14x + 49 – 289 = 0
⇒ 2x² + 14x – 240 = 0
⇒ x² + 7x – 120 = 0
अब b² – 4ac = (7)² – 4 × 1 × (120)
= 49 + 280
= 529 > 0
अतः दिए गए द्विघात समीकरण के दो वास्तविक मूल है और इसलिए खम्भे को पार्क की परिसीमा पर गाड़ा जा सकता है।
अब x² + 7x – 120 = 0
⇒ x² + (15 – 8)x – 120 = 0
⇒ x² + 15x – 8x – 120 = 0
⇒ (x² + 15x) (8x + 120) = 0
⇒ x(x + 15) – 8 (x + 15) = 0
⇒ (x + 15 ) (x – 8 ) = 0
⇒ x + 15= 0 और x 8 = 0
⇒ x = – 15 और x = 8
∵ x खम्भे और फाटक B के बीच की दूरी है। अतः यह कभी भी ऋणात्मक नहीं हो सकती है।
अतः x = – 12 को छोड़ देते हैं।
अतः x = 8 मी और x + 7 = 8 + 7 = 15 मी
अतः खम्भे से फाटक की दूरी 15 मीटर तथा फाटक B से 8 मीटर है।

प्रश्न 5.
500 किमी की एक हवाई उड़ान में एक वायुयान खराब मौसम के कारण धीनी गति से चला। पूरी उड़ान की औसत चाल 200 किमी / घंटा घट गई तथा उड़ान का समय 30 मिनट बढ़ गया। उड़ान का मूल समय ज्ञात कीजिए ।
हल :
माना वायुयान की सामान्य चाल x किमी / घंटा है।
वायुयान की घटी चाल = (x – 200) किमी / घंटा
दूरी = 600 किमी
600 किमी दूरी तय करने में वायुयान को लगा समय = दूरी / चाल = \(\frac{600}{x}\)घंटे
नई चाल से 600 किमी दूरी तय करने में लगा समय = \(\frac{600}{x-200}\)घंटे
प्रश्नानुसार,

⇒ x² – 200x = 2400
⇒ x² – 200x – 2400 = 0
⇒ x² – 600x + 400x – 2400 = 0
⇒ x(x – 600) + 400(x – 600) = 0
⇒ (x – 600) (x + 400) = 0
यदि x – 600 = 0 तो x = 600
और यदि x + 400 = 0, तो x = – 400
∵ वायुयान की चाल ऋणात्मक नहीं तो सकती, इसलिए x ≠ – 400
∴ वायुयान की सामान्य चाल = 600 किमी / घंटा
अतः उड़ान का मूल समय = दूरी / चाल = \(\frac{600}{600}\) = 1 घंटा

प्रश्न 6.
एक रेलगाड़ी 480 किमी की दूरी एकसमान चाल से चलती है। यदि उसकी चाल 8 किमी / घंटा कम हो, यह उसी दूरी को तय करने में 3 घंटे अधिक लेती है। रेलगाड़ी की मूल चाल ज्ञात कीजिए।
हल :
माना रेलगाड़ी की मूल चाल किमी/घंटा है।
तब रेलगाड़ी की नई घटी हुई चाल (x – 8) किमी / घंटा है।
दूरी = 480 किमी
प्रश्नानुसार,
\(\frac{480}{x-8}-\frac{480}{x}\) = 3
[∵ समय = दूरी / चाल]
⇒ \(\frac{480[x-(x-8)]}{x(x-8)}\) = 3
⇒ 480 × 8 = 3x (x – 8)
⇒ x² – 8x = 1280
⇒ x² – 8x – 1280 = 0
⇒ x² – 40x + 32x – 1280 = 0
⇒ x(x – 40) + 32(x – 40) = 0
⇒ (x – 40) (x + 32) = 0
यदि x – 40 = 0 तो x = 40
और यदि x + 32 = 0 तो x = – 32, जो कि असम्भव हैं, क्योंकि चाल ऋणात्मक नहीं हो सकती।
अतः रेलगाड़ी की मूल चाल 40 किमी/घंटा है।

प्रश्न 7.
एक तेज चलने वाली रेलगाड़ी 600 किमी की यात्रा में एक धीमी चलने वाली रेलगाड़ी से 3 घंटे कम समय लेती है। यदि धीमी चलने वाली रेलगाड़ी की चाल, तेज चलने वाली रेलगाड़ी की चाल से 10 किमी / घंटा कम है, तो दोनों गाड़ी की चाल ज्ञात कीजिए।
हल :
माना तेज चलने वाली रेलगाड़ी की चाल x किमी / घंटा है,
तब
धीमी चलने वाली रेलगाड़ी की चाल (x – 10) किमी / घंटा होगी।
तेज चलने वाली गाड़ी द्वारा 600 किमी की यात्रा में लिया गया समय = \(\frac{600}{x}\) घंटे
धीमी चलने वाली गाड़ी द्वारा 600 किमी. की यात्रा में लिया गया समय = \(\frac{600}{x-10}\) घंटे
प्रश्नानुसार,
\(\frac{600}{x-10}-\frac{600}{x}\) = 3
⇒ \(\frac{600[(x-(x-10)]}{x(x-10)}\) = 3
⇒ 600 × [(x – (x + 10)] = 3x(x – 10)
⇒ 6000 = 3x(x – 10)
⇒ x(x – 10) = 2000
⇒ x² – 10x – 2000 = 0
⇒ x² – 50x + 40x – 2000 = 0
⇒ x (x – 50) + 40 (x – 50) = 0
⇒ (x – 50) (x + 40) = 0
यदि x – 50 = 0, तो x = 50
और यदि x + 40 = 0 तो x = – 40; जो कि असम्भव है।
अत: तेज चलने वाली रेलगाड़ी की चाल = 50 किमी / घंटा
तथा धीमी चलने वाली रेलगाड़ी की चाल = (50 – 10) किमी / घंटा = 40 किमी / घंटा

प्रश्न 8.
दो प्राकृत संख्याओं का अंतर 5 है, तथा उनके प्रतिलोमों का अंतर \(\frac{1}{10}\) है। संख्याएँ ज्ञात कीजिए।
हल :
माना दो प्राकृत संख्याएँ और x + 5 हैं।
प्रश्नानुसार,
⇒ \(\frac{1}{x}-\frac{1}{x+5}\) = \(\frac{1}{10}\)
⇒ \(\frac{(x+5)-x}{x(x+5)}\) = \(\frac{1}{10}\)
⇒ \(\frac{5}{x^2+5 x}\) = \(\frac{1}{10}\)
⇒ x² + 5x = 50
⇒ x² + 5x – 50 =0
⇒ x² + 10x – 5x – 50 = 0
⇒ x(x + 10) – 5(x + 10) = 0
⇒ (x + 10) (x – 5) = 0
यदि x + 100, तो x = – 10; जो कि असम्भव है, क्योंकि कि प्राकृत संख्याएँ ऋणात्मक नहीं होती।
यदि x – 5 = 0, तो x = 5
तथा x + 5 = 5 + 5 = 10
अतः दो प्राकृत संख्याएँ 5 और 10 है।

प्रश्न 9.
एक व्यक्ति के पास एक टूर (यात्रा) के दौरान खर्च के लिए ₹ 4200 हैं। यदि वह अपना दूर 3 दिन बढ़ा दे उसे अपना प्रतिदिन का व्यय ₹70 कम करना पड़ता है। उसके दूर की मूल अवधि ज्ञात कीजिए।
हल :
माना व्यक्ति के टूर की अवधि दिन है।
प्रतिदिन का व्यय = \(\frac{4200}{x}\)
यदि दूर 3 दिन बढ़ा दिया जाए, तब प्रतिदिन का व्यय = \(\frac{4200}{x+3}\)
प्रश्नानुसार,
\(\frac{4200}{x}-\frac{4200}{x+3}\) = 70
⇒ \(\frac{4200[x+3-x]}{x(x+3)}\) = 70
⇒ 4200 × 3 = 70x (x + 3)
⇒ \(\frac{4200 \times 3}{70}\) = x² + 3x
⇒ x² + 3x – 180 = 0
⇒ x + 15x – 12x – 180 = 0
⇒ x(x + 15) – 12 (x + 15) = 0
⇒ (x + 15) (x – 12) = 0
यदि x + 15 = 0, तो x = – 15; जो कि असम्भव है, क्योंकि दिनों की संख्या ऋणात्मक नहीं हो सकती।
और यदि x – 12 = 0, तो x = 12
अतः यात्रा की अवधि 12 दिन है।

प्रश्न 10.
तीन क्रमागत धनपूर्णांक ऐसे हैं कि पहले के वर्ग तथा अन्य दो कि गुणनफल को जोड़ने पर 46 प्राप्त होता है। पूर्णांक ज्ञात कीजिए।
हल :
माना तीन क्रमागत धनपूर्णांक x (x + 1) तथा (x + 2) हैं।
प्रश्नानुसार,
x² + (x + 1)(x + 2) = 46
x² + x + 2x + x + 2 = 46
2x² + 3x + 2 – 46 = 0
2x² + 3x – 44 = 0
2x² + 11x – 8x – 44 = 0
x(2x + 11) – 4(2x + 11) = 0
(2x + 11) (x – 4) = 0
यदि 2x + 11 = 0, तो x = – \(\frac{11}{2}\), असम्भव क्योंकि ऋणात्मक है।
यदि x – 4 = 0, तो x = 4
∴ x + 1 = 4 + 1 = 5 और x + 2 = 4 + 2 = 6
अतः अभीष्ट धनपूर्णांक संख्याएँ 4, 5 और 6 हैं।

प्रश्न 11.
कुछ विद्यार्थियों ने पिकनिक पर जाने की योजना बनाई खाने का कुल बजट ₹ 2000 रखा गया परन्तु 5 विद्यार्थियों के न आने पर प्रति विद्यार्थी खाने पर खर्च ₹ 20 बढ़ गया। कितने विद्यार्थी पिकनिक पर गए तथा प्रत्येक विद्यार्थी ने खाने के लिए कितनी राशि दी ?
हल :
माना पिकनिक पर x विद्यार्थी गए।
कुल धन राशि = ₹ 2000
∴ प्रत्येक विद्यार्थी द्वारा दी गई राशि = \(\frac{2000}{x}\)
यदि 5 विद्यार्थी न आते तब प्रत्येक विद्यार्थी द्वारा दी गई राशि = \(\frac{2000}{x-5}\)
प्रश्नानुसार,
\(\frac{2000}{x-5}-\frac{2000}{x}\) = 20
\(\frac{2000[x-(x-5)]}{x(x-5)}\) = 20
2000 × 5 = 20x (x – 5)
500 = x² – 5x
x² – 5x – 500 = 0
x² – 25x + 20x – 500 = 0
x – (x – 25) + 20(x – 25) = 0
(x – 25) (x + 20) = 0
यदि x – 25 = 0, तो x = 25
और यदि x + 20 = 0 तो x = – 20 (असम्भव)
अतः पिकनिक पर गए विद्यार्थी = 25
प्रत्येक विद्यार्थी द्वारा दी गई राशि = ₹ \(\frac{2000}{25}\) = ₹ 80

प्रश्न 12.
एक ऐसे आयताकार पार्क को बनाना है जिसकी चौड़ाई उसकी लम्बाई से 3 मी कम है। इसका क्षेत्रफल पहले से निर्मित समद्विबाहु त्रिभुजाकार पार्क जिसका आधार आयाताकार पार्क की चौड़ाई के बराबर तथा ऊँचाई 12 मी. है, से 4 वर्ग मी. अधिक हो। इस पार्क की लम्बाई और चौड़ाई ज्ञात कीजिए।
हल :
माना पार्क की लम्बाई x मी है।
पार्क की चौड़ाई (x – 3) मी होगी।
आयताकार पार्क का क्षेत्रफल = x (x – 3) वर्ग मी समद्विबाहु त्रिभुजाकार पार्क का आधार = आयताकार पार्क की चौड़ाई = (x – 3) मी ऊँचाई = 12 मी
समद्विबाहु त्रिभुजाकार पार्क का आधार
= \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × (x – 3) × 12
= 6 (x – 3) वर्ग मी
प्रश्नानुसार,
आयताकार पार्क का क्षेत्रफल = त्रिभुजाकार पार्क का क्षेत्रफल + 4
x(x – 3) = 6(x – 3) + 4
x² – 3x = 6x – 18 + 4
x² – 3x – 6x + 14 = 0
x² – 9x + 14 = 0
x² – 7x – 2x + 14 = 0
x(x – 7) – 2(x – 7) = 0
(x – 7)(x – 2) = 0
यदि x – 7 = 0, तो x = 7
और यदि x – 2 = 0 तो x = 2 जो कि असम्भव है, क्योंकि अगर लम्बाई 2 मी. है तो चौड़ाई (x – 3) मी = – 1 मी होगी जो कि ऋणात्मक है।
अतः पार्क की लम्बाई = 7 मी
तथा चौड़ाई = (7 – 3) मी = 4 मी

प्रश्न 13.
कुछ लम्बाई वाले एक कपड़े की कुल लागत ₹ 200 है। यदि यह कपड़ा 5 मीटर अधिक लम्बा हो तथा प्रत्येक मीटर कपड़े की लागत ₹ 2 कम हो, तो कपड़े की कुल लागत में कोई परिवर्तन नहीं होगा। कपड़े का वास्तविक प्रति मीटर मूल्य ज्ञात कीजिए तथा कपड़े की लम्बाई भी ज्ञात कीजिए।
हल :
माना, कपड़े की लम्बाई x मी हैं तथा कपड़े के प्रत्येक मीटर का मूल्य y है।
प्रश्नानुसार,
xy = 200 ……..(i)
यदि कपड़े की लम्बाई 5 मी अधिक होतो तथा प्रत्येक मीटर का मूल्य ₹2 कम होता तो,
(x + 5)(y – 2) = 200
xy – 2x + 5y – 10 = 200 ……..(ii)
समीकरण (i) व (ii) को बराबर करने पर,
xy = xy – 2x + 5y – 10
2x – 5y = 10 ……..(iii)
2x – 5 × \(\frac{200}{x}\) = – 10 (समीकरण (i) से y = \(\frac{200}{x}\))
2x – \(\frac{1000}{x}\) = – 10
2x² – 1000 = – 10x
2x² + 10x – 1000 = 0
x² + 5x – 500 = 0
x² + 25x – 20x – 500 = 0
x(x + 25) – 20(x + 25) = 0
(x – 20)(x + 25) = 0
यदि x – 20 = 0, तो x = 20
और x + 25 = 0 तो x = – 25; जो कि असम्भव है, क्योंकि लम्बाई ऋणात्मक नहीं होती।
अब x × y = 200
20 × y = 200
y = 10
अतः कपड़े की लम्बाई 20 मीटर है तथा प्रत्येक मीटर का मूल्य ₹ 10 है।

प्रश्न 14.
दो पानी के नल एक साथ एक टैंक को 1\(\frac{7}{8}\) घंटों में भर सकते हैं। बड़े व्यास वाला नल टैंक को भरने में, कम व्यास वाले नल से 2 घंटे कम समय लेता है। प्रत्येक नल द्वारा अलग से टैंक को भरने का समय ज्ञात कीजिए।
हल :
माना छोटा नल टैंक को भरने में x घंटे लेता है।
∴ बड़ा नल टैंक को भरने में (x – 2) घंटे लेगा।
अब, 1 घंटे में बड़े नल द्वारा भरा गया पानी = \(\frac{1}{x-2}\)
1 घंटे में छोटे नल द्वारा भरा गया पानी = \(\frac{1}{x}\)
तथा 1 घंटे में दोनों नल द्वारा भरा गया पानी = \(\frac{8}{15}\)
\(\frac{1}{x}+\frac{1}{x-2}\) = \(\frac{8}{15}\)
\(\frac{x-2+x}{x(x-2)}\) = \(\frac{8}{15}\)
\(\frac{2 x-2}{x(x-2)}\) = \(\frac{8}{15}\)
\(\frac{x-1}{x(x-2)}\) = \(\frac{4}{15}\)
15x – 15 = 4x² – 8x
4x² – 8x – 15x + 15 = 0
4x² – 23x + 15 = 0
4x² – 20x – 3x + 15 = 0
4x(x – 5) – 3(x – 5) = 0
(x – 5) (4x – 3) = 0
यदि x – 5 = 0, तो x = 5
और यदि 4x – 3 = 0, तो x = \(\frac{3}{4}\) जो कि अमान्य है।
अतः छोटा नल को टैंक भरने में 5 घण्टे लगेंगे एवं बड़े नल को 3 घण्टे लगेंगे।

प्रश्न 15.
निम्न समीकरणों के मूल ज्ञात कीजिए :
(i) 8x² – 2x – 3 = 0
(ii) 14x² + 17x – 6 = 0
(iii) 3x² – 4\(\sqrt{3}\)x + 4 = 0
(iv) x² + 5x – (a² + a – 6) = 0
हल :
(i) दिया है,
8x² – 2x – 3 = 0
⇒ 8x² – 6x + 4x – 3 = 0
⇒ 2x(4x – 3) + 1(4x – 3) = 0
⇒ (4x – 3)(2x + 1) = 0
यदि 4x – 3 = 0, तो x = \(\frac{3}{4}\)
और यदि 2x + 1 = 0, तो x = –\(\frac{1}{2}\)
अत: x = \(\frac{3}{4}\), –\(\frac{1}{2}\)

(ii) दिया है, 14x² + 17x – 6 = 0
⇒ 14x² + 21x – 4x – 6 = 0
⇒ 7x(2x + 3) – 2(2x + 3) = 0
⇒ (2x + 3)(7x – 2) = 0
यदि 2x + 3 = 0, x = – \(\frac{3}{2}\)
और यदि 7x – 2 = 0, तो x = \(\frac{2}{7}\)
अत: x = –\(\frac{3}{2}\), \(\frac{2}{7}\)

(iii) दिया है,
3x² – 4\(\sqrt{3}\)x + 4 = 0
3x² – 2\(\sqrt{3}\)x – 2\(\sqrt{3}\)x + 4 = 0
\(\sqrt{3}\)x(\(\sqrt{3}\) – 2) – 2(\(\sqrt{3}\) – 2) = 0
(\(\sqrt{3}\) – 2) (\(\sqrt{3}\) – 2) = 0
यदि \(\sqrt{3}\)x – 2 = 0 तो x = \(\frac{2}{\sqrt{3}}\)
अतः x = \(\frac{2}{\sqrt{3}}\), \(\frac{2}{\sqrt{3}}\)

(iv) दिया है,
x² + 5x – (a² + a – 6) = 0
यहाँ, a² + a – 6 = a² + 3a – 2a – 6
= a(a + 3) – 2(a + 3)
= (a + 3)(a – 2)
∴ x² + 5x – (a – 3)(a – 2) = 0
x² + (a + 3)x – (a – 2)x – (a + 3)(a – 2) = 0
x[x + a + 3] – (a – 2)[x + a + 3] = 0
(x – a + 2)(x + a + 3) = 0
यदि x – a + 2 = 0, x = a – 2
और यदि x + a + 3 = 0, तो x = – (a + 3)
अत: x = (a – 2) और – (a + 3)

प्रश्न 16.
x के लिए हल कीजिए:

हल :

⇒ (4x + 1)(5x + 1) = 3(x² + 5x + 4)
⇒ 20x² + 4x + 5x + 1 = 3x² + 15x + 12
⇒ 17x² – 6x – 11 = 0
⇒ 17x² – 17x + 11x – 11 = 0
⇒ 17x(x – 1) + 11(x – 1) = 0
⇒ (x – 1)(17x + 11) = 0
⇒ x = 1 या x = \(\frac{-11}{17}\)
दिया है x ≠ 1, अतः x = \(\frac{-11}{17}\)

(ii) दिया है, \(\frac{1}{2 x-3}+\frac{1}{x-5}\) = 1\(\frac{1}{9}\)
\(\frac{x-5+2 x-3}{(2 x-3)(x-5)}\) = \(\frac{10}{9}\)
\(\frac{3 x-8}{2 x^2-13+15}\) = \(\frac{10}{9}\)
9(3x – 8) = 10 (2x² – 13x + 15)
27x – 72 = 20x² – 130x + 150
20x² – 157x + 222 = 0
20x² – 120x – 37x + 222 = 0
20x(x – 6) – 37 (x – 6) = 0
(x – 6) (20x – 37) = 0
(x – 6 ) = 0 या 20x – 37 = 0
अत: x = 6 या x = \(\frac{37}{20}\)

(iii)

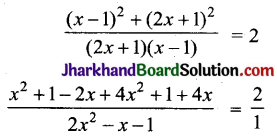
5x² + 2x + 2 = 2(2x² – x – 1)
5x² + 2x + 2 = 4x² – 2x – 2
x² + 4x + 4 = 0
(x + 2)² = 0
या तो x + 2 = 0 या x + 2 = 0
अतः x = – 2, -2

प्रश्न 17.
दो नल एक साथ टैंक को 3\(\frac{1}{13}\) घण्टे में भर सकते हैं। यदि एक नल टैंक को भरने में दूसरे नल से 3 घण्टे अधिक लेता है, तो प्रत्येक नल टैंक को भरने में कितना समय लेगा ?
हल :
माना कि टैंक एक नल से x घण्टे में भरता है। अत: टैंक दूसरे नल से (x + 3) घण्टे में भरेगा।
टैंक को दोनों नल एक साथ भरते हैं = 3\(\frac{1}{13}\)
= \(\frac{40}{13}\) घण्टे में
प्रश्नानुसार,

13x² + 39x = 80x + 120
13x² – 41x – 120 = 0
13x² – 65x + 24x – 120 = 0
13x(x – 5) + 24 (x – 5) = 0
(x – 5)(13x + 24) = 0
यदि x – 5 = 0 तो x = 5
और यदि 13x + 24 = 0 तो x = – \(\frac{24}{13}\), जो कि संभव नहीं है।
अतः एक नल टैंक भरेगा = 5 घण्टे में।
और दूसरा नल टैंक भरेगा = (x – 3) = 8 घण्टे में ।

प्रश्न 18.
एक रेलगाड़ी 300 किमी की दूरी एकसमान चाल से तय करती है। यदि रेलगाड़ी की चाल 5 किमी / घंटा बढ़ा दी जाए, तो यात्रा में 2 घंटे कम समय लगता है। रेलगाड़ी की मूल चाल ज्ञात कीजिए।
हल :
माना, रेलगाड़ी की मूल चाल = x किमी / घंटा
रेलगाड़ी की नई चाल = (x + 5) किमी / घंटा
दूरी = 300 किमी
प्रश्नानुसार,
\(\frac{300}{x}-\frac{300}{x+5}\) = 2
⇒ \(\frac{300(x+5-x)}{(x)(x+5)}\) = 2
⇒ 1500 = 2(x² + 5x)
⇒ 1500 = 2x² + 10x
⇒ 2x² + 10x – 1500 = 0
⇒ x² + 5x – 750 = 0
⇒ x² + 30x – 25x – 750 = 0
⇒ x(x + 30) – 25 (x + 30) = 0
⇒ (x + 30)(x – 25) = 0
यदि x + 30 = 0 तो x = – 30, जो अमान्य है।
और यदि x – 25 = 0 तो x = 25
अतः रेलगाड़ी की मूल चाल = 25 किमी / घण्टा ।

प्रश्न 19.
A एक कार्य को करने में B से 6 दिन कम लेता है। यदि A और B दोनों एक साथ काम करते हुए इसे 4 दिन में कर सकते हैं, तो B इस कार्य को समाप्त करने में कितने दिन लेगा?
हल :
माना B कार्य को x दिन में समाप्त कर सकता है। तो A कार्य को (x – 6) दिन में समाप्त करेगा।
दोनों मिलकर कार्य 4 दिन में समाप्त करते हैं।
प्रश्नानुसार, \(\frac{1}{x}+\frac{1}{x-6}\) = \(\frac{1}{4}\)
⇒ \(\frac{x-6+x}{(x)(x-6)}\) = \(\frac{1}{4}\)
⇒ 4(2x – 6) = x² – 6x
⇒ 8x – 24 = x² – 6x
⇒ x² – 14x + 24 = 0
⇒ x² – 12x – 2x + 24 = 0
⇒ x (x – 12) – 2 (x – 12) = 0
⇒ (x – 12) (x – 2) = 0
यदि x – 12 = 0 तो x = 12
और यदि x – 2 = 0 तो x = 2 (अमान्य हैं।)
अतः B कार्य को करने में 12 दिन लेगा।
A कार्य को करने में 6 दिन लेगा।

प्रश्न 20.
एक नाव की शांत जब में चाल 15 किमी / घंटा है। यह नाव 30 किमी धारा के विपरीत दिशा में जाकर पुन: उसी जगह 4 घंटे 30 मिनट में वापस लौट आती है। धारा की चाल ज्ञात कीजिए।
हल :
माना धारा की चाल x किमी / घंटा है।
प्रश्नानुसार,

अतः धारा की चाल 5 किमी / घण्टा ।

प्रश्न 21.
एक आयताकार खेल का विकर्ण उसकी छोटी भुजा से मी अधिक लम्बा है। यदि बड़ी भुजा छोटी भुजा से 20 मी. अधिक हो, तो खेत की भुजाएँ ज्ञात कीजिए।
हल :
माना खेत की छोटी भुजा = x मी
∴ खेत की बड़ी भुजा = (x + 20) मी
और खेत का विकर्ण = (x + 40) मी
पाइथागोरस प्रमेय से,
(विकर्ण)² = शेष दोनों भुजाओं के वर्गों का योग
⇒ (x + 40)² = x² + (x + 20)²
⇒ x² + 1600 + 80x = x² + x² + 400 + 40x
⇒ x² – 2x² + 80x – 40 + 1600 – 400 = 0
⇒ – x² – 40x + 1200 = 0
⇒ x² + 40x – 1200 = 0
⇒ x² + 60x – 20x – 1200 = 0
⇒ x(x + 60) – 20(x + 60) = 0
⇒ (x + 60) (x – 20) = 0
यदि x + 60 = 0, तो x = – 60 जो कि असम्भव है, क्योंकि भुजा की लम्बाई ऋणात्मक नहीं हो सकती।
और यदि x – 20 = 0 तो x = 20
अतः खेत की छोटी भुजा = 20 मी
तथा खेत की बड़ी भुजा = (20 + 20) मी = 40 मी.

प्रश्न 22.
एक आयताकार खेत का विकर्ण उसकी छोटी भुजा से 25 मी अधिक लंबा है। यदि बड़ी भुजा छोटी भुजा से 23 मी अधिक है, तो खेत की भुजाएँ ज्ञात कीजिए ।
हल :
माना रेलगाड़ी की चाल x किमी / घंटा है।
300 किमी दूरी तय करने में लगा समय = \(\frac{300}{x}\) घंटे
रेलगाड़ी की नई चाल = (x + 10) किमी / घंटा
नई चाल से 300 किमी दूरी तय करने में लगा समय = \(\frac{300}{x+10}\) घंटे
प्रश्नानुसार,
\(\frac{300}{x}-\frac{300}{x+10}\) = 1
⇒ \(\frac{300[x+10-x]}{x(x+10)}\) = 1
⇒ 300 × 10 = x(x + 10)
⇒ x² + 10x – 3000 = 0
⇒ x² + 60x – 50x – 3000 = 0
⇒ x(x + 60) – 50 (x + 60) = 0
⇒ (x + 60) (x – 50) = 0
यदि x + 60 = 0, तो x = – 60; असम्भव क्योंकि चाल ऋणात्मक नहीं होती।
और यदि x – 50 = 0 तो x = 50
अतः रेलगाड़ी की चाल = 50 किमी / घंटा

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. ऐसा व्यंजक जिसमें चर की घात ……………….. होती है, द्विघात बहुपद कहलाता है।
2. समीकरण x² + bx + c = 0 के मूल बराबर हैं, यदि ………………. है।
3. द्विघात समीकरण 3x² – 2x + 4 = 0 के मूल ……………….. होंगे।
4. समीकरण 9x² = 10 का मानक रूप ………………….. है।
5. प्रत्येक द्विघात समीकरण के अधिक से अधिक ………………. वास्तविक मूल हो सकते हैं।

हल :

1. 2
2. b² – 4c = 0
3. काल्पनिक
4. 9x² + 0x – 10 = 0
5. दो

निम्न में से सत्य / असत्य कथन छाँटिए :

प्रश्न (ख)

1. द्विघात समीकरण ax² + bx + c = 0 का विविक्तर, D = b² + 4ac होता है।
2. यदि b² – 4ac > 0 तथा पूर्ण वर्ग हो, तो मूल वास्तविक, परिमेय तथा असमान होते हैं।
3. यदि b² – 4ac > 0 तथा पूर्ण वर्ग न हो, तो मूल वास्तविक, अपरिमेय तथा असमान होते हैं।
4. यदि b² – 4ac < 0 तो मूल काल्पनिक होते हैं।
5. यदि b² – 4ac = 0 तो मूल काल्पनिक, परिमेय तथा असमान होते हैं।

हल :

1. असत्य,
2. सत्य,
3. सत्य,
4. सत्य,
5. असत्य

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
बहुपद x² – 3x – m (m + 3) के शून्यक हैं:
(A) m, m + 3
(B) – m, m + 3
(C) m, – (m + 3)
(D) – m, – (m + 3)
हल :
शून्यक के लिए : x² – 3x – m(m + 3) = 0
x² – (3 + m – m)x – m(m + 3) = 0
x² – (m + 3)x + mx – m(m + 3) = 0
x[x – (m + 3)] + m[x – (m + 3)] = 0
[x – (m + 3)] (x + m) = 0
यदि [x – (m + 3)] = 0, तो x = m + 3
यदि x + m = 0, तो x = – m
अत: विकल्प (B) सही है।

प्रश्न 2.
द्विघात समीमरण x² – 0.04 = 0 के मूल हैं:
(A) ± 0.2
(B) ± 0.02
(C) 0.4
(D) 2
हल :
दिया है, x² – 0.04 = 0
x² = 0.04 = \(\frac{4}{100}\)
x = ± \(\sqrt{\frac{4}{100}}\)
= ± \(\frac{2}{10}\) = ± 0.2
अत: सही विकल्प (A) है।

प्रश्न 3.
λ का वह मान जिसके लिए (x² + 4x + λ) एक पूर्ण वर्ग है, है:
(A) 16
(B) 9
(C) 1
(D) 4
हल :
दिया है, x² + 4x + λ
= (x)² + 2(2) x + λ
= (x)² + 2(2) x + (2)²
= (x + 2)², जो कि एक पूर्ण वर्ग है।
∴ λ = (2)² = 4
अत: सही विकल्प (D) है।

प्रश्न 4.
द्विघात समीकरण x² – 4x + k = 0 के दो भिन्न वास्तविक मूल होंगे, यदि
(A) k = 4
(B) k > 4
(C) k = 16
(D) k < 4
हल :
दो भिन्न वास्तविक मूलों के लिए प्रतिबन्ध :
B² – 4AC > 0
⇒ (-4)² – 4 × 1 × k > 0
⇒ 16 – 4k > 0
⇒ – 4k > – 16
⇒ k < 4
अत: सही विकल्प (D) है।

प्रश्न 5.
यदि द्विघात समीकरण 2x² + kx + 2 = 0 के मूल समान हों, तो का मान है :
(A) 4
(B) ± 4
(C) – 4
(D) = 0
हल :
मूलों के समान होने के लिए प्रतिबन्ध :
B² – 4AC = 0
⇒ (k)² – 4 × 2 × 2 = 0
⇒ k² – 16 = 0
⇒ k² = 16
⇒ k = ± 4
अत: सही विकल्प (B) है।

प्रश्न 6.
द्विघात समीकरण 2x² – 4x + 3 = 0 के मूल हैं:
(A) वास्तविक तथा बराबर
(B) वास्तविक तथा भिन्न
(C) वास्तविक नहीं
(D) वास्तविक
हल :
यहाँ B² – 4AC = (-4)² – 4 × 2 × 3
= 16 – 24 = – 8
⇒ B² – 4AC < 0
अत: सही विकल्प (C) है।

प्रश्न 7.
समीकरण ax² + bx + c = 0, a ≠ 0 के मूल वास्तविक नहीं होंगे यदि :
(A) b² < 4ac
(B) b² > 4ac
(C) b² = 4ac
(D) b = 4ac
हल :
सही विकल्प (A) है।

प्रश्न 8.
द्विघात समीकरण px² + qx + r =0, p ≠ 0 के मूल समान होंगे यदि :
(A) p² < Apr
(B) p² > 4qr
(C) p² = 4pr
(D) p² = 4qr
हल :
सही विकल्प (C) है।

प्रश्न 9.
द्विघात समीकरण 2x² – x – 6 = 0 के मूल है :
(A) – 2, \(\frac{3}{2}\)
(B) 2, – \(\frac{3}{2}\)
(C) – 2, – \(\frac{3}{2}\)
(D) 2, \(\frac{3}{2}\)
हल :
दिया गया द्विघात समीकरण है :
2x² – x – 6 = 0
⇒ 2x² – (4 – 3) x – 6 = 0
⇒ 2x² – 4x + 3x – 6 = 0
⇒ (2x² – 4x) + (3x – 6) = 0
⇒ 2x(x – 2) + 3(x – 2) = 0
⇒ (x – 2) (2x + 3) = 0
⇒ x = – 2 = 0 या 2x + 3 = 0
⇒ x = 2 या x = \(\frac{-3}{2}\)
अत: विकल्प (B) सही है।

प्रश्न 10.
द्विघात समीकरण 2x² – \(\sqrt{5}\)x + 1 = 0 के :
(A) दो भिन्न वास्तविक मूल है
(B) दो बराबर वास्तविक मूल है
(C) कोई वास्तविक मूल नहीं है
(D) दो से अधिक वास्तविक मूल है।
हल :
सही विकल्प (C) है।

प्रश्न 11.
यदि f(x) = ax² + bx + c और c = \(\frac{b^2}{4 a}\) हो, तो f(x) = 0 के मूल होंगे :
(A) वास्तविक और बराबर
(B) वास्तविक और असमान
(C) वास्तविक नहीं
(D) इनमें से कोई नहीं
हल :
सही विकल्प (A) है।

प्रश्न 12.
यदि p(x) एक बहुपद में चर x इस प्रकार है कि p(h) = 0 हो तो h, p(x) का
(A) मूल है
(B) गुणनखण्ड है
(C) शून्यक है
(D) इनमें से कोई नहीं ।
हल :
सही विकल्प (C) है।

प्रश्न 13.
बहुपद p(x) में x इस तरह कि p (h) = 0 हो, तो p(x), p(x – h) :
(A) मूलं है.
(B) गुणनखण्ड है
(C) शून्यक है
(D) इनमें से कोई नहीं
हल:
सही विकल्प (B) है।

प्रश्न 14.
दो संख्याएँ ज्ञात कीजिए जिनका योग 27 और गुणनफल 182 हो :
(A) 13 और 14
(C) 17 और 10
(B) 15 और 12
(D) इनमें से कोई नहीं
हल :
सही विकल्प (A) है।

प्रश्न 15.
यदि द्विघात समीकरण x² (a² + b) + 2x( ac + bad) + (c2 + 2) = 0 के मूल बराबर हों तो :
(A) ad = – bc
(B) ad = ± bc
(C) ad = bc
(D) इनमें से कोई नहीं
हल :
सही विकल्प (A) है।