JAC Class 10 Maths Important Questions Chapter 5 समांतर श्रेढ़ियाँ

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 5 समांतर श्रेढ़ियाँ Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 5 समांतर श्रेढ़ियाँ

लयूत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
यदि किसी A. P. के प्रथम 12 पदों का योग 468 है तथा इसका सार्वअंतर 6 है, तो 10वाँ पद ज्ञात कीजिए।
हल :
दिया है,
S_n = 468, d = 6, n = 12
a₁₀ = ?
हम जानते हैं :
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
468 = \(\frac{12}{2}\)[2a + (12 – 1)6]
468 = 6(2a + 66)
= 12a + 396
a = \(\frac{468-396}{12}=\frac{72}{12}\)
a = 6
∴ a₁₀ = a + (n – 1)d
= 6 + (10 – 1)6
= 6 + 9 × 6 = 6 + 54
a₁₀ = 60.

प्रश्न 2.
एक समान्तर श्रेणी का 14वाँ पद उसके 8वें पद का दुगना है। यदि उसका छटा पद – 8 है, तो उसके प्रथम 20 पदों का योगफल ज्ञात कीजिए।
हल :
माना समान्तर श्रेणी का प्रथम पद = a
तथा सर्वाअंतर = d
∴ समान्तर श्रेढी के nth पद
a_n = a + (n – 1)d
इस प्रकार a₁₄ = a + (14 – 1)d
= a + 13d
a₈ = a + (8 – 1)d = a + 7d
a₆ = a + (6 – 1)d = a + 5d
प्रश्नानुसार-
a₁₄ = 2a₈
⇒ a + 13d = 2(a + 7d)
⇒ a + d = 0 ………..(1)
इसी प्रकार,
a₆ = a + 5d = – 8 ………..(2)
समी (1) व (2) को हल करने पर,
a = 2, d = – 2
∴ S₂₀ = \(\frac{20}{2}\) [2 × z + (20 – 1) (- z)]
S₂₀ = – 340
अतः प्रथम 20 पदों का योगफल = – 340.

प्रश्न 3.
1 से 100 तक के मध्य की 6 से विभाजित होने वाली संख्याओं का योगफल ज्ञात कीजिए।
हल :
1 से 100 तक के मध्य की 6 से विभाज्य संख्याएँ है….
6, 12, 18, 24, …, 96
स्पष्ट है कि उपर्युक्त संख्याएँ समान्तर श्रेढी में हैं।
यहाँ a = 6, d = 12 – 6 = 6 तथा a_n = 96
अत: a_n = 96
⇒ a + (n – 1)d = 96
⇒ 6 + (n – 1) × 6 = 96
⇒ (n – 1) × 6 = 96 – 6 = 90
⇒ n – 1 = \(\frac{90}{6}\) = 15
⇒ n = 15 + 1 = 16
∵ हम जानते हैं कि
S_n = \(\frac{n}{2}\)(a + l)
⇒ S₁₆ = \(\frac{16}{2}\)(6 + 96)
⇒ S₁₆ = 8 × 102
⇒ S₁₆ = 816
अतः S₁₆ = 816

प्रश्न 4.
समीकरण हल कीजिए :
1 + 4 + 7 + 10 +……+ x = 287.
हल :
दिया गया समीकरण है :
1 + 4 + 7 + 10 +………+ x = 287
स्पष्ट है कि यह एक समान्तर श्रेढी है।
यहाँ a = 1, d = 4 – 13, a_n = x तथा S_n = 287
∵ a_n = x
⇒ a + (n – 1)d = x
⇒ 1 + (n – 1) × 3 = x
⇒ 1 + 3n – 3 = x
⇒ x = 3n – 2 ……………(i)
और S_n = 287
⇒ \(\frac{n}{2}\)(a + l) = 287
⇒ \(\frac{n}{2}\)(1 + x) = 287
⇒ \(\frac{n}{2}\)(1 + 3n – 2) = 287
[समी. (i) का प्रयोग करने पर]
⇒ n(3n – 1) = 574
⇒ 3n² – n – 574 = 0
श्रीधराचार्य सूत्र से –
n = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

∵ n एक प्राकृतिक धन पूर्णांक है। अतः n = \(\frac{-41}{3}\) को छोड़ देते हैं।
अत: n = 14
n का मान समीकरण (i) में रखने पर
x = 3 × 14 – 2
= 42 – 2 = 40
अतः x = 40.

प्रश्न 5.
A. P. 17, 15, 13 के कितने पद लिए जाएँ ताकि उनका योग 81 हो।
हल :
a = 17, d = 15 – 17 = – 2
S_n = 81
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
81 = \(\frac{n}{2}\)[2 × 17 + (n – 1) × (- 2)]
81 = \(\frac{n}{2}\)[34 – 2n + 2]
= n[17 – n + 1]
= n[18 – n]
81 = 18n – n²
n² – 18n + 81 = 0
n² – 9n – 9n + 81 = 0
n(n – 9) – 9 (n – 9) = 0
(n – 9) (n – 9) = 0
n = 9.

प्रश्न 6.
चार क्रमागत संख्याएँ जोकि समान्तर श्रेढी में हैं, का योग 32 है। प्रथम और अन्तिम संख्याओं का गुणनफल मध्य संख्याओं के गुणनफल से 7 : 15 के अनुपात में हो। वह संख्याएँ ज्ञात करो ।
हल :
माना चार क्रमागत संख्याएँ हैं-
a – 3d, a – d, a + d, a + 3d
प्रश्नानुसार,
संख्याओं का योग = 32
⇒ (a – 3d) + (a – d) + (a + d) + (a + 3d) = 32
⇒ 4a = 32
⇒ a = \(\frac{32}{4}\) = 8
तथा \(\frac{(a-3 d)(a+3 d)}{(a-d)(a+d)}\) = \(\frac{7}{15}\)
⇒ \(\frac{a^2-9 d^2}{a^2-d^2}\) = \(\frac{7}{15}\)
⇒ \(\frac{64-9 d^2}{64-d^2}\) = \(\frac{7}{15}\) [∵ a = 8]
⇒ 960 – 135d² = 448 – 7d²
⇒ 960 – 448 = 135d² – 7d²
⇒ 512 = 128d²
⇒ d² = \(\frac{512}{128}\) = 4
⇒ d = ± 2
अतः a – 3d = 8 – 3 × 2 = 2
a – d = 8 – 2 = 6
a + d = 8 + 2 = 10
a + 3d = 8 + 3 × 2 = 14
अतः अभीष्ट संख्याएँ हैं-
2, 6, 10, 14.

प्रश्न 7.
यदि एक समान्तर श्रेढी के m पदों का योग ‘n’ तथा n पदों का योग ‘m’ हो, तो सिद्ध कीजिए कि (m + n) पदों का योगफल – (m + n) होगा।
हल :
माना दी गई श्रेढी का प्रथम पद a तथा सार्वअन्तर d हैं।
दिया है S_m = n
⇒ \(\frac{m}{2}\){2a + (m – 1)d} = n
⇒ 2am + m(m-1)d = 2n ……..(1)
तथा S_n = m
⇒ \(\frac{n}{2}\){2a + (n – 1)d} = m
⇒ 2am + n(n – 1)d = 2m …….(ii)
समीकरण (i) में से समीकरण (ii) को घटाने पर,
2a(m – n) + {m(m – 1) n (n-1)} d = 2n – 2m
⇒ 2a(m – n) + {(m² – n²) – (m – n)} d
= – 2(m – n)
⇒ 2a + (m + n – 1)d = – 2 ………….(iii)
[दोनों पक्षों में (m – n) से भाग देने पर]
अब S_m+n = \(\frac{m+n}{2}\){2a + (m + n – 1)d}
⇒ \(\frac{(m+n)}{2}\)(-2) [(iii) के प्रयोग से]
⇒ S_m+n = – (m + n)
अतः S_m+n = – (m + n) इति सिद्धम् ।

प्रश्न 8.
यदि एक समान्तर श्रेढी का m वाँ पद \(\frac{1}{n}\) तथा n वाँ पद \(\frac{1}{m}\) हो, तो दर्शाइए कि mn पदों का योगफल \(\frac{1}{2}\) (mn + 1) होगा।
हल :
माना दी गई समान्तर श्रेढी का प्रथम पद a तथा सार्वअन्तर d है।
दिया है : a_m = \(\frac{1}{n}\)
⇒ a + (m – 1)d = \(\frac{1}{n}\) ……..(i)
तथा a_n = \(\frac{1}{m}\)
⇒ a + (n – 1)d = \(\frac{1}{m}\) …………….(ii)
समीकरण (i) में से समीकरण (ii) को घटाने पर,
(m – n)d = \(\frac{1}{n}-\frac{1}{m}\)
⇒ (m – n)d = \(\frac{m-n}{m n}\)
⇒ d = \(\frac{1}{mn}\)
समीकरण (i) में d = \(\frac{1}{mn}\) रखने पर,
a + (m – 1)\(\frac{1}{mn}\) = \(\frac{1}{n}\)
⇒ a + \(\frac{1}{n}\) – \(\frac{1}{mn}\) = \(\frac{1}{n}\)
⇒ a = \(\frac{1}{mn}\)
∴ अभीष्ट योगफल S_mn = \(\frac{mn}{2}\){2a + (mn – 1)d}
⇒ S_mn = \(\frac{mn}{2}\){\(\frac{2}{mn}\) + (mn – 1) × \(\frac{1}{mn}\)}
⇒ S_mn = \(\frac{1}{2}\)(mn + 1)
अत: mn पदों का योगफल
= \(\frac{1}{2}\)(mn + 1) इति सिद्धम् ।

प्रश्न 9.
एक समान्तर श्रेढी के प्रथम n पदों केयोगफल को S_n द्वारा दर्शाया जाता है। इस श्रेढी में यदि S₅ + S₇ = 167 तथा S₁₀ = 235 है, तो समान्तर श्रेणी ज्ञात कीजिए ।
हल :
माना श्रेढी का प्रथम पद = a
और सार्वअंतर = d
n पदों का योगफल
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
दिया है,
S₅ + S₇ = 167
⇒ \(\frac{5}{2}\)(2a + 4d) + \(\frac{7}{2}\)(2a + 6d) = 167
⇒ 5a + 10d + 7a + 21d = 167
⇒ 12a + 31d = 167 ……….. (1)
इसी प्रकार,
S₁₀ = 235
⇒ \(\frac{10}{2}\)(2a + 9d) = 235
⇒ 2a + 9d = 47 ……….. (2)
समी. (1) व (2) से,
a = 1 और d = 5
अत: अभीष्ट A. P. 1, 6, 11… है ।

प्रश्न 10.
दर्शाइए कि उस A. P का योग, जिसका प्रथम पद a, द्वितीय पद b और अन्तिम पद c हो \(\frac{(a+c)(b+c-2 a)}{2(b-a)}\) के बराबर है।
हल :
दिया है,
प्रथम पद = a
द्वितीय पद = b
∴ सार्वअन्तर (d) = ba
अन्तिम पद (l) = c
माना कि समान्तर श्रेढी में पद है।
∴ a_n = c
⇒ a + (n – 1) × d = c
⇒ a + (n – 1) × (b – a) = c
⇒ (n – 1) (b – a) = c – a
⇒ (n – 1) = \(\frac{c-a}{b-a}\)
⇒ n = \(\frac{c-a}{b-a}\) + 1
⇒ n = \(\frac{c-a+b-a}{b-a}\)
⇒ n = \(\frac{b+c-2 a}{b-a}\)
अब S_n = \(\frac{n}{2}\)[a + l]
⇒ S_n = \(\frac{(b+c-2 a)}{2(b-a)}\)[a + c]
⇒ S_n = \(\frac{(a+c)(b+c-2 a)}{2(b-a)}\) इति सिद्धम् ।

प्रश्न 11.
एक मोटर कार A स्थान से B स्थान तक 175 किमी दूरी 70 किमी / घंटा समान गति से सभी 10 हरे यातायात्रा सिग्नलों को पार करती है। भारी यातायात के कारण यह प्रथम सिग्नल पर एक मिनट, दूसरे सिग्नल पर 3 मिनट, तीसरे सिग्नल पर 5 मिनट एवम् इसी प्रकार दसवें सिग्नल पर 19 मिनट रूकती हैं। स्थान B तक पहुँचने में इसे कुल कितना समय लगेना उपयुक्त गणितीय विधि से हल कीजिए ।
हल :
यहाँ, हम देखते हैं कि 10 सिग्नलों पर लगा समय समान्तर श्रेढी में हैं।

प्रथम पद a = 1, तथा सार्वअन्तर d = 3 – 1 = 2
∴ 10 सिग्नलों को पार करने के लगा समय = 1 + 3 + 5 + 5 + 9 + 11 + 13 + 15 + 17 + 19
= \(\frac{10}{2}\)[2 × 1 + (10 – 1) × 2]
= 5 [2 + 18] = 5 × 20 = 100 मिनट
= \(\frac{10}{60}\) घंटे = \(\frac{5}{3}\)घंटे
∴ A से B तक पहुँचाने में लगा कुल समय
= (\(\frac{175}{70}+\frac{5}{3}\))घंटे = (\(\frac{35}{14}+\frac{5}{3}\))घंटे
= (\(\frac{35 \times 3+5 \times 14}{42}\))घंटे = \(\frac{175}{42}\)घंटे
= 4\(\frac{1}{6}\) घंटे = 4 घंटे 10 मिनट

प्रश्न 12.
उस A. P. के प्रथम 15 पदों का योग ज्ञात कीजिए, जिसका पाँचवा और नवाँ पद क्रमश: 26 और 42 है।
हल :
माना सं. क्षे. का प्रथम पद a तथा सार्वअन्तर d है।
स.क्षे. का पाँचवाँ पद,
a₅ = a + (n – 1)d
⇒ 26 = a + (5 – 1)d
⇒ 26 = a + 4d ………..(i)
स.क्षे. का नव पद, a₉ = a + (9 – 1)d
42 = a + 8d ………….(ii)
समीकरण (ii) में से समीकरण (i) घटाने पर
a + 8d = 42
a + 4d = 26
4d = 16
d = 4
समीकरण (i) में d = 4 रखने पर
a + 4 × 4 = 26
a = 26 – 8 = 18
स.क्षे. के 15 पदों को योग
= [2 × 18 + (15 – 1) × 4]
= [36 + 56]
= 15 × 92
= 690

प्रश्न 13.
एक कार A स्थान से B स्थान पर 260 किमी दूरी 65 किमी / घंटा समान गति से सभी 13 हरे यातायात सिग्नलों को पार करती है। भारी यातायात के कारण यह प्रथम सिग्नल पर 4 मिनट, दूसरे सिग्नल पर 7 मिनट, तीसरे सिग्नल पर 10 मिनट एवम् इसी प्रकार तेरहवें सिग्नल पर 40 मिनट रूकती है। स्थान B तक पहुँचने इसे कुल कितना समय होगा? उपयुक्त गणितीय विधि से हल कीजिए।
हल :

A से B तक पहुँचने में लगा कुल समय
= \(\frac{260}{65}\)घंटे + \(\frac{13}{2}\)[2 × 4 + (13 – 1) × 3] मिनट
= \(\frac{20}{5}\)घंटे + \(\frac{13}{2}\) [8 + 36] मिनट
= 4 घंटे + \(\frac{13}{2}\) × 44 मिनट = 4 घंटे + 286 मिनट
= 4 घंटे + 46 मिनट = 8 घंटे 46 मिनट

प्रश्न 14.
दर्शाइए कि (a – b)², (a² + b²), (a + b)² एक समान्तर श्रेणी में हैं।
हल :
माना a₁ = (a – b)², a₂ = (a² + b²), a₃ = (a + b)²
a₂ – a₁ = (a² + b²) – (a – b)²
= (a² + b²) – (a² + b² – 2ab)
= a² + b² – a² – b² + 2ab = 2ab … (i)
तथा
a₃ – a₂ = (a + b)² – (a² + b²)
= a² + b² + 2ab – a² – b²
= 2ab ……………(ii)
समीकरण (i) व (ii) से,
∵(a² + b²) – (a – b)² = (a + b)² – (a² + b²)
a₂ – a₁ = a₃ – a₂
अत: (a – b)², (a² + b²), (a + b²) एक स.क्षे. मैं हैं।

प्रश्न 15.
एक स. क्षे. के प्रथम 7 पदों का योग 63 है और इसके अगले 7 पदों का योग 161 है। स. क्षे. ज्ञात कीजिए ।
हल :
माना स.क्षे. का प्रथम पद ‘a’ तथा सार्व अन्तर ‘d’ है।
स. क्षे. के प्रथम 7 पदों का योग,
S_n = \(\frac{n}{2}\)[2a+ (n – 1)d]
S₇ = \(\frac{7}{2}\)[2a + (7 – 1)d]
63 = \(\frac{7}{2}\)(2a + 6d)
⇒ \(\frac{1}{2}\)(2a + 6d) = 9
⇒ a + 3d = 9
a = 9 – 3d ……………(i)
प्रश्नानुसार,
S₁₄ – S₇ = 161
\(\frac{14}{2}\)[2a + (14 – 1)d] – 63 = 161
\(\frac{14}{2}\)[2a + (14 – 1)d] = 161 + 63
7[2(9 – 3d) + 13d] = 224
18 – 6d + 13d = \(\frac{224}{7}\)
7d = 32 – 18
d = \(\frac{14}{7}\) = 2
समीकरण (i) से, a = 9 – 3 × 2 = 3
अतः समान्तर श्रेढी हैं :
a, a + d, a + 2d, a + 3d, ……………..
= 3, 5, 7, 9, …………

प्रश्न 16.
एक समान्तर श्रेणी के सभी 11 पदों का योगफल ज्ञात कीजिए, जिसका मध्य पद 30 है।
हल :
माना स. क्षे. का प्रथम पद a तथा सार्वअन्तर d है।
∵ स. क्षे. में 11 पद हैं।
∴ मध्य पद = (\(\frac{n+1}{2}\)) वाँ पद = (\(\frac{11+1}{2}\))वाँ पद = 5वाँ पद
a₅ = a + (5 – 1)d
30 = a + 5d ……………(i)
स. क्षे. के 11 पदों का योग = \(\frac{11}{2}\)[2a + (11 – 1)d]
= \(\frac{11}{2}\)[2a + 10d]
= \(\frac{11}{2}\) × 2(a + 5d)
= 11 × 30 = 330

प्रश्न 17.
निम्न समीकरण को हल कीजिए: 1 + 5 + 9 + 13 + ……………. + x = 1326
हल :
यहाँ, प्रथम पद, a = 1
सार्वअन्तर, d = 5 – 1 = 4
प्रश्नानुसार,
S_n = 1326
⇒ \(\frac{n}{2}\)[2 × 1 + (n – 1)4] = 1326
⇒ \(\frac{n}{2}\)(2 + 4n – 4) = 1326
⇒ \(\frac{n}{2}\)(4n – 2) = 1326
⇒ n(2n – 1) = 1326
⇒ 2n² – n – 1326 = 0
⇒ 2n² – 52n + 51n – 1326 = 0
⇒ 2n(n – 26) + 51(n – 26) = 0
⇒ (n – 26) (2n + 51) = 0
यदि n – 26 = 0 तो n = 26
और यदि 2n + 51 = 0, तो n = \(\frac{-51}{2}\) असम्भव, क्योंकि ‘n’ एक प्राकृतिक संख्या है।
अर्थात् n = 14 है।
प्रश्नानुसार,
14वाँ पद = x
⇒ a + (14 – 1)d = x
⇒ 1 + 13 × 4 = x
अतः x = 53

प्रश्न 18.
यदि संख्याएँ a, 7, b, 23, c एक समान्तर श्रेढी में है, तो a, b तथा c के मान ज्ञात कीजिए।
हल :
माना स. क्षे. का सार्व अन्तर d है।
प्रश्नानुसार,
a₂ = 7
a + (2 – 1)d = 7
a + d = 7 ……………(i)
तथा a₄ = 23
a + (4 – 1)d = 23
a + 3d = 23 ……………(ii)
समीकरण (ii) में से समीकरण (i) घटाने पर

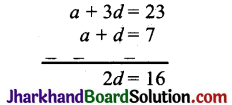
समीकरण (i) में, d = 8 रखने पर
a + 8 = 7
⇒ a = 7 – 8 = – 1
तीसरा पद, a₃ = a + (3 – 1)d
b = – 1 + 2 × 8 = 15
पाँचवाँ पद,
a₅ = a + (5 – 1)d
c = – 1 + 4 × 8 = 31.
अतः a = – 1, b = 15, c = 31

प्रश्न 19.
समानान्तर श्रेणी
20, 19\(\frac{1}{4}\), 18\(\frac{1}{2}\), 17\(\frac{3}{4}\), ………… का कौन-सा पद प्रथम ऋणात्मक पद है?
हल :
प्रश्नानुसार, समानान्तर श्रेणी
20, 19\(\frac{1}{4}\), 18\(\frac{1}{2}\), 17\(\frac{3}{4}\), …….. = 20, \(\frac{77}{4}\), \(\frac{37}{2}\), \(\frac{71}{4}\), ………..
यहाँ, a = 20, d = \(\frac{77}{4}\) – 20 = \(\frac{77-80}{4}\) = \(\frac{-3}{4}\)
माना पहला ऋणात्मक पद a_n है।

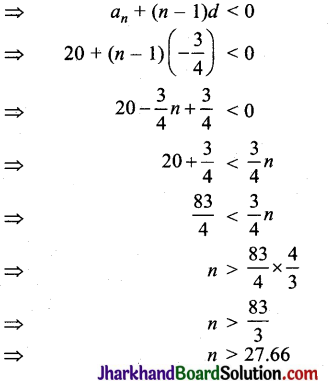
अतः दी गयी समानान्तर श्रेणी का 28वाँ पद प्रथम ऋणात्मक पद होगा।

प्रश्न 20.
यदि दो समानान्तर श्रेणियों के प्रथम पदों के योगफलों का अनुपात (7+ 1) (4 + 27) है, तो उनके 9वें पदों का अनुपात ज्ञात कीजिए।
हल :
दिया है, समानान्तर श्रेणियों के प्रथम n पदों के योगफलों का अनुपात :

अतः दो समानान्तर श्रेणियों के 9वें पदों का अनुपात = 24 : 19

प्रश्न 21.
n के किस मान के लिए, दो समानान्तर श्रेणियों 63, 65, 67, ….. तथा 3, 10, 17 ……… के n वें पद समान होंगे?
हल :
पहल समानान्तर श्रेणी 63, 65, 67, …………..
a = 63, d = 65 – 63 = 2
a_n = a + (n – 1)d
= 63 + (n – 1)d
= 63 + 2n – 2 = 61 + 2n
दूसरी समानान्तर श्रेणी 3, 10, 17, ………..
a = 3, d = 10 – 3 = 7
a_n = a + (n – 1)d
= 3 + (n – 1) (7) = 3 + 7n – 7
= 7n – 4
प्रश्नानुसार
61 + 2n = 7n – 4
61 + 4 = 7n – 2n
65 = 5n
n = \(\frac{65}{5}\) = 13
अतः दोनों समानान्तर क्षेणियों का 13वाँ पद समान हैं।

प्रश्न 22.
एक समान्तर श्रेढी के प्रथम 6 पदों का योग 42 है। इसके 10वें पद तथा 30वें पद में अनुपात 1 : 3 का है। इस समान्तर श्रेढी का प्रथम पद तथा 13वाँ पद ज्ञात कीजिए।
हल :
माना स.क्षे. का प्रथम पद a तथा सार्व अन्तर d है।
स. क्षे. का 6 पदों का योग,
S₆ = \(\frac{6}{2}\)[2a + (6 – 1)d]
⇒ 42 = 3 (2a + 5d)
⇒ 2a + 5d = 14 ………(i)
10वें तथा 30वें पद में अनुपात 1 : 3

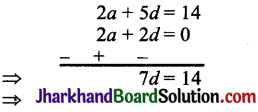
समीकरण (i) में d = 2 रखने पर
2a + 5 × 2 = 14
⇒ 2a = 14 – 10
⇒ a = \(\frac{4}{2}\) = 2
अतः स.क्षे. का 13वाँ पद = 2 + (13 – 1) × 2
= 2 + 24 = 26

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. संख्याओं के एक निश्चित नियमानुसार क्रम को ………………. कहते हैं।
2. वह श्रेणी जिसमें अगल पद, पहले पदे में एक निश्चित संख्या जोड़ने अथवा घटाने पर प्राप्त होती है, ………….. श्रेणी कहलाती है।
3. समान्तर श्रेणी का …………… धनात्मक, ऋणात्मक या शून्य हो सकता है।
4. यदि समान्तर श्रेणी में पदों की संख्या निश्चित है, तो उसे ……………… समान्तर श्रेणी कहते हैं।
5. यदि 3k – 2, 4k – 6 तथा k + 2 एक समान्तर श्रेणी के क्रमित पद हैं, तो k का मान ………….. हैं।

हल :

1. अनुक्रम
2. समान्तर
3. सार्व अन्तर,
4. परिमित,
5. 2.

निम्न में सत्य / असत्य ज्ञात कीजिए :

प्रश्न (ख)

1. यदि समान्तर श्रेणी में पदों की संख्या अपरिमित है, तो उसे परिमित समान्तर श्रेणी कहते हैं।
2. श्रेणी 21, 18, 15, …………… का 8वाँ पद शून्य है।
3. श्रेणी 5, 9, 13 …………. 185 में अन्तिम पद से पहले पद की और 9वीं पद 152 है।
4. दो अंकों की 30 संख्याएँ उसे भाग्य हैं।
5. समान्तर श्रेणी 3, 15, 27, 39, ….. का 31वाँ पद 21 वे पद से 120 अधिक है।

हल :

1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. सत्य।

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
एक समान्तर श्रेणी का प्रथम पद p है तथा सार्वअन्तर q है, तो उसका 10वाँ पद है :
(A) q + 9p
(B) p – 9q
(C) p + 9g
(D) 2p + 9q
हल :
a10 = a + (n – 1)d
⇒ a10 = p + (10 – 1) × q
⇒ a10 = p + 9q
अत: सही विकल्प (C) है।

प्रश्न 2.
x का मान जिसके लिए 2x, (x + 10) तथा (3x + 2) एक समान्तर श्रेणी के क्रमिक पद हैं, है:
(A) 6
(B) – 6
(C) 18
(D) – 18
हल :
∵ दिए गए पद स.क्षे. के क्रमिक पद हैं।
∴ (x + 10) – 2x = (3x + 2) – (x + 10)
⇒ – x + 10 – 2x = 3x + 2 – x – 10
⇒ – x + 10 = 2x – 8
⇒ – x – 2x = – 8 – 10
⇒ – 3x = – 18
⇒ x = 6
अत: सही विकल्प (A) है।

प्रश्न 3.
समांतर श्रेणी \(\frac{1}{p}, \frac{1-p}{p}, \frac{1-2 p}{p}\), ……………… का सार्वअंतर है :
(A) 1
(B) \(\frac{1}{p}\)
(C) – 1
(D) – \(\frac{1}{p}\)
हल :
सार्व अंतर = \(\frac{1-p}{p}-\frac{1}{p}=\frac{1-p-1}{p}\)
= \(\frac{-p}{p}\)
= – 1
अत: सही विकल्प (C) है।

प्रश्न 4.
समान्तर श्रेणी a, 3a, 5a, …………. का n वाँ पद है :
(A) na
(B) (2n – 1) a
(C) (2n + 1)a
(D) 2na
हल :
प्रथम पद, A = a
सार्वअन्तर
D = 3a – a = 2a
∴ n वाँ पद = A + (n – 1) D
= a + (n – 1) × 2a
= a + 2na – 2a
= 2na – a
= (2n – 1)a
अत: सही विकल्प (B) है।

प्रश्न 5.
समान्तर श्रेणी 5, 9, 13, ………., 185 में कितने पद हैं?
(A) 31
(B) 51
(C) 46
(D) 40
हल :
प्रथम पद, a = 5
सार्वअन्तर, d = 9 – 5 = 4
पदों की संख्या, n = ?
∵ an = a + (n – 1)d
⇒ 185 = 5 + (n – 1) × 4
⇒ n – 1 = \(\frac{180}{4}\) = 45
⇒ n = 45 + 1 = 46
अतः सही विकल्प (C) है।

प्रश्न 6.
उस समान्तर श्रेणी, जिसका n वाँ पद an = (3n + 7) है, का सार्वअंतर है :
(A) 3
(B) 7
(C) 10
(D) 6
हल :
n वाँ पद,
an = 3n + 7
प्रथम पद, a1 = 3 × 1 + 7 = 10
द्वितीय पद, a2 = 3 × 2 + 7 = 13
सार्व अंतर, = a2 – a1 = 13 – 10 = 3
अत: सही विकल्प (A) है।

प्रश्न 7.
एक समांतर श्रेणी का प्रथम पद 5 है तथा अंतिम पद 45 है। यदि सभी पदों को योगफल 400 हो, तो पदों की संख्या है :
(A) 20
(B) 8
(C) 10
(D) 16
हल :
दिया है, a = 5, l = 45, Sn = 400
∵ Sn = \(\frac{n}{2}\)(a + l)
⇒ 400 = \(\frac{n}{2}\) (5 + 45)
⇒ n = \(\frac{400 \times 2}{50}\) = 16
अत: सही विकल्प (D) है।

प्रश्न 8.
एक समान्तर श्रेणी – 15 – 11 – 7, …………… 49 का 9 वाँ पद है
(A) 32
(B) 0
(C) 17
(D) 13
हल :
दियाहै,
a = – 15, d = – 11 – (-15) = – 11 + 5 = 4 तथा n = 9
an = a + (n – 1)d
a9 = – 15 + (9 – 1) × 4
= – 15 + 32 = 17
अत: सही विकल्प (C) है।

प्रश्न 9.
निम्नलिखित में से कौन-सी समांतर श्रेढी नहीं है?
(A) – 1.2, 0.8, 2.8, ………….
(B) 3, 3 + \(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\),….
(C) \(\frac{4}{3}, \frac{7}{3}, \frac{9}{3}, \frac{12}{3}\), ………………..
(D) \(\frac{-1}{5}, \frac{-2}{5}, \frac{-3}{5}\), …………..
हल :
(C) में सार्वअन्तर समान नहीं है।
\(\frac{7}{3}-\frac{4}{3}=\frac{3}{3}\)
तथा \(\frac{9}{3}-\frac{7}{3}=\frac{2}{3}\)
अर्थात् \(\frac{7}{3}-\frac{4}{3} \neq \frac{9}{3}-\frac{7}{3}\)
अंत: सही विकल्प (C) है।

प्रश्न 10.
समान्तर श्रेणी 5, 8, 11, ………. 47 का अंतिम पद से (प्रथम पद की ओर) दूसरा पद है:
(A) 50
(B) 45
(C) 44
(D) 41
हल :
दिया है, a = 5, d = 8 – 5 = 3, l = 47 तथा n = 2
स. क्षे. का अंत से n वाँ पद = l – (n – 1)d
= 47 – (2 – 1) × 3
= 47 – 3 = 44
अत: सही विकल्प (C) है।

प्रश्न 11.
दी गई श्रेढी 2,\(\frac{5}{2}\), 3, \(\frac{7}{2}\), ………….. A.P. में है, तो इसका 3 वाँ पद होगा : (A) – 3
(B) 3
(C) 2
(D) 4
हल :
a = 2, d = \(\frac{5}{2}\) – 2 = \(\frac{5-4}{2}=\frac{1}{2}\)
an = a + (n – 1)d
∴ a3 = 2 + (3 – 1) × \(\frac{1}{2}\)
= 2 + 2 × \(\frac{1}{2}\) = 2 + 1 = 3
अत: सही विकल्प (B) है।

प्रश्न 12.
समान्तर श्रेढी 21, 42, 63, 84, ………….. का कौन-सा पद 210 है ?
(A) 9th
(B) 10th
(C) 11th
(D) 12th
हल :
दी गयी समान्तर श्रेढी है :
21, 42, 63, 84, ………. 210
यहाँ a = 21, d = 42 – 21 = 21 तथा an = 210
∴ an = 210
a + (n – 1)d = 210
⇒ 21 + (n – 1) × 21 = 210
(n – 1) × 21 = 210 – 21 = 189
(n – 1) = \(\frac{189}{21}\) = 9
n = 9 + 1 = 10
अत: विकल्प (B) सही है।

प्रश्न 13.
3 के प्रथम पाँच गुणजों का योगफल है :
(A) 45
(B) 55
(C) 65
(D) 75
हल :
3 के प्रथम पाँच गुणज हैं :
3, 6, 9, 12, 15
यहाँ a = 3, n = 3 तथा l = 15
सूत्र Sn = \(\frac{n}{2}\)(a + l) से
S5 = \(\frac{5}{2}\)(3 + 15)
⇒ S5 = \(\frac{5}{2}\) × 18 = 45
अत: सही विकल्प (A) है।

प्रश्न 14.
m के किस मान के लिए 10, m, – 2 समान्तर श्रेढी में होंगे:
(A) m = 4
(B) m = 3
(C) m = 2
(D) m = 1
हल :
a2 – a1 = a2 – a2
⇒ m – 10 = – 2 – m
⇒ m + m = – 2 + 10
2m = 8
m = \(\frac{8}{2}\)
m = 4
अत: सही विकल्प (A) है।

प्रश्न 15.
यदि एक समान्तर श्रेढी का n वाँ पद (2n + 1) है, तो उसके प्रथम तीन पदों का योगफल है :
(A) 6n + 3
(B) 15
(C) 12
(D) 21
हलं :
दिया गया है:
an = 2n + 1
n = 1, 2, 3 रखने पर
a1 = 2 × 1 + 1 = 3
a2 = 2 × 2 + 1 = 5
a3 = 2 × 3 + 1 = 7
अतः समान्तर श्रेढी है-
3, 5, 7,…
सार्वअन्तर (d) = 5 – 3 = 2
या 7 – 5 = 2
प्रथम तीन पदों का योगफल (Sn)
= \(\frac{n}{2}\) [2a + (n – 1) × d)]
= \(\frac{3}{2}\) [2 × 3 + (3 – 1) × 2]
= \(\frac{3}{2}\) [6 + 4]
= \(\frac{3}{2}\) × 10 = 15
अत: विकल्प (B) सही है।