JAC Class 10 Maths Important Questions Chapter 6 त्रिभुज

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 6 त्रिभुज Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 6 त्रिभुज

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
दी गई आकृति में रेखाखण्ड XY, त्रिभुज ABC की भुजा AC के समान्तर है तथा त्रिभुज को दो समान भागों में बाँटती है। अनुपात \(\frac{AX}{AB}\) ज्ञात कीजिए।

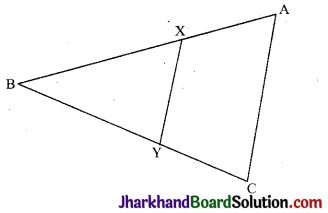
हल :
दिया है
XY || AC
ΔBXY और ΔBAC में
∠BXY = ∠BAC (संगत कोण)
∠BYX = ∠BCA (संगत कोण)
∴ ΔBXY ~ ΔBAC (AA समरूपता गुणधर्म से )

⇒ \(\frac{AX}{AB}\) = \(\frac{2-\sqrt{2}}{2}\)
अतः \(\frac{AX}{AB}\) = \(\frac{2-\sqrt{2}}{2}\)
∴ AY : AB = (2 – \(\sqrt{2}\)) : 2

प्रश्न 2.
BE और CF एक समकोण ΔABC की माध्यिकाएँ है तथा इस Δ का कोण A समकोण है। सिद्ध कीजिए : 4 (BE² + CF²) = 5BC².
हल :
दिया है : BE तथा CF समकोण ΔABC की माध्यिकाएँ है तथा ∠A = 90° हैं।

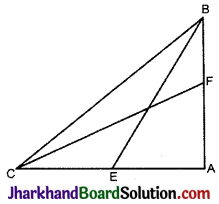
सिद्ध करना है: 4(BE² + CF²) = 5BC²
उपपत्ति: समकोण ΔABC में,
BC² = AB² + AC² ……….(1)
समकोण ΔABE में,
BE² = AE² + AB²
BE² = (\(\frac{AC}{2}\))² + AB²
[∵ BE, ΔABC की माध्यिका है
∴ AE = CE = \(\frac{1}{2}\)AC]
BE² = \(\frac{A C^2}{4}\) + 4AB² ……………(2)
अब समकोण ΔCAF में,
CF² = CA² + AF²
CF² = AC² + (\(\frac{AB}{2}\))²
[∵ BF, ΔABC की माध्यिका है
∴ AF = BF = \(\frac{1}{2}\)AB]
CF² = AC² + \(\frac{A B^2}{4}\)
4CF² = 4AC² + AB² …………(3)
समी. (2) और (3) को जोड़ने पर
4 (BE² + CF²) = AC² + 4AB² + 4AC² + AB²
4 (BE² + CF²) = 5 (AC² + AB²)
4 (BE² + CF²) = 5BC²
[समी. (1) के प्रयोग से] इति सिद्धम् ।

प्रश्न 3.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के परिमापों का अनुपात किन्हीं दो संगत भुजाओं के अनुपात के समान होता है।
हल :
दिया है: ΔABC ~ ΔDEF

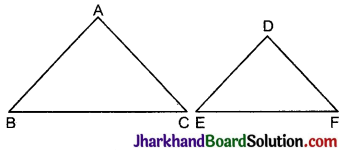
सिद्ध करना है :

प्रश्न 4.
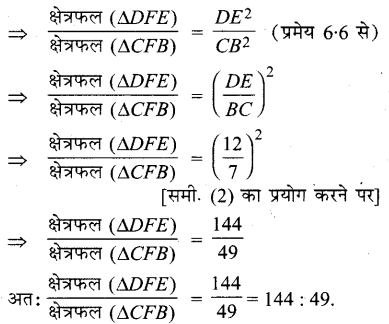
दी गई आकृति में DE || BC तथा AD : DB = 7 : 5 है, तो क्षेत्रफल (ΔDEF) / क्षेत्रफल (ΔCFB) का मान ज्ञात कीजिए।

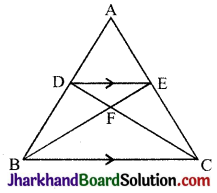
हल :
दिया है
DE || BC तथा AD : DB = 7 : 5
ΔADE तथा ΔABC में,
∠ADE = ∠ABC (संगत कोण)
∠AED = ∠ACB (संगत कोण)
∴ ΔADE ~ ΔABC (AA समरूपता गुणधर्म से)
\(\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}\) ……………(1)
[समरूप त्रिभुज की संगत भुजाएँ समानुपाती होती हैं।]
परन्तु AD : DB = 7 : 5

ΔDFE तथा ΔCFB में
∠DEF = ∠CBF (एकान्तर कोण)
∠DFE = ∠CFB(शीर्षाभिमुख कोण)
∴ ΔDFE ~ ΔCFB
(AA समरूपता गुणधर्म से)

प्रश्न 5.
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गये समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
हल :
दिया है : समकोण त्रिभुज ABC की भुजाओं AB, BC तथा AC पर समबाहु त्रिभुज खींचे गए हैं।
सिद्ध करना है : ar (ΔABN) + ar (ΔBCL) = ar(ΔACM)

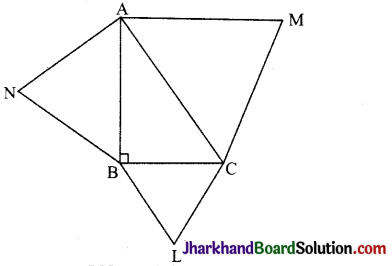
उपपत्ति : ∵ ΔABN तथा ΔACM के प्रत्येक कोण 60° का होगा ।
अतः ΔABN ~ ΔACM (AA समरूपता गुणधर्म से)

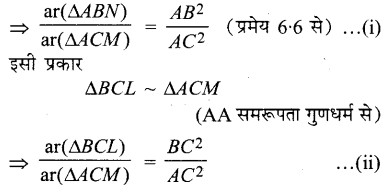
प्रश्न 6.
दिया है कि ΔABC ~ ΔPQR, यदि \(\frac{AB}{PQ}=\frac{1}{3 }\) है, तो ar(ΔABC) / ar(ΔPQR) का मान ज्ञात कीजिए।
हल :
दिया है, ΔABC ~ ΔPQR

प्रश्न 7.
निम्न आकृति में, ∠D = ∠E तथा \(\frac{AB}{DB}=\frac{AE}{EC}\) है, तो सिद्ध कीजिए कि ΔBAC एक समद्विबाहु त्रिभुज है।

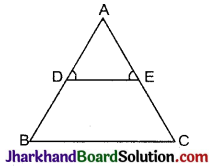
हल :
ΔADE
∠D = ∠E (दिया है)
⇒ AD = AE
(∵ बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।)
दिया है, \(\frac{AD}{DB}=\frac{AE}{EC}\)
⇒ \(\frac{AD}{DB}=\frac{AD}{EC}\) [समी. (i) से]
⇒ DB = EC …………….(ii)
समीकरण (i) व (ii) को जोड़ने पर,
AD + DB = AE + EC
⇒ AB = AC
अत: ΔABC एक समद्विबाहु त्रिभुज हैं।

प्रश्न 8.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है कि D, BC का मध्य बिन्दु है । त्रिभुजों ABC और BDE के क्षेत्रफलों में अनुपात ज्ञात कीजिए।
हल :
हम जानते हैं कि समबाहु त्रिभुज समरूप होते हैं,
अर्थात् ΔABC ~ ΔBDE
∵ D, BC का मध्य बिन्दु है,
∴ BC = 2BD ……….(i)

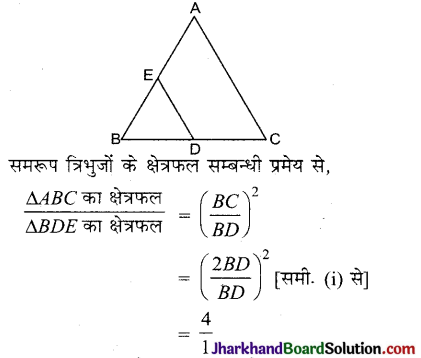
अत: ΔABC का क्षे. ΔBDE का क्षे. = 4 : 1

प्रश्न 9.
निम्न चित्र में, MN || BC और AM : MB = 1 : 2, तो ΔAMN का क्षेत्रफल / ΔABC का क्षेत्रफल का मान ज्ञात कीजिए।

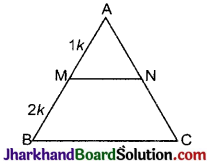
हल :
दिया है, AM = 1K और MB = 2K
∴ AB = AM + MB = 1K + 2K = 3K
ΔAMN और ΔABC में,
∠A = ∠A (उभयनिष्ठ)
∠AMN = ∠ABC (संगत कोण)
∴ ∠AMN ~ ∠ABC (AA समरूपता से)
समरूप त्रिभुजों के क्षेत्रफल के प्रमेय से,

प्रश्न 10.
निम्न चित्र में, यदि AD ⊥ BC, तो सिद्ध कीजिए कि AB² + CD² = BD² + AC²

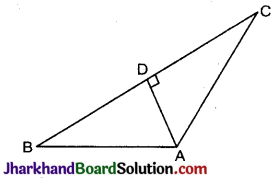
हल :
समकोण ΔADC मे, पाइथागोरस प्रमेय से,
AC² = AD² + CD²
⇒ AD² = AC² – CD² ……….(i)
पुन: समकोण ΔADB में, पाइथागोरस प्रमेय से
AB² = AD² + BD²
⇒ AD² = AB² – BD² ……….(ii)
समीकरण (i) और (ii) से,
AB² – BD² = AC² – CD²
⇒ AB² + CD² = AC² + BD² इति सिद्धम्

प्रश्न 11.
निम्न चित्र में, यदि ΔABC ~ ΔDEF तथा उनकी भुजाओं की लम्बाइयाँ (सेमी में) उन पर अंकित है, तो प्रत्येक त्रिभुज की भुजाओं की लम्बाई ज्ञात कीजिए।

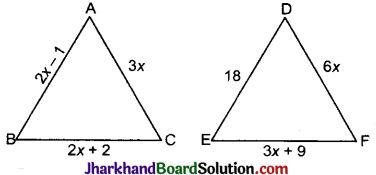
हल :
दिया है, ΔABC ~ ΔDEF

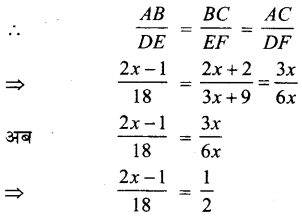
⇒ 4x – 2 = 18
⇒ x = \(\frac{20}{4}\) = 5
ΔABC में,
AB = 2x – 1 = 2 × 5 – 1 = 9 इकाई
BC = 2x + 2 = 2 × 5 + 2 = 12 इकाई
CD = 3x = 3 × 5 = 15 इकाई
ΔDEF में,
DE = 18 इकाई
EF = 3x + 9 = 3 × 5 + 9 = 24 इकाई
DF = 6x = 6 × 5 = 30 इकाई

प्रश्न 12.
चित्र में, यदि PQ || BC तथा PR || CD है, तो सिद्ध कीजिए कि \(\frac{QB}{AQ}=\frac{DR}{AR}\)

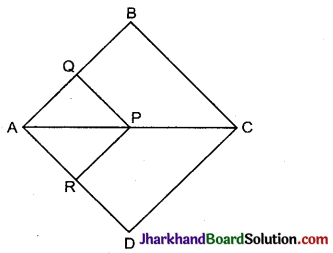
हल :
ΔABC में, PQ || BC
∴ आधारभूत आनुपातिकता प्रमेय से,
\(\frac{AQ}{QB}=\frac{AP}{PC}\) ………….(i)
पुन: ΔADC में,
PR || CD
∴ आधारभूत आनुपातिकता प्रमेय से,
\(\frac{AR}{RD}=\frac{AP}{PC}\) ………….(ii)
समीकरण (i) व (ii) से,
\(\frac{AQ}{QB}=\frac{AR}{RD}\)
अतः \(\frac{QB}{AQ}=\frac{DR}{AR}\) (इति सिद्धम्)

प्रश्न 13.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 16 : 81 है तो इनकी भुजाओं का अनुपात ज्ञात कीजिए।
हल :
समरूप त्रिभुजों के क्षेत्रफल के प्रमेय से,
समरूप त्रिभुज के क्षेत्रफलों का अनुपात = संगत भुजाओं के वर्गों का अनुपात
⇒ 16 : 81 = संगत भुजाओं के वर्गों का अनुपात
⇒ संगत भुजाओं का अनुपात = \(\sqrt{\frac{16}{81}}\) = \(\frac{4}{4}\) = 4 : 9

प्रश्न 14.
निम्न आकृति में, ABC एक त्रिभुज है। यदि \(\frac{AD}{AB}=\frac{AE}{AC}\), तो सिद्ध कीजिए DE || BC है ।

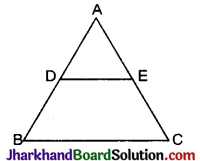
हल :

आधारभूत आनुपातिकता प्रमेय के विलोम से DE || BC (इति सिद्धम)

प्रश्न 15.
यदि दो समरूप त्रिभुजों की संगत माध्यिकाओं का अनुपात 9 : 16 है, तो इनके क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
∵ दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के वर्ग के अनुपात के बराबर होता है ।
∴ क्षेत्रफलों का अनुपात = (9)² : (16)² = 81 : 256

प्रश्न 16.
दो समरूप त्रिभुजों के परिमाप क्रमश: 25 सेमी तथा 15 सेमी है। यदि पहले त्रिभुज की एक भुजा की लंबाई 9 सेमी है, तो दूसरे त्रिभुज की संगत भुजा की लंबाई ज्ञात कीजिए।
हल :
माना दूसरे त्रिभुज की संगत भुजा की लंबाई x सेमी है।
∵ समरूप त्रिभुज की संगत भुजा की लंबाई का अनुपात उनके परिमाप के अनुपात के बराबर होता है।
∴ \(\frac{25}{15}=\frac{9}{x}\)
⇒ x = \(\frac{15 \times 9}{25}\) = 5.4 सेमी
अत: दूसरे त्रिभुज की संगत भुजा = 5.4 सेमी

प्रश्न 17.
चित्र में ΔABC में, DE || BC है तथा AD = 2.4 सेमी, AB = 3 सेमी और AC = 8 सेमी है, तो AE की लम्बाई क्या है?

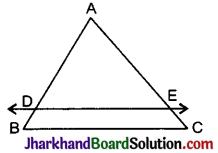
हल :
चित्र में,
DE || BC
तथा
AD = 2.4 सेमी
AB = 3.2 सेमी
AC = 8 सेमी

प्रश्न 18.
निम्न आकृति में, ΔABC तथा ΔXYZ दर्शाए गए हैं। यदि ABC = 3.8 सेमी, AC = 3\(\sqrt{3}\) सेमी, BC = 6 सेमी, XY = 6\(\sqrt{3}\) सेमी, XY = 7.6 सेमी, YZ = 12 सेमी तथा ∠A = 65°, ∠B = 70° हों, तो ∠Y का मान ज्ञात कीजिए।
हल :
ΔABC में,
∠A + ∠B + ∠D = 180°
65° + 70° + ∠C = 180°
∠C = 180° – 135° = 45°
अब ΔABC और ΔXYZ में

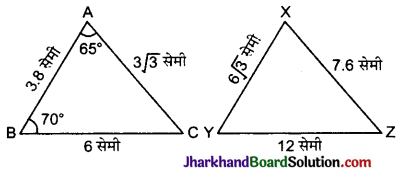
अर्थात् ΔABC ~ ΔXYZ
∴ ∠A = ∠X = 65°, ∠B = ∠Z = 70°
तथा ∠C = ∠Y = 45°

प्रश्न 19.
निम्न चित्र में, समबाहु त्रिभुज ABC में, AD ⊥ BC, BE ⊥ AC तथा CF ⊥ AB है। सिद्ध कीजिए:
4(AD² + BE² + CF²) = 9AB²

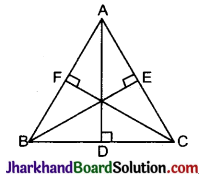
हल :
ΔADB और ΔADC में,
और AB = AC (दिया है)
∠B = ∠C (प्रत्येक कोण 60° है।)
और ∠ADB = ∠ADC (प्रत्येक कोण 90° है।)
∴ ΔADB ≅ ΔADC
⇒ BD = DC
⇒ BD = DC = \(\frac{1}{2}\)BC
∵ ΔADB एक समकोण त्रिभुज है,
∴ AB² = AD² + BD²
⇒ AB² = AD² + (\(\frac{BC}{2}\))²
⇒ AB² = AD² + \(\frac{B C^2}{4}\)
⇒ 4AB² = 4AD² + AB²
⇒ 3AB² = 4AD² …………(i)
इसी प्रकार से, ABEC एक समकोण त्रिभुज है,
∴ BC² = BE² + EC²
⇒ AB² = BE² + (\(\frac{AC}{2}\))²
[∵ BC = AB और EC = AE = \(\frac{AC}{2}\)]
⇒ AB² = BE² + (\(\frac{AC}{2}\))²
⇒ 4AB² = 4BE² + AC²
⇒ 4AB² = 4BE² + AB² [∵ AB = AC]
⇒ 3AB² = 4BE² …………..(ii)
अब समकोण ΔBFC में,
BC² = BF² + CF²
⇒ AB² = (\(\frac{AB}{2}\))² + CF²
⇒ AB² = \(\frac{A B^2}{4}\) + CF²
⇒ 4AB² = AB² + 4CF²
⇒ 3AB² = 4CF² ……..(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर
9AB = 4(AD² + BE² + CF²) इति सिद्धम

प्रश्न 20.
दी गई आकृति में, ABC एक समद्विबाहु त्रिभुज है, जिसका कोण C है तथा AC = 4 सेमी है। AB की लम्बाई ज्ञात कीजिए।

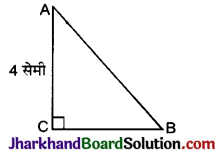
हल :
दिया है, ΔABC एक समद्विबाहु त्रिभुज है,
∠C = 90° तथा AC = 4 सेमी
∴ ΔABC एक समद्विबाहु त्रिभुज है। अतः
BC = AC
ΔABC में, पाइथागोरस प्रमेय से,
AB² = AC² + BC²
AB² = AC² + AC² (∵BC = AC)
= 2 × AC²
= 2 × 4²
= 32
⇒ AB = \(\sqrt{32}\)
AB = 4\(\sqrt{2}\) सेमी

प्रश्न 21.
कर्ण BC पर एक ही तरफ दो समकोण त्रिभुज ABC, DBC बनाए गए है। यदि AC तथा BD एक- दूसरे बिन्दु पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि :
AP × PC = BP × DP
हल :
दिया है, ΔABC तथा ΔDBC समकोण त्रिभुज हैं।
ΔABC व ΔDBC में,
∠BAC = ∠BDC = 90°
∠BPA = ∠CPD (शीर्षाभिमुख होगा )

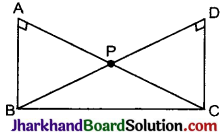
अत: AA समरूपता में,
ΔABC ~ ΔDBC
\(\frac{AP}{BP}=\frac{DP}{PC}\)
[∵ समरूप त्रिभुजों की संगत भुजाओं का अनुपात समान होता है।]
⇒ AP × PC = DP × BP इति सिद्धम्

प्रश्न 22.
दी गई आकृति में, DE || BC, AD = 1 सेमी तथा BD = 2 सेमी है। ΔABC तथा ΔADE के क्षेत्रफलों में क्या अनुपात है?

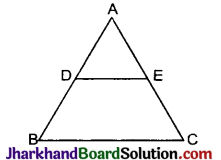
हल :
दिया है, DE || BC, AD = 1 सेमी तथा BD = 2 सेमी
चूँकि, DE || BC
इसीलिए, ∠ADE = ∠DBC ( संगत कोण)

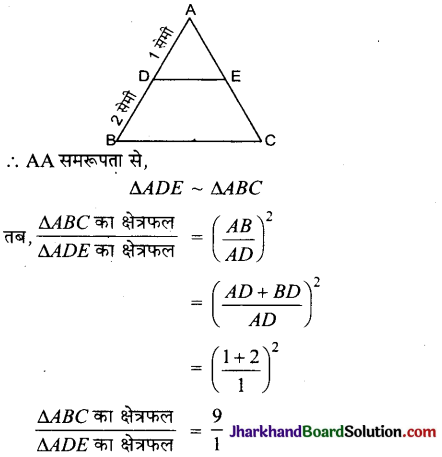
अतः ar(ΔABC) : ar(ΔADE) = 9 : 1

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. दो आकृतियाँ, जिनके आकार समान हों, परन्तु उनकी आमाप समान न हो, ……………… कहलाती हैं।
2. दो आकृतियाँ जिनके आकार तथा आमाप दोनों समान हों, …………. आकृतियाँ कहलाती है।
3. दो त्रिभुज समरूप होते हैं यदि उनके संगत कोण ……………….. हों ।
4. त्रिभुजों की समरूपता को प्रकट करने के लिए उनक शीर्षों की संगतताओं को सही …………….. में लिखना आवश्यक है।
5. यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करें, तो वह तीसरी भुजा के होती है।

हल :

1. समरूप,
2. सर्वांगसम
3. समान,
4. क्रम,
5. समांतर ।

निम्न में सत्य / असत्य ज्ञात कीजिए :

प्रश्न (ख)

1. दो समरूप त्रिभुजों के क्षेत्रफल त्रिभुजों की संगत भुजाओं के वर्गों के अनुपात में होते हैं।
2. एक समद्विबाहु त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
3. यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो पहली भुजा का सम्मुख कोण अधिक कोण होता है।
4. पाइथागोरस प्रमेय के बौधायन प्रमेय के नाम से भी जाना जाता है।
5. सभी वृत्त सर्वागसम होते हैं।

हल :

1. सत्य,
2. असत्य,
3. असत्य,
4. सत्य,
5. असत्य ।

(ग) बहुविकल्पात्मक प्रश्न :

प्रश्न 1.
यदि ΔABC ~ ΔDEF इस प्रकार है कि AB = 1.2 सेमी तथा DE = 1.4 सेमी है, तो त्रिभुजों ABC तथा DEF के क्षेत्रफलों में अनुपात है:
(A) 49 : 36
(B) 6 : 7
(C) 7 : 6
(D) 36 : 49
हल :
ΔABC ~ ΔDEF

अत: सही विकल्प (D) है।

प्रश्न 2.
चित्र में, ABC एक समद्विबाहु समकोण त्रिभुज है जिसका समकोण C है। अतः
(A) AB² = 2AC²
(B) BC² = 2AB²
(C) AC² = 2AB²
(D) AB² = 4AC²

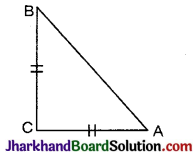
हल :
समकोण समद्विबाहु ΔABC में,
AB² = AC² + BC²
AB² = AC² + (AC) ² [∵ BC = AC]
AB² = AC² + AC²
AB² = 2AC²
अत: सही विकल्प (A) हैं।

प्रश्न 3.
चित्र में, DE || BC है। यदि \(\frac{AB}{DB}\) = \(\frac{3}{2}\) तथा AE = 2.7 सेमी है, तो EC बराबर है :

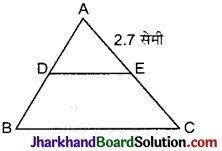
(A) 2.0 सेमी
(B) 1.8 सेमी
(C) 4.0 सेमी
(D) 2.7 सेमी
हल :
ΔABC में DE || BC
∴ आधारभूत समानुपातिक प्रमेय से,

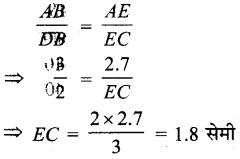
अत: सही विकल्प (B) है।

प्रश्न 3.
यदि ΔABC ~ ΔDEF हो एवं AB = 10 सेमी, DE = 8 सेमी हो, तो ΔABC का क्षेत्रफल : ΔDEF का क्षेत्रफल होगा :
(A) 25 : 16
(B) 16 : 25
(C) 4 : 5
(D) 5 : 4
हल :
ΔABC ~ ΔDEF

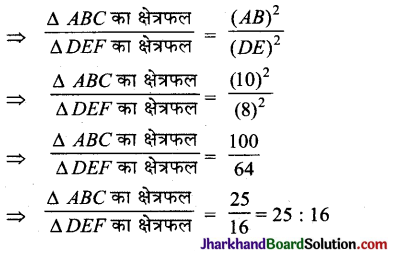
अत: सही विकल्प (A) है।

प्रश्न 4.
ΔABC में यदि D, BC का मध्य- बिन्दु इस प्रकार है कि \(\frac{AB}{AC}=\frac{BD}{DC}\) हो एवं ∠B = 70°, ∠C = 70° हो, तो ∠BAD की माप होगी :
(A) 60°
(B) 30°
(C) 20°
(D) 50°
हल :
ΔABC में,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 70° + 70° = 180°

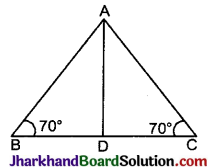
⇒ ∠A = 180° – 140°
∴ ∠A = 40°
अतः \(\frac{AB}{AC}=\frac{BD}{DC}\) और ∠B = ∠C
⇒ ΔABD ~ ΔACD
(SAS समरूपता कसौटी से )
∴ ∠BAD और ∠DAC आपस में बराबर होंगे।
∠BAD + ∠DAC = 40°
⇒ 2∠BAD = 40°
∴ ∠BAD = \(\frac{40°}{2}\) = 20°
अत: सही विकल्प (C) है।

प्रश्न 5.
दी गई आकृति में, XY || QR, \(\frac{PQ}{XQ}=\frac{7}{3}\) तथा PR = 6.3 सेमी है, तो YR बराबर है :
(A) 2.7 सेमी
(B) 18.9 सेमी
(C) 2.1 सेमी
(D) 0.9 सेमी

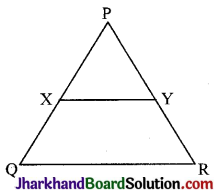
हल :
दिया है
त्रिभुज PQR में XY || QR, \(\frac{PQ}{XQ}\) = \(\frac{7}{3}\) तथा PR = 6.3 सेमी।
आधारभूत आनुपातिक प्रमेय से,

अत: विकल्प (A) सही है।

प्रश्न 6.
एक 12 मीटर लम्बी ऊर्ध्वाधर छड़ की जमीन पर छाया की लम्बाई 8 मीटर लम्बी है। यदि इसी समय एक मीनार की छाया की लम्बाई 40 मीटर हो, तो मीनार की ऊँचाई होगी :
(A) 60 मीटर
(B) 60 सेमी
(C) 40 सेमी
(D) 80 सेमी
हल :
माना ऊर्ध्वाधर AB छड़ है और BC उसकी छाया है। PQ मीनार है और CQ उसकी छाया है।

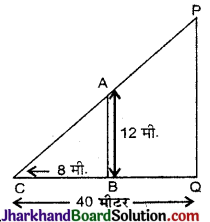
ΔABC और ΔPQC में,
∠ACB = ∠PCQ (उभयनिष्ठ)
∠ABC = ∠PQC (प्रत्येक 90°)
कोण-कोण समरूपता गुणधर्म से,
ΔABC ~ ΔPOC
∴ \(\frac{AB}{PQ}=\frac{BC}{QC}\) (∵ समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं)
⇒ \(\frac{12}{PQ}=\frac{8}{40}\)
∴ PQ = \(\frac{40 \times 12}{8}\)
= 5 × 12 = 60 मीटर
अतः सही विकल्प (A) है।

प्रश्न 7.
आकृति में, DE || BC है यदि AD = x, DB = x – 2, AE = x + 2 तथा EC = x – 1 हो, तो x का मान होगा :

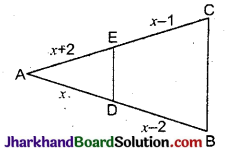
(A) 3
(B) 2
(C) 4
(D) 1
हल :
ΔABC में,
DE || BC
\(\frac{AD}{BD}=\frac{AE}{EC}\)
⇒ \(\frac{x}{x-2}=\frac{x+2}{x-1}\)
⇒ x(x – 1) = (x – 2) (x + 2)
⇒ x² – x = x² – 4
∴ x = 4
अत: सही विकल्प (C) है।

प्रश्न 8.
आकृति में ΔACB ~ ΔAPQ है यदि BC = 8 सेमी, BA = 6.5 सेमी, PQ = 4 सेमी और AP = 2.8 सेमी हो, तो 40 का मान होगा :

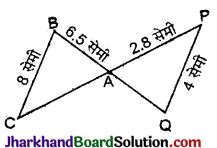
(A) 5.6 सेमी
(B) 6.8 सेमी
(C) 10.5 सेमी
(D) 3.25 सेमी
हल :
ΔACB ~ ΔAPQ

अत: सही विकल्प (D) है।

प्रश्न 9.
यदि ΔABC में AB = 5 सेमी, BC = 12 सेमी और AC = 13 सेमी है, तो ∠B का मान होगा:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
हल :
ΔABC में,
(AB)² + (BC)² = (5)² + (12)²
= 25 + 144 = 169
= (AC)²
∴ AB² + BC² = AC²
पाइथागोरस प्रमेय के विलोम से,
ΔABC समकोण त्रिभुज है जिसमें
∠B = 90°
अत: सही विकल्प (C) है।

प्रश्न 10.
दो समरूप ΔABC और ΔPQR हैं जिनके क्षेत्रफल क्रमशः 100 सेमी² तथा 144 सेमी² है और ΔABC की ऊँचाई 6 सेमी है तो ΔPQR की ऊँचाई होगी :
(A) 12 सेमी
(B) 6.3 सेमी
(C) 7.2 सेमी
(D) 4.8 सेमी
हल :
हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत ऊँचाइयों के वर्गों के अनुपात के समान होता है। माना ΔPQR की संगत ऊँचाई x सेमी है।

अत: सही विकल्प (C) है।

प्रश्न 11.
यदि ΔABC और ΔDEF में \(\frac{AB}{DE}=\frac{BC}{FD}\) हो, तो वे समरूप होंगे, यदि :
(A) ∠B = ∠E
(B) ∠A = ∠D
(C) ∠B = ∠D
(D) ∠A = ∠F
हल :
सही विकल्प (C) है।

प्रश्न 12.
यदि ΔDEF और ΔPQR में ∠D = ∠Q और ∠R = ∠E हो, तो निम्नलिखित में से कौन-सा सही नहीं है?
(A) \(\frac{EF}{PR}=\frac{DF}{PQ}\)
(B) \(\frac{DE}{PQ}=\frac{EF}{RP}\)
(C) \(\frac{DE}{QR}=\frac{DF}{PQ}\)
(D) \(\frac{EF}{RP}=\frac{DE}{QR}\)
हल :
सही विकल्प (B) है।

प्रश्न 13.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 16 : 81 है, तो त्रिभुजों की भुजाओं का अनुपात होगा :
(A) 4 : 9
(B) 16 : 81
(C) 9 : 4
(D) 2 : 3
हल :
हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के समान होता है ।
अतः दोनों भुजाओं का अनुपात = 4 : 9
अत: सही विकल्प (A) है।