JAC Class 10 Maths Notes Chapter 1 वास्तविक संख्याएँ

Students should go through these JAC Class 10 Maths Notes Chapter 1 वास्तविक संख्याएँ will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 1 वास्तविक संख्याएँ

भूमिका :
हमने पिछली कक्षाओं में प्राकृतिक संख्याओं, पूर्ण संख्याओं, परिमेय संख्याओं अपरिमेय संख्याओं व वास्तविक संख्याओं के विषय में पढ़ा है। हमने इनके गुणों के विषय में भी पढ़ा है स्मरण करें कि वास्तविक संख्याएँ परिमेय संख्याओं और अपरिमेय संख्याओं का समूह होती हैं।

इस अध्याय में हम \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\) आदि की अपरिमेयता सिद्ध करने, परिमेय संख्याओं का दशमलव प्रसार, सांत आवर्ती दशमलवं प्रसार, यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग, अंकगणित की आधारभूत प्रमेव यूक्लिड विभाजन प्रमेविका आदि के विषय में अध्ययन करेंगे।
→ वास्तविक संख्याएँ (Real Numbers) : परिमेय संख्या और अपरिमेय संख्याओं के समूह को वास्तविक संख्याएँ कहते हैं।
जैसे 3, 5, \(\sqrt{7}\), \(\frac{-\sqrt{3}}{2}\) आदि।

→ परिमेय संख्याएँ (Rational numbers): वे संख्याएँ जिनका दशमलव प्रसार सांत अथवा असांत आवर्ती होता परिमेय संख्याएँ कहलाती हैं। इन्हें \(\frac{p}{q}\) (जहाँ q ≠ 0) के रूप में लिखा जा सकता है।
जैसे- \(\frac{2}{4}\), 3, \(\frac{1}{3}\) आदि।

→ अपरिमेय संख्याएँ (Irrational numbers): वे संख्याएँ जिनका दशमलव प्रसार असांत तथा अनावर्ती होता है. अपरिमेय संख्याएँ कहलाती हैं।
जैसे- \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt[3]{4}\), π आदि ।

→ पूर्णांक (Integers): शून्य प्राकृतिक संख्याओं एवम् ऋणात्मक प्राकृतिक संख्याओं के समूह की पूणांक कहते हैं।
जैसे- -9, -8, 0, 5, 4, आदि।

→ सम संख्याएँ (Even numbers): वे संख्याएँ जो 2 से विभाजित होती हैं, सम संख्याएँ कहलाती है।
जैसे- 2, 4, 6, 8, 10 ….. (सम संख्याओं में इकाई का अंक 0, 2, 4, 6, 8 होता है।)

→ विषम संख्याएँ (Odd numbers): वे संख्याएँ जो 2 से विभाजित नहीं होती हैं, विषम संख्याएँ कहलाती हैं।
जैसे- 1, 3, 5, 7, 9, …. (विषम संख्याओं में इकाई का अंक 1, 3, 5, 9 होता है।)

→ अभाज्य संख्याएँ (Prime numbers): वे संख्याएँ जिनके सिर्फ दो गुणनखंड (1 व स्वयं) होते हैं, अभाज्य संख्याएँ कहलाती हैं अथवा वे संख्याएँ जो या स्वयं से विभाजित होती हैं, अभाज्य संख्या कहलाती हैं।
जैसे- 2, 5, 7, 11, 13, ….. ( सबसे छोटी अभाज्य संख्या 2 होती है।)

→ भाज्य संख्याएँ (Composite numbers): वे संख्याएँ जिनके और स्वयं के अलावा कम से कम एक और “गुणनखण्ड हो, भाज्य संख्याएँ कहलाती हैं।
जैसे- 4, 6, 8, 9, 10, 12, …
महत्वपूर्ण बिन्दु: 1 न तो अभाज्य संख्या है और न ही भाज्य संख्या।

→ सांत दशमलव प्रसार (Terminating decimal expansion): जिन परिमेय संख्याओं के हर 2ⁿ × 5^m के रूप में होते हैं, उनके दशमलव प्रसार सांत होते हैं।
जैसे \(\frac{2}{4}\) = 0.5, \(\frac{1}{5}\), 0.2, \(\frac{10}{25}=\frac{2}{5}\) = 0·4

→ असांत आवर्ती दशमलव प्रसार (Non-terminating recurring decimal expansion): जिन परिमेय संख्याओं के हर 2ⁿ × 5^m के रूप में नहीं होते हैं, उन परिमेय संख्याओं के दशमलव प्रसार असांत आवर्ती होते हैं।
जैसे \(\frac{1}{3}\) = 0.333, …. \(\frac{17}{6}\) = 2.8333…

→ लघुत्तम समापवर्त्य (LCM): दी गयी संख्याओं के छोटे से छोटे सार्वगुणज को लघुत्तम समापवर्त्य कहते हैं।

→ महत्तम समापवर्त्य (HCF): दी गयी संख्याओं के बड़े से बड़े सार्व गुणनखंड को महत्तम समापवर्तक कहते हैं।

पूर्णांकों की भाजकता तथा धनात्मक पूर्णांकों के दो महत्वपूर्ण गुण-
(i) यूक्लिड विभाजन एल्गोरिथ्म ( कलन विधि) (Euclid’s Division Algorithm ): यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग इस अध्याय में दो धनात्मक पूर्णांकों के महत्तम समापवर्तक (HCF) परिकलित करने में करेंगे।
(ii) अंकगणित की आधारभूत प्रमेय (Fundamental Theorem of Arithmetic ): अंकगणित की आधारभूत प्रमेय का प्रयोग दो अनुप्रयोगों में करेंगे:
(i) प्रथम अनुप्रयोग में कुछ संख्याओं जैसे \(\sqrt{2}\), \(\sqrt{3}\) और \(\sqrt{5}\) आदि की अपरिमेयता सिद्ध करने में करेंगे। (ii) किसी दी गई संख्या के अभाज्य गुणनखण्ड ज्ञात करने में करेंगे।

यूक्लिड विभाजन प्रमेविका :
यूक्लिड प्रथम यूनानी गणितज्ञ थे, जिन्होंने समतल ज्यामिति के अध्ययन हेतु एक नई विचारधारा को प्रारम्भ किया जिसमें से एक यूक्लिड विभाजन प्रमेयिका है। इसके अनुसार एक धनात्मक पूर्णांक a को किसी अन्य धनात्मक पूर्णांक b से विभाजित करने पर भागफल q और शेषफल r प्राप्त होता है तथा शेषफल r या तो शून्य होता है या भाजक b से छोटा होता है अर्थात् 0 ≤ r < b होता है।

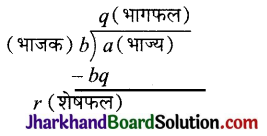
यही यूक्लिड की विभाजन प्रमेयिका है।
इसे औपचारिक रूप से निम्न प्रकार व्यक्त कर सकते हैं:
यदि a और b दो धनात्मक पूर्णांक हैं तो दो ऐसे अद्वितीय पूर्णांक q और r विद्यमान होते हैं कि
a = bq + r, जहाँ 0 ≤ r < b
ध्यान रहे कि या शून्य भी हो सकते हैं।
साधारण शब्दों में, भाज्य (a) = भाजक (b) × भागफल (q) + शेषफल (r)

अंकगणित की आधारभूत प्रमेय :
प्रत्येक भाज्य संख्या को अभाज्य संख्याओं के एक गुणनफल के रूप में व्यक्त (गुणनखंडित) किया जा सकता है तथा यह गुणनखंडन अभाज्य गुणनखंडों के आने वाले क्रम के बिना अद्वितीय होता है अर्थात् इस पर कोई ध्यान दिए बिना कि अभाज्य गुणनखंड किस क्रम में आ रहे हैं।

उदाहरण के लिए :
44 एक भाज्य संख्या है। इसे 2 × 2 × 11 अथवा 11 × 2 × 2 के रूप में लिखा जा सकता है। यदि हम 2 × 2 × 11 अथवा 11 × 2 × 2 के क्रम पर ध्यान नहीं देते अर्थात् यदि 2 × 2 × 11 और 11 × 2 × 2 में कोई अन्तर नहीं है, तो यह गुणनखण्ड अद्वितीय भी है।
दो संख्याओं के म. स. तथा ल.स. में सम्बन्ध- दो संख्याओं के म. स. तथा ल.स. का गुणनफल उन संख्याओं के गुणनफल के बराबर होता है। अर्थात्
म.स. (H.C.F.) × ल.स. (L.C.M.) = एक संख्या (a) × दूसरी संख्या (b)
यदि दो संख्याएँ a और b हों, तो
H.C.F. × L.C.M. = a × b
इस मुख्य सम्बन्ध की सहायता से निम्नांकित सम्बन्ध भी लिखे जा सकते हैं-
(i) H.C.F. = \(\frac{a \times b}{\text { L.C.M }}\)
(ii) L.C.M. = \(\frac{a \times b}{\text { H.C.F. }}\)
(iii) a = \(\frac{\text { H.C.F. } \times \text { L.C.M. }}{b}\)
(iv) b = \(\frac{\text { H.C.F. } \times \text { L.C.M. }}{a}\)

अपरिमेय संख्याओं का पुनभ्रमण :
अपरिमेय संख्याएँ: वे संख्याएँ जिनका दशमलव प्रसार असान्त (Non-terminating) और अनावर्ती (Non-repeating) हो, अपरिमेय संख्याएँ कहलाती हैं। इन संख्याओं को \(\frac{p}{q}\) के रूप में व्यक्त नहीं किया जा सकता; जहाँ p और q पूर्णांक है और q ≠ 0.
उदाहरण : \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{15}\), π, \(\frac{-\sqrt{2}}{\sqrt{3}}\), 0.10110111011110…….. इत्यादि।
हम विरोधाभास विधि द्वारा संख्याओं की अपरिमेयता को सिद्ध करते हैं।

परिमेय संख्याओं और उनके दशमलव प्रसारों का पुनभ्रमण :
कोई भी परिमेय संख्या जिसका दशमलव प्रसार सांत है, उसे हम एक ऐसी परिमेय संख्या के रूप में लिख सकते हैं जिसका हर 10 की कोई घात होती है अर्थात् कोई भी 10 की धनात्मक घात को 2 और 5 की घातों के गुणनफल के रूप में व्यक्त कर सकते हैं।
जैसे 10ⁿ = (2 × 5)ⁿ ⇒ 2ⁿ × 5ⁿ
10² = 2² × 5²
10³ = 2³ × 5³ इत्यादि
अतः जिन परिमेय संख्याओं के दशमलव प्रसार सांत होते हैं, उनके हर 2ⁿ × 5^m के रूप में होते हैं।