JAC Class 10 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Students should go through these JAC Class 10 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

भूमिका (Introduction) :
पिछली कक्षाओं में हम ठोस आकृतियों जैसे घनाभ, घन, शंकु, बेलन और गोला के पृष्ठीय क्षेत्रफल तथा आयतन के बारे में अध्ययन कर चुके है। इस अध्याय में पिछले ज्ञान का उपयोग करते हुए दो या दो से अधिक ठोस आकृतियों के संयोजन से बनी आकृतियों के पृष्ठीय क्षेत्रफल तथा आयतन का अध्ययन करेंगे। हम ऐसी ठोस आकृतियों के बारे में भी अध्ययन करेंगे जो एक शंकु को उसके आधार के समान्तर एक तल द्वारा काटने पर प्राप्त होते है। उदाहरण के लिए बाल्टी, ग्लास, फ्रिक्शन क्लच आदि।
→ ठोस (Solid) : वस्तुएँ जिनकी अन्तरिक्ष में तीन भुजाएँ अर्थात् (लम्बाई, चौड़ाई, ऊँचाई) हों ठोस कहलाते हैं।
→ आयतन (Volume) : किसी ठोस द्वारा अन्तरिक्ष के घेरे गए स्थान के परिमाण को उसका आयतन कहते हैं।
→ पृष्ठीय क्षेत्रफल (Surface area) : किसी ठोस के सभी पृष्ठों के क्षेत्रफलों के योग को उसका पृष्ठीय क्षेत्रफल कहते हैं।
→ वक्त पृष्ठीय क्षेत्रफल (Lateral surface area) : किसी ठोस के आधार क्षेत्रफलों को छोड़कर शेष बचे सभी पृष्ठों के क्षेत्रफलों के योग को वक्र पृष्ठीय क्षेत्रफल कहते हैं।
→ घनाभ (Cuboid): छ: आयताकार पृष्ठों से घिरी ठोस बन्द आकृति को घनाभ कहते हैं।
→ घन (Cube) : यदि घनाभ की प्रत्येक कोर लम्बाई में समान हो, तो उसे घन कहते हैं।
→ लम्ब वृत्तीय शंकु का छिन्नक (Frustum of a right circular cone) : यदि किसी लम्ब वृत्तीय शंकु को उसके आधार के समान्तर किसी तल द्वारा काटा जाये तो कटने वाले तल तथा आधार के बीच के भाग को शंकु का छिन्नक कहते हैं।

घन (Cube) और घनाभ (Cuboid) :
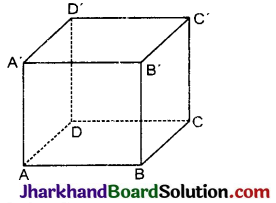
घनाभ (Cuboid) : यदि समान्तर षट्फलक का प्रत्येक फलक आयत हो, तो उसे घनाभ कहते हैं। घनाभ को आयतफलकी ठोस भी कहते हैं जैसे ईंट, सन्दूक, कमरा आदि घनाभ हैं घनाभ में छः पृष्ठ (फलक), 8 शीर्ष व 12 कोरें होती हैं।
चित्र से स्पष्ट है कि घनाभ के आमने-सामने के फलक परस्पर समान होते हैं।

1. घनाभ के फलक ABCD का क्षेत्रफल = फलक A’B’CD’ का क्षेत्रफल = लम्बाई × चौड़ाई
2. घनाभ के फलक ADD’A’ का क्षेत्रफल = फलक BCC’B’ का क्षेत्रफल = चौड़ाई × ऊँचाई
3. घनाभ के फलक ABB’A’ का क्षेत्रफल = फलक DCC’D’ का क्षेत्रफल = ऊँचाई × ऊँचाई
4. घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2 (लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई) वर्ग इकाई
5. घनाभ की चारों दीवारों का क्षेत्रफल = 2 × ऊँचाई (लम्बाई + चौड़ाई) वर्ग इकाई
अथवा
= (ऊँचाई × परिमाप) वर्ग इकाई।

घन (Cube) : यदि घनाभ का प्रत्येक फलक वर्गाकार हो, तो उसे घन कहते हैं। अर्थात् घन की लम्बाई, चौड़ाई और ऊँचाई बराबर होती हैं।
∴ घन का प्रत्येक पृष्ठ वर्गाकार होता है।
घन के एक पृष्ठ का क्षेत्रफल = (भुजा)²
∴ घन के 6 पृष्ठों का क्षेत्रफल = 6(भुजा)²
अतः घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 6(भुजा)² वर्ग इकाई

घन और घनाभ के विकर्ण (Diagonals of Cube and Cuboid)
घन या घनाभ के समान्तर फलक के दो सम्मुख शीर्षों को मिलाने वाली रेखा विकर्ण कहलाती है अतः घन एवं मैं कुल 4 विकर्ण होते हैं।
1. घनाभ के विकर्ण की लम्बाई =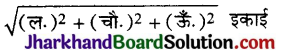
2. घन के विकर्ण की लम्बाई = भुजा \(\sqrt{3}\) इकाई
घन और घनाभ का आयतन (Volume of Cube and Cuboid)
प्रत्येक ठोस आकृति स्थान घेरती है। अतः ठोस आकृति द्वारा घेरे गये स्थान की माप को आयतन कहा जाता है।
घनाभ का आयतन = (लम्बाई × चौड़ाई × ऊँचाई ) घन इकाई तथा घन का आयतन = (भुजा)³ घन इकाई।

लम्बवृत्तीय बेलन और शंकु :
लम्बवृत्तीय बेलन (Right Circular Cylinder) :
परिभाषा- किसी ‘आयत’ की एक भुजा को स्थिर रखकर उसके परित: आयत को घुमाने पर बने ठोस को लम्बवृत्तीय बेलन कहते हैं।
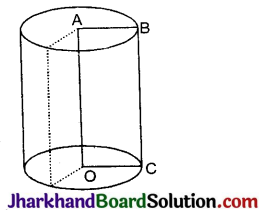
संलग्न चित्र में आयत OABC की भुजा OA को स्थिर मानकर उसके परितः आयत को घुमाने पर बने लभ्यवृत्तीय बेलन को दिखाया गया है।
स्थिर भुजा OA की लम्बाई को बेलन की ऊँचाई कहते हैं तथा बिन्दु O और A इसके वृत्तीय सिरों के केन्द्र कहलाते हैं। OC अथवा AB इसके वृत्तीय आधार की त्रिज्या हैं। आयत को उसकी किसी एक भुजा के परितः घुमाने पर लम्बवृत्तीय बेलन प्राप्त होता है।

लम्बवृत्तीय बेलन से सम्बन्धित सूत्र
1. बेलन के आधार का क्षेत्रफल = वृत्त का क्षेत्रफल = πr² वर्ग इकाई
2. बेलन के आधार की लम्बाई = वृत्त की परिधि = 2πr इकाई
3. बेलन के वक्रपृष्ठ का क्षेत्रफल (C.S.A.) = आधार की परिधि × ऊँचाई
= 2πrh वर्ग इकाई
4. बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल (T.S.A.) = वक्रपृष्ठ का क्षेत्रफल + दोनों वृत्तीय आधारों का क्षेत्रफल
= 2πrh + 2πr² = 2πr (h + r) वर्ग इकाई
5. बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई = πr² × h = πr2h घन इकाई

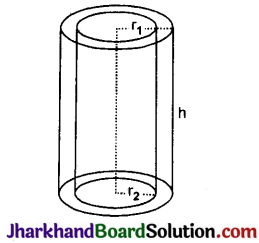
खोखला बेलन (Hollow Cylinder)- यदि r₁ व r₂ खोखले बेलन की बाह्य और अन्तः त्रिज्याएँ हों तथा ऊँचाई h हो तो :
1. खोखले बेलन के प्रत्येक सिरे का क्षेत्रफल = π(r₁² – r₂²)
2. खोखले बेलन के वक्रपृष्ठ का क्षेत्रफल = बाह्य पृष्ठ का क्षेत्रफल + अन्तः पृष्ठ का क्षेत्रफल
= 2πr₁h + 2πr₂h = 2π(r₁ + r₂)h
3. खोखले बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल = वक्रपृष्ठ का क्षेत्रफल + 2 × (एक सिरे का क्षेत्रफल)
= 2π(r₁ + r₂)h + 2π(r₁² – r₂²)
= 2π(r₁ + r₂)h + 2π(r₁ + r2) (r₁ – r₂)
= 2π(r₁ + r₂) (h + r₁ – r₂)
4. खोखले बेलन का आयतन = बाह्य बेलन का आयतन – अन्तः बेलन का आयतन
= πr₁²h – πr₂²h = π(r₁² – r₂²)h

लम्बवृत्तीय शंकु (Right Circular Cone) :
परिभाषा- किसी समकोण त्रिभुज की समकोण बनाने वाली दो भुजाओं में से एक को स्थिर मानकर, त्रिभुज को उसके परितः घुमाने पर बने ठोस को लम्बवृत्तीय शंकु कहते हैं।
चित्र में समकोण ΔVOA को भुजा OV के परित: घुमाने पर प्राप्त लम्बवृत्तीय शंकु को दिखाया गया है, जिसका शीर्ष V तथा वृत्तीय आधार का केन्द्र O है।

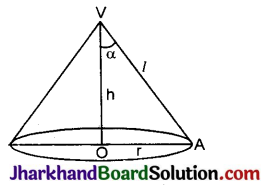
यहाँ शंकु की ऊँचाई = OV = h
शंकु की तिरछी ऊँचाई = VA = l
शंकु के आधार की त्रिज्या = ∠OAP = α
शंकु का अर्द्ध-शीर्ष कोण
समकोण ΔVOA में, VA² = OV² + OA²
l² = h² + h²
l = \(\sqrt{h^2+r^2}\)
शंकु की तिरछी ऊँचाई (l) = \(\sqrt{h^2+r^2}\)

लम्बवृत्तीय शंकु से सम्बन्धित सूत्र :
1. शंकु का वक्रपृष्ठीय क्षेत्रफल (C.S.A.) = \(\frac{1}{2}\) × वृत्तीय आधार की परिधि × तिरछी ऊँचाई
= \(\frac{1}{2}\) × 2πr × l = πrl
2. शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल (T.S.A.) = वक्र पृष्ठ + वृत्तीय आधार का क्षेत्रफल
= πrl + πr² = πr(l + r)
3. शंकु का आयतन = \(\frac{1}{3}\) × वृत्तीय आधार का क्षेत्रफल × ऊँचाई = \(\frac{1}{3}\)πr²h
यदि शंकु का अर्द्ध-शीर्ष कोण α हो तो उसकी :
(i) ऊँचाई (h) = r cot α
(ii) तिर्यक ऊँचाई (l) = r cosec α

गोला (Sphere) :
जब किसी वृत्त या अर्द्धवृत्त को उसके व्यास के सापेक्ष परिक्रमण कराया जाता है, तो एक ठोस आकृति प्राप्त होती है जिसे गोला कहते हैं। वृत्त का केन्द्र, त्रिज्या और व्यास गोले के केन्द्र, त्रिज्या और व्यास होंगे।

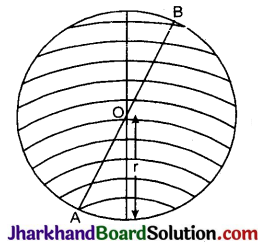
यदि गोले की त्रिज्या r हो, तो
1. गोले का पृष्ठीय क्षेत्रफल = 4πr²
2. गोले का आयतन = \(\frac{4}{3}\)πr³

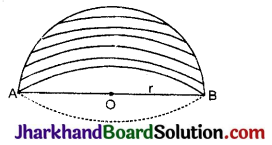
यदि अर्द्ध गोले की त्रिज्या r हो, तो
1. अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr²
2. अर्द्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2πr² + πr² = 3πr²
3. अर्द्ध गोले का आयतन = \(\frac{2}{3}\)πr³

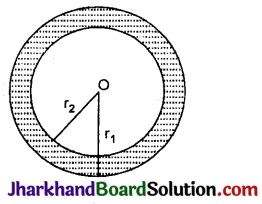
गोलीय कोश (खोखला गोला) (Spherical shell)- दो संकेन्द्रीय गोलों से सीमाबद्ध आकृति को गोलीय कोश कहते हैं।
यदि गोलीय कोश की बाह्य त्रिज्या r₁ और अन्तः त्रिज्या r₂ हो, तो
1. गोलीय कोश का आयतन = \(\frac{4}{3}\)π(r₁³ – r₂³)
2. गोलीय कोश की मोटाई = r₁ – r₂.

ठोसों के संयोजन का पृष्ठीय क्षेत्रफल :
निम्नांकित चित्रों में बनी आकृतियों पर ध्यान दीजिए:

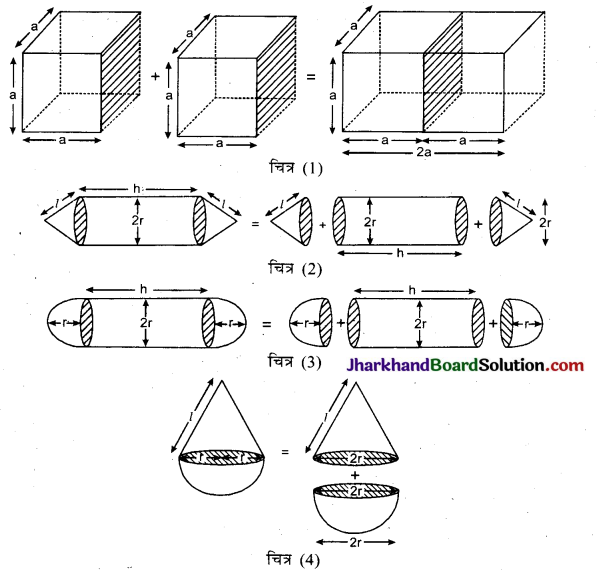
चित्र (1) में दो घनों को संयुक्त करके एक आयतफलकी बनाया गया है।
चित्र (2) में दी गई आकृति एक बेलन के दोनों सिरों पर समान परिच्छेद क्षेत्रफल के दो शंकु जोड़कर बनाई गई है।
चित्र (3) में दी गई आकृति एक बेलन के दोनों सिरों पर समान परिच्छेद क्षेत्रफल के दो अर्द्धगोलों को संयुक्त कर बनाई गई है।
चित्र (4) में दी गई आकृति समान आधार वाले अर्द्धगोले पर शंकु के संयोजन से बनाई गई है।
नोट : (1) किसी संयुक्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल (T.S.A.) उसके खण्डों के सम्पूर्ण पृष्ठीय क्षेत्रफलों के योग से कम होता है और क्षेत्रफल में यह कमी उस क्षेत्रफल के बराबर होती है जो खण्डित भागों को संयुक्त करने पर विलुप्त हो जाता है।
(2) यदि संयुक्त ठोस के सभी खण्ड वक्र संयुक्त पृष्ठीय हैं, तो
संयुक्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = संयुक्त ठोस के खण्डों के वक्र पृष्ठों के क्षेत्रफल का योग
तथा संयुक्त ठोस का आयतन = संयुक्त ठोस के खण्डों के आयतनों का योग।

ठोसों के संयोजन का आयतन :
दो ठोसों के संयोजन से बने ठोस आकृति का आयतन वास्तव में दोनों के आयतनों के योग के बराबर होता है।
आयतन से सम्बन्धित सूत्र :
1. घनाभ का आयतन = ल. × चौ. × ॐ.
2. घन का आयतन = भुजा³
3. बेलन का आयतन = πr²h
4. शंकु का आयतन = \(\frac{1}{3}\)πr²h
5. खोखले बेलन का आयतन = π(r₁² – r₂²)h, जहाँ r₁ > r₂
6. गोले का आयतन = \(\frac{4}{3}\)πr³
7. अर्द्धगोले का आयतन = \(\frac{2}{3}\)πr³
8. खोखले गोले (गोलीय कोश) का आयतन = \(\frac{4}{3}\)π(r₁³ – r₂³), जहाँ r₁ > r₂

आयतन सम्बन्धी इकाइयाँ
1 लीटर = 1000 घन सेमी
1000 लीटर = 1 घन मीटर
1 किलो लीटर = 1 घन मीटर
1 घन सेमी = 10 × 10 × 10 = 1000 घन मिमी
1 घन मीटर = 100 × 100 × 100
= 1000000 घन सेमी

एक ठोस का एक आकार से दूसरे आकार में रूपान्तरण :
इस खण्ड में हम एक ठोस को एक रूप से दूसरे रूप में परिवर्तित करते हैं, तो इस पूरी स्थिति में दोनों आकारों का आयतन समान रहता है।
जैसे-जूस की एक बोतल को कुछ गिलासों में समान मात्रा में बाँट दें। अब हम गिलासों की संख्या ज्ञात करना चाहेंगे।
[जूस की बोतल का आयतन] = n[गिलासों का आयतन],
जहाँ गिलासों की संख्या है।

लम्बवृत्तीय शंकु का छिन्नक (Frustum of a Right Circular Cone) :
छिन्नक : यदि किसी लम्बवृत्तीय शंकु को उसके आधार के समान्तर तल द्वारा काटा जाता है, तो वह भाग जो शंकु के आधार तथा काटने वाले तल के बीच है, छिन्नक कहलाता है।

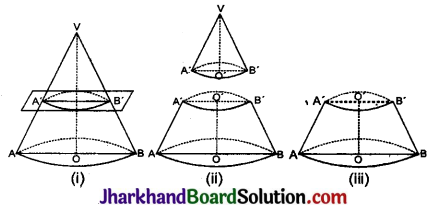
चित्र (i) में लम्बवृत्तीय शंकु VAB को उसके वृत्तीय आधार के समान्तर एक तल द्वारा काटा जाता है जिसका केन्द्र O तथा व्यास AB है। शीर्ष / वाले भाग को हटा दिया जाता है, जैसा कि चित्र (ii) में दिखाया गया है। शेष हुआ भाग ABB ‘A’ चित्र (iii) में दिखाया गया है, यह शंकु VAB का छिन्नक है वृत्तीय पृष्ठ AOB तथा A’O’B’ छिन्नक के वृत्तीय सिरे कहलाते हैं।
अतः लम्बवृत्तीय शंकु के छिन्नक के दो असमान वृत्तीय आधार होते हैं और एक वक्र पृष्ठ होता है।
छिन्नक की ऊँचाई: छिन्नक की ऊँचाई या मोटाई दोनों वृत्तीय आधारों के बीच की लम्बीय दूरी होती है।
छिन्नक की ऊँचाई OO’ = VO – VO’ (चित्र iii)
छिन्नक की तिर्यक ऊंचाई : छिन्नक के दोनों वृत्तीय आधारों पर एक ही दिशा में खींची समान्तर त्रिज्याओं के बाहरी बिन्दुओं को मिलाने वाले रेखाखण्ड की लम्बाई को छिन्नक की तिर्यक ऊँचाई कहते हैं।
चित्र में, छिन्नक ABA’B’ की तिर्यक ऊँचाई AA’ या BB’ हैं।
स्पष्ट है कि AA’ = VA – VA’
तथा BB’ = VB – VB’
अतः छिन्नक की तिर्यक ऊँचाई शंकुओं VAB और VA’B’ की तिर्यक ऊँचाइयों के अन्तर के बराबर होती है।

लम्बवृत्तीय शंकु के छिन्नक का आयतन और पृष्ठीय क्षेत्रफल :
शंकु के छिन्नक का आयतन = \(\frac{1}{3}\)π(r₁² – r₁ r₂ + r₂²)h
शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π(r₁ + r₂)l

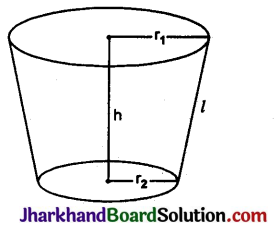
शंकु के छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल + वृत्तीय आधारों का पृष्ठीय क्षेत्रफल
= π(r₁ + r₂)l + πr₁² + πr₁²
= π[(r₁ + r₂)l + r₁² + r₂²]
शंकु के छिन्नक की (तिर्यक) ऊँचाई = \(\sqrt{\left(r_1-r_2\right)^2+h^2}\)