JAC Class 10 Maths Notes Chapter 3 दो चरों वाले रखिक समीकरण का युग्म

Students should go through these JAC Class 10 Maths Notes Chapter 3 दो चरों वाले रखिक समीकरण का युग्म will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 3 दो चरों वाले रखिक समीकरण का युग्म

भूमिका :
हम पिछली कक्षाओं में सरल समीकरणों अर्थात् प्रथम घात ( रैखिक) तथा एक अज्ञात राशि (चर) के समीकरण का अध्ययन कर चुके हैं। व्यापक रूप में इन्हें ax + b = 0 या ax + b = c के द्वारा निरूपित किया जाता है, जहाँ a, b, c वास्तविक संख्याएँ हैं। a ≠ 0 तथा x चर है। हम यह भी जानते हैं कि ax + b = 0, a ≠ 0 का हल x = –\(\frac{b}{a}\) होता है तथा x = –\(\frac{b}{a}\) समीकरण ax + b = 0 का मूल (Root) कहलाता है।
इस अध्याय में हम दो चरों वाले रैखिक समीकरण युग्म को बीजगणितीय तथा आलेखीय विधियों से हल करेंगे।

दो चरों में रैखिक समीकरण युग्म :
समीकरण ax + by + c = 0 दो चरों वाले रैखिक समीकरण का व्यापक रूप कहलाता है जिसमें a, b, c वास्तविक संख्याएँ होती हैं तथा a ≠ 0, b ≠ 0. जैसे- 3x + 4y + 7 = 0, -5y + x = -2 तथा 2x + \(\frac{3}{11}\)y = 1 आदि दो चरों वाले रेखीय समीकरणों के कुछ उदाहरण हैं।
यदि समीकरण ax + by + c = 0 में a ≠ 0, b = 0 हो, तो यह समीकरण परिवर्तित होकर ax + c = 0 रूप ले लेती है जो कि एक घर में रैखिक समीकरण है। इसी प्रकार यदि तो ax + by + c = 0 परिवर्तित होकर by + c = 0 के रूप में आ जाती है जो कि पुनः एक चर y में रैखिक समीकरण है।
दो चरों में दो रैखिक समीकरण एक रैखिक समीकरणों का युग्म कहलाता है। ऐसे समीकरणों के युग्म को युगपत समीकरण भी कहते हैं।
a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 रैखिक समीकरण युग्म का सबसे व्यापक रूप है। जहाँ a₁, b₁, c₁, a₂, b₂, c₂ ऐसी वास्तविक संख्याएँ हैं कि
a₁² + b₁² ≠ 0, a₂² + b₂² ≠ 0.

दो चरों वाले रैखिक समीकरण युग्म का हल : दो चरों वाले रैखिक समीकरण को हल करने की दो विधियाँ हैं-
(i) लेखाचित्र विधि (Graphical Method),
(ii) बीजगणितीय विधि (Algebraic Method)

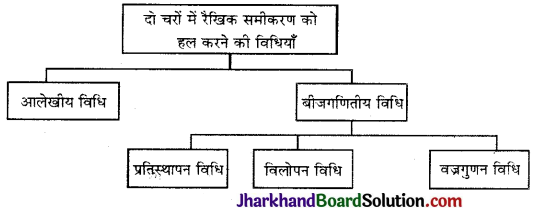
लेखाचित्र विधि (Graphical Method)
दो चरों वाले रैखिक समीकरण युग्म का ग्राफीय हल :
(i) सबसे पहले समीकरण युग्म का एक समीकरण लिखिए।
(ii) अब x का कोई पूर्णांक मान लेकर समीकरण में x के स्थान पर प्रतिस्थापित कर, चर y का मान निकाल लेते हैं।
(iii) यदि x का मान a तथा y का मान b प्राप्त होता है, तो एक बिन्दु (a, b) को ग्राफ पर अंकित करते हैं।
(iv) पुन: इसी प्रकार x का अन्य कोई दूसरा पूर्णांक समीकरण में प्रतिस्थापित कर y का मान निकाल लेते हैं।
(v) यदि अब x का मान c तथा y का मान d प्राप्त होता है तब बिन्दु (c, d) को ग्राफ पर अंकित करते हैं।
(vi) अब इन दोनों अंकित बिन्दुओं से ग्राफ पेपर पर आलेख खींचते हैं।
(vii) इस प्रकार पहले समीकरण का आलेख एक सरल रेखा प्राप्त होती है।
(viii) अब समीकरण युग्म का दूसरा समीकरण लेकर, ऊपर बताए गये बिन्दुओं के अनुसार दूसरे समीकरण का भी आलेख खींचते हैं।
(ix) दूसरे समीकरण का आलेख भी एक सरल रेखा प्राप्त होती है।
(x) ये दोनों सरल रेखाएँ परस्पर काटेंगी (Intersecting lines) या फिर समान्तर (Parallel lines) होंगी अथवा सम्पाती (Conincident lines) होंगी।

सम्पाती हो तो समीकरण युग्म के अनन्त (अपरिमित) सार्व हल प्राप्त होंगे-
इस प्रकार आलेखीय निरूपण निम्न प्रकार प्राप्त होता है-

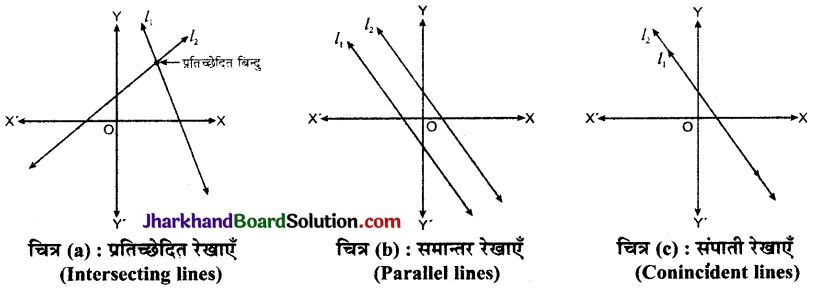
रेखीय समीकरणों के संगत व असंगत युग्म :
संगत युग्म (Consistent pair) : यदि समीकरणों के निकाय a₁x + b₁y + c₁ = 0; a₂x + b₂y + c₂ = 0 के हल विद्यमान हैं, तो दिया गया समीकरण निकाय संगत निकाय कहलाता है।
संगत निकाय के निम्न दो प्रकार हैं :
(i) दो प्रतिच्छेदी रेखाएँ निरूपित करेगा अर्थात् अद्वितीय हल (Unique solution) होते हैं।
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
(ii) दो सम्पाती रेखाएँ निरूपित करेगा अर्थात् अनन्त हल (Infinitely many solutions) होते हैं।
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
असंगत युग्म (Inconsistent pair) : जब समीकरण निकाय a₁x + b₁y + c₁ = 0; a₂x + b₂y + c₂ = 0 का कोई भी हल विद्यमान नहीं होता तब वह निकाय असंगत निकाय कहलाता है।
(iii) दो समान्तर रेखाएँ निरूपित करेगा अर्थात् कोई हल नहीं (No solution) होते हैं।
\(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

रैखिक समीकरण युग्म का ग्राफीय विधि से हल में रेखाओं का व्यवहार :
दो चरों वाले दो समीकरणों के निकाय को निरूपित करने वाली रेखाओं के व्यवहार और हलों के होने या न होने का सार संक्षेप में निम्न प्रकार है-
(i) रेखाएँ केवल एक बिन्दु पर प्रतिच्छेद करें, तो समीकरणों का एक अद्वितीय हल होगा। – संगत समीकरण युग्म ।
(ii) रेखाएँ समान्तर भी हो सकती हैं तो इस स्थिति में समीकरणों का कोई हल नहीं होगा। – असंगत समीकरण युग्म।
(iii) रेखाएँ सम्पाती हो सकती हैं, समीकरणों के अपरिमित रूप से अनेक हल होंगे।
आश्रित (संगत) समीकरण युग्म रेखाओं के सामान्य समीकरणों को इस प्रकार निरूपित कर सकते हैं :
a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0
जहाँ a₁, a₂, b₁, b₂, c₁, c₂ वास्तविक संख्याएँ हैं (a₁ ≠ 0, b₁ ≠ 0, a₂ ≠ 0, b₂ ≠ 0)
(i) प्रतिच्छेद करें तो \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\); समीकरण: युग्म संगत होगा और उसका एक और केवल एक ही (अद्वितीय) हल होगा।
(ii) सम्पाती हों तो \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\); समीकरण युग्म संगत होगा और उसके अपरिमित रूप से अनेक हल होंगे।
(iii) समान्तर हों तो \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\); समीकरण युग्म असंगत होगा और उसका कोई हल नहीं होगा।
किसी भी रेखाओं के युग्म के लिए विलोम भी सत्य है।

एक रैखिक समीकरण युग्म को हल करने की बीजगणितीय विधि (Algebraic Method to Solve a Pair of Linear Equations in Two Variables) :
रैखिक समीकरण युग्म को हल करने की तीन बीजीय विधियाँ हैं-
(1) प्रतिस्थापन विधि (Method of Substitution)
(2) विलोपन विधि (Method of Elimination)
(3) वज्रंगुणन विधि (Method of Cross multiplication)

प्रतिस्थापन विधि क्रियाविधि (Working Rule) :
चरण 1. किसी एक समीकरण से एक चर x को दूसरे चर के पदों के रूप में लिख लेते हैं।
चरण 2. y के पदों में प्राप्त x के इस मान को युग्म के शेष दूसरे समीकरण में x के स्थान पर प्रतिस्थापित करके y का मान निकाल सकते हैं।
चरण 3. y के इस मान को किसी एक समीकरण में प्रतिस्थापित कर x का मान निकाल सकते हैं।

निराकरण या विलोपन विधि (Elimination Method) :
इस विधि में एक चर का विलोपन करते हैं या उसे हटा देते हैं। यह विधि कभी-कभी प्रतिस्थापन विधि से अधिक सुविधाजनक रहती है।
गुणांकों को बराबर करके हल सर्वप्रथम हम दोनों युगपत् समीकरणों को ऐसे शून्येतर गुणांकों अर्थात् शून्य को छोड़कर अन्य गुणांकों से गुणा करके दोनों समीकरणों में एक अज्ञात राशि या y के गुणांक बराबर कर लेते हैं। अब दोनों समीकरणों को आवश्यकतानुसार जोड़कर या घटाकर समान गुणांकों वाली राशि को विलुप्त करते हैं। अब हमें एक अज्ञात राशि वाला समीकरण प्राप्त होता है जिसे हल करके अज्ञात राशि का मान ज्ञात करते हैं इस मान को किसी भी एक समीकरण में प्रतिस्थापित कर दूसरी अज्ञात राशि का मान ज्ञात कर लेते हैं।

वज्रगुणन विधि (Method of Cross Multiplication) :
इस विधि में दोनों समीकरणों को इस प्रकार लिख लेते हैं कि उनके दायें पक्ष में शून्य हो ।
माना समीकरण a₁x + b₁y + c₁ = 0.
तथा a₂x + b₂y + c₂ = 0 हैं।
अब निम्न प्रकार लिखकर x और y के मान ज्ञात कर लेते हैं-
\(\frac{x}{b_1 c_2-b_2 c_1}=\frac{y}{c_1 a_2-c_2 a_1}=\frac{1}{a_1 b_2-a_2 b_1}\)
उपर्युक्त हल को स्मरणीय रूप में निम्न प्रकार लिखकर प्राप्त किया जा सकता है-

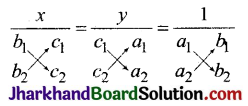
इस आरेख के अनुसार नीचे की ओर तीर वाली (↓) संख्याओं के गुणनफल में से ऊपर की ओर तीर वाली (↑) संख्याओं के गुणनफल को घटाकर लिखा जा सकता है।
अथवा
\(\frac{x}{b_1 c_2-b_2 c_1}=\frac{y}{c_1 a_2-c_2 a_1}=\frac{1}{a_1 b_2-a_2 b_1}\)

दो चरों के रैखिक समीकरणों के युग्म में बदले जा सकने वाले समीकरण :
यदि समीकरण ax + by + c = 0 के रूप में नहीं है अर्थात् \(\frac{a}{x}+\frac{b}{y}+c\) = 0 के रूप में है, तो इसे रैखिक समीकरण के रूप में निम्न प्रकार बदला जा सकता है :
माना \(\frac{1}{x}\) = P और \(\frac{1}{y}\) = q प्रतिस्थापित करने पर,
ap + bq + c = 0 प्रकार का रैखिक समीकरण बना कर हल करते हैं।