JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.3

जब तक अन्यथा न कहा जाए, π = \(\frac {22}{7}\) लीजिए ।

प्रश्न 1.
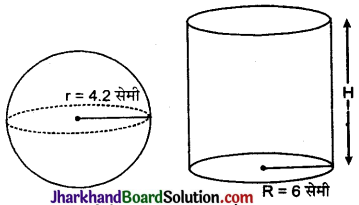
त्रिज्या 4.2 सेमी वाले धातु के एक गोले को पिघलाकर त्रिज्या 6 सेमी वाले एक बेलन के रूप में ढाला जाता है। बेलन की ऊँचाई ज्ञात कीजिए।
हल :
दिया है,
गोले की त्रिज्या (r) = 4.2 सेमी
बेलन की त्रिज्या (R) = 6 सेमी
माना कि बेलन की ऊँचाई = H सेमी

ढालने पर गोले का आयतन और0 बेलन का आयतन बराबर होगा।
गोले का आयतन = बेलन का आयतन

अत: बेलन की ऊँचाई = 2.74 सेमी

प्रश्न 2.
क्रमशः 6 सेमी, 8 सेमी और 10 सेमी त्रिज्याओं वाले धातु के तीन ठोस गोलों को पिघलाकर एक बड़ा ठोस गोला बनाया जाता है। इस गोले की त्रिज्या ज्ञात कीजिए।
हल :
दिया है,
पहले गोले की त्रिज्या (r₁) = 6 सेमी
दूसरे गोले की त्रिज्या (r₂) = 8 सेमी
तीसरे गोले की त्रिज्या (r₃) = 10 सेमी
माना कि नए बने गोले की त्रिज्या R सेमी है।
∵ तीनों गोलों को पिघलाकर एक बड़ा गोला बनाया जाता है।
∴ बड़े गोले का आयतन = तीनों गोलों के आयतनों का योग

अतः बड़े गोले की त्रिज्या = 12 सेमी

प्रश्न 3.
7 मीटर व्यास वाला तथा 20 मीटर गहरा एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैलाकर 22 मीटर x 14 मीटर वाला एक चबूतरा बनाया गया है। इस चबूतरे की ऊँचाई ज्ञात कीजिए।
हल :
दिया है, कुएँ का व्यास = 7 मीटर
कुएँ की त्रिज्या (r) = \(\frac {7}{2}\) मीटर
और कुएँ की गहराई (h) = 20 मीटर
कुएँ से निकाली मिट्टी का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 20
= 770 घन मीटर
चबूतरे की लम्बाई (L) = 22मी
तथा चौड़ाई (B) = 14 मी
माना चबूतरे की ऊँचाई H मीटर है।
चबूतरे का आयतन = L × B × H घन मीटर
= 22 × 14 × H घन मीटर
प्रश्नानुसार,
चबूतरे का आयतन = कुएँ से निकाली गई मिट्टी का आयतन
22 × 14 × H = 770
∴ H = \(\frac{770}{22 \times 14}\) = 2.5 मीटर
अतः चबूतरे की ऊँचाई = 2.5 मीटर

प्रश्न 4.
3 मीटर व्यास का एक कुआँ 14 मीटर की गहराई तक खोदा जाता है। इससे निकली हुई मिट्टी को कुएँ के चारों ओर 4 मीटर चौड़ी एक वृत्ताकार वलय (ring) बनाते हुए, समान रूप से फैलाकर एक प्रकार का बाँध बनाया जाता है। इस बाँध की ऊँचाई ज्ञात कीजिए।
हल :
दिया है,
∵ कुएँ का व्यास = 3 मीटर
तथा गहराई (h) = 14 मीटर
∴ कुएँ से निकली मिट्टी का आयतन = πr²h
कुएँ की त्रिज्या (r) = \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2}\) × 14
= \(\frac{22 \times 3 \times 3}{2}\) = 99 घन मीटर
∵ कुएँ की त्रिज्या = \(\frac {3}{2}\) मीटर है और कुएँ के चारों ओर 4 मीटर चौड़ा वृत्ताकार वलय बनाया गया है।
∴ कुएँ की बाहरी त्रिज्या (r₁) = \(\frac {3}{2}\) + 4 = \(\frac {11}{2}\) मीटर
तथा भीतरी त्रिज्या (r₂) = \(\frac {3}{2}\) मीटर
∴ वृत्ताकार वलय का क्षेत्रफल = πr₁² – πr₂²

माना बाँध की ऊँचाई h मीटर है।
तब बाँध की मिट्टी का आयतन = 88 × h घन मीटर
अब बाँध की मिट्टी का आयतन = कुएँ से निकाली गई मिट्टी का आयतन
88 × h = 99
∴ h = \(\frac{99}{88}=\frac{9}{8}\)
= 1.125 मीटर
अतः बाँध की ऊँचाई = 1.125 मीटर

प्रश्न 5.
व्यास 12 सेमी और ऊँचाई 15 सेमी वाले एक लम्बवृत्तीय बेलन के आकार का बर्तन आइसक्रीम से पूरा भरा हुआ है। इस आइसक्रीम को ऊँचाई 12 सेमी और व्यास 6 सेमी वाले शंकुओं में भरा जाना है, जिनका ऊपरी सिरा अर्द्धगोलाकार होगा। उन शंकुओं की संख्या ज्ञात कीजिए जो इस आइसक्रीम से भरे जा सकते हैं।
हल :
दिया है,
बेलनाकार बर्तन का व्यास = 12 सेमी
∴ बेलनाकार बर्तन की त्रिज्या (r₁) = 6 सेमी
तथा बेलनाकार बर्तन की ऊँचाई (h₁) = 15 सेमी
∴ बेलनाकार बर्तन का आयतन = πr₁²h₁
= π × (6)² × 15
= 540π घन सेमी
∴ आइसक्रीम का कुल आयतन = 540π घन सेमी
शंकु की त्रिज्या (r₂) = \(\frac {6}{2}\) = 3 सेमी
तथा ऊँचाई (h₂) = 12 सेमी
∴ शंकु का आयतन = \(\frac {1}{3}\)πr₂²h₂ = \(\frac {1}{3}\)π × (3)² × 12
= 36π घन सेमी
शंकु के मुँह पर अर्द्धगोलाकार आइसक्रीम का आयतन
= \(\frac {2}{3}\)πr₂³
= \(\frac {2}{3}\)π × (3)³ = 18π घन सेमी
∴ आइसक्रीम से भरे शंकु का आयतन = 36π + 18π = 54π घन सेमी
∴ शंकुओं की संख्या
= आइसक्रीम का कुल आयतन / 1 शंकु में भरी आइसक्रीम का आयतन
= \(\frac {540π}{54π}\) = 10
अतः आइसक्रीम द्वारा भरे जाने वाले शंकुओं की संख्या = 10

प्रश्न 6.
विमाओं 5.5 सेमी × 10 सेमी × 3.5 सेमी वाला एक घनाभ बनाने के लिए 1.75 सेमी व्यास और 2 मिमी मोटाई वाले कितने चाँदी के सिक्कों को पिघलाना पड़ेगा ?
हल :
माना चाँदी के n सिक्के पिघलाने पड़ेंगे।
प्रत्येक सिक्के की त्रिज्या r = \(\frac {1.75}{2}\)सेमी
= \(\frac {175}{200}\)
= \(\frac {7}{8}\) सेमी
और प्रत्येक सिक्के की ऊँचाई h = 2 मिमी
= \(\frac {2}{10}\) सेमी = \(\frac {1}{5}\)
∴ प्रत्येक सिक्के का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{8} \times \frac{7}{8} \times \frac{1}{5}\)
= \(\frac {77}{160}\) घन सेमी
∴ n सिक्कों का आयतन = \(\frac {77}{160}\)n घन सेमी
घनाभ का आयतन = 5.5 × 10 × 3.5
= 192.5 घन सेमी
∵ चाँदी के n सिक्कों को घनाभ बनाया गया
∴ n सिक्कों का आयतन = घनाभ का आयतन
⇒ \(\frac {77}{160}\)n = 192.5
⇒ n = \(\frac{192.5 \times 160}{77}\) = 400
अत: चाँदी के सिक्कों की संख्या = 400

प्रश्न 7.
32 सेमी ऊँची और आधार त्रिज्या 18 सेमी वाली एक बेलनाकार बाल्टी रेत से भरी हुई है। इस बाल्टी को भूमि पर खाली किया जाता है और इस रेत की एक शंक्वाकार ढेरी बनाई जाती है। यदि शंक्वाकार ढेरी की ऊँचाई 24 सेमी है, तो इस ढेरी की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए।
हल :
बेलनाकार बाल्टी की त्रिज्या (R) = 18 सेमी
बेलनाकार बाल्टी की ऊँचाई (H) = 32 सेमी
शंकु की ऊँचाई (h) = 24 सेमी

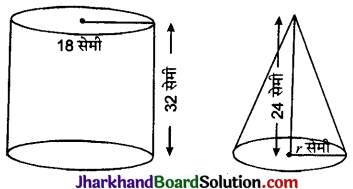
माना कि शंकु की त्रिज्या r सेमी तथा तिर्यक ऊँचाई l सेमी है।
बाल्टी में रेत का आयतन = शंक्वाकार ढेरी का आयतन

अतः ढेरी की तिर्यक ऊँचाई (l) = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(36)^2+(24)^2}\)
= \(\sqrt{1296+576}\)
= \(\sqrt{1872}\)
= \(\sqrt{9 \times 4 \times 4 \times 13}\)
= 3 × 2 × 2 × \(\sqrt{13}\)
= 12\(\sqrt{13}\)
या l = 143.27 सेमी
अतः ढेरी की त्रिज्या = 36 सेमी
तथा तिर्यक ऊँचाई = 12\(\sqrt{13}\) अथवा 43.27 सेमी।

प्रश्न 8.
6 मीटर चौड़ी और 1.5 मीटर गहरी एक नहर में पानी 10 किमी / घण्टा की चाल से बह रहा है। 30 मिनट में, यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी, जबकि सिंचाई के लिए 8 सेमी गहरे पानी की आवश्यकता होती है?
हल :
दिया है,
नहर की चौड़ाई = 6 मीटर
नहर में पानी की गहराई = 1.5 मीटर
नहर में पानी की चाल = 10 किमी/ घण्टा
= \(\frac{10 \times 1000}{60}\) मीटर / मिनट
= \(\frac {500}{3}\)मीटर/मिनट
1 मिनट में नहर में बहे पानी की लम्बाई = \(\frac {500}{3}\)मी.
नहर घनाभ के आयतन के बराबर पानी प्रति मिनट में स्थानान्तरित करेगी।
∵ 1 मिनट में स्थानान्तरित पानी का आयतन
= 6 × 1.5 × \(\frac {500}{3}\)मी³
∴ 30 मिनट में स्थानान्तरित पानी का आयतन
= 30 × 6 × 1.5 × \(\frac {500}{3}\)
= 45000 घन मीटर
सिंचाई के लिए 8 सेमी या \(\frac {8}{100}\) मीटर गहरे पानी की आवश्यकता है।
∴ 30 मिनट में स्थानान्तरित पानी का आयतन = खेत में पानी का आयतन
45000 घन मीटर = खेत का क्षेत्रफल × पानी का ऊँचाई
या 45000 = खेत का क्षेत्रफल × \(\frac {8}{100}\)
∴ खेत का क्षेत्रफल = \(\frac{45000 \times 100}{8}\)
= 562500 मीटर²
= \(\frac {562500}{10000}\)हेक्टेअर
= 56.25 हेक्टेअर
अत: नहर द्वारा 30 मिनट में सिंचित क्षेत्र का क्षेत्रफल = 56.25 हेक्टेअर ।

प्रश्न 9.
एक किसान अपने खेत में बनी 10 मीटर व्यास वाली और 2 मीटर गहरी एक बेलनाकार टंकी को, आन्तरिक व्यास 20 सेमी वाले एक पाइप द्वारा नहर से जोड़ता है। यदि पाइप में पानी 3 किमी प्रति घण्टा की चाल से बह रहा है तो कितने समय बाद टंकी पूरी भर जाएगी ?
हल :
दिया है,
टंकी का व्यास = 10 मीटर
∴ त्रिज्या r = 5 मीटर
और टंकी की गहराई h = 2 मीटर
∴ बेलनाकार टंकी का आयतन = πr²h
= π × (5)² × 2
= 50π घन मीटर
पाइप का व्यास = 20 सेमी
त्रिज्या = \(\frac {20}{2}\) = 10 सेमी
= \(\frac{10}{100}=\frac{1}{10}\) मीटर
पाइप में पानी की चाल 3 किमी / घण्टा
= \(\frac{3 \times 1000}{60}\) मीटर/मिनट
= 50 मीटर / मिनट
1 मिनट में बहे पानी की लम्बाई = 50 मी
पाइप, बेलन के आयतन के बराबर पानी प्रति मिनट में स्थानान्तरित करेगा।
यदि टंकी को भरने में n मिनट का समय लगता है, तो n मिनट में स्थानान्तरित पानी का आयतन = बेलनाकार टंकी का आयतन
⇒ n × π × (\(\frac {1}{10}\))² × 50 = 50π
⇒ n = \(\frac{50 \pi \times 100}{50 \pi \times 1}\)
⇒ n = 100 मिनट
अतः टंकी 100 मिनट में पूरी भर जाएगी।