JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.4

जब तक अन्यथा न कहा जाए π = \(\frac {22}{7}\) लीजिए ।

प्रश्न 1.
पानी पीने वाला एक गिलास लीजिए । वाले एक शंकु के छिन्नक के आकार का है। दोनों वृत्ताकार सिरों के व्यास 4 सेमी और 2 सेमी हैं। इस गिलास की धारिता ज्ञात कीजिए ।
हल :
दिया है,
गिलास के ऊपरी सिरे का व्यास = 4 सेमी

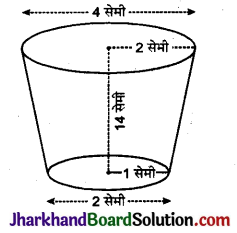
∴ ऊपरी सिरे की त्रिज्या (r₁) = \(\frac {4}{2}\) = 2 सेमी
गिलास के निचले सिरे की त्रिज्या (r₂) = \(\frac {2}{2}\) = 1 सेमी
सेमी गिलास की ऊँचाई (h) = 14 सेमी
शंकु के छिन्नक के आकार के गिलास का आयतन

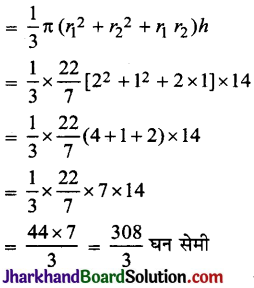
अतः गिलास की धारिता = 102\(\frac {2}{3}\) घन सेमी

प्रश्न 2.
एक शंकु के छिन्नक की तिर्यक ऊंचाई 4 सेमी है तथा इसके वृत्तीय सिरों के परिमाप (परिधियाँ) 18 सेमी और 6 सेमी हैं। इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
शंकु के छिन्नक की तिर्यक ऊँचाई l = 4 सेमी माना ऊपरी सिरे की त्रिज्या r₁ और निचले सिरे की त्रिज्या r₂ है।

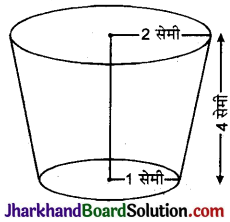
∴ ऊपरी सिरे की परिधि = 18 सेमी
⇒ 2πr₁ = – 18
⇒ r₁ = \(\frac {18}{2π}\) = \(\frac {9}{π}\)सेमी
निचले सिरे की परिधि = 6 सेमी
⇒ 2πr₂ = 6
⇒ r₂ = \(\frac{6}{2 \pi}=\frac{3}{\pi}\)सेमी
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π(r₁ + r₂)l
= π[\(\frac {9}{π}\) + \(\frac {3}{π}\)] × 4
= 12 × 4
= 48 वर्ग सेमी
अतः छिन्नक का वक्र पृष्ठीय क्षेत्रफल = 48 वर्ग सेमी

प्रश्न 3.
एक तुर्की टोपी शंकु के एक छिन्नक के आकार की है( देखिए आकृति) । यदि इसके खुले सिरे की त्रिज्या 10 सेमी है, ऊपरी सिरे की त्रिज्या 4 सेमी है और टोपी की तिर्यक ऊँचाई 15 सेमी है, तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए ।

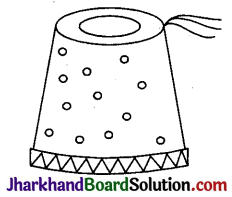
हल :
दिया है,
छिन्नक के निचले सिरे की त्रिज्या (r₁) = 10 सेमी
छिन्नक के ऊपरी सिरे की त्रिज्या (r₂) = 4 सेमी

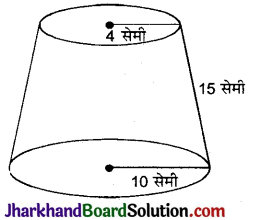
छिन्नक की तिर्यक ऊँचाई (l) = 15 सेमी
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πl(r₁ + r₂)
= \(\frac {22}{7}\) × 15 (10 + 4)
= \(\frac {22}{7}\) × 15 × 14
= 22 × 30 = 660 वर्ग सेमी
बन्द (ऊपरी) सिरे का क्षेत्रफल = πr₂² = \(\frac {22}{7}\) × 4 × 4
= \(\frac {352}{7}\) = 50.28 वर्ग सेमी
प्रयुक्त पदार्थ का कुल क्षेत्रफल = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + बन्द सिरे का क्षेत्रफल
= 660 + 50.28 = 710.28 वर्ग सेमी
अंतः प्रयुक्त पदार्थ का कुल क्षेत्रफल
= 710.28 वर्ग सेमी

प्रश्न 4.
धातु की चादर से बना और ऊपर से खुला एक बर्तन शंकु के एक छिन्नक के आकार का है, जिसकी ऊँचाई 16 सेमी है तथा निचले और ऊपरी सिरों की त्रिज्याएँ क्रमशः 8 सेमी और 20 सेमी हैं। ₹20 प्रति लीटर की दर से, इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। साथ ही, इस बर्तन को बनाने के लिए प्रयुक्त धातु की चादर का मूल्य ₹8 प्रति 100 सेमी की दर से ज्ञात कीजिए। (π = 3.14)
हल :
दिया है,
बर्तन के ऊपरी सिरे की त्रिज्या (r₁) = 20 सेमी
बर्तन के निचले सिरे की त्रिज्या (r₂) = 8 सेमी

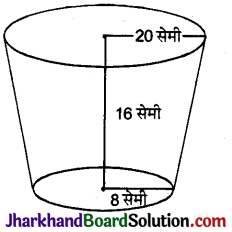
बर्तन की ऊँचाई (h) = 16 सेमी

बर्तन की धारिता = 10449.92 घन सेमी
अतः बर्तन में दूध का आयतन = बर्तन की धारिता
= 10449.52 घन सेमी
= \(\frac {10449.52}{1000}\)
= 10.45 लीटर
∵ 1 लीटर दूध का मूल्य = ₹ 20
∴ 10.45 लीटर दूध का मूल्य = ₹ 10.45 × 20
= ₹ 209
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π(r₁ + r₂)l
= 3.14 (20 + 8) × 20
= 3.14 × 28 × 20
= 1758.4 वर्ग सेमी
बर्तन के निचले आधार का क्षेत्रफल = πr₂² = 3.14 × (8)²
= 3.14 × 64
= 200.96 वर्ग सेमी
बर्तन बनाने के लिए प्रयुक्त धातु
= छिन्नक का वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल
= (1758.4 + 200.96) सेमी²
= 1959.36 सेमी²
∴ 100 सेमी² धातु की चादर का मूल्य = ₹ 8
∴ 1 सेमी² धातु की चादर का मूल्य = ₹ \(\frac {8}{100}\)
∴ 1959.36 सेमी² धातु की चादर का मूल्य
= ₹ \(\frac {8}{100}\) × 1959.36
= ₹ 156.748 = ₹ 156.75
अतः दूध का मूल्य = ₹ 209
और चादर का मूल्य = ₹ 156.75

प्रश्न 5.
20 सेमी ऊँचाई और शीर्ष कोण (vertical angle) 60° वाले एक शंकु को उसकी ऊंचाई के बीचों-बीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समान्तर है।
यदि इस प्राप्त शंकु के छिन्नक को व्यास \(\frac {1}{16}\) सेमी वाले एक तार के रूप में बदल दिया जाता है, तो तार की लम्बाई ज्ञात कीजिए ।
हल :
चित्र में किसी शंकु के आधार का व्यास A’OA है तथा शीर्ष V है। शंकु का शीर्ष कोण A’VA = 60° है, तब शंकु का अर्द्धशीर्ष कोण α = 30°
शंकु की ऊँचाई = 20 सेमी है


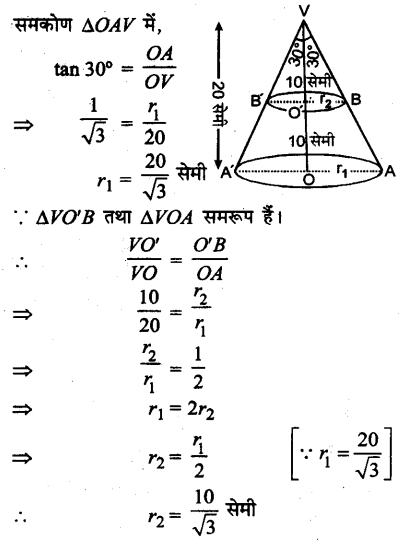
∵ बेलनाकार तार का व्यास = \(\frac {1}{16}\) सेमी
∵ बेलनाकार तार की त्रिज्या (r) = \(\frac {1}{32}\) सेमी
माना खींचे जाने वाले तार की लम्बाई l सेमी है।
तार का आयतन = πr²l
= π × \(\frac {1}{32}\) × \(\frac {1}{32}\) × l = \(\frac {πl}{1024}\) घन सेमी
∵ तार शंकु के छिन्नक से खींचा जाता है।
∴ तार का आयतन = छिन्नक का आयतन
\(\frac {πl}{1024}\) = \(\frac {7000}{9}\)π
l = \(\frac {7000π}{9}\) × \(\frac {1024}{π}\)सेमी
= \(\frac {70}{9}\) × 1024 मीटर
= \(\frac {71680}{9}\) मीटर
= 7964.44 मीटर
अतः तार की लम्बाई = 7964.44 मीटर