JAC Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.3

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 बहुपद Exercise 2.3

प्रश्न 1.
विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए :
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
हल:
(i) p(x) = x³ – 3x² + 5x – 3 तथा
g(x) = x² – 2
माना भागफल q(x) और शेषफल r(x) है।
यूक्लिड की विभाजन एल्गोरिथ्यम से,
p(x) = g(x).q(x) + r(x)

अर्थात

अत: भागफल q(x) = x – 3
शेषफल r(x) = 7x – 9
(ii) p(x) = x⁴ – 3x² + 4x + 5
g(x) = x² + 1 – x ⇒ x² – x + 1
माना भागफल q(x) तथा शेषफल r(x) है।
यूक्लिड विभाजन एल्गोरिथ्म से,

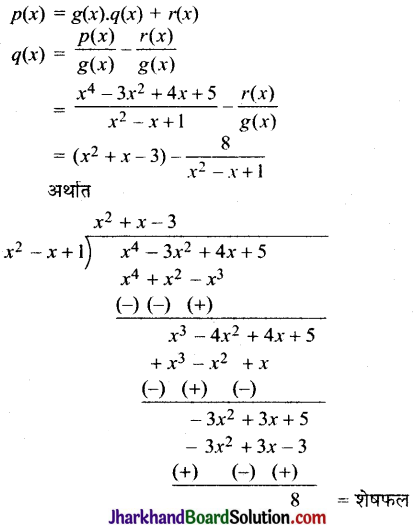
अत: भागफल q(x) = x² + x – 3
तथा शेषफल r(x) = 8
(iii) p(x) = x⁴ – 5x + 6
g(x) = 2 – x²
माना भागफल q(x) तथा शेषफल r(x) है।
यूक्लिड की विभाजन एल्गोरिथ्म से,
p(x) = g(x).q(x) + r(x)

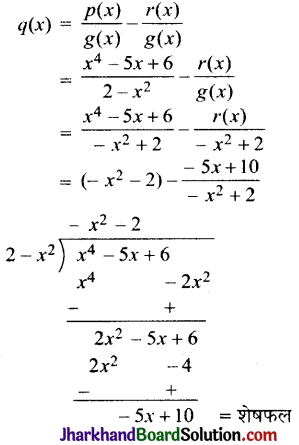
अत: भागफल q(x) = – x² – 2
तथा शेषफल r(x) = -5x + 10

प्रश्न 2.
प्रथम बहुपद से द्वितीय बहुपद को भाग करके, जाँच कीजिए कि क्या प्रथम बहुपद, द्वितीय बहुपद का एक गुणनखण्ड है:
(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
हल:
(i)

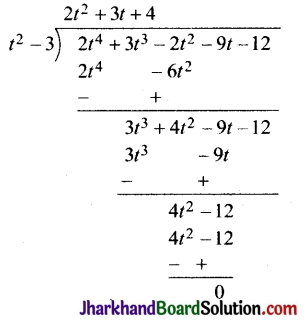
∵ शेषफल शून्य है।
∴ विभाजन एल्गोरिथ्म से,
2t⁴ + 3t³ – 2t² – 9t – 12 = (t² – 3) (2t² + 3t + 4) + 0
अतः t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12 का एक गुणनखण्ड है।

∵ शेषफल शून्य है।
∴ विभाजन एल्गोरिथ्म प्रमेय से,
3x⁴ + 5x³ – 7x² + 2x + 2 = (x² + 3x + 1) (3x² – 4x + 2) + 0
अत: x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2 का एक गुणनखण्ड है।

(iii) माना g(x) = x³ – 3x + 1
p(x) = x⁵ – 4x³ + x² + 3x + 1

∴ शेषफल r(x) = 2
भागफल q(x) = x² – 1
∵ शेषफल शून्य नहीं है।
अत: g(x), p(x) का गुणनखण्ड नहीं है।

प्रश्न 3.
3x⁴ + 6x³ – 2x² – 10x – 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक \(\sqrt{\frac{5}{3}}\) और –\(\sqrt{\frac{5}{3}}\) है।
हल:
∵ \(\sqrt{\frac{5}{3}}\) और –\(\sqrt{\frac{5}{3}}\) दिए गए बहुपद के शून्यक है।
∴ \(\left(x-\sqrt{\frac{5}{3}}\right)\left(x+\sqrt{\frac{5}{3}}\right)=\left(x^2-\frac{5}{3}\right)\)
दिए गए बहुपद का एक गुणनखण्ड होगा।
∴ बहुपद 3x⁴ + 6x³ – 2x² – 10x – 5 को x² – \(\frac{5}{3}\) से भाग देने पर,

∴ बहुपद के दिये गये शून्यक के अलावा अन्य शून्यक निम्न होंगे :
x + 1 = 0 या x + 1 = 0
⇒ x = -1 या x = -1
अतः दिए गए बहुपद के अन्य शून्यक -1 और -1 हैं।

प्रश्न 4.
यदि x³ – 3x² + x + 2 को एक बहुपद g(x) से भाग देने पर भागफल और शेषफल क्रमश: x – 2 और -2x + 4 हैं, तो g(x) ज्ञात कीजिए।
हल:
भाज्य p(x) = x³ – 3x² + x + 2
भाजक g(x) = ज्ञात करना है
भागफल q(x) = x – 2
शेषफल r(x) = -2x + 4
∴ यूक्लिड विभाजन प्रमेयिका से,
p(x) = g(x).q(x) + r(x)
g(x) = \(\frac{p(x)-r(x)}{q(x)}\)
p(x), q(x) और r(x) के मान रखने पर,

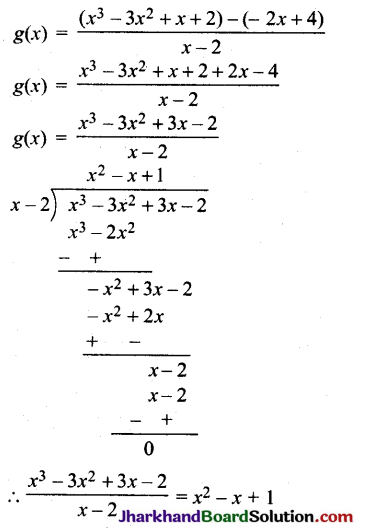
अत: g(x) = x² – x + 1

प्रश्न 5.
बहुपदों p(x), g(x), q(x) और (x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को सन्तुष्ट करते हों तथा
(i) घात p(x) = घात q(x)
(ii) घात q(x) = घात (x)
(iii) घात r(x) = 0.
हल:
(i) हमें p(x) व q(x) ऐसा चाहिए कि
p(x) की घात = q(x) की घात
तब p(x) की घात = g(x) की घात · q(x) की घात
⇒ g(x) की घात शून्य होनी चाहिए।
माना कि p(x) = 4x² + 8x + 12 तथा g(x) = 4
p(x) को g(x) से विभाजित करने पर

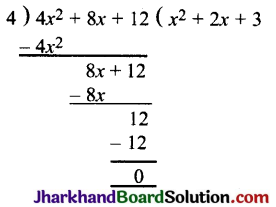
अतः q(x) = x² + 2x + 3 तथा r(x) = 0
विभाजन एल्गोरिथ्म से
4x² + 8x + 12 = 4(x² + 2x + 3) + 0
अथवा p(x) = g(x) · q(x) + r(x)
∴ p(x) की घात = q(x) की घात = 2
अतः p(x) = 4x² + 8x + 12
q(x) = x² + 2x + 3
g(x) = 4
r(x) = 0

(ii) q(x) की घात = r(x) की घात
p(x) = g(x).q(x) + r(x)
माना कि p(x) = x³ – x² + 4x + 1
तथा g(x) = x² + 1
p(x) को g(x) से विभाजित करने पर

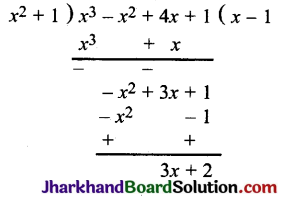
∴ q(x) = x – 1 तथा r(x) = 3x + 2
विभाजन एल्गोरिथ्म से
x³ – x² + 4x + 1 = (x² + 1) (x – 1) + 3x + 2
अथवा p(x) = g(x) · q(x) + r(x)
∴ q(x) की घात = r(x) की घात = 1
अतः p(x) = x³ – x² + 4x + 1
g(x) = x² + 1, q(x) = x – 1 तथा
r(x) = 3x + 2

(iii) घात (x) = 0
माना कि p(x) = x³ + x² – x + 2
तथा g(x) = x² – 1
p(x) को g(x) से विभाजित करने पर

अतः q(x) = x + 1 तथा r(x) = 3
विभाजन एल्गोरिथ्म से
x³ + x² – x + 2 = (x² – 1 ) (x + 1) + 3
अथवा p(x) = g(x) · q(x) + r(x)
r(x) की घात = 0
अतः p(x) = x³ + x² – x + 2
g(x) = x² – 1
q(x) = x + 1 तथा
अतः r(x) = 3.