Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.3 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Exercise 3.3
प्रश्न 1.
निम्न रैखिक समीकरण युग्म को प्रतिस्थापन विधि से हल कीजिए :
(i) x + y = 14
x – y = 4
(ii) s – t = 3
\(\frac{s}{3}+\frac{t}{2}=6\)
(iii) 3x – y = 3
9x – 3y = 9
(iv) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
(v) \(\sqrt{2}\)x + \(\sqrt{2}\)y = 0
\(\sqrt{2}\)x – \(\sqrt{8}\)y = 0
(vi) \(\frac{3 x}{2}-\frac{5 y}{3}=-2\)
\(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\)
हल:
(i) दिया गया रैखिक समीकरण युग्म
x + y = 14 …..(i)
x – y = 4 …..(ii)
समीकरण (i) से,
⇒ x = 14 – y
x का यह मान समीकरण (ii) में प्रतिस्थापित करने पर,
(14 – y) – y = 4
14 – y – y = 4.
-2y = 4 – 14
-2y = -10
∴ y = \(\frac{-10}{-2}\) = 5
y का मान समीकरण (i) में रखने पर,
x + 5 = 14
⇒ x = 14 – 5
∴ x = 9
अतः रैखिक समीकरण युग्म का हल x = 9 तथा y = 5
(ii) दिया गया रैखिक समीकरण युग्म
s – t = 3 …..(i)
\(\frac{s}{3}+\frac{t}{2}=6\)
समीकरण (i) से,
5 = 3 + t
s का यह मान समीकरण (ii) में प्रतिस्थापित करने पर
\(\frac{3+t}{3}+\frac{t}{2}=6\)
⇒ \(\frac{2(3+t)+3 t}{6}=6\)
⇒ \(\frac{6+2 t+3 t}{6}=6\)
⇒ 5t + 6 = 36
⇒ 5t = 36 – 6
⇒ 5t = 30
∴ t = \(\frac{30}{5}\) = 6
समीकरण (i) मैं का मान रखने पर,
s – 6 = 3
∴ s = 3 + 6 = 9
अंतः रैखिक समीकरण युग्म का हल s = 9 और t = 6
(iii) दिया गया रैखिक समीकरण युग्म
3x – y = 3 …..(i)
9x – 3y = 9 …..(ii)
समीकरण (i) से,
y = 3x – 3
y का यह मान समीकरण (ii) में प्रतिस्थापित करने पर,
9x – 3 (3x – 3) = 9
⇒ 9x – 9x + 9 = 9
⇒ 9 = 9
यह कथन x के सभी मानों के लिए सत्य है। फिर भी हम x का कोई विशेष मान हल के रूप में प्राप्त नहीं करते। इसलिए y का भी कोई मान प्राप्त नहीं कर सकते हैं।
इस प्रकार की स्थिति तभी पैदा होती है जब दोनों समीकरण एक जैसे हों।
अत: समीकरण (i) व (ii) के अपरिमित रूप से अनेक हल हैं।
(iv) दिया गया रैखिक समीकरण युग्म :
0.2x + 0.3y = 1.3 …..(i)
और 0.4x + 0.5y = 2.3 …..(ii)
समीकरण (i) से,
\(\frac{2}{10} x+\frac{3}{10} y=\frac{13}{10}\)
⇒ 2x + 3y = 13 …..(iii)
समीकरण (ii) से,
\(\frac{4}{10} x+\frac{5}{10} y=\frac{23}{10}\)
⇒ 4x + 5y = 23 ….(iv)
समीकरण (iii) से,
2x = 13 – 3y
x = \(\frac{13-3 y}{2}\)
x का यह मान समीकरण (iv) में प्रतिस्थापित करने पर,
\(\frac{13-3 y}{2}\) + 5y = 23
⇒ 2(13 – 3y) + 5y = 23
⇒ 26 – 6y + 5y = 23
⇒ – y =23 – 26 = -3
∴ y = 3
y का यह मान समीकरण (iii) में प्रतिस्थापित करने पर,
2x + 3 × 3 = 13
⇒ 2x + 9 = 13
⇒ 2x = 13 – 9
⇒ 2x = 4 ⇒ x = \(\frac{4}{2}\) = 2
अत: दिये गये रैखिक समीकरण युग्म का हल x = 2 और y = 3
(v) दिया गया रैखिक समीकरण युग्म
\(\sqrt{2}\)x + \(\sqrt{3}\)y =0 …..(i)
\(\sqrt{3}\)x – \(\sqrt{8}\)y = 0 ….. (ii)
समीकरण (i) से,
\(\sqrt{2}\)x = –\(\sqrt{3}\)y
⇒ x = \(\frac{-\sqrt{3}}{\sqrt{2}} y\) ….. (iii)
x का मान समीकरण (ii) में रखने पर,

y का मान समीकरण (iii) में रखने पर,
∵ x = \(-\frac{\sqrt{3}}{\sqrt{2}} y\)
∴ x = \(-\frac{\sqrt{3}}{\sqrt{2}} \times 0=0\)
⇒ x = 0
अत: दिये गये रैखिक समीकरण युग्म का हल
x = 0 तथा y = 0
(vi) दिया गया रैखिक समीकरण युग्म

x का यह मान समीकरण (ii) में प्रतिस्थापित करने पर,
\(2\left[\frac{10 y-12}{9}\right]\) + 3y = 13
\(\frac{20 y-24}{9}\) + 3y = 13
\(\frac{20 y-24+27 y}{9}\) = 13
⇒ 20y – 24 + 27y = 13 × 9
⇒ 47y = 117 + 24
⇒ 47y = 141
∴ y = \(\frac{141}{47}\) = 3
समीकरण (i) मैं y = 3 रखने पर,
9x – 10 × 3 = – 12
9x – 30 = – 12
9x = – 12 + 30 = 18
x = \(\frac{18}{9}\) = 2
अतः दिए गये रैखिक समीकरण युग्म का हल x = 2 और y = 3 हैं।
![]()
प्रश्न 2.
2x + 3y = 11 और 2x – 4y = -24 को हल कीजिए और इससे ‘m’ का वह मान ज्ञात कीजिए जिसके लिए y = mx + 3 हो।
हल:
दिया गया रैखिक समीकरण युग्म :
2x + 3y = 11 …..(i)
2x – 4y = -24 …..(ii)
समीकरण (i) से,
2x = 11 – 3y ⇒ x = \(\frac{11-3 y}{2}\) …..(iii)
x का यह मान समीकरण (ii) में प्रतिस्थापित करने पर,
\(2\left(\frac{11-3 y}{2}\right)\) – 4y = -24
⇒ 11 – 3y – 4y = -24
– 7y = – 24 – 11
– 7y = – 35
∴ y = \(\frac{-35}{-7}\) = 5
y का यह मान समीकरण (iii) में रखने पर,
x = \(\frac{11-3 \times 5}{2}\)
= \(\frac{11-15}{2}\)
= \(\frac{-4}{2}\) = -2
∴ x = -2
x और y के मान दिये गये समीकरण y = mx + 3 में रखने पर,
5 = m × -2 + 3
या 5 = -2m + 3
या 2m = 3 – 5
या 2m = – 2
या m = \(\frac{-2}{2}\)
∴ m = -1
अतः दिए गए रैखिक समीकरण का हल
x = -2, y = 5 और m = -1
![]()
प्रश्न 3.
निम्न समस्याओं में रैखिक समीकरण युग्म बनाइए और उनके हल प्रतिस्थापन विधि द्वारा ज्ञात कीजिए:
(i) दो संख्याओं का अन्तर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है। उन्हें ज्ञात कीजिए।
(ii) दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18° अधिक है। उन्हें ज्ञात कीजिए।
(iii) एक क्रिकेट टीम के कोच ने 7 बल्ले तथा 6 गेंदें ₹ 3,800 में खरीदीं। बाद में उसने 3 बल्ले तथा 5 गेंदें ₹ 1,750 में खरीदीं। प्रत्येक बल्ले और प्रत्येक गेंद का मूल्य ज्ञात कीजिए।
(iv) एक नगर में टैक्सी के भाड़े में एक नियत भाड़े के अतिरिक्त चली गई दूरी पर प्रति किमी के हिसाब से भाड़ा सम्मिलित किया जाता है। 10 किमी दूरी के लिए भाड़ा ₹ 105 है तथा 15 किमी के लिए भाड़ा ₹ 155 है। नियत भाड़ा तथा प्रति किमी भाड़ा क्या है? एक व्यक्ति को 25 किमी यात्रा करने के लिए कितना भाड़ा देना होगा ?
(v) यदि किसी भिन्न के अंश और हर दोनों में 2 जोड़ दिया जाए, तो वह \(\frac{9}{11}\) हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए, तो वह \(\frac{5}{6}\) हो जाती है। वह भिन्न ज्ञात कीजिए।
(vi) पाँच वर्ष बाद जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जाएगी। पाँच वर्ष पूर्व जैकब की आयु उसके पुत्र की आयु की सात गुनी थी उनकी वर्तमान आयु क्या है?
हल:
(i) माना एक संख्या x तथा दूसरी संख्या y है।
∵ एक संख्या दूसरी संख्या की 3 गुनी है।
⇒ x = 3y …..(i)
यहाँ x, y से बड़ा है।
दोनों संख्याओं का अन्तर 26 है।
∴ x – y = 26 …..(ii)
समीकरण (i) से x का मान समीकरण (ii) में प्रतिस्थापित करने पर,
3y – y = 26 ⇒ 2y = 26 ⇒ y = \(\frac{26}{2}\) ⇒ y = 13
समीकरणं (i) में y = 13 रखने पर,
x = 3 × 13 = 39
अत: अभीष्ट संख्याएँ x = 39 और y = 13
(ii) माना बड़ा कोण x° तथा छोटा कोण y° है।
कोण x° और y° एक-दूसरे के संपूरक हैं।
∴ x + y = 180° …..(i)
बड़ा कोण छोटे कोण से 18° अधिक है।
∴ x = y + 18° …..(ii)
समीकरण (ii) से x का मान समीकरण (i) में प्रतिस्थापित करने पर,
⇒ y + 18° + y = 180°
⇒ 2y +18° = 180°
⇒ 2y = 180° – 18° = 162°
∴ y = \(\frac{162}{2}\) = 81°
y का यह मान समीकरण (ii) में रखने पर,
x = 81° + 18° = 99°
अतः बड़ा कोण 99° और छोटा कोण 81° है।
(iii) माना एक बल्ले का मूल्य ₹ x तथा एक गेंद का मूल्य ₹ y है।
∴ 7 बल्लों का मूल्य = ₹ 7x
और 6 गेंदों का मूल्य = ₹ 6y
प्रश्नानुसार,
7x + 6y = 3800 …..(i)
पुनः 3 बल्लों का मूल्य = ₹ 3x
और 5 गेंदों का मूल्य = ₹ 5y
प्रश्नानुसार,
3x + 5y = 1750 …..(ii)
समीकरण (i) से,
7x = 3800 – 6y
⇒ x = \(\frac{3800-6 y}{7}\) …..(iii)
x का यह मान समीकरण (ii) में प्रतिस्थापित करने पर
\(3\left[\frac{3800-6 y}{7}\right]\) + 5y = 1750
⇒ \(\frac{11400-18 y+35 y}{7}\) = 1750
⇒ 11400 – 18y + 35y = 1750 × 7
⇒ 11400 + 17y = 12250
⇒ 17y = 12250 – 11400
⇒ 17y = 850
∴ y = \(\frac{850}{17}\) = 50
y का यह मान समीकरण (iii) में प्रतिस्थापित करने पर
x = \(\frac{3800-6 \times 50}{7}=\frac{3800-300}{7}\)
x = \(\frac{3500}{7}\)
∴ x = 500
अतः एक बल्ले का मूल्य = ₹ 500
और एक गेंद का मूल्य = ₹ 50
(iv) मान लीजिए टैक्सी का निश्चित किराया = ₹ x
और एक किमी यात्रा का किराया = ₹ y
पहली शर्त के अनुसार,
x + 10y = 105 …..(i)
दूसरी शर्त के अनुसार,
x + 15y = 155 …..(ii)
समीकरण (i) से,
x = 105 – 10y ….. (iii)
x का यह मान समीकरण (ii) में प्रतिस्थापित करने पर,
105 – 10y + 15y = 155
⇒ 5y = 155 – 105
⇒ 5y = 50
∴ y = \(\frac{50}{5}\) = 10
y का यह मान समीकरण (iii) में रखने पर,
x = 105 – 10 × 10
⇒ x = 105 – 100
∴ x = 5
अतः टैक्सी का निश्चित किराया = ₹ 5
और प्रति किमी यात्रा का किराया = ₹ 10
साथ ही 25 किमी यात्रा का किराया = x + 25y = 5 + 25 × 10
= 5 + 250
= 255 रुपये।
(v) माना भिन्न का अंश x तथा हर y है।
तब भिन्न = \(\frac{x}{y}\)
भिन्न के अंश व हर में 2 जोड़ने पर भिन्न \(\frac{x+2}{y+2}\) होगी।
प्रशनानुसार, \(\frac{x+2}{y+2}=\frac{9}{11}\)
⇒ 11(x + 2) = 9 (y + 2)
⇒ 11x + 22 = 9y + 18
⇒ 11x = 9y + 18 – 22
⇒ 11x = 9y – 4
⇒ x = \(\frac{(9 y-4)}{11}\) …..(i)
भिन्न के अंश व हर में 3 जोड़ने पर भिन्न \(\frac{x+3}{y+3}\) होगी।
प्रश्नानुसार, \(\frac{x+3}{y+3}=\frac{5}{6}\)
⇒ 6(x + 3 ) = 5(y + 3)
⇒ 6x + 18 = 5y + 15
⇒ 6x – 5y = 15 – 18
⇒ 6x – 5y = – 3 …..(ii)
समीकरण (i) से x का मान समीकरण (ii) में प्रतिस्थापित करने पर,
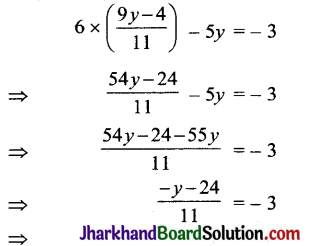
⇒ – y – 24 = – 3 × 11
⇒ – y = – 33 + 24
⇒ -y = -9
⇒ y = 9.
y का मान समीकरण (i) में रखने पर,
⇒ \(\frac{9 \times 9-4}{11}\)
⇒ \(\frac{81-4}{11}=\frac{77}{11}\)
∴ x = 7
∴ रैखिक समीकरण युग्म का हल : x = 7, y = 9
अतः भिन्न = \(\frac{7}{9}\)
(vi) माना जैकब की वर्तमान आयु x वर्ष है।
और उसके पुत्र की वर्तमान आयु y वर्ष है।
5 वर्ष बाद जैकब की आयु = (x + 5) वर्ष तथा 5 बाद पुत्र की आयु = (y + 5) वर्ष
प्रश्नानुसार,
5 वर्ष के बाद जैकब की आयु = 3 × (5 वर्ष बाद उसक पुत्र की आयु)
x + 5 = 3 × (y + 5)
⇒ x + 5 = 3y + 15
⇒ x = 3y + 15 – 5
⇒ x = 3y + 10
5 वर्ष पूर्व जैकब की आयु (x – 5) वर्ष और 5 वर्ष पूर्व उसके पुत्र की आयु = (y – 5) वर्ष
प्रश्नानुसार,
5 वर्ष पूर्व जैकब की आयु = 7 × (5 वर्ष पूर्व उसके पुत्र की आयु)
x – 5 = 7 × (y – 5)
x – 5 = 7y – 35
x – 7y = -35 + 5
x – 7y = – 30 ….(ii)
समीकरण (i) से x का मान समीकरण (ii) में प्रतिस्थापित करने पर,
(3 y + 10) – 7y = 30
⇒ 3y + 10 – 7y = -30
⇒ – 4y = -30 – 10
⇒ – 4y = – 40
∴ y = \(\frac{-40}{-4}\) = 10
y का यह मान समीकरण (i) में प्रतिस्थापित करने पर,
x = 3 × 10 + 10
⇒ x = 30 + 10
∴ x = 40
