JAC Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.7

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.7 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Exercise 3.7

प्रश्न 1.
दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अन्तर है। अनी के पिता धरम की आयु अनी की आयु की दुगनी और बीजू की आयु अपनी बहन कैथी की आयु की दुगनी है। कैथी और धरम की आयु में अन्तर 30 वर्ष है। अनी और बीजू की आयु ज्ञात कीजिए।
हल:
माना अनी की आयु = x वर्ष
तथा बीजू की आयु = y वर्ष
प्रश्नानुसार,
x – y = 3 …..(i)
या y – x = 3
⇒ -x + y = 3 …..(ii)
और अनी के पिता की आयु = 2 × अनी की आयु
= 2x वर्ष
बीजू की आयु = कैथी की आयु का दुगना

प्रश्नानुसार, धरम, कैथी से 30 वर्ष बड़ा है।
∴ \(2 x-\frac{y}{2}=30\)
⇒ \(\frac{4 x-y}{2}=30\)
⇒ 4x – y = 60 …..(iii)
समीकरण (i) में से समीकरण (iii) को घटाने पर,

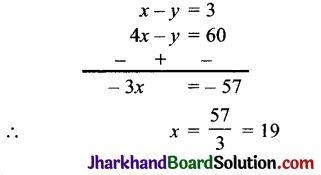
x का यह मान समीकरण (ii) में रखने पर,
19 – y = 3
⇒ -y = 3 – 19
⇒ -y = – 16 ∴ y = 16
पुन: समीकरण (2) तथा समीकरण (3) को जोड़ने पर
-x + y = 3
4x – y = 60
3x = 63
⇒ x = \(\frac{63}{3}\) = 21
x का मान समी. (2) में रखने पर,
– 21 + y = 3 ⇒ y= 3 + 21 = 24
अनी की आयु 19 वर्ष और बीजू की आयु 16 वर्ष है या अनी की आयु 21 वर्ष तथा बीजू की आयु 24 वर्ष है।

प्रश्न 2.
एक मित्र दूसरे से कहता है कि ‘यदि मुझे एक सौ रुपये दे दो, तो मैं आपसे दो गुना धनी बन जाऊँगा।’ दूसरा उत्तर देता है, ‘यदि आप मुझे दस रुपये दे दें, तो मैं आपसे छः गुना धनी बन जाऊँगा। बताइए कि उनकी क्रमशः क्या सम्पत्तियाँ हैं ?
हल:
माना A और B दो दोस्त हैं। A के पास ₹ x तथा B के पास रु. हैं।
का धन ₹ (x + 100)
प्रथम शर्तानुसार A का धन = ₹(x + 100)
B का धन = ₹(y – 100)
∵ A का धन = 2 × B का धन
x + 100 = 2 × (y – 100)
⇒ x + 100 = 2y – 200
⇒ x – 2y = – 300 …..(i)
तथा द्वितीय शर्तानुसार,
B का धन = ₹ (y + 10),
A का धन = ₹ (x – 10)
B का धन = 6 × A का धन
y + 10 = 6 × (x – 10)
y + 10 = 6x – 60
6x – y = 60 + 10
6x – y = 70 …..(ii)
समीकरण (ii) में 2 से गुणा करने पर,
12x – 2y = 140 …..(iii)
समीकरण (iii) में से समी. (i) को घटाने पर,

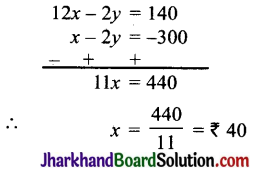
x का यह मान समीकरण (i) में रखने पर
40 – 2y = -300
– 2y = – 300 – 40
– 2y = – 340
2y = 340
y = \(\frac{340}{2}\) = ₹ 170
अतः पहले मित्र के पास धन = ₹ 40
और दूसरे मित्र के पास धन = ₹ 170

प्रश्न 3.
एक रेलगाड़ी एक समान चाल से एक निश्चित दूरी तय करती है। यदि गाड़ी 10 किमी/घण्टा अधिक तेज चलती होती, तो इसे नियत समय से 2 घण्टे कम लगते और यदि रेलगाड़ी 10 किमी/ घण्टा धीमी चलती होती, तो इसे नियत समय से 3 घण्टे अधिक लगते। रेलगाड़ी द्वारा तय की गई दूरी ज्ञात कीजिए।
हल:
माना कि रेलगाड़ी की चाल = x किमी / घण्टा
और रेलगाड़ी द्वारा लिया गया = y घण्टा
रेलगाड़ी द्वारा तय की गई दूरी = चाल × समय
= x × y
= xy किमी
रेलगाड़ी के तेज चलने पर चाल = (x + 10 ) किमी / घण्टा
रेलगाड़ी द्वारा लिया गया समय = (y – 2) घण्टे
दूरी = (x + 10 ) (y – 2)
⇒ xy = xy – 2x + 10y – 20
⇒ 2x – 10y = – 20 …..(i)
रेलगाड़ी के धीमी गति से चलने पर चाल = (x – 10) किमी / घण्टा
समय = (y + 3) घण्टे
दूरी = चाल × समय
⇒ xy = (x – 10) × (y + 3)
⇒ xy = xy + 3x – 10y – 30
⇒ 3x – 10y = 30 …..(ii)
समीकरण (ii) में से (i) को घटाने पर,

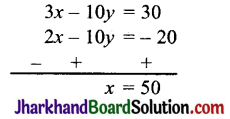
∴ x = 50
समीकरण (i) में x का मान रखने पर,
2 × 50 – 10y = -20
100 – 10y = – 20
-10y = -20 – 100
– 10y = -120
y = \(\frac{-120}{-10}\) = 12
अतः रेलगाड़ी की चाल = 50 किमी / घण्टा
रेलगाड़ी द्वारा लिया गया समय = 12 घण्टे
∴ रेलगाड़ी द्वारा तय की गई दूरी = चाल × समय
= 50 × 12
= 600 किमी।

प्रश्न 4.
एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा होना है। यदि प्रत्येक पंक्ति में 3 विद्यार्थी अधिक होते तो 1 पंक्ति कम होती। यदि पंक्ति में 3 विद्यार्थी कम होते तो 2 पंक्तियाँ अधिक बनतीं कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।
हल:
माना प्रत्येक पंक्ति में विद्यार्थियों की संख्या x है
तथा कुल पंक्तियों की संख्या y है
∴ कुल विद्यार्थियों की संख्या = xy
स्थिति I: यदि प्रत्येक पंक्ति में 3 विद्यार्थी अधिक हैं
तब इस स्थिति में पंक्तियों की संख्या (y – 1) हो जाती है।
xy = (x + 3) (y – 1)
⇒ xy = xy – x + 3y – 3
⇒ x – 3y = – 3 …..(i)
स्थिति II: यदि प्रत्येक पंक्ति में 3 विद्यार्थी कम हैं तब इस स्थिति में पंक्तियों की संख्या (y + 2) हो जाती है।
xy = (x – 3) (y + 2)
⇒ xy = xy + 2x – 3y – 6
⇒ 2x – 3y = 6 …..(ii)
समीकरण (i) में 2 से गुणा करने पर,
2x – 6y = – 6 …..(iii)
समीकरण (iii) में से (ii) को घटाने पर,

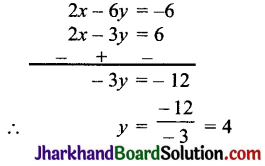
y का मान समीकरण (i) में रखने पर,
⇒ x – 3y = – 3
⇒ x – 3 × 4 = -3
⇒ x – 12 = – 3
x = – 3 + 12
∴ x = 9
अतः कक्षा में विद्यार्थियों की कुल संख्या = 9 × 4 = 36

प्रश्न 5.
एक ΔABC में, ∠C = 3 ∠B = 2 (∠A + ∠B) है। त्रिभुज के तीनों कोण ज्ञात कीजिए।
हल:
माना त्रिभुज के कोण A, B तथा C हैं।
तब ∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠B = 180° – ∠C
∠C = 3∠B = 2 (∠A + ∠B)
∠C = 2 (∠A + ∠B)
⇒ ∠C = 2 (180° – ∠C)
[क्योंकि ∠A + ∠B = 180° – ∠C]
⇒ ∠C = 360° – 2∠C
⇒ ∠C + 2∠C = 360°
⇒ 3∠C = 360°
∴ C = \(\frac{360^{\circ}}{3}\) = 120°
अब ∠C = 3∠B
⇒ 3∠B = 120°
∴ ∠B = \(\frac{120^{\circ}}{3}\) = 40°
परन्तु ∠A + ∠B + ∠C = 180°
⇒ ∠A + 40° + 120° = 180°
⇒ ∠A = 180° – 160°
∠A = 20°
अतः Δ के कोण ∠A = 20°
∠B = 40°
∠C = 120°

प्रश्न 6.
समीकरणों 5x – y = 5 और 3x – y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष पर बने त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
हल:
दिया गया समीकरण युग्म है
5x – y = 5 …..(i)
3x – y = 3 …..(ii)
समीकरण (i) से,
⇒ y = 5x – 5
x = 0 रखने पर, y = 5 × 0 – 5 = 0 – 5 = -5
x = 1 रखने पर, y = 5 × 1 – 5 = 0
x = 2 रखने पर, y = 5 × 2 – 5
= 10 – 5 = 5
x के विभिन्न मानों के लिए सारणी :

x	0	1	2
y	-5	0	5

समीकरण (ii) से,
⇒ y = 3x – 3
x = 0 रखने पर, y = 3 × 0 – 3 = -3
x = 1 रखने पर, y = 3 × 1 – 3 = 0
x= 2 रखने पर, y = 3 × 2 – 3 = 3
x के विभिन्न मानों के लिए सारणी:

x	0	1	2
y	-3	0	3

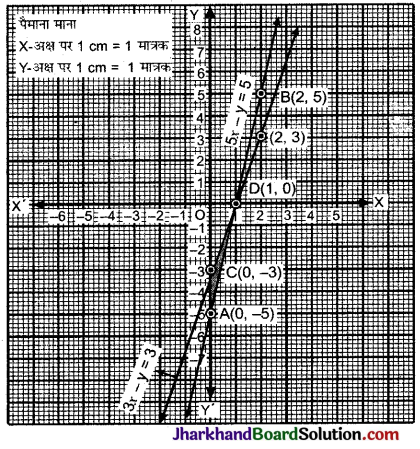
बिन्दुओं (0, -5), (1, 0) तथा (2, 5) को ग्राफ पेपर पर आलेखित करने पर समीकरण 5x – y = 5 की एक सरल रेखा प्राप्त होती है।
इसी प्रकार बिन्दुओं (0, -3), (1, 0) और (2, 3) को ग्राफ पेपर पर आलेखित करने पर समीकरण 3xy – 3 की सरल रेखा प्राप्त होती है।
इन रेखाओं से y-अक्ष पर बना छायांकित त्रिभुज ACD है जिसके निर्देशांक A(0, -5), C(0, -3) और D(1, 0) हैं।
माना x₁ = 0, y₁ = -5, x₂ = 0, y₂ = – 3
तथा x₃ = 1, y₃ = 0
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\) [0(- 3 – 0) + 0{0 – (-5)} + 1 {-5 – (-3)}]
= \(\frac{1}{2}\) [0 + 0 + 1(- 5 + 3)]
= \(\frac{1}{2}\) (-2) = -1 वर्ग मात्रक
त्रिभुज के शीषों के निर्देशांक (1, 0), (0, -3), (0, -5) है।
∵ क्षेत्रफल ऋणात्मक नहीं हो सकता। अतः त्रिभुज का क्षेत्रफल 1 वर्ग मात्रक होगा।

प्रश्न 7.
निम्नलिखित रैखिक समीकरणों के युग्मों को हल कीजिए-
(i) px + qy = p – q
qx – py = p + q
(ii) ax + by = c
bx + ay = 1 + c
(iii) \(\frac{x}{a}-\frac{y}{b}=0\)
ax + by = a² + b²
(iv) (a – b)x + (a + b)y = a² – 2ab – b²
(a + b) (x + y) = a² + b²
(v) 152x – 378y = -74
-378x + 152y = -604
हल:
(i) दिया गया रैखिक समीकरण युग्म
px + qy = p – q …(1)
और qx – py = p + q …(2)

समीकरण (1) को से और समीकरण (2) को p से गुणा करने पर,

घटाने पर,
y के इस मान को समीकरण (1) में रखने पर,
px + q(-1) = p – q
⇒ px – q = p – q
⇒ px= p – q + q
⇒ px = p
∴ x = 1
अतः x = 1 और y = -1

(ii) दिया गया रैखिक समीकरण युग्म
ax + by = c
⇒ ax + by – c = 0 …..(i)
तथा bx + ay = 1 + c
⇒ bx + ay – (1 + c) = 0 …..(ii)
वज्रगुणन विधि से समी. (i) एवं (ii) को हल करने पर

(iii) दिया गया रैखिक समीकरण युग्म
\(\frac{x}{a}-\frac{y}{b}=0\)
⇒ \(\frac{b x-a y}{a b}\) = 0
⇒ bx – ay = 0 …..(i)
और ax + by = a² + b²
⇒ ax + by – (a² + b²) = 0 …..(ii)
वज्रगुणन विधि से हल करने पर,

अतः समीकरण के अभीष्ट हल x = a और y = b हैं।

(iv) दिया गया रैखिक समीकरण युग्म
(a – b)x + (a + b)y = a² – 2ab – b²
ax – bx + ay + by = a² – 2ab – b² …..(i)
और (a + b) (x + y) = a² + b²
⇒ ax + bx + ay + by = a² + b² …..(ii)
समीकरण (i) में से (ii) को घटाने पर,

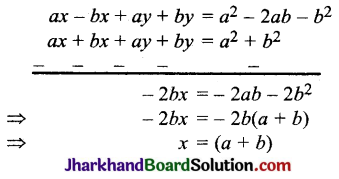
x के इस मान को समीकरण (i) में रखने पर,
(a – b) (a + b) + (a + b)y = a² – 2ab – b²
⇒ a² – b² + (a + b)y = a² – 2ab – b²
⇒ (a + b)y = a² – 2ab – b² – a² + b²
⇒ (a + b)y = -2ab
∴ y = \(\frac{-2 a b}{a+b}\)
अतः x = (a + b)
और y = \(-\frac{2 a b}{a+b}\)

(v) दिया गया समीकरण युग्म
152x – 378y = -74 …..(1)
-378x + 152y = -604 …..(2)
समीकरण (1) व समीकरण (2) को जोड़ने पर,
-226x – 226y = -678
⇒ -226(x + y) = -678
⇒ x + y = \(\frac{-678}{-226}\)
∴ x + y = 3 …..(3)
समीकरण (1) मैं से समीकरण (2) को घटाने पर,
(152x – 378y) – (-378x + 152y) = – 74 – (-604)
⇒ 152x – 378y + 378x – 152y = – 74 + 604
⇒ 530x – 530y = 530
⇒ 530(x – y) = 530
∴ x – y = 1 …..(4)
समीकरण (3) व समीकरण (4) को जोड़ने पर,
x + y + x – y = 3 + 1
⇒ 2x = 4
⇒ x = \(\frac{4}{2}\)
∴ x = 2
x = 2 समीकरण (3) में रखने पर,
⇒ 2 + y = 3
⇒ y = 3 – 2 ⇒ y = 1
अत: समीकरण के अभीष्ट हल x = 2 और y = 1 हैं।

प्रश्न 8.
ABCD एक चक्रीय चतुर्भुज है। इस चक्रीय चतुर्भुज के कोण ज्ञात कीजिए।

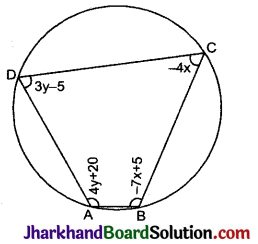
हल:
∵ ABCD एक चक्रीय चतुर्भुज है।
∴ ∠A + ∠C = 180°
⇒ 4y + 20 + (- 4x ) = 180°
या – 4x + 4y = 180° – 20° = 160°
या x – y = – 40° …..(1)
और ∠B + ∠D = 180°
तो -7x + 5 + 3y – 5 = 180°
या -7x + 3y = 180°
या 7x – 3y = – 180° …..(2)
समीकरण (1) से y = x + 40 समीकरण (2) में प्रतिस्थापित करने पर,
7x – 3(x + 40) = – 180
⇒ 7x – 3x – 120 = -180
⇒ 4x = – 180 + 120
⇒ 4x = -60
∴ x = \(\frac{-60}{4}\) = -15
x का यह मान समीकरण (1) में रखने पर,
– 15 – y = – 40
⇒ – y = -40 + 15
⇒ – y = – 25 ⇒ y = 25
तब ∠A = 4y + 20 = 4 × 25 + 20 = 120°
∠B = – 7x + 5 = (-7) × (-15) + 5
= 110°
∠C = – 4x = – 4 × – 15 = 60°
∠D = 3y – 5 = 3 × 25 – 5 = 70°