JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.6

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.6 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.6

प्रश्न 1.
आकृति में, PS कोण QPR का सम-द्विभाजक है। सिद्ध कीजिए कि \(\frac{Q S}{S R}=\frac{P Q}{P R}\) है।
हल:
दिया है : ΔPQR में, PS कोण QPR का सम-द्विभाजक है अर्थात् ∠1 = ∠2 है।

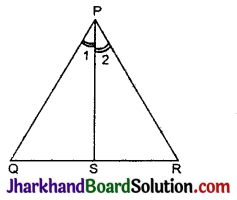
सिद्ध करना है :
\(\frac{Q S}{S R}=\frac{P Q}{P R}\)
रचना: R से एक रेखा PS के समान्तर खींचते हैं जो OP को बढ़ाने पर T पर मिलती है।
उपपत्ति: ΔQRT में,
PS || TR

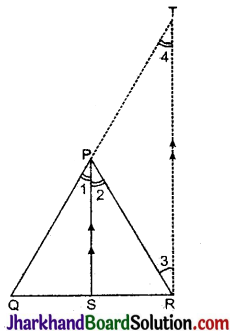
∠2 = ∠3, (एकान्तर कोण)
∠1 = ∠4, (संगत कोण)
परन्तु ∠1 = ∠2, (दिया है)
∴ ∠3 = ∠4
ΔPRT में. ∠3 = ∠4, (ऊपर सिद्ध किया है)
PT = PR (समान भुजाओं के सम्मुख कोण)
ΔQRT में, PS || TR
\(\frac{Q P}{P T}=\frac{Q S}{S R}\) (आधारभूत समानुपातिक प्रमेय से)
\(\frac{Q P}{P R}=\frac{Q S}{S R}\) (∵ PT = PR)
या \(\frac{P Q}{P R}=\frac{Q S}{S R}\)

प्रश्न 2.
दी गई आकृति में D, ΔABC के कर्ण AC पर स्थित एक बिन्दु है जिसमें BD ⊥ AC तथा DM ⊥ BC और DN ⊥ AB है। सिद्ध कीजिए कि:

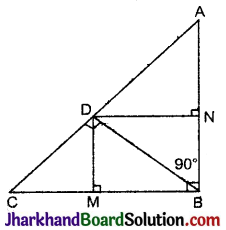
(i) DM² = DN × MC
(ii) DN² = DM × AN
हल:
दिया है: समकोण ΔABC में ∠ABC = 90°, BD ⊥ AC, DM ⊥ BC तथा DN ⊥ AB
सिद्ध करना है:
(i) DM² = DN × MC
(ii) DN² = DM × AN
उपपत्ति: समकोण ΔABC में,
BD ⊥ AC
∴ ΔBDC ~ ΔABC और ΔADB ~ ΔABC
∴ ΔBDC ~ ΔADB (प्रमेय 6.7 से)
तथा ΔBDC और ΔADB समकोणिक त्रिभुज हैं।
(i) ∵ समकोण ΔBDC में,
DM ⊥ BC (दिया है)
ΔDMC ~ ΔBMD (प्रमेय 6.7 से)
⇒ \(\frac{M C}{D M}=\frac{D M}{B M}\)
(∵ दो समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं)
⇒ DM² = BM × MC …(1)
∵ चतुर्भुज BMDN में,
∠B = 90°, ∠M = 90° तथा ∠N = 90°
∴ चतुर्भुज BMDN एक आयत है।
BM = DN …(2)
समीकरण (1) व (2) से
DM² = DN × MC

(ii) ∵ समकोण ΔADB में,
DN ⊥ AB
ΔAND ~ ΔDNB (प्रमेयं 6.7 से)
\(\frac{D N}{B N}=\frac{A N}{D N}\)
(∵ दो समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं)
DN² = BN × AN …(3)
∵ चतुर्भुज BMDN एक आयत है।
BN = DM …(4)
समीकरण (3) व (4) से,
DN² = DM × AN

प्रश्न 3.
दी गई आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° तथा AD ⊥ CB है। सिद्ध कीजिए कि AC² = AB² + BC² + 2BC.BD है।

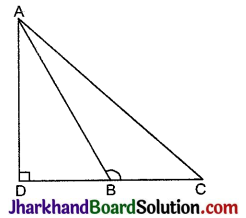
हल:
दिया है: ΔABC में, ∠ABC > 90° तथा AD ⊥ CB है।
सिद्ध करना है: AC² = AB² + BC² + 2BC.BD
उपपत्ति: समकोण ΔADB में,
AB² = AD² + BD² …(1)
पुन: समकोण ΔADC में,
AC² = AD² + DC²
⇒ AC² = AD² + (BD + BC)²
(∵ DC = BD + BC)
⇒ AC² = AD² + BD² + BC² + 2BD.BC
समीकरण (1) से, AD² + BD² का मान रखने पर,
अतः AC² = AB² + BC² + 2BD.BC

प्रश्न 4.
दी गई आकृति में, ABC एक त्रिभुज है जिसमें ∠ABC < 90° है तथा AD ⊥ BC है। सिद्ध कीजिए कि AC² = AB² + BC² – 2BC.BD हैं।

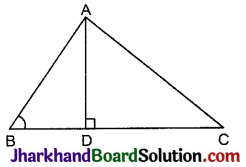
हल:
दिया है: त्रिभुज ABC जिसमें ∠ABC < 90° तथा AD ⊥ BC है।
सिद्ध करना है: AC² = AB² + BC² – 2BC.BD
उपपत्ति: ∵ AD ⊥ BC
∴ ΔADB और ΔADC समकोणीय त्रिभुज हैं।
समकोण ΔADB में,
AB² = AD² + BD² …(1)
समकोण ΔADC में,
AC² = AD² + DC² …(2)
समीकरण (2) में से (1) को घटाने पर,
AC² – AB² = DC² – BD²
= (DC + BD) (DC – BD)
= BC (DC – BD)
{∵ DC + BD = BC}
= BC (BC – BD – BD) {∵ DC BC-BD}
= BC (BC – 2BD)
⇒ AC² – AB² = BC² – 2BC × BD
⇒ AC² = AB² + BC² – 2BC.BD

प्रश्न 5.
दी गई आकृति में, AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि :

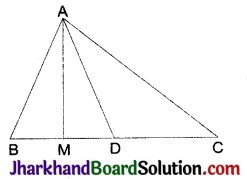
(i) AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^2\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^2\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC2
दिया है: ΔABC, जिसमें BC का मध्यबिन्दु D है क्योंकि AD माध्यिका है। AM, BC पर लम्ब हैं और AC > AB.
सिद्ध करना है :
(i) AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^2\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^2\)
(iii) AC² + AB²= 2AD² + \(\frac{1}{2}\)BC²
उपपत्ति: (i) समकोण ΔAMD में,
AD² = AM² + DM²
AM² = AD² – DM² …(1)
समकोण ΔAMC में,
AC² = AM² + MC² …(2)
समीकरण (1) तथा (2) से
AC² = (AD² – DM²) + MC²
⇒ AC² = (AD² – DM²) + (DM + DC)²
(∵ MC = DM + DC)
⇒ AC² = AD² – DM² + DM² + DC² + 2DM.DC
⇒ AC² = AD² + DC² + 2DM.DC,

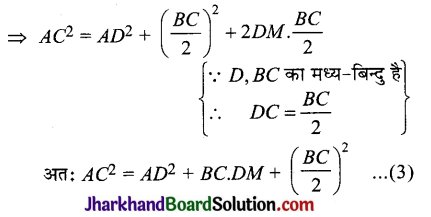
(ii) समकोण ΔAMB में,
AB² = AM² + BM²
= (AD² – DM²) + BM²
[समी. (1) का प्रयोग करने पर]
= (AD² – DM²) + (BD – DM)²
= AD² – DM² + BD² + DM² – 2BD.DM
= AD² + BD² – 2BD.DM

∴ AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^2\)
अत: AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^2\) …(4)

(iii) समीकरण (3) व (4) को जोड़ने पर,
AB² + AC² = 2AD² + 2 × \(\frac{1}{4}\)BC²
= 2AD² + \(\frac{1}{2}\)BC²
अतः AB² + AC² = 2AD² + \(\frac{1}{2}\)BC²

प्रश्न 6.
सिद्ध कीजिए कि एक समान्तर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
हल:
दिया है: ABCD एक समान्तर चतुर्भुज है जिसके विकर्ण AC और BD परस्पर बिन्दु O पर काटते हैं।
सिद्ध करना है :
AC² + BD² = AB² + BC²2 + CD² + DA²
रचना: A से BD पर AE तथा C से BD पर CF लम्ब खींचे।

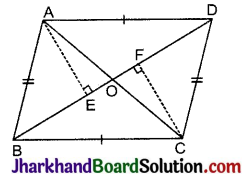
उपपत्ति: ABCD एक समान्तर चतुर्भुज है और AC तथा BD उसके विकर्ण हैं जो परस्पर O बिन्दु पर काटते हैं।
∴ AO = OC और OB = OD और AB = CD
समकोण ΔAEB में,
AB² = AE² + BE²
= AE² + (OB – OE)²
= AE² + (\(\frac{1}{2}\)BD – OE)²
= AE² + BD² + OE² – 2 × \(\frac{1}{2}\)BD.OE
= \(\frac{1}{4}\)BD² + (AE² + OE²) – BD.OE
∵ ΔAOE समकोण त्रिभुज है
∴ AE² + OE² = AO² = \(\left(\frac{1}{2} A C\right)^2\)
= \(\frac{1}{4}\)BD² + \(\left(\frac{1}{2} A C\right)^2\) – BD.OE
⇒ AB² = \(\frac{1}{4}\)BD² + \(\frac{1}{4}\)AC² – BD.OE …(1)
पुन: समकोण ΔAED में,
DA² = AE² + ED²
= AE² + (OD + OE)²
= AE² + \(\left(\frac{1}{2} BD+O E\right)^2\)
= AE² + \(\frac{1}{4}\)BD² + OE² + 2·\(\frac{1}{2}\)BD.OE
= (AE² + OE²) + \(\frac{1}{4}\)BD² + BD.OE,
(∵ AE² + OE² = AO² ΔAEO समकोण Δ है)
= AO² + \(\frac{1}{4}\)BD² + BD.OE
= \(\left(\frac{1}{2} A C\right)^2\) + \(\frac{1}{4}\)BD² + BD.OE
(∵ OA = \(\frac{1}{2}\)AC)
⇒ DA² = \(\frac{1}{4}\)BD² + \(\frac{1}{4}\)AC² + BD.OE …(2)
समीकरण (1) व (2) को जोड़ने पर,
AB² + DA² = \(\frac{1}{4}\)BD² + \(\frac{1}{4}\)BD² + \(\frac{1}{4}\)AC² + \(\frac{1}{4}\)AC²
⇒ AB² + DA² = \(\frac{2}{4}\)BD² + \(\frac{2}{4}\)AC²
⇒ AB² + DA² = \(\frac{1}{2}\)BD² + \(\frac{1}{2}\)AC²
= AB² + DA² = \(\frac{1}{4}\)(BD² + AC²) …(3)
समीकरण (3) में AB = CD और DA = BC रखने पर
CD² + BC² = \(\frac{1}{2}\)(BD² + AC²) …(4)
समीकरण (3) व (4) को जोड़ने पर,
AB² + BC² + CD² + DA² = \(\frac{1}{2}\)(BD² + AC²) + \(\frac{1}{2}\)(BD² + AC²)
अत: AB² + BC² + CD² + DA² = BD² + AC²

प्रश्न 7.
दी गई आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिन्दु पर प्रतिच्छेद करती हैं।

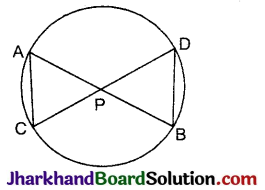
सिद्ध कीजिए कि:
(i) ΔAPC ~ ΔDPB
(ii) AP. PB = CP. DP
हल:
दिया है: एक वृत्त की AB व CD दो जीवाएँ हैं जो एक-दूसरे को बिन्दु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है:
(i) ΔAPC ~ ΔDPB.
(ii) AP.PB = CP.DP

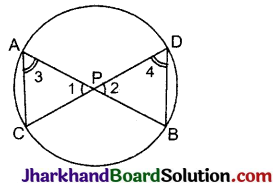
उपपत्ति: (i) ΔAPC और ΔDPB में,
∠1 = ∠2 (शीर्षाभिमुख कोण)
∠3 =∠4 (एक ही वृत्तखण्ड के कोण )
∴ A-A समरूपता कसौटी से, ΔAPC ~ ΔDPB

(ii) ΔAPC ~ ΔDPB, (ऊपर प्रमाणित )
⇒ \(\frac{A P}{D P}=\frac{P C}{P B}\)
(यदि दो त्रिभुज समरूप हों तो उनकी संगत भुजाएँ समानुपाती होती हैं)
⇒ AP.PB = PC.DP

प्रश्न 8.
दी गई आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि :

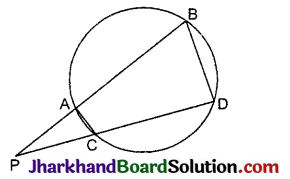
(i) ΔPAC ~ ΔPDB
(ii) PA.PB = PC.PD
हल:
दिया है: AB और CD एक वृत्त की दो जीवाएँ हैं जो बढ़ाने पर एक-दूसरे को वृत्त के बाहर बिन्दु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है:
(i) ΔPAC ~ ΔPDB
(ii) PA.PB = PC.PD

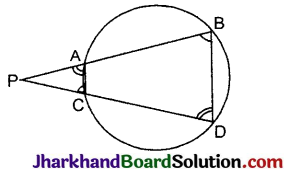
रचना : रेखाखण्ड AC व BD को मिलाया।
उपपत्ति: (i) ΔPAC और ΔPDB में,
∠P = ∠P (उभयनिष्ठ)
∠PAC = ∠PDB (∵ चक्रीय चतुर्भुज का बाह्य कोण अन्तः सम्मुख कोण के बराबर होता है।)
A-A समरूपता कसौटी से,
ΔPAC ~ ΔPDB

(ii) ΔPAC ~ ΔPDB (ऊपर सिद्ध किया है)
\(\frac{P A}{P D}=\frac{P C}{P B}\)
(यदि दो Δ समरूप हैं तो उनकी संगत भुजाएँ समानुपाती होती हैं)
PA.PB = PC.PD

प्रश्न 9.
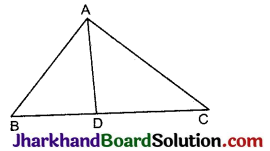
दी गई आकृति में त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि \(\frac{B D}{C D}=\frac{A B}{A C}\) है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।

हल:
दिया है: ΔABC की भुजा BC पर एक बिन्दु D ऐसा है कि \(\frac{B D}{C D}=\frac{A B}{A C}\) है।

सिद्ध करना है AD, ∠BAC का समद्विभाजक है अर्थात् ∠1 = ∠2
रचना: BA को उसकी सीध में E तक इतना बढ़ाया कि AE = AC हो।
उपपत्ति: आकृति में
\(\frac{B D}{C D}=\frac{A B}{A C}\) (दिया है)
परन्तु AC = AE (रचना से)
\(\frac{B D}{C D}=\frac{A B}{A E}\)
⇒ AD || EC
(आधारभूत आनुपातिकता प्रमेय के विलोम से)
⇒ ∠1 = ∠3 (संगत कोण)
∠2 = ∠4 (एकांतर कोण)
परन्तु ∠3 = ∠4 (∵ AC = AE)
⇒ ∠1 = ∠2
⇒ AD, ∠BAC का समद्विभाजक है।

प्रश्न 10.
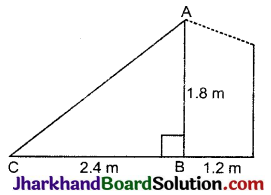
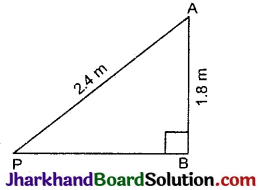
नाजिमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाजिमा से दूरी 3.6m है और छड़ के सिरे के ठीक नीचे पानी की सतह पर स्थित बिन्दु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है। (देखिए आकृति) यदि वह डोरी को 5 cm/s की दर से अन्दर खींचे, तो 12 सेकण्ड के बाद नाजिमा की काँटे से क्षैतिज दूरी कितनी होगी ?
हल:
समकोण ΔABC में,
AB = 1.8m
BC = 2.4m
∠B = 90°

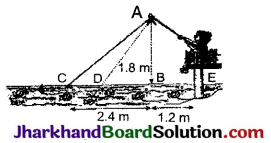
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ AC² = (1.8)² + (2.4)²
⇒ AC² = 3.24 + 5.76
∴ AC = 3 मीटर
बाहर वाली डोरी की लम्बाई = 3 मी

12 सेकण्ड में 5 सेमी/से. की दर से खींची गई डोरी की लम्बाई
= (5 × 12) सेमी.
= 60 सेमी = 0.60 मीटर
∴ शेष बची डोरी की लम्बाई = (3 – 0.6) मी. = 2.4 मी.
दूसरी अवस्था में PB ज्ञात करने के लिए,

PB² = PA² – BA²
= (2.4)² – (1.8)²
= 5.76 – 3.24 = 2.52
⇒ PB = \(\sqrt{2.52}\) = 1.59 (लगभग)
अतः 12 सेकण्ड बाद नाजिमा की काँटे से क्षैतिज दूरी = (1.59 + 1.2) मी.
= 2.79 मी. (लगभग)
अतः डोरी की लम्बाई और 12 सेकण्ड के बाद नाजिमा की काँटे से क्षैतिज दूरी क्रमश: 3 मीटर और 2.79 मीटर है।