JAC Class 10 Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.2

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 निर्देशांक ज्यामिति Exercise 7.2

प्रश्न 1.
उस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (-1, 7) और (4, -3) को मिलाने वाले रेखाखण्ड को 2 : 3 के अनुपात में विभाजित करता है।
हल:
माना अभीष्ट बिन्दु P के निर्देशांक (x, y) हैं।

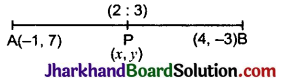
विभाजन सूत्र से:

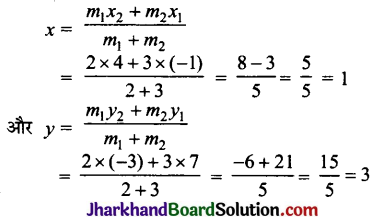
अतः अभीष्ट बिन्दु के निर्देशांक (1, 3) हैं।

प्रश्न 2.
बिन्दुओं (4, -1) और (-2, -3) को जोड़ने वाले रेखाखण्ड को सम त्रिभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
हल:
माना कि P (x₁, y₁) और Q (x₂, y₂) अभीष्ट बिन्दु हैं जो बिन्दुओं A(4, -1) और B (-2, -3) को जोड़ने वाले रेखाखण्ड को सम त्रिभाजित करते हैं।
माना कि AP = PQ = BQ = x
∴ PB = x + x = 2x
तथा AQ = x + x = 2x
अब \(\frac{A P}{P B}=\frac{x}{2 x}=\frac{1}{2}\) = 1 : 2
तथा \(\frac{A Q}{B Q}=\frac{2 x}{x}=\frac{2}{1}\) = 2 : 1
अर्थात् बिन्दु P, AB को 1 : 2 के अनुपात मैं तथा बिन्दु Q, AB को 2 : 1 के अनुपात में विभाजित करता है।


∴ अभीष्ट बिन्दु Q के निर्देशांक (2, –\(\frac{7}{3}\)) हैं।
अत: P और Q के अभीष्ट निर्देशांक (2, –\(\frac{5}{3}\)) और (0, –\(\frac{7}{3}\)) हैं।

प्रश्न 3.
आपके स्कूल में खेलकूद क्रियाकलाप आयोजित करने के लिए, एक आयताकार मैदान ABCD में, चूने से परस्पर 1 मीटर की दूरी पर पंक्तियाँ बनाई गई हैं। AD के अनुदिश परस्पर 1 मीटर की दूरी पर 100 गमले रखे गए हैं, जैसा कि आकृति में दर्शाया गया है। निहारिका दूसरी पंक्ति में AD के \(\frac{1}{4}\) भाग के बराबर की दूरी दौड़ती है और वहाँ एक हरा झण्डा गाड़ देती है। प्रीत आठवीं पंक्ति में AD के \(\frac{1}{5}\) भाग के बराबर की दूरी दौड़ती है और वहाँ एक लाल झण्डा गाड़ देती है।
(i) दोनों झण्डों के बीच की दूरी क्या है ?
(ii) यदि रश्मि को एक नीला झण्डा इन दोनों झण्डों को मिलाने वाले रेखाखण्ड पर ठीक आधी दूरी (बीच में) पर गाड़ना हो, तो उसे अपना झण्डा कहाँ गाड़ना चाहिए ?

हल:
(i) ∵ भुजा AD पर 1 मीटर की दूरी पर 100 गमले रखे गए हैं।
∴ AD = 100 मीटर
निहारिका के झण्डे की स्थिति = दूसरी पंक्ति में AD के \(\frac{1}{4}\) भाग के बराबर दूरी
= \(\frac{1}{4}\) × 100 = 25 मीटर
∴ हरे झण्डे के निर्देशांक (2, 25) हैं।
प्रीत के झण्डे (लाल) की स्थिति = आठवीं पंक्ति में AD के \(\frac{1}{5}\) भाग के बराबर दूरी
= \(\frac{1}{5}\) × 100 = 20 मीटर
∴ लाल झण्डे के निर्देशांक (8,20) हैं।
∴ हरे और लाल झण्डे के बीच की दूरी
= \(\sqrt{(8-2)^2+(20-25)^2}\)
= \(\sqrt{36+25}=\sqrt{61}\) मीटर

(ii) रश्मि को इन दोनों झण्डों को मिलाने वाले रेखाखण्ड के मध्य बिन्दु पर नीला झण्डा गाड़ना है, तब मध्य-बिन्दु के निर्देशांक
= \(\left(\frac{2+8}{2}, \frac{25+20}{2}\right)\)
= \(\left(5, \frac{45}{2}\right)\)
= (5, 22.5)
अतः रश्मि को पाँचवीं पंक्ति में AD के अनुदिश 22.5 मीटर की दूरी पर झण्डा गाड़ना चाहिए।

प्रश्न 4.
बिन्दुओं (-3,10) और (6, -8) को जोड़ने वाले रेखाखण्ड को बिन्दु (-1, 6) किस अनुपात में विभाजित करता है?
हल:
माना बिन्दुओं (-3, 10) और (6, -8) को जोड़ने वाले रेखाखण्ड को बिन्दु (-1, 6), K : 1 में विभाजित करता है, तब

⇒ – K – 1 = 6K – 3
⇒ – K – 6K = – 3 + 1
⇒ -7K = – 2
⇒ K = \(\frac{2}{7}\)
⇒ \(\frac{K}{1}\) = \(\frac{2}{7}\)
अत: अभीष्ट अनुपात K : 1 = 2 : 7

प्रश्न 5.
वह अनुपात ज्ञात कीजिए जिसमें बिन्दुओं A(1, -5) और B(-4, 5) को मिलाने वाला रेखाखण्ड X-अक्ष से विभाजित होता है। इस विभाजन बिन्दु के निर्देशांक भी ज्ञात कीजिए।
हल:
माना कि x-अक्ष पर अभीष्ट बिन्दु P (x, 0) है जो A(1, -5) और B(-4, 5) को मिलाने वाले रेखाखण्ड को K : 1 के अनुपात में विभाजित करता है।

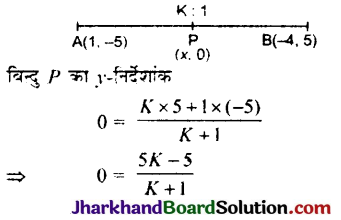
⇒ 5K – 5 = 0
⇒ 5K = 5
⇒ K = \(\frac{5}{5}\) = 1
∴ K = 1
∴ बिन्दु P का अभीष्ट अनुपात = 1 : 1
अब बिन्दु P का x-निर्देशांक

अतः अभीष्ट बिन्दु के निर्देशांक (-\(\frac{3}{2}\), 0) हैं।

प्रश्न 6.
यदि बिन्दु (1, 2), (4, y), (x, 6) और (3, 5), इसी क्रम में लेने पर एक समान्तर चतुर्भुज के शीर्ष हों, तो x और ज्ञात कीजिए।
हल:
माना कि A(1, 2), B(4, y), C(x, 6) तथा D(3, 5) एकं समान्तर चतुर्भुज के शीर्षों के निर्देशांक है।
चूँकि ABCD एक समान्तर चतुर्भुज है, इसलिए इसके विकर्ण AC तथा BD परस्पर समदभीजित करते हैं।
AC के मध्य बिन्दु के निर्देशांक = \(\left(\frac{1+x}{2}, \frac{2+6}{2}\right)\)
= \(\left(\frac{1+x}{2}, 4\right)\)
BD के मध्य बिन्दु के निर्देशांक = \(\left(\frac{4+3}{2}, \frac{y+5}{2}\right)\)
= \(\left(\frac{7}{2}, \frac{y+5}{2}\right)\)
∵ AC और BD परस्पर समद्विभाजित करते हैं।
∴ AC का मध्यबिन्दु वही होगा जो BD का है।
∴ \(\frac{1+x}{2}=\frac{7}{2}\)
⇒ 1 + x = 7 या x = 6
और \(\frac{y+5}{2}\) = 4
⇒ y + 5 = 8 या y = 3
अत: x = 6, y = 3

प्रश्न 7.
बिन्दु के निर्देशांक ज्ञात कीजिए, जहाँ AB एक वृत्त का व्यास है जिसका केन्द्र (2, -3) है तथा B के निर्देशांक (1, 4) हैं।
हल:
केन्द्र के निर्देशांक = (2, -3)
बिन्दु B के निर्देशांक = (1, 4)

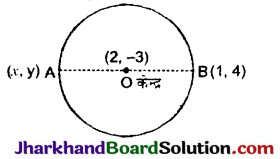
माना बिन्दु A के निर्देशांक (x, y) हैं।
बिन्दु O, व्यास AB का मध्य-बिन्दु है।

⇒ 4 = x + 1 और -6 = y + 4
⇒ x = 4 – 1 और y = – 6 – 4
∴ x = 3 और y = -10
अतः अभीष्ट बिन्दु’ के निर्देशांक (3, -10) हैं।

प्रश्न 8.
यदि A और B क्रमश: (-2, -2) और (2, -4) हों, तो बिन्दु को निर्देशांक ज्ञात कीजिए ताकि AP = \(\frac{3}{7}\)AB हो, और P रेखाखण्ड AB पर स्थित है।
हल:
माना कि अभीष्ट बिन्दु P (x, y) हैं।

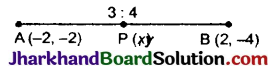
दिया है:
AP = \(\frac{3}{2}\)AB …(i)
परन्तु PB = AB – AP
⇒ PB = AB – AP
⇒ PB = AB – \(\frac{3}{7}\)AB
PB = \(\frac{7 A B-3 A B}{7}\)
PB = \(\frac{4}{7}\)AB ….(ii)
समी. (i) व (ii) से,
∴ AP : PB = \(\frac{3}{7}\)AB : \(\frac{4}{7}\)AB
⇒ AP : PB = 3 : 4
∴ बिन्दुओं A और B को बिन्दु P, 3 : 4 के अनुपात में विभाजित करता है।
∴ बिन्दु P के निर्देशांक3

प्रश्न 9.
बिन्दुओं A(-2, 2) और B(2, 8) को जोड़ने वाले रेखाखण्ड AB को चार बराबर भागों में विभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
हल:
माना कि C, D और E अभीष्ट बिन्दु हैं जो बिन्दुओं A(-2, 2) और B (2, 8) को मिलाने वाले रेखाखण्ड को चार बराबर भागों में विभाजित करते हैं।

अब D, A और B का मध्यबिन्दु है: C, A और D का मध्य- बिन्दु है E, D और B का मध्य बिन्दु है।
∴ AC = CD = DE = EB
अब A और B के मध्य बिन्दु D के निर्देशांक
= \(\left(\frac{-2+2}{2}, \frac{2+8}{2}\right)\)
= (0, 5)
A और D के मध्य बिन्दु C के निर्देशांक
= \(\left(\frac{-2+0}{2}, \frac{2+5}{2}\right)\)
= \(\left(-1, \frac{7}{2}\right)\)
D और B के मध्य बिन्दु E के निर्देशांक
= \(\left(\frac{2+0}{2}, \frac{8+5}{2}\right)\)
= \(\left(1, \frac{13}{2}\right)\)
अतः AB को चार बराबर भागों में विभाजित करने वाले बिन्दुओं के निर्देशांक (0, 5), \(\left(-1, \frac{7}{2}\right)\) और \(\left(1, \frac{13}{2}\right)\)

प्रश्न 10.
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष, इसी क्रम में (3, 0), (4, 5), (-1, 4) और (-2, -1) हैं।
हल:
माना समचतुर्भुज ABCD के शीर्षो के निर्देशांक A(3, 0), B (4, 5), C (-1, 4) और D (-2, -1) हैं।

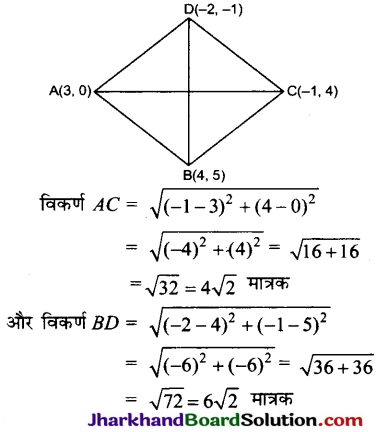
समचतुर्भुज ABCD का क्षेत्रफल
= \(\frac{1}{2}\) × पहला विकर्ण × दूसरा विकर्ण
= \(\frac{1}{2}\) × 4\(\sqrt{2}\) × 6\(\sqrt{2}\)
= \(\frac{1}{2}\) × 24 × 2 = 24 वर्ग मात्रक
अतः समचतुर्भुज का क्षेत्रफल = 24 वर्ग मात्रक ।