JAC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.4

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.4

Question 1.
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A (2, – 2) and B (3, 7).
Answer:
Let the line 2x + y – 4 = 0 divide the line segment joining the point A (2, – 2) and B (3, 7) at point M (a, b) in the ratio k : 1.
Then, the coordinates of point M are
(\(\frac{3 k+2}{k+1}, \frac{7 k-2}{k+1}\)) = (a, b)
∴ a = \(\frac{3k+2}{k+1}\)
and b = \(\frac{7k-2}{k+1}\) …… (1)
Now, the point M also lies on line 2x + y – 4 = 0.
Hence, (a, b) must satisfy
2x + y – 4 = 0
∴ 2a + b – 4 = 0
∴ 2(\(\frac{3k+2}{k+1}\)) + (\(\frac{7k-2}{k+1}\)) – 4 = 0 [From (1)]
∴ 6k + 4 + 7k – 2 – 4k – 4 = 0
∴ 9k – 2 = 0
∴ k = \(\frac{2}{9}\)
Hence, the ratio k : 1 = \(\frac{2}{9}\) : 1 = 2 : 9.
Thus, the line 2x + y – 4 = 0 divides the line segment joining the points A (2, – 2) and B (3, 7) in the ratio 2 : 9.

Question 2.
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Answer:
Points A (x, y), B(1, 2) and C(7,0) are collinear.
∴ Area of ΔABC = 0
∴ \(\frac{1}{2}\)[x(2 – 0) + 1 (0 – y) + 7 (y – 2)] = 0
∴ 2x – y + 7y – 14 = 0
∴ 2x + 6y – 14 = 0
∴ x + 3y – 7 = 0
Thus, x + 3y – 7 = 0 is the required relation between x and y.

Question 3.
Find the centre of the circle passing through the points (6, – 6), (3, – 7) and (3, 3).
Answer:
Let A (6, 6), B (3, 7) and C(3, 3) be the given points and P(x, y) be the centre of the circle passing through these points. Then, P is equidistant from all the points A, B and C.
∴ PA = PB = PC
∴ PA² = PB² = PC²
Now, PA² = PB² gives
(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²
∴ x² – 12x + 36 + y² + 12y +36 = x² – 6x + 9 + y² + 14y + 49
∴ – 6x – 2y = – 14
∴ 3x + y = 7 …………..(1)
Again, PA² = PC² gives
(x – 6)² + (y + 6)² = (x – 3)² + (y – 3)²
∴ x² – 12x + 36 + y² + 12y + 36 = x² – 6x + 9 + y² – 6y + 9
∴ – 6x + 18y = – 54
∴ x – 3y = 9 …………..(2)
Multiplying equation (1) by 3, we get
9x + 3y = 21
Adding equations (2) and (3), we get 10x = 30
10x = 3
∴ x = 3
Substituting x = 3 in 3x + y = 7, we get 9 + y = 7. i.e., y = – 2
∴ The coordinates of P are (3, – 2).
Thus, the centre of the circle passing through the given points is (3, – 2).

Question 4.
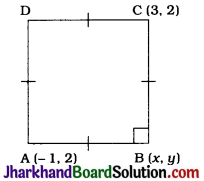
The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.

Answer:
Let ABCD be the given square in which A(-1, 2) and C(3, 2) are given vertices and B and D are to be found.
Let the coordinates of B be (x, y).
In ΔABC, ∠B = 90° and AB = BC.
AB = BC
∴ AB² = BC²
∴ (x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²
∴ x² + 2x + 1 + y² – 4y + 4 = x² – 6x + 9 + y² – 4y + 4
∴ 8x = 8
∴ x = 1
In ΔABC,
∠B = 90°
Hence, by Pythagoras theorem,
AB² + BC² = AC²
∴ (x + 1)² + (y – 2)² + (x – 3)² + (y – 2)² = (3 + 1)² + (2 – 2)²
∴ x² + 2x + 1 + y² – 4y + 4 + x² – 6x + 9 + y² – 4y + 4 = 16
∴ 2x² – 4x + 2y² – 8y + 18 – 16 = 0
∴ 2(1)² – 4(1) + 2y² – 8y + 2 = 0 (Substituting x = 1)
∴ 2 – 4 + 2y² – 8y + 2 = 0
∴ 2y² – 8y = 0
∴ 2y (y – 4) = 0
∴ 2y = 0 or y – 4 = 0
∴ y = 0 or y = 4
These two values of y gives us the y-coordinates of B and D while the single value of x suggests that the x-coordinate of B and D is same. Thus, the coordinates of the other two vertices are (1, 0) and (1, 4) respectively.

Question 5.
The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the given figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

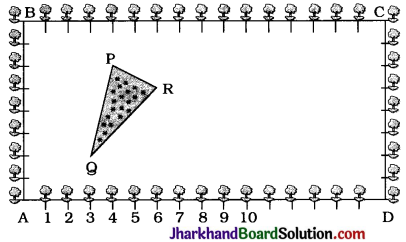
1. Taking A as origin, find the coordinates of the vertices of the triangle.
2. What will be the coordinates of the vertices of ΔPQR if C is the origin? Also calculate the areas of the triangles in these cases. What do you observe?
Answer:
1. Taking A as the origin and AB and AD as the y-axis and the x-axis respectively, we get the coordinates of points as A (0, 0), B(0, 8), D(16, 0) and C(16, 8).
Then, the vertices of ΔPQR are P (4, 6), 9 (3, 2) and R (6, 5).
Area of ΔPQR
= \(\frac{1}{2}\)[4(2 – 5) + 3(5 – 6) + 6(6 – 2)]
= \(\frac{1}{2}\)[- 12 – 3 + 24]
= \(\frac{9}{2}\) sq units

2. Taking C as the origin and CB and CD as positive x-axis and y-axis respectively, we get C(0, 0), B(16, 0), D (0, 8) and A (16, 8) as the vertices of quadrilateral ABCD. Then, the vertices of ΔPQR are P (12, 2), Q (13, 6) and R(10, 3).
Area of ΔPQR
= \(\frac{1}{2}\)[12(6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac{1}{2}\)[36 + 13 – 40]
= \(\frac{9}{2}\)sq units
We observe that the area of ΔPQR is same in both the cases.
Note: In second case, if we take CB and CD as negative x-axis and y-axis, then the vertices of ΔPQR will be P(-12, -2), Q(-13,-6) and R(-10,-3). Still the area of ΔPQR would not change.

Question 6.
The vertices of a ΔABC are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that \(\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}\). Calculate the area of the ΔADE and compare it with the area of ΔABC.
Answer:

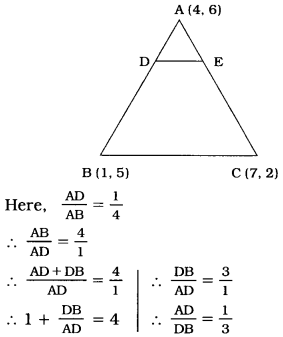
Similarly, \(\frac{AE}{EC}=\frac{1}{3}\)
Now, D divides the join of A (4, 6) and B(1, 5) in the ratio 1:3.
Then the coordinates of D are

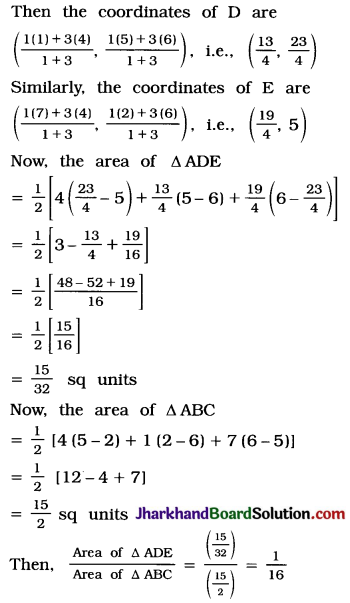
So, area of ΔADE : area of ΔABC = 1 : 16
Thus, the area of ΔADE is \(\frac{15}{32}\) sq units and the ratio of areas of ΔADE and ΔABC is 1 : 16.

Question 7.
Let A (4, 2), B (6, 5) and C(1, 4) be the vertices of AABC.
1. The median from A meets BC at D. Find the coordinates of the point D.
2. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
3. Find the coordinates of points Q and R on medians BE and CF respectively such that BQ:QE=2:1 and CR : RF = 2:1.
4. What do you observe? [Note: The point which is common to all the three medians is called the centroid and this point divides each median in the ratio 2:1.]
5. If A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) and the vertices of ΔABC, find the coordinates of the centroid of the triangle.

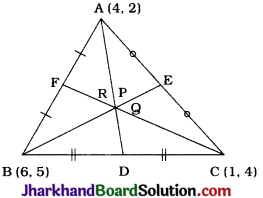
Answer:
1. AD is a median. Hence, D is the midpoint of BC.
Then, the coordinates of D, by midpoint formula, are (\(\frac{6+1}{2}, \frac{5+4}{2}\))
= (\(\frac{7}{2}\), \(\frac{9}{2}\)).

2. Point P divides AD in the ratio 2 : 1.
∴ Coordinates of P by section formula, are (\(\frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}, \frac{2\left(\frac{9}{2}\right)+2}{2+1}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))

3. BE is a median. Hence, E is the midpoint of AC.
Then, the coordinates of E, by midpoint formula, are
(\(\frac{4+1}{2}, \frac{2+4}{2}\)) = (\(\frac{5}{2}\), 3).
Now, Q divides BE in the ratio 2 : 1.
∴ Coordinates of Q, by section formula, are (\(\frac{2\left(\frac{5}{2}\right)+1(6)}{2+1}, \frac{2(3)+1(5)}{2+1}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))
CF is a median, Hence, F is the midpoint of AB.
Then, the coordinates of F, by midpoint formula are (\(\frac{4+6}{2}, \frac{2+5}{2}\)) = (5, \(\frac{7}{2}\)).
Point R divide CF in the ratio 2 : 1.
∴ Coordinates of R, by section formula, are (\(\frac{2(5)+1(1)}{2+1}, \frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))

4. Here, we observe that points P(\(\frac{11}{3}\), \(\frac{11}{3}\)), Q(\(\frac{11}{3}\), \(\frac{11}{3}\)) and R(\(\frac{11}{3}\), \(\frac{11}{3}\)) are the same points. i.e., P = Q = R.
This means that all the three medians are concurrent at point P (or Q or R).
This point is called the centroid of the triangle which is usually denoted by letter G. Centroid of a triangle divides each of its medians in the ratio 2 : 1 from the vertex side.

5. Now, the coordinates of the vertices of ΔABC are A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃).
AD, BE and CF are medians.
Hence, D, E and F are the midpoints of BC, AC and AB respectively.

Note: Now, with this formula, we can verify the answers received in part (2) and (3), as (\(\frac{4+6+1}{3}, \frac{2+5+4}{3}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))

Question 8.
ABCD is a rectangle formed by the points A(-1, -1), B(1, 4), C (5, 4) and D (5, 1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Answer:

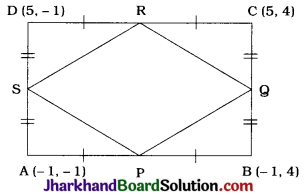
In rectangle ABCD, P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Then, the coordinates of P, Q, R and S are obtained as

So, in quadrilateral PQRS,
PQ² = QR² = RS² SP2 but PR² ≠ QS², i.e..
PQ = QR = RS = SP but PR ≠ QS
So, in quadrilateral PQRS, all the sides are equal but diagonals are not equal.
Hence, PQRS is a rhombus.