Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Exercise 8.1
Question 1.
Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° – sin² 60°

Solution :
(i) sin 60° cos 30° + sin 30° cos 60°
\(\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\) + \(\frac{1}{2} \times \frac{1}{2}\)
\(\frac{3}{4}+\frac{1}{4}\) = 1
(ii) 2 tan² 45° + cos² 30° – sin² 60°
2(tan 45)² + (cos 30)² – (sin 60)²
2(1)² + (\(\frac{\sqrt{3}}{2}\))² – (\(\frac{\sqrt{3}}{2}\))² = 2

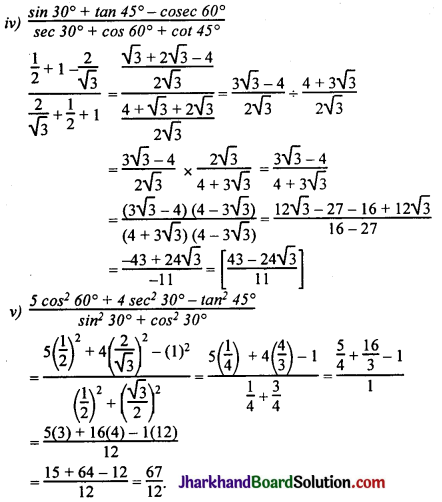
![]()
Question 2.
Choose the correct option and justify your choice:
(i) \(\frac{2 \tan 30^{\circ}}{1+\tan ^2 30^{\circ}}\)
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
Solution :
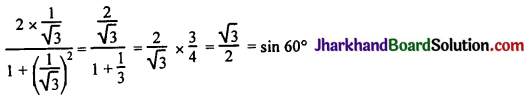
(ii) \(\frac{1-\tan ^2 45^{\circ}}{1+\tan ^2 45^{\circ}}\) =
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0
Solution :
\(\frac{1-(-1)^2}{1+(1)^2}=\frac{0}{2}\) = 0
(iii) sin 2A = 2 sin A is true when A =
(A) 0°
(B) 30°
(C) 45°
(D) 60°
Solution :
sin 2A = sin 0° = 0
2 sin A = 2 sin 0° = 2(0) = 0.
(iv) \(\frac{2 \tan 30^{\circ}}{1-\tan ^2 30^{\circ}}\) =
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°
Solution :
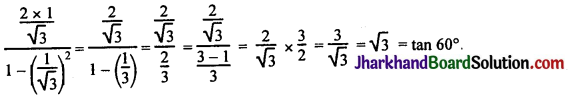
Question 3.
If tan (A + B) = \(\sqrt{3}\) and tan (A – B) = \(\frac{1}{\sqrt{3}}\), 0° < A + B ≤ 90°; A > B, find A and B.
Solution :
tan(A + B) = \(\sqrt{3}\)
tan 60° = \(\sqrt{3}\)
∴ A + B = 60°
tan (A – B) = \(\frac{1}{\sqrt{3}}\)
tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ A – B = 30°
∴ \(\hat{\mathbf{A}}\) = 45°, \(\hat{\mathbf{B}}\) = 15°
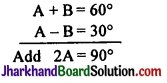
A + B = 60°
45 + B = 60°
B = 60 – 45 = 15
∴ B = 15°
![]()
Question 4.
State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution :
i) Let A = 30°, B = 60°.
sin 30° = \(\frac{1}{2}\)
sin 30 + sin 60°
sin (A + B) = sin 90° = 1
sin 60° = \(\frac{\sqrt{3}}{2}\)
\(\frac{1}{2}+\frac{\sqrt{3}}{2}\) = \(\frac{1+\sqrt{3}}{2}\)
sin (A+B) sin A + sin B
False.
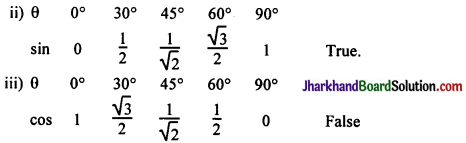
iv) [θ = 0] sin 0 = 0
cos 0 = 1
θ = 30° sin 30° = \(\frac{1}{2}\)
cos 30° = \(\frac{\sqrt{3}}{2}\)
θ = 45° sin 45° = \(\frac{1}{\sqrt{2}}\)
cos 45° = \(\frac{1}{\sqrt{2}}\)
θ = 60° sin 60° = \(\frac{\sqrt{3}}{2}\)
cos 60° = \(\frac{1}{2}\)
θ = 90° sin 90° = 1
cos 90° = 0
False, because it is true only for θ = 45°.
(v) cot A = \(\frac{cos A}{sin A}\) . cot 0° = \(\frac{cos 0°}{sin 0°}\) = \(\frac{1}{0}\) = Undefined. True.