Jharkhand Board JAC Class 9 Maths Important Questions Chapter 6 रेखाएँ और कोण Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 6 रेखाएँ और कोण
प्रश्न 1.
निम्नलिखित वाक्यों में रिक्त स्थानों की पूर्ति कीजिए-
(i) दो आसन्न कोण एक रेखीय युग्म बनाते हैं, यदि वे ……………… हों ।
(ii) यदि एक किरण एक रेखा पर खड़ी है तो इस प्रकार बने दो आसन्न कोणों का योग ………………….. होता है।
(iii) यदि दो आसन्न कोणों का योग 180° हो तो वे एक ………………. बनाते हैं।
(iv) दो आसन्न कोणों का शीर्ष बिन्दु …………. ही होता है।
(v) यदि दो शीर्षाभिमुख कोणों में से एक x° हो तो दूसरा कोण …………….. होगा।
(vi) यदि दो रेखाऐं एक दूसरे पर लम्ब हों तो वे परस्पर ……………. होती हैं।
(vii) यदि दो रेखाओं को एक तियक रेखा काटे और इस प्रकार बने संगत कोण बराबर हों, तो वे रेखाएँ परस्पर ……………… होती हैं।
(viii) यदि दो समान्तर रेखाओं को एक तिर्यक रेखा काटे तो इस प्रकार बने एकान्तर कोण ……………….. होते हैं।
(ix) दो आसन्न सम्पूरक कोणों के समद्विभाजक एक दूसरे पर ……………….. होते हैं।
(x) त्रिभुज की किसी भुजा को बढ़ाने पर ………………. बनता है, जो के मानों के योग के बराबर होता है।
हल :
(i) सम्पूरक कोण
(ii) 180°
(iii) रेखीय युग्म,
(iv) एक
(v) x°
(vi) समान्तर
(vii) समान्तर,
(viii) समान,
(ix) लम्ब
(x) शीर्षाभिमुख कोण, अंत: अभिमुख कोणों ।
![]()
प्रश्न 2.
चित्र में प्रतिवर्ती कोण ∠POQ बराबर है :
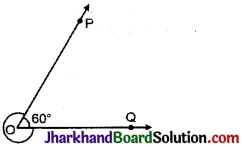
(A) 60°
(B) 120°
(C) 300°
(D) 360°.
हल :
∵ किसी बिन्दु पर समस्त कोणों का योग = 360°
∴ दीर्घ ∠POQ = 360° – लघु ∠POQ = 360° – 60° = 300°
अत: विकल्प (C) सही है।
प्रश्न 3.
चित्र में दो समान्तर रेखाओं l तथा m को एक तिर्यक् रेखा n, बिन्दुओं G तथा H पर काट रही है। इस प्रकार बनने वाले कोण चित्र में अंकित हैं। यदि ∠1 न्यूनकोण हो, तो बताइए निम्न में से कौन-सा कथन असत्य है :
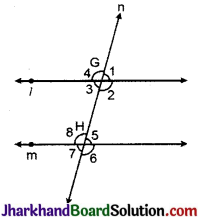
(A) ∠1 + ∠2 = 180°
(B) ∠2 + ∠5 = 180°
(C) ∠3 + ∠8 = 180°
(D) ∠2 + ∠6 = 180°
हल :
∠1 + ∠2 = 180° (रैखिक कोण युग्म)
∠2 + ∠5 = 180° (संगत अन्तः कोणों का योग)
∠3 + ∠8 = 180° (संगत अन्तः कोणों का योग)
∠1 + ∠2 = 180°
न्यूनकोण + ∠2 = 180°
⇒ ∠2 = 180° – न्यूनकोण
⇒ ∠2 = अधिक कोण
⇒ ∠2 = ∠6 (संगतकोण)
अतः अधिक कोण अधिक कोण > 180°
![]()
प्रश्न 4.
चित्र में दो समान्तर रेखाओं a तथा b को एक तिर्यक रेखा c बिन्दुओं A तथा B पर काटती है। A तथा B पर बनने वाले कोण चित्र में अंकित हैं। चित्र में बताइए कि निम्न में से कौन-से कोण युग्म का समान होना आवश्यक नहीं है:
(A) ∠1, ∠2
(B) ∠1, ∠3
(C) ∠1, ∠5
(D) ∠2, ∠8
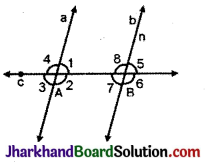
हल :
∠1 और ∠2 तब तक बराबर नहीं हो सकते जब तक कि तिर्यक रेखा c, भुजाओं a तथा b पर लम्ब न हो।
∠1 = ∠3 (शीर्षाभिमुख कोण)
∠1 = ∠5 (संगत कोण)
∠2 = ∠8 (एकान्तर कोण)
∵ ∠1 व ∠2 का समान होना आवश्यक नहीं है।
अतः विकल्प (A) सही है।
प्रश्न 5.
निम्न में पूरक कोण युग्म नहीं है:
(A) 60°, 30°
(B) 56°, 34°
(C) 0°, 90°
(D) 150°, 30°.
हल :
पूरक कोण युग्म का योग 90° होता है।
अतः विकल्प (D) सही है।
प्रश्न 6.
निम्न में सम्पूरक कोण युग्म नहीं है:
(A) 90°, 90°
(B) 32°, 58°
(C) 0°, 180°
(D) 76°, 104°
हल :
सम्पूरक कोण युग्म का योग 180° होता है।
अतः विकल्प (B) सही हैं।
![]()
प्रश्न 7.
चित्र में दर्शाए कोण ∠AOB तथा ∠BOC हैं:
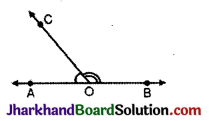
(A) पूरक कोण
(B) सम्पूरक कोण
(C) आसन्न कोण
(D) उपर्युक्त में से कोई नहीं।
हल :
किरण AOB के बिन्दु पर दो आसन्न कोण ∠AOB तथा ∠BOC हैं।
अत: विकल्प (D) सही है।
प्रश्न 8.
चित्र में दो सरल रेखाएँ AB तथा CD एक-दूसरे को O बिन्दु पर प्रतिच्छेद कर रही हैं और इस प्रकार बिन्दु O पर बने कोण अंकित हैं। यहाँ ∠x – ∠y का मान है :
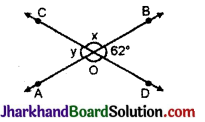
(A) 56°
(B) 118°
(C) 620
(D) 180°.
हल :
∠BOC + ∠BOD = 180° (रैखिक युग्म कोण)
x + 62° = 180°
x = 180° – 62° = 118°
अत: विकल्प (A) सही है।
[∵ ∠x – ∠y = 118° – 62° = 56°]
![]()
प्रश्न 9.
चित्र से बताइए कि निम्न में कौन-सा युग्म, संगत कोण नहीं हैं:
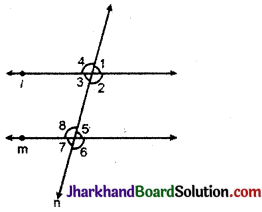
(A) ∠1, ∠5
(B) ∠2, ∠6
(C) ∠3, ∠7
(D) ∠3, ∠5
हल :
∠3 और ∠5 एकान्तर कोण हैं। अन्त तीन संगत कोण हैं। अतः विकल्प (D) सही है।
प्रश्न 10.
चित्र में रेखाएँ l तथा m समान्तर हैं, तो ∠x का मानज्ञात कीजिए । कारण भी स्पष्ट कीजिए।
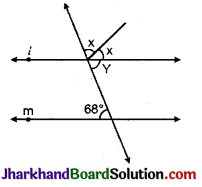
हल :
∠y = 68° (एकान्तर कोण)
∠y + ∠x + ∠x = 180° (रेखिक कोण युग्म)
⇒ 68° + 2∠x = 180°
⇒ 2∠x = 180° – 68°
⇒ 2∠x = 112°
⇒ ∠x = \(\frac {112°}{2}\)
∴ ∠x = 56°
![]()
प्रश्न 11.
चित्र में, ∠AOB, ∠COD एवं ∠EOF ज्ञात कीजिए ।
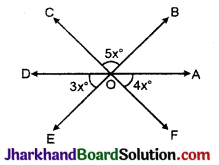
हल :
दिया है, CF और BE, दो रेखाएँ एक-दूसरे को प्रतिच्छेद कर रही हैं,
∴ ∠COB = ∠EOF (शीर्षाभिमुख कोण)
5x° = ∠EOF
∴ ∠EOF = 5x°
अत: ∠AOF + ∠EOF + ∠DOE = 180°
[∵ DOA एक सरल रेखा है]
4x° + 5x° + 3x° = 180°
⇒ 12x° = 180°
⇒ x° = \(\frac {180°}{12}\)
∴ x° = 15°
अतः
∠AOB = ∠DOE (शीर्षाभिमुख कोण)
= 3x° = 3 × 15° = 45°
∠COD = ∠AOF (शीर्षाभिमुख कोण)
= 4x° = 4 × 15° = 60°
∠EOF = ∠COB (शीर्षाभिमुख कोण)
= 5x° = 5 × 15° = 75°
अत: ∠AOB, ∠COD और ∠EOF क्रमश: 45°, 60° और 75° हैं।
प्रश्न 12.
चित्र में, ∠POR और ∠QOR एक रैखिक कोण युग्म बनाते हैं। यदि a – b = 80°, तो a और b का मान ज्ञात कीजिए।
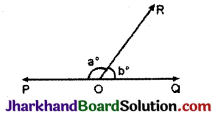
हल :
दिया है, ∠a तथा ∠b रैखिक युग्म हैं
अतः a + b = 180° …………..(i)
एवं a – b = 80° …………..(ii) (दिया है)
समीकरण (i) और (ii) को जोड़ने पर,
2a = 260°
∴ a = \(\frac {260°}{2}\) = 130°
a का मान समीकरण (i) में रखने पर,
⇒ 130° + b = 180°
⇒ b = 180° – 130°
∴ b = 50°
अतः a = 130°, b = 50°
प्रश्न 13.
आकृति में रेखाएँ PQ और RS परस्पर बिन्दु O पर प्रतिच्छेद करती हैं यदि ∠POR : ∠ROQ = 5 : 7 हो, तो सभी कोण ज्ञात करो ।
हल :
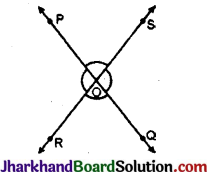
∠POR + ∠ROQ = 180° (रैखिक कोण युग्म)
∵ ∠POR : ∠ROQ = 5 : 7 (दिया है)
माना ∠POR = 5x, तथा ∠ROQ = 7x
∴ 5x + 7x = 180°
12x = 180°
x = \(\frac {180°}{2}\) = 15°
∴ ∠POR = 5 × 15 = 75°
तथा ∠ROQ = 7 × 15 = 105°
अत: ∠POS = ∠ROQ = 105° (शीर्षाभिमुख कोण)
और ∠SOQ = ∠POR = 75° (शीर्षाभिमुख कोण)
प्रश्न 14.
आकृति में, OP, OQ, OR और OS चार किरणें हैं। सिद्ध कीजिए कि
∠POQ + ∠QOR + ∠SOR + ∠POS = 360° है।
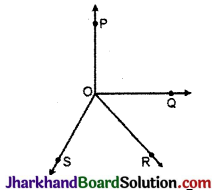
हल :
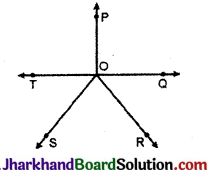
किरण QO को T बिन्दु तक आगे बढ़ाया। TOQ सरल रेखा हैं।
∴ ∠TOP + ∠POQ = 180° ……….(1)
(रैखिक कोण युग्म)
इसी प्रकार, किरण OS, रेखा TOQ पर खड़ी है।
⇒ ∠TOS +∠SOQ= 180° (रैखिक कोण युग्म)
परन्तु ∠SOQ = ∠SOR + ∠QOR है।
⇒ ∠TOS + ∠SOR + ∠QOR = 180° … (2)
अब (1) और (2) को जोड़ने पर,
∠TOP + ∠POQ + ∠TOS + ∠SOR + ∠QOR
= 180° + 180°
[∵ ∠TOP + ∠TOS = ∠POS]
= ∠POQ + ∠QOR + ∠SOR + ∠POS
= 360°. इति सिद्धम् ।
![]()
प्रश्न 15.
आकृति में AB || CD और CD || EF है। साथ ही EA ⊥ AB है। यदि ∠BEF = 55° है, तो x, y और z के मान ज्ञात कीजिए।
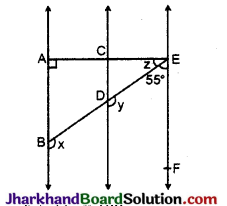
हल :
y + 55° = 180°
(CD || EF, तिर्यक रेखा ED के एक ही ओर के अन्त:कोण)
⇒ y = 180° – 55° = 125°
x = y (संगत कोण)
∴ x = 125°
∵ AB || CD और CD || EF
∴ AB || EF होगी।
⇒ ∠EAB + ∠FEA = 180° (अन्तःकोण)
⇒ 90° + z + 55° = 180°
∴ z = 180° – 90° – 55°
= 35°
अतः x y और z के मान क्रमशः 125°, 125° और 350° हैं।
प्रश्न 16.
यदि दो समान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेदित करती है, तो सिद्ध कीजिए कि अन्तः कोणों के समद्विभाजकों से एक आयत बनता है।
हल :
दिया है AB || CD तथा तिर्यक रेखा EF || AB व CD को क्रमश: P तथा Q पर काटती है अन्तः कोणों के समद्विभाजक क्रमश: PR व QR बिन्दु R पर तथा ∠BPQ एवं ∠PQD के समद्विभाजक PS व QS बिन्दु S पर काटते हैं।
उपपत्ति: AB || CD, व तिर्यक रेखा EF उन्हें P तथा Q पर काटती है।
∴ ∠APQ = ∠PQD (एकान्तर कोण )
⇒ \(\frac {1}{2}\)∠APQ = \(\frac {1}{2}\)∠PQD
⇒ ∠2 = ∠4
परन्तु ∠2 व ∠4 एकान्तर कोण युग्म है।
∴ RP || QS ………..(i)
इसी प्रकार ∠1 = ∠3
∴ PS || QR …….(ii)
(i) व (ii) से
PSQR एक समान्तर चतुर्भुज है ….(iii)
परन्तु ∠APQ + ∠BPQ = 180°
⇒ \(\frac {1}{2}\)∠APQ + \(\frac {1}{2}\)∠BPQ = \(\frac {1}{2}\) × 180°
⇒ ∠2 = ∠1 = 90°
⇒ ∠RPS = 90°
∴ PS QR एक आयत हैं। इति सिद्धम्
![]()
प्रश्न 17.
चित्र में AB || DC हो, तो दिए गए कोणों से ∠x, ∠y तथा ∠z ज्ञात कीजिए।
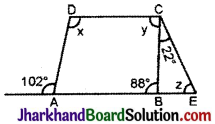
हल :
AB || DC
∴ x = 102° (एकान्तर कोण)
और 88° = 22° + z (CBE का बहिष्कोण)
z° = 88° – 22° = 66°
और ∵ AB || DC
∴ y + 88° = 180°
(एक ही ओर के अन्तः कोणों का योग)
∴ ∠y = 180° – 88°
∴ ∠y = 92°
अतः ∠x = 102°, y = 92°, z = 66°
प्रश्न 18.
दिए गए चित्र से ∠x तथा ∠y के माप ज्ञात कीजिए। यदि ∠x – ∠y = 10° हो ।
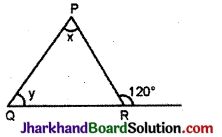
हल :
∠x – ∠y = 10° (दिया है) … (i)
और ∠x + ∠y = 120°
(बहिष्कोण = दोनों अन्तराभिमुख अन्तः कोणों का योगफल) … (ii)
(i) व (ii) को जोड़ने पर
⇒ 2∠x = 130° ⇒ ∠x = 65°
समी. (ii) से,
65° + ∠y = 120°
∴ ∠y = 120° – 65° = 55°.
अतः ∠x = 65° तथा ∠y = 55°
![]()
प्रश्न 19.
आकृति में, ΔABC की भुजाओं AB और AC को क्रमशः E और D तक बढ़ाया गया है। यदि ∠CBE और ∠BCD के समद्विभाजक क्रमश: BO और CO बिन्दु O पर मिलते हैं, तो सिद्ध कीजिए कि
∠BOC = 90° – \(\frac {1}{2}\)∠BAC
हल :
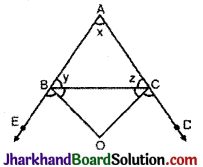
किरण BO, ∠CBE की समद्विभाजक है।
∴ ∠CBO = \(\frac {1}{2}\)∠CBE
= \(\frac {1}{2}\)(180° – y)
= 90° – \(\frac {z}{2}\) ………….(1)
इसी प्रकार, किरण CO, ∠BCD की समद्विभाजक
∠BCO = \(\frac {1}{2}\)∠BCD = \(\frac {1}{2}\)(180° – z)
= 90° – \(\frac {z}{2}\) ……….(2)
ΔBOC में,
∠BOC + ∠BCO + ∠CBO = 180° ……….(3)
समीकरण (1) व (2) के मान (3) में रखने पर,
∠BOC + 90° – \(\frac {z}{2}\) + 90° – \(\frac {y}{2}\) = 180°
∠BOC = \(\frac{z}{2}+\frac{y}{2}\)
∠BOC = \(\frac {1}{2}\)(y + z)
[∵ त्रिभुज के तीनों कोणों का योग (x + y + z) = 180°]
y + z = 180° – x
\(\frac {1}{2}\)(y + z) = \(\frac {1}{2}\)(180 – x)
∠BOC = \(\frac {1}{2}\)(180° – x)
= \(\frac {1}{2}\) × 180° – \(\frac {x}{2}\)
अतः ∠BOC = 90° – \(\frac {1}{2}\)∠BAC. इति सिद्धम् ।
प्रश्न 20.
निम्न चित्र में m और n दो समतल दर्पण हैं जो परस्पर लम्बवत है। दिखाइए कि आपतित किरण CA, परावर्तित किरण BD के समान्तर है।
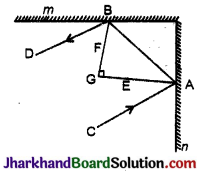
हल :
दिया है: m ⊥ n तथा
आ CA, n पर आपतित व BD, m पर परावर्तित किरणें हैं।
सिद्ध करना है : CA || BD
रचना : AE ⊥ n तथा BF ⊥ Lin खींचे
उपपत्ति : AE ⊥ n तथा BF ⊥ m एवं m ⊥ n
∴ BF ⊥ AE या BG ⊥ GA
ΔBGA = 90°
एवं ∠GAB + ∠GBA + ∠BGA = 180°
(त्रिभुज के अन्त कोणों का योग)
⇒ ∠GAB + ∠GBA + 90° = 180°
⇒ ∠GAB + ∠GBA = 90° ……………..(i)
∵ आपतन कोण परावर्तन कोण
∴ ∠CAG = ∠GAB ……(i)
⇒ ∠GBA = \(\frac {1}{2}\)∠CAB … (ii)
इसी प्रकार ∠CAG = \(\frac {1}{2}\)∠ABD … (iii)
(i), (ii) तथा (iii) से
⇒ \(\frac {1}{2}\)∠CAB + \(\frac {1}{2}\)∠ABD = 90°
⇒ ∠CAB + ∠ABD = 180°
किन्तु में तिर्यक रेखा के एक ही ओर के कोण हैं
अत: CA || BD इति सिद्धम्
![]()
प्रश्न 21.
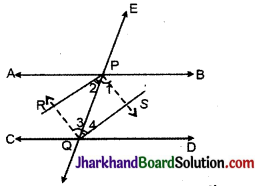
यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों के एक युग्म के समद्विभाजक परस्पर समान्तर हों, तो सिद्ध करो कि दोनों रेखाएँ भी परस्पर समान्तर होती हैं।
हल :
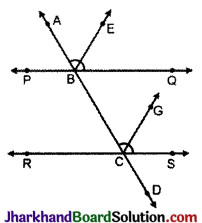
दिया है : एक तिर्यक रेखा AD दो रेखाओं PQ और RS को B व C बिन्दु पर प्रतिच्छेद करती है। किरण BE, ∠ABQ की समद्विभाजक और किरण CG, ∠BCS की समद्विभाजक है तथा BE || CG है।
सिद्ध करना है : PQ || RS
उपपत्ति: किरण BE, ∠ABQ की समद्विभाजक है।
∴ ∠ABE = \(\frac {1}{2}\)∠ABQ ……. (1)
इसी प्रकार, किरण CG, ∠BCS की समद्विभाजक है।
∴ ∠BCG = \(\frac {1}{2}\)∠BCS …….. (2)
∵ BE || CG है और AD तिर्यक काटती है।
∴ ∠ABE = ∠BCG (संगत कोण)
समी (1) और (2) से मान रखने पर,
\(\frac {1}{2}\)∠ABQ = \(\frac {1}{2}\)∠BCS (संगत कोण)
⇒ ∠ABQ = ∠BCS
∴ PQ || RS. इति सिद्धम् ।
प्रश्न 22.
निम्न आकृति में, ∠ABC और ∠BCA के कोण समद्विभाजक बिन्दु O पर परस्पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि ∠BOC = 90° + \(\frac {1}{2}\)∠A.
हल :
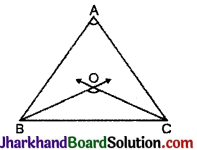
दिया है ΔABC में ZABC तथा ∠BCA के समद्विभाजक BO तथा CO बिन्दु पर एक-दूसरे को काटते हैं।
सिद्ध करना है: ∠BOC = 90° + \(\frac {1}{2}\)∠A
उपपत्ति : ∵BO, ∠ABC की समद्विभाजक है।
∴ ∠OBC = \(\frac {1}{2}\)∠ABC
इसी प्रकार CO, ∠BCA की समद्विभाजक है।
∴ ∠OCB = \(\frac {1}{2}\)∠BCA
⇒ ∠OBC + ∠OCB = \(\frac {1}{2}\)∠ABC + \(\frac {1}{2}\)∠BCA … (1)
ΔABC से, ∵ ∠ABC + ∠BCA + ∠A = 180°
⇒ \(\frac {1}{2}\)∠ABC + \(\frac {1}{2}\)∠BCA + \(\frac {1}{2}\)∠A = \(\frac {1}{2}\) × 180°
⇒ \(\frac {1}{2}\)∠ABC + \(\frac {1}{2}\)∠BCA = 90° – \(\frac {1}{2}\)∠A …..(2)
समी (2) में समी. (1) का मान रखने पर,
∠BOC + ∠OCB = 90° – \(\frac {1}{2}\)∠A …………..(3)
ΔOBC से, ∠OBC + ∠OCB + ∠BOC = 180°
समीकरण (3) से मान रखने पर
90° – \(\frac {1}{2}\)∠A + ∠BOC = 180°
∴ ∠BOC = 90° + \(\frac {1}{2}\)∠A इति सिद्धम् ।
![]()
प्रश्न 23.
सिद्ध करो कि किसी चतुर्भुज के चारों कोणों का योगफल चार समकोण के बराबर होता है।
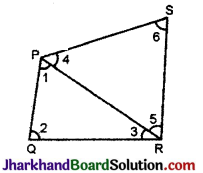
हल :
दिया है
चतुर्भुज PQRS
रचना : PR को मिलाया, अत: रेखा PR, चतुर्भुज PQRS को दो त्रिभुओं PQR तथा SPR में बाँटती है।
ΔPQR में, ∠1 + ∠2 + ∠3 = 180° … (i)
एवं ΔPSR में ∠4 + ∠5 + ∠6 = 180° …(ii)
समीकरण (i) तथा (ii) से,
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°
या (∠1 + ∠4) + ∠2 + (∠3 + ∠5) + ∠6 = 360°
या ∠P + ∠Q + ∠R + ∠S = 360°
या ∠P + ∠Q + ∠R + ∠S = 4 × 90°
या ∠P + ∠Q + ∠R + ∠S = 4 समकोण । इति सिद्धम् ।
प्रश्न 24.
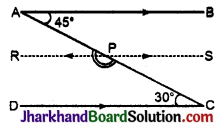
दिये गये चित्र में AB और CD दो समान्तर रेखाओं के बीच विन्दु P इस प्रकार है किं ∠PAB 45° तथा ∠PCD = 30° तो बृहत कोण APC का मान ज्ञात कीजिए।
हल :
बिन्दु P से AB रेखा के समान्तर RS रेखा खींची।
अतः
∠BAP = ∠APR = 45° (एकान्तर कोण)
इसी प्रकार, ∠SPC = ∠PCD = 30° (एकान्तर कोण)
अव ∠RPC = 180° – 30° = 150°
∴ ∠APC = ∠APR + ∠RPC
= 45° + 150°
∴ ∠APC = 195°.
![]()
प्रश्न 25.
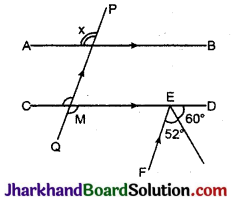
दिये गये चित्र में AB || CD तथा PQ || EF तो ∠x का मान ज्ञात कीजिए।
हल :
∠DEF = 60° + 52° = 112°
∠EMQ = ∠DEF (संगत कोण)
परन्तु
∠PMC = ∠EMQ
= 112° (शीर्षाभिमुख कोण)
∴ ∠x = ∠PMC (संगत कोण)
∴ ∠x = 112°
प्रश्न 26.
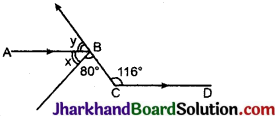
दी गई आकृति में AB || CD हैं तो ∠x तथा के मान ज्ञात कीजिए।
हल :
(i) ∠ABC = ∠BCD (एकान्तर कोण)
∵ ∠x + 80° = 116
∴ ∠x = 116° – 80°
= 36°
(ii) परन्तु
∠y + ∠x + 80° = 180°,
(सरल रेखा पर बने कोण)
⇒ ∠y + 80° + 36° = 180°
⇒ ∠y = 180 – 80 – 36 = 180° – 116°
∴ ∠y = 64°
![]()
प्रश्न 27.
दिये गये चित्र में यदि, QT ⊥ PR, ∠TQR = 40°, ∠SPR = 30° है तो x तथा y के मान ज्ञात कीजिए।
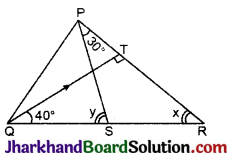
हल :
(i) ΔTQR में, ∠T = 90° (∵ OT⊥PR)
∴ 90° + 40° + x = 180°
(त्रिभुज के अन्तःकोणों का योग )
⇒ ∠x = 180° – 40° – 90° = 180° – 130°
∴ ∠x = 50°.
(ii) ΔPSR में,
∠y, ΔPSR का बहिष्कोण है।
∴ ∠y = 30° + x = 30° + 50°
∴ ∠y = 80°.