Jharkhand Board JAC Class 9 Maths Important Questions Chapter 7 त्रिभुज Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 7 त्रिभुज
प्रश्न 1.
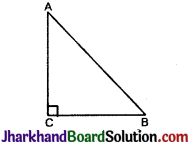
समकोण त्रिभुज ABC में कोण C समकोण हो, तो बड़ी भुजा होगी:
(A) AB
(B) BC
(C) CA
(D) कोई नहीं।
हल :
समकोण के सामने वाली भुजा AB (कर्ण) सबसे बड़ी होगी।
अत: सही विकल्प ‘A’ है।
![]()
प्रश्न 2.
किसी त्रिभुज की किन्हीं दो भुजाओं का अन्तर उसकी तीसरी भुजा से होता है:
(A) अधिक
(B) समान
(C) कम
(D) आधा।
हल :
किसी त्रिभुज की किन्हीं दो भुजाओं का अन्तर उसकी तीसरी भुजा से कम होता है।
अतः सही विकल्प ‘C’ है।
प्रश्न 3.
त्रिभुज के तीनों शीर्ष लम्बों का योग उसके परिमाप से होता है:
(A) अधिक
(B) समान
(C) आधा
(D) कम।
हल :
त्रिभुज के तीनों शीर्ष लम्बों का योग, त्रिभुज के परिमाप से कम होता है।
अतः सही विकल्प ‘D’ है।
प्रश्न 4.
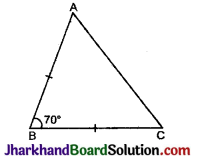
चित्र में, ∠A का मान होगा : यदि AB = BC एवं ∠B = 70°।
(A) 70°
(B) 40°
(C) 55°
(D) 90°.
हल :
चित्र में, ΔABC एक समद्विबाहु 4 है।
AB = BC
∴ ∠C = ∠A
हम जानते हैं कि
∠A + ∠B + ∠C = 180°
⇒ ∠A + 70° + ∠A = 180°
⇒ 2∠A = 180° – 70°
⇒ 2∠A = 110°
⇒ ∠A = \(\frac {110°}{2}\)
∴ ∠A = 55°
अतः सही विकल्प ‘C’ है।
![]()
प्रश्न 5.
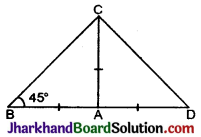
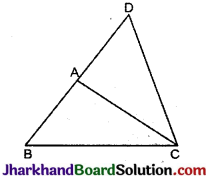
एक समद्विबाहु त्रिभुज ABC में, AB = AC तथा ∠B = 45° है, एवं भुजा BA को D तक इस प्रकार बढ़ाया कि AB = AD हो, तो ∠BCD की माप होगी :
(A) 70°
(B) 90°
(C) 60°
(D) 45°
हल :
AB = AC ……………(i)
∠ACB = ∠B
(समान भुजाओं के सम्मुख कोण समान होते हैं)
∠ACB = 45°
∠A + ∠B + ∠CAB = 180°
(त्रिभुज के अन्तः कोणों का योग )
45° + 45° + ∠CAB = 180°
∠CAB = 180° – 90° = 90°
तथा ∠CAD = ∠CAB = 90°
अब AB = AD (दिया है)
तब AD = AC (∵ AC = AB)
ΔACD समकोण समद्विबाहु D में, (माना)
∴ ∠C = ∠D = x°
तब
∠A + ∠C + ∠D = 180°
90° + x + x° = 180°
2x = 180 – 90° = 90°
x° = 45°
∴ ∠BCD = 45° + 45° = 90°
अतः सही विकल्प ‘B’ है।
प्रश्न 6.
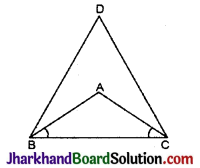
चित्र में, AB = AC एवं ∠ABD = ∠ACD हो, तो ΔBDC होगा :
(A) समबाहु त्रिभुज
(B) समद्विबाहु त्रिभुज
(C) समानकोणिक त्रिभुज
(D) विषमबाहु त्रिभुज ।
हल :
AB = AC (दिया है)
∴ ∠ABC = ∠ACB …….(i)
(समान भुजाओं के सामने के कोण)
∠ABD = ∠ACD (दिया है) …(ii)
(i) व (ii) को जोड़ने पर,
∠ABC + ∠ABD = ∠ACB + ∠ACD
∠DBC = ∠DCB
∴ BD = DC
(समान कोणों की सम्मुख भुजाएँ )
अत: ΔBCD एक समद्विबाहु 4 है।
अतः सही विकल्प ‘B’ है।
![]()
प्रश्न 7.
चित्र में ΔABC में, AB = AC एवं AD ⊥ BC हो, न्तो भुजा AD समद्विभाजक होगी :
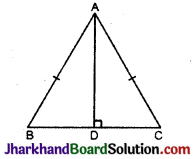
(A) कोण 4 की
(B) भुजा BC की
(C) कोण A एवं भुजा BC की
(D) किसी की नहीं।
हल :
चित्र में, AB = AC (दिया है)
AD ⊥ BC (दिया है)
ΔABD तथा ΔADC में,
AB = AC (दिया है)
∠ADB = ∠ADC (समकोण)
∠ABD = ∠ACD (समान कोणों के सम्मुख कोण)
∴ ΔABD ≅ ΔADC (ASA)
∴ ∠BAD = ∠CAD
तथा BC = DC
अतः भुजा AD, ∠A और भुजा BC की समद्विभाजक है।
अतः सही विकल्प ‘C’ है।
प्रश्न 8.
किसी त्रिभुज की बराबर भुजाओं के सम्मुख कोण …………… होते हैं।
हल :
बराबर।
प्रश्न 9.
चित्र में, भुजा AB एवं AC में सम्बन्ध लिखिए।
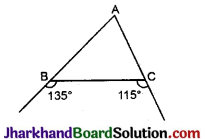
हल :
यहाँ बहिष्कोण B = 135°
∴ ∠ABC + 135° = 180°
∴ ∠ABC = 180° – 135° = 45°
और बहिष्कोण C = 115°
∠ACB + 115° = 180°
∴ ∠ACB = 180° – 115° = 65°
अब ∠ACB > ∠ABC
AB > AC
(बड़े कोण की सम्मुख भुजा बड़ी होती है)
![]()
प्रश्न 10.
यदि ΔABC में, AB = AC तथा ∠A < 60° हो, भुजा BC एवं AC में सम्बन्ध लिखिए।
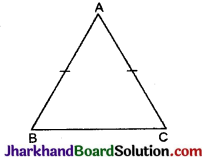
हल :
ΔABC में दियां, ∠A < 60° ……..(i)
∵ AB = AC
∴ ∠B = ∠C (समान भुजाओं के सम्मुख कोण)
हम जानते हैं कि ΔABC में, किसी त्रिभुज के तीनों कोणों का योग 180° होता है।
∠A + ∠B + ∠C = 180°
∵ ∠A < 60° और ∠B = ∠C
∴ ∠B = ∠C > 60° और ∠A < 60° (दिया है)
अब ∠B = ∠C > ∠A
⇒ ∠B > ∠A (सम्मुख भुजाओं के कोण)
⇒ AC > BC
⇒ BC < AC
प्रश्न 11.
चित्र में, चतुर्भुज ABCD के ∠ABC = ∠ABD एवं AC = BD हो, तो सिद्ध कीजिए कि ΔABC ≅ ΔABD.
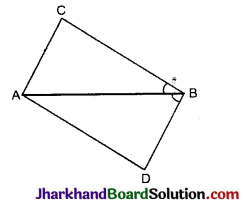
हल :
दिया है चतुर्भुज ABCD में
∠ABC = ∠ABD, AC = BD.
सिद्ध करना है: ΔABC ≅ ΔABD
उपपत्ति: ΔABC और ΔABD में.
BC = BD (दिया हैं)
∠ABC = ∠ABD (दिया है)
AB = AB (उभयनिष्ठ)
अतः भुजा कोण-भुजा
ΔABC ≅ ΔABD (SAS नियम) इति सिद्धम् ।
![]()
प्रश्न 12.
चित्र में त्रिभुज में कोई अन्तःबिन्दु O हो, तो सिद्ध कीजिए कि
(BC + AB + AC) < 2 (OA + OB + OC).
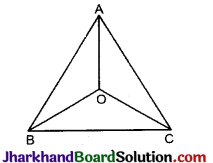
हल :
दिया है ΔABC में, O अन्त: बिन्दु है।
सिद्ध करना है
(BC + AB + AC) < 2 (OA + OB + OC).
उपपत्ति ΔAOB में, AO + BO > AB …(i) (Δ की दो भुजाओं का योग )
इसी प्रकार ΔBOC में, OB + OC > BC ….(ii)
इसी प्रकार ΔAOC में, OC + OA > AC ….(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर
(AO + BO) + (OB + OC) + (OC + OA) > AB + BC + AC
2(OA + OB + OC) > AB + BC + AC
या AB + BC + AC < 2(OA + OB + OC) इति सिद्धम् ।
प्रश्न 13.
निम्नांकित आकृति में PQRS एक चतुर्भुज है जिसके विकर्ण PR और Q5 बिन्दु पर प्रतिच्छेदित करते है। दिखाइये कि
(i) PQ + QR + RS + SP > PR + QS तथा
(ii) PQ + QR + RS + SP < 2 (PR + QS)
हल :
दिया है: चतुर्भुज PQRS में विकर्ण PR तथा QS एक दूसरे को O पर काटते हैं। सिद्ध करना है
(i) PQ + QR + RS + SP > PR + QS तथा
(ii) PQ + QR + RS + SP < 2(PR + QS)
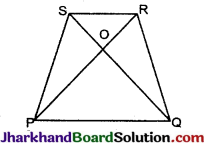
उपपत्ति : चूँकि त्रिभुज में किन्हीं दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
∴ ΔPQR से, PQ + QR > PR ……….(i)
ΔRSP में RS + SP > PR ………. (ii)
ΔQRS में OR + RS > QS ………. (iii)
ΔPQS में PQ + SP > QS …………(iv)
(i), (ii), (iii) और (iv) को जोड़ने पर,
2PQ + 2QR + 2RS + 2SP > 2(PR + QS)
⇒ PQ + QR + RS + SP > PR + QS इति सिद्धम् ।
पुन: ΔOPQ में
OP + OQ > PQ ………(v)
ΔOQR में OQ + OR > QR ……(vi)
ΔORS में OR + OS > RS ………(vii)
ΔOSP में OS + OP > SP ……..(viii)
(v), (vi), (vii) और (viii) को जोड़ने पर
2OP + 2OR + 2OQ + 2OS > PQ + QR + RS + SP
2(OP + OR + OQ + OS) > PQ + QR + RS + SP
2(PR+ QS) > PQ+QR + RS + SP
PQ + QR + RS + SP < 2 (PR + QS) इति सिद्धम् ।
![]()
प्रश्न 14.
सिद्ध कीजिए कि त्रिभुज की तीनों भुजाओं का योग उसकी तीनों माध्यिकाओं के योग से अधिक होता है।
हल :
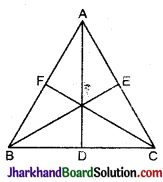
दिया है ABC में, माध्यिकाए AD BE और सिद्ध करना है AB + BC + AC > AD + BE + CE
उपपत्ति: हम जानते हैं कि किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा पर खींची गई माध्यिका के दुगुने से अधिक होता है। चित्र में 4 शीर्ष से
खींची गई भुजा BC पर AD माध्यिका है।
⇒ AB + AC > 2AD ……….(i)
B शीर्ष से खींची गई भुजा CA पर BE माध्यिका है।
⇒ BC + AB > 2BE …….(ii)
C शीर्ष से खींची गई भुजा AB पर CF माध्यिका है।
⇒ AC + BC > 2CF …………. (iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर,
(AB + AC) + (BC + AB) + (AC + BC) > 2AD + 2BE + 2CF
⇒ 2(AB + BC + AC) > 2 (AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF इति सिद्धम् ।
प्रश्न 15.
शलभ दो वस्तुओं के मध्य की दूरी मालूम करना चाहता है, परन्तु इन दोनों वस्तुओं के मध्य एक रुकावट है (जैसा कि चित्र में दिखाया गया है।), जिसके कारण वह यह दूरी सीधे नाप कर ज्ञात नहीं कर सकता।
इस कठिनाई को दूर करने के लिए वह दिमाग लड़ाता है। पहले वह एक बिन्दु O ऐसा लेता है जिससे A और B दोनों दिखाई दें और वह एक खम्भा स्थापित करता है। फिर रेखा AO की सीध में एक बिन्दु पर खम्भा इस प्रकार स्थापित करता है कि AO = OD इसी प्रकार वह एक तीसरा खम्भा C पर स्थापित करता है, जिससे BO = CO। तब वह CD को नापता है और देखता हैकि CD = 170 मी. सिद्ध कीजिए कि A तथा B के मध्य की दूरी भी 170 मीटर है।
हल :
दिया है AD = OD, BO = CO व CD = 170
सिद्ध करना है: AB = CD = 170 मीटर
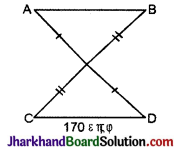
उपपत्ति: ΔAOB व ΔDOC में,
∠AOB = ∠COD (शीर्षाभिमुख कोण)
OA = OD (दिया है)
OB = OC (दिया है)
∴ ΔAOB ≅ ΔDOC (ASS)
∴ AB = CD
∴ AB = 170 मीटर इति सिद्धम् ।
![]()
प्रश्न 16.
निम्नांकित आकृति में AC = BC, ∠DCA = ∠ECB तथा ∠DBC = ∠EAC सिद्ध कीजिए कि ΔDBC और ΔEAC सर्वांगसम हैं और DC = EC
हल :
दिया है : AB = BC, ∠DCA = ∠ECB
तथा ∠DBC = ∠EAC,
सिद्ध करना है ΔDBC ≅ ΔEAC
तथा DC = EC
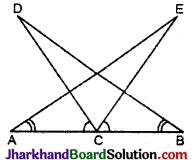
उपपत्ति:
∠ECB = ∠DCA (दिया है)
⇒ ∠ECB + ∠ECD = ∠DCA + ∠ECD
(दोनों पक्षों में ∠ECD जोड़ने पर )
⇒ ∠DCB = ∠ECA ………….(i)
अब, ΔDBC व ΔEAC में
∠DCA = ∠ECA ((i) से)
BC = AC (दिया है)
∠DBC = ∠EAC (दिया है)
∴ ΔDBC ≅ ΔEAC (ASA)
∴ DC = EC इति सिद्ध ।
प्रश्न 17.
निम्न आकृति में, ΔABC में, AB = AC और CF क्रमश: ∠B और ∠C के समद्विभाजक हैं। सिद्ध कीजिए कि ΔEBC ≅ ΔFCB.
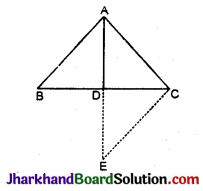
हल :
दिया है ΔABC में, AB = AC व BF तथा CF
क्रमश: ∠B और ∠C के समद्विभाजक हैं।
सिद्ध करना है:
ΔEBC ≅ ΔFCB.
उपपत्ति
ΔMBC में, ΔBAC
∴ ∠B = ∠C (समान भुजओं के सम्मुख कोण)
⇒ ∠ABC = ∠ACB
⇒ \(\frac {1}{2}\)∠ABC = \(\frac {1}{2}\)∠ACB
⇒ ∠EBC = ∠FCB ……..(i)
अब ΔEBC और ΔFCB में,
∠EBC = ∠FCB [समीकरण (i) से]
BC = BC (उभयनिष्ठ भुजा)
∠ECB = ∠FBC [∵ ∠ABC = ∠ACB ]
ΔEBC ≅ ΔFCB. (ASA से) इति सिद्धम् ।
![]()
प्रश्न 18.
यदि त्रिभुज के किसी कोण का समद्विभाजक सम्मुख भुजा को भी समद्विभाजित करता है, तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु है ।
हल :
दिया हुआ माना त्रिभुज ABC में
कोण ∠BAC का समद्विभाजक, सम्मुख भुजा BC को समद्विभाजित करता है।
सिद्ध करना है : AB = AC
रचना : भुजा AD, ∠A
तथा भुजा BC को समद्विभाजित करती है। AD को E तक इस प्रकार बढ़ाया कि AD = DE।
E और C को मिलाया।
उपपत्ति :
ΔADB और ΔEDC में,
BD = DC (दिया है)
AD = DE (रचना से)
∠ADB = ∠EDC (शीर्षाभिमुख कोण)
∴ ΔADB ≅ ΔEDC (SSA)
⇒ AB = EC ………….(i)
और ∠BAD = ∠CED (एकान्तर कोण)
लेकिन ∠BAD = ∠CAD (दिया है)
∴ ∠CAD = ∠CED
⇒ AC = EC [∵ समान भुजाओं के सम्मुख कोण]
⇒ AC = AB [समीकरण (i) से]
अत: ΔABC एक समद्विबाहु त्रिभुज है। इति सिद्धम् ।
प्रश्न 19.
सम्मुख आकृति में, ΔABC समद्विबाहु में AB = AC हैं तथा दो माध्यिकाएँ BD तथा CE सिद्ध कीजिए कि BD = CE.
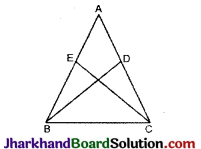
हल :
दिया है : समद्विबाहु त्रिभुज ABC में, AB = AC और BD तथा CE शीर्षों B तथा C से खींची गयी माध्यिकाएँ है।
सिद्ध करना है : BD = CE.
उपपत्ति : ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∴ ∠ABC = ∠ACB (समान भुजाओं के सम्मुख कोण)
∴ ∠EBC = ∠DCB ……..(1)
∵ BD, भुजा AC की माध्यिका है
∴ CD = \(\frac {1}{2}\)AC या AC = 2CD
इसी प्रकार
∴ BE = \(\frac {1}{2}\) AB या AB = 2BE
∵ ΔABC समद्विबाहु त्रिभुज है जिसमें भुजा AC = AB
∴ 2CD = 2BE ⇒ CD = BE
अब ΔBCE तथा ΔBCD में,
भुजा BE = भुजा CD, अभी सिद्ध किया है
∠EBC = ∠DCB, समीकरण (1) से
BC = BC, दोनों त्रिभुजों में उभयनिष्ठ भुजा है
ΔBCE ≅ ΔBCD (SAS) इति सिद्धम् ।
![]()
प्रश्न 20.
निम्न आकृति में यदि AB = EF, BC = DE, AB ⊥ BD तथा FE ⊥ CE, तो सिद्ध कीजिए कि ΔABD = ΔFEC
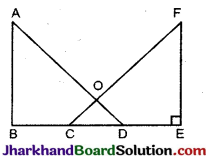
हल :
BC = DE (दिया है)
∴ BC + CD = CD + DE
(दोनों पक्षों में CD जोड़ने पर)
⇒ BD = CE …(i)
अब ΔMBD और ΔFEC में
AB = EF (दिया है)
∠ABD =∠FEC = 90° (∵ AB ⊥ BD और FE ⊥ CE)
BD = CE …(i) से]
अतः ΔABD ≅ ΔFEC इति सिद्धम्
प्रश्न 21.
ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA को D तक इस प्रकार बढ़ाया गया है कि AB = AD सिद्ध कीजिए कि ∠BCD समकोण है।
हल :
त्रिभुज ABC में
AB = BC (दिया है) …….(i)
∠ABC = ∠ACB …….(ii)
(समान भुजाओं के सम्मुख कोण)
AB = AD (दिया है ) … (iii)
∠ADC = ∠DCA ….(iv)
(समान भुजाओं के सम्मुख कोण)
(ii) और (iii) को जोड़ने पर
∠ABC +∠ADC = ∠ACB + ∠DCA
∠ABC + ∠ADC = ∠BCD ……(v)
∠ABC + ∠ADC + ∠BCD = 180°
(त्रिभुज के अन्त कोणों का योग)
∠BCD + ∠BCD = 180° [(v) से]
2 ∠BCD = \(\frac {180°}{2}\)
∠BCD = 90° इति सिद्धम् ।
प्रश्न 22.
सिद्ध कीजिए कि त्रिभुज के तीनों शीर्ष लम्बों का योग उस त्रिभुज के परिमाप से कम होता है।
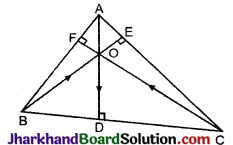
हल :
दिया है ΔABC में शीर्षों A, B तथा C से क्रमशः सम्मुख भुजाओं पर डाले गए लम्ब AD, BE तथा CF
सिद्ध करना है :
AD + BE + CF < AB + BC + CA
उपत्ति : ΔABD में, ∠ADB = 90°
∴ AD < AB ………..(i)
ΔBEC में, BE ⊥ AC
∴ BE < BC …..(ii)
इसी प्रकार, ΔACF में,
CF ⊥ AB
∴ CF < AC …(iii)
(i), (ii) और (iii) को जोड़ने पर,
AD + BE + CF < AB + BC + AC इति सिद्धम्
![]()
प्रश्न 23.
रिक्त स्थानों की पूर्ति कीजिए :
(i) यदि कोई बिन्दु दो बिन्दुओं को मिलाने वाले रेखाखण्ड के लम्ब समद्विभाजक पर स्थित हो, तो वह दिए हुए बिन्दुओं से …………… होता है।
(ii) बिन्दुओं का ऐसा समुच्चय जो कुछ दिए हुए प्रतिबन्धों को संतुष्ट करता है, …………… कहलाता है।
(iii) किसी ऐसे बिन्दु का बिन्दु पथ जो स्थिर बिन्दुओं से समदूरस्थ है, दोनों बिन्दुओं को मिलाने वाले रेखाखण्ड का ……… होता है।
(iv) यदि कोई बिन्दु दो प्रतिच्छेदी रेखाओं के मध्य बने कोण के समद्विभाजक पर स्थित हो, तो वह दोनों रेखाओं से ………….. होता है।
(v) किसी त्रिभुज के शीर्ष और सम्मुख भुजा के मध्य बिन्दु को मिलाने वाली रेखाखण्ड ……………. कहलाती है।
हल :
(i) समदूरस्थ
(ii) बिन्दुपथ,
(iii) लम्ब समद्विभाजक,
(iv) समदूरस्थ
(v) माध्यिका