Jharkhand Board JAC Class 9 Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल
प्रश्न 1.
यदि किसी समलम्ब की समान्तर भुजाएँ a व b हैं तथा उनके बीच की लम्बवत दूरी h है तो उसके क्षेत्रफल का सूत्र होगा :
(A) 2h(\(\frac {a}{b}\))
(B) 2h(a + b) h
(C) a.b.h
(D) \(\frac {1}{2}\)(a + b)h.
हल :
विकल्प ‘D’ सही है।
![]()
प्रश्न 2.
किसी त्रिभुज का क्षेत्रफल उसकी भुजा और संगत शीर्षलम्ब के गुणन का होता है।
(A) दो गुना
(B) बराबर का
(C) एक तिहाई
(D) आधा
हल :
विकल्प ‘D’ सही है।
प्रश्न 3.
समान्तर चतुर्भुज का प्रत्येक विकर्ण उसको समान क्षेत्रफल वाले जिन दो प्रान्तों में विभाजित करता हैं, उनका आकार होता है :
(A) समचतुर्भुजाकार
(B) त्रिभुजाकार
(C) समान्तर चतुर्भुजाकार
(D) विषमबाहु चतुर्भुजाकार
हल :
विकल्प ‘B’ सही है।
प्रश्न 4.
एक त्रिभुज का आधार 6 सेमी और ऊँचाई 5 सेमी है, तो क्षेत्रफल होगा :
(A) 15 सेमी²
(B) 25 सेमी²
(C) 30 सेमी²
(D) 36 सेमी²
हल :
Δ का क्षेत्रफल = \(\frac {1}{2}\) × आधार × ऊँचाई
= \(\frac {1}{2}\) × 6 × 5 सेमी²
= 3 × 5 सेमी² = 15 सेमी²
सही विकल्प ‘A’ है।
![]()
प्रश्न 5.
एक समान्तर चतुर्भुज का आधार 5 सेमी और ऊंचाई 4 सेमी है, तो क्षेत्रफल होगा :
(A) 10 वर्ग सेमी
(B) 20 वर्ग सेमी
(C) 18 वर्ग सेमी
(D) 40 वर्ग सेमी।
हल :
समान्तर चतुर्भुज का क्षेत्रफल आधार × ऊंचाई
= 5 × 4 सेमी² = 20 सेमी²
सही विकल्प ‘B’ है।
प्रश्न 6.
एक समान्तर चतुर्भुज और त्रिभुज क्षेत्रफल में समान हैं और एक ही आधार पर स्थित हैं। यदि समान्तर चतुर्भुज की ऊंचाई 2 सेमी हो, तो त्रिभुज की ऊँचाई है:
(A) 4 सेमी
(B) 1 सेमी
(C) 2 सेमी
(D) 3 सेमी।
हल :
Δ का क्षेत्रफल = समान्तर चतुर्भुज का क्षेत्रफल (दिया है)
\(\frac {1}{2}\) × आ. × ॐ. = आ. × स. च. की ऊँचाई
∴ त्रिभुज की ऊँ. = 2 × स. च. की ऊँचाई
= 2 × 2 = 4 सेमी
अतः विकल्प ‘A’ सही है।
प्रश्न 7.
ABCD एक समान्तर चतुर्भुज है, जिसमें AB = 10 सेमी है। AB और AD भुजाओं के शीर्षलम्ब 7 सेमी व 8 सेमी है। AD की लम्बाई है:
(A) 8.75 सेमी
(B) 8.25 सेमी
(C) 7.75 सेमी
(D) 9 सेमी
हल :
समान्तर चतुर्भुज का क्षेत्रफल = आधार × संगत शीर्षलम्ब
पुन:
= AB × DM
= 10 × 7 = 70 सेमी² …….(i)
ar (|| ABCD) = AD × BN
= AD × 8 …….(ii)
(i) और (ii) से
AD × 8 = 70
AD = \(\frac {70}{8}\) = 8.75 सेमी
अतः विकल्प ‘A’ सही है।
![]()
प्रश्न 8.
चित्र में ABCD का क्षेत्रफल होगा :
(A) 12 सेमी²
(B) 8 सेमी²
(C) 10 सेमी²
(D) 9 सेमी²
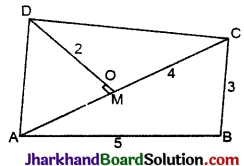
हल :
☐ABCD का क्षेत्रफल
= ar (ΔABC) + ar (ΔADC)
= \(\frac {1}{2}\) × 4 × 3 + \(\frac {1}{2}\) × 4 × 2
= 6 + 4 = 10 सेमी²
अतः विकल्प ‘C’ सही है।
प्रश्न 9.
एक समान्तर चतुर्भुज की दो क्रमागत लम्बाई 15 सेमी तथा 12 सेमी है। यदि 15 सेमी भुजाकी भुजाओं की भुजाओं के दूरी 6 सेमी हो तो 12 सेमी भुजाओं की दूरी होगी :
(A) 8 सेमी
(B) 7.5 सेमी
(C) 12 सेमी
(D) 6 सेमी.
हल :
समान्तर चतुर्भुज का क्षेत्रफल = आधार × संगत शीर्ष लम्ब
= 15 × 6 = 90 सेमी²
पुनः माना 12 सेमी भुजाओं के मध्य की दूरी = x
∴ 12 × x = 90
x = \(\frac {90}{12}\) = 7.5 सेमी
अतः विकल्प ‘B’ सही है।
प्रश्न 10.
यदि किसी Δ की तीनों भुजाएँ क्रमशः a, b तथा c हैं तो उसकी अर्द्धमाप होगी :
(A) abc
(B) \(\frac {a + b + c}{2}\)
(C) \(\frac {abc}{2}\)
(D) a + b + c
हल :
त्रिभुज का परिमाप = a + b + c
त्रिभुज का अर्द्धमाप = \(\frac {a + b + c}{2}\)
अतः विकल्प ‘B’ सही है।
![]()
11. रिक्त स्थानों की पूर्ति करो :
प्रश्न (i)
त्रिभुज का क्षेत्रफल समान्तर चतुर्भुज के क्षेत्रफल का ………………. कल होता है।
हल :
आधा
प्रश्न (ii)
किसी आकृति का तलीय क्षेत्र का परिमाण या माप उस आकृति का ………. कहलाता है।
हल :
क्षेत्रफल ।
प्रश्न (iii)
एक ही आधार और बराबर क्षेत्रफल वाले त्रिभुज समान ………… के बीच स्थित होते हैं।
हल :
समान्तर रेखाओं ।
प्रश्न (iv)
त्रिभुज की माध्यिका, त्रिभुज को ………………………. वाले दो त्रिभुजों में विभाजित करती है।
हल :
बराबर क्षेत्रफल ।
![]()
प्रश्न (v)
समातर चतुर्भुज की कोई भी भुजा इसका ……………….. हो सकती है।
हल :
आधार।
प्रश्न (vi)
4 सेमी भुजा वाले वर्ग का क्षेत्रफल ………………….. भुजाओं वाले आयत के क्षेत्रफल के बराबर होता है।
हल :
8 सेमी तथा 2 सेमी।
प्रश्न (vii)
किसी समबाहु त्रिभुज की भुजाओं के मध्य-बिन्दुओं को मिलाने से बने त्रिभुज का क्षेत्रफल मूल त्रिभुज के क्षेत्रफल का …………. होता है।
हल :
एक चौथाई।
प्रश्न (viii)
ऐसी आकृति जिसकी चारों भुजाएँ तो बराबर होती हैं किन्तु कोण नहीं ………………… कहलाता है।
हल :
समचतुर्भुज ।
प्रश्न (ix)
किसी समकोण त्रिभुज का परिगत केन्द्र, उसके …………… भुजा पर स्थित होता है।
हल :
कर्ण।
![]()
प्रश्न (x)
समान आधार तथा समान समान्तर रेखाओं के मध्य बने समचतुर्भुज तथा आयत के क्षेत्रफलों में आयत का क्षेत्रफल ………………….. होता है।
हल :
कम।
प्रश्न 12.
सिद्ध करो कि यदि एक त्रिभुज और एक समान्तर चतुर्भुज, एक ही आधार पर और उन्हीं दो समान्तर रेखाओं के बीच में हों, तो त्रिभुज का क्षेत्रफल, समान्तर चतुर्भुज के क्षेत्रफल का आधा होता है।
हल :
दिया है ΔVAB और ||gm ABCD, इस प्रकार हैं कि V, D और C संरेख हैं।
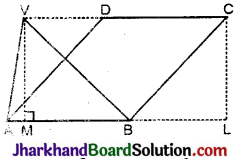
सिद्ध करना है : ar (ΔVAB) = \(\frac {1}{2}\)ar (||gm ABCD).
रचना : CL ⊥ AB खींचा जो बढ़ी हुई रेखा AB के बिन्दु L पर मिलती है, और VM ⊥ AB, जो रेखा AB को M बिन्दु पर मिलती है।
उपपत्ति : V, D और C संरेख हैं और DC || AB,
∴ VM = CL, …….(1)
(समान्तर रेखाओं के बीच की दूरी )
अब ar (ΔVAB) = \(\frac {1}{2}\)VM × AB …….. (2)
ar (||gm ABCD) = CL × AB ………..(3)
समीकरण (2) से,
ar (ΔVAB) = \(\frac {1}{2}\) × VM × AB
ar (ΔVAB) = \(\frac {1}{2}\) × CL × AB …………(4) [∵ VM = CL]
समीकरण (3) एवं (4) से,
ar (ΔVAB) = \(\frac {1}{2}\)ar (||gm ABCD).
इति सिद्धम् ।
प्रश्न 13.
सिद्ध करो कि समलम्ब चतुर्भुज का क्षेत्रफल, उसकी समान्तर भुजाओं के मध्य लम्बवत दूरी और समान्तर भुजाओं के योगफल के गुणनफल का आधा होता है।
हल :
दिया है समलम्ब चतुर्भुज ABCD, जिसमें AB || CD
AL ⊥ DC और CN ⊥ AB है।
AB = a, DC = b, AL = CN = h (माना)
सिद्ध करना है :
ar (समलम्ब चतुर्भुज ABCD) = \(\frac {1}{2}\)h × (a + b).
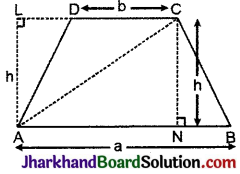
रचना : A और C को मिलाया।
उपपत्ति : AC, चतुर्भुज ABCD का विकर्ण है।
∴ ar (समलम्ब चतुर्भुज ABCD)
= ar (ΔABC) + ar (ΔACD)
अब, ar (ΔABC) = \(\frac {1}{2}\)h × a …….(i)
ar (ΔACD) = \(\frac {1}{2}\)h × b ………….(ii)
समीकरण (i) और (ii) को जोड़ने पर,
∵ ar (ΔABC) + ar (ΔACD)
= \(\frac {1}{2}\)h × a + \(\frac {1}{2}\)h × b
= \(\frac {1}{2}\)h × (a + b)
इति सिद्धम् ।
![]()
प्रश्न 14.
एक समबाहु त्रिभुज के शीर्षलम्ब की लम्बाई और क्षेत्रफल ज्ञात कीजिए जिसकी भुजा की लम्बाई a है।
हल :
एक समबाहु त्रिभुज जिसकी भुजा की लम्बाई a है।
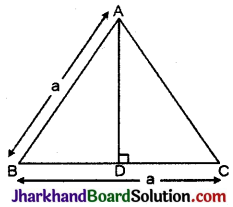
अतः
AB = BC = CA = a
त्रिभुज का शीर्षलम्ब AD है।
BD = \(\frac {1}{2}\)BC
[समबाहु Δ में प्रत्येक शीर्षलम्ब सम्मुख भुजा को समद्विभाजित करता है।]
∴ BD = \(\frac {1}{2}\) × a = \(\frac {a}{2}\)
ΔABD में, ∠D समकोण है, अत: पाइथागोरस प्रमेय से,

प्रश्न 15.
चित्र में यदि ΔABC एवं ΔDBC एक ही आधार BC पर स्थित हैं, तो सिद्ध कीजिए कि
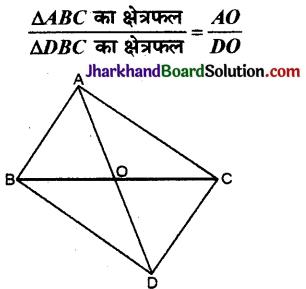
हल :
दिया है ΔABC और ΔDBC का आधार BC है।
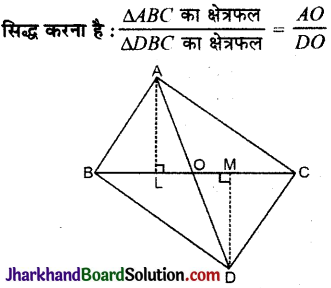
रचना : A तथा D से AL ⊥ BC तथा DM ⊥ BC डालें।
ΔALO और ΔDMO में,
∠ALO = ∠DMO (प्रत्येक 90°)
∠AOL = ∠DOM (शीर्षाभिमुख कोण)
ΔALO ~ ΔDMO (AAA नियम)
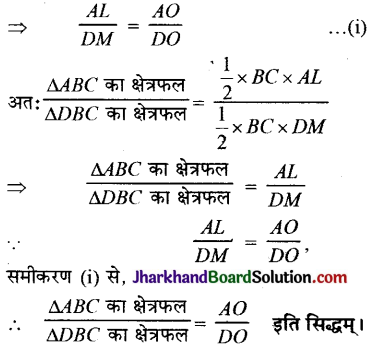
![]()
प्रश्न 16.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफल संगत माध्यिकाओं के वर्गों के अनुपात में होते हैं।
हल :
दिया है : समरूप त्रिभुज ABC और DEF में AP और DQ माध्यिकाएँ हैं।
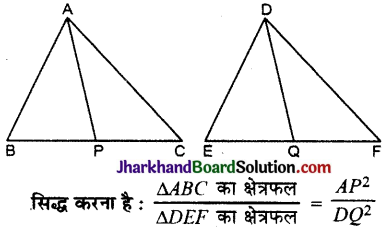
उपपत्ति: हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के समान होता है (मूलभूत समानुपातिक प्रमेय)

प्रश्न 17.
दो त्रिभुज के आधार क्रमशः 8 सेमी व 6 सेमी हैं। यदि उनकी ऊंचाई क्रमशः 6 सेमी व 8 सेमी हो, तो उनके क्षेत्रफल का अनुपात ज्ञात कीजिए।
हल :
पहले त्रिभुज का क्षेत्रफल = \(\frac {1}{2}\)आधार × ऊँचाई
= \(\frac {1}{2}\) × 8 × 6
= 24 वर्ग सेमी
दूसरे त्रिभुज का क्षेत्रफल = \(\frac {1}{2}\) × 6 × 8
= 24 वर्ग सेमी
अतः अनुपात = पहले त्रिभुज का क्षेत्रफल / दूसरे त्रिभुज का क्षेत्रफल
= \(\frac{24}{24}=\frac{1}{1}\)
अतः दोनों त्रिभुजों के क्षेत्रफल का अनुपात = 1 : 1
![]()
प्रश्न 18.
दो त्रिभुज एक ही आधार पर एवं समान समान्तर रेखाओं के बीच स्थित हैं। एक त्रिभुज की ऊंचाई 5 सेमी तथा क्षेत्रफल 18 वर्ग सेमी. है। दूसरे त्रिभुज की ऊँचाई ज्ञात कीजिए।
हल :
दो त्रिभुज ABC तथा त्रिभुज DBC एक ही आधार BC पर तथा एक ही समान्तर रेखाओं BR तथा PQ के मध्य स्थित हैं। अतः दोनों त्रिभुजों का क्षेत्रफल समान होगा।
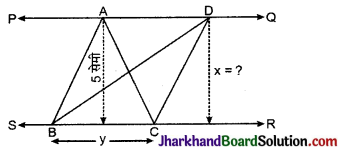
अत: त्रिभुज ABC का क्षे. = \(\frac {1}{2}\) × आधार × ऊँचाई
18 = \(\frac {1}{2}\) × आधार × 5
∴ आधार = \(\frac{2 \times 18}{5}=\frac{36}{5}\)
∴ आधार (y) = 7.2 सेमी
दूसरे त्रिभुज का क्षे. = \(\frac {1}{2}\) × आधार × ऊँचाई
18 = \(\frac {1}{2}\) × y × x
18 = \(\frac {1}{2}\) × 7.2 × x
∴ x = \(\frac{18 \times 2}{7.2}\)
= \(\frac{18 \times 20}{72}\) = 5
∴ दूसरे त्रिभुज DBC की ऊँचाई (x) = 5 सेमी
अतः ऊंचाई: = 5 सेमी।
प्रश्न 19.
एक समचतुर्भुज का एक विकर्ण दूसरे विकर्ण से दोगुना है। यदि उस समचतुर्भुज का क्षेत्रफल 80 वर्ग सेमी हो तो उसकी भुजा की लम्बाई ज्ञात कीजिए।
हल :
माना, सम चतुर्भुज ABCD की प्रत्येक भुजा की लम्बाई = a सेमी
माना, समचतुर्भुज के एक विकर्ण की लम्बाई = x सेमी
समचतुर्भुज का क्षेत्रफल = \(\frac {1}{2}\) × (x × 2x)
= x2 वर्ग सेमी
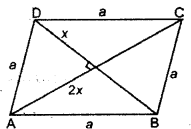
चूंकि समचतुर्भुज के विकर्ण एक दूसरे को समकोण पर समद्विभाजिक करते हैं। अतः ∠AOD एक समकोण त्रिभुज है, जिसका ΔAOD = 90°

अतः समचतुर्भुज की भुजा की लम्बाई = 10 सेमी
![]()
प्रश्न 20.
एक नहर की अनुप्रस्थ काट का आकार समलम्ब है। यदि नहर के ऊपरी सिरे की चौड़ाई 10 मी, तली की 6 मी तथा अनुप्रस्थ काट का क्षेत्रफल 72 वर्ग मीटर हो तो उसकी गहराई ज्ञात कीजिए। समलम्ब की अन्य भुजाओं की लम्बाई भी बताइए।
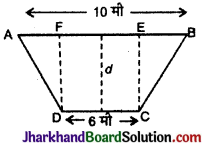
हल :
माना अनुप्रस्थ काट की गहराई = d मीटर की दूरी = d मीटर समलम्ब ABCD का क्षेत्रफल = \(\frac {1}{2}\)(AB + BC) × d
72 = \(\frac {1}{2}\)(10 + 6) × d
72 × 2 = 16 d
d = \(\frac{72 \times 2}{16}\) = 9
नहर की गहराई = 9 मीटर
समलम्ब की अन्य दो भुजाएँ AD = BC
ΔAFD में, ∠AFD = 90°
AF = \(\frac{10-6}{2}\) = 2, DF = d = 9
AD = \(\sqrt{2^2+9^2}=\sqrt{4+81}=\sqrt{85}\)मीटर