Students should go through these JAC Class 9 Maths Notes Chapter 12 Heron’s Formula will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 12 Heron’s Formula
Mensuration:
A branch of mathematics which concerns itself with measurement of lengths, areas and volumes of plane and solid figure is called Mensuration.
→ Perimeter: The perimeter of a plane figure is the length of its boundary. In case of a triangle or a polygon, the perimeter is the sum of the lengths of its sides.
→ Units of Perimeter: The unit of perimeter is the same as the unit of length i.e. centimetre (cm), metre (m), kilometre (km) etc.
1 centimetre (cm) = 10 milimetres (mm)
1 decimetre (dm) = 10 centimetres
1 metre (m) = 10 decimetres
= 100 centimetres
= 1000 milimetres
1 decametre (dam) = 10 metres
= 1000 centimetres
1 hectometre (hm) = 10 decametres
= 100 metres
1 kilometre (km) = 1000 metres
= 100 decametres
= 10 hectometres
![]()
Area:
The area of a plane figure is the measure of the surface enclosed by its boundary.
The area of a triangle or a polygon is the measure of the surface enclosed by its sides.
→ Units of Area:
The various units of measuring area are, square centimetre (cm2), square metre (m2), hectare etc.
1 square centrimetre (cm2)
= 1 cm × 1 cm
= 10 mm × 10 mm
= 100 sq.mm.
1 square decimetre (dm2)
= 1 dm × dm
= 10 cm × 10 cm
= 100 sq. cm.
1 square metre (m2)
= 1 m × 1 m
= 10 dm × 10 dm
= 100 sq. dm
1 square decametre (dam2)
= 1 dam × 1 dam
= 10 m × 10 m
= 100 sq.m.
1 square hectometre (hm2)
= 10 dam × 10 dam
= 100 sq. dam
(or 1 hectare) = 10000 sq. m.
1 square kilometre (km2)
= 1 km × 1 km
= 10 hm × 10 hm
= 100 sq. hm.
→ Heron’s formula:
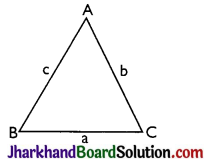
In ΔABC if sides of triangle BC, CA, and AB are a, b, c respectively then
perimeter = 2s = a + b + c
Area = \(\sqrt{s(s-a)(s-b)(s-c)}\)
→ Perimeter and Area of a Triangle:
Right-angled triangle:
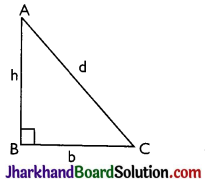
For a right-angled triangle, let b be the base, h be the perpendicular and d be the hypotenuse. Then
(A) Perimeter = b + h + d
(B) Area = \(\frac{1}{2}\)(Base × Height) = \(\frac{1}{2}\)bh
(C) Hypotenuse, d = \(\sqrt{b^2+h^2}\) [Pythagoras theorem]
Isosceles right-angled triangle:
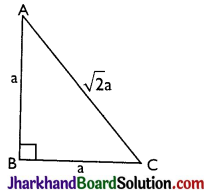
For an isosceles right-angled triangle, let a be the equal sides, then
(A) Hypotenuse = \(\sqrt{a^2+a^2}=\sqrt{2} a\)
(B) Perimeter = 2a + \(\sqrt{2}\)a
(C) Area = \(\frac{1}{2}\)(Base × Height) = \(\frac{1}{2}\)(a × a) = \(\frac{1}{2}\)a2.
Equilateral triangle:
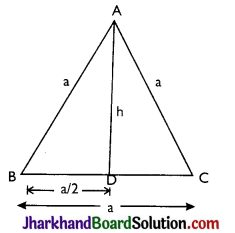
For an equilateral triangle, let each side be a, and the height of the triangle be h, then
(A) ∠A = ∠B = ∠C = 60°
(B) ∠BAD = ∠CAD = 30°
(C) AB = BC = AC = a(say)
(D) BD = DC = \(\frac{\mathrm{a}}{2}\)
(E) \(\left(\frac{\mathrm{a}}{2}\right)^2\) + h2 = a2 ⇒ h2 = \(\frac{3 \mathrm{a}^2}{4}\)
∴ Height (h) = \(\frac{\sqrt{3}}{2} \mathrm{a}\)
(F) Area = \(\frac{1}{2}\)(Base × Height)
= \(\frac{1}{2} \times \mathrm{a} \times \frac{\sqrt{3}}{2} \mathrm{a}=\frac{\sqrt{3}}{4} \mathrm{a}^2\)
(G) Perimeter = a + a + a = 3a.