JAC Class 9 Maths Important Questions Chapter 9 Areas of Parallelograms and Triangles

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 9 Areas of Parallelograms and Triangles Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 9 Areas of Parallelograms and Triangles

Question 1.
In a parallelogram ABCD; AB = 8 cm. The altitudes corresponding to sides AB and AD are respectively 4 cm and 5 cm. Find AD.

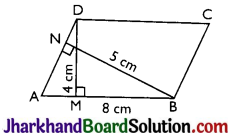
Solution :
We know that, Area of a parallelogram
= Base × Corresponding altitude
∴ Area of parallelogram
ABCD = AD × BN = AB × DM
⇒ AD × 5 = 8 × 4
⇒ AD = \(\frac{8 \times 4}{5}\) = 6.4 cm.

Question 2.
ABCD is a quadrilateral and BD is one of its diagonals as shown in the figure. Show that the quadrilateral ABCD is a parallelogram and find its area.

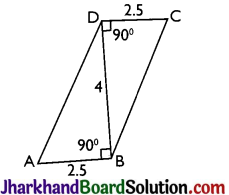
Solution :
From figure, the transversal DB is intersecting a pair of lines DC and AB such that
∠CDB = ∠ABD = 90°.
As these angles form a pair of alternate interior angles
∴ DC || AB.
Also, DC = AB = 2.5 units.
∴ Quadrilateral ABCD is a parallelogram. Now, area of parallelogram ABCD
= Base × Corresponding altitude
= 2.5 × 4 = 10 sq. units

Question 3.
In figure, E is any point on median AD of a ΔABC. Show that ar(ABE) = ar(ACE).

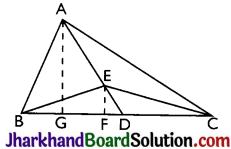
Solution :
Construction: From A, draw AG ⊥ BC and from E, draw EF ⊥ BC.
Proof: ar(ΔABD) = \(\frac {BD × AG}{2}\)
ar(ΔADC) = \(\frac{\mathrm{DC} \times \mathrm{AG}}{2}\)
But, BD = DC [∵ D is the mid-point of BC as AD is the median]
∴ ar(ΔABD) = ar(ΔADC) ……………(i)
Again, ar(ΔEBD) = \(\frac{\mathrm{BD} \times \mathrm{EF}}{2}\)
ar(ΔEDC) = \(\frac{\mathrm{DC} \times \mathrm{EF}}{2}\)
But, BD = DC
∴ ar(ΔEBD) = ar(ΔEDC) …….(ii)
Subtracting (ii) from (i), we get
ar(ΔABD) – ar(ΔEBD)
= ar(ΔADC) – ar(ΔEDC)
⇒ ar(ΔABE) = ar(ΔACE)
Hence, proved.

Question 4.
Triangles ABC and DBC are on the same base BC; with A, D on opposite sides of the line BC, such that ar(ΔABC) = ar(ΔDBC). Show that BC bisects AD.

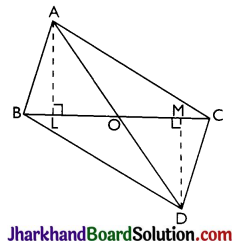
Solution :
Construction: Draw AL ⊥ BC and DM ⊥ BC.
Proof: ar(ΔABC) = ar(ΔDBC) (Given)
⇒ \(\frac{\mathrm{BC} \times \mathrm{AL}}{2}=\frac{\mathrm{BC} \times \mathrm{DM}}{2}\)
⇒ AL = DM ………….(i)
Now in Δs OAL and OMD
AL = DM [From (i)]
⇒ ∠ALO = ∠DMO [Each = 90°]
⇒ ∠AOL = ∠MOD [Vert. opp. ∠s]
∴ ΔOAL ≅ ΔODM [By AAS]
∴ OA = OD [By CPCT]
i.e., BC bisects AD. Hence, proved.

Question 5.
ABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that the area of ΔBED = \(\frac {1}{4}\) area of ΔABC.

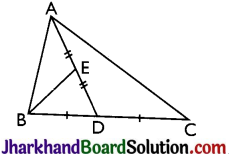
Solution :
Given: A ΔABC in which D is the midpoint of BC and E is the mid-point of AD.
To prove: ar(ΔBED) = \(\frac {1}{4}\)ar(ΔABC).
Proof: ∵ AD is a median of ΔABC
∴ ar(ΔABD) = ar(ΔADC)
= \(\frac {1}{2}\)ar(ΔABC) ……..(i)
[∵ Median of a triangle divides it into two triangles of equal area]
Again,
∵ BE is a median of ΔABD.
∴ ar(ΔBEA) = ar(ΔBED)
= \(\frac {1}{2}\)ar(ΔABD) ……..(ii)
[∵ Median of a triangle divides it into two triangles of equal area]
∴ ar(ΔBED) = \(\frac {1}{2}\)ar(ΔABD)
= \(\frac {1}{2}\) × \(\frac {1}{2}\)ar(ΔABC) [From (i)]
∴ ar(ΔBED) = \(\frac {1}{4}\)a(ΔABC). [From (ii)]

Question 6.
Prove that the area of an equilateral triangle is equal to \(\frac{\sqrt{3}}{4}\)a², where a is the side of the triangle.

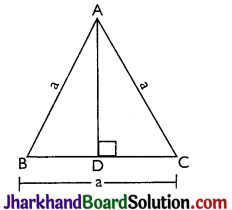
Solution :
Draw AD ⊥ BC
⇒ ΔABD ≅ ΔACD
[By RHS congruence rule]
∴ BD = DC [By CPCT]
∴ BD = DC = \(\frac {a}{2}\)
In right-angled ΔABD
AD² = AB² – BD²
= a² – (\(\frac {a}{2}\))² = a² – \(\frac{a^2}{4}=\frac{3 a^2}{4}\)
AD = \(\frac{\sqrt{3} a}{2}\)
Area of ΔABC = \(\frac {1}{2}\)BC × AD
= \(\frac {1}{2}\)a × \(\frac{\sqrt{3} a}{2}=\frac{\sqrt{3} a^2}{4}\)
Hence, proved.

Question 7.
In figure, P is a point in the interior of rectangle ABCD. Show that
(i) ar(ΔAPD) + ar(ΔBPC)
= \(\frac {1}{2}\)ar(rect. ABCD)

(ii) ar(APD) + ar(PBC)
= ar(APB) + ar(PCD)

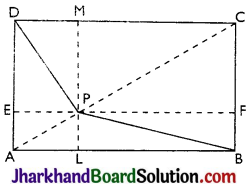
Solution :
Given: A rect. ABCD and P is a point inside it. PA, PB, PC and PD have been joined.
To prove:
(i) ar(ΔAPD) + ar(ΔBPC)
= \(\frac {1}{2}\)ar(rect. ABCD)

(ii) ar(ΔAPD) + ar(ΔBPC)
= ar(ΔAPB) + ar(ΔCPD).
Construction :
Draw EPF || AB
and LPM || AD.
Proof: EPF || AB and DA cuts them,

(i) ∠EAB = 90° [As each angle of a rectangle is of 90°]
∴ ∠DEP = ∠EAB = 90° [Corresponding angles]
∴ PE ⊥ AD
Similarly, PF ⊥ BC; PL ⊥ AB and PM ⊥ DC.
∴ ar(ΔAPD) + ar(ΔBPC)
= (\(\frac {1}{2}\) × AD × PE) + ar (\(\frac {1}{2}\) × BC × PF)
= \(\frac {1}{2}\)AD (PE + PF) [∵ BC = AD]
= \(\frac {1}{2}\) × AD × EF = \(\frac {1}{2}\) × AD × AB [∵ EF = AB]
= \(\frac {1}{2}\) × ar(rectangle ABCD)

(ii) ar(ΔAPB) + ar(PCD)
= (\(\frac {1}{2}\) × AB × PL) + (\(\frac {1}{2}\) × DC × PM)
= \(\frac {1}{2}\) × AB × (PL + PM) [∵ DC = AB]
= \(\frac {1}{2}\) × AB × LM
= \(\frac {1}{2}\) × AB × AD [∵ LM = AD]
= \(\frac {1}{2}\) × ar(rect. ABCD).
= ar(ΔAPD) + ar(PBC)
= ar(ΔAPB) + ar(PCD)
Hence, proved.

Multiple Choice Questions

Question 1.
The sides BA and DC of the parallelogram ABCD are produced as shown in the figure then

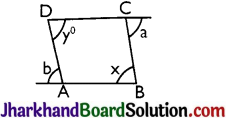
(a) a + x = b + y
(b) a + y = b + a
(c) a + b = x + y
(d) a – b = x – y
Solution :
(c) a + b = x + y

Question 2.
The sum of the interior angles of polygon is three times the sum of its exterior angles. Then numbers of sides in polygon is
(a) 6
(b) 7
(c) 8
(d) 9
Solution :
(d) 9

Question 3.
In the following figure, AP and BP are angle bisectors of ∠A and ∠B which meet at a point P of the parallelogram ABCD. Then 2∠APB =

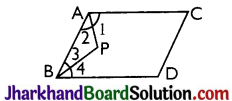
(a) ∠A + ∠B
(b) ∠A + ∠C
(c) ∠B + ∠D
(d) 2∠C + ∠D
Solution :
(a) ∠A + ∠B

Question 4.
In a parallelogram ABCD, AO and BO are respectively the angle bisectors of ∠A and ∠B (see figure). Then measure of ∠AOB is

(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution :
(d) 90°

Question 5.
In a parallelogram ABCD, ∠D = 60° then the measurement of ∠A is
(a) 120°
(b) 65°
(c) 90°
(d) 75°
Solution :
(a) 120°

Question 6.
In the adjoining figure ABCD, the angles x and y are

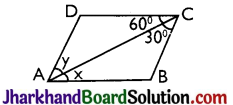
(a) 60°, 30°
(b) 30°, 60°
(c) 45°, 45°
(d) 90°, 90°
Solution :
(a) 60°, 30°

Question 7.
In the parallelogram PQRS (see figure), the values of ∠SQP and ∠QSP are

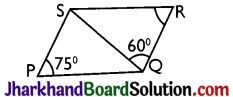
(a) 45°, 60°
(b) 60°, 45°
(c) 70°, 35°
(d) 35°, 70°
Solution :
(a) 45°, 60°

Question 8.
In parallelogram ABCD, AB = 12 cm. The altitudes corresponding to the sides CD and AD are respectively 9 cm and 11 cm. Find AD.

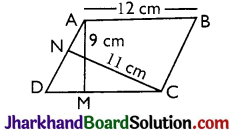
(a) \(\frac {108}{11}\) cm
(b) \(\frac {108}{10}\) cm
(c) \(\frac {99}{10}\) cm
(d) \(\frac {108}{17}\) cm
Solution :
(a) \(\frac {108}{11}\) cm

Question 9.
In ΔABC, AD is a median and P is a point on AD such that AP : PD = 1 : 2 then the area of ΔABP =
(a) \(\frac {1}{2}\) × Area of ΔABC
(b) \(\frac {2}{3}\) × Area of ΔABC
(c) \(\frac {1}{3}\) × Area of ΔABC
(d) \(\frac {1}{6}\) × Area of ΔABC
Solution :
(d) \(\frac {1}{6}\) × Area of ΔABC

Question 10.
In ΔABC if D is a point on BC and divides it in the ratio 3 : 5 i.e., if BD : DC = 3 : 5 then, ar(AADC): ar(ΔABC) = ?
(a) 3 : 5
(b) 3 : 8
(c) 5 : 8
(d) 8 : 3
Solution :
(b) 3 : 8