Jharkhand Board JAC Class 9 Maths Important Questions Chapter 6 Lines and Angles Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 6 Lines and Angles
Question 1.
Two supplementary angles are in the ratio 4 : 5, find the angles.
Solution :
Let angles be 4x and 5x.
∵ Angles are supplementary
∴ 4x + 5x = 180°
⇒ 9x = 180°
⇒ x = \(\frac {180°}{2}\) = 20°
∴ Angles are 4 × 20° and 5 × 20° i.e., 80° and 100°
![]()
Question 2.
If an angle differs from its complement by 10°, find the angle.
Solution :
Let angle be x° then its complement is 90° – x°.
Now given, x° – (90° – x°) = 10°
⇒ x° – 90° + x° = 10°
⇒ 2x° = 10° + 90° = 100°
⇒ x° = \(\frac {100°}{2}\) = 50°
∴ Required angle is 50°.
Question 3.
In figure, OP and OQ bisects ∠BOC and ∠AOC respectively. Prove that ∠POQ = 90°.
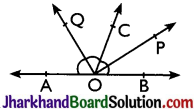
Solution :
∵ OP bisects ∠BOC
∴ ∠POC = \(\frac {1}{2}\)∠BOC ………(i)
Also OQ bisects ∠AOC
∠COQ = \(\frac {1}{2}\)∠AOC ………(ii)
∵ OC stands on AB
∴ ∠AOC + ∠BOC = 180°[Linear pair]
⇒ \(\frac {1}{2}\)∠AOC + \(\frac {1}{2}\)∠BOC = \(\frac {1}{2}\) × 180°
⇒ ∠COQ + ∠POC = 90° [Using (i) and (ii)]
⇒ ∠POQ = 90°
![]()
Question 4.
In figure, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠DOE and ∠BOF.
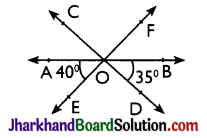
Solution :
Given, ∠AOE = 40° and ∠BOD = 35°
Clearly, ∠AOC = ∠BOD
(Vertically opposite angles)
⇒ ∠AOC = 35°
⇒ ∠BOF = ∠AOE
[Vertically opposite angles]
⇒ ∠BOF = 40°
Now, ∠AOB = 180° [Straight angle]
⇒ ∠AOC + ∠COF + ∠BOF = 180°
[Angles sum property]
⇒ 35° + ∠COF + 40° = 180°
⇒ ∠COF = 180° – 75° = 105°
Now, ∠DOE = ∠COF
[Vertically opposite angles]
∴ ∠DOE = 105°
Question 5.
In figure if l || m, n || p and ∠1 = 85° find ∠2.
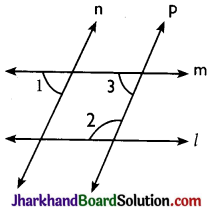
Solution :
∵ n || p and m is transversal
∴ ∠1 = ∠3 = 85° [Corresponding angles]
Also, m || l and p is transversal
∴ ∠2 + ∠3 = 180°
[Consecutive interior angles]
⇒ ∠2 + 85° = 180°
⇒ ∠2 = 180° – 85°
⇒ ∠2 = 95°
Multiple Choice Questions
Question 1.
If two lines are intersected by a transversal, then each pair of corresponding angles so formed is
(a) Equal
(b) Complementary
(c) Supplementary
(d) None of these
Solution :
(a) Equal
![]()
Question 2.
Two parallel lines have:
(a) a common point
(b) two common points
(c) no common point
(d) infinite common points
Solution :
(c) no common point
Question 3.
An angle is 14° more than its complement then angle is:
(a) 38°
(b) 52°
(c) 50°
(d) none of these
Solution :
(a) 38°
Question 4.
The angle between the bisectors of two adjacent supplementary angles is:
(a) acute angle
(b) right angle
(c) obtuse angle
(d) none of these
Solution :
(c) obtuse angle
Question 5.
If one angle of triangle is equal to the sum of the other two then triangle is:
(a) acute triangle
(b) obtuse triangle
(c) right triangle
(d) none of these
Solution :
(c) right triangle
![]()
Question 6.
Point x is in the interior of ∠BAC. If ∠BAC = 70° and ∠BAX = 42° then ∠XAC =
(a) 28°
(b) 29°
(c) 27°
(d) 30°
Solution :
(a) 28°
Question 7.
If the supplement of an angle is three times its complement, then angle is:
(a) 40°
(b) 35°
(c) 50°
(d) 45°
Solution :
(d) 45°
Question 8.
Two angles whose measures are a and b are such that 2a – 3b = 60° then \(\frac {4a}{5b}\) = _______, if they form a linear pair :
(a) 0
(b) 8/5
(c) \(\frac {12}{5}\)
(d) \(\frac {2}{3}\)
Solution :
(c) \(\frac {12}{5}\)
Question 9.
Which one of the following statements is not false?
(a) If two angles are forming a linear pair, then each of these angles is of measure 90°
(b) Angles forming a linear pair can both be acute angles.
(c) One of the angles forming a linear pair can be obtuse angle.
(d) Bisectors of the adjacent angles form a right angle.
Solution :
(c) One of the angles forming a linear pair can be obtuse angle.
![]()
Question 10.
Which one of the following is correct?
(a) If two parallel lines are intersected by a transversal, then alternate interior angles are equal
(b) If two parallel lines are intersected by a transversal then sum of the interior angles on the same side of transversal is 180°
(c) If two parallel lines are intersected by a transversal then corresponding angles are equal.
(d) All of these
Solution :
(d) All of these