Jharkhand Board JAC Class 9 Maths Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 11 रचनाएँ Exercise 11.1
प्रश्न 1.
एक दी हुई किरण के प्रारम्भिक बिन्दु पर 90° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल:
रचना: 1. किरण \(\overrightarrow{O A}\) खाँची।
2. इसके आरम्भिक बिन्दु को केन्द्र मानकर किसी भी त्रिज्या का एक चाप CDE लगाया जो OA को बिन्दु पर काटता है।
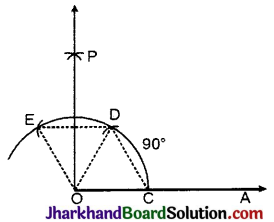
3. C को केन्द्र मानकर समान त्रिज्या का चाप खींचा जो चाप CDE को D पर काटता है।
4. D को केन्द्र मानकर समान त्रिज्या का चाप खींचा जो CDE को E पर काटता है।
5. D और E को केन्द्र मानकर, तथा समान त्रिज्या से दो चाप लगाए जो एक-दूसरे को P बिन्दु पर काटते हैं।
6. OP को मिलाया। इस प्रकार ∠AOP = 90°.
सत्यापन: रचना, OE, ED, DO तथा CD को मिलाया।
अब क्योंकि OC = CD = OD
∴ ΔOCD एक समबाहु त्रिभुज है।
अतः ∠COD = 60°.
पुनः OD = DE = EO
∴ ΔODE भी एक समबाहु त्रिभुज है।
अतः ∠DOE = 60°.
चूँकि OP, ∠DOE को समद्विभाजित करता है। अतः ∠POD = 30°.
अब, ∠AOP = ∠COD + ∠DOP
= 60° + 30° = 90°.
![]()
प्रश्न 2.
एक दी हुई किरण के प्रारम्भिक बिन्दु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल:
रचना: 1. किरण \(\overrightarrow{O A}\) खींची।
2. O को केन्द्र मानकर कोई भी त्रिज्या लेकर एक चाप खींचा, जो OA को B बिन्दु पर काटता है।
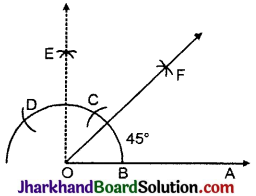
3. B को केन्द्र मानकर समान त्रिज्या से चाप खींचा जो पहले खींचे गए चाप को बिन्दु C पर काटता है अब बिन्दु C को केन्द्र तथा समान त्रिज्या लेकर चाप खींचा जो पहले चाप को D बिन्दु पर काटता है।
4. C. बिन्दु से CD की आधी से अधिक त्रिज्या लेकर एक चाप खींचा।
5. इस प्रकार बिन्दु D को केन्द्र मानकर समान त्रिज्या का दूसरा चाप लगाया जो पहले चाप को E पर काटता है।
6. OE को मिलाया। इस प्रकार ∠AOE = 90°.
7. ∠AOE का समद्विभाजक OF खींचा। इस प्रकार ∠AOF = 45°.
सत्यापन : रचना में, ∠AOE = 90° और OF, ∠AOE का समद्विभाजक है।
∴ ∠AOF = \(\frac{1}{2}\)∠AOE
= \(\frac{1}{2}\) × 90° = 45°.
प्रश्न 3.
निम्नलिखित मापों के कोणों की रचना कीजिए:
(i) 30°
(ii) \(22 \frac{1}{2}^{\circ}\)
(iii) 15°
हल:
रचना करनी है : 30° कोण की।
विश्लेषण: 30° = \(\frac{1}{2}\) × 60°
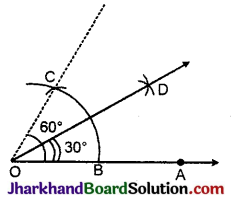
रचना: (1) किरण \(\overrightarrow{O A}\) खींची।
(2) किरण \(\overrightarrow{O A}\) के अन्त्य बिन्दु O को केन्द्र मानकर कोई त्रिज्या OB लेकर एक चाप लगाया।
(3) पुनः B को केन्द्र मानकर उसी त्रिज्या से एक अन्य चाप खींचा जो पहले चाप को बिन्दु C पर काटता है।
(4) बिन्दु C तथा B को केन्द्र मानकर चाप लगाए जो परस्पर D बिन्दु पर काटते हैं।
(5) OD को मिलाती हुवी रेखा खींची।
इस प्रकार ∠AOD = 30° जो अभीष्ट कोण है।
(ii) रचना करनी है: \(22 \frac{1}{2}^{\circ}\) के कोण की।
विश्लेषण: 90° के कोण का समद्विभाजक खींचने पर 45° का कोण प्राप्त होता है और पुनः 45° के कोण का समद्विभाजक खाँचने पर \(22 \frac{1}{2}^{\circ}\) का कोण प्राप्त होता है।
रचना : (1) एक किरण \(\overrightarrow{O A}\) खींचकर उसके अन्त्य बिन्दु O पर 90° का कोण बनाती हुयी रेखा OT खींची।
(2) ∠TOA = 90° का समद्विभाजक OC खींचा
∴ ∠COA = 45°
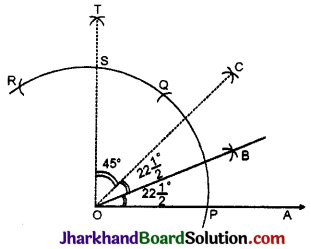
(3) ∠COA – 45° का समद्विभाजक रेखाखण्ड OB खींचा। इस प्रकार \(22 \frac{1}{2}^{\circ}\) के दो कोण प्राप्त होते हैं।
अतः ∠BOA = \(22 \frac{1}{2}^{\circ}\) जो अभीष्ट कोण है।
(iii) रचना करनी है: 15° के कोण की।
विश्लेषण: 60° के कोण का अर्द्धक 30° का कोण बनाया। अब 30° के कोण का अर्द्धक कर 15° का कोण बनाते हैं।
रचना: (1) किरण OA खींचकर उसके अन्त्य बिन्दु O पर 60° बनाते हुए चाप लगाया। ∠COA = 60°.
(2) ∠COA का समद्विभाजक OD खींचा जो ∠DOA = 30° बनाता है।
(3) ∠DOA का समद्विभाजक OE खींचा।
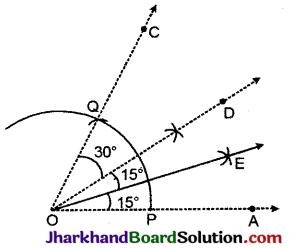
इस प्रकार ∠AOE = \(\frac{1}{2}\) × 30° = 15°
अत: ∠AOE = 15° जो कि अभीष्ट कोण है।
![]()
प्रश्न 4.
निम्नलिखित कोणों की रचना कीजिए और चाँदे द्वारा मापकर पुष्टि कीजिए:
(i) 75°
(ii) 105°
(iii) 135°.
हल:
(i) रचना करनी है: 75° के कोण की।
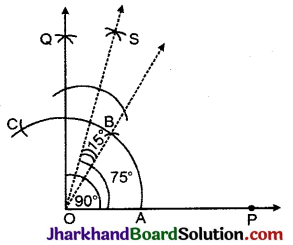
विश्लेषण: 75° = 90° – 15°
= 90° – [30° के कोण का \(\frac{1}{2}\)]
रचना : (1) ∠BOP = 60° बनाते हुए किरण OB तथा ∠POQ = 90° बनाते हुए किरण \(\overline{O Q}\) खींची।
(2) ∠BOQ = (90° – 60° = 30°) का समद्विभाजक OS खींचा, जिससे ∠QOS = 15°.
(3) स्पष्ट है कि
∠POS = ∠POQ – ∠QOS
= 90° – 15° = 75°
अतः ∠POS अभीष्ट कोण है।
(ii) रचना करनी है 105° के कोण की।
विश्लेषण: 60° + 30° + \(\left(30^{\circ} \times \frac{1}{2}\right)\) = 105°
अथवा 90° + \(\left(30^{\circ} \times \frac{1}{2}\right)\) = 105°
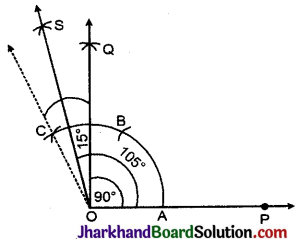
रचना: (1) किरण \(\overline{O P}\) के अन्त्य बिन्दु O पर ∠COP = 120° बनाती हुयी रेखा CO तथा ∠QOP = 90° बनाती हुवी रेखा OQ खींची।
(2) ∠QOC का समद्विभाजक OS खींचा जिससे ∠QOS = 15°।
इस प्रकार, ∠POS = 90° + 15° = 105° जोकि अभीष्ट कोण है।
(iii) रचना करनी है: 135° के कोण की।
विश्लेषण: 135° = 90° + 45°.
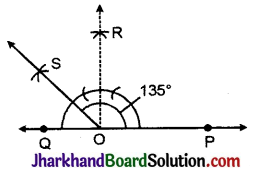
रचना: (1) रेखाखण्ड \(\overline{O P}\) के अन्त्य बिन्दु O पर 90° का कोण बनाती हुयी रेखा \(\overline{O P}\) खींची। इस प्रकार ∠ROQ = ∠ROP = 90°.
(2) ∠QOR का समद्विभाजक OS खींचा।
तब ∠POS = 90° + 45° = 135° जोकि अभीष्ट कोण है।
![]()
प्रश्न 5.
एक समबाहु त्रिभुज की रचना कीजिए, जब इसकी भुजा दी हो। कारण सहित रचना कीजिए।
हल:
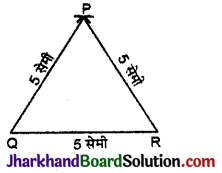
रचना:
(1) रेखाखण्ड QR = 5 सेमी (माना) खींचा।
(2) Q और R को केन्द्र मान कर तथा 5 सेमी त्रिज्या लेकर दो चाप लगाए जो परस्पर P बिन्दु पर काटते हैं।
(3) PQ और PR को मिलाया। इस प्रकार ΔPQR अभीष्ट समबाहु त्रिभुज है।