Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 त्रिभुज Ex 7.3 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 7 त्रिभुज Exercise 7.3
प्रश्न 1.
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि :
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) APकोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BCका लम्ब समद्विभाजक है।
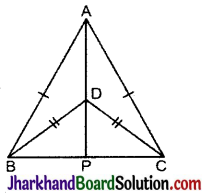
हल:
(i) ΔABD तथा ΔACD में,
AB = AC [दिया है]
BD = DC [दिया है]
और AD = AD [उभयनिष्ठ]
∴ भुजा भुजा-भुजा सर्वांगसमता गुण से,
ΔABD ≅ ΔACD इति सिद्धम्।
(ii) ΔABP तथा ΔACP में.
AB = AC [दिया है]
∠BAP = ∠PAC
[∵ ΔABD ≅ ΔACD
या ∠BAD = ∠DAC
या ∠BAP = ∠PAC]
और AP = AP [उभयनिष्ठ]
ΔABP ≅ ΔACP. [SAS नियम]
इति सिद्धम्।
(iii) ∵ ΔABD ≅ ΔACD
∴ ∠BAD = ∠DAC
⇒ AD, ∠A को समद्विभाजित करता है। …(i)
ΔBDP तथा ΔCDP में,
BD = CD [दिया है]
BP = PC
[∵ ΔABP ≅ ΔACP या BP = PC]
तथा DP = DP [उभयनिष्ठ]
∴ ΔBDP ≅ ΔPDC [SAS नियम]
⇒ DP, ∠D को समद्विभाजित करता है। …(ii)
समीकरण (i) + (ii)
AP, ∠A तथा ∠D को समद्विभाजित करता है। इति सिद्धम्।
(iv) ∵ AP, BC पर स्थित है।
∠APB + ∠APC = 180° [समान्तर युग्म]
परन्तु ∠APB = ∠APC [सिद्ध किया है]
∴ ∠APB = ∠APC = \(\frac{1}{2}\)
तथा BP = PC [सिद्ध किया है]
या AP, BC का लम्ब समद्विभाजक है।
इति सिद्धम्।
![]()
प्रश्न 2.
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD, रेखाण्ड BC को समद्विभाजित करता है।
(ii) AD, कोण 4 को समद्विभाजित करता है।
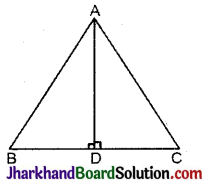
हल:
(i) AD, शीर्ष A से खींचा गया लम्ब है, जो कि समद्विबाहु ΔABC के आधार BC के सम्मुख है।
AB = AC, ∠ADC = ∠ADB = 90°
अब ΔADB तथा ΔADC में,
AB = AC [दिया है]
∴ AD = AD [उभयनिष्ठ है]
तथा ∠ADC = ∠ADB [प्रत्येक 90°]
∴ ΔADB ≅ ΔADC [AAS नियम]
व BD = DC
तथा ∠BAC =∠DAC
∴ AD, BC को समद्विभाजित करता है। इति सिद्धम्।
(ii) ΔADB = ΔADC
अत: ∠BAD ∠CAD
इति सिद्धम् ।
⇒ AD, ∠A को समद्विभाजित करता है। इति सिद्धम्।
प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक-दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर हैं (देखिए आकृति)।
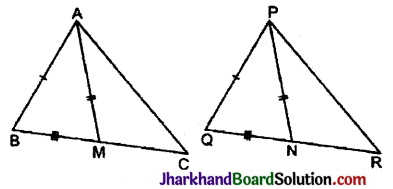
दर्शाइए कि :
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR.
हल:
ΔABC तथा ΔPQR में,
AB = PQ
BC = QR
तथा AM = PN
चूँकि AM तथा PN क्रमश: ΔABC तथा ΔPQR की माध्यिकाएँ हैं।
और BC = QR [दिया है]
⇒ \(\frac{1}{2}\)BC = \(\frac{1}{2}\)QR
⇒ BM = QN
अब, ΔABM तथा ΔPQN में,
AB = PQ [दिया है]
BM = QN
तथा AM = PN [दिया है]
ΔΑΒΜ ≅ ΔΡQΝ [sss नियम]
⇒ ∠B = ∠Q
अब ΔABC तथा ΔPQR में,
AB = PQ [दिया है]
∠B = ∠Q
BC = QR [दिया है]
∴ ΔABC = ΔPQR, [SAS नियम]
![]()
प्रश्न 4.
BE और CF त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं। R.H.S. सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।
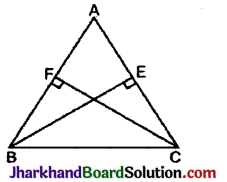
हल:
ΔBCF तथा ΔCBE में,
∠BFC = ∠CEB [∵ प्रत्येक 90°]
BC = BC [उभयनिष्ठ]
FC = EB (दिया है)
∴ ΔBCF ≅ ΔCBE (RHS नियम)
⇒ ∠FBC = ∠ECB
या ∠ABC = ∠ACB
⇒ AB = AC
∴ ΔABC एक समद्विबाहु त्रिभुज है। इति सिद्धम्।
प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। AP ⊥ BC खींचकर दर्शाइए कि ∠B ≅ ∠C है।
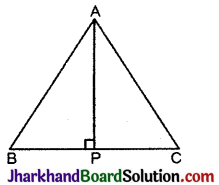
हल:
ΔABP तथा ΔACP में,
AB = AC [दिया है]
AP = AP [उभयनिष्ठ]
∠APB = ∠APC [प्रत्येक 90°]
ΔABP ≅ ΔACP (RHS नियम)
या ∠B = ∠C इति सिद्धम्।