Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 संख्या पद्धति Ex 1.3 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 1 संख्या पद्धति Exercise 1.3
प्रश्न 1.
निम्नलिखित भिन्नों को दशमलव के रूप में लिखिए और बताइए कि प्रत्येक का दशमलव प्रसार किस प्रकार का है ?
(i) \(\frac{36}{100}\)
उत्तर:
\(\frac{36}{100}\) = 0.36, सांत।
(ii) \(\frac{1}{11}\)
उत्तर:
भाग विधि द्वारा :

∴ \(\frac{1}{11}\) = 0.090909…..
= \(0 . \overline{09}\) असांत और आवृत्ति ।
(iii) 4\(\frac{1}{8}\) = \(\frac{33}{8}\)
उत्तर:
भाग विधि द्वारा:

∴ 4\(\frac{1}{8}\) = 4.125, सांत।
(iv) \(\frac{3}{13}\)
उत्तर:
भाग विधि द्वारा:

\(\frac{3}{13}\) = 0.23076923….
= \(0 . \overline{230769}\), असांत और आवृत्ति (पुनरावृत्ति)।
(v) \(\frac{2}{11}\)
हल:
भाग विधि द्वारा :

∴ \(\frac{2}{11}\) = 0.1818 = \(0 . \overline{18}\), असांत और पुनरावृत्ति ।
(vi) \(\frac{329}{400}\)
हल:
भाग विधि द्वारा:

∴ \(\frac{329}{400}\) = 0.8225, सान्त।
![]()
प्रश्न 2.
आप जानते हैं कि \(\frac{1}{7}\) = \(0 . \overline{142857}\) है। वास्तव में, लम्बा भाग दिए बिना क्या आप यह बता सकते हैं कि \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) के दशमलव प्रसार क्या हैं? यदि हाँ, तो कैसे ?
हल:
हाँ, उपर्युक्त सभी 1, 4, 2, 8, 5, 7 आवृत्ति (पुनरावृत्ति) दशमलव हैं।
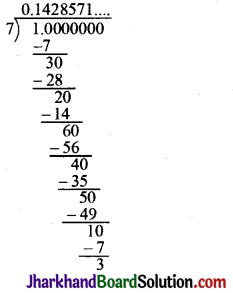

प्रश्न 3.
निम्नलिखित को \(\frac{p}{q}\) के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है:
(i) \(0 . \overline{6}\), (ii) \(0.4 \overline{7}\), (iii) \(0 . \overline{001}\).
हल:
(i) माना x = \(0 . \overline{6}\)
x = 0.666…. …(1)
∵ यहाँ केवल एक आवृत्ति अंक है। इसलिए समीकरण (1) में 10 से गुणा करने पर,
10x = 10 × 0.666….
या 10x = 6.666…. …(2)
समी. (2) मैं से समी. (1) घटाने पर,
9x = 6
⇒ x = \(\frac{6}{9}\)
या x = \(\frac{2}{3}\)
अतः \(0 . \overline{6}\) = \(\frac{2}{3}\)
(ii) प्रथम विधि : माना x = \(0.4 \overline{7}\) …(1)
∵ दशमलव बिन्दु के दायीं ओर बिना बार (रेखा) के एक अंक है।
∴ अतः दोनों पक्षों में 10 से गुणा करने पर,
10x = 10 × \(0.4 \overline{7}\) ⇒ 10x = \(4 . \overline{7}\) ….. (ii)
पुन: समी. (i) के दोनों पक्षों में 100 से गुणा करने पर
100x = \(47 . \overline{7}\) ……..(iii)
समी. (iii) में से समी. (ii) घटाने पर,
90x = 43
⇒ x = \(\frac{43}{90}\)
अत: \(0.4 \overline{7}\) = \(\frac{43}{90}\)
(iii) \(0 . \overline{001}\)
माना x = \(0 . \overline{001}\)
⇒ x = 0.001001001…. …(1)
यहाँ दशमलव बिन्दु के बाद तीन आवृत्ति अंक हैं।
अत: समी. (1) को (10)3 = 1000 से गुणा करने पर,
1000x = 1.001001…. …(2)
समी. (2) में से समी. (1) को घटाने पर,
1000x – x = (1.001001…) – (0.001001….)
⇒ 999x = 1
⇒ x = \(\frac{1}{999}\)
अतः \(0 . \overline{001}\) = \(\frac{1}{999}\)
![]()
प्रश्न 4.
0.99999…. को \(\frac{p}{q}\) के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित हैं ? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।
हल:
माना x = 0.99999….. …..(1)
∵ यहाँ केवल एक आवृत्ति अंक है अतः समीकरण (1) में 10 से गुणा करने पर,
10x = 10 × 0.99999….
10x = 9.999…. …(2)
समी. (2) में से सभी (1) को घटाने पर,
⇒ 9x = 9
∴ x = 1
अतः 0.9999…. = 1
क्योंकि 0.9999…. अनन्त तक होगा। अतः 1 और 0.9999…. में कोई अन्तर नहीं है अतः ये लगभग समान हैं।
प्रश्न 5.
\(\frac{1}{17}\) के दशमलव प्रसार में अंकों के पुनरावृत्ति खण्ड में अंकों की अधिकतम संख्या क्या हो सकती है ? अपने उत्तर की जाँच करने के लिए विभाजन क्रिया कीजिए।
हल:
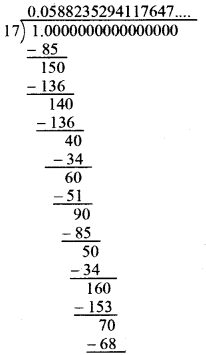
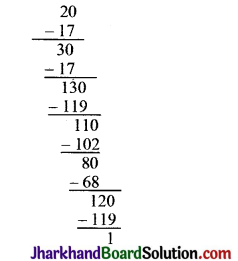
अतः \(\frac{1}{17}\) = \(0 . \overline{0588235294117647}\)
\(\frac{1}{17}\) के दशमलव प्रसार में पुनरावृत्ति अंकों की अधिकतम संख्या 16 है।
प्रश्न 6.
\(\frac{p}{q}\)(q ≠ 0) के रूप की परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड नहीं है और जिसका सांत दशमलव (निरूपण) प्रसार है। क्या आप यह अनुमान लगा सकते हैं कि 9 को कौन-सा गुण अवश्य सन्तुष्ट करना चाहिए ?
हल:
\(\frac{p}{q}\)(q ≠ 0) के रूप में कुछ ऐसी परिमेय संख्याएँ लेते हैं जिसमें और पूर्णांक हों तथा जिनके के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड न हो और सांत दशमलव हो।
माना \(\frac{1}{2}, \frac{1}{4}, \frac{7}{8}, \frac{37}{25}, \frac{8}{125}, \frac{17}{20}, \frac{31}{16}\) आदि ऐसी परिमेय संख्याएँ हैं।
अब हर में ऐसी प्राकृत संख्या से गुणा करते हैं जिससे हर 10 या 10 की घात का प्राप्त हो।

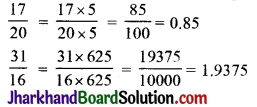
उपरोक्त परिमेय संख्याओं में प्रत्येक के हर का एक गुणनखण्ड 2 अथवा 5 है, तभी हर को 10 या 10 की किसी घात के रूप में प्राप्त किया जा सकता है।
यदि परिमेय संख्या जो मानक रूप में हो और हर में 2 और 5 के अलावा और कोई अभाज्य गुणनखण्ड न हो तब और केवल तब सांत दशमलव निरूपित होता है।
![]()
प्रश्न 7.
ऐसी तीन संख्याएं लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हों।
हल:
हम जानते हैं कि सभी अपरिमेय संख्याओं का दशमलव प्रसार अनवसानी अनावर्ती होता है।
अतः \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\)….. इत्यादि का दशमलव प्रसार अनवसानी अनावर्ती है।
ऐसी संख्या को सीधे दशमलव प्रसार के रूप में भी व्यक्त किया जा सकता है।
a = 0.04004000400004…..
b = 0.505005000500005…..
c = 0.007000700007…..
प्रश्न 8.
परिमेय संख्याओं \(\frac{5}{7}\) और \(\frac{9}{11}\) के बीच तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
हल:
\(\frac{5}{7}\) और \(\frac{9}{11}\)

\(\frac{5}{7}\) और \(\frac{9}{11}\) के मध्य अनन्त अपरिमेय संख्याएँ हो सकती हैं। इसमें से तीन अपरिमेय संख्याएँ निम्नलिखित हैं :
0.75075007500075000075………
0.767076700767000767………
और 0.808008000800008………
![]()
प्रश्न 9.
बताइए कि निम्नलिखित संख्याओं में कौन-कौन संख्याएँ परिमेय और कौन-कौन संख्याएँ अपरिमेय हैं:
(i) \(\sqrt{23}\)
(ii) \(\sqrt{225}\)
(iii) 0.3796
(iv) 7.478478…….
(v) 1·101001000100001………
हल:
(i) संख्या \(\sqrt{23}\) मे 23 पूर्ण वर्ग नहीं है।
\(\sqrt{23}\) अपरिमेय संख्या है।
(ii) \(\sqrt{225}\) = \(\sqrt{3 \times 3 \times 5 \times 5}\)
= 3 × 5 = 15

अतः \(\sqrt{225}\) = 15 एक परिमेय संख्या है।
(iii) 0.3796
सांत दशमलव संख्या है।
∴ 0.3796 एक परिमेय संख्या है।
(iv) 7.478478…..
एक आवृत्ति लेकिन पुनरावृत्ति है।
∴ यह परिमेय संख्या है।
(v) 1.101001000100001…..
यह एक आवृत्ति है लेकिन पुनरावृत्ति नहीं है।
∴ यह अपरिमेय संख्या है।