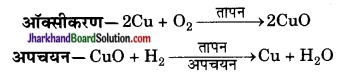Class 10

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Exercise 4.4

प्रश्न 1.
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का अस्तित्व हो, तो उन्हें ज्ञात कीजिए:
(i) 2x² – 3x + 5 = 0
(ii) 3x² – 4\(\sqrt{3}\)x + 4 = 0
(iii) 2x² – 6x + 3 = 0
हल:
(i) दिया गया समीकरण है:
2x² – 3x + 5 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = – 3 तथा c = 5
विविक्तकर (D) = b² – 4ac
= (- 3)² – 4 × 2 × 5
= 9 – 40
= -31 < 0
अतः दी गई द्विघात समीकरण का कोई वास्तविक मूल नहीं है।

(ii) दिया गया द्विघात समीकरण है:
3x² – 4\(\sqrt{3}\)x + 4 = 0
इसकी तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 3, b = – 4\(\sqrt{3}\), c = 4
∴ विविक्तकर (D) = b² – 4ac
= (-4\(\sqrt{3}\))² – 4 × 3 × 4
= 48 – 48 = 0
अतः दी गई द्विघात समीकरण के मूल वास्तविक और बराबर होंगे।
अब श्रीधराचार्य सूत्र से,
x = \(\frac{-b \pm 4 \sqrt{D}}{2 a}\)
= \(\frac{-(-4 \sqrt{3}) \pm \sqrt{0}}{2 \times 3}=\frac{4 \sqrt{3}}{6}\)
= \(\frac{2 \sqrt{3}}{3} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{2 \times 3}{3 \times \sqrt{3}}=\frac{2}{\sqrt{3}}\)
अतः द्विघात समीकरण के मूल \(\frac{2}{\sqrt{3}}\) और \(\frac{2}{\sqrt{3}}\)

(iii) दिया गया द्विघात समीकरण है : 2x² – 6x + 3 = 0 है।
इसकी तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
∴ विविक्तकर (D) = b² – 4ac
a = 2, b = – 6, c =3
= (- 6)² – 4 × 2 × 3
= 36 – 24 = 12 > 0
∴ दी गई द्विघात समीकरण के मूल वास्तविक और भिन्न-भिन्न होंगे।
अब श्रीधराचार्य सूत्र से समीकरण के मूल

प्रश्न 2.
निम्न प्रत्येक द्विघात समीकरण में k का ऐसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों :
(i) 2x² + kx + 3 = 0
(ii) kx(x – 2) + 6 = 0
हल:
(i) दिया गया समीकरण है:
2x² +kx +3 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = k तथा c = 3
विविक्तकर D = b² – 4ac
= k² – 4 × 2 × 3
= k² – 24
समीकरण के मूल बराबर तब होंगे, जब विविक्तकर
D = 0 हो
अर्थात् k² – 24 = 0
⇒ k² = 24
⇒ k = ±\(\sqrt{24}\) = ±2\(\sqrt{6}\)
अतः मूल बराबर होने के लिए ±2\(\sqrt{6}\) होना चाहिए।

(ii) दिया गया समीकरण
kx(x – 2) + 6 = 0
या kx² – 2kx + 6 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = k, b = -2k तथा c = 6
विविक्तकर D =b² – 4ac
= (-2k)² – 4 × k × 6
= 4k² – 24k
= 4k(k – 6)
समीकरण के मूल बराबर तब होंगे, जब विविक्तकर
D = 0 हो
अर्थात् 4k(k – 6) = 0
⇒ k = 0 या k – 6 = 0
⇒ k = 0 या k = 6
अतः समीकरण के बराबर होने के लिए k = 6 होना चाहिए क्योंकि k = 0 प्रतिबन्धित होता है।

प्रश्न 3.
क्या एक ऐसी आम की बगिया बनाना सम्भव है जिसकी लम्बाई, चौड़ाई से दुगनी हो और उसका क्षेत्रफल 800 मी’ हो ? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल:
माना कि एक आयताकार बगिया की चौड़ाई = x मी
आयताकार बगिया की लम्बाई = 2x मी
आयताकार बगिया का क्षेत्रफल = लम्बाई × चौड़ाई
= [2x × x] मी²
= 2x² मी²
प्रश्नानुसार, 2x² = 800
⇒ x² = \(\frac{800}{2}\) = 400
⇒ x = ±\(\sqrt{400}\)
⇒ x = ±20
∵ आयताकार बगिया की लम्बाई ऋणात्मक नहीं हो सकती इसलिए हम x = – 20 को छोड़ देते हैं।
∴ x = 20
∴ आयताकार बगिया की चौड़ाई = 20 मी
और आयताकार बगिया की लम्बाई = (2 × 20) मी
= 40 मी

प्रश्न 4.
क्या निम्न स्थिति सम्भव है ? यदि है, तो उनकी वर्तमान आयु ज्ञात कीजिए। दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पूर्व उनकी आयु (वर्षो में) का गुणनफल 48 था।
हल:
माना कि पहले मित्र की आयु = x वर्ष
∵ दोनों की आयु का योग 20 वर्ष है।
दूसरे मित्र की आयु = (20 – x) वर्ष
चार वर्ष पूर्व,
पहले मित्र की आयु = (x – 4) वर्ष
दूसरे मित्र की आयु = (20 – x – 4) वर्ष
= (16 – x) वर्ष
और उनका गुणनफल = (x – 4) (16 – x)
= 16x – x² – 64 + 4x
= – x + 20x – 64
प्रश्नानुसार,
-x² + 20x – 64 = 48
⇒ -x² + 20x – 64 – 48 = 0
⇒ -x² + 20x – 112 = 0 …..(1)
इसकी मानक समीकरण ax² + bx + c = 0 से तुलना करने पर,
a = -1, b = 20, c = -112
∴ विविक्तकर (D) = b² – 4ac
= (20)² – 4 × (1) × (-112)
=400 – 448 = -48 < 0
∵ मूल वास्तविक नहीं होंगे।
इसलिए x का कोई भी मान द्विघात समीकरण (1) को सन्तुष्ट नहीं कर सकता है।
अतः दी गई स्थिति सम्भव नहीं है।

प्रश्न 5.
क्या परिमाप 80 मी तथा क्षेत्रफल 400 मी² के एक पार्क को बनाना सम्भव है? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल:
माना आयताकार पार्क की लम्बाई = x मी
एवं चौड़ाई = y मी
∴ आयताकार पार्क का परिमाप = 2(x + y) मी
और आयताकार पार्क का क्षेत्रफल = xy मी²
प्रश्न की प्रथम शर्त के अनुसार,
2 (x + y) = 80
⇒ x + y = \(\frac{80}{2}\)
⇒ x + y = 40
⇒ y = 40 – x …..(1)
प्रश्न की दूसरी शर्त के अनुसार,
xy = 400
समीकरण (1) से y का मान रखने पर,
x(40 – x) = 400
⇒ 40x – x² = 400
⇒ x² – 40x + 400 = 0
इसकी तुलना मानक समीकरण ax² + bx + c = 0 से करने पर,
a = 1, b = – 40, c = 400
विविक्तकर (D) = b² – 4ac
= (-40)² – 4 × 1 × 400
= 1600 – 1600 = 0
अतः इस द्विघात समीकरण के मूल वास्तविक और बराबर होंगे।
अब श्रीधराचार्य सूत्र से, x = \(\frac{1}{2}\)
= \(\frac{1}{2}\)
∴ x = 20 मी
तथा y = 40 मी – 20 मी = 20 मी
∴ आयताकार पार्क की लम्बाई और चौड़ाई की माप बराबर अर्थात् 20 मीटर है।
अतः दिया गया आयताकार पार्क का अस्तित्व सम्भव है और यह एक वर्ग है।

Students must go through these JAC Class 10 Science Notes Chapter 7 नियंत्रण एवं समन्वय to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 7 नियंत्रण एवं समन्वय

→ तंत्रिका कोशिका (न्यूरॉन)-सन्देश संवहन की संरचनात्मक एवं क्रियात्मक इकाई है।

→ केन्द्रीय तन्त्रिका तन्त्र-तंत्रिका तन्त्र जो जन्तुओं में मस्तिष्क और मेरूरज्जु का बना होता है।

→ हॉर्मोन-शरीर की क्रियात्मक प्रक्रियाओं को नियन्त्रित करने के लिए विशेष रसायन होते हैं जिन्हें हॉर्मोन कहते हैं।

→ पादप हॉर्मोन-पौधों द्वारा स्नावित हॉर्मोन जो विभिन्न कार्य करते हैं। ये हैं-

• ऑक्सिन
• जिबरलिन
• साइटोकाइनिन
• वृद्धिरोधक।

→ संवेदी तंत्रिका कोशिकाएँ-ये संवेदी अंगों से उद्दीपनों को लेकर मस्तिष्क तक पहुँचाती हैं।

→ चालक तंत्रिका कोशिकाएँ-ये उद्दीपनों के प्रत्युत्तर को कार्यकारी अंगों तक पहुँचाती हैं।

→ अन्तः स्रावी ग्रन्थियाँ-नलिकाविहीन ग्रन्थियाँ जो हॉर्मोन स्रावित करती हैं।

→ डेन्ड्राइट्स-तंत्रिका कोशिकाओं के कोशिकाय बहुशाखी प्रवर्ध।

→ ऐक्सोन-तंत्रिका कोशिका का बहुत अधिक लम्बा व अशाखी प्रबन्ध है।

→ मस्तिष्क-केन्द्रीय तन्त्रिका तन्त्र का वह भाग जो अत्यन्त कोमल तथा संवेदनशील होता है।

→ मस्तिष्क के भाग-मस्तिष्क के तीन भाग होते हैं-

• अग्रमस्तिष्क
• अनुमस्तिष्क
• प्रमस्तिष्क।

→ अन्त:स्रावी ग्रन्थियाँ-थॉयराइड, पेंक्रियास, एड्रिनल, पीयूष, अण्डाशय आदि अन्तःस्तावी ग्रन्थियाँ हैं।

→ मेरुरज्जु-पश्च मस्तिष्क की मेड्यूला ऑब्लांगेटा खोपड़ी के महारन्ध्र छिद्र से निकलकर कशेरुकाओं की तन्त्रिका नाल से होती हुई अन्त तक फैली रहती है और इसे मेरुरज्जु कहते हैं।

→ प्रतिवर्ती क्रियाएँ-किसी उद्दीपन से होने वाली स्वचालित जल्दी से और अनैच्छिक क्रिया को प्रतिवर्ती क्रिया कहते हैं।

→ तंत्रिका आवेग-तंत्रिका कोशिकाओं का (रासायनिक या विद्युत) संकेत भेजना।

Students must go through these JAC Class 10 Science Notes Chapter 6 जैव प्रक्रम to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 6 जैव प्रक्रम

→ जैव प्रक्रम वह सभी प्रक्रम जो सम्मिलित रूप से अनुरक्षण का कार्य करते हैं जैव प्रक्रम कहलाता है।

→ पोषण – किसी जीव द्वारा पोषक पदार्थों को ग्रहण करना तथा उनका उपयोग करना पोषण कहलाता है।

→ स्वपोषी पोषण – स्वपोषी पोषण में पर्यावरण से सरल अकार्बनिक पदार्थ लेकर तथा बाह्य ऊर्जा स्रोत जैसे सूर्य का उपयोग करके उच्च ऊर्जा वाले जटिल कार्बनिक पदार्थों का संश्लेषण करना है।

→ विषमपोषी पोषण – विषमपोषी पोषण में दूसरे जीवों द्वारा तैयार किए जटिल पदार्थों का अंतर्ग्रहण होता है।

→ मनुष्य में पोषण- मनुष्य में खाए गए भोजन का विखंडन भोजन नली के अंदर कई चरणों में होता है तथा पाचित भोजन क्षुद्रांत्र में अवशोषित करके शरीर की सभी कोशिकाओं में भेज दिया जाता है।

→ श्वसन प्रक्रम में ग्लूकोज़ जैसे जटिल कार्बनिक यौगिकों का विखंडन होता है जिससे ए.टी.पी. का उपयोग कोशिका में होने वाली अन्य क्रियाओं को ऊर्जा प्रदान करने के लिए किया जाता है।

→ श्वसन वायवीय या अवायवीय हो सकता है। वायवीय श्वसन से जीव को अधिक ऊर्जा प्राप्त होती है।

→ उत्सर्जन – उपापचयी क्रियाओं के फलस्वरूप शरीर में उत्पन्न होने वाले वर्ज्य पदार्थों का शरीर से निष्कासन उत्सर्जन कहलाता है।

→ उत्सर्जी अंग जो अंग उत्सर्जी पदार्थों को शरीर से बाहर निकालते हैं उत्सर्जी अंग कहलाते हैं।

→ मनुष्य में उत्सर्जी अंग-वृक्क, त्वचा, फुफ्फुस, आँत तथा यकृत उत्सर्जी अंग हैं।

→ फेफड़ा – यह कार्बन डाइ ऑक्साइड तथा जल का उत्सर्जन करता है।

→ यकृत- कोलेस्टरॉल, पित्तवर्णक, निष्क्रिय स्टेयरॉयड, हार्मोन तथा वसा का उत्सर्जन करता है।

→ आँत – यकृत द्वारा उत्पन्न पदार्थों का उत्सर्जन करती है।

→ नेफ्रॉन-वृक्क की संरचनात्मक एवं क्रियात्मक इकाई है।

→ त्वचा- इनमें अनेक स्वेद ग्रन्थियाँ होती हैं जो जल व लवण का निष्कासन करती हैं।

→ पौधों में उत्सर्जी अंग-पौधों में उत्सर्जी अंग नहीं पाए जाते हैं।

→ निम्न श्रेणी के जन्तुओं में उत्सर्जन विसरण द्वारा होता है।

→ मनुष्य में मुख्य उत्सर्जी अंग- वृक्क।

→ मनुष्य में सहायक उत्सर्जी अंग- त्वचा, यकृत, फेफड़े।

→ मनुष्य में ऑक्सीजन, कार्बन डाइ ऑक्साइड, भोजन तथा उत्सर्जी उत्पाद सरीखे पदार्थों का वहन परिसंचरण तंत्र का कार्य होता है। परिसंचरण तंत्र में हृदय, रुधिर तथा रुधिर वाहिकाएँ होती हैं।

→ उच्च विभेदित पादपों में जल, खनिज लवण, भोजन तथा अन्य पदार्थों का परिवहन संवहन ऊतक का कार्य है जिसमें जाइलम तथा फ्लोएम होते हैं।

→ मनुष्य में उत्सर्जी उत्पाद विलेय नाइट्रोजनी यौगिक के रूप वृक्क में वृक्काणु (नेफ्रॉन) द्वारा निकाले जाते हैं।

→ पादपों में उत्सर्जन पादप अपशिष्ट पदार्थों से छुटकारा प्राप्त करने के लिए विविध तकनीकों का उपयोग करते हैं। उदाहरण के लिए अपशिष्ट पदार्थ कोशिका रिक्तिका में संचित किए जा सकते हैं या गोंद व रेजिन के रूप में तथा गिरती पत्तियों द्वारा दूर किया जा सकता है ये अपने आसपास की मृदा में उत्सर्जित कर देते हैं।

Students must go through these JAC Class 10 Science Notes Chapter 5 तत्वों का आवर्त वर्गीकरण to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 5 तत्वों का आवर्त वर्गीकरण

→ डॉबेराइनर के त्रिक-सन् 1817 में जर्मन रसायनज्ञ वुल्फगांग डॉबेराइनर ने समान गुणधर्मों वाले तत्त्वों को समूहों में व्यवस्थित करने का प्रयास किया-

• तीन-तीन तत्त्वों वाले कुछ समूहों को चुना एवं उन समूहों को त्रिक कहा गया।
• त्रिक के तीनों तत्त्वों को उनके परमाणु द्रव्यमान के आरोही क्रम में रखने पर बीच वाले तत्त्व का परमाणु द्रव्यमान, अन्य दो तत्त्वों के परमाणु द्रव्यमान का औसत होता है।

→ न्यूलैंड्स का अष्टक सिद्धान्त-

• अंग्रेज वैज्ञानिक जॉन न्यूलैंड्स ने सबसे कम परमाणु द्रव्यमान वाले तत्त्व से आरम्भ कर 56वें तत्त्व थोरियम तक आरोही क्रम में तत्त्वों को व्यवस्थित किया।
• न्यूलैंड्स ने देखा कि प्रत्येक आठवें तत्त्व का गुणधर्म पहले तत्त्व के समान है। उन्होंने इसकी तुलना संगीत के अष्टक से की और इसलिए उन्होंने इसे अष्टक का सिद्धान्त कहा।

→ न्यूलैंड्स का अष्टक सिद्धान्त केवल हल्के तत्त्वों के लिए ही ठीक से लागू हो पाया था।

→ न्यूलैंड्स के अष्टक नियम की सीमाएँ-

• न्यूलैंड्स ने कल्पना की कि प्रकृति में केवल 56 तत्त्व विद्यमान हैं और भविष्य में किसी अन्य तत्त्व की खोज नहीं होगी। बाद में कई नये तत्त्वों की खोज हुई जिसके गुणधर्म, अष्टक सिद्धान्त से मेल नहीं खाते थे।
• न्यूलैंड्स का अष्टक का सिद्धान्त केवल कैल्सियम तक ही लागू होता था क्योंकि कैल्सियम के प्रत्येक आठवें तत्त्व का गुणधर्म पहले तत्त्व से नहीं मिलता था।

→ मेण्डलीफ की आवर्त सारणी-

• मेण्डलीफ ने तत्त्वों को उनके परमाणु द्रव्यमान के आरोही क्रम तथा रासायनिक गुणधर्मों के आधार पर वर्गीकृत किया।
• मेण्डलीफ की आवर्त सारणी में ऊर्ध्व स्तंभ को समूह तथा क्षैतिज पंक्तियों को आवर्त कहते हैं।

→ मेण्डलीफ के आवर्त सारणी का सिद्धान्त-

• तत्त्वों के गुणधर्म उनके परमाणु द्रव्यमान का आवर्तफलन होते हैं।
• मेण्डलीफ की आवर्त सारणी में आठ Group तथा 6 Period होते हैं।
• उस समय तक 63 तत्त्व ज्ञात थे, जिनके ऊपर मेण्डलीफ ने प्रयोग किया।

→ मेण्डलीफ की आवर्त सारणी की उपलब्धियाँ-

• मेण्डलीफ ने अपनी आवर्त सारणी में कुछ रिक्त स्थान छोड़ दिये और इनसे सम्बन्धित तत्त्वों के अस्तित्व की भविष्यवाणी की थी तथा उनके गुणों का भी अनुमान किया। इसलिए यह नये तत्त्वों की खोज के लिए प्रेरित करती है।
• अक्रिय गैसों की खोज होने पर सारणी में छेड़छाड़ किये बिना ही इन्हें नये समूह में रखा गया।

→ मेण्डलीफ के वर्गीकरण की सीमाएँ-

• वह अपनी सारणी में हाइड्रोजन को सही स्थान नहीं दे पाये। इसे क्षारीय धातु के साथ Group I में रखा गया परन्तु ये हैलोजन की तरह भी द्विपरमाणुक अणु के रूप में पायी जाती है और धातुओं तथा अधातुओं के साथ सहसंयोजक यौगिक बनाती है।
• समस्थानिकों की खोज होने पर सारणी में इन्हें उचित स्थान देने में कठिनाई आती है।

→ आधुनिक आवर्त सारणी-

• हेनरी मोज्ले ने कहा कि तत्त्व के परमाणु द्रव्यमान की तुलना में उसका परमाणु संख्या अधिक आधारभूत गुणधर्म है।
• आधुनिक आवर्त नियम-तत्त्वों के गुणधर्म उनकी परमाणु संख्या का आवर्त फलन होते हैं।
• आवर्त सारणी में तत्त्वों की स्थिति से उनकी रासायनिक अभिक्रियाशीलता का पता चलता है।
• आधुनिक आवर्त सारणी में 18 ऊर्ध्व स्तंभ हैं, जिन्हें समूह (Group) कहा जाता है तथा 7 क्षैतिज पंक्तियाँ हैं, जिन्हें आवर्त (Period) कहा जाता है।

→ आधुनिक आवर्त सारणी की प्रवृत्ति-

• संयोजकता – किसी भी तत्त्व की संयोजकता उसके परमाणु के सबसे बाहरी कोश में उपस्थित संयोजकता इलेक्ट्रॉनों की संख्या से निर्धारित होती है।
• परमाणु साइज – (a) समूह में – जब किसी ग्रुप में नीचे बढ़ते हैं तब परमाणु साइज में वृद्धि होती है, क्योंकि ऊपर से नीचे जाने पर एक एक कोश की वृद्धि होती जाती है।, (b) आवर्त में आवर्त में बायें से दायें ओर जाने पर परमाणु त्रिज्या घटती है क्योंकि नाभिक में आवेश के बढ़ने से यह इलेक्ट्रॉनों को नाभिक की ओर खींचता है जिससे परमाणु का साईज घट जाता है।
• धात्विक अभिलक्षण – धात्विक अभिलक्षण आवर्त में घटता है तथा समूह में नीचे जाने पर बढ़ता है।
• धातुओं के ऑक्साइड क्षारीय तथा अधातुओं के ऑक्साइड सामान्यतः अम्लीय होते हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.1

प्रश्न 1.
कोष्ठकों में दिए गए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिए:
(i) सभी वृत्त ……… होते हैं। (सर्वांगसम, समरूप)
(ii) सभी वर्ग ………. होते हैं। (समरूप, सर्वांगसम)
(iii) सभी……… त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (a) उनके संगत कोण ………….. हों तथा (b) उनकी संगत भुजाएँ ………. हों । (बराबर, समानुपाती)
हल:
(i) समरूप,
(ii) समरूप,
(iii) समबाहु,
(iv) (a) बराबर (b) समानुपाती।

प्रश्न 2.
निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ।
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।
हल:
(i) 1. समबाहु त्रिभुजों का युग्म समरूप आकृतियाँ हैं।
2. वर्गों का युग्म समरूप आकृतियाँ हैं।

(ii) 1. एक त्रिभुज और एक चतुर्भुज ऐसी आकृतियों का युग्म बनाती हैं जो समरूप नहीं हैं।
2. एक वर्ग और एक समचतुर्भुज ऐसी आकृतियों का युग्म बनाती हैं जो समरूप नहीं हैं।

प्रश्न 3.
बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं :

हल:
दोनों चतुर्भुज समरूप हैं क्योंकि उनके संगत कोण बराबर हैं।

Students must go through these JAC Class 10 Science Notes Chapter 4 कार्बन एवं इसके यौगिक to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 4 कार्बन एवं इसके यौगिक

→ कार्बन एक सर्वतोमुखी तत्त्व है जो सभी जीवों एवं हमारे उपयोग में आने वाली वस्तुओं का आधार है, जैसे- भोजन, दवा, कपड़े आदि।

→ कार्बनिक यौगिक कार्बन में बहुत बड़ी संख्या में यौगिक बनाने का गुण है। इन यौगिकों को कार्बनिक यौगिक कहते हैं। इनमें कार्बन तथा हाइड्रोजन के अतिरिक्त नाइट्रोजन ऑक्सीजन, हैलोजन और गंधक आदि भी हो सकते हैं।

→ अपररूपता-तत्त्वों का एक गुण जिसके द्वारा कोई तत्व ऐसे कई रूपों में पाया जाता है जिनके भौतिक गुण भिन्न-भिन्न हों और रासायनिक गुण समान हों, अपरूपता कहलाते हैं।

→ हाइड्रोकार्बन – कार्बन तथा हाइड्रोजन से बने यौगिकों को हाइड्रोकार्बन कहते हैं।

→ संतृप्त हाइड्रोकार्बन (ऐल्केन) – वे हाइड्रोकार्बन जिनमें कार्बन की चारों संयोजकताएँ एकल सहबंध द्वारा संतुष्ट होती हैं, संतृप्त हाइड्रोकार्बन कहलाते हैं। इनका सामान्य रासायनिक सूत्र C_nH_2n+2 है।

→ असंतृप्त हाइड्रोकार्बन-जिन हाइड्रोकार्बन में दो कार्बन परमाणुओं के मध्य द्विबंध अथवा त्रिबंध होता है, उन्हें असंतृप्त हाइड्रोकार्बन कहते हैं।

→ एल्कीन – इन असंतृप्त हाइड्रोकार्बन का सामान्य सूत्र C_nH_2n होता है। इनमें कार्बन के दो परमाणु के मध्य एक द्विबंध होता है।

→ एल्काइन – इन असंतृप्त हाइड्रोकार्बन का सामान्य रासायनिक सूत्र C₂H_2n-2 होता है। इनमें दो कार्बन परमाणुओं में एक त्रिबंध होता है।

→ सहसंयोजी आबंध – दो परमाणुओं के बीच इलेक्ट्रॉन के एक युग्म की साझेदारी के द्वारा बनने वाले आबंध, सहसंयोजी आबंध कहलाते हैं।

→ कार्बन की चतुः संयोजकता एवं श्रृंखलन प्रकृति के कारण यह कई यौगिक बनाता है।

→ अपने-अपने बाहरी कोशों को पूर्ण रूप से भरने के लिए दो परमाणुओं के बीच इलेक्ट्रॉनों की साझेदारी से सहसंयोजक आबंध बनता है।

→ ऐल्कोहॉल-वे कार्बन यौगिक होते हैं जिनमें एक या एक से अधिक हाइड्रॉक्सिल ग्रुप (OH) हो तथा जिनका सामान्य सूत्र C_n H_2n+1OH हों। इसमें Al- kane के ‘6’ के स्थान पर (ol) जोड़ देते हैं।

→ विषम परमाणु- यौगिकों में हाइड्रोजन प्रतिस्थापित करने वाले तत्त्वों को विषम परमाणु कहते हैं।

→ संकलन अभिक्रियाएँ वे क्रियाएँ जो कार्बन- कार्बन के बीच द्वि-आबंध या त्रि-आबंध होने पर वे अन्य अणुओं से क्रिया करके योगात्मक उत्पादक बनाता है तथा द्वि-आबंध या त्रि-आबंध एकल आबंध में परिवर्तित हो जाता है।

→ प्रतिस्थापन अभिक्रियाएँ – वे अभिक्रियाएँ हैं जिनमें किसी यौगिक के सभी परमाणु एक-एक करके अन्य परमाणुओं से विस्थापित हो जाते हैं।

→ समावयवता – वह घटना जिसमें दो या अधिक यौगिकों के अणुसूत्र तो एक ही हों लेकिन संरचना भिन्न होने के कारण गुण भिन्न हो जाते हैं।

→ प्रकार्यात्मक समूह (Functional Group):

• परमाणु या परमाणुओं का समूह जो कार्बनिक यौगिक की अभिक्रियाशीलता बताती है और उसके विशिष्ट गुणधर्मों (अथवा क्रियाओं) को सुनिश्चित करता है, प्रकार्यात्मक समूह कहलाते हैं।
• यौगिकों का विशिष्ट गुण कार्बन श्रृंखला की लम्बाई और प्रकृति पर निर्भर नहीं करता है।

→ ऐल्कोहॉल, ऐल्डिहाइड, कीटोन एवं कार्बोक्सिलिक अम्ल जैसे समूह कार्बन यौगिकों अभिलाक्षणिक गुण प्रदान करते हैं।

→ कार्बन तथा उसके यौगिक हमारे ईंधन के प्रमुख स्रोत हैं।

→ कार्बनिक यौगिक एथेनॉल एवं एथेनॉइक अम्ल का हमारे दैनिक जीवन में काफी महत्त्व है।

→ साबुन एवं अपमार्जक की प्रक्रिया अणुओं में जलरागी तथा जलविरागी दोनों समूहों की उपस्थिति पर आधारित है। इसकी मदद से तैलीय मैल का पायस बनता है और बाहर निकलता है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Exercise 4.1

प्रश्न 1.
जाँच कीजिए कि क्या निम्न द्विघात समीकरण है:
(i) (x + 1)² = 2(x – 3 )
(ii) x² – 2x = (-2) (3 – x)
(iii) (x – 2) (x + 1) = (x – 1) (x + 3)
(iv) (x – 3) (2x + 1) = x (x + 5)
(v) (2x – 1) (x – 3) = (x + 5)
(vi) x² + 3x + 1 = (x – 2)²
(vii) (x + 2)³ = 2x(x² – 1)
(viii) x³ – 4x² – x + 1 = (x – 2)³
हल:
(i) दिया गया समीकरण है:
(x + 1)² = 2(x – 3)
[सूत्र (a + b)² = a² + 2ab + b² से]
⇒ x² + 2x + 1 = 2x – 6
⇒ x² + 2x + 1 – 2x + 6 = 0
⇒ x² + 7 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

(ii) दिया गया समीकरण है:
x² – 2x = (- 2) (3 – x)
⇒ x² – 2x = – 6 + 2x
⇒ x² – 2x – 2x + 6 = 0
⇒ x² – 4x + 6 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

(iii) दिया गया समीकरण
(x – 2) (x + 1) = (x – 1) (x + 3)
⇒ x(x + 1) – 2 (x + 1) = x (x + 3) – 1 (x + 3)
⇒ x² + x – 2x – 2 = x² + 3x – x – 3
⇒ x² + x – 2x – 2 – x² – 3x + x + 3 = 0
⇒ 3x + 1 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 1 है।
अतः समीकरण, द्विघात समीकरण नहीं है।

(iv) दिया गया समीकरण
(x – 3) (2x + 1) = x(x + 5)
⇒ 2x² + x – 6x – 3 = x² + 5x
⇒ 2x² – 5x – 3 – x² – 5x = 0
⇒ x² – 10x – 3 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः समीकरण द्विघात समीकरण है।

(v) दिया गया समीकरण
(2x – 1) (x – 3) = (x + 5) (x – 1)
2x² – 6x – x + 3 = x² – x + 5x – 5
2x² – 7x + 3 = x² + 4x – 5
2x² – 7x + 3 – x² – 4x + 5 = 0
x² – 11x + 8 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

(vi) दिया गया समीकरण
x² + 3x + = (x – 2)²
⇒ x² + 3x + 1 = x² + 4 – 4x
⇒ x² + 3x + 1 – x² – 4 + 4x = 0
⇒ 7x – 3 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 1 है।
अतः दिया गया समीकरण द्विघात समीकरण नहीं है।

(vii) दिया गया समीकरण
(x + 2)³ = 2x(x² – 1)
⇒ x³ + (2)³ + 3 × x × 2 (x + 2) = 2x³ – 2x
⇒ x³ + 8 + 6x² + 12x = 2x³ – 2x = 0
⇒ x³ + 8 + 6x² + 12x – 2x³ + 2x = 0
⇒ -x³ + 6x² + 14x + 8 = 0
∵ यहाँ x की उच्चतम घात 3 है।
अतः यह एक द्विघात समीकरण नहीं है।

(viii) दिया गया समीकरण
x³ – 4x² – x + 1 = (x – 2)³
⇒ x³ – 4x² – x + 1 = x³ – (2)³ – 3 × x × 2 (x – 2)
⇒ x³ – 4x² – x + 1 = x³ – 8 – 6x² + 12x = 0
⇒ x³ – 4x² – x + 1 – x³ + 8 + 6x² – 12x = 0
⇒ 2x² – 13x + 9 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

प्रश्न 2.
निम्नलिखित स्थितियों को द्विघात समीकरणों के रूप में निरूपित कीजिए :
(i) एक आयताकार भूखण्ड का क्षेत्रफल 528 मीटर 2 है। क्षेत्र की लम्बाई (मीटरों में) चौड़ाई के दुगने से एक अधिक है। हमें भूखण्ड की लम्बाई और चौड़ाई ज्ञात करनी हैं।
(ii) दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 306 है। हमें पूर्णांकों को ज्ञात करना है।
(iii) रोहन की माँ उससे 26 वर्ष बड़ी है। उनकी आयु (वर्षो में) का गुणनफल अब से तीन वर्ष पश्चात् 360 हो जाएगा। हमें रोहन की वर्तमान आयु ज्ञात करनी है।
(iv) एक रेलगाड़ी 480 किमी की दूरी समान चाल से तय करती है। यदि इसकी चाल 8 किमी/घण्टा कम होती, तो वह उसी दूरी को तय करने में 3 घण्टे अधिक लेती। हमें रेलगाड़ी की चाल ज्ञात करनी है।
हल:
(i) माना भूखण्ड की चौड़ाई x मीटर है।
∵ भूखण्ड की लम्बाई, उसकी चौड़ाई के दुगुने से 1 मीटर अधिक है।
∴ भूखण्ड की लम्बाई = (2 × चौड़ाई) + 1
= (2 × x + 1)
= (2x + 1) मीटर
∵ आयताकार भूखण्ड का क्षेत्रफल = ल. × चौ.
= (2x + 1) × x
= (2x² + x) वर्ग मीटर
दिया है भूखण्ड का क्षेत्रफल = 528 वर्ग मीटर
∴ 2x² + x = 528
या 2x² + x – 528 = 0
अतः अभीष्ट द्विघात समीकरण :
2x² + x – 528 = 0

(ii) माना पहला धन पूर्णांक है तथा दूसरा क्रमागत धन पूर्णांक x + 1 है,
∴ पूर्णांकों का गुणनफल = x × (x + 1) = x² + x
प्रश्नानुसार, x² + x = 306
x² + x – 306 = 0
अतः अभीष्ट द्विघात समीकरण:
x² + x – 306 = 0

(iii) माना रोहन की वर्तमान आयु = x वर्ष तथा उसकी माँ उससे 26 वर्ष बड़ी है।
∴ रोहन की माँ की वर्तमान आयु = (x + 26) वर्ष
तीन वर्ष बाद रोहन की आयु = (x + 3) वर्ष
तथा तीन वर्ष बाद रोहन की माँ की आयु = (x + 26) + 3 = (x + 29) वर्ष
∴ रोहन और उसकी माँ की आयु का गुणनफल = (x + 3) (x + 29 ) वर्ष
प्रश्नानुसार,
⇒ (x + 3) (x + 29) = 360
⇒ x² + 29x + 3x + 87 = 360
⇒ x² + 32x + 87 – 360 = 0
⇒ x² + 32x – 273 = 0
अतः अभीष्ट द्विघात समीकरण :
x² + 32x – 273 = 0

(iv) माना रेलगाड़ी की चाल x किमी/घण्टा है।
निर्धारित दूरी = 480 किमी
रेलगाड़ी द्वारा लिया गया समय

यदि रेलगाड़ी की चाल 8 किमी / घण्टा कम हो अर्थात् चाल (x – 8) किमी / घण्टा होती तो रेलगाड़ी द्वारा 480 किमी दूरी चलने में लगा समय

⇒ 3x² – 24x = 3840
⇒ 3x² – 24x – 3840 = 0
⇒ 3(x² – 8x – 1280) = 0
⇒ x² – 8x – 1280 = 0
अतः अभीष्ट द्विघात समीकरण : x² – 8x – 1280 = 0

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.4

प्रश्न 1.
A. P. 121, 117, 113, का कौन-सा पद सबसे पहला ऋणात्मक पद होगा ?
हल:
दी गई A. P. है : 121 117, 113, …
प्रथम पद a = a₁ = 121; a₂ = 117; a₃ = 113
सार्वन्तर d = a₂ – a₁ = 117 – 121 = – 4
सूत्र a_n = a + (n – 1)d का प्रयोग करने पर,
⇒ a_n = 121 + (n – 1 ) (- 4)
= 121 – 4n + 4
= 125 – 4n
प्रश्नानुसार,
a_n < 0
⇒ 125 – 4n < 0
⇒ 4n > 125
⇒ n > \(\frac{125}{4}\)
⇒ n > 31\(\frac{1}{4}\)
⇒ n > 31.25
⇒ n < 32
क्योंकि n एक पूर्णांक है।
अत: 32वाँ पद पहला ऋणात्मक पद होगा।

प्रश्न 2.
किसी AP के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है। इस A. P. के प्रथम 16 पदों का योग ज्ञात कीजिए।
हल:
माना दी गई A.P का प्रथम पद a तथा सार्वअन्तर d है।
तीसरा पद a₃ = a + (3 – 1)d = a + 2d
सातवाँ पद a₇ = a + (7 – 1)d = a + 6d
प्रश्नानुसार,
तीसरे और सातवें पदों का योग = 6
या a₃ + a₇ = 6
⇒ a + 2d + a + 6d = 6
⇒ 2a + 8d = 6
⇒ a + 4d = 3 …(1)
पुन: प्रश्नानुसार, a₃ × a₇ = 8
⇒ (a + 2d)(a + 6d) = 8
⇒ a² + 8ad + 12d² = 8 …(2)
समीकरण (1) के वर्ग में से समीकरण (2) को घटाने पर,
(a + 4d)² – (a² + 8ad + 12d²) = (3)² – 8
⇒ a² + 8ad + 16d² – a² – 8ad – 12d² = 9 – 8
4d² = 1
∴ d = ±\(\frac{1}{2}\)
तव a + 4d = 3 में d = \(\frac{1}{2}\) रखने पर,
a + 4 × \(\frac{1}{2}\) = 2
⇒ a + 2 = 3
∴ a = 1
पुन: a + 4d = 3 में d = –\(\frac{1}{2}\) रखने पर,
a + 4 × (-\(\frac{1}{2}\)) = 3
⇒ a – 2 = 3
∴ a = 5

स्थिति I. a = 1, d = \(\frac{1}{2}\)
प्रथम 16 पदों का योग
S₁₆ = \(\frac{16}{2}\) [2a + (16 – 1)d]
= 8[2 + 15 × \(\frac{1}{2}\)]
= 8 × \(\frac{19}{2}\) = 4 × 19 = 76
अतः 16 पदों का योग = 76

स्थिति II. a = 5, d = –\(\frac{1}{2}\)
∴ प्रथम 16 पदों का योग

अतः 16 पर्दों का योगफल = 20.

प्रश्न 3.
एक सीणी के क्रमागत डण्डे परस्पर 25 सेमी की दूरी पर हैं (देखिए आकृति)। डण्डों की लम्बाई एकसमान रूप से घटती जाती है तथा सबसे निचले डंडे की लम्बाई 45 सेमी है और सबसे ऊपर वाले डण्डे की लम्बाई 25 सेमी है। यदि ऊपरी और निचले डण्डे के बीच की दूरी 2\(\frac{1}{2}\) मीटर है, तो डण्डों को बनाने के लिए लकड़ी की कितनी लम्बाई की आवश्यकता होगी ?

हल:
प्रथम व अन्तिम डण्डे के बीच की दूरी
= 2\(\frac{1}{2}\) मीटर = 250 सेमी
और दो क्रमागत डण्डों के बीच की दूरी = 25 सेमी
∴ सीणी में डण्डों की संख्या

∵ प्रथम डण्डे की लम्बाई (a) = 25 सेमी और अन्तिम डण्डे की लम्बाई (l) = 45 सेमी
∴ 11 डण्डों में प्रयुक्त लकड़ी की कुल माप
= 2\(\frac{1}{2}\)(a + l) = \(\frac{1}{2}\)(25 + 4)
\(\frac{11}{2}\) × 70 = 11 × 35
= 385 सेमी = 3.85 मीटर
अतः सीणी के डण्डों में प्रयुक्त लकड़ी की लम्बाई = 385 सेमी या 3.85 मीटर।

प्रश्न 4.
एक पंक्ति के मकानों को क्रमागत रूप से संख्या 1 से 49 तक अंकित किया गया है। दर्शाइए कि x का एक ऐसा मान है किx से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। x का मान ज्ञात कीजिए।
हल:
मकानों पर क्रमागत रूप से अंकित संख्याएँ :
1, 2, 3, 4, 5, 6, …… 47, 48, 49 है।
x एक ऐसी संख्या है कि x के एक ओर की संख्याओं का योग = x के दूसरी ओर की संख्याओं का योग
अर्थात् 1 से x – 1 तक की संख्याओं का योग
= x + 1 से 49 तक की संख्याओं का योग
अनुक्रम की सभी संख्याओं में सार्वअन्तर d = 1 है।
तब से x – 1 तक की संख्याओं का योग, a = 1, n = x – 1

और x + 1 से 49 तक की संख्याओं का योग
= S₄₉ – S_x
(∵ S_x+1 नहीं होगा क्योंकि x के बाद ही x + 1 प्रारम्भ होगा)

अतः x का मान 35 है।

प्रश्न 5.
एक फुटबाल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीणियाँ बनी हुई हैं। इन सीणियों में से प्रत्येक की लम्बाई 50 मीटर है और वह ठोस कंक्रीट (concrete) की बनी हैं। प्रत्येक सीणी में \(\frac{1}{4}\) मीटर की बनाई है और \(\frac{1}{2}\) मीटर का फैलाव (चौड़ाई) है। (देखिए आकृति)। इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।

हल:
प्रत्येक सौणी की लम्बाई 50 मीटर और चौड़ाई \(\frac{1}{2}\) मीटर है सीणियों की संख्या 15 है। प्रत्येक सीणी की जमीन से ऊँचाई एक समान्तर श्रेढी (A.P.) का अनुक्रम है-
\(\frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}, \frac{5}{4}, \frac{6}{4}, \ldots, \frac{15}{4}\)
अतः पहली सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{1}{4}=\frac{50}{8}\) घन मीटर
दूसरी सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{2}{4}=\frac{100}{8}\) घन मीटर
तीसरी सीणी में लगी कंक्रीट का आयतन
\(=50 \times \frac{1}{2} \times \frac{3}{4}=\frac{150}{8}\) घन मीटर
चौथी सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{4}{4}=\frac{200}{8}\) घन मीटर
अतः चबूतरा बनाने में लगे कंक्रीट का कुल आयतन

अतः चबूतरे में लगी कंक्रीट का कुल आयतन = 750 घन मीटर

Jharkhand Board JAC Class 10 Science Important Questions Chapter 1 रासायनिक अभिक्रियाएँ एवं समीकरण Important Questions and Answers.

JAC Board Class 10 Science Important Questions Chapter 1 रासायनिक अभिक्रियाएँ एवं समीकरण

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
किस नियम पर, रासायनिक समीकरण का संतुलित करना आधारित है?
उत्तर:
रासायनिक समीकरण का संतुलित करना द्रव्यमान संरक्षण के नियम पर आधारित है।

प्रश्न 2.
रासायनिक समीकरण में प्रतीक (↓) एवं (↑) क्या प्रदर्शित करते हैं?
उत्तर:
प्रतीक (↑) गैसीय उत्पाद व प्रतीक (↓) अवक्षेप (ठोस) उत्पाद दर्शाता है।

प्रश्न 3.
जलीय अवस्था क्या है?
उत्तर:
किसी अभिकारक या उत्पाद का जल में विलयन उसकी जलीय अवस्था कहलाती है।

प्रश्न 4.
भोजन के पाचन में किस प्रकार की अभिक्रिया होती है?
उत्तर:
भोजन के पाचन में वियोजन अभिक्रिया होती है।

प्रश्न 5.
श्वसन में किस प्रकार की अभिक्रिया होती है?
उत्तर:
श्वसन में उपचयन एवं ऊष्माक्षेपी अभिक्रिया होती है।

प्रश्न 6.
वियोजन अभिक्रियाओं में ऊर्जा किस रूप में ली जाती है?
उत्तर:
वियोजन अभिक्रियाओं में ऊर्जा ऊष्मा, प्रकाश या विद्युत के रूप में ली जाती है।

प्रश्न 7.
अभिकारक व उत्पाद क्या है?
उत्तर:
अभिकारक – ऐसे पदार्थ जो रासायनिक अभिक्रियाओं में भाग लेते हैं अभिकारक कहलाते हैं।

उत्पाद – ऐसे पदार्थ जो रासायनिक अभिक्रिया के फलस्वरूप प्राप्त होते हैं उत्पाद कहलाते हैं।

प्रश्न 8.
बिना बुझे हुए चूने का रासायनिक सूत्र लिखिए।
उत्तर:
CaO.

प्रश्न 9.
रासायनिक अभिक्रियाओं से क्या समझते हैं? उदाहरण दीजिए।
उत्तर:
रासायनिक अभिक्रियाएँ- जब एक या एक से अधिक पदार्थ आपस में क्रिया करके नये पदार्थ का निर्माण करते हैं तो ऐसी अभिक्रियाओं को रासायनिक अभिक्रियाएँ कहते हैं।

उदाहरण – आयरन को सल्फर के साथ गर्म करने पर फेरस सल्फाइड बनता है।

प्रश्न 10.
एथिलीन पर हाइड्रोजन की क्रिया से एथेन बनता है, क्यों?
उत्तर:
एथिलीन एक असंतृप्त हाइड्रोकार्बन है जिसमें कार्बन परमाणु द्विआबन्ध द्वारा जुड़े होते हैं। जब ये हाइड्रोजन से क्रिया करते हैं तो इसका द्विआबन्ध टूट जाता है और नया एकल आबन्ध, आबन्ध द्वारा संतृप्त हाइड्रोजन एथेन बनाते हैं। यह योगशील अभिक्रिया के कारण होता है।

प्रश्न 11.
एकल विस्थापन अभिक्रिया किसे कहते हैं?
उत्तर:
एक विस्थापन अभिक्रिया – जब किसी यौगिक में उपस्थित एक तत्त्व या (एक परमाणु) को किसी दूसरे यौगिक के एक तत्त्व या (एक परमाणु), द्वारा हटाकर स्वयं उसका स्थान ले लेता है तो उसे एकल विस्थापन अभिक्रिया कहते हैं।
उदाहरण: CuSO₄ + Zn → ZnSO₄ + Cu

प्रश्न 12.
उपचयन व अपचयन अभिक्रियाओं को हम किस दूसरे नाम से जानते हैं?
उत्तर:
रेडॉक्स अभिक्रिया (Redox Reaction )।

प्रश्न 13.
उस अभिक्रिया का नाम बताइए जिसमें अविलेय लवण प्राप्त होता है?
उत्तर:
अवक्षेपण अभिक्रिया।

प्रश्न 14.
बेरियम सल्फेट तथा सोडियम क्लोराइड किन अभिकारकों से प्राप्त किये जा सकते हैं?
उत्तर:

1. Na₂SO₄ ( सोडियम सल्फेट)
2. BaCl₂ (बेरियम क्लोराइड)

प्रश्न 15.
अभिक्रिया की गति प्रभावित करने वाले प्रमुख कारक कौन से हैं?
उत्तर:

1. अभिकारकों की प्रकृति
2. ताप
3. सांद्रण
4. उत्प्रेरक।

प्रश्न 16.
ऊष्माक्षेपी अभिक्रियाएँ किन्हें कहते हैं?
उत्तर:
ऊष्माक्षेपी अभिक्रियाएँ – वे रासायनिक अभिक्रियाएँ जिसमें ऊष्मा उत्पन्न या उत्सर्जित होती है, ऊष्माक्षेपी अभिक्रियाएँ कहलाती हैं।
उदाहरण – 1 मोल कार्बन और 1 मोल ऑक्सीजन संयोग करती है तो 1 मोल कार्बन डाइऑक्साइड बनती है तथा 44.3 k cal. ऊष्मा उत्पन्न होती है।
C + O₂ → CO₂ + 44.3 kcal

प्रश्न 17.
उत्क्रमणीय अभिक्रिया किसे कहते हैं?
उत्तर:
उत्क्रमणीय अभिक्रियाएँ वे अभिक्रियाएँ जो समान परिस्थितियों में अग्र एवं पश्च दोनों दिशाओं में होती हैं और किसी भी दिशा में पूर्णता को नहीं पहुँचतीं उत्क्रमणीय अभिक्रियाएँ कहलाती हैं।

उदाहरण – जब फॉस्फोरस पेण्टाक्लोराइड को गर्म किया जाता है तब यह अपघटित होकर फ़ॉस्फोरस ट्राइ- इसे ठण्डा करने पर पुनः क्लोराइड तथा क्लोरीन देता है। फॉस्फोरस पेण्टाक्लोराइड प्राप्त हो जाता है।
PCl₅ ⇌ PCl₃ + Cl₂

लघु उत्तरीय प्रश्न

प्रश्न 1.
रासायनिक साम्य किसे कहते हैं? सिद्ध कीजिए कि इसकी प्रकृति गतिज होती है।
उत्तर:
रासायनिक साम्य- किसी उत्क्रमणीय अभिक्रिया की वह अवस्था जिसमें अग्र व विपरीत दोनों अभिक्रियाओं के वेग बराबर हो जाते हैं, रासायनिक साम्यावस्था कहलाती है।
एक परखनली में कैडमियम क्लोराइड (CaCl₂) के अम्लीय विलयन में H₂S प्रवाहित करने पर कैडमियम सल्फाइड (Cds) का पीला अवक्षेप प्राप्त होता है।

इस स्थिति में सान्द्र HCl की कुछ बूँदें मिलाने पर अवक्षेप घुल जाता है और साफ विलयन प्राप्त हो जाता है। प्राप्त विलयन में H₂S गैस प्रवाहित करने पर पुनः पीला अवक्षेप प्राप्त होता है। इस प्रयोग से सिद्ध होता है। कि रासायनिक साम्य की प्रकृति गतिज होती है।

प्रश्न 2.
ऊष्मीय वियोजन और आयनिक वियोजन में अन्तर लिखिए।
उत्तर:
ऊष्मीय वियोजन और आयनिक वियोजन में अन्तर

ऊष्मीय वियोजन	आयनिक वियोजन
1. ऊष्मीय वियोजन ऊष्मा के द्वारा होता है।	1. आयनिक वियोजन विलयन बनाने पर होता है।
2. ऊष्मीय वियोजन में उत्पाद उदासीन अणु होते हैं।	2. आयनिक वियोजन में उत्पाद आयन होते हैं।
3. ऊष्मीय वियोजन के लिये माध्यम आवश्यक नहीं है।	3. आयनिक वियोजन के लिए माध्यम आवश्यक नहीं है।
4. ऊष्मीय वियोजन में उत्पाद पृथक किये जा सकते हैं।	4. आयनिक वियोजन के उत्पाद पृथक नहीं किये जा सकते।
5. उदाहरण-	5. उदाहरण-

प्रश्न 3.
निम्नलिखित में से कौन-से परिवर्तन ऊष्माशोषी और कौन-से ऊष्माक्षेपी प्रकृति के हैं-
(a) फेरस सल्फेट का अपघटन
(b) सल्फ्यूरिक अम्ल का तनुकरण
(c) सोडियम हाइड्रॉक्साइड का जल में विलीन होना
(d) अमोनियम क्लोराइड का जल में विलीन होना।
उत्तर:
(b) तथा (c) ऊष्माक्षेपी हैं क्योंकि इन परिवर्तनों में ऊष्मा मुक्त होती है।
(a) तथा (d) ऊष्माशोषी हैं, क्योंकि इन परिवर्तनों में ऊष्मा अवशोषित होती है।

प्रश्न 4.
‘X’ समूह 2 के एक तत्त्व का ऑक्साइड है जो सीमेंट उद्योग में बहुत अधिक उपयोग में आता है। यह तत्त्व हड्डियों में भी उपस्थित रहता है। जल में अभिकृत कराने पर यह ऑक्साइड एक विलयन बनाता है, जो लाल लिटमस को नीला कर देता है। ‘X’ को पहचानिए तथा सम्बन्धित रासायनिक अभिक्रियाओं को भी लिखिए।
उत्तर:
X = कैल्सियम ऑक्साइड (बिना बुझा हुआ चूना)

प्रश्न 5.
प्राकृतिक गैस का दहन किस प्रकार की अभिक्रिया है? रासायनिक समीकरण द्वारा स्पष्ट कीजिए।
उत्तर:
यह एक ऊष्माक्षेपी रासायनिक अभिक्रिया है, क्योंकि उत्पाद के निर्माण के साथ-साथ ऊष्मा भी उत्पन्न होती है।

प्रश्न 6.
निम्नलिखित अभिक्रियाओं में अपचायक को पहचानिए-
(a) Fe₂O₃ + 3CO → 2Fe + 3CO₂
(b) 4NH₃ + 5O₂ → 4NO + 6H₂O
उत्तर:
(a) कार्बन मोनॉक्साइड (CO)।
(b) अमोनिया (NH₃)।

प्रश्न 7.
निम्नलिखित अभिक्रियाओं में किसका ऑक्सीकरण तथा किसका अपचयन हुआ है?
(a) MnO₂(aq) + 4HCl(aq) → MnCl₂ (aq) + 2H₂O(l) + Cl₂(g)
(b) CuO(s) + H₂(g) → Cu(s) + H₂O(l)
उपर्युक्त अभिक्रियाओं का क्या नाम है?
उत्तर:
(a) HCl का उपचयन (ऑक्सीकरण) तथा MnO₂ का अपचयन हुआ है।

(b) H₂ का उपचयन तथा CuO का अपचयन हुआ है।
इन अभिक्रियाओं को उपचयन- अपचयन अथवा रेडॉक्स अभिक्रियाएँ कहते हैं।

प्रश्न 8.
क्या होता है जब आयरन धातु के टुकड़े को कॉपर सल्फेट विलयन में डुबोया जाता है?
उत्तर:
लोहे के टुकड़े का रंग भूरा हो जाता है तथा विलयन का रंग हरा हो जाता है। अभिक्रिया इस प्रकार होती है-

प्रश्न 9.
क्या होता है जब एक टुकड़ा-
(a) जिंक धातु का कॉपर सल्फेट विलयन में डाला जाता है।
(b) ऐलुमिनियम धातु का तनु हाइड्रोक्लोरिक अम्ल में डाला जाता है।
(c) सिल्वर धातु को कॉपर सल्फेट विलयन में डाला जाता है।
यदि अभिक्रिया सम्पन्न होती हो तो संतुलित रासायनिक समीकरण भी लिखिए।
उत्तर:
(a) चूँकि जिंक (Zn), कॉपर (Cu) से अधिक क्रियाशील धातु है इसलिए CuSO₄ से Cu को विस्थापित कर देता है तथा जिंक सल्फेट का विलयन प्राप्त होता है।

यह विस्थापन अभिक्रिया का एक उदाहरण है।

(b) इसी प्रकार Al, हाइड्रोजन (H₂) से अधिक क्रियाशील है, इसलिए तनु HCl से H₂ गैस मुक्त कर देता है।

(c) Ag(s) + CuSO₄ (aq) → कोई अभिक्रिया नहीं क्योंकि Ag, Cu से कम क्रियाशील धातु है अतः CuSO₄ से Cu को विस्थापित नहीं कर पाती है।

प्रश्न 10.
विलोपन अभिक्रिया से क्या तात्पर्य है? एक उदाहरण द्वारा समझाइये।
उत्तर:
विलोपन अभिक्रिया वह सहसंयोजक रासायनिक अभिक्रिया जिसमें किसी यौगिक के अणु से एक सरल अणु निष्कासित (विलोपित) होता है विलोपन अभिक्रिया कहलाती है।

उदाहरण – जब एथिल ब्रोमाइड पर ऐल्कोहॉलीय पोटैशियम हाइड्रॉक्साइड की क्रिया करते हैं तो एक सरल अणु जल निष्कासित होता है।

प्रश्न 11.
उत्क्रमणीय एवं अनुत्कमणीय अभिक्रियाओं में अन्तर बताइये।
उत्तर:
उत्क्रमणीय एवं अनुत्क्रमणीय अभिक्रियाओं में अन्तर

उत्क्रमणीय अभिक्रियाएँ	अनुत्क्रमणीय अभिक्रियाएँ
1. ये अभिक्रियाएँ अग्र एवं पश्च दोनों दिशाओं में होती हैं।	1. ये अभिक्रियाएँ एक ही दिशा में चलती हैं।
2. इन अभिक्रियाओं में उत्पाद पुन: संयोजित होकर क्रियाकारकों को बनाते हैं।	2. इन अभिक्रियाओं में उत्पाद पुनः संयोजित नहीं होते हैं।
3. ये अभिक्रियाएँ कभी पूर्ण नहीं होतीं।	3. ये अभिक्रियाएँ पूर्णता को प्राप्त होती हैं।
4. उदाहरण-	4. उदाहरण-

प्रश्न 12.
कारण स्पष्ट करते हुए बताइए कि निम्नांकित परिवर्तन भौतिक हैं अथवा रासायनिक-
(i) गर्म करने पर मोम का पिघलना
(ii) मोमबत्ती का जलना
(iii) भोजन का पाचन
(iv) विद्युत् धारा प्रवाहित होने से तार का गर्म होना
(v) विद्युत धारा प्रवाहित होने से जल का हाइड्रोजन एवं ऑक्सीजन में विघटन
(vi) शुष्क चूने को जल में मिलाने पर जल का गर्म हो जाना
(vii) शर्करा घोलने पर का कुछ ठण्डा हो जाना
(viii) कॉपर सल्फेट विलयन में लोहे के टुकड़े डालने पर उनके रंग का काले से लाल हो जाना।
उत्तर:
(i) गर्म करने पर मोम का पिघलना भौतिक परिवर्तन है, क्योंकि इसमें मोम की केवल भौतिक अवस्था
(ठोस → द्रव) बदलती है-मोम की आणविक संरचना में कोई परिवर्तन नहीं होता।

(ii) मोमबत्ती का जलना-रासायनिक परिवर्तन है. क्योंकि मोम की ऑक्सीजन के साथ रासायनिक अभिक्रिया से नये पदार्थ (CO₂ तथा H₂O) बनते हैं।

(iii) भोजन का पाचन – भोजन का पाचन रासायनिक परिवर्तन है, क्योंकि पाचन क्रिया में अनेक रासायनिक अभिक्रियाओं यौगिक नये यौगिकों में परिवर्तित हो जाते हैं।

(iv) विद्युत् धारा प्रवाहित होने से तार का गर्म होना – भौतिक परिवर्तन है, क्योंकि इससे तार की भौतिक में ही परिवर्तन होता है-तार की संरचना नहीं बदलती।

(v) विद्युत् धारा प्रवाहित होने से जल का हाइड्रोजन एवं ऑक्सीजन में विघटन- यह रासायनिक परिवर्तन है क्योंकि जल से नये पदार्थ हाइड्रोजन एवं ऑक्सीजन बनते हैं।

(vi) शुष्क चूने को जल में मिलाने पर जल का गर्म हो जाना – यह रासायनिक परिवर्तन है, क्योंकि चूना (CaO) तथा जल (H₂O) के रासायनिक संयोग से नया पदार्थ Ca(OH)₂ बनता है।

(vii) शर्करा घोलने पर जल का कुछ ठण्डा हो ना- भौतिक परिवर्तन है, क्योंकि विलयन बनने पर शर्करा एवं जल का मिश्रण बनता है, कोई नया पदार्थ नहीं।

(viii) कॉपर सल्फेट विलयन लोहे के टुकड़े डालने पर उसके रंग का काले से लाल हो जाना – रासायनिक परिवर्तन है, क्योंकि कॉपर सल्फेट के विघटन से नया पदार्थ कॉपर बनता है जो लोहे के टुकड़ों पर एकत्र हो जाता है।

प्रश्न 13.
कारण देते हुए निम्नांकित अभिक्रियाओं को ऊष्माक्षेपी एवं ऊष्माशोषी में वर्गीकृत कीजिए-
(i) 2NH₃ → N₂ + 3H₂ – 24 किलो कैलोरी
(ii) 2SO₂ + O₂ → 2SO₃ + 25 किलो कैलोरी
(iii) N₂ + O₂ + 45 किलो कैलोरी → 2NO
उत्तर:

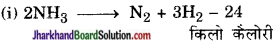
उपर्युक्त अभिक्रिया को निम्नवत् लिखा जा सकता है-
2 NH₃ + 24 किलो कैलोरी N₂ + 3H₂
चूँकि अभिक्रिया सम्पन्न कराने हेतु NH₃ को 24 किलो कैलोरी ऊष्मा देना आवश्यक है अतः यह ऊष्माशोषी अभिक्रिया है।

(ii) 2SO₂ + O₂ → 2SO₃ + 25 किसी कॅलोरी अभिक्रिया में SO₃ के साथ 25 किलो कैलोरी ऊष्मा भी प्राप्त होती है अतः यह ऊष्माक्षेपी अभिक्रिया है।

(iii) N₂ + O₂ + 45 किलो कैलोरी → NO
अभिक्रिया सम्पन्न होने के लिए N₂ तथा O₂ के साथ 45 किलो कैलोरी ऊष्मा भी देना आवश्यक है अतः यह ऊष्माशोषी अभिक्रिया है।

प्रश्न 14.
निम्नलिखित समीकरणों को संतुलित कीजिए-
(i) H₂ + Br₂ → HBr
(ii) Na + O₂ → Na₂O
(iii) P + O₂ → P₂O₅
(iv) CO + O₂ → CO₂
(v) NaOH + H₂SO₄ → Na₂SO₄ + H₂O
उत्तर:
(i) H₂ + Br₂ → HBr
H तथा Br के परमाणुओं की संख्या दोनों ओर समान करने के लिए HBr में 2 से गुणा करने पर
H₂ + Br₂ → 2HBr

(i) Na + O₂ → Na₂O
O की संख्या समान करने के लिए दाहिनी ओर 2 का गुणा करने पर
Na + O₂ → 2 Na₂O
अब Na की संख्या समान करने के लिए Na में 4 का गुणा करने पर

O के 1 परमाणु से Na के दो परमाणु संयोग करके 1 अणु Na₂O बनाते हैं। अतः बायीं ओर O के 2 परमाणुओं से संयोग हेतु Na के 4 परमाणु चाहिए तथा इससे 2 अणु
Na₂O के बनेंगे।
अतः 4 Na + O₂ → 2Na₂O

(iii) P + O₂ → P₂O₅
P₂O₅ सूत्र के अनुसार P के 2 परमाणुओं परमाणु संयोग करते हैं। अतः P के 2 परमाणु लेने पर या O के 5 परमाणु 2 1/2 अणु लेने होंगे।
2P + 2 1/2 O₂ → P₂O₅
परन्तु 1/2 अणु का कोई अर्थ नहीं है-अतः पूरे समीकरण में 2 का गुणा करने पर
4P + 5O₂ → 2P₂O₅

(iv) CO + O₂ → CO₂
चूँकि O का एक परमाणु CO के एक अणु से संयोग करके CO₂ बनाता है, O के दो परमाणु (O₂), से CO के दो अणु संयोग करके 2 अणु CO₂ बनायेंगे। अतः
2CO + O₂ → 2CO₂

(v) NaOH + H₂SO₄ → Na₂SO₄ + H₂O
Na परमाणुओं की संख्या के संतुलन हेतु बायीं ओर NaOH के 2 अणु होने चाहिए। तदनुसार
2 NaOH + H₂SO₄ → Na₂SO₄ + H₂O
अब H परमाणुओं की संख्या के संतुलन हेतु दाहिनी ओर H₂O के दो अणु होने चाहिए – अतः
2NaOH + H₂SO₄ → Na₂SO₄ + 2H₂O

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
‘रासायनिक अभिक्रिया’ से क्या तात्पर्य है? इसके विभिन्न प्रकारों को, प्रत्येक का एक उदाहरण देकर स्पष्ट कीजिए।
उत्तर:
रासायनिक अभिक्रियाएँ (Chemical Reactions) जब कभी भी तत्त्व आपसी संयोग द्वारा यौगिकों का निर्माण करते हैं तब हम कह सकते हैं कि रासायनिक अभिक्रिया हुई। अथवा जब कभी भी भी यौगिक अपघ होकर दूसरे यौगिकों को बनाते हैं, तो रासायनिक अभिक्रियाएँ सम्पन्न होती हैं। अतः “ऐसी क्रियाएँ जिसमें एक या एक या एक से अधिक पदार्थों में उपस्थित परमाणुओं के पुनर्गठन के फलस्वरूप भिन्न पदार्थ या पदार्थों का निर्माण है, रासायनिक अभिक्रिया कहलाती है।”

उपर्युक्त परिभाषा से यह निष्कर्ष ष्कर्ष निकलता है कि रासायनिक अभिक्रिया ऐसी अभिक्रियाएँ हैं जिनके फलस्वरूप नये गुण वाले नये पदार्थ निर्मित होते हैं।

दूसरे शब्दों में “जब एक पदार्थ को किसी दूसरे पदार्थ के साथ क्रिया कराके अथवा कोई पदार्थ अकेले अपघटित होकर एक या एक से अधिक पदार्थ की रचना करता है तो यह क्रिया ही रासायनिक अभिक्रिया ही रासायनिक अभिक्रिया है।

उदाहरणस्वरूप, हाइड्रोजन एवं ऑक्सीजन के मिश्रण में जब चिनगारी की जाती है तब जल निर्मित होता है। इस प्रक्रिया में हाइड्रोजन एवं ऑक्सीजन के अणुओं में उपस्थित परमाणु पुनर्संगठित होकर जल के अणुओं की रचना करते हैं। इस अभिक्रिया को हम साधारणत: रासायनिक समीकरण के रूप में व्यक्त करते हैं।
हाइड्रोजन + ऑक्सीजन → जल
2H₂ + O₂ → 2H₂O
ऊपर व्यक्त अभिक्रिया में हाइड्रोजन एवं ऑक्सीजन अभिकारक हैं। तीर (→) का निशान यह सूचित कर रहा है कि अभिक्रिया हो रही है एवं निर्मित यौगिक जल को उत्पाद कहते हैं।

रासायनिक अभिक्रियाएँ मुख्यतः निम्नलिखित प्रकारों की होती हैं-

• योगात्मक रासायनिक अभिक्रिया (Addition Chemical Reaction)
• प्रतिस्थापन रासायनिक अभिक्रिया (Substitu-tion Chemical Reaction)
• वियोजन अभिक्रिया (Dissociation)
• अपघटन अभिक्रिया (Decomposition)
• उभय-अपघटन (Double Decomposition)

(1) योगात्मक रासायनिक अभिक्रिया (Addition Chemical Reaction) – जिस अभिक्रिया में दो या दो से अधिक पदार्थ आपस में संयोग करके केवल एक पदार्थ बनाते हैं तथा कोई भी अन्य पदार्थ नहीं बनता उसे योगात्मक रासायनिक अभिक्रिया कहते हैं।
उदाहरण-

(2) प्रतिस्थापन रासायनिक अभिक्रिया ( Substi tution Chemical Reaction) – जिस अभिक्रिया में किसी यौगिक के अणु के किसी एक परमाणु या समूह के स्थान पर कोई दूसरा परमाणु या समूह जाता है, उसे प्रतिस्थापन रासायनिक अभिक्रिया कहते हैं।
उदाहरण-

(3) वियोजन अभिक्रिया (Dissociation Reaction ) – ऐसी रासायनिक अभिक्रियाएँ, जिनमें कोई पदार्थ रासायनिक अभिक्रिया को प्रेरित करने वाले कारणों (जैसे – ताप, दाब आदि) में परिवर्तन करने से दो अथवा से अधिक पदार्थों में विभक्त हो जाता तथा उपर्युक्त कारण हटा देने से पुनः मूल पदार्थ बन जाता है, वियोजन कहलाती है। वियोजन एक उत्क्रमणीय (Reversible) अभिक्रिया है। वियोजन अभिक्रियाएँ मुख्यतः दो प्रकार की होती हैं-
(i) ऊष्मीय वियोजन (Thermal Disso- ciation)- जब किसी यौगिक को गर्म करने से उसके अणु दो अथवा दो से अधिक छोटे अणुओं में परिवर्तित हो जाते हैं और ठण्डा करने पर वे फिर से मिलकर मूल
यौगिक बनाते हैं तब इस अभिक्रिया को ऊष्मीय अथवा तापीय वियोजन कहते हैं।
उदाहरणार्थ-

(ii) आयनिक वियोजन (Ionic Dissocia- tion) – किसी विद्युत् अपघद्य (Electrolyte) अथवा विद्युत्-संयोजी यौगिक (Electrovalent COmpound) को जल में घोला जाता है अथवा उच्च ताप तक गर्म करके गलित किया जाता है तो अणुओं का धनात्मक तथा ऋणात्मक आयनों में वियोजन हो जाता है। ये आयन विलयन में या गलित अवस्था में भी पुन: संयोजित होकर अणु बनाते रहते हैं। इस क्रिया को आयनिक वियोजन कहते हैं।
उदाहरण-
NaCl ⇌ Na⁺ + cr^–
H₂SO₄ ⇌ 2.H⁺ + SO^—

(4) अपघटन अभिक्रिया (Decomposition Reaction) – इस प्रकार की अभिक्रिया में किसी पदार्थ का अणु दो या दो से अधिक छोटे अणुओं या परमाणुओं में स्थायी रूप से विभक्त हो जाता है। यह क्रिया मुख्यत: दो प्रकार से से होती है-
(i) ऊष्मीय अपघटन अभिक्रिया (Thermal Decomposition Reaction) – वह रासायनिक अभिक्रिया जिसमें किसी पदार्थ को गर्म करने पर दो या दो से अधिक अवयवों में टूट जाय, परन्तु ठण्डा करने पर पुनः मूल पदार्थ न उसे ऊष्मीय अपघटन अभिक्रिया कहा जाता है। जैसे-

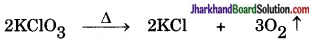
पोटैशियम क्लोरेट पोटैशियम क्लोराइड ऑक्सीजन गैस

(∆ चिन्ह ‘गरम करने’ अथवा ‘ऊष्मा’ को व्यक्त करता है)

(ii) विद्युत्-अपघटन अभिक्रिया (Electrolytic Decomposition Reaction) – इस प्रकार की क्रिया किसी विद्युत अपघट्य के विलयन या गलित अवस्था में विद्युत्-धारा प्रवाहित करने से होती है।
उदाहरणतः

(5) उभय अपघटन (Double Decomposi tion Reaction) – जिस रासायनिक अभिक्रिया में यौगिकों के आयनों या अवयवों की आपस में अदला-बदली होकर नये यौगिक बनते हैं, उसे उभय-अपघटन अभिक्रिया कहते हैं।
उदाहरण-

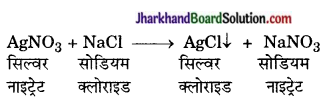
ये अभिक्रियाएँ मुख्यतः ऐसे दो यौगिकों के जलीय विलयनों के मिलाने से होती हैं, जिनमें से एक धनात्मक तथा एक ऋणात्मक आयन मिलकर कोई अविलेय यौगिक बनाते हैं. हैं, जो अवक्षेप अवक्षेप (Precipitate) 1 के रूप में विलयन से अलग हो जाता है। समीकरण में ↓ का चिन्ह, अवक्षेप को व्यक्त करता है।

प्रश्न 2.
रासायनिक समीकरण’ क्या होता है? इससे क्या “क्या जानकारियाँ मिलती हैं? कोई एक उदाहरण देकर बताइए एवं इसकी कमियाँ बताइए।
उत्तर:
रासायनिक समीकरण (Chemical Equation):
किसी भी रासायनिक परिवर्तन में एक या एक से अधिक पदार्थ परस्पर क्रिया करके नये पदार्थ (एक या अधिक) बनाते हैं। ऐसे परिवर्तन को गणितीय समीकरणों की भाँति एक समीकरण से व्यक्त किया जा सकता है। किसी रासायनिक परिवर्तन को व्यक्त करने वाले ऐसे समीकरण को रासायनिक समीकरण कहते हैं।

अभिक्रिया लिखने की विधि (Method of Written Reaction) – अभिक्रिया करने वाले अभिकारक (Reactants) समीकरण के या चिन्ह के बायीं ओर तथा अभिक्रिया के फलस्वरूप बने परिणामी पदार्थ (उत्पाद – Products) चिन्ह के दायीं ओर लिखे जाते हैं।

धन (+) चिन्ह दो या दो से अधिक अभिकारकों के बीच लगाया जाता है तथा परिणामी पदार्थों के बीच भी इसका प्रयोग कहते हैं। समीकरण के दोनों ओर प्रत्येक तत्त्व के परमाणुओं की संख्या समान कर ली जाती है अर्थात् समीकरण को सन्तुलित कर लिया जाता है। गैसों को सदैव अणु के रूप में लिखा जाता है
जैसे – Cl₂, O₂, N₂, H₂ आदि।

इस विधि से सिल्वर नाइट्रेट और हाइड्रोक्लोरिक अम्ल (तनु) की क्रिया के समीकरण को निम्नलिखित ढंग से लिख सकते हैं-
AgNO₃ + HCl = AgCl + HNO₃
किसी रासायनिक समीकरण से निम्नलिखित जानकारी मिलती है-

• अभिकर्मक तत्त्वों तथा यौगिकों के नाम एवं संघटन
• उत्पादों के नाम एवं संघटन
• रासायनिक अभिक्रिया में अभिकर्मकों तथा उत्पादों का द्रव्यमानात्मक अनुपात
• अभिकर्मक गैसों तथा उत्पादित गैसों का (समान दाब तथा ताप पर) आयतनात्मक अनुपात।

उदाहरणतः समीकरण

से ज्ञात होता है कि-
(i) नाइट्रोजन गैस तथा हाइड्रोजन गैस संयोग करके अमोनिया (NH₃) गैस गैस बनाती हैं।

(ii) अमोनिया में नाइट्रोजन का 1 परमाणु तथा हाइड्रोजन के तीन परमाणु होते हैं।

(iii) रासायनिक क्रिया में द्रव्यमान के अनुसार नाइट्रोजन तथा हाइड्रोजन [2 × 14/6 × 1 = ] 14 : 3 के अनुपात में क्रिया करती है तथा इससे 17 भाग अमोनिया उत्पन्न होती है। [∵ नाइट्रोजन का परमाणु भार = 14 तथा हाइड्रोजन का परमाणु-भार = 1]

(iv) दोनों अभिकर्मक तथा उत्पाद गैसे हैं। आयतन , इनका अनुपात, इनके अणुओं की संख्या के अनुपात में होता है। अत: समान दाब तथा ताप पर अभिक्रिया में नाइट्रोजन, हाइड्रोजन तथा अमोनिया का अनुपात 1:3:2 होगा – अर्थात् 1 1 लीटर नाइट्रोजन तथा 3 लीटर हाइड्रोजन के संयोग से 2 लीटर अमोनिया बनेगी।

रासायनिक समीकरण की कमियाँ (Demerits of Chemical Equation) – रासायनिक समीकरण से यह ज्ञात नहीं होता कि-

• अभिकर्मकों की ली गयी तथा उत्पादों की उत्पन्न मात्राएँ क्या हैं।
• अभिक्रिया दाब एवं ताप की किन दशाओं में होती है।
• अभिक्रिया एकदिशीय (अनुत्क्रमणीय) है अथवा उत्क्रमणीय।
• अभिक्रिया में ऊर्जा अवशोषित होती है अथवा मुक्त।

प्रश्न 3.
संतुलित रासायनिक समीकरण की क्या पहचान है? किसी असंतुलित समीकरण को अनुमान विधि से संतुलित करने की क्रिया, एक सरल उदाहरण देकर समझाइए।
उत्तर:
संतुलित रासायनिक समीकरण (Balanced Chemical Equation) रासायनिक अभिक्रियाओं में न तो परमाणु नष्ट होते हैं, न नये परमाणु बनते हैं और न ही एक तत्त्व के परमाणु से किसी दूसरे तत्त्व का परमाणु बनता है। अतः रासायनिक समीकरण में उसके दोनों पक्षों में प्रत्येक तत्त्व के परमाणुओं की मात्रा समान होनी चाहिए। तभी वह समीकरण रासायनिक क्रिया को सही रूप में व्यक्त करता है। इस प्रकार के समीकरण को संतुलित समीकरण (Balanced Equation) कहते हैं।

उदाहरणतः हाइड्रोजन तथा ऑक्सीजन गैसों के संयोग से जल बनने की क्रिया को निम्नवत् लिखा जा सकता है-

उपर्युक्त समीकरण अभिक्रिया के अभिकर्मकों तथा उत्पाद को तो व्यक्त करता है परन्तु इसमें समीकरण के दोनों पक्षों में ऑक्सीजन परमाणुओं की संख्या समान नहीं है– अर्थात् यह समीकरण संतुलित नहीं है। संतुलित करने पर इसका स्वरूप निम्नवत् जाता है-
2H₂ + O₂ → 2H₂O
समीकरण सन्तुलन का उदाहरण (अनुमान विधि) (Examples of Equation Balance) – सरल रासायनिक समीकरणों को (जिनमें दो से अधिक अभिकर्मक न हों), तत्त्वों के परमाणुओं को गिनकर, संतुलित किया जा सकता है। इसे अनुमान विधि भी कहते हैं। यद्यपि इस विधि में भी परमाणुओं की संख्या का संतुलन अनुमान मैं नहीं, वरन् गणितीय विधि से ही किया जाता है।]
उदाहरण 1.
H₂ + O₂ → H₂O
(i) समीकरण के बाएँ पक्ष में दो 0 परमाणु हैं परन्तु दाहिने पक्ष में केवल एक, अतः दाहिने पक्ष में 2 अणु लेने से 0 परमाणुओं का संतुलन हो जाता है अर्थात्
H₂ + O₂ → 2H₂O

(ii) अब दाहिने पक्ष में H के कुल 4 परमाणु बाएँ पक्ष में केवल 2 अतः बायीं ओर H₂ में 2 का गुणा करने से H का संतुलन हो जाता है-
2H₂ + O₂ → 2H₂O
अत: यह संतुलित समीकरण है।

प्रश्न 4.
(क) ‘मन्द’ तथा ‘तीव्र’ अभिक्रिया से क्या तात्पर्य है? एक-एक उदाहरण देकर बताइए।
(ख) रासायनिक अभिक्रिया की गति को मुख्यतः कौन-से कारक प्रभावित करते हैं?
उत्तर:
(क) मन्द अभिक्रियाएँ (Slow Reae- tions) – कुछ रासायनिक अभिक्रियाओं के पूरा होने में अधिक समय लगता है जैसे लोहे की वस्तु पर ऑक्सीजन की क्रिया से जंग (Rust) लगना किसी लोहे की वस्तु के पूरी तरह जंग में परिवर्तित होने में अनेक वर्ष लग सकते हैं। ऐसी क्रियाओं को मन्द अभिक्रियाएँ (Slow Reactions) कहते हैं।

मन्द अभिक्रियाओं में अभिकर्मकों का उत्पादों में परिवर्तन धीरे-धीरे अर्थात् अधिक समय में होता है।

उदाहरण- सल्फ्यूरिक अम्ल (H₂SO₄) की उपस्थिति में एथिल ऐल्कोहॉल (C₂H₅OH) ऐसीटिक अम्ल (CH₃COOH) से क्रिया करके एथिल ऐसीटेट (CH₃COOC₂H₅) और जल (H₂O) बनाता है। इस अभिक्रिया को पूर्ण होने में अनेक मिनट लगते हैं। अतः यह एक मंद अभिक्रिया है।

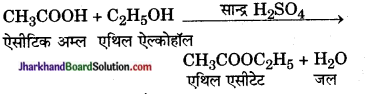
तीव्र – अभिक्रियाएँ (Rapid Reactions ) – तीव्र अभिक्रियाएँ अत्यन्त कम समय में ही पूरी हो जाती हैं। अभिकर्मकों को मिलाने पर इनके पूरे होने का समय 106 सेकण्ड (माइक्रो सेकण्ड ) के कोटिमान का होता है। तीव्र अभिक्रियाएँ मुख्यतः आयनों अथवा आयनिक यौगिकों के बीच होती हैं।

उदाहरण – सिल्वर नाइट्रेट (AgNO₃) के विलयन को जब सोडियम क्लोराइड (NaCl) के विलयन में डालते तो सिल्वर क्लोराइड (AgCl) का तत्काल सफेद अवक्षेप (Precipitate) बनता है। यह एक तात्क्षणिक (Instan- taneous) अभिक्रिया है। अभिक्रिया है, क्योंकि आयनों के बीच होती है।

(ख) रासायनिक अभिक्रियाओं की गति को प्रभावित करने वाले प्रमुख कारक निम्नलिखित हैं- ताप, दाब, अभिकर्मकों की मात्राएँ तथा उत्प्रेरकों की उपस्थिति अथवा अनुपस्थिति। कुछ अभिक्रियाएँ नमी, प्रकाश आदि से भी प्रभावित होती हैं।

प्रश्न 5.
विस्थापन अभिक्रिया को उदाहरण सहित समझाइए।
अथवा
एकल विस्थापन अभिक्रिया एवं द्वि-विस्थापन अभिक्रिया को उदाहरण सहित समझाइये।
उत्तर:
विस्थापन अभिक्रिया – जब रासायनिक अभिक्रिया में एक तत्त्व (या पदार्थ) किसी दूसरे तत्त्व (या पदार्थ) को उसके यौगिक में से हटाकर स्वयं उसका स्थान ले लेता है तो उसे विस्थापन अभिक्रिया कहते हैं। ये दो प्रकार की होती हैं-
(i) एकल विस्थापन अभिक्रिया- किसी यौगिक में उपस्थित एक तत्त्व या (एक परमाणु) को इसके यौगिक के एक तत्त्व या (एक परमाणु) द्वारा हटाकर स्वयं उसका स्थान ले लेना एकल विस्थापन अभिक्रिया कहलाती है।

उदाहरण- कॉपर सल्फेट विलयन में जिंक धातु का टुकड़ा डालने पर जिंक द्वारा कॉपर का विस्थापन करके जिंक सल्फेट बनाता है।

द्वि-विस्थापन अभिक्रिया- ऐसी रासायनिक अभिक्रियाएँ जिसमें दो यौगिकों द्वारा परस्पर आयनों का विनिमय कर नये यौगिकों का निर्माण करते हैं तो इस क्रिया को द्वि-विस्थापन अभिक्रिया कहते हैं।

उदाहरण – जब सोडियम क्लोराइड के जलीय विलयन में सिल्वर नाइट्रेट विलयन मिलाते हैं तो आयनों का विनिमय कर सिल्वर क्लोराइड और सोडियम नाइट्रेट प्राप्त होता है।
Na⁺ Cl^– + Ag⁺ NO^–₃ → AgCl + NaNO₃

प्रश्न 6.
निम्नलिखित रासायनिक अभिक्रियाओं को परिभाषित कीजिए तथा एक-एक उदाहरण भी दीजिए-
(a) संयोजन अभिक्रिया
(b) वियोजन अभिक्रिया
(c) विस्थापन अभिक्रिया
(d) द्विविस्थापन अभिक्रिया
(e) उपचयन एवं अपचयन अभिक्रिया
उत्तर:
(a) संयोजन अभिक्रिया – ऐसी अभिक्रिया जिसमें या दो से अधिक अभिकारक मिलकर एक उत्पाद का निर्माण करते हैं, उसे संयोजन अभिक्रिया कहते हैं।
2Mg + O₂ → 2MgO

(b) वियोजन या अपघटन अभिक्रिया – इसमें एकल पदार्थ वियोजित होकर दो या दो से अधिक पदार्थ बनाते हैं। वियोजन के लिए ऊष्मा, प्रकाश या विद्युत ऊर्जा की आवश्यकता होती है।

(c) विस्थापन अभिक्रिया – ऐसी अभिक्रिया जिसमें अधिक क्रियाशील तत्त्व, कम क्रियाशील तत्त्व को उसके यौगिक से विस्थापित कर दे, विस्थापन अभिक्रिया कहलाती है।

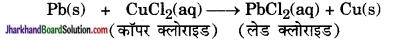
यहाँ लेड (Pb), कॉपर (Cu) की अपेक्षा अधिक क्रियाशील तत्त्व है, जो Cu को CuCl₂ से हटा देता है।

(d) द्विविस्थापन अभिक्रिया – वे अभिक्रियाएँ जिसमें अभिकारकों के बीच आयनों का आदान-प्रदान होता है, उन्हें द्विविस्थापन अभिक्रियाएँ कहते हैं।
Na₂SO₄(aq) + BaCl₂(aq) → BaSO₄(s) + 2NaCl(aq)
यहाँ Ba²⁺+ तथा SO₄^2- आयनों की अभिक्रिया से BaSO₄ अवक्षेप का निर्माण होता है।

(e) उपचयन – अपचयन अभिक्रिया – ऑक्सीजन का योग या हाइड्रोजन का ह्रास ऑक्सीकरण या उपचयन कहलाता है जबकि ऑक्सीजन का ह्रास या हाइड्रोजन का योग अपचयन कहलाता है।

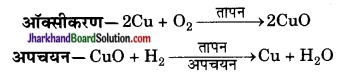
प्रश्न 7.
कारण देते हुए निम्नलिखित अभिक्रियाओं का प्रकार बताइए-
(i) Zn + 2 HCl → ZnCl₂ + H₂
(ii) N₂ + 3H₂ → 2NH₃
(iii) CaO + CO₂ → CaCO₃
(iv) HCl ⇌ H⁺ + Cl^–
(v) AgNO₃ + KCl → KNO₃ + AgCl
(vi) HNO₃ + NaOH → NaNO₃ + H₂O
(vii) 2CO + O₂ → 2CO₂
(viii) C₂H₅Br + NaOH → C₂H₅OH + NaBr

उत्तर:
(i) Zn + 2 HCl → ZnCl₂ + H₂
यह प्रतिस्थापन अभिक्रिया है- क्योंकि HCl अणु से Zn परमाणु H परमाणु को हटाकर उसका स्थान लेता है।

(ii) N₂ + 3H₂ → 2NH₃
योगात्मक अभिक्रिया है- क्योंकि N₂ तथा H₂ के संयोग से NH₃ अणु बनता है।

(iii) CaO + CO₂ → CaCO₃
योगात्मक अभिक्रिया है, जिसमें CaO अणु तथा CO₂ अणु का संयोजन होकर CaCO₃ अणु बनता है।

(iv) HCl ⇌ H⁺ + Cl^–
आयनिक- वियोजन की अभिक्रिया है, जिसमें HCl अणु का H⁺ तथा CH^– आयनों में विघटन तथा इनका पुनः संयोजन होता रहता है।

(v) AgNO₃ + KCl → KNO₃ + AgCl
उभय- अपघटन अभिक्रिया है, क्योंकि AgNO₃ तथा KCI के धनात्मक तथा ऋणात्मक आयनों के विनिमय से नये अण बनते हैं।

(vi) HNO₃ + NaOH → NaNO₃ + H₂O
उदासीनीकरण अभिक्रिया है क्योंकि अम्ल (HNO₃) तथा क्षार (NaOH) की पारस्परिक अभिक्रिया से जल तथा लवण (NaNO₃) बनते हैं।

(vii) 2CO + O₂ → 2CO₂
योगात्मक अभिक्रिया है जिसमें CO तथा O₂ के संयोग से CO₂ बनता है।

(viii) C₂H₅Br + NaOH → C₂H₅OH + NaBr
प्रतिस्थापन अभिक्रिया है जिसमें C₂H₅ Br अणु से Br का प्रतिस्थापन OH द्वारा होता है।

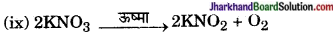
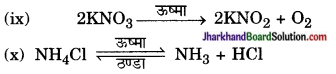
ऊष्मीय अपघटन है, क्योंकि ऊष्मा के प्रभाव से KNO₃ का अपघटन होता है तथा KNO₂ एवं O₂ बनते हैं।

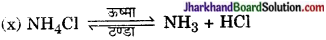
ऊष्मीय वियोजन की अभिक्रिया है- क्योंकि ऊष्मा के प्रभाव से NH₄Cl का अणु NH₃ तथा HCl में विघटित होता है तथा ये परस्पर पुनः संयोजित होकर NH₄Cl बनाते रहते हैं।

बहुविकल्पीय प्रश्न

निर्देश- प्रत्येक प्रश्न में दिये गये वैकल्पिक उत्तरों में से सही विकल्प चुनिए-

1. नौसादर को गर्म करने पर यह अमोनिया और हाइड्रोजन क्लोराइड में टूट जाता है, ठण्डे में दोनों के संयोग से नौसादर बन जाता है। यह अभिक्रिया है-
(a) ऊष्मीय वियोजन
(c) ऊष्मीय अपघटन
(b) विस्थापन
(d) अपघटन
उत्तर:
(a) ऊष्मीय वियोजन

2. तप्त निकिल चूर्ण की उपस्थिति में ऐसिटिलीन तथा हाइड्रोजन की अभिक्रिया कहलाती है-
(a) विस्थापन अभिक्रिया
(b) योगात्मक अभिक्रिया
(c) वियोजन अभिक्रिया
(d) अपघटन अभिक्रिया
उत्तर:
(b) योगात्मक अभिक्रिया

3. क्यूप्रिक सल्फेट के विलयन में जब लोहे का टुकड़ा डाला जाता है तो आयरन, कॉपर हटाकर फेरस सल्फेट बनाता है। यह अभिक्रिया है-
(a) प्रतिस्थापन अभिक्रिया
(b) अपघटन अभिक्रिया
(c) योगात्मक अभिक्रिया
(d) वियोजन अभिक्रिया
उत्तर:
(a) प्रतिस्थापन अभिक्रिया

4. निम्नलिखित में ऊष्माशोषी अभिक्रिया है-
(a) H₂ + Cl₂ → 2HCl + 44.12 किलो कैलोरी
(b) S + O₂ → SO₂ + 71.0 किलो कैलोरी
(c) C + O₂ → CO₂ + 94.45 किलो कैलोरी
(d) H₂ + I₂ → 2Hl – 11.82 किलो कैलोरी
उत्तर:
(d) H₂ + I₂ → 2Hl – 11.82 किलो कैलोरी

5. निम्नलिखित में ऊष्माक्षेपी अभिक्रिया है-
(a) C + O₂ → CO₂ + 94.45 किलो कैलोरी
(b) H₂ + I₂ → 2HI – 11.82 किलो कैलोरी
(c) N₂₊ + O₂ → 2NO – 43.2 किलो कैलोरी
(d) C + 2S → CS₂ – 15.4 किलो कैलोरी
उत्तर:
(a) C + O₂ → CO₂ + 94.45 किलो कैलोरी

6. NH₄Cl ⇌ NH₄⁺ + Cl^– अभिक्रिया है-
(a) ऊष्मीय अपघटन
(b) आयनिक वियोजन
(c) ऊष्मीय वियोजन
(d) विद्युत् अपघटन
उत्तर:
(c) ऊष्मीय वियोजन

7. निम्नलिखित में योगात्मक अभिक्रिया है-
(a) Zn + H₂SO₄ → ZnSO₄ + H₂
(b) 2KBr + Cl₂ → 2KCl + Br₂
(c) 2H₂ + O₂ → 2H₂O
(d) 2Hgo → 2Hg + O₂
उत्तर:
(c) 2H₂ + O₂ → 2H₂O

8. जिन अभिक्रियाओं में आयनों के विनिमय से नये यौगिक बनते हैं, उन्हें कहते हैं-
(a) प्रतिस्थापन अभिक्रिया
(b) उभय अपघटन
(c) योगात्मक अभिक्रिया
(d) वियोजन
उत्तर:
(b) उभय अपघटन

9. निम्न अभिक्रिया में किस पदार्थ का अपचयन हुआ है?
3MnO₂ + 4Al → 3Mn + 2AlO₃
(a) MnO₂
(b) Al
(c) AlO₃
(d) Mn
उत्तर:
(a) MnO₂

10. निम्न अभिक्रिया एक उदाहरण है-

(a) संयोजन अभिक्रिया
(b) वियोजन अभिक्रिया
(c) विस्थापन अभिक्रिया
(d) द्विविस्थापन अभिक्रिया
उत्तर:
(c) विस्थापन अभिक्रिया

11. अपघटन अभिक्रिया का उदाहरण है-
(a) 2KClO₃ → 2KCl (s) + 3O₂ (g)
(b) Zn + CuSO₄ → ZnSO₄ + Cu
(c) Mg + 2HCH → MgCl₂+ H₂
(d) CaO + H₂O → Ca(OH)₂
उत्तर:
(a) 2KClO₃ → 2KCl (s) + 3O₂ (g)

12. लेड (II) नाइट्रेट के घोल (विलयन) में पोटैशियम आयोडाइड का घोल मिलाने पर किस रंग का अवक्षेप प्राप्त होता है?
(a) पीला
(c) लाल
(b) नीला
(d) भूरा
उत्तर:
(a) पीला

13. जब कॉपर सल्फेट के घोल में लोहे की कील या पत्ती डुबोई जाए तो विलयन (घोल) किस रंग का हो जाता है?
(a) नीला
(b) रंगहीन
(c) नाल
(d) हरा
उत्तर:
(d) हरा

14. लेड मल्फेट का रासायनिक सूत्र है-
(a) Pb₂SO₄
(b) Pb(SO₄)₂
(c) PbSO₄
(d) Pb(SO₄)₃
उत्तर:
(c) PbSO₄

15. निम्नलिखित में से कौन-से ऊष्माशोषी प्रक्रिया हैं?
(i) सल्फ्यूरिक अम्ल का तनुकरण
(ii) शुष्क बर्फ का ऊर्ध्वपातन (सबलिमेशन)
(iii) जनवाप्प का संघनन
(iv) जल का जलवाष्प में बदलना।
(a) (i) और (iii)
(c) केवल (iii)
(b) केवल (ii)
(d) (ii) और (iv)
उत्तर:
(d) (ii) और (iv)

16. दी गई अभिक्रिया, SO₂ (g) + 2H₂S (g) → 2H₂O(g) + 3S(s), में अपचायक (Reducing agent) है-
(a) SO₂
(b) H₂O
(c) H₂S
(d) S
उत्तर:
(c) H₂S

17. मीथेन के दहन (Combustion) से प्राप्त होता है-
(a) CO₂
(b) H₂O
(c) CO₂ और H₂ O दोनों
(d) CO और H₂O दोनों
उत्तर:
(c) CO₂ और H₂ O दोनों

18. सिल्वर ब्रोमाइड (AgBr) का वियोजन किस ऊर्जा के कारण होता है?
(a) ऊष्मा
(b) प्रकाश
(c) विद्युत
(d) पवन
उत्तर:
(b) प्रकाश

19. दीवारों पर सफेदी करने के दो-तीन दिन बाद चमक आती है-
(a) क्योंकि CaO, H₂O से अभिक्रिया कर CO₂ बनाता है।
(b) क्योंकि Ca(OH)₂, CO₂ से अभिक्रिया कर CaCO₃ बनाता है।
(c) क्योंकि Ca(OH)₂, H₂O से अभिक्रिया कर CaCO₃ बनाता है।
(d) क्योंकि C, O₂ से अभिक्रिया कर CO₂ बनाता है।
उत्तर:
(b) क्योंकि Ca(OH)₂, CO₂ से अभिक्रिया कर CaCO₃ बनाता है।

20. निम्नलिखित अभिक्रियाओं में से द्विविस्थापन अभिक्रिया के उदाहरण हैं-
(i) Pb + CuCl₂ → PbCl₂ + Cu
(ii) Na₂SO₄ + BaCl₂ → BaSO₄ + 2NaCl
(iii) C + O₂ → CO₂
(iv) CH₄ + 2O₂ → CO₂ + 2H₂O
(a) (i) और (iv)
(b) केवल (ii)
(c) (i) और (ii)
(d) (iii) और (iv)
उत्तर:
(b) केवल (ii)

रिक्त स्थानों की पूर्ति कीजिए

1. ऐसी अभिक्रिया जिसमें दो या दो से अधिक पदार्थ अभिक्रिया करके एक नया पदार्थ बनाते हैं, उसे …………… कहते हैं।
2. ऐसी अभिक्रिया जिसमें एक पदार्थ विघटित होकर दो या दो से अधिक सरल पदार्थ बनाता है, …………… कहलाता है।
3. जो पदार्थ गलित अवस्था में या विलयन में विद्युत-धारा का वहन करता है, …………… कहलाता है।
4. जिन अभिक्रियाओं में ऊष्मा मुक्त होती है, वे अभिक्रियाएँ …………… कहलाती हैं।
5. ऐसी अभिक्रिया जिसमें किसी यौगिक में उपस्थित एक तत्त्व दूसरे तत्त्व द्वारा विस्थापित होता है, …………… कहलाता है।

उत्तर:

1. संयोजन अभिक्रिया
2. विघटन अभिक्रिया
3. विद्युत अपघट्य
4. उत्क्रमणीय अभिक्रियाएँ
5. विस्थापन अभिक्रिया।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.2

प्रश्न 1.
निम्नलिखित सारणी में रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a सार्वअन्तर d और nवाँ पद a_n है-

हल:
(i) a = 7, d = 3, n = 8
∵ a_n = a + (n – 1)d
∴ a₈ = 7 + (8 – 1)3
= 7 + 21 = 28
अत: a₈ = 28

(ii) a = – 18, a = 10, a_n = 0
∵ a_n = a + (n – 1)d
∴ a₁₀ = -18 + (10 – 1)d
⇒ 0 = -18 + 9d
⇒ 9d = 18
∴ d = \(\frac{18}{9}\) = 2
अत: d = 2

(iii) d = -3, n = 18, a_n = -5
∵ a_n = a + (n – 1)d
∴ a₁₈ = a + (18 – 1) (-3)
⇒ -5 = a – 51
∴ a = – 5 + 51 = 46

(iv) a = – 18.9, d = 2.5, a_n = 3.6
∵ a_n = a + (n – 1)d
∴ 3.6 = -18.9 + (n – 1) 2.5
⇒ 3.6 + 18.9 = (n – 1) 2.5
⇒ (n – 1)2.5 = 22.5
⇒ n – 1 = \(\frac{22.5}{2.5}\) = 9
∴ n = 9 + 1 = 10

(v) a = 3.5, d = 0, n = 105
∵ a_n = a + (n – 1)d
∴ a_n = 43.5 + (105 – 1)0
a_n = 3.5 + 0 = 3.5

प्रश्न 2.
निम्नलिखित में सही उत्तर चुनिए और उसका औचित्य दीजिए-
(i) A.P. : 10, 7, 4, … का 30वीं पद है-
(A) 97 (B) 77 (C) – 77 (D) – 87
(ii) A.P. : -3, –\(\frac{1}{2}\), 2, … का 11वाँ पद है-
(A) 28 (B) 22 (C) -38 (D) -48\(\frac{1}{2}\)
हल:
(i) A.P. : 10, 7, 4, … का 30वाँ पद
यहाँ a = 10, d = 7 – 10 = -3 तथा n = 30
∵ a_n = a + (n – 1)d
∴ a₃₀ = 10 + (30 – 1) × -3
= 10 + 29 × -3 = 10 – 87 = -77
अतः विकल्प (C) सही है।

(ii) A.P.: -3, –\(\frac{1}{2}\), 2, … का 11वाँ पद
यहाँ a = – 3, d = –\(\frac{1}{2}\) – (-3) = –\(\frac{1}{2}\) + 3 = \(\frac{5}{2}\)
n = 11
a_n = a + (n – 1)d
a₁₁ = -3 + (11 – 1) × \(\frac{5}{2}\)
= – 3 + 10 × \(\frac{5}{2}\)
= -3 + 25 = 22
अतः विकल्प (B) सही है।

प्रश्न 3.
निम्नलिखित समान्तर श्रेढियों में रिक्त खानों (boxes) के पदों को ज्ञात कीजिए :

हल:
(i) पहला पद a = 2 तीसरा पद a₃ = 26,
दूसरा पद a₂ = ?
माना सार्वअन्तर है।
अब a₃ = a + 2d
⇒ 26 = 2 + 2d
⇒ 2d = 26 – 2 = 24
⇒ d = 12
∴ दूसरा पद a₂ = a + d = 2 + 12 = 14
अतः रिक्त बॉक्स का पद a₂ = 14

(ii) पहला पद a = ?, दूसरा पद a₂ = 13, तीसरा पद a₃ = ?, चौथा पद d₄ = 3
माना सार्वअन्तर d है a₂ = a + d
⇒ 13 = a + d …(1)
तथा a₄ = a + 3d
⇒ 3 = a + 3d …(2)
समीकरण (2) में से (1) को घटाने पर,
2d = – 10 ⇒ d = -5
समीकरण (1) से, 13 = a + d
⇒ 13 = a – 5 ⇒ a = 18
∴ तीसरा पद a₃ = a + 2d
= 18 + 2 × (-5)
⇒ a₃ = 8
अतः रिक्त बॉक्सों के पद क्रमश: 18 व 8 हैं।

(iii) पहला पद a = 5, चौथा पद a₄ = 9\(\frac{1}{2}\), दूसरा पद a₂ = ? तीसरा पद a₃ = ?
माना सार्वअन्तर d है।

अतः रिक्त बाक्सों के पद क्रमशः 6\(\frac{1}{2}\) और 8 हैं।

∵ पहला पद a = -4 और माना सार्वअन्तर d है।
6वाँ पद = a + (6 – 1)d
= a + 5d
∵ a + 5d = 6
⇒ – 4 + 5d = 6
⇒ 5d = 6 + 4 = 10
⇒ 5d = 10
∴ d = \(\frac{10}{5}\) = 2
तब दूसरा पद a₂ = a + d = – 4 + 2 = – 2
तीसरा पद a₃ = a₂ + d = – 2 + 2 = 0
चौथा पद a₄ = a₃ + d = 0 + 2 = 2
पाँचवाँ पद a₅ = a₄ + d = 2 + 2 = 4

माना पहला पद a और सार्वअन्तर d है।
दूसरा पद = a + d = 38 …(i)
और छठवाँ पद = a + (6 – 1)d
⇒ a + 5d = -22 …(ii)
समीकरण (ii) में से (i) को घटाने पर,
(a + 5d) – (a + d) = – 22 – 38
⇒ 5d – d = 60
⇒ 4d = 60
∴ d = \(\frac{-60}{4}\) = -15
∴ समीकरण (i) से,
a + d = 38
⇒ a + (-15) = 38
∴ a = 38 + 15 = 53
तब पहला पद a₁ = 53
तीसरा पद a₃ = a₂ + d = 38 – 15 = 23
चौथा पद a₄ = a₃ + d = 23 – 15 = 8
पाँचवाँ पद a₅ = a₄ + d = 8 – 15 = – 7
अतः रिक्त बॉक्सों में क्रमिक प्रविष्टियाँ

प्रश्न 4.
A.P. 3, 8, 13, 18, … का कौन-सा पद 78 है ?
हल:
दी गई A. P. : 3, 8, 13, 18, ….
यहाँ a = 3
d = 8 – 3 = 5
माना पद 78 है।
∴ a_n = 78
∵ a_n = a + (n – 1)d
⇒ 78 = 3+ (n – 1)5
⇒ 78 = 3 + 5n – 5
⇒ 78 = 5n – 2
⇒ 5n = 78 – 2
⇒ 5n = 80
∴ n = \(\frac{80}{5}\) = 16
अतः 16वाँ पद 78 है।

प्रश्न 5.
निम्नलिखित समान्तर श्रेढियों में से प्रत्येक श्रेठी में कितने पद हैं ?
(i) 7, 13, 19, …., 205
(ii) 18, 15, 13, …., -47
हल:
(i) दी गई समान्तर श्रेढी (A.P.) : 7, 13, 19, ….., 205
यहाँ a = 7 तथा d = 13 – 7 = 6
माना दी गई A. P. में n पद हैं
nवाँ पद a_n = 205
a_n = 205
⇒ a + (n – 1)d = 205
⇒ 7 + (n – 1)6 = 205
⇒ 7 + 6n – 6 = 205
⇒ 1 + 6n = 205
⇒ 6n = 205 – 1 = 204
∴ n = \(\frac{204}{6}\) = 34
अतः दी गई A. P. में 34 पद हैं।

(ii) दी गई समान्तर श्रेढी (A.P.):
18, 15\(\frac{1}{2}\), 13, …, – 47
यहाँ पहला पद a = 18
तथा सार्वअन्तर d = 15\(\frac{1}{2}\) – 18
= \(\frac{31}{2}-18=\frac{31-36}{2}\)
= \(-\frac{5}{2}\)
माना दी गई श्रेढी में पद हैं।
n पद a_n = -47
a + (n – 1)d = -47
⇒ 18 + (n – 1) × \(\left(-\frac{5}{2}\right)\) = -47
\(-\frac{5(n-1)}{2}\) = -47 – 18 = -65
(n – 1) \(\frac{(-65) \times 2}{-5}\) = 26
n = 26 + 1 = 27
अतः दी गई श्रेढी (A.P.) में 27 पद हैं।

प्रश्न 6.
क्या A.P. : 11, 8, 5, 2… का एक पद -150 है ? क्यों ?
हल:
दी गई A. P. : 11, 8, 5, 2 …
यहाँ पहला पद a = 11 तथा सार्वअन्तर d = 8 – 11
= -3
माना nवाँ पद (a_n) = -150 है।
⇒ a_n = -150
⇒ a + (n – 1)d = -150
⇒ 11 + (n – 1) × (-3) = -150
⇒ -3(n – 1) = -150 – 11 = -161
⇒ (n – 1) = \(\frac{-161}{-3}\)
= 53.6 (लगभग)
∴ n = 53.6 + 1 = 54.6
⇒ n का मान एक पूर्ण संख्या नहीं है।
अतः दी गई A.P का कोई पद -150 नहीं है।

प्रश्न 7.
उस A. P. का 31वाँ पद ज्ञात कीजिए, जिसका 11वाँ पद 38 है और 16वाँ पद 73 है।
हल:
माना A.P का प्रथम पद a तथा सार्वअन्तर d है।
तब 11वाँ पद a₁₁ = 38
a + (11 – 1)d = 38
a + 10d = 38 …(i)
और 16वाँ पद a₁₆ = 73
⇒ a + (16 – 1)d = 73
⇒ a + 15d = 73 …(ii)
समीकरण (ii) में से (i) को घटाने पर,
(a + 15d) – (a + 10d) = 73 – 383
⇒ a + 15d – a – 10d = 35
⇒ 5d = 35
∴ d = \(\frac{35}{5}\) = 7
समीकरण (i) में d का मान रखने पर,
⇒ a + 10 × 7 = 38
⇒ a + 70 = 38
∴ a = 38 – 70 = -32
श्रेढी का 31वाँ पद
a₃₁ = a + (31 – 1)d
= – 32 + 30 × 7
= – 32 + 210 = 178
अत: A.P का 31वाँ पद = 178

प्रश्न 8.
एक A.P में 50 पद हैं, जिसका तीसरा पद 12 है और अन्तिम पद 106 है। इसका 29वाँ पद ज्ञात कीजिए।
हल:
माना कि A.P का प्रथम पद ‘a’ और सार्वअन्तर ‘d’ है। दिया है कि,
तीसरा पद a₃ = 12
a + (3 – 1)d = 12 [∵ a_n = a + (n – 1)d]
⇒ a + 2d = 12 ….(1)
और अन्तिम पद = a50 = 106
a + (50 – 1)d = 106
⇒ a + 49d = 106 …(2)
समीकरण (2) में से (1) को घटाने पर,

d का यह मान समीकरण (1) में प्रतिस्थापित करने पर,
a + 2 × 2 = 12
⇒ a + 4 = 12
∴ a = 12 – 4 = 8
अब श्रेढी का 29वीं पद
a₂₉ = a + (29 – 1)d
= 8 + 28 × 2 = 8 + 56 = 64
अत: A.P का 29वाँ पद = 64

प्रश्न 9.
यदि किसी A. P. के तीसरे और नौवें पद क्रमशः 4 और -8 हैं, तो इसका कौन-सा पद शून्य होगा ?
हल:
माना कि A.P का प्रथम पद ‘a’ और सार्वअन्तर ‘d’ है।
दिया है, तीसरा पद a₃ = 4
a + (3 – 1)d = 4 [a_n = a + (n – 1)d से]
⇒ a + 2d = 4 ….(1)
और a₉ = – 8
a + (9 – 1)d = -8
a + 8d = -8 ….(2)
समीकरण (2) मैं से (1) को घटाने पर,

d का यह मान समीकरण (1) में प्रतिस्थापित करने पर,
a + 2 (-2) = 4
या a – 4 = 4
∴ a = 4 + 4 = 8
अब माना कि श्रेढी का व पद शून्य होगा, तब
nवाँ पद a_n = 0
∴ a + (n – 1)d = 0
⇒ 8 + (n – 1) × (-2) = 0
⇒ – 2 (n – 1) = – 8
⇒ (n – 1) = 4
∴ n = 5
अत: दी गई A. P. का 5वाँ पद शून्य होगा।

प्रश्न 10.
किसी A.P. का 17वाँ पद उसके 10वें पद से 7 अधिक है। इसका सार्वअन्तर ज्ञात कीजिए।
हल:
माना A.P. का प्रथम पद a तथा सार्वअन्तर d है।
तब 17वाँ पद a₁₇ = a + (17 – 1)d
= a + 16d
10वाँ पद a₁₀ = a + (10 – 1)d
= a + 9d
∵17वाँ पद, 10 वें पद से 7 अधिक है।
a₁₇ – a₁₀ = 7
⇒ (a + 16d) – (a + 9d) = 7
⇒ 7d = 7
∴ d = 1
अतः श्रेढी का सार्वअन्तर = 1

प्रश्न 11.
A. P. : 3, 15, 27, 39, … का कौन-सा पद उसके 54वें पद से 132 अधिक होगा ?
हल:
माना अभीष्ट पद व पद है।
दी गई A. P.: 3, 15, 27, 39, …
प्रथम पद a = 3 तथा सार्वअन्तर d = 15 – 3 = 12
तब श्रेढी का 54वाँ पद a₅₄ = a + (54 – 1)d
= 3 + 53 × 12
=3 + 636 = 639
⇒ nवाँ पद = 54वें पद से 132 अधिक
= 639 + 132 = 771
nवाँ पद a_n = 771
⇒ a + (n – 1)d = 771
⇒ 3 + (n – 1) 12 = 771
⇒ (n – 1)12 = 771 – 3 = 768
n – 1 = \(\frac{768}{12}\) = 64
∴ n = 64 + 1 = 65
अतः श्रेढी का 65वाँ पद 54वें पद से 132 अधिक है।

प्रश्न 12.
दो समान्तर श्रेडियों का सार्वअन्तर समान है। यदि इनके 100वें पदों का अन्तर 100 है, तो इनके 1000 वें पदों का अन्तर क्या होगा ?
हल:
माना पहली A.P का प्रथम पद तथा सार्वअन्तर d है और दूसरी A. P. का प्रथम पद 4 तथा सार्वअन्तर है क्योंकि सार्वअन्तर समान हैं।
पहली श्रेढी का 100वाँ पद = a + (100 – 1)d
= a + 99d
दूसरी श्री का 100वाँ पद = A + (100 – 1) d
= A + 99d
∴ दोनों श्रेढियों के 100वें पदों का अन्तर = (A + 99d) – (a + 99d)
= A – a
प्रश्नानुसार, A – a = 100 …(1)
पहली श्रेढी का 1000वाँ पद = a +(1000 – 1)d = a + 999d
दूसरी श्रेढी का 1000वाँ पद = A + (1000 – 1)d = A + 999d
∴ दोनों श्रेढियों के 1000 वें पदों का अन्तर = (A + 999d) – (a + 999d) = A – a
∴ दोनों श्रेढियों के 1000वें पदों का अन्तर A – a = 100 (समी. 1 से)
अतः 1000वें पदों का अन्तर = 100

प्रश्न 13.
तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं ?
हल:
तीन अंकों की संख्याओं की सूची 100, 101, 102, ….., 999,
3 अंकों की 7 से विभाज्य प्रथम संख्या = 105 और अन्तिम संख्या = 994
तब 7 से विभाज्य 3 अंकीय संख्याओं की सूची-
105, (105 + 7), (105 + 7 + 7),… 994 = 105, 112, 119, …, 994
माना ऐसी कुल संख्याएँ n हैं।
प्रथम संख्या a = 105, सार्वअन्तर d = 7,
∴ nवाँ पद a_n = 994
⇒ a + (n – 1)d = 994
⇒ 105 + (n – 1) × 7 = 994
⇒ (n – 1) × 7 = 994 – 105 = 889
⇒ (n – 1) = \(\frac{889}{7}\) = 127
∴ n = 127 + 1 = 128
अतः 7 से विभाव्य तीन अंकों वाली संख्याएँ = 128

प्रश्न 14.
10 और 250 के बीच में 4 के कितने गुणज हैं ?
हल:
10 से बड़ा 4 का पहला गुणज = 12
250 से छोटा 4 का पहला गुणज = 248
∵ 10 और 250 के बीच 4 के गुणजों की श्रेढी निम्न होगी :
12, 16, 20, 24, ….., 248
माना गुणजों की संख्या n है।
पहला पद a = 12, सार्वअन्तर d = 16 – 12 = 4
तब nवाँ पद, a_n = 248
a + (n – 1)d = 248
12 + (n – 1)4 = 248
12 + 4n – 4 = 248
4n = 248 + 4 – 12= 240
n = \(\frac{240}{4}\) = 60
अतः 10 और 250 के बीच 4 के गुणजों की संख्या 60 है।

प्रश्न 15.
n के किस मान के लिए, दोनों समान्तर श्रेतियों 63, 65, 67,… और 3, 10, 17, … के वें पद बराबर होंगे ?
हल:
पहली समान्तर श्रेढी 63, 65, 67, ….
प्रथम पद a = 63, सार्वअन्तर d = 65 – 63 = 2
∴ श्रेढ़ी का nवाँ पद a_n = a + (n – 1)d
= 63 + (n – 1)2
= 63 + 2n – 2
= 61 + 2n
दूसरी समान्तर श्रेढी = 3, 10, 17, …..
प्रथम पद a’ = 3, सार्वअन्तर d’ = 10 – 3 = -7
इस श्रेढी का nवाँ पद a_n‘ = a’ + (n – 1)d’
= 3 + (n – 1)7
-= 3 + 7n – 7 = 7n – 4
प्रश्नानुसार,
पहली A.P का nवाँ पद = दूसरी A.P का nवाँ पद
⇒ 61 + 2n = 7n – 4
⇒ 2n – 7n = – 4 – 61
⇒ – 5n = -65
n = \(\frac{-65}{-5}\) = 13
अतः दोनों समान्तर श्रेढियों के 13वें पद बराबर होंगे।

प्रश्न 16.
वह A. P. ज्ञात कीजिए जिसका तीसरा पद 16 है और 7वाँ पद 5वें पद से 12 अधिक है।
हल:
माना कि A.P का प्रथम पद a और सार्वअन्तर d है।
दिया है a₃ = 16
a + (3 – 1)d = 16
⇒ a + 2d = 16 …(1)
प्रश्न के अनुसार, a₇ – a₅ = 12
[a + (7 – 1)d] – [a + (5 – 1) d] = 12
⇒ a + 6d – a – 4d = 12
⇒ 2d = 12
∴ d = \(\frac{12}{2}\) = 6
d का यह मानं समीकरण (1) में प्रतिस्थापित करने पर,
a + 2(6) = 16
∴ a = 16 – 12 = 4
A.P. = a, a + d, a + 2d,…
= 4, 4 + 6, 4 + 2 × 6,…
= 4, 10, 16,…
अतः वाँछित A. P. है, 4, 10, 16, 22….

प्रश्न 17.
A. P. : 3, 8, 13, …, 253 में अन्तिम पद से 20वाँ पद ज्ञात कीजिए।
हल:
दी गई A. P.: 3, 8, 13, …., 253
प्रथम पद a = 3
सार्वअन्तर d = 8 – 3 = 5
अन्तिम पद a_n = 253
समान्तर श्रेढी का nवाँ पद
an = a + (n – 1)d
253 = 3 + (n – 1) × 5
253 = 3 + 5n – 5
5n = 253 + 2
5n = 255
∴ n = \(\frac{255}{5}\) = 51
समान्तर श्रेढी के अन्तिम पद से 20वाँ पद
= (पदों की संख्या) – 20 + 1
= 51 – 20 + 1 = 32वाँ पद
∴ A.P के अन्तिम पद से 20वाँ पद = आरम्भ से 32वाँ पद
∵ a_n = a + (n – 1)d
a₃₂ = 3 + (32 – 1) × 5
= 3 + 31 × 5
= 3 + 155 = 158
अत: A.P के अन्तिम पद से 20वाँ पद = 158

द्वितीय विधि :
यहाँ प्रथम पद a = 3, सार्वअन्तर d = 8 – 3 = 5
अन्तिम पद a_n = 253
सूत्र: अन्त rवाँ पद = a_n – (r – 1)d
अन्त से 20वाँ पद = 253 – (20 – 1)5
= 253 – 19 × 5
= 253 – 95 = 158
अत: A. P. के अन्तिम पद से 20वाँ पद 158 है।

प्रश्न 18.
किसी A. P. के चौथे और 8वें पदों का योग 24 है तथा छठे और 10वें पदों का योग 44 है। इस A. P. के ‘प्रथम तीन पद ज्ञात कीजिए।
हल:
माना A.P का प्रथम पद a और सार्वअन्तर d है।
∵ चौथा पद a₄ + 8वाँ पद a₈ = 24
⇒ [a + (4 – 1)d] + [a + (8 – 1)d] = 24
⇒ a + 3d + a + 7d = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 …(1)
∵ 6वाँ पद a₆ + दसवाँ पद a₁₀ = 44
⇒ [a + (6 – 1)d] + [a + (10 – 1)d] = 44
⇒ a + 5d + a + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22 … (2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(a + 7d) – (a + 5d) = 22 – 12
⇒ a + 7d – a – 5d = 10
⇒ 2d = 10 ⇒ d = 5
d का मान समीकरण (1) में रखने पर,
a + 5 × 5 = 12
⇒ a + 25 = 12
∴ a = -13
अब श्रेढी का पहला पद a = -13
दूसरा पद a₂ = a + d = -13 + 5 = -8
तीसरा पद a₃ = a₂ + d = – 8 + 5= -3
अतः वांछित A.P. के प्रथम तीन पद = -13, – 8, -3

प्रश्न 19.
सुब्बाराव ने 1995 में ₹ 5000 के मासिक वेतन पर कार्य आरम्भ किया और प्रत्येक वर्ष ₹ 200 की वेतन वृद्धि प्राप्त की। किस वर्ष में उसका वेतन ₹ 7000 हो गया ?
हल:
पहले वर्ष में प्रारम्भिक वेतन = ₹ 5000 प्रति मास
दूसरे वर्ष में वेतन = ₹ 5000 + ₹ 200
= ₹ 5200 प्रति मास
तीसरे वर्ष में वेतन = ₹ 5200 + ₹ 200
= ₹ 5400 प्रति मास
इस प्रकार प्रत्येक वर्ष के वेतन (रु. में) 5000, 5200, 5400…… एक समान्तर श्रेढी बनाते हैं,
जिसका प्रथम पद a = 5000 तथा सार्वअन्तर d = 200
माना n वर्ष बाद वेतन ₹ 7000 होगा।
तब nवाँ पद = 7000
⇒ a + (n – 1)d = 7000
⇒ 5000 + (n – 1)200 = 7000
⇒ (n – 1) × 200 = 7000 – 5000
⇒ (n – 1) × 200 = 2000
⇒ (n – 1) = \(\frac{2000}{200}\) = 10
∴ n = 10 + 1 = 11
अतः 11 वें वर्ष में अर्थात 2006 में सुब्बाराव का वेतन ₹ 7000 होगा।

प्रश्न 20.
रामकली ने किसी वर्ष के प्रथम सप्ताह में ₹ 5 की बचत की और फिर अपनी साप्ताहिक बचत ₹ 1.75 बणाती गई। यदि वें सप्ताह में उसकी साप्ताहिक बचत ₹ 20.75 हो जाती है, तो n ज्ञात कीजिए।
हल:
माना प्रथम पद a तथा सार्वअन्तर d है
प्रथम सप्ताह की बचत = ₹ 5
प्रति सप्ताह बचत में वृद्धि = ₹ 1.75
यह स्पष्ट है कि यह एक A.P. है
प्रथम पद a = 5, d = 1.75
nवें सप्ताह में उसकी बचत a_n = 20.75
∵ a_n = a + (n – 1)d
⇒ 20.75 = 5 + (n – 1) × 1.75
⇒ 20.75 = 5 + 1.75n – 1.75
⇒ 1.75n = 20.75 – 5 + 1.75
⇒ 1.75n = 17.5
n = \(\frac{17.5}{1.75}\) ⇒ n = 0
अतः 10वें सप्ताह में रामकली की बचत ₹ 20.75

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.1

प्रश्न 1.
निम्नलिखित स्थितियों में से किन स्थितियों में सम्बद्ध संख्याओं की सूची A. P. है और क्यों ?
(i) प्रत्येक किलोमीटर के बाद का टैक्सी का किराया, जबकि प्रथम किलोमीटर के लिए किराया ₹ 15 है और प्रत्येक अतिरिक्त किलोमीटर के लिए किराया ₹ 8 है।
(ii) किसी बेलन (cylinder) में उपस्थित हवा की मात्रा, जबकि वायु निकालने वाला पम्प प्रत्येक बार बेलन की शेष हवा का \(\frac{1}{4}\) भाग बाहर निकाल देता है।
(iii) प्रत्येक मीटर की खुदाई के बाद, एक कुआँ खोदने में आई लागत, जबकि प्रथम मीटर खुदाई की लागत ₹ 150 है और बाद में प्रत्येक मीटर खुदाई की लागत ₹ 50 बणती जाती है।
(iv) खाते में प्रत्येक वर्ष का मिश्रधन, जबकि ₹ 10000 की राशि 8% वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है।
हल:
(i) यदि टैक्सी का पहले किमी का किराया a₁, दूसरे किमी का किराया a₂ तथा वें किमी का किराया a_n से व्यक्त किया जाए तो
प्रश्नानुसार,
a₁ = 15
a₂ = 15 + 8 = 23
a₃ = 23 + 8 = 31
अब सार्वअन्तर (d) = a₂ – a₁ = 23 – 15 = 8
और a₃ – a₂ = 31 – 23 = 8
∵ a₃ – a₂ = a₂ – a₁
अर्थात् सार्वअन्तर समान हैं।
∴ दी गई स्थिति A.P. (समान्तर श्रेढी) के रूप की है।

(ii) माना कि एक बेलन में उपस्थित हवा की मात्रा को x मात्रक से तथा प्रत्येक पम्प के बाद हवा की शेष मात्रा को a₂, a₃, a₄ से व्यक्त किया जाता है।
प्रश्न के अनुसार,

और आगे भी इसी प्रकार से….
अब सार्वअन्तर,

यहाँ a₃ – a₂ ≠ a₂ – a₁
∵ सार्वअन्तर समान नहीं है।
∴ दी गई स्थिति A.P का रूप नहीं है।

(iii) माना कि एक कुआँ खोदने के nवें मीटर की लागत को a_n से व्यक्त किया जाए तो.
प्रश्न के अनुसार, a₁ = ₹ 150
a₂ = ₹ (150 + 50) = ₹ 200
a₃ = ₹ (200 + 50) = ₹ 250
और आगे भी इसी प्रकार से…..
अब सार्वअन्तर
a₃ – a₂ = ₹ (250 – 200) = ₹ 50
a₂ – a₁ = ₹ (200 – 150) = ₹ 50
यहाँ a₃ – a₂ = a₂ – a₁ = ₹ 50
सार्वअन्तर समान हैं।
अतः दी गई स्थिति A. P. (समान्तर श्रेढी) के रूप की है।

(iv) खाते में जमा किए गए धन के लिए भिन्न वर्षों के मिश्रधन:
मूलधन P = ₹ 10000
ब्याज की दर R% = 8%


निरीक्षण से ही स्पष्ट है कि
A₂ – A₁ ≠ A₃ – A₂
अतः मिश्रधन A.P. (समान्तर श्रेढी) में नहीं हैं।

प्रश्न 2.
दी हुई A. P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्वअन्तर d निम्नलिखित हैं:
(i) a = 10, d = 10,
(ii) a = -2, d = 0
(iii) a = 4, d = – 3,
(iv) a = -1, d = \(\frac{1}{2}\)
(v) a = -1.25, d = -0.25
हल:
(i) दिया है, प्रथम पद (a) = 10
और सार्व अन्तर (d) = 10
∴ a₁ = प्रथम पद (a) = 10
a₂ = a + d = 10 + 10 = 20
a₃ = a + 2d = 10 + 2 × 10 = 30
a₄ = a + 3d = 10 + 3 × 10 = 40
अत: A.P के प्रथम चार पद 10, 20, 30, 40 हैं।

(ii) दिया हुआ है कि प्रथम पद (a) = 22
और सार्वअन्तर (d) = 0
∴ a₁ = a = -2
a₂ = a + d = 2 + 0 = 2
a₃ = a + 2d = -2 + 2 × 0 = -2
a₄ = a + 3d = 2 + 3 × 0 = -2
अत: A.P. के प्रथम चार पद -2, -2, -2, -2, हैं ।

(iii) दिया हुआ है, प्रथम पद (a) = 4
और सार्वअन्तर (d) = -3
∴ a₁ = a = 4
a₂ = a + d = 4 + (-3) = 1
a₃ = a + 2d = 4 + 2 × (-3) = -2
a₄ = a + 3d = 4 + 3 × (-3) = – 5
अत: A.P. के प्रथम चार पद 4, 1, 2, 5 हैं।

(iv) दिया है कि प्रथम पद a = -1
और सार्वअन्तर d = \(\frac{1}{2}\)
∴ a₁ = a = -1
a₂ = a + d
= \(-1+\frac{1}{2}=\frac{-1}{2}\)
a₃ = a + 2d
= \(-1+2\left(\frac{1}{2}\right)\)
– 1 + 1 = 0
a₄ = a + 3d
= \(-1+3\left(\frac{1}{2}\right)\)
= \(\frac{-2+3}{2}=\frac{1}{2}\)
अत: A.P. के प्रथम चार पद -1, –\(\frac{1}{2}\), 0, \(\frac{1}{2}\) हैं।

(v) दिया हैं कि प्रथम पद = a = -1.25
और सार्वअन्तर (d) = -0.25
∴ a₁ = a = – 1.25
a₂ = a + d = – 1.25 – 0.25 = -1.50
a₃ = a + 2d = – 1.25 + 2(-0.25)
= -1.25 – 0.50 = -1.75
a₄ = a + 3d = – 1.25 + 3(-0.25)
= – 1.25 – 0.75 = -2
अत: A.P. के प्रथम चार पद -1.25, -1.50, 1.75, – 2. हैं।

प्रश्न 3.
निम्नलिखित में से प्रत्येक A. P. के लिए प्रथम पद तथा सार्वअन्तर लिखिए:
(i) 3, 1, -1, -3,…
(ii) -5, 1, 3, 7,…
(iii) \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots\)
(iv) 0.6, 1.7, 2.8, 3.9,…
हल:
(i) दी गई A.P. = 3, 1, -1, -3, …
यहाँ a₁ = 3, a₂ = 1
a₃ = -1, a₄ = -3
प्रथम पद a = a₁ = 3
सार्वअन्तर d = a₂ – a₁ = 1 – 3 = -2
अत: प्रथम पद 3 तथा सार्वअन्तर = -2

(ii) दी गई A. P. = -5, -1, 3, 7, …
यहाँ a₁ = -5
a₂ = -1
a₃ = 3
a₄ = 7
प्रथम पद a₁ = -5
सार्वन्तर d = a₂ – a₁ = – 1 – (-5) = – 1 + 5 = 4
अतः प्रथम पद = -5 तथा सार्वन्तर = 4

(iii) दी गई A.P. = \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots \ldots\)
यहाँ a₁ = \(\frac{1}{3}\),
a₂ = \(\frac{5}{3}\),
a₃ = \(\frac{9}{3}\),
a₄ = \(\frac{13}{3}\)
प्रथम पद a = a₁ = \(\frac{1}{3}\)
सार्वन्तर d = a₂ – a₁ = \(\left(\frac{5}{3}-\frac{1}{3}\right)\)
= \(\frac{5-1}{3}=\frac{4}{3}\)
अतः प्रथम पद = \(\frac{1}{3}\) तथा सार्वअन्तर = \(\frac{4}{3}\)

(iv) दी गई A.P. = 0.6, 1.7, 2.8, 3.9, …
a₁ = 0.6, a₂ = 1.7
a₃ = 2.8, a₄ = 3.9
प्रथम पद a = a₁ = 0.6
सार्वअन्तर d = a₂ – a₁ = 1.7 – 0.6 = 1.1
अत: प्रथम पद = 0.6 तथा सार्वअन्तर = 1.1

प्रश्न 4.
निम्नलिखित में से कौन-कौन A.P. हैं ? यदि कोई A.P. है, तो इसका सार्वअन्तर ज्ञात कीजिए और इनके तीन और पद लिखिए:
(i) 2, 4, 8, 16, …
(ii) 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …
(iii) -1.2, -3.2, -5.2, -7.2,
(iv) -10, -6, -2, 2,…
(v) 3, 3 + \(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\),…
(vi) 0.2, 0.22, 0.222, 0.2222,
(vii) 0, -4, -8, -12,…
(viii) \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \ldots\)
(ix) 1, 3, 9, 27, …
(x) a, 2a, 3a, 4a, …
(xi) a, a², a³, a⁴, …
(xii) \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\),…
(xiii) \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\),…
(xiv) 1², 3², 5², 7², …
(xv) 1², 5², 7², 7³, …
हल:
(i) दिया हुआ अनुक्रम 2, 4, 8, 16, …
यहाँ a₁ = 2, a₂ = 4, a₃ = 8, a₄ = 16
दो क्रमागत पदों का अन्तर (सार्वअन्तर)
d = a₂ – a₁ = 4 – 2 = 2
a₃ – a₂ = 8 – 4 = 4
a₄ – a₃ = 16 – 8 = 8
∵ दो क्रमागत पदों का अन्तर समान नहीं है,
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A.P. नहीं है।

(ii) दिया गया अनुक्रम 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …
यहाँ a₁ = 2, a₂ = \(\frac{5}{2}\), a₃ = 3, a₄ = \(\frac{7}{2}\)
∵ दो क्रमागत पदों का अन्तर (सार्वअन्तर)

दो क्रमागत पदों का अन्तर समान है। सार्वअन्तर = \(\frac{1}{2}\) हैं।
∴ दिया गया अनुक्रम A.P. है।
अगले तीन पद

अत: दिये गये अनुक्रम के अगले तीन पद 4, \(\frac{9}{2}\) और 5 हैं।

(iii) दिया गया अनुक्रम -1.2, -3.2, -5.2, -7.2, …
यहाँ a₁ = -1.2, a₂ = -3.2, a₃ = -5.2, a₄ = -7.2
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = – 3.2 – (-1.2) = – 2.0
a₃ – a₂ = -5.2 – (-3.2) = -2.0
a₄ – a₃ = -7.2 – (-5.2) = -2.0
∵ दो क्रमागत पदों का अन्तर समान (-2.0) है।
∴ सार्वन्तर d = -2.0 और दिया गया अनुक्रम एक A.P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= -7.2 + (-2) = -9.2
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= -9.2 + (-2) = -11.2
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
-11.2 + (-2) = -13.2
अतः दिए गए अनुक्रम के अगले तीन पद -9.2, -11.2, -13.2 हैं।

(iv) दिया हुआ अनुक्रम -10, 6, – 2, 2,…
यहाँ a₁ = -10, a₂ = -6, a₃ = -2, a₄ = 2
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = -6 – (-10) = – 6 + 10 = 4
a₃ – a₂ = – 2 – (-6) = – 2 + 6 = 4
a₄ – a₃ = 2 – (-2) = 2 + 2 = 4
∵ दो क्रमागत पदों का अन्तर समान (4) है।
∴ सार्वअन्तर d = 4 और दिया गया अनुक्रम एक A.P. हैं।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= 2 + 4 = 6
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= 6 + 4 = 10
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= 10 + 4 = 14
अतः दिए गए अनुक्रम के अगले तीन पद 6, 10, 14 हैं।

(v) दिया हुआ अनुक्रम 3, 3 + \(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\),…
यहाँ a₁ = 3, a₂ = 3 + \(\sqrt{2}\), a₃ = 3 + 2\(\sqrt{2}\), a₄ = 3 + 3\(\sqrt{2}\)
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = (3+ \(\sqrt{2}\)) – 3 = \(\sqrt{2}\)
a₃ – a₂ = (3 + 2\(\sqrt{2}\)) – (3 + \(\sqrt{2}\)) = \(\sqrt{2}\)
a₄ – a₃ = (3 + 3\(\sqrt{2}\)) – (3 + 2\(\sqrt{2}\))= \(\sqrt{2}\)
∵ दो क्रमागत पद का अन्तर समान (\(\sqrt{2}\)) है।
∴ सार्वअन्तर d = \(\sqrt{2}\) और दिया गया अनुक्रम एक A. P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
3 + 3\(\sqrt{2}\) + \(\sqrt{2}\)
= 3 + \(\sqrt{2}\)(3 + 1) = 3 + 4\(\sqrt{2}\)
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= 3 + 4\(\sqrt{2}\) + \(\sqrt{2}\)
= 3 + \(\sqrt{2}\)(4 + 1) = 3 + 5\(\sqrt{2}\)
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= 3 + 5\(\sqrt{2}\) + \(\sqrt{2}\)
= 3 + \(\sqrt{2}\)(5 + 1) = 3 + 6\(\sqrt{2}\)
अतः दिए गए अनुक्रम के अगले तीन पद
3 + 4\(\sqrt{2}\), 3 + 5\(\sqrt{2}\), 3 + 6\(\sqrt{2}\) है।

(vi) दिया हुआ अनुक्रम
0.2, 0.22, 0.222, 0.2222, …
यहाँ a₁ = 0.2, a₂ = 0.22, a₃ = 0.222, a₄ = 0.2222,
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = 0.22 – 0.2 = 0.02
a₃ – a₂ = 0.222 – 0.22 = 0.002
a₄ – a₃ = 0.2222 – 0.222 = 0.0002
दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A. P. नहीं है।

(vii) दिया हुआ अनुक्रम 0, -4, -8, -12, ….
यहाँ a₁ = 0, a₂ = -4, a₃ = -8, a₄ = -12
दो क्रमागत पदों का अन्तर :
a₂ – a₁ = – 4 – 0 = -4
a₃ – a₂ = – 8 – (-4)
= – 8 + 4 = -4
a₄ – a₃ = – 12 – (-8)
= – 12 + 8 = -4
दो क्रमागत पदों का अन्तर समान है सार्वअन्तर = -4 है। अतः दिया गया अनुक्रम A.P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= – 12 + (-4) = -16
पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= – 16 + (-4) = -20
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= -20 + (-4) = -24
अतः दिए गये अनुक्रम के अगले तीन पद -16, -20 और -24 हैं।

(viii) दिया हुआ अनुक्रम \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \ldots\)

a₄ – a₃ = \(-\frac{1}{2}-\left(-\frac{1}{2}\right)\)
= \(-\frac{1}{2}+\frac{1}{2}\) = 0
दो क्रमागत पदों का अन्तर समान है। सार्वअन्तर = 0 है अतः दिया गया अनुक्रम एक A.P. है।
पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= \(-\frac{1}{2}+0=-\frac{1}{2}\)
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= \(-\frac{1}{2}+0=-\frac{1}{2} \)
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= \(-\frac{1}{2}+0=-\frac{1}{2}\)
दिए गए अनुक्रम के अगले तीन पद \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\) है।

(ix) दिया हुआ अनुक्रम 1, 3, 9, 27,…
यहाँ a₁ = 1, a₂ = 3, a₃ = 9, a₄ = 27
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = 3 – 1 = 2
a₃ – a₂ = 9 – 3 = 6
a₄ – a₃ = 27 – 9 = 18
दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A.P. में नहीं है।

(x) दिया हुआ अनुक्रम a, 2a, 3a, 4a…..
यहाँ a₁ = a, a₂ = 2a, a₃ = 3a, a₄ = 4a
दो क्रमागत पद का अन्तर d:
a₂ – a₁ = 2a – a = a
a₃ – a₂ = 3a – 2a = a
a₄ – a₃ = 4a – 3a = a
∵ दो क्रमागत पर्दों का अन्तर समान (a) है।
अतः सार्वन्तर d = a तथा दिया गया अनुक्रम एक A. P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= 4a + a = 5a
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= 5a + a = 6a
सातवाँ पद a₇ = छटा पद a₇ + सार्वअन्तर d
= 6a + a = 7a
अतः दिए गए अनुक्रम के अगले तीन पद 5a, 6a, 7a है।

(xi) दिया हुआ अनुक्रम यहाँ a, a², a³, a⁴, ….
यहाँ a₁ = a, a₂ = a², a₃ = a³‚ a₄ = a⁴
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = a² – a = a(a – 1)
a₃ – a₂ = a³ – a² = a²(a – 1)
∵ दो क्रमागत पद का अन्तर समान नहीं है।
अर्थात a₂ – a₁ ≠ a₃ – a₂
अतः दिया गया अनुक्रम एक A. P. नहीं है।

(xii) दिया हुआ अनुक्रम \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\)……
यहाँ a₁ = \(\sqrt{2}\), a₂ = \(\sqrt{8}\), a₃ = \(\sqrt{18}\), a₄ = \(\sqrt{32}\)
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = \(\sqrt{8}\) – \(\sqrt{2}\) = \(\sqrt{2}\)(\(\sqrt{4}\) – 1)
= \(\sqrt{2}\) (2 – 1) = \(\sqrt{2}\)
a₃ – a₂ = \(\sqrt{18}\) – \(\sqrt{8}\) = \(\sqrt{2}\)(\(\sqrt{9}\) – \(\sqrt{4}\))
= \(\sqrt{2}\)(3 – 2) = \(\sqrt{2}\)
a₄ – a₃ = \(\sqrt{32}\) – \(\sqrt{18}\) = \(\sqrt{2}\)(\(\sqrt{19}\) – \(\sqrt{9}\))
= \(\sqrt{2}\)(4 – 3) = \(\sqrt{2}\)
दो क्रमागत पदों का अन्तर समान (\(\sqrt{2}\)) है।
अतः सार्वअन्तर d = \(\sqrt{2}\) तथा दिया गया अनुक्रम एक A.P. है।
तब 5वाँ पद a₅ = 4वाँ पद + सार्वअन्तर d.
= \(\sqrt{32}\) + \(\sqrt{2}\)
= \(\sqrt{2}\)(\(\sqrt{16}\) + 1) = \(\sqrt{2}\)(4 + 1)
= 5\(\sqrt{2}\) = \(\sqrt{25}\) × \(\sqrt{2}\) = \(\sqrt{50}\)
6वाँ पद a₆ = 5वाँ पद + सार्वअन्तर d
= \(\sqrt{50}\) + \(\sqrt{2}\) = \(\sqrt{2}\)(\(\sqrt{25}\) + 1)
= \(\sqrt{2}\)(5 + 1) = 6\(\sqrt{2}\)
= \(\sqrt{36}\) × \(\sqrt{2}\) = \(\sqrt{72}\)
7वाँ पद a₇ = 6वीं पद + सार्वअन्तर d
= \(\sqrt{72}\) + \(\sqrt{2}\) = \(\sqrt{2}\)(\(\sqrt{36}\) + 1)
= \(\sqrt{2}\)(6 + 1) = 7\(\sqrt{2}\)
= \(\sqrt{49}\) × \(\sqrt{2}\) = \(\sqrt{98}\)
अतः दिए गए अनुक्रम के अगले तीन पद \(\sqrt{50}\), \(\sqrt{72}\), \(\sqrt{98}\) हैं।

(xiii) दिया हुआ अनुक्रम \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\), …
a₁ = \(\sqrt{3}\), a₂ = \(\sqrt{6}\), a₃ = \(\sqrt{9}\), a₄ = \(\sqrt{12}\)
दो क्रमागत पदों का अन्तर d
a₂ – a₁ = \(\sqrt{6}\) – \(\sqrt{3}\) = \(\sqrt{3}\) (\(\sqrt{2}\) – 1) = 0.717
a₃ – a₂ = \(\sqrt{9}\) – \(\sqrt{6}\) = \(\sqrt{3}\)(\(\sqrt{3}\) – \(\sqrt{2}\)) = 0.530
∵ दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात a₂ – a₁ ≠ a₃ – a₂
अतः दिया गया अनुक्रम एक A.P. नहीं है।

(xiv) दिया हुआ अनुक्रम 1², 3², 5², 7², ….
a₁ = 1², a₂ = 3², a₃ = 5², a₄ = 7²
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = 3² – 1² = 9 – 1 = 8
a₃ – a₂ = 5² – 3² = 25 – 9 = 16
a₄ – a₃ = 7² – 5² = 49 – 25 = 24
∵ दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A.P. नहीं है।

(xv) दिया गया अनुक्रम 1², 5², 7², 7³, ….
यहाँ a₁ = 1², a₂ = 5², a₃ = 7², a₄ = 7³
दो क्रमागत पर्दों का अन्तर d:
a₂ – a₁ = 5² – 1² = 25 – 1 = 24
a₃ – a₂ = 7² – 5² = 49 – 25 = 24
a₄ – a₃ = 7³ – 7² = 73 – 49 = 24
चूँकि दो क्रमागत पदों का अन्तर समान है।
अतः सार्वअन्तर d = 24
तथा दिया गया अनुक्रम A.P. है।
पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर
= 73 + 24 = 97
छठवाँ पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर
= 97 + 24 = 121
छठवाँ पद a₇ = छठवाँ पद a₆ + सार्वअन्तर
= 121 + 24 = 145
अत: दिये गये अनुक्रम के अगले तीन पद 97, 121 और 145 हैं।