Jharkhand Board JAC Class 10 Maths Important Questions Chapter 12 वृतों से संबंधित क्षेत्रफल Important Questions and Answers.
JAC Board Class 10th Maths Important Questions Chapter 12 वृतों से संबंधित क्षेत्रफल
लयूतरात्मक / निबन्धात्मक प्रश्न
प्रश्न 1.
14 सेमी. व्यास वाले वृत्त की परिधि ज्ञात कीजिए।
हल:
दिया है,
वृत्त का व्यास = 14 सेमी.
हम जानते हैं,
त्रिज्या r = \(\frac{14}{2}\) = 7 सेमी
वृत्त की परिधि = 2πr
= 2 × \(\frac{22}{7}\) × 7
= 44 सेमी.।
प्रश्न 2.
त्रिज्या 21 सेमी वाले वृत्त का एक चाप केन्द्र पर 60° का कोण अन्तरित करता है, तो संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है :
वृत्त की त्रिज्या (r) = 21 सेमी.
माना कि चाप AB केन्द्र पर 60° का कोण अन्तरित करता है।
संगत दीर्घ त्रिज्यखण्ड का कोण
(θ) = 360° – 60°
= 300°
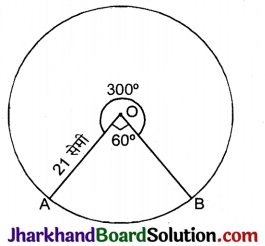
संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल
= \(\frac{\pi r^2 \theta}{360^{\circ}}\)
= \(\frac{22}{7} \times \frac{21^2 \times 300^{\circ}}{360^{\circ}}\)
= \(\frac{22 \times 3 \times 21 \times 5}{6}\)
= 11 × 21 × 5
= 1155 सेमी.2
अतः संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल = 1155 सेमी.2 ।
![]()
प्रश्न 3.
आकृति में छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। यदि AB = 5 सेमी., AC = 12 सेमी. और O वृत्त का केन्द्र है।
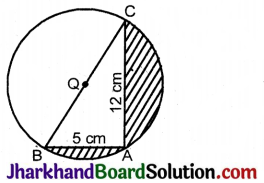
हल:
स्पष्टत: ∠BAC अर्द्धवृत्त में बना कोण है।
इसलिए यह समकोण Δ है।
पाइथागोरस प्रमेय से,
BC2 = AB2 + AC2
BC2 = 52 + 122
= 25 + 144
BC2 = 169
∴ BC = 13 सेमी.
वृत्त की त्रिज्या R = \(\frac{13}{2}\) सेमी.
अब छायांकित भाग का क्षे. = अर्द्धवृत्त का क्षे. – ΔABC का क्षे.
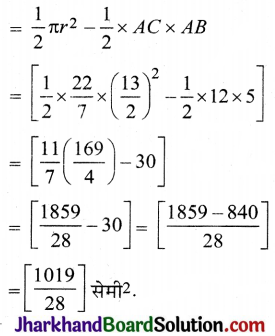
प्रश्न 4.
चित्र में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
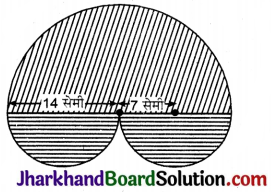
हल:
दिया है बड़े अर्द्धवृत्त की त्रिज्या = 14 सेमी
बड़े अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr2
= \(\frac{1}{2} \times \frac{22}{7} \times(14)^2\)
= \(\frac{1}{2} \times \frac{22}{7} \times 14 \times 14\)
= 308 वर्ग सेमी
प्रत्येक छोटे अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr2
= \(\frac{1}{2} \times \frac{22}{7} \times(7)^2\)
= \(\frac{1}{2} \times \frac{22}{7} \times 7 \times 7\)
= 77 वर्ग सेमी
अतः अभीष्ट छायांकित भाग का क्षेत्रफल = (308 + 77 +77) वर्ग सेमी
= 462 वर्ग सेमी
अतः अभीष्ट छायांकित भाग का क्षेत्रफल = 462 सेमी2
![]()
प्रश्न 5.
एक 6 सेमी त्रिज्या के वृत्त का व्यास PQRS इस प्रकार है कि PQ, QR और RS बराबर हैं। चित्रानुसार PQ और QS को व्यास मानकर अर्द्धवृत्त खींचे गये हैं। छायांकित भाग का परिमाप और क्षेत्रफल ज्ञात कीजिए।
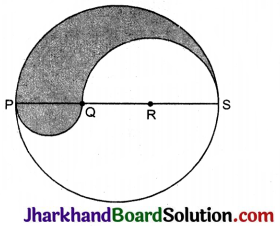
हल:
दिया है : वृत्त की त्रिज्या = 6 सेमी
∴ वृत्त का व्यास PS = 12 सेमी
PQ = QR = RS = \(\frac{12}{3}\) = 4 सेमी
QS = QR + RS = (4 + 4) = 8 सेमी
अतः अभीष्ट परिमाप = 6 सेमी त्रिज्या वाले अर्द्धवृत्त का चाप + 4 सेमी त्रिज्या वाले अर्द्धवृत्त का चाप + 2 सेमी त्रिज्या वाले अर्द्धवृत्त का चाप
= [π × 6 + π × 4 + π × 2] सेमी
= 12π सेमी
और अभीष्ट क्षेत्रफल = PS व्यास वाले अर्द्धवृत्त का क्षेत्रफल + PQ व्यास वाले अर्द्धवृत्त का क्षेत्रफल – QS व्यास वाले अर्द्धवृत्त का क्षेत्रफल

अतः अभीष्ट छायांकित भाग का क्षेत्रफल = 37.71 सेमी2।
प्रश्न 6.
दी गई आकृति में, एक वृत्त के चतुथांश OAQB के अन्तर्गत एक वर्ग OPQR बना हुआ है। यदि वृत्त की त्रिज्या 6\(\sqrt{2}\) सेमी है, तो छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। [π = \(\frac{22}{7}\) लीजिए]
हल:
∵ OPQR एक वर्ग है।
माना OP = PQ = QR = OR = x सेमी
दिया है, OR = 6\(\sqrt{2}\) सेमी
समकोण त्रिभुज OPQ में,
OQ2 = OP2 + PQ2 (पाइथागोरस प्रमेय से)
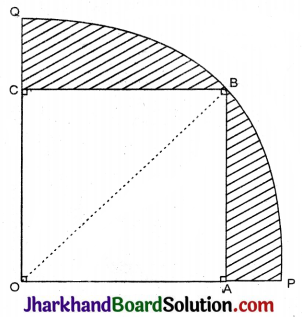
(6\(\sqrt{2}\))2 = x2 + x2
72 = 2x2
x2 = 36
x = 6 सेमी
त्रिज्यखण्ड का कोण (θ) = 90°
चतुर्थांश OPBQ का क्षेत्रफल
= \(\frac{\pi r^2 \theta}{360^{\circ}}\)
= \(\frac{22}{7} \times \frac{(6 \sqrt{2})^2 \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{396}{7}\) सेमी2
वर्ग OABC का क्षेत्रफल = 6 × 6 = 36 सेमी.2
छायांकित क्षेत्र का क्षेत्रफल = चतुर्थाश OPBQ का क्षेत्रफल – वर्ग OABC का क्षेत्रफल
= \(\frac{396}{7}\) – 36
= 20.5 सेमी.2
अतः छायांकित भाग का क्षेत्रफल = 20.5 सेमी.2
![]()
प्रश्न 7.
छायांकित भाग का क्षेत्रफल ज्ञात कीजिए यदि केन्द्र O पर संकेन्द्रीय वृत्तों की त्रिज्या क्रमशः 21 सेमी तथा 42 सेमी तथा ∠AOC = 60° है।
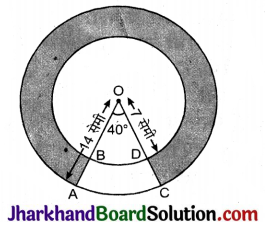
हल:
दिया है,
त्रिज्यखण्ड AOC की त्रिज्या (r1) = 42 सेमी
त्रिज्यखंड BOD की त्रिज्या (r2) = 21 सेमी
तथा त्रिज्यखंड कोण (θ) = 60°
क्षेत्र ABDC का क्षेत्रफल = त्रिज्यखण्ड AOC का क्षेत्रफल – त्रिज्यखण्ड BOD का क्षेत्रफल
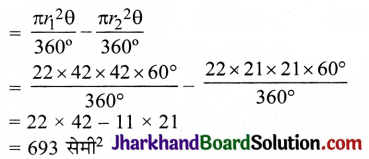
गोलाकार रिंग का क्षेत्रफल = \(\frac{22}{7}\) × (42)2 – \(\frac{22}{7}\) × (21)2
= \(\frac{22}{7}\) × [1764 – 441]
= \(\frac{22}{7}\) × 1323 = 4158 सेमी2
अतः अभीष्ट छायांकित भाग का क्षेत्रफल = 4158 – 693
= 3465 सेमी2
अतः अभीष्ट छायांकित भाग का क्षेत्रफल = 3465 सेमी2
प्रश्न 8.
एक डार्टबोर्ड की प्रथम रिंग (ring I) के अन्तः तथा बाह्य व्यास क्रमश: 32 सेमी तथा 34 सेमी और दूसरी रिंग (ring II) के अन्तः तथा बाह्य व्यास क्रमशः 19 सेमी तथा 21 सेमी हैं। इन दोनों रिगों का कुल क्षेत्रफल ज्ञात कीजिए।
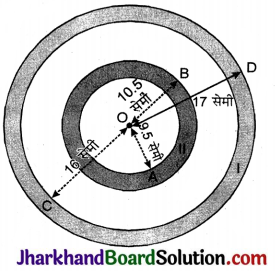
हल:
दिया है,
रिंग के व्यास क्रमशः 34 सेमी तथा 32 सेमी.
अतः रिंग की त्रिज्याएँ होगी R = \(\frac{34}{2}\) = 17 सेमी,
r = \(\frac{32}{2}\) = 16 सेमी.
रिंग II के व्यास क्रमश: 21 सेमी तथा 19 सेमी.
अतः रिंग II की त्रिज्याएँ होगी r1 = \(\frac{21}{2}\) = 10.5 सेमी r2 = \(\frac{19}{2}\) = 9.5 सेमी.
प्रथम रिंग का क्षेत्रफल = πR2 – πr2
= \(\frac{22}{7}\) × (17)2 – \(\frac{22}{7}\)(16)2
= \(\frac{22}{7}\)(172 – 162)
= \(\frac{22}{7}\) × 33 सेमी2
दूसरी रिंग का क्षेत्रफल = πr12 – πr22
= \(\frac{22}{7}\) × (10.5)2 – \(\frac{22}{7}\) × (9.5)2
= \(\frac{22}{7}\) × [(10.5)2 – (9.5)2]
= \(\frac{22}{7}\) × 20 सेमी2
अतः दोनों रिंगों का कुल क्षेत्रफल = \(\frac{22}{7}\) × 33 + \(\frac{22}{7}\) × 20
= \(\frac{22}{7}\) × (33 + 20)
= \(\frac{22}{7}\) × 53 = 166.57 सेमी2
अतः दोनों रिंगों का कुल क्षेत्रफल = 166.57 सेमी2।
प्रश्न 9.
एक कागज आयत ABCD आकार का है जिसमें AB = 40 सेमी तथा AD = 28 सेमी है। यदि इसमें से BC व्यास का एक अर्द्ध वृत्ताकार भाग काट लिया जाता है तो शेष भाग का क्षेत्रफल ज्ञात कीजिए।
हल:
आयत ABCD की लम्बाई AB = 40 सेमी और चौड़ाई AD = 28 सेमी
∴ आयत ABCD का क्षेत्रफल = AB × AD
= 40 × 28
= 1120 सेमी2
अर्द्धवृत्त का व्यास AD = 28 सेमी
अर्द्धवृत्त की त्रिज्या = \(\frac{28}{2}\) = 14 सेमी
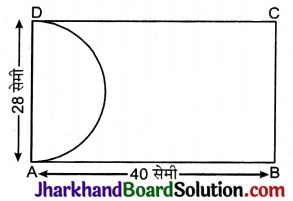
आयत ABCD से काटे गये अर्द्धवृत्ताकार भाग का क्षेत्रफल
= \(\frac{1}{2}\)πr2 = \(\frac{1}{2} \times \frac{22}{7} \times 14 \times 14\)
= 22 × 14 = 308 सेमी2
∴ शेष भाग का क्षेत्रफल
= आयत ABCD का क्षेत्रफल – अर्द्धवृत्त का क्षेत्रफल
= 1120 – 308 वर्ग सेमी
= 812 वर्ग सेमी
अत: शेष भाग का क्षेत्रफल = 812 सेमी2
![]()
प्रश्न 10.
14 सेमी. त्रिज्या वाले वृत्त के उस लघु वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए जिसका केन्द्रीय कोण 60° है। संगत दीर्घ वृत्तखण्ड का क्षेत्रफल भी ज्ञात कीजिए। [π = \(\frac{22}{7}\) लीजिए]
हल:
वृत्त की त्रिज्या = 14 सेमी.
मूल बिन्दु O से जीवा AB द्वारा बना कोण 60° है।
अब वृत्त का क्षेत्रफल = πr2 = \(\frac{22}{7}\) × 142
= 616 सेमी2
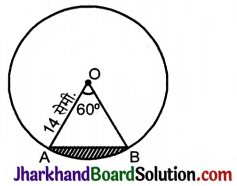
त्रिज्यखण्ड AOB का क्षे. = πr2 × \(\frac{60}{360}\)
= 616 × \(\frac{1}{6}\)
= 102.67 सेमी.2 (लगभग)
ΔOAB में,
AO = OB (वृत्त की त्रिज्या)
∴ ∠OBA = ∠OAB
(त्रिभुज में समान भुजाओं के सम्मुख कोण बराबर होते हैं)
अब ∠OAB + ∠OBA + ∠AOB = 180°
⇒ 2∠OAB = 180° – 60° – 120° [∵ ∠OBA = ∠OAB]
⇒ ∠OAB = 60°
इस प्रकार ΔAOB समबाहु त्रिभुज है।
∴ ΔAOB का है. = \(\frac{\sqrt{3}}{4}\)OA2
= \(\frac{\sqrt{3}}{4}\)(14)2
= 196 × \(\frac{\sqrt{3}}{4}\)
= 84.87 सेमी.2 (लगभग)
लघु वृत्त खण्ड का क्षेत्रफल = AOB का क्षे. – ΔAOB का क्षे.
= 102.67 – 84.87
= 17.8 सेमी2 (लगभग)
अब दीर्घ वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षे. – लघु खण्ड का क्षे.
= 616 – 17.8
= 598.2 सेमी2 (लगभग)।
प्रश्न 11.
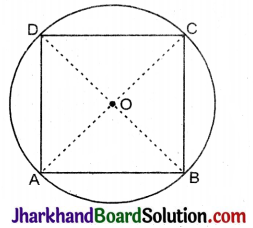
56 मीटर भुजा वाले एक वर्गाकार बगीचे ABCD के AB व CD भुजा पर दो वृत्ताकार फूलों की क्यारियाँ बनाई गई हैं। यदि प्रत्येक वृत्ताकार क्यारी का केन्द्र बगीचे के विकणों का प्रतिच्छेद बिन्दु O है, तो बगीचे और क्यारियों के क्षेत्रफलों का योग ज्ञात कीजिए।
हल:
दिया है, वर्ग की भुजा 56 मी.
∵ AC और BD वर्ग के विकर्ण है तथा हम जानते हैं कि वर्ग के विकर्ण एक दूसरे को 90° पर समद्विभाजित करते हैं तथा बराबर होते हैं।
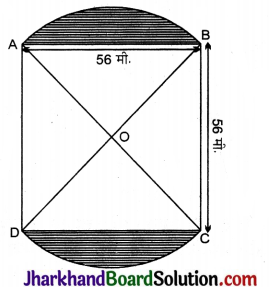
∠AOB = 90°
माना कि AO = OB = x मी. [∵ \(\frac{1}{2}\)AC = \(\frac{1}{2}\)BD]
समकोण त्रिभुज AOB में,
AB2 = AO2 + OB2 (पाइथागोरस प्रमेय से)
⇒ 562 = x2 + x2
⇒ 562 = 2x2
⇒ x2 = \(\frac{56 \times 56}{2}\)
⇒ x2 = 28 × 56
⇒ x = \(\sqrt{28 \times 56}\) मी.
अब त्रिज्यखण्ड OAB की त्रिज्या = \(\sqrt{28 \times 56}\) मी.
तथा त्रिज्यखण्ड कोण (θ) = 90°.
वृत्ताकार क्यारी AB का क्षेत्रफल = त्रिज्यखण्ड OAB का क्षेत्रफल – समकोण ΔAOB का क्षेत्रफल
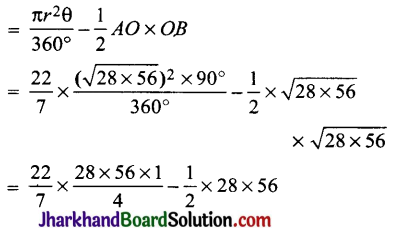
= 22 × 56 – 28 × 28
= 1232 – 784 = 448 मी.2
इसी प्रकार वृत्ताकार क्यारी CD का क्षेत्रफल = 448 मी.2
वर्गाकार बगीचे ABCD का क्षेत्रफल
= 56 × 56 = 3136 मी.2
अब वर्गाकार बगीचे का क्षेत्रफल + वृत्ताकार क्यारियों का क्षेत्रफल
= 3136 + 448 + 448
= 4032 वर्ग मीटर
अत: वर्गाकार बगीचे का क्षेत्रफल व वृत्ताकार क्यारियों के क्षेत्रफलों का योग = 4032 वर्ग मीटर।
प्रश्न 12.
दी गई आकृति में, दर्शाए गए वृत्त खंड का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त की त्रिज्या 21 सेमी हैं तथा ∠AOB = 120° है। [π = \(\frac{22}{7}\) लीजिए]
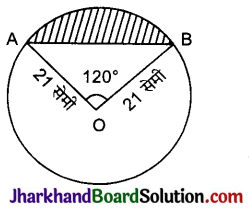
हल:
वृत्तखण्ड का क्षेत्रफल = त्रिज्यखण्ड OAYB का क्षेत्रफल – ΔOAB का क्षेत्रफल
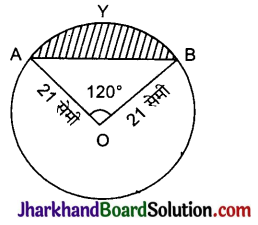
अब, त्रिज्यखण्ड OAYB का क्षेत्रफल
= \(\frac{120^{\circ}}{360^{\circ}}\) × π × 21 × 21
= \(\frac{120^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 21 × 21
= 462 सेमी2 …..(i)
अब, OM ⊥ AB खींचिए
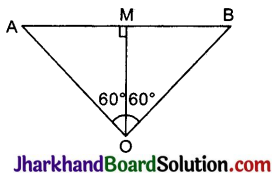
ΔAMO तथा ΔBMO में,
OM = OM (उभयनिष्ठ) (S)
∠AMO = ∠BMO = 90° (A)
∠MOA = ∠MOB = 60° (A)
अतः AAS सर्वांगसमता द्वारा
∠AMO = ∠BMO
माना OM = x सेमी है।
इसीलिए ΔOMA में,
\(\frac{O M}{O A}\) = cos 60°
\(\frac{x}{21}=\frac{1}{2}\)
x = \(\frac{21}{2}\)
अत: OM = \(\frac{21}{2}\) सेमी

इसलिए वृत्तखंड AYB का क्षेत्रफल = \(\left(462-\frac{441}{4} \sqrt{3}\right)\)
= \(\frac{21}{4}\)(88 – 21\(\sqrt{3}\)) सेमी2
![]()
प्रश्न 13.
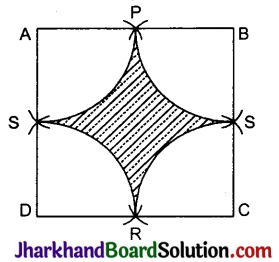
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए वर्ग ABCD के शीर्षों A, B, C तथा D को केन्द्र मानकर खींची गई चायें भुजाओं AB, BC, CD तथ DA के मध्य बिन्दुओं क्रमश: P, Q, R तथा S पर दो-दो के जोड़ों में काटती हैं तथा वर्ग की भुजा 12 सेमी है। [π = 3.14 लीजिए]
हल:
ज्ञात है ABCD एक वर्ग हैं तथा P, Q, R व S वर्ग को भुजाओं के मध्य बिन्दु हैं।
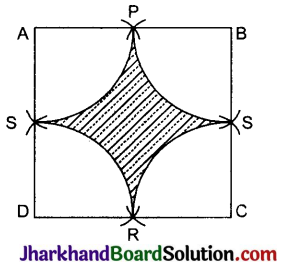
त्रिज्याखण्ड की त्रिज्या, r = \(\frac{a}{2}\)
= \(\frac{12}{2}\) = 6 सेमी
छायांकित भाग का क्षेत्रफल = वर्ग में क्षेत्रफल – 4 × त्रिज्यखण्ड का क्षेत्रफल
= (a)2 – 4 × \(\frac{1}{4}\)πr2
= (12)2 – 3.14 × (6)2
= 144 – 11.04 = 30.96 सेमी2
प्रश्न 14.
दी गई आकृति में, प्रत्येक 3 सेमी व्यास के तीन अर्द्धवृत्त, 4.5 सेमी व्यास का एक वृत्त तथा 4.5 सेमी त्रिज्या का एक अर्धवृत्त बनाए गए हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
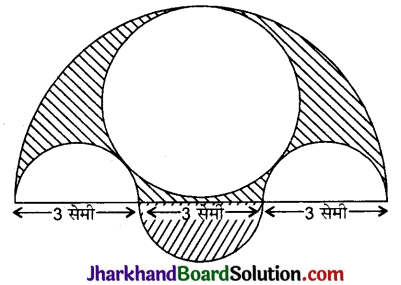
हल:
दिया है, बड़े अर्द्धवृत्त की त्रिज्या = 4.5 सेमी
बड़े अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πR2
= \(\frac{1}{2} \times \frac{22}{7}\) × 4.5 × 4.5
आन्तरिक वृत्त का व्यास = 4.5 सेमी
⇒ r = \(\frac{4.5}{2}\) सेमी
आन्तरिक वृत्त का व्यास = πr2
= \(\frac{22}{7} \times \frac{4.5}{2} \times \frac{4.5}{2}\)
छोटे अर्द्धवृत्त का व्यास = 3 सेमी
⇒ r = \(\frac{3}{2}\) सेमी
छोटे अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr2
= \(\frac{1}{2} \times \frac{22}{7} \times \frac{3}{2} \times \frac{3}{2}\)
छायांकित भाग का क्षेत्रफल = बड़े अर्द्धवृत्त का क्षेत्रफल + पहले छोटे अर्द्धवृत्त का क्षेत्रफल – अन्तः वृत्त का क्षेत्रफल – दो छोटे अर्द्धवृत्तों पर क्षेत्रफल

= \(\frac{11}{7} \times \frac{90}{4}-\frac{22}{7} \times \frac{29.25}{4}\)
= \(\frac{990-643.5}{28}\)
= 12.37 सेमी2 (लगभग)
प्रश्न 14.
दी गई आकृति में, ABCD एक आयत हैं जिसकी विमाएँ 21 सेमी × 14 सेमी हैं। BC की व्यास मान का एक अर्द्ध खींचा गया है। आकृति में छायांकित भाग का क्षेत्रफल तथा परिमाप ज्ञात कीजिए।
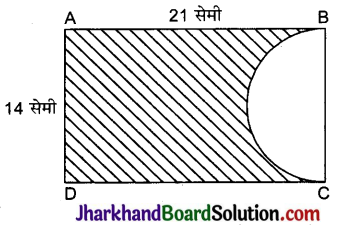
हल:
छायांकित भाग का क्षेत्रफल = अद्यतन का क्षेत्रफल – अर्द्धवृत्त का क्षेत्रफल
= l × b – \(\frac{1}{2}\)πr2
= 21 × 14 – \(\frac{1}{2} \times \frac{22}{7}\) × 7 × 7
= 294 – 77
= 217 सेमी2
छायांकित भाग का परिमाप = 2l + b + πr
= 2 × 21 + 14 + \(\frac{22}{7}\) × 7
= 42 + 14 + 22
= 78 सेमी
![]()
प्रश्न 15.
दी गई आकृति में, ΔABC एक समकोण त्रिभुज है जिसमें ∠A = 90° है। AB, AC व BC की व्यास मानकर अर्द्धवृत्त खींचे गए हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
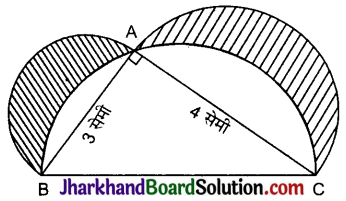
हल:
समकोण ΔABC में पाइथागोरस प्रमेय से,
BC2 = AB2 + BC2
= (3)2 + (4)2
= 9 + 16 = 25
BC = \(\sqrt{25}\) = 5 सेमी
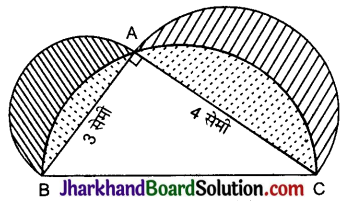
व्यास BC से निर्मित अर्द्धवृत्त का क्षेत्रफल
= \(\frac{1}{2}\)πr2
= \(\frac{1}{2} \times \pi\left(\frac{5}{2}\right)^2=\frac{25}{8} \pi\) सेमी2
व्यास AB से निर्मित अर्द्धवृत्त का क्षेत्रफल
= \(\frac{1}{2}\)πr2
= \(\frac{1}{2} \pi\left(\frac{3}{2}\right)^2=\frac{9}{8} \pi\) सेमी2
व्यास AC से निर्मित अर्द्धवृत्त का क्षेत्रफल
= \(\frac{1}{2}\)πr2
= \(\frac{1}{2} \pi\left(\frac{4}{2}\right)^2=\frac{16}{8} \pi\) सेमी2
समकोण ΔBAC का क्षेत्रफल = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × 3 × 4 = 6 सेमी2
बिन्दुपूर्ण क्षेत्र का क्षेत्रफल = (\(\frac{25}{8}\)π – 6) सेमी2
छायांकित भाग का क्षेत्रफल
= \(\frac{16}{8} \pi+\frac{9}{8} \pi-\left(\frac{25}{8} \pi-6\right)\)
= \(\frac{16}{8} \pi+\frac{9}{8} \pi-\frac{25}{8} \pi+6\)
= 6 सेमी2
प्रश्न 16.
22 सेमी लम्बी एक तार को एक वृत्त की चाप के रस में इस प्रकार मोड़ा गया कि वह वृत्त के केन्द्र पर 60° का कोण अंतरित करती है। वृत्त की त्रिज्या ज्ञात कीजिए। [π = \(\frac{22}{7}\) लीजिए]
हल:
माना त्रिज्या r सेमी है।
चाप की लम्बाई = 22 सेमी

⇒ \(\frac{\pi r \theta}{180^{\circ}}=22\)
⇒ \(\frac{22 \times r \times 60^{\circ}}{7 \times 180^{\circ}}=22\)
⇒ r = \(\frac{22 \times 180 \times 7}{22 \times 60}=21\) सेमी
अतः वृत्त की त्रिज्या = 21 सेमी
प्रश्न 17.
वृत्त के एक तिज्यखंड को परिधि 16.4 सेमी है। यदि त्रिज्या 5.2 सेमी है, तो त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है,
r = 5.2 सेमी
त्रिज्यखण्ड की परिधि = 16.4 सेमी
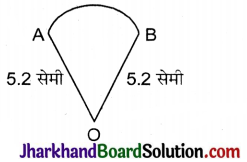
⇒ r + r + चाप AB की लम्बाई = 16.4
⇒ 5.2 + 5.2 + l = 16.4
⇒ l = 16.4 – 10.46 = 6 सेमी
त्रिज्यखंड का क्षेत्रफल = \(\frac{1}{2}\)lr
= \(\frac{1}{2}\) × 5.2 × 6 = 15.6 सेमी2
![]()
प्रश्न 18.
निम्न आकृति में, ABCD एक समान्तर चतुर्भुज है। भुजा AB को व्यास तथा बिन्दु O को केन्द्र मानते हुए एक अर्धवृत्त खींचा गया है जो D से होकर गुजरता है यदि AB = 12 सेमी तथा OD ⊥ AB, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14)
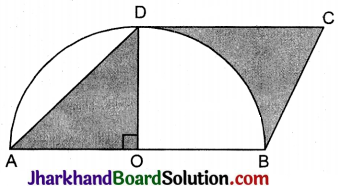
हल:
दिया है, समान्तर चतुर्भुज ABCD की भुजा AB = 12 सेमी
∵ OD ⊥ AB
तथा O, AB का मध्यबिन्दु है।
∴ AO = OB = \(\frac{12}{2}\) = 6 सेमी
∵ OD = OA = 6 सेमी
समान्तर चतुर्भुज ABCD का क्षेत्रफल = AB × OD
= 12 × 6 सेमी
= 72 वर्ग सेमी
चतुर्थांश BOD का क्षेत्रफल = \(\frac{\pi r^2 \theta}{360^{\circ}}\)
= \(\frac{3.14 \times(6)^2 \times 90^{\circ}}{360^{\circ}}\)
= 28.26 सेमी
अतः छायांकित भाग का क्षेत्रफल = समान्तर चतुर्भुज ABCD का क्षेत्रफल – चतुर्थाश OBD का क्षेत्रफल
= (72 – 28.26) सेमी2
= 43.64 सेमी2
प्रश्न 19.
एक वृत्त के त्रिज्यखण्ड का परिमाप 31 सेमी है। यदि वृत्त की त्रिज्या 6.5 सेमी है, तो त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है, वृत्त की त्रिज्या = 6.5 सेमी
वृत्त के त्रिज्यखंड का परिमाप = 31 सेमी

⇒ l + 2r = 31

वस्तुनिष्ठ प्रश्न
रिक्त स्थानों की पूर्ति कीजिए :
प्रश्न (क).
1. नियति बिंदु को वृत्त पर ……………… कहते हैं।
2. वृत्त की परिधि पर स्थित किन्ही दो बिन्दुओं को मिलाने वाले रेखाखण्ड को वृत्त की …………………. कहते हैं।
3. वृत्त के केन्द्र से होकर जाने वाली जीवा, वृत्त का ………………. कहलाती है।
4. वृत्त की परिधि पर किसी सतत् भाग को वृत्त का ………………. कहते हैं।
5. वृत्त के एक-चौथाई भाग को वृत्त का ………………. कहते हैं।
उत्तर:
1. केन्द्र,
2. जीवा,
3. व्यास,
4, चाप,
5. चतुर्थांश।
![]()
निम्न में सत्य / असत्य बताइए :
प्रश्न (ख).
1. किसी चाप द्वारा वृत्त के केन्द्र पर अंतरित कोण को चाप का केन्द्रीय कोण कहते हैं।
2. किसी वृत्त का पूरा एक चक्कर चलने में तय की दूरी उसका क्षेत्रफल कहलाती है।
3. किसी वृत्त की त्रिज्या उस वृत्त को दो बराबर भागों में विभाजित करती है।
4. ऐसी रेखा को, जो वृत्त के किन्हीं दो भिन्न बिन्दुओं पर प्रतिच्छेद करती है, वृत्त की छेदक रेखा कहते हैं।
5. लघुचाप से घिरे त्रिज्यखण्ड को लघु त्रिज्यखण्ड कहते हैं।
उत्तर:
1. सत्य,
2. असत्य,
3. असत्य,
4. सत्य,
5. सत्य।
(ग) बहुविकल्पीय प्रश्न :
प्रश्न 1.
10 सेमी त्रिज्या वाले वृत्त की एक जीवा वृत्त के केन्द्र पर समकोण अंतरित करती है, जो जीवा की लम्बाई है :
(A) \(\frac{5}{\sqrt{2}}\)
(B) 5\(\sqrt{2}\)
(C) 10\(\sqrt{2}\)
(D) 10\(\sqrt{3}\)
हल:
दिया है, वृत्त की त्रिज्या OA = OB = 10 सेमी
तथा ∠AOB = 90°
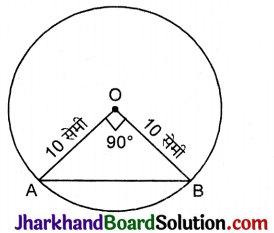
समकोण ΔAOB में,
AB2 = OA2 + OB2
= (10)2 + (10)2
= 100 + 100 = 200
AB = \(\sqrt{100 \times 2}\) = 10\(\sqrt{2}\) सेमी
अतः सही विकल्प (C) है।
प्रश्न 2.
यदि एक वृत्त की परिधि और एक वर्ग का परिमाप बराबर है, तो-
(A) वृत्त का क्षेत्रफल = वर्ग का क्षेत्रफल
(B) वृत्त का क्षेत्रफल > वर्ग का क्षेत्रफल
(C) वृत्त का क्षेत्रफल < वर्ग का क्षेत्रफल
(D) वृत्त और वर्ग के क्षेत्रफलों के बीच के संबंध में निश्चित रूप से कुछ नहीं कहा जा सकता।
हल:
सही विकल्प (B) है।
![]()
प्रश्न 3.
वृत्त के चतुर्थाश का परिमाप क्या होगा यदि वृत्त की त्रिज्या r हो :
(A) \(\frac{\pi+2 r}{r}\)
(B) πr + 2r
(C) \(\frac{\pi r+r}{r}\)
(D) \(\frac{\pi r+4 r}{2}\)
हल:
सही विकल्प (D) है।
प्रश्न 4.
एक वृत्त की त्रिज्या 5 सेमी है इस वृत्त के 9 सेमी लम्बाई के चाप द्वारा बने त्रिज्यखण्ड का क्षेत्रफल है:
(A) 45 वर्ग सेमी
(B) 22.5 वर्ग सेमी
(C) 67.5 वर्ग सेमी
(D) 2.25 वर्ग सेमी
हल:
दिया है, वृत्त की त्रिज्या (r) = 5 सेमी
वृत्त के चाप की लम्बाई (l) = 9 सेमी
हम जानते हैं, त्रिज्यखण्ड का क्षेत्रफल
A = \(\frac{1}{2}\) × l × r
= \(\frac{1}{2}\) × 9 × 5 = \(\frac{45}{2}\)
= 22.5 वर्ग सेमी
अत: सही विकल्प (B) है।
प्रश्न 5.
एक वृत्त की परिधि 22 सेमी. है। उसके चतुर्थांश का क्षेत्रफल (वर्ग सेमी. में) है-
(A) \(\frac{77}{2}\)
(B) \(\frac{77}{4}\)
(C) \(\frac{77}{8}\)
(D) \(\frac{77}{16}\)
हल:
दिया है,
वृत्त की परिधि = 22 सेमी.
⇒ 2πr = 22 [जहाँ r वृत्त की त्रिज्या है]
⇒ r = \(\frac{22}{2 \pi}=\frac{22 \times 7}{2 \times 22}=\frac{7}{2}\) सेमी.
वृत्त के चतुर्थाश का क्षेत्रफल = \(\frac{1}{4}\)πr2
= \(\frac{1}{4} \times \frac{22}{7} \times\left(\frac{7}{2}\right)^2\)
= \(\frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)
= \(\frac{77}{8}\) वर्ग सेमी.
अत: विकल्प (C) सही है।
![]()
प्रश्न 6.
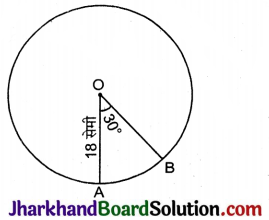
चित्र में वृत्त का केन्द्र O है। वृत्त की त्रिज्या 18 सेमी है तथा ∠AOB = 30° है, तो लघु चाप AB की लम्बाई है :
(A) 2π
(B) 3π
(C) 6π
(D) 4π
हल:
दिया है : वृत्त की त्रिज्या (r) = 18 सेमी
∠AOB = θ = 30°
हम जानते हैं कि लघु चाप की लम्बाई = \(\frac{\pi r \theta}{180^{\circ}}\)
= \(\frac{\pi \times 18 \times 30^{\circ}}{180^{\circ}}\)
= \(\frac{\pi \times 18}{6}=3 \pi\)
अत: सही विकल्प (B) है।
प्रश्न 7.
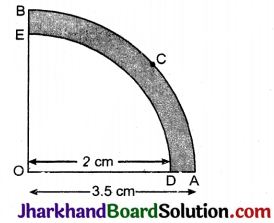
आकृति में, OACB केन्द्र O और त्रिज्या 3.5 सेमी वाले एक वृत्त का चतुर्थाश है। यदि OD = 2 सेमी हो तो छायांकित भाग का क्षेत्रफल ज्ञात, कीजिए:
(A) 6.485 सेमी2
(B) 5.485 सेमी2
(C) 4.485 सेमी2
(D) 3.485 सेमी2
हल:
छायांकित भाग का क्षेत्रफल = \(\frac{1}{4}\)π(R2 – r2)
जहाँ R = बाहरी त्रिज्या r = आन्तरिक त्रिज्या है।
= \(\frac{1}{4} \times \frac{22}{7}\) [(3.5)2 – (2)2]
= \(\frac{22}{28}\)[12.25 – 4]
= \(\frac{22}{28}\) × 8.25
= \(\frac{181.5}{28}\) सेमी2
= 6.482 सेमी2
अत: सही विकल्प (A) हैं।
प्रश्न 8.
यदि वृत्त के त्रिज्यखण्ड का क्षेत्रफल, वृत्त के क्षेत्रफल का \(\frac{1}{12}\) वाँ भाग हो तो त्रिज्यखण्ड का कोण होगा :
(A) 20°
(B) 30°
(C) 40°
(D) 50°
हल:
वृत्त का क्षेत्रफल = πr2
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi r^2 \theta}{360^{\circ}}\)
प्रश्नानुसार,
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{1}{12}\) (वृत्त का क्षेत्रफल)
⇒ \(\frac{\pi r^2 \theta}{360^{\circ}}=\frac{1}{12} \pi r^2\)
⇒ \(\frac{\theta}{360^{\circ}}=\frac{1}{12}\)
⇒ θ = \(\frac{360^{\circ}}{12}\)
∴ θ = 30°
अत: सही विकल्प (B) है।
प्रश्न 9.
भुजा 6 सेमी. वाले एक वर्ग के अन्तर्गत खींचे जा सकने वाले वृत्त का क्षेत्रफल है-
(A) 36π सेमी.2
(B) 18π सेमी.2
(C) 12π सेमी.2
(D) 9π सेमी.2
हाल:
दिया है :
वर्ग ABCD की भुजा = 6 सेमी.
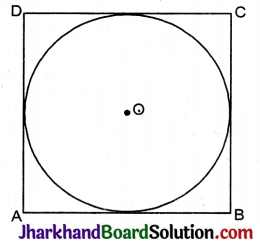
वर्ग के अन्तर्गत खींचे जा सकने वाले वृत्त की त्रिज्या (r) = \(\frac{6}{2}\) = 3 सेमी.
वृत्त का क्षेत्रफल = πr2
= π × (3)2
= 9π सेमी.2
अत: विकल्प (D) सही है।
![]()
प्रश्न 10.
त्रिज्या 8 सेमी वाले एक वृत्त के अन्तर्गत खींचा जा सकने वाले वर्ग का क्षेत्रफल है-
(A) 256 सेमी2
(B) 128 सेमी2
(C) 64\(\sqrt{2}\) सेमी2
(D) 64 सेमी2
हल:
दिया है :
वृत्त की त्रिज्या (r) = 8 सेमी.
∴ वृत्त का व्यास = 2 × 8 = 16. सेमी.
∵ हम जानते हैं कि वृत्त के अन्तर्गत खींचे जा सकने वाले वर्ग के विकर्ण वृत्त के केन्द्र पर समद्विभाजित करते हैं।
अत: AC = 16 सेमी.
माना कि वर्ग की भुजा = x सेमी.
समकोण त्रिभुज ABC मैं
AB2 + BC2 = AC2 (पाइथागोरस प्रमेय से)
⇒ x2 + x2 = 162
⇒ 2x2 = 256
⇒ x2 = \(\frac{256}{2}\) = 128
x = \(\sqrt{128}\) = \(\sqrt{8 \times 8 \times 2}\)
x = 8\(\sqrt{2}\) सेमी.
वर्ग का क्षेत्रफल = 8\(\sqrt{2}\) × 8\(\sqrt{2}\)
= 128 सेमी.2
अतः विकल्प (B) सही है।
प्रश्न 11.
यदि एक वृत्त का परिमाप एक वर्ग के परिमाप के बराबर है, तो उसके क्षेत्रफलों का अनुपात है-
(A) 22 : 7
(B) 14 : 11
(C) 7 : 22
(D) 11 : 14
हल:
माना कि वृत्त की त्रिज्या r तथा वर्ग की भुजा x है।
दिया है :
वृत्त का परिमाप = वर्ग का परिमाप
⇒ 2πr = 4 × x

वृत्त का क्षेत्रफल : वर्ग का क्षेत्रफल = 14 : 11
आत विकल्प (B) सही है।
प्रश्न 12.
यदि π = \(\frac{22}{7}\) लें, तो 35 सेमी, व्यास वाले एक पहिए द्वारा एक चक्कर में तय की गयी दूरी (मीटर में) है-
(A) 2.2
(B) 1.1
(C) 9.625
(D) 96.25
हल:
दिया है :
पहिए का व्यास = 35 सेमी.
∴ पहिए की त्रिज्या (r) = \(\frac{35}{2}\) सेमी.
पहिए द्वारा 1 चक्कर में तय की गयी दूरी = पहिए की परिधि
= 2πr
= 2 × \(\frac{22}{7} \times \frac{35}{2}\)
= 110 सेमी.
= 1.1 मीटर
अतः विकल्प (B) सही है।
![]()
प्रश्न 13.
व्यासों 36 सेमी, और 20 सेमी वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या है-
(A) 56 सेमी.
(B) 42 सेमी.
(C) 28 सेमी.
(D) 16 सेमी.
हल:
दिया है दो वृत्तों के व्यास 36 सेमी, 20 सेमी. है। अतः इनकी त्रिज्याएँ क्रमशः r1 = \(\frac{36}{2}\) = 18 सेमी., r2 = \(\frac{20}{2}\) = 10 सेमी.।
माना वाँछित वृत्त की त्रिज्या R सेमी है।
प्रश्नानुसार
दिये गये वृत्तों की परिधियों का योग = बाँछित वृत्त की परिधि
⇒ 2πr1 + 2πr2 = 2πR
⇒ 2π(r1 + r2) = 2πR
⇒ (18 + 10) = \(\frac{2 \pi \times R}{2 \pi}\)
⇒ 28 = R
⇒ R = 28 सेमी.
अत: विकल्प (C) सही है।
प्रश्न 14.
AB वृत्त का व्यास है AC = 6 सेमी और BC = 8 सेमी। छायांकित भाग का क्षेत्रफल होगा :
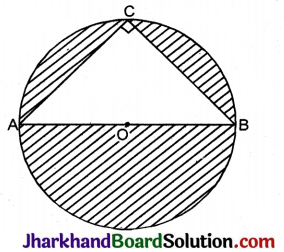
(A) 54.2 सेमी2
(B) 54.3 सेमी2
(C) 54.4 सेमी2
(D) 54.57 सेमी2
हल:
छायांकित भाग का क्षेत्रफल = वृत्त का क्षेत्रफल – ΔABC का क्षेत्रफल
= πr2 – \(\frac{1}{2}\) × AC × BC
दिया है : AB वृत्त का व्यास है।
∵ ∠ACB अर्द्धवृत्त में बंना कोण है। ∠ACB = 90°
समकोण ΔACB में,
AB = \(\sqrt{A C^2+B C^2}\)
= \(\sqrt{6^2+8^2}\)
= \(\sqrt{36+64}=\sqrt{100}\)
∴ AB (व्यास) = 10 सेमी
अतः त्रिज्या (r) = \(\frac{10}{2}\) = 5 सेमी
∴ छायांकित भाग का क्षेत्रफल = वृत्त का क्षेत्रफल – समकोण ΔABC का क्षेत्रफल
= πr2 – \(\frac{1}{2}\) × AC × BC
= \(\frac{22}{7}\) × 5 × 5 – \(\frac{1}{2}\) × 6 × 8
= \(\frac{550}{7}-\frac{24}{1}\)
= 78.57 – 24
= 54.57 सेमी2
अत: सही विकल्प (D) है।
![]()
प्रश्न 15.
त्रिज्याओं 24 सेमी और 7 सेमी. वाले दो वृत्तों के क्षेत्रफलों के योग के बराबर क्षेत्रफल वाले एक वृत्त का व्यास है-
(A) 31 सेमी.
(B) 25 सेमी.
(C) 62 सेमी.
(D) 50 सेमी.
हल:
दिया है,
दो वृत्तों की त्रिज्याएँ r1 = 24 सेमी., r2 = 7 सेमी.
माना कि वाँछित वृत्त की त्रिज्या R सेमी है।
प्रश्नानुसार,
दिए गए दो वृत्तों के क्षेत्रफलों का योग = वाँछित वृत्त का क्षेत्रफल
= πr12 + πr22 = πR
= π(r12 + r22) = πR2
(242 + 72) = \(\frac{\pi R^2}{\pi}\)
576 + 49 = R2
R2 = 625
R = \(\sqrt{625}\)
= 25 सेमी.
अतः वाँछित वृत्त का व्यास = 2 × 25
= 50 सेमी.
अत: विकल्प (D) सही है।