JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.5

Question 1.
Which of the following pairs of linear equations has a unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross-multiplication method:
1. x – 3y – 3 = 0
3x – 9y – 2 = 0
2. 2x + y = 5
3x + 2y = 8
3. 3x – 5y = 20
6x – 10y = 40
4. x – 3y – 7 = 0
3x – 3y – 15 = 0
Solution:
1. x – 3y – 3 = 0 and 3x – 9y – 2 = 0
Here, a₁ = 1; a₂ = 3; b₁ = -3; b₂ = -9; c₁ = -3 and c₂ = -2.
Now, \(\frac{a_1}{a_2}=\frac{1}{3}, \quad \frac{b_1}{b_2}=\frac{-3}{-9}=\frac{1}{3}\) and \(\frac{c_1}{c_2}=\frac{-3}{-2}=\frac{3}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Hence, the given pair of linear equations has no solution.

2. 2x + y – 5 = 0 and 3x + 2y – 8 = 0
Here, a₁ = 2; a₂ = 3; b₁ = 1; b₂ = 2; c₁ = -5 and c₂ = -8.
Now, \(\frac{a_1}{a_2}=\frac{2}{3}, \quad \frac{b_1}{b_2}=\frac{1}{2}\) and \(\frac{c_1}{c_2}=\frac{-5}{-8}=\frac{5}{8}\)
Here, \(\frac{1}{2}\)
Hence, the given pair of linear equations has a unique solution.
Now,


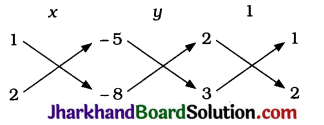
Thus, the unique solution of the given pair of linear equations is x = 2, y = 1.

3. 3x – 5y – 20 = 0 and 6x – 10y – 40 = 0
Here, a₁ = 3, a₂ = 6, b₁ = -5, b₂ = -10, c₁ = -20 and c₂ = -40.
Now, \(\frac{a_1}{a_2}=\frac{3}{6}=\frac{1}{2}\), \(\frac{b_1}{b_2}=\frac{-5}{-10}=\frac{1}{2}\) and \(\frac{c_1}{c_2}=\frac{-20}{-40}=\frac{1}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Hence, the given pair of linear equations has infinitely many solutions.

4. x – 3y – 7 = 0 and 3x – 3y – 15 = 0
Here, a₁ = 1, a₂ = 3, b₁ = -3, b₂ = -3, c₁ = -7 and c₂ = -15.
Now, \(\frac{a_1}{a_2}=\frac{1}{3}, \frac{b_1}{b_2}=\frac{-3}{-3}=1\) and \(\frac{c_1}{c_2}=\frac{-7}{-15}=\frac{7}{15}\)
Here, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, the given pair of linear equations has a unique solution.
Now,

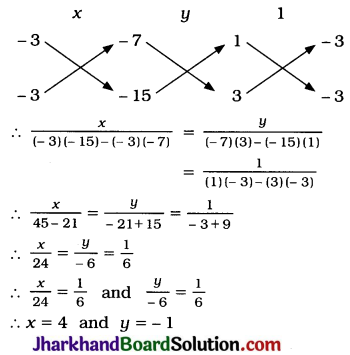
Thus, the unique solution of the given pair of linear equations is x = 4, y = -1.

Question 2.
1. For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
2. For which value of k will the following pair of linear equations have no solution ?
3x + y = 1
(2k – 1)x + (k – 1) y = 2k + 1
Solution:
1. For the given pair of equations, we express them in the standard form as:
2x + 3y – 7 = 0 and
(a – b)x + (a + b)y – (3a + b – 2) = 0
Here, A₁ = 2; A₂ = a – b; B₁ = 3; B₂ = a + b; C₁ = -7 and C₂ = -(3a + b – 2)
Then, \(\frac{\mathrm{A}_1}{\mathrm{~A}_2}=\frac{2}{a-b}, \frac{\mathrm{B}_1}{\mathrm{~B}_2}=\frac{3}{a+b}\) and \(\frac{C_1}{C_2}=\frac{-7}{-(3 a+b-2)}=\frac{7}{3 a+b-2}\)
For the pair of equations to have infinite number of solution, we must have

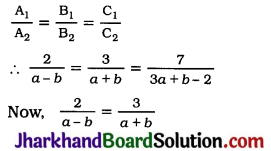
∴ 2(a + b) = 3(a – b)
∴ 2a + 2b = 3a – 3b
∴ 5b = a
∴ a = 5b ………..(1)
Again, \(\frac{3}{a+b}=\frac{7}{3 a+b-2}\)
∴ 3 (3a + b – 2) = 7(a + b)
∴ 9a + 3b – 6 = 7a + 7b
∴ 2a – 4b = 6
∴ 2 (5b) – 4b = 6 [from (1), a = 5b]
∴ 6b = 6
∴ b = 1
Now, a = 5b
∴ a = 5(1)
∴ a = 5
Thus, for a = 5 and b = 1, the given pair of linear equations will have an infinite number of solutions.

2. We express the given equations in the standard form as:
3x + y – 1 = 0 and
(2k – 1)x + (k – 1)y – (2k + 1) = 0.
Here, a₁ = 3; a₂ = 2k – 1; b₁ = 1; b₂ = k – 1; c₁ = -1 and c₂ = -(2k + 1).
Then, \(\frac{a_1}{a_2}=\frac{3}{2 k-1}, \quad \frac{b_1}{b_2}=\frac{1}{k-1}\) and \(\frac{c_1}{c_2}=\frac{-1}{-(2 k+1)}=\frac{1}{2 k+1}\)
For the pair of equations to have not solution, we must have
\(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
∴ \(\frac{3}{2 k-1}=\frac{1}{k-1} \neq \frac{1}{2 k+1}\)
\(\frac{3}{2 k-1}=\frac{1}{k-1}\)
∴ 3(k – 1) = 2k – 1
∴ 3k – 3 = 2k – 1
∴ k = 2
For k = 2.
\(\frac{a_1}{a_2}=\frac{3}{2(2)-1}=1\), \(\frac{b_1}{b_2}=\frac{1}{2-1}=1\) and \(\frac{c_1}{c_2}=\frac{1}{2(2)+1}=\frac{1}{5}\)
Thus, k = 2 satisfies \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Thus, for k = 2, the given pair of linear equations has no solution.

Question 3.
Solve the following pair of linear equations by the substitution and cross-multiplication methods:
8x + 5y = 9
3x + 2y = 4
Solution:
1. Substitution method:
8x + 5y = 9 ……….(1)
3x + 2y = 4 ……….(2)
From equation (2), we get y = \(\frac{4-3 x}{2}\)
Substituting y = \(\frac{4-3 x}{2}\) in equation (1).
we get
8x + 5(\(\frac{4-3 x}{2}\)) = 9
∴ 16x + 5(4 – 3x) = 18 (Multiplying by 2)
∴ 16x + 20 – 15x = 18
∴ x = -2
Substituting x = -2 in y = \(\frac{4-3 x}{2}\), we get
∴ y = \(\frac{4-3(-2)}{2}\)
∴ y = 5
Thus, the solution of the given pair of linear equations is x = -2, y = 5.

2. Cross-multiplication method:
We express both the equations in the standard form as:
8x + 5y – 9 = 0 and 3x + 2y – 4 = 0
Here, a₁ = 8; b₁ = 5; c₁ = -9; a₂ = 3; b₂ = 2 and c₂ = -4.
Now, we arrange the coefficients as required in cross-multiplication method as:

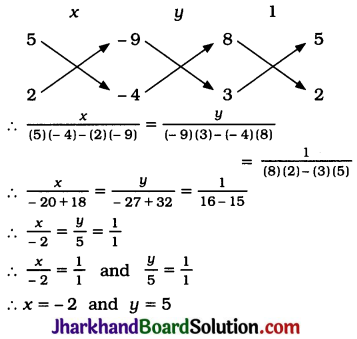
Thus, the solution of the given pair of linear equations is x = -2, y = 5.

4. Form the pair of linear equations in the following problems and find their solutions. (if they exist) by any algebraic method:

Question 1.
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay ₹ 1000 as hostel charges whereas a student B, who takes food for 26 days, pays ₹ 1180 as hostel charges. Find the fixed charges and the cost of food per day.
Solution:
Let the fixed monthly charge be ₹ x and the cost of food per day be ₹ y.
Then, from the give data, we get the following pair of linear equations:
x + 20y = 1000 ……….(1)
x + 26y = 1180 ………..(2)
These equations in standard form are:
x + 20y – 1000 = 0 ……….(3)
x + 26y – 1180 = 0 ……….(4)
Now, we solve the equation by cross-multiplication method.

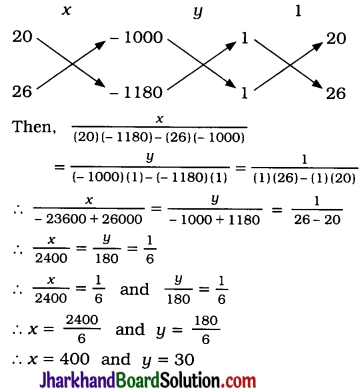
Thus, monthly fixed charge is ₹ 400 and the cost of food per day is ₹ 30.
Note: Here, the elimination method would be much easter, but we have solved. it by cross-multiplication method to show more applications of that method.

Question 2.
A fraction becomes \(\frac{1}{3}\) when 1 is subtracted from the numerator and it becomes \(\frac{1}{4}\) when 8 is added to its denominator. Find the fraction.
Solution:
Let the numerator and the denominator of the required fraction be x and y respectively.
Then, the required fraction = \(\frac{x}{y}\)
By the given data, we get
\(\frac{x-1}{y}=\frac{1}{3}\)
∴ 3x – 3 = y
∴ 3x – y = 3 ……….(1)
Also, \(\frac{x}{y+8}=\frac{1}{4}\)
∴ 4x = y +8
∴ 4x – y = 8 …………(2)
Subtracting equation (1) from equation (2),
we get
(4x – y) – (3x – y) = 8 – 3
∴ 4x – y – 3x + y = 5
∴ x = 5
Substituting x = 5 in equation (1),
we get
3(5) – y = 3
∴ 15 – 3 = y
∴ y = 12
Hence, the required fraction = \(\frac{x}{y}=\frac{5}{12}\)

Question 3.
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solution:
Suppose Yash gave x right answers and y wrong answers.
Then, from the given data, we get
3x – y = 40 ………(1)
and 4x – 2y = 50, i.e.. 2x – y = 25 ……….(2)
We express the equations in the standard form as
3x – y – 40 = 0 ………(3)
2x – y – 25 = 0 ………(4)
Then,

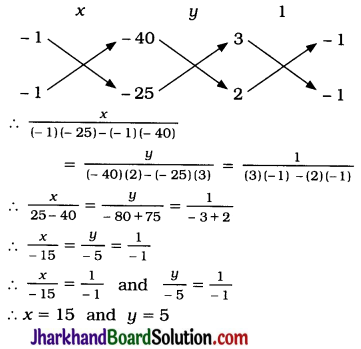
Then, the total number of questions in the test = x + y = 15 + 5 = 20.
Thus, there were 20 questions in the test.

Question 4.
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
Solution:
Let the speed of the car starting from A be x km/hour and the speed of the car starting from B be y km/hour such that x > y. If the cars travel in the same direction and meet, they should be travelling in the direction from A towards B as the car starting from A is faster than the car starting from B.

Suppose the cars meet at place P after 5 hours, when they travel in the same direction. Then, the distance travelled in 5 hours by the car starting from A= 5x km = AP (Distance = Speed × Time) Similarly, the distance travelled in 5 hours by the car starting from B = 5y km = BP.
Now, AB = 100 km
∴ AP – BP = 100
∴ 5x – 5y = 100
∴ x – y = 20 (Dividing by 5) ………(1)

Suppose the cars meet at place Q after 1 hour when they travel in opposite directions.
Then, distance travelled in 1 hour by the car starting from A = x km = AQ
Similarly, distance travelled in 1 hour by the car starting from B = y km = BQ.
Now, AB = 100 km
∴ AQ + BQ = 100
∴ x + y = 100 ………(2)
Adding equations (1) and (2), we get
(x – y) + (x + y) = 20 + 100
∴ 2x = 120
∴ x = 60
Substituting x = 60 in equation (2), we get
60 + y = 100
∴ y = 40
Thus, the speeds of the cars starting from A and B are 60 km/hour and 40 km/hour respectively under the assumption that x > y.

Question 5.
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solution:
Let the length of the rectangle be x units and its breadth be units.
Area of a rectangle = Length × Breadth
∴ Area of given rectangle = xy square units
According to the first condition given,
new reduced length = (x – 5) units,
new increased breadth = (y + 3) units and new reduced area = (xy – 9) square units.
Then, Length × Breadth = Area of a rectangle gives
(x – 5) (y + 3) = xy – 9
∴ xy + 3x – 5y – 15 = xy – 9
∴ 3x – 5y – 6 = 0 ……….(1)
Similarly, from the second condition given,
new increased length = (x + 3) units.
new increased breadth = (y + 2) units and
new increased area = (xy + 67) square units.
Again, Length × Breadth = Area of a rectangle gives
(x + 3)(y + 2) = xy + 67
∴ xy + 2x + 3y + 6 = xy + 67
∴ 2x + 3y – 61 = 0 ………..(2)
We solve these equations (1) and (2) by cross-multiplication method.


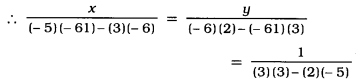
∴ x = \(\frac{323}{19}\) and y = \(\frac{171}{19}\)
∴ x = 17 and y = 9
Thus, the length and the breadth of the given rectangle are 17 units and 9 units respectively.