Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 Triangles Ex 6.4 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 6 Triangles Exercise 6.4
Question 1.
Let ΔABC ~ ΔDEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution :
ΔABC ~ ΔDEF

![]()
Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution :
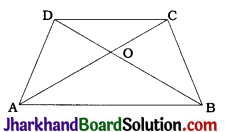
In trapezium ABCD, AB || CD and diagonals AC and BD intersect at O.
Then, in ΔAOB and ΔCOD.
∠OAB = ∠OCD (Alternate angles)
∠OBA = ∠ODC (Alternate angles)
∠AOB = ∠COD (Vertically opposite angles)
∴ By AAA criterion, ΔAOB ~ ΔCOD.

Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar (ABC) / ar (DBC) = \(\frac{AO}{DO}\)
Solution :
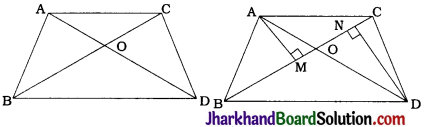
Draw AM ⊥ BC and DN ⊥ BC.
Then, ar (ABC) = \(\frac{1}{2}\) × BC × AM and
ar (DBC) = \(\frac{1}{2}\) × BC × DN
In ΔAMO and ΔDNO
∠AMO = ∠DNO (Right angles)
∠AOM = ∠DON (Vertically opposite angles)
∴ By AA criterion, ΔAMO ~ ΔDNO.
∴ \(\frac{AM}{DN}=\frac{AO}{DO}\) ……………….(2)
From (1) and (2), ar (ABC) / ar (DBC) = \(\frac{AO}{DO}\)
![]()
Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution :
Given: ΔABC ~ ΔPQR and ar (ABC) = ar (PQR)
To prove : ΔABC ≅ ΔPQR
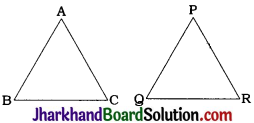
Proof: ΔABC ~ ΔPQR

∴ AB = PQ, BC = QR and CA = RP
∴ By SSS criterion for congruence of triangles, ΔABC = ΔPOR.
Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Solution :
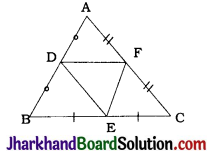
In ΔABC, D, E and F are the mid-points of sides AB, BC and CA respectively.
Then, EF || AB and DE || AC
∴ EF || AD and DE || AF
∴ ADEF is a parallelogram.
∴ ∠A = ΔDEF
(Opposite angles of parallelogram)
Similarly, we can prove that ∠B = ∠EFD and ∠C = ∠EDF
Now, in ΔABC and ΔEFD,
∠A = ∠E, ∠B = ∠F and ∠C = ∠D
∴ By AAA criterion, ΔABC ~ ΔEFD.
∴ ar (DEF) / ar(ABC) = (\(\frac{EF}{AB}\))² ………………(1)
In ΔABC, E and F are the mid-points of BC and CA respectively.
∴ EF = \(\frac{1}{2}\)AB ………………(2)
(Alternately: ADEF is a parallelogram.
∴ EF = AD = \(\frac{1}{2}\)AB)
From (1) and (2),

![]()
Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution :
Given: ΔABC ~ ΔPQR, AD and PM are medians of triangles ABC and PQR respectively.
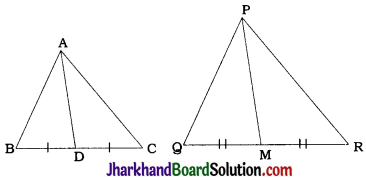
Proof :
In ΔABC, AD is a median ∴ BD = \(\frac{1}{2}\)BC
In ΔPQR, PM is a median ∴ QM = \(\frac{1}{2}\)QR.
ΔABC ~ ΔPQR
∴ ∠B = ∠Q and \(\frac{AB}{PQ}=\frac{BC}{QR}\)
∴ ∠ABD = ∠PQM and \(\frac{AB}{PQ}=\frac{BD}{QM}\)
So, by SAS criterion ΔABD ~ ΔPQM.
∴ \(\frac{AB}{PQ}=\frac{AD}{PM}\) ……………(1)
Now, ΔABC ~ ΔPQR
∴ ar (ABC) / ar (PQR) = (\(\frac{AB}{PQ}\))²
∴ ar (ABC) / ar (PQR) = (\(\frac{AD}{PM}\))² [By (1)]
Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of an equilateral triangle described on one of its diagonals.
Solution :
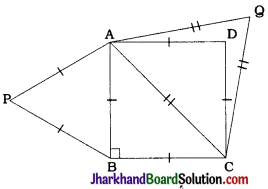
ABCD is a square. PAB, is an equilateral triangle described on side AB and QAC is an equilateral triangle described on diagonal AC.
In ΔABC, ∠B = 90° and AB = BC (Properties of a square)
Then, AC² = AB² + BC² (Pythagoras theorem)
∴ AC² = AB² + AB²
∴ AC² = 2AB²
∴ \(\frac{\mathrm{AB}^2}{\mathrm{AC}^2}\) = \(\frac{1}{2}\)
∴ (\(\frac{18}{36}\))
ΔPAB is an equilateral triangle.
∴ ∠P = ∠A = ∠B = ∠60°
ΔQAC is an equilateral triangle.
∴ ∠Q = ∠A = ∠C = 60°
Thus, in ΔPAB and ΔQAC,
∠P = ∠Q and ∠A = ∠A and ∠B = ∠C
∴ By AAA criterion, ΔPAB ~ ΔQAC.
∴ ar (PAB) / ar(QAC) = (\(\frac{AB}{AC}\))²
∴ ar (PAB) / ar(QAC) = \(\frac{1}{2}\) [By (1)]
∴ ar (PAB) = \(\frac{1}{2}\)ar (QAC)
Thus, the area of an equilateral triangle described on a side of a square is half the area of an equilateral triangle described on one of its diagonals.
Tick the correct answer and justify:
Question 8.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution :
The correct answer is (C) 4 : 1.
ΔABC and ΔBDE are equilateral triangles.
Hence, any of their correspondences is a similarity.

![]()
Question 9.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution :
The correct answer is (D) 16 : 81.
By theorem 6.6.
Ratio of areas of two similar triangles
= (Ratio of their corresponding sides)²
= (4 : 9)²
= (\(\frac{4}{9}\))²
= 16 : 81