JAC Class 10 Maths Important Questions Chapter 14 सांख्यिकी

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 14 सांख्यिकी Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 14 सांख्यिकी

लघूत्तरात्मक/निबन्धात्मक प्रश्न :

प्रश्न 1.
निम्न बंटन का बहुलक ज्ञात कीजिए :

हल:
बहुलक के लिए, दिये गये आँकड़ों में अधिकतम बारम्बारता 61 है।
इसका संगत वर्ग-अंतराल 60 – 80 है।
बहुलक वर्ग = 60 – 80
l = 60, f₁ = 61, f₀ = 52, f₂ = 38, h = 20

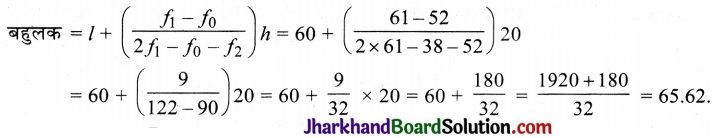
प्रश्न 2.
यदि नीचे दिए हुए बंटन का माध्यम 28.5 हो तो x और y के मान ज्ञात कीजिए।

हल:

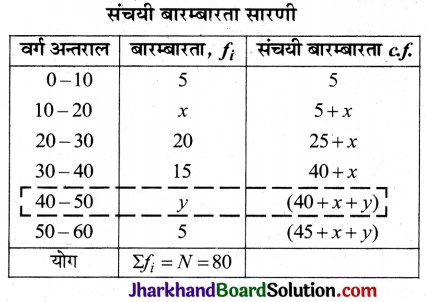
परन्तु बारम्बारता का योग Σf_i = N = 80 है। अंतिम संचयी बारम्बारताओं के योग के बराबर होता है।
∴ 45 + x + y = 80
⇒ x + y = 80 – 45
⇒ x + y = 35 ……(1)
अब \(\frac{N}{2}=\frac{80}{2}=40\)
तथा बंटन का माध्यक = 28.5 है।
जोकि वर्ग अंतराल 20 – 30 में स्थिति है।
माध्यम वर्ग = 20 – 30
l = 20, f = 20, c = 5 + x और h = 10

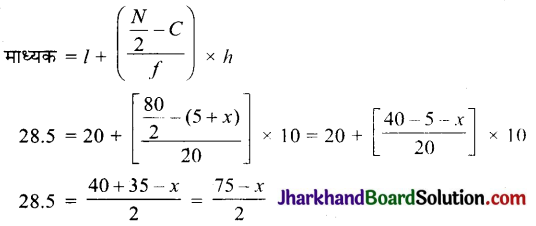
57 = 75 – x
x = 18
x का मान समी. (1) में रखने पर 18 + y = 35
अतः y = 17

प्रश्न 3.
नीचे दिए गए बंटन का माध्य 50 हो तो x व y के मान ज्ञात कीजिए :

वर्ग अन्तराल	बारंबारता
0 – 20	17
20 – 40	x
40 – 60	32
60 – 80	y
80 – 100	19
योग	120

हल:
संचयी बारम्बारता सारणी

वर्ग अन्तराल	बारंबारता	संचयी बारंबारता c.f.
0 – 20	17	17
20 – 40	X	17 + x
40 – 60	32	(49 + x)
60 – 80	Y	(49 + x + y)
80 – 100	19	(68 + x + y)
योग	Σfi = N = 120

परन्तु बारम्बारताओं का योग Σf_i = N = 120 है अंतिम संचयी बारम्बारता वर्ग बारम्बारताओं के योग के बराबर होता है।
68 + x + y = 120
x + y = 120 – 68
x + y = 52 …..(1)
अब \(\frac{N}{2}=\frac{120}{2}=60\)
तथा बंटन का माध्यक = 50 है।
जोकि वर्ग अन्तराल 40 – 60 में स्थिति है।
माध्यक वर्ग = 40 – 60
l = 40, f = 32, c = 17 + x और h = 20

⇒ 50 = 320 + 215 – 5x
⇒ 400 – 535 = -5x ⇒ 5x = 135 ⇒ x = 27
x का मान समीकरण (1) में रखने पर
27 + y = 52
y = 25

प्रश्न 4.
निम्नलिखित आँकड़ों का माध्यक 525 है। यदि बारम्बारताओं का योग 100 है तो x और y के मान ज्ञात कीजिए।

वर्ग-अन्तराल	बारम्बारता
0 – 100	2
100 – 200	5
200 – 300	x
300 – 400	12
400 – 500	17
500 – 600	20
600 – 700	y
700 – 800	9
800 – 900	7
900 – 1000	4

हल:

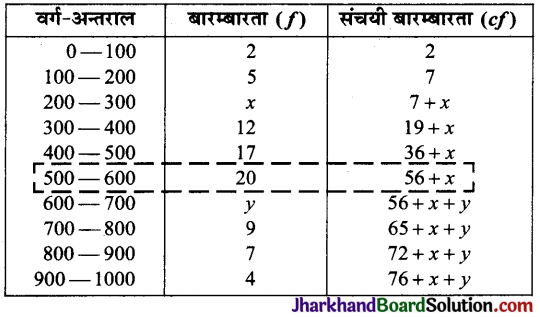
दिया है : Σ(f) = N = 100
अतः 76 + x + y = 100 ⇒ x + y = 100 – 76 = 24 …..(1)
माध्यक 525 है जो वर्ग 500 – 600 में स्थित है।
∴ l = 500; ƒ = 20, C = 36 + x, h = 100

x = 14 – 5
∴ x = 9
समीकरण (1) से, 9 + y = 24
⇒ y = 24 – 9
∴ y = 15
अतः x = 9 और y = 15

प्रश्न 5.
गणित की एक परीक्षा में 30 विद्यार्थियों द्वारा प्राप्त किए गए अंकों का बंटन निम्नलिखित है :

इन आँकड़ों से कल्पित माध्य विधि से माध्य ज्ञात कीजिए एवम् बहुलक भी ज्ञात कीजिए।
हल:
माना कि कंल्पित माध्य (A) = 47.5

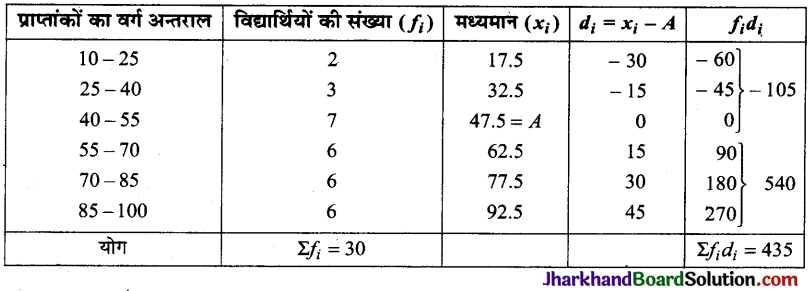
समान्तर माध्य (x) = A + \(\frac{\Sigma f_i d_i}{\Sigma f_i}\) = 47.5 + \(\frac{435}{30}\)
= 47.5 + 14.5 = 62
दी गयी सारणी से स्पष्ट है कि सबसे अधिक बारम्बारता 7 है।
अतः 7 के संगत वर्ग अन्तराल 40 – 55 है। अतः बहुलक वर्ग 40 – 55 होगा।
l = 40, f₀ = 3, f₁ = 7, ƒ₂ = 6 तथा h = 15

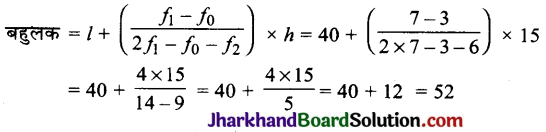
अतः माध्य = 62 तथा बहुलक = 52

प्रश्न 6.
निम्न बंटन का कल्पित माध्य मानकर माध्यx ज्ञात कीजिए :

हल:

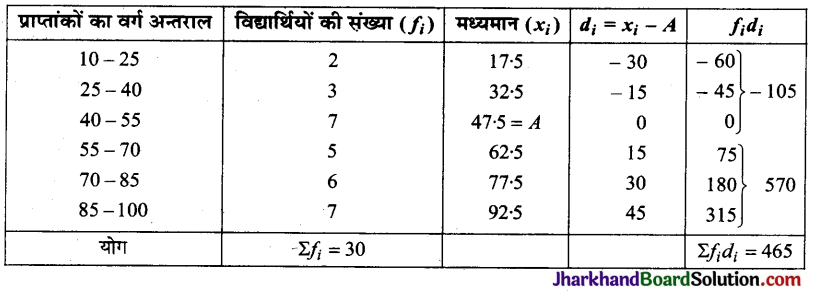
समान्तर माध्य (x) = A + \(\frac{\Sigma f_i d_i}{\Sigma f_i}\)
= 47.5 + \(\frac{465}{30}\)
= 47.5 + 15.5 = 63
दी गयी सारणी से स्पष्ट है कि सबसे अधिक बारम्बारता 7 है।

प्रश्न 7.
एक मेडिकल की प्रवेश परीक्षा में 400 विद्यार्थियों के प्राप्तांक निम्न सारणी में दर्शाये गए हैं :

उपर्युक्त बंटन को एक ‘से कम’ प्रकार के संचयी बारम्बारता बंटन में बदलिए और उसका तोरण खींचिए।
हल:
‘से कम’ प्रकार का संचयी बारम्बारता बंटन

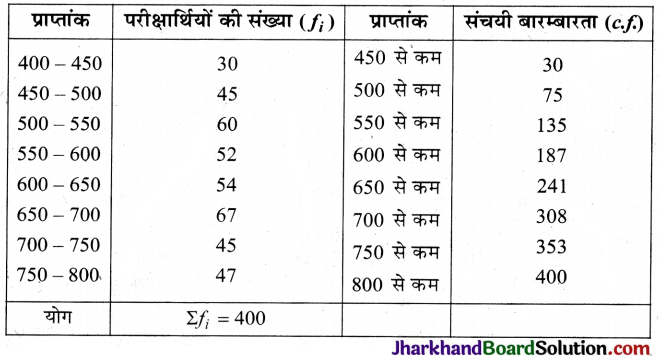
(i) बिन्दुओं A(450, 30); B(500, 75); C(550, 135); D(600, 187); E(650, 241); F(700, 308); G(750, 353) और H(800, 400) को ग्राफ पेपर पर उचित पैमाना मानकर अंकित किया।
(ii) इन सभी बिन्दुओं को हाथ से जोड़कर ‘से कम प्रकार’ का तोरण खींचा।

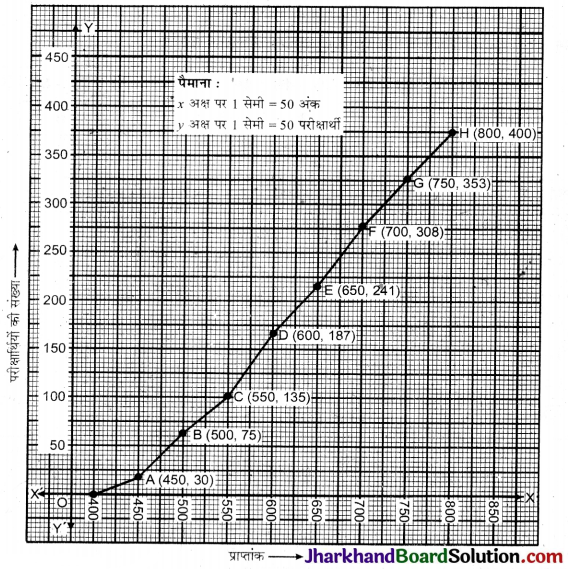
अत: ABCDEFG ही अभीष्ट तोरण है।

प्रश्न 8.
कक्षा X के 60 विद्यार्थियों के अंक निम्नवत् हैं :

इस बंटन को ‘कम प्रकार’ के बंटन में बदलिए। तोरण वक्र खींचकर माध्यक ज्ञात कीजिए।
हल:
‘कम प्रकार’ का संचयी बारम्बारता बंटन

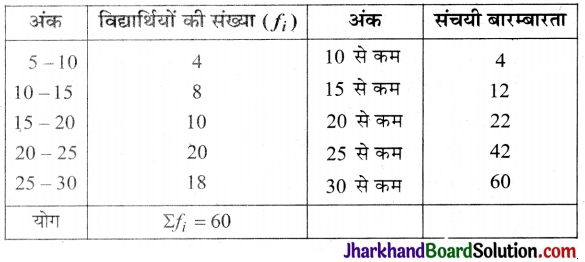
अब बिन्दुओं A(10, 4), B(15, 12), C(20, 22), D(25, 42), E(30, 60) को ग्राफ पेपर पर अंकित किया। अब सभी बिन्दुओं को हाथ से जोड़ते हुए तोरण खींचा।

माध्यक के लिए :
(i) Y-अक्ष पर 30 विद्यार्थियों पर एक बिन्दु अंकित किया।
(ii) इस बिन्दु से X-अक्ष के समान्तर रेखा खींची जो वक्र को P बिन्दु पर काटती है।
(iii) बिन्दु P का भुज ज्ञात किया जो कि 22 है।
अतः माध्यक = 22 अंक।

प्रश्न 9.
किसी मोहल्ले के एक शॉपिंग कॉम्प्लेक्स (shopping complex) की 30 दुकानों द्वारा अर्जित किए गए वार्षिक लाभों से निम्नलिखित बारम्बारता बंटन प्राप्त होता है।

लाभ (लाख रु. में)	दुकानों की संख्या
5 से अधिक या बराबर	30
10 से अधिक या बराबर	28
15 से अधिक या बराबर	16
20 से अधिक या बराबर	14
25 से अधिक या बराबर	10
30 से अधिक या बराबर	7
35 से अधिक या बराबर	3

उपर्युक्त आँकड़ों से (i) ‘अधिक प्रकार’ का तोरण वक्र खींचिए।
(ii) एक ही अक्षों पर दोनों तोरण खींचिए। इसके बाद माध्यक लाभ ज्ञात कीजिए।
हल:
(i) बिन्दुओं A(5, 30); B(10, 28); C(15, 16); D(20, 14); E(25, 10); F(30, 7) और G(35, 3) को उचित पैमाना मानकर ग्राफ पेपर पर अंकित करते हैं। सभी बिन्दुओं को एक मुक्त हस्त से जोड़ते हुए तोरण खीचते है।
अत: A B C D E F G ही अभीष्ट तोरण है।

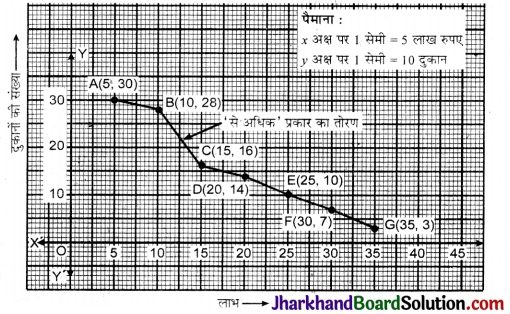
(ii) दिये गये बारम्बारता बंटन से, वर्ग-अन्तराल, संगत बारम्बारताएँ और संचयी बारम्बारता सारणी बनाते हैं।

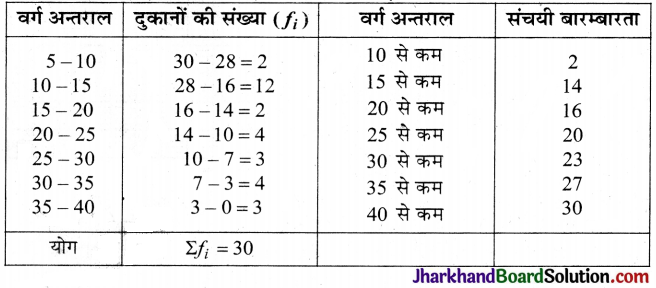
अब बिन्दुओं (10, 2); (15, 14); (20, 16); (25, 20); (30, 23); (35, 27); (40, 30) को ग्राफ पेपर पर अंकित करते हैं। इन सभी बिन्दुओं को मुक्त हस्त से जोड़कर ‘कम प्रकार’ का तोरण खींचते हैं।
इस वक्र को ‘अधिक प्रकार’ के वक्र के साथ आलेखित करने से दोनों प्रकार के वक्र एक ही अक्ष पर प्राप्त हो जाते हैं।

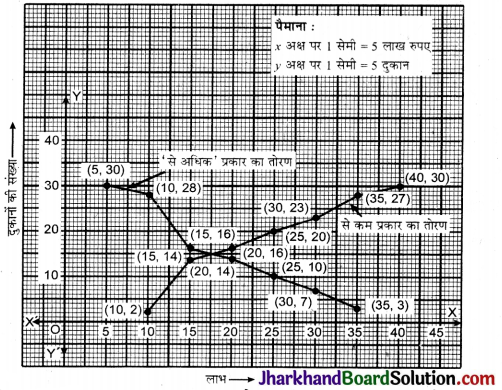
दोनों तोरण के प्रतिच्छेद बिन्दु से क्षैतिज अक्ष पर लम्ब डालने पर प्राप्त लाभ माध्यक होगा।
अतः माध्यक = ₹ 17.5 लाख

प्रश्न 10.
निम्न बारंबारता का बहुलक 36 है। लुप्त बारंबारता (f) का मान ज्ञात कीजिए :

हल:
दिए गए बारंबारता बंटन का बहुलक 36 है, इसलिए बहुलक वर्ग 30-40 है।
∴ l = 30, f₀ = f, f₁ = 16, f₂ = 12 तथा h = 10

⇒ 6 × (20 – f) = (16 – f) × 10
⇒ 120 – 6f = 160 – 10f
⇒ 10f – 6f = 160 – 120
⇒ 4f = 40
⇒ f = 10
अतः लुप्त बारंबारता, f = 10.

प्रश्न 11.
निम्न आँकड़ों का बहुलक ज्ञात कीजिए :

हल:

वर्ग	बारम्बारता
0 – 20	6
20 – 40	8
40 – 60	10 = f0
60 – 80	12 = f1
80 – 100	6 = f2
100 – 120	5
120 – 140	3

∵ अधिकतम बारंबारता = 12
∴ बहुलक वर्ग = 60 – 80
∴ l = 60, f₀ = 10, f₁ = 12, f₂ = 6, h = 20
अब बहुलक = \(60+\left(\frac{12-10}{2 \times 2-10-6}\right) \times 20\)
= \(60+\frac{2}{8} \times 20\)
= 60 + 5 = 65

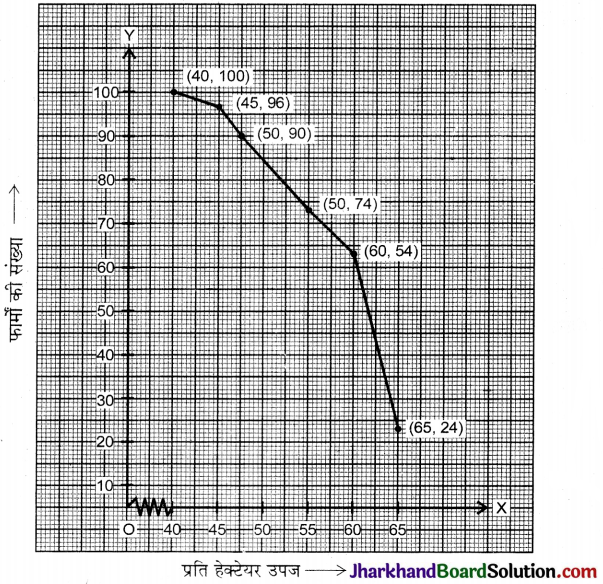
प्रश्न 12.
निम्न तालिका एक गाँव की 100 फार्मों में गेहूँ की प्रति हैक्टेयर (क्विंटलों में) उपज के आँकड़ें दर्शाता है :

उपरोक्त बंटन को ‘से अधिक’ प्रकार के बंटन में बदलकर उसका तोरण खींचिए।
हल:

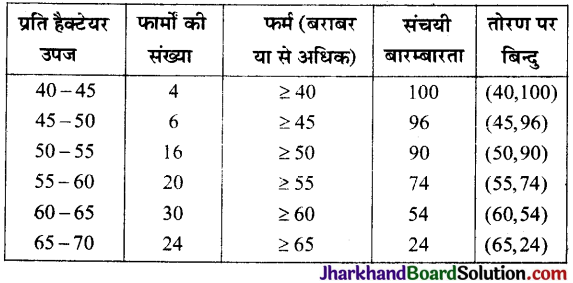
अब तोरण बिन्दुओं को ग्राफ पर अंकित करके मुक्त हस्त से वक्र खींचते हैं जैसे कि निम्न आकृति में दर्शाया गया है।
इस प्रकार प्राप्त वक्र को “से अधिक प्रकार” का तोरण कहते हैं।

प्रश्न 13.
निम्न बारंबारता बंटन का बहुलक ज्ञात कीजिए।

हल:

यहाँ अधिकतम वर्ग बारंबारता 16 है तथा इस बारंबारता का संगत वर्ग 30 – 40 है।
अतः बहुलक वर्ग 30 – 40 है।
अब बहुलक़ वर्ग = 30 – 40
बहुलक वर्ग की निम्न सीमा (l) = 30 तथा वर्ग माप (h) = 10
f₁ = 16, f₀ = 10 तथा f₂ = 12

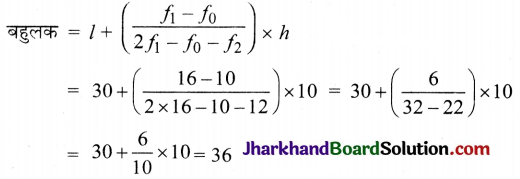
प्रश्न 14.
नीचे दी गई सारणी में 280 लोगों का वेतन मान दर्शाया गया है :

वेतन (हजार ₹ में)	लोगों की संख्या
5 – 10	49
10 – 15	133
15 – 20	63
20 – 25	15
25 – 30	6
30 – 35	7
35 – 40	4
40 – 45	2
45 – 50	1

उपर्युक्त आँकड़ों से माध्यक वेतन मान ज्ञात कीजिए।
हल:

वेतन	बारंबारता	संचयी बारंबारता
5 – 10	49	49
10 – 15	133	182
15 – 20	63	245
20 – 25	15	260
25 – 30	6	266
30 – 35	7	273
35 – 40	4	277
40 – 45	2	279
45 – 50	1	280
	N = 280

\(\frac{N}{2}=\frac{280}{2}\) = 140
माध्यम वर्ग = 10 – 15
f = 133
c.f. = 49
h = 5

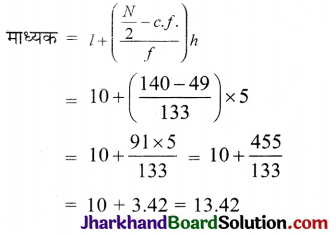
अतः लोगों का माध्यक वेतन ₹ 13.42 है।

प्रश्न 15.
निम्नलिखित बंटन को ‘से कम प्रकार’ के बंटन में बदलिए और फिर उसका तोरण खींचिए :

वर्ग अन्तराल	बारंबारता
30 – 40	7
40 – 45	5
50 – 60	8
60 – 70	10
70 – 80	6
80 – 90	6
90 – 100	8

हल:

वर्ग अन्तराल	बारंबारता	तोरण बिन्दु
40 से कम	7	(40, 7)
50 से कम	12	(50, 12)
60 से कम	20	(60, 20)
70 से कम	30	(70, 30)
80 से कम	36	(80, 36)
90 से कम	42	(90, 42)
100 से कम	50	(100, 50)

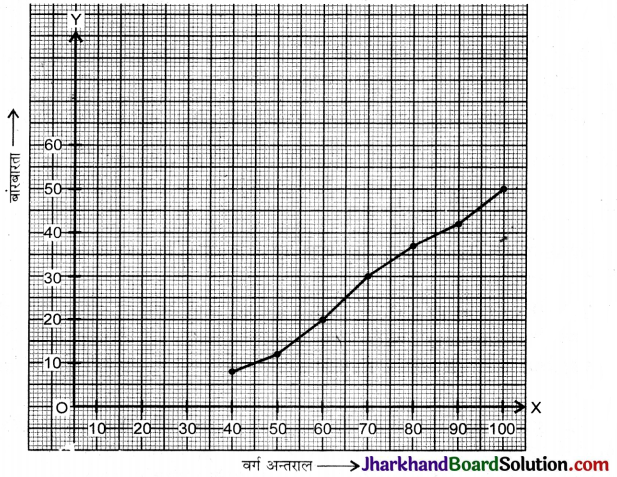
अब तोरण बिन्दुओं को ग्राफ पर अंकित करके मुक्त-हस्त से वक्र खींचते हैं। जैसे कि निम्न आकृति में दर्शाया गया है। इस प्राकर प्राप्त वक्र को “से कम प्रकार” का तोरण कहते हैं।

वस्तुनिष्ठ प्रश्न :

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क).

1. ऐसे आँकड़े जिनका व्यवस्थितिकरण वर्गों के रूप में होता है, ……………… आँकड़े कहलाते हैं।
2. यदि कोई प्रेक्षण वर्ग की उच्च सीमा में आता है, तो उसे अगले ……………… में लेते हैं।
3. जिस प्रेक्षण की बारंबारता अधिकतम होती है वह उन प्रेक्षणों का ……………… कहलाता है।
4. 100 प्रेक्षणों वाले एक बंटन के ‘से कम प्रकार’ का तोरण तथा ‘से अधिक प्रकार’ का तोरण बिन्दु (58, 50) पर प्रतिच्छेद करते हैं। इस बंटन का माध्यक ……………… है।
5. माध्यक वर्ग वह वर्ग है जिसकी संचयी बारंबारता ……………… से अधिक तथा समीपतय होती है।

उत्तर:

1. वर्गीकृत,
2. अन्तराल,
3. बहुलक,
4. 58,
5. \(\frac{n}{2}\)

निम्न में सत्य / असत्य बताइए :

प्रश्न (ख).

1. अधिकतम बारंबारता वाले वर्ग को माध्यिका वर्ग कहते हैं।
2. f₀ बहुलक वर्ग से ठीक अगले वर्ग की बारंबारता होती है।
3. संचयी बारंबारता दो प्रकार की होती है-‘से कम प्रकार’ तथा ‘से अधिक प्रकार’ की।
4. सभी प्रेक्षणों के योगफल को, प्रेक्षणों की कुल संख्या से भाग देने पर माध्यक प्राप्त होता है।
5. माध्यकं = 3 × बहुलक – 2 × बहुलक

उत्तर:

1. असत्य,
2. असत्य,
3. सत्य,
4. असत्य,
5. असत्य

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
एक बंटन का माध्य तथा माध्यक क्रमशः 14 तथा 15 है। अतः बहुलक का मान होगा :
(A) 16
(B) 17
(C) 17
(D) 13
हल:
बहुलक 3 × माध्यक – 2 × माध्य
= 3 × 15 – 2 × 14
= 45 – 28
= 17
अत: सही विकल्प (B) है।

प्रश्न 2.
बारम्बारता बंटन के माध्य, मध्यिका तथा बहुलक के बीच निम्न सम्बन्ध है :
(A) बहुलक = 3 माध्य – 2 माध्यिका
(B) बहुलक = 3 मध्यिका – 2 माध्य
(C) बहुलक = 2 माध्यिका – 3 माध्य
(D) बहुलक = माध्यिका + 2 माध्य।
हल:
बारम्बारता बंटन के लिए माध्य, माध्यिका और बहुलक के बीच निम्नलिखित सम्बन्ध होता है-
बहुलक = 3 मध्यका – 2 माध्य
अत: सही विकल्प (B) है।

प्रश्न 3.
यदि x_i वर्गीकृत आँकड़ों के वर्गअन्तरालों के मध्य बिन्दु हैं, f_i इनकी संगत बारम्बारताएँ हैं तथा माध्य \(\bar{x}\) है, तो Σ(f_ix_i – \(\bar{x}\)) बराबर है :
(A) 0
(B) -1
(C) 1
(D) 2
हल:
सही विकल्प (A) है।

प्रश्न 4.
वर्गीकृत आँकड़ों की ‘से कम प्रकार’ और ‘से अधिक प्रकार’ की संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के भुज से आँकड़ों का प्राप्त होना है :
(A) माध्य
(B) माध्यक
(C) बहुलक
(D) उपरोक्त सभी
हल:
सही विकल्प (B) है।

प्रश्न 5.
संचयी बारम्बारता सारणी का उपयोग होता है, ज्ञात करने में :
(A) माध्य
(B) बहुलक
(C) माध्यक
(D) सभी में।
हल:
संचयी बारम्बारता सारणी माध्यक ज्ञात करने के लिए सहायक होती है। अतः सही विकल्प (C) है।

प्रश्न 6.
दिए गए सूत्र \(\bar{X}\) = a + h\(\bar{x}\) में, u_i का मान होगा :
(A) h(x_i – a)
(B) \(\frac{x_i-a}{h}\)
(C) \(\frac{a-x_i}{h}\)
(D) \(\frac{x_i+a}{h}\)
हल:
u_i = \(\frac{x_i-a}{h}\) होता है।
अत: सही विकल्प (B) होगा।

प्रश्न 7.
निम्न बंटन पर विचार कीजिए-

माध्यक वर्ग और बहुलक वर्ग की निम्न सीमाओं का योग है :
(A) 15
(B) 25
(C) 30
(D) 35
हल:
दिए गए आँकड़ों में अधिकतम बारम्बारता 20 है। इसके संगत वर्ग अन्तराल 15 – 20 है । अत: बहुलक वर्ग = 15 – 20 होगा।
माध्यक के लिए,

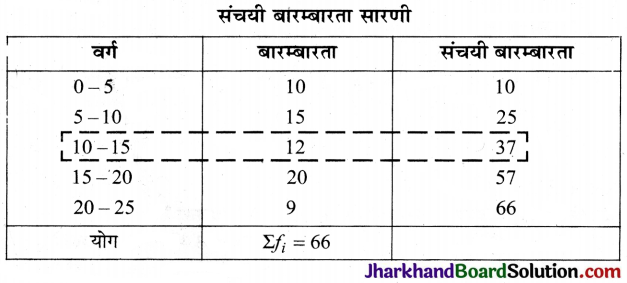
यहाँ N = 66 ⇒ \(\frac{N}{2}=\frac{66}{2}\) = 33
33 से ठीक बड़ी संचयी बारम्बारता 37 के संगत वर्ग अन्तराल 10 – 55 है।
अतः माध्यक वर्ग = 10 – 15
अतः माध्यक वर्ग और बहुलक वर्ग की निम्न सीमाओं का योग 10 + 15 = 25
अत: सही विकल्प (B) है।

प्रश्न 8.
निम्नलिखित बारम्बारता बंटन में 25 वर्ष से कम आयु के विद्यार्थियों की संख्या है :

(A) 8
(B) 6
(C) 17
(D) 25
हल:

आयु (वर्षो में)	विद्यार्थियों की संख्या
10 से कम	3
15 से कम	9
20 से कम	17
25 से कम	25
30 से कम	27

अतः उपर्युक्त सारणी में 25 वर्ष से कम आयु के विद्यार्थियों की संख्या 25 होगी।
अत: सही विकल्प (D) है।

प्रश्न 9.
बंटन :

प्राप्तांक	विद्यार्थियों की संख्या
0 से अधिक या उसके बराबर	63
10 से अधिक या उसके बराबर	58
20 से अधिक या उसके बराबर	55
30 से अधिक या उसके बराबर	51
40 से अधिक या उसके बराबर	48
50 से अधिक या उसके बराबर	42

के लिए वर्ग 30 – 40 की बारम्बारता है :
(A) 3
(B) 4
(C) 48
(D) 51
हल:
दी गयी संचयी बारम्बारता सारणी को सामान्य बारम्बारता सारणी में परिवर्तित करेंगे।

प्राप्तांक	विद्यार्थियों की संख्या
0 – 10	63 – 58 = 5
10 – 20	58 – 55 = 3
20 – 30	55 – 51 = 4
30 – 40	51 – 48 = 3
40 – 50	48 – 42 = 6

अतः वर्ग 30 – 40 की बारम्बारता 3 है।
अत: सही विकल्प (A) है।

प्रश्न 10.
यदि 5, 7, 9, x का समान्तर माध्य 9 हो, तो x का मान है :
(A) 11
(B) 15
(C) 18
(D) 16
हल:

⇒ 9 × 4 = 21 + x
⇒ 36 = 21 + x
∴ x = 36 – 21 = 15
अत: सही विकल्प (B) है।

प्रश्न 11.
बंटन :

के लिए, माध्यक वर्ग की उपरि सीमा और बहुलक वर्ग की निम्न सीमा का अन्तर है :
(A) 0
(B) 19
(C) 20
(D) 38
हल:
दिए आँकड़ों में अधिकतम बारम्बारता 20 है। इसके संगत वर्ग अन्तराल 125 – 145 है। अत: बहुलक वर्ग = 125 – 145 होगा।
माध्यक के लिए संचयी बारम्बारता सारणी

वर्ग	बारम्बारता (fi)	संचयी बारम्बारता (cf)
65 – 85	4	4
85 – 105	5	9
105 – 125	13	22
125 – 145	20	42
145 – 165	14	56
165 – 185	7	63
185 – 205	4	67
योग	Σfi = 67

यहाँ N = 67 ⇒ \(\frac{N}{2}=\frac{67}{2}\) = 33.5
33.5 से ठीक बड़ी संचयी बारम्बारता 42 के संगत वर्ग अन्तराल 125 – 145 है। अतः माध्यक वर्ग = 125 – 145.
∴ माध्यक वर्ग की उपरि सीमा और बहुलक वर्ग की निम्न सीमा का अन्तर 145 – 125 = 20
अतः सही विकल्प (C) है।

प्रश्न 12.
चार छात्रों के सांख्यिकी में प्राप्तांक 53, 75, 42, 70 हैं। उनके प्राप्तांकों का समान्तर माध्य है :
(A) 42
(B) 64
(C) 60
(D) 56
हल:

= \(\frac{240}{4}\)
= 60
अतः सही विकल्प (C) है।

प्रश्न 13.
बंटन 3, 5, 7, 4, 2, 1, 4, 3, 4 का बहुलक है :
(A) 7
(B) 4
(C) 3
(D) 1
हल:
ऊपर दी गई सारणी को देखने से स्पष्ट होता है कि 4 की बारम्बारता सबसे अधिक (3 बार है)। अतः इसका बहुलक 4 होगा।
अत: सही विकल्प (B) है।

प्रश्न 14.
किसी स्कूल के छात्रों की संख्या उनकी आयु के अनुसार निम्न प्रकार है :

इसका बहुलक है :
(A) 41
(B) 12
(C) 3
(D) 17
हल:
ऊपर की सारणी से स्पष्ट होता है कि बारम्बारता 41 सबसे अधिक है तथा इसका संगत आयु वर्ग 12 है। अतः इसका बहुलक 12 होगा।
अत: सही विकल्प (B) है।

प्रश्न 15.
बंटन 2, 3, 4, 7, 5, 1 का माध्यक होगा :
(A) 4
(B) 7
(C) 11
(D) 3.5
हल:
पदों को आरोही क्रम में रखने पर 1, 2, 3, 4, 5, 7
यहाँ पदों की संख्या N = 6 जो कि सम है, अतः


अत: सही विकल्प (D) है।

प्रश्न 16.
बंटन 1, 3, 2, 5, 9 का माध्यक होगा :
(A) 3
(B) 4
(C) 2
(D) 20
हल:
पदों को आरोही क्रम में रखने पर, 1, 2, 3, 5, 9
यहाँ पदों की संख्या (N) = 5 है जो कि विषम है।
माध्यक = \(\frac{1}{2}\) वें पद का मान = \(\frac{1}{2}\) वें पद का मान
= \(\frac{1}{2}\) वें पद का मान
= 3 वें पद का मान = 3
अत: सही विकल्प (A) है।