JAC Class 10 Maths Important Questions Chapter 15 प्रायिकता

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 15 प्रायिकता Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 15 प्रायिकता

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्रायिकताओं का योग लिखिए।
हल:
किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्रायिकताओं का योग 1 होता है।

प्रश्न 2.
एक थैले में 3 लाल और 5 काली गेंदें हैं। इस थैले में से एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता क्या है कि गेंद काली नहीं है ?
हल:
थैले में गेंदों की कुल संख्या = 3 लाल + 5 काली = 8
∴ कुल सम्भव परिणाम = 8
काली गेंद न होने की घटना के अनुकूल परिणामों की संख्या = 3
∴ गेंद काली न होने की प्रायिकता = \(\frac{3}{8}\)

प्रश्न 3.
दो पासों को एक साथ फेंका जाता है। इसकी प्रायिकता क्या है कि दोनों पासों पर आने वाली संख्याओं का योग 7 है।
हल:
जब दो पासों को एक साथ फेंका जाता है तब सम्भावित परिणामों की संख्या = 6 × 6 = 36
दोनों पासों पर आने वाली ऐसी संख्याएँ जिनका योग 7 है :
(1, 6), (2, 5), (3, 4), (4, 3), (5, 2) और (6, 1)
∴ अनुकूल परिणामों की संख्या = 6
दोनों पासों पर आने वाली संख्याओं का योग 7 की प्रायिकता = \(\frac{6}{36}=\frac{1}{6}\)

प्रश्न 4.
52 पत्तों की अच्छी प्रकार से फेंटी गई ताश की एक गड्डी में से यादृच्छया एक पत्ता निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाला गया पत्ता-
(i) लाल रंग का बादशाह है।
(ii) एक बेगम अथवा गुलाम है।
हल:
ताश की गड्डी में 52 पत्ते होते हैं तथा एक पत्ता 52 तरीकों से निकाला जा सकता है।
∴ कुल सम्भावित परिणामों की संख्या = 52
(i) माना कि लाल रंग का बादशाह होने की घटनां R है।
अतः घटना (R) के अनुकूल परिणामों की संख्या = 2
P(R) = \(\frac{2}{52}=\frac{1}{26}\)

(ii) माना कि एक गुलाम अथवा बेगम होने की घटना A है।
∴ घटना (A) के अनुकूल परिणामों की संख्या = 8
∴ P(A) = \(\frac{8}{52}=\frac{2}{13}\)
अत: (I) P(R) = \(\frac{1}{26}\), (ii) P(A) = \(\frac{2}{13}\)

प्रश्न 5.
52 पत्तों की ताश की एक गड्डी में से सभी बादशाह, बेगम तथा इक्के निकाल दिए गए। शेष बचे पत्तों को भली प्रकार फेंटने के पश्चात् उनमें से एक पत्ता निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाला पत्ता-
(i) एक काले रंग का तस्वीर वाला पत्ता है।
(ii) एक लाल रंग का पत्ता है।
हल:
ताश की गड्डी में कुल पत्तों की संख्या = 52
बादशाह, बेगम तथा इक्के के पत्तों की संख्या = 12
बादशाह, बेगम तथा इक्के के पत्तों को निकालने के बाद शेष बचे पत्तों की संख्या 52 – 12 = 40
∴ कुल सम्भव परिणामों की संख्या = 40
(i) माना कि निकाले गए पत्ते की काले रंग के तस्वीर वाले पत्ते होने की घटना ‘A’ है।
40 पत्तों में काले रंग के तस्वीर वाले पत्तों की संख्या = 2
∴ घटना (A) के अनुकूल परिणामों की संख्या = 2
⇒ P(A) = \(\frac{2}{40}=\frac{1}{20}\)

(ii) माना कि निकाले गए पत्ते की लाल रंग का होने की घटना ‘B’ है।
लाल रंग के पत्तों की संख्या = 20
∴ घटना (B) के अनुकूल परिणामों की संख्या = 20
⇒ P(B) = \(\frac{20}{40}=\frac{1}{2}\)
अत: (i) P(A) = \(\frac{1}{20}\)
(ii) P(B) = \(\frac{1}{2}\)

प्रश्न 6.
एक पेटी में 30 डिस्क हैं, जिन पर 1 से 30 तक संख्याएँ अंकित हैं। यदि इस पेटी में से एक डिस्क यादृच्छया निकाली जाती है तो इसकी प्रायिकता ज्ञात कीजिए कि इस डिस्क पर अंकित होगी-
(i) दो अंकों की एक संख्या
(ii) एक पूर्ण वर्ग संख्या
हल:
दिया है : पेटी में कुल डिस्क = 30
(i) 30 डिस्क में से दो अंकों की संख्याएँ हो सकती हैं-
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
दो अंकों की डिस्क के अनुकूल परिणाम = 21 डिस्क संभावित परिणाम = 30
अतः यादृच्छया दो अंकों की एक संख्या होने की प्रायिकता

(ii) एक पूर्ण वर्ग संख्या = 4, 9, 16, 25
अनुकूल परिणाम = 4
संभावित परिणाम = 30
अतः यादृच्छया एक पूर्ण वर्ग संख्या होने की प्रायिकता = \(\frac{4}{30}=\frac{2}{15}\)

प्रश्न 7.
अच्छी तरह से फेंटी गई एक ताश की गड्डी से एक पत्ता यादृच्छया निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाला गया पत्ता-
(i) हुकुम का पत्ता है या एक इक्का है
(ii) एक काले रंग का बादशाह है
(iii) न तो गुलाम है तथा न ही बादशाह है
(iv) या तो बादशाह हैं या बेगम है
हल:
कुल पत्तों की संख्या = 52
(i) हुकुम और इक्का के पत्तों की संख्या 13 + 3 = 16
हुकुम और इक्का के निकलने की प्रायिकता = \(\frac{16}{52}=\frac{4}{13}\)
(ii) गड्डी में काले रंग का बादशाह = 2
काले रंग के बादशाह की प्रायिकता = \(\frac{2}{52}=\frac{1}{26}\)
(iii) गुलाम और बादशाह के पत्तों की संख्या = 4 + 4 = 8
एक गड्डी में न तो गुलाम है तथा न ही बादशाह के पत्तों की संख्या = 52 – 8 = 44
न गुलाम न बादशाह होने की प्रायिकता = \(\frac{44}{52}=\frac{11}{13}\)
(iv) एक गड्डी में बादशाह और बेगम के पत्तों की संख्या = 4 + 4 = 8
या तो बादशाह या बेगम होने की प्रायिकता = \(\frac{8}{52}=\frac{2}{13}\)

प्रश्न 8.
दो भिन्न पासों को एक साथ उछाला गया दोनों पासों के ऊपरी तलों पर आई संख्याओं का गुणनफल 6 आने की प्रायिकता ज्ञात कीजिए।
हल:
जब दोनों पासों को एक साथ फेंका जाता है तो संभावित परिणामों की संख्या 6 × 6 = 36
दोनों पासों पर संख्याओं का गुणनफल 6 प्राप्त होने की अनुकूल स्थितियाँ = (1, 6), (6, 1), (2, 3), (3, 2)
दोनों पासों का गुणनफल 6 होने के अनुकूल परिणामों की संख्या = 4
अभीष्ट परिणाम = \(\frac{4}{36}=\frac{1}{9}\)

प्रश्न 9.
एक जार में केवल लाल, नीली तथा नारंगी रंग की गेंदें हैं। यादृच्छया एक लाल रंग की गेंद के निकालने की प्रायिकता \(\frac{1}{4}\) है। इसी प्रकार उसी जार से यादृच्छया एक नीली गेंद निकालने की प्रायिकता \(\frac{1}{3}\) है। यदि नारंगी की कुल गेंदें 10 हैं, तो बताइए कि जार में कुल कितनी गेंदें हैं।
हल:
माना लाल, नीली तथा नारंगी गेंद निकालने की प्रायिकता क्रमश: E₁, E₂, E₃ है।
हम जानते हैं,
P(E₁) = \(\frac{1}{4}\)
P(E₂) = \(\frac{1}{3}\)
P(E₃) = 1 – PE₂ – PE₁
P(E₃) = \(1-\frac{1}{3}-\frac{1}{4}\)
P(E₃) = \(\frac{5}{12}\)
हमयह भी जानते हैं कि

कुल गेदों की संख्या = \(\frac{120}{5}\) = 24
अतः जार में गेंदों की कुल संख्या = 24 है।

प्रश्न 10.
एक जार में केवल नीले, काले तथा हरे कंचे हैं। इस जार में से यादृच्छया एक नीले कंचे के निकालने की प्रायिकता \(\frac{1}{5}\) है तथा उसी जार में से एक काले कंधे के यादृच्छयता निकालने की प्रायिकता \(\frac{1}{4}\) है। यदि जार में 11 हरे रंग के कंचे हैं, तो जार में कुल कंचों की संख्या ज्ञात कीजिए।
हल:
दिया है,
जार से नीले कंचे निकालने की प्रायिकता P(x) = \(\frac{1}{5}\)
जार से काले कंचे निकालने की प्रायिकता P(y) = \(\frac{1}{4}\)
जार में हरे कंचों की कुल संख्या = 11
माना, जार से हरे कंचे निकालने की प्रायिकता P(z) है।
अतः P(x) + P(y) + P(z) = 1

प्रश्न 11.
एक पिग्गी बैंक में, ₹ 1 के सौ सिक्के, ₹ 2 के 25 सिक्के, फू 5 के 15 सिक्के और ₹ 10 के दस सिक्के हैं। यदि पिग्गी बैंक को हिलाकर उल्टा करने पर कोई एक सिक्का गिरने के परिणाम समप्रायिक हैं, तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का :
(i) ₹ 2 का होगा ?
(ii) ₹ 5 का होगा ?
हल:
कुल सम्भव परिणामों की संख्या = 100 + 25 + 15 + 10 = 150
(i) अनुकूल परिणामों की संख्या = 25
∴ ₹ 2 का सिक्का गिरने की प्रायिकता = \(\frac{25}{150}=\frac{1}{6}\)
(ii) अनुकूल परिणामों की संख्या = 15
∴ ₹ 5 का सिक्का गिरने की प्रायिकता = \(\frac{15}{150}=\frac{1}{10}\)

प्रश्न 12.
एक डिब्बे में 7 लाल कंचे, 10 सफेद कंचे और 5 हरे कंचे हैं। इस डिब्बे में से एक कंचा यादृच्छया निकाला जाता है। इसकी प्रायिकता क्या है कि निकाला गया कंचा (i) लाल नहीं है? (ii) सफेद है ? (iii) हरा है?
हल:
कुल सम्भव परिणामों की संख्या = 7 + 10 + 5 = 22
(i) अनुकूल परिणामों की संख्या = 7
लाल कंचे के निकलने की प्रायिकता = \(\frac{7}{22}\)
∴ लाल कंचे के न निकलने की प्रायिकता = \(1-\frac{7}{22}\)
= \(\frac{22-7}{22}=\frac{15}{22}\)
(ii) अनुकूल परिणामों की संख्या = 10
सफेद कंचे के निकलने की प्रायिकता = \(\frac{10}{22}=\frac{5}{11}\)
(iii) अनुकूल परिणामों की संख्या = 5
हरे कंचे के निकलने की प्रायिकता = \(\frac{5}{22}\)

प्रश्न 13.
दो विभिन्न पासों को एक साथ उछाला गया। निम्न के आने की प्रायिकता ज्ञात कीजिए :
(i) एक द्विक आना।
(ii) दोनों पासों पर आई संख्याओं का योग 10 आना।
हल:
दो पासों को एक साथ उछालने पर आने वाले कुल परिणाम = 36
(i) एक द्विक आने के संभावित परिणाम = [(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)]
कुल सम्भावित परिणामों की संख्या = 6
P (एक द्विक आना) = संभावित परिणाम / कुल परिणाम
= \(\frac{6}{36}=\frac{1}{6}\)
(ii) संख्याओं का योग 10 आने के संभावित परिणाम = [(4, 6), (5, 5) (6, 4)]
कुल संभावित परिणामों की संख्या = 5
P (योग 10) = संभावित परिणाम / कुल परिणाम
= \(\frac{6}{36}=\frac{1}{12}\)

प्रश्न 14.
1 से 100 के बीच की संख्याओं में से यादृच्छया एक संख्या चुनी गई। प्रायिकता ज्ञात कीजिए कि यह संख्या
(i) 8 से भाज्य है।
(ii) 8 से भाज्य नहीं है।
हल:
1 और 100 के बीच आने वाली कुल संख्या = 98
(i) 8 से भाज्य संख्या
= {(8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96}
कुल संभावित परिणामों की संख्या = 12
P(8 से भाज्य संख्या) = संभावित परिणाम / कुल परिणाम
= \(\frac{12}{98}=\frac{6}{49}\)

(ii) P(8 से अभाज्य संख्या)
\(P \bar{E}\) = 1 – P(E)
= 1 – \(\frac{6}{49}\) = \(\frac{43}{49}\)

प्रश्न 15.
एक थेले में 5 लाल गेंदे तथा कुछ नीली गेंदे हैं। यदि थैले में से यादृच्छया एक नीली गेंद निकालने की प्रायिकता, एक लाल गेंद के निकलने की प्रायिकता की तीन गुना है, तो थैले में नीली गेंदों की संख्या ज्ञात ‘कीजिए।
हल:
थैले में लाल गेंदों की संख्या = 5
माना थैले में नीली गेंदों की संख्या x है।
∴ थैले में से एक लाल गेंद निकालने की प्रायिकता = \(\frac{5}{x+5}\)
तथा थैले में से एक नीली गेंद निकालने की प्रायिकता = \(\frac{x}{x+5}\)
प्रश्नानुसार, \(\frac{x}{x+5}=3 \times \frac{5}{x+5}\)
⇒ \(\frac{x}{x+5}=\frac{15}{x+5}\)
⇒ x = 15
अतः थैले में नीली गेंदों की संख्या = 15

प्रश्न 16.
किसी यादृच्छया लिए गए वर्ष के नवम्बर मास में 5 रविवार होने की प्रायिकता ज्ञात कीजिए।
हल:
यादृच्छया लिए गए वर्ष के नवम्बर मास में 4 पूर्ण सप्ताह तथा 2 अन्य दिन होते हैं।
ये दो अन्य दिन निम्न में से कोई भी हो सकते हैं:
(सोम, मंगल), (मंगल, बुध), (बुध, गुरु), (गुरु, शुक्र), (शुक्ल, शनि), (शनि, रवि), (रवि, सोम)
पाँच रविवार होने के लिए अनुकूल परिणाम (शनि, रवि) तथा (रवि सोम)
अत: वांछित प्रायिकता = \(\frac{2}{7}\) ₹

प्रश्न 17.
तीन बच्चों वाले एक परिवारों में, कम-से-कम दो लड़के होने की प्रायिकता ज्ञात कीजिए।
हल:
तीन बच्चों वाले परिवारों में बच्चों के होने के परिणाम निम्नलिखित हैं :
{BBB, BBG, BGB, GBB, GGB, GBG, BGG, GGG}
कुल सम्भव परिणामों की संख्या = 8
कम-से-कम दो लड़के होने के अनुकूल परिणाम = {BBB, BBG BGB, GBB}
अनुकूल परिणामों की संख्या = 4
∴ कम से कम दो लड़के होने की प्रायिकता = \(\frac{4}{8}=\frac{1}{2}\)

वस्तुनिष्ठ प्रश्न :

(क) रिक्त स्थानों की पूर्ति कीजिए :
1. यदि P(E’) ‘नहीं की’ प्रायिकता 0.95 है, तो P(E) की प्रायिकता …………… होगी।
2. एक सिक्के को एक बार उछाला जाता है। इसे पट नहीं आने की प्रायिकता …………… है।
3. एक निश्चित घटने वाली घटना की प्रायिकता ……………. होती है।
4. अंग्रेजी वर्णमाला में से एक अक्षर यदृच्छया चुने जाने पर उसके व्यंजक होने की प्रायिकता ……………… है।
5. यदि किसी के जीतने की प्रायिकता 0.07 है तो उसके हारने की प्रायिकता …………….. है।
उत्तर:
1. 0.05,
2. \(\frac{1}{2}\)
3. 1
4. \(\frac{21}{26}\)
5. 0.93

(ख) निम्न में सत्य / असत्य बताइए :
1. एक पासा एक बार उछाले जाने पर 3 से छोटी संख्या प्राप्त करने की प्रायिकता \(\frac{1}{3}\) है।
2. 52 पत्तों की एक गड्डी में से एक लाल रंग के बादशाह आने की प्रायिकता \(\frac{1}{26}\) है।
3. यदि कल वर्षा होने की प्रायिकता 0.85 है, तो वर्षा न होने की प्रायिकता 0.58 है।
4. दो पासों को एक साथ फेंकने पर दोनों पासों पर संख्याओं का योग 13 आने की प्रायिकता \(\frac{2}{13}\) है।
5. यदि पासों के एक युग्म को एक बार उछाला गया, तो योगफल 8 आने की प्रायिकता \(\frac{5}{36}\) है।
उत्तर:
1. सत्य,
2. सत्य,
3. असत्य,
4. असत्य,
5. सत्य

बहुविकल्पीय प्रश्न :

प्रश्न 1.
एक थैले में 3 लाल, 5 काली तथा 7 सफेद गेंदे हैं। इस थैले में से एक गेंद को यादृच्छया निकाला जाता है। निकाली गई गेंद काली नहीं है, इसकी प्रायिकता है :
(A) \(\frac{1}{3}\)
(B) \(\frac{9}{15}\)
(C) \(\frac{5}{10}\)
(D) \(\frac{2}{3}\)
हल:
कुल गेंदे, n(S) = 3 + 5 + 7 = 15
अनुकूल परिणामों की संख्या = 5
∴ एक काली गेंद निकलने की प्रायिकता

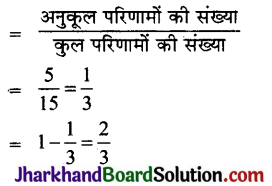
अत: सही विकल्प (D) है।

प्रश्न 2.
संख्याओं 1, 2, 3, ……. 15 से यादृच्छया 4 का एक गुणज चुने जाने की प्रायिकता है:
(A) \(\frac{4}{15}\)
(B) \(\frac{2}{15}\)
(C) \(\frac{1}{15}\)
(D) \(\frac{1}{5}\)
हल:
कुल परिणाम की संख्या = 5
अनुकूल परिणाम = {4, 8, 12}
अनुकूल परिणामों की संख्या = 3
∴ 4 का गुणज चुने जाने की प्रायिकता = \(\frac{3}{15}=\frac{1}{5}\)
सही विकल्प (D) है।

प्रश्न 3.
दो सिक्के एक साथ उछाले गए। अधिक से अधिक एक चित आने की प्रायिकता है:
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{3}{4}\)
हल:
सम्भव परिणाम = {HT, HH, TH, TT}
कुल सम्भव परिणामों की संख्या = 4
अनुकूल परिणाम = {HT, TH}
अनुकूल परिणामों की संख्या = 2
अधिक से अधिक एक चित आने की प्रायिकता = \(\frac{2}{4}=\frac{1}{2}\)
सही विकल्प (B) है।

प्रश्न 4.
अच्छी प्रकार से फेंटी गई 52 पत्तों की ताश की गड्डी में से एक पत्ता यदृच्छया निकाला गया है। एक गुलाम के आने की प्रायिकता क्या है?
(A) \(\frac{3}{26}\)
(B) \(\frac{1}{52}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{3}{52}\)
हल:
कुल सम्भव परिणामों की संख्या = 52
अनूकूल परिणामों की संख्या = 4
∴ गुलाम के आने की प्रायिकता = \(\frac{4}{52}=\frac{1}{13}\)
सही विकल्प (C) है।

प्रश्न 5.
किसी असम्भव घटना के होने की प्रायिकता है:
(A) 1
(B) \(\frac{3}{4}\)
(C) परिभाषित नहीं
(D) 0
हल:
सही विकल्प (D) हैं।

प्रश्न 6.
52 ताशों की एक गड्डी में से एक ताश निकाला जाता है। इसके लाल रंग का मुख कार्ड होने की प्रायिकता है :
(A) \(\frac{3}{26}\)
(B) \(\frac{1}{52}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{3}{52}\)
हल:
ताश की गड्डी में कार्डों की कुल संख्या = 52
∴ कुल सम्भव परिणामों की संख्या = 52
लाल रंग के मुख कार्डों की संख्या = 6
∴ घटना के अनुकूल परिणामों की संख्या = 6
ताश की गड्डी में मुख कार्ड होने की प्रायिकता = \(\frac{6}{52}=\frac{3}{26}\)
अत: सही विकल्प (A) है।

प्रश्न 7.
52 ताशों की एक गड्डी में से एक कार्ड निकाला जाता है। कार्ड का ईंट का इक्का न होना घटना E है। E के अनुकूल परिणामों की संख्या है:
(A) 4
(B) 13
(C) 48
(D) 51
हल:
गड्डी में ताशों की कुल संख्या = 52
ताश की गड्डी में से एक कार्ड निकाला जाता है।
कार्ड का ईंट का इक्का न होना घटना E है।
∴ E के अनुकूल परिणामों की संख्या = 52 – 1 = 51
अत: सही विकल्प (D) है।

प्रश्न 8.
कोई लड़की यह परिकलित करती है कि उसके द्वारा एक लाटरी में प्रथम पुरुस्कार जीतने की प्रायिकता 0.08 है। यदि 6000 टिकट बेचे गए हैं तो उस लड़की ने कितने टिकट खरीदे हैं ?
(A) 40
(B) 240
(C) 480
(D) 750
हल:
बेचे गए टिकटों की संख्या = 6000
∴ कुल सम्भव परिणामों की संख्या = 6000
माना कि लड़की द्वारा खरीदे गए टिकटों की संख्या = x
∴ घटना के अनुकूल परिणामों की संख्या = x
प्रथम पुरुस्कार जीतने की प्रायिकता

⇒ x = 0.08 × 6000
⇒ x = 480
अत: सही विकल्प (C) है।

प्रश्न 9.
ताश की गड्डी में एक काले रंग के गुलाम न होने की प्रायिकता होगी :
(A) \(\frac{1}{26}\)
(B) \(\frac{3}{4}\)
(C) \(\frac{11}{52}\)
(D) \(\frac{25}{26}\)
हल:
ताश की गड्डी में कुल पत्तों की संख्या = 52
अतः कुल सम्भावित परिणामों की संख्या = 52
ताश की गड्डी में काले रंग के गुलाम (हुकम, चिढ़ी) होने के अनुकूल परिणामों की संख्या = 2
ताश की गड्डी में काले रंग के गुलाम होने की प्रायिकता = \(\frac{2}{52}=\frac{1}{26}\)
ताश की गड्डी में काले रंग के गुलाम न होने की प्रायिकता = \(1-\frac{1}{26}=\frac{25}{26}\)
अत: सही विकल्प (D) है।

प्रश्न 10.
एक थैले में कार्ड हैं जिन पर 2, 3, 4, …, 11 संख्याएँ अंकित हैं। थैले में से यादृच्छया एक कार्ड निकाला गया है। निकाले गए कार्ड पर एक अभाज्य संख्या होने की प्रायिकता है:
(A) \(\frac{1}{2}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{3}{10}\)
(D) \(\frac{5}{9}\)
हल: थैले में कार्डों पर अंकित संख्याएँ हैं :
2, 3, 4, ………., 11
थैले में कार्डों की संख्या = 10
कार्डों पर अंकित अभाज्य संख्याएँ हैं :
2, 3, 5, 7, 11
कार्ड पर एक अभाज्य संख्या होने के अनुकूल परिणामों की संख्या = 5
∴ कार्ड पर एक अभाज्य संख्या होने की प्रायिकता = \(\frac{5}{10}=\frac{1}{2}\)
अतः सही विकल्प (A) है।

प्रश्न 11.
एक बक्से में कार्ड हैं जिन पर 6 से 50 तक की संख्याएँ अंकित हैं। बक्से में से यादृच्छया एक कार्ड निकाला गया। इस कार्ड पर अंकित संख्या के एक पूर्ण वर्ग होने की प्रायिकता है:
(A) \(\frac{1}{45}\)
(B) \(\frac{2}{15}\)
(C) \(\frac{1}{9}\)
(D) \(\frac{4}{45}\)
हल:
बक्से में कार्डों पर 6 से 50 तक की संख्याएँ अंकित हैं।
कुल सम्भव परिणामों की संख्या = 45
कार्डों पर अंकित पूर्ण वर्ग संख्याएँ हैं:
9, 16, 25, 36, 49
कार्ड पर पूर्ण वर्ग संख्या होने के अनुकूल परिणामों की संख्या = 5
कार्ड पर पूर्ण वर्ग संख्या होने की प्रायिकता = \(\frac{5}{45}=\frac{1}{9}\)
अतः सही विकल्प (C) है।

प्रश्न 12.
एक पासे को एक बार फेंका जाता है। एक विषम संख्या के आने की प्रायिकता है :
(A) 1
(B) \(\frac{1}{9}\)
(C) \(\frac{4}{6}\)
(D) \(\frac{2}{6}\)
हल:
एक पासे को एक बार फेंका जाता है तो पासे के पृष्ठों पर आने वाली संख्याएँ हैं :
{1, 2, 3, 4, 5, 6}
∴ सम्भव परिणामों की संख्या = 6
तथा अभाज्य संख्याएँ हैं : {1, 3, 5}
अभाज्य संख्या आने के अनुकूल परिणामों की संख्या = 3
अभाज्य संख्या आने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)
अतः सही विकल्प (B) है।

प्रश्न 13.
किसी स्कूल में पाँच सदन A, B, C, D और E हैं। किसी कक्षा में 23 विद्यार्थी हैं, जिनमें से 4 सदन A से, 8 सदन B से, 5 सदन C से 2 सदन D से तथा शेष सदन E से हैं। इनमें से एक विद्यार्थी को कक्षा का मॉनीटर बनाने के लिए चुना जाता है। चुने गए इस विद्यार्थी के सदनों A, B और C से न होने की प्रायिकता है :
(A) \(\frac{4}{23}\)
(B) \(\frac{6}{23}\)
(C) \(\frac{8}{23}\)
(D) \(\frac{17}{23}\)
हल:
कक्षा में विद्यार्थियों की कुल संख्या = 23
सदन A, B तथा C में विद्यार्थियों की संख्या का योग = 4 + 8 + 5 = 17
कुल सम्भव परिणामों की संख्या = 23
घटना के अनुकूल परिणामों की संख्या = 17
विद्यार्थी के सदनों A, B और C से होने की प्रायिकता = \(\frac{17}{23}\)
विद्यार्थी के सदनों A, B और C से न होने की प्रायिकता = \(1-\frac{17}{23}=\frac{6}{23}\)
अतः सही विकल्प (B) है।

प्रश्न 14.
यदि दो पासों को एक साथ फेंका जाता है तो दोनों पाँसों पर एक ही संख्या प्राप्त होने की प्रायिकता होगी :
(A) \(\frac{1}{6}\)
(B) \(\frac{5}{6}\)
(C) \(\frac{1}{36}\)
(D) इनमें से कोई नहीं
हल:
जब दोनों पासों को एक साथ फेंका जाता है तो सम्भावित परिणामों की संख्या = 6 × 6= 36
दोनों पाँसों पर एक जैसी संख्या प्राप्त होने की अनुकूल स्थितियाँ
(1, 1); (2, 2); (3, 3); (4, 4); (5, 5); (6, 6)
दोनों पासों पर एक जैसी संख्या प्राप्त होने के अनुकूल परिणामों की संख्या = 6
अभीष्ट प्रायिकता = \(\frac{6}{36}=\frac{1}{6}\)
अंत: सही विकल्प (A) है।

प्रश्न 15.
इसकी प्रायिकता कि यादृच्छिक रूप से चुने गए एक ऐसे वर्ष में, जो अधिवर्ष (leap year) न हो 53 रविवार हों, निम्नलिखित हैं :
(A) \(\frac{1}{7}\)
(B) \(\frac{2}{7}\)
(C) \(\frac{3}{7}\)
(D) \(\frac{5}{7}\)
हल:
एक साधारण वर्ष (Non leap year) में 365 दिन होते हैं।
365 दिन में 52 सप्ताह व 1 दिन होते हैं।
अर्थात् 365 दिन में 52 सप्ताह में 52 रविवार होंगे जो 1 दिन बचा है। वह निम्न में से एक हो सकता है।
रविवार, सोमवार, मंगलवार, बुधवार, गुरूवार, शुक्रवार, शनिवार
∴कुल सम्भव परिणामों की संख्या = 7
रविवार आने की घटना के अनुकूल परिणामों की संख्या = 1
रविवार होने की प्रायिकता = \(\frac{1}{7}\)
अत: सही विकल्प (A) है।