JAC Class 9 Maths Important Questions Chapter 1 संख्या पद्धति

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 1 संख्या पद्धति Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 1 संख्या पद्धति

वस्तुनिष्ठ प्रश्न :

प्रश्न 1.
\(2^{\frac{2}{3}} \cdot 2^{\frac{1}{2}}\) का मान होगा :
(A) 26
(B) 4
(C) 6
(D) – 2
हल :

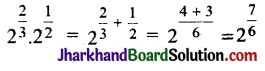
अतः सही विकल्प ‘A’ है।

प्रश्न 2.
(\(\sqrt{m}\) – \(\sqrt{m}\))(\(\sqrt{11}\) + \(\sqrt{7}\)) का मान होगा :
(A) 172
(B) 18
(C) 4
(D) 77
हल:
(\(\sqrt{m}\) – \(\sqrt{m}\))(\(\sqrt{11}\) + \(\sqrt{7}\))
= (\(\sqrt{11}\))² – (\(\sqrt{7}\))²
= 11 – 7 = 4
अतः सही विकल्प ‘C’ है।

प्रश्न 3.
अपरिमेय संख्या होगी :
(A) \(\frac {2}{4}\)
(B) \(\sqrt{3}\)
(C) \(\sqrt{9}\)
(D) \(\frac {3}{4}\)
हल :
अपरिमेय संख्या \(\sqrt{3}\) है।
अतः सही विकल्प ‘B’ है।

प्रश्न 4.
अनवसानी आवर्ती संख्या होगी :
(A) \(\frac {1}{3}\)
(B) \(\frac {1}{2}\)
(C) \(\frac {7}{8}\)
(D) \(\frac {3}{2}\)
हल :
अनवसानी आवर्ती में अंश में हर का भाग देने पर शेषफल आता है अर्थात् शेषफल 0 (शून्य) नहीं आता है तथा भागफल की पुनरावृत्ति होती रहती है। \(\frac {1}{3}\) = 0.333…
अत: सही विकल्प ‘A’ है।

प्रश्न 5.
समस्त परिमेय और अपरिमेय संख्याओं का संग्रह कहलाता है:
(A) पूर्णांक संख्याएँ
(B) वास्तविक संख्याएँ
(C) प्राकृत संख्याएँ
(D) सांत परिमेय संख्याएँ
हल :
परिमेय और अपरिमेय संख्याओं के संग्रह को वास्तविक संख्याएँ कहते हैं।
अतः सही विकल्प ‘B’ है।

प्रश्न 6.
\(\frac{1}{\sqrt{3}}\) किस प्रकार की संख्या है ?
(A) परिमेय
(B) अपरिमेय
(C) प्राकृत संख्या
(D) पूर्णांक संख्या
हल:
\(\frac{1}{\sqrt{3}}\) में अंश (1) परिमेय संख्या है और हर (\(\sqrt{3}\)) अपरिमेय संख्या है।
परिमेय संख्या / अपरिमेय संख्या = अपरिमेय संख्या
अतः सही विकल्प ‘B’ है।

प्रश्न 7.
यदि किसी संख्या के अंश में हर का भाग देने पर शेषफल शून्य प्राप्त होता है, तो वह होगा :
(A) असांत दशमलव
(B) असांत अनावर्ती
(C) सांत एवं असांत दोनों
(D) सांत दशमलव ।
हल :
जब किसी भिन्न के अंश में हर का भाग देने पर शेषफल शून्य प्राप्त होता है, वह भिन्न परिमेय सांत दशमलव भिन्न कहलाती है।
अतः सही विकल्प ‘D’ है।

प्रश्न 8.
0.333…. को \(\frac {p}{q}\) के रूप में लिखा जा सकता है:
(A) \(\frac {1}{0.3}\)
(B) \(\frac {3}{10}\)
(C) \(\frac {1}{3}\)
(D) इनमें से कोई नहीं।
हल:
0.333… = \(0 . \overline{3}\)
माना x = \(0 . 3\overline{3}\)
10x = \(3 . \overline{3}\)
9x = 3 (घटाने पर)
x = \(\frac{3}{9}=\frac{1}{3}\)
सही विकल्प ‘C’ है।

प्रश्न 9.
किसी परिमेय और अपरिमेय संख्या का अन्तर होगा :
(A) परिमेय
(B) अपरिमेय
(C) सांत दशमलव
(D) इनमें से कोई नहीं
हल :
परिमेय तथा अपरिमेय संख्याओं का अन्तर सदैव अपरिमेय होता है।
अतः विकल्प ‘B’ सही है।

प्रश्न 10.
(\(\sqrt{3}\))⁶ का मान होगा :
(A) 3\(\sqrt{3}\)
(B) 3
(C) 9
(D) 27.
हल :
(\(\sqrt{3}\))⁶ = \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\)
= 3 × 3 × 3
= 27
अत: सही विकल्प ‘D’ है।

लघु उत्तरीय प्रश्न :

प्रश्न 11.
– 2 और 5 के बीच तीन परिमेय संख्याएँ ज्ञात कीजिए।
हल :

प्रश्न 12.
निम्नलिखित संख्याओं को दशमलव संख्या में व्यक्त कीजिए तथा दशमलव प्रसार का प्रकार बताइए :
(i) \(\frac {3}{11}\)
(ii) \(\frac {1}{7}\)
(iii) \(\frac {1}{16}\)
हल :

प्रश्न 13.
\(0 . \overline{361}\) को परिमेय संख्या में बदलिए ।
हल :
माना कि x = \(0 . \overline{361}\)
x = 0.361361361 …….(1)
समी. (1) में 1000 से गुणा करने पर,
1000x = 361.361361 …….(2)
समी (2) में से समी (1) घटाने पर
999x = 361
∴ x = \(\frac {361}{999}\)
⇒ अतः \(0 . \overline{361}\) = \(\frac {361}{999}\)

प्रश्न 14.
निम्नलिखित को सरल कीजिए:
(i) x² × x^-2 × x^-3
(ii) 2x³ ÷ 2x^-3
(iii) \(\frac{x}{\sqrt{5}+1}\) = \(\frac{\sqrt{5}-1}{x}\)
(iv) (2\(\sqrt{5}\) + 1) + (1 – 2\(\sqrt{5}\)) – 2.
हल :
(i) x² × x^-2 × x^-3 = x^2-2-3
= x^2-5
= x^-3 = \(\frac{1}{x^3}\)

(ii) 2x³ ÷ 2x^-3 = \(\frac {2}{2}\) x^3-(-3)
= x³⁺³ = x⁶

(iii) \(\frac{x}{\sqrt{5}+1}\) = \(\frac{\sqrt{5}-1}{x}\)
x × x = (\(\sqrt{5}\) – 1)(\(\sqrt{5}\) + 1)
x² = (\(\sqrt{5}\))² – (1)² = 5 – 1
x² = 4
x = ±2.

(iv) (2\(\sqrt{5}\) + 1)+(1 – 2\(\sqrt{5}\)) – 2
= (2\(\sqrt{5}\) – 2\(\sqrt{5}\)) + (1 + 1) – 2
= 0 + 2 – 2 = 0

प्रश्न 15.
वास्तविक संख्या रेखा पर \(\sqrt{3}\) का स्थान निर्धारित कीजिए।
हल :
सबसे पहले XY रेखा खींची। रेखा पर बिन्दु O पर 0 (शून्य) से इकाई लम्बाई (1 इकाई) पर बिन्दु 4 लिया। बिन्दु 4 पर लम्ब AB = 1 इकाई खींचा। O और B को मिलाया है।

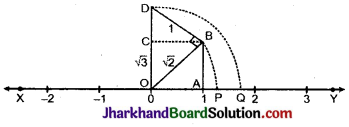
अब OB के B बिन्दु पर एकांक लम्बाई का लम्ब BD खींचा तथा O और D को मिलाया। OD = \(\sqrt{(\sqrt{2})^2+(1)^2}\) = \(\sqrt{3}\) प्राप्त होता है। O को केन्द्र मानकर OD त्रिज्या का चाप खींचा, जो संख्या रेखा को बिन्दु पर काटता है। अत: बिन्दु Q अपरिमेय संख्या \(\sqrt{3}\) को निरूपित करता है।

प्रश्न 16.
सिद्ध कीजिए कि \(\sqrt{3}\) अपरिमेय संख्या है।
हल :
भाग विधि से वर्गमूल :

∴ \(\sqrt{3}\) = 1.732050807…………
अतः असांत अनावर्ती अपरिमेय संख्या है। इति सिद्धम्

प्रश्न 17.
\(\frac{\sqrt{3}-1}{\sqrt{3}+1}\) = a + b\(\sqrt{3}\)
तब a तथा b के मान ज्ञात कीजिए।
हल :
दी हुई संख्या में (\(\sqrt{3}\) – 1) का अंश और हर में गुणा करने पर,

प्रश्न 18.
[(1)³ + (2)³ + (3)³]\(\frac {-5}{2}\) का मान ज्ञात कीजिए ।
हल :
[(1)³ + (2)³ + (3)³]\(\frac {-5}{2}\)
⇒ [1 + 8 + 27]\(\frac {-5}{2}\)
⇒ (36)\(\frac {-5}{2}\)
⇒ [(6)²]^-5/2
⇒ (6)^{2×\(\frac {-5}{2}\)}
⇒ \(\frac{1}{(6)^5}\)
⇒ \(\frac {1}{7776}\)

प्रश्न 19.
यदि धनात्मक संख्याएँ हैं, तो का मान ज्ञात कीजिए।
\(\sqrt{x^{-1} y} \cdot \sqrt{y^{-1} z} \cdot \sqrt{z^{-1} x}\)
हल :

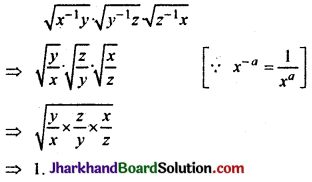
प्रश्न 20.
6\(\sqrt{5}\) को 3\(\sqrt{5}\) से गुणा कीजिए।
हल :
6\(\sqrt{5}\) × 3\(\sqrt{5}\) = 6 × 3 × \(\sqrt{5}\) × \(\sqrt{5}\)
= 18 × 5 = 90.

प्रश्न 21.
\(\frac{3}{\sqrt{8}}\) का परिमेयकरण कीजिए।
हल :
\(\sqrt{8}\) का अंश और हर में गुणा करने पर,

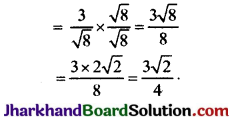
प्रश्न 22.
यदि b = \(\sqrt[5]{243}\) हो, तो b का मान ज्ञात कीजिए।
हल :
b = \(\sqrt[5]{243}\)
⇒ b = (243)^1/5
= (3 × 3 × 3 × 3 × 3)^1/5
= [(3)⁵]^1/5
= 3^5×1/5
∴ b = 3

प्रश्न 23.
\(\frac{3}{\sqrt{48}-\sqrt{75}}\) का मान क्या होगा ?
हल :

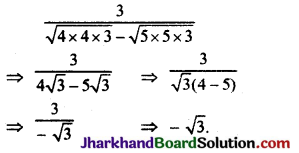
प्रश्न 24.
\(\frac{1}{3+\sqrt{2}}\) के हर का परिमेयकरण कीजिए।
हल :
अंश और हर में (3 – \(\sqrt{2}\)) का गुणा करने पर,
\(\frac{3-\sqrt{2}}{(3+\sqrt{2}) \times(3-\sqrt{2})}\) ⇒ \(\frac{3-\sqrt{2}}{(9-2)}\)
{∵ a² – b² = (a+b) (a – b)}
⇒ \(\frac{3-\sqrt{2}}{7}\)

प्रश्न 25.
यदि (x)^y = 128, तो x तथा y का मान ज्ञात कीजिए ।
हल :
(x)^y = 128 = (2)⁷
x^y = 2⁷
आधार तथा घातकी तुलना करने पर,
x = 2
y = 7.