JAC Class 9 Maths Important Questions Chapter 10 Circles

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 10 Circles Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 10 Circles

Question 1.
In figure, AB = CB and is the centre of the circle. Prove that BO bisects ∠ABC.

Solution :
Given: In figure, AB = CB and O is the centre of the circle.
To Prove : BO bisects ∠ABC.
Construction: Join OA and OC.
Proof: In ΔOAB and ΔOCB,
OA = OC [Radii of the same circle]
AB = CB [Given]
OB = ОВ (Common)
∴ ΔOAB ≅ ΔOCB [By SSS]
∴ ∠ABO = ∠CBO [By CPCT]
⇒ BO bisects ∠ABC. Hence, Proved.

Question 2.
In figure, AB = AC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC.

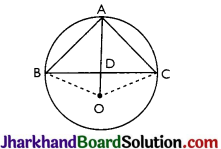
Solution :
Given: In figure, AB = AC and O is the centre of the circle.
To Prove: OA is the perpendicular bisector of BC.
Construction: Join OB and OC.
Proof: AB = AC [Given]
∴ chord AB = chord AC.
[∵ If two arcs of a circle are congruent, then their corresponding chords are equal.]
∴ ∠AOB = ∠AOC ……(i) [∵ Equal chords of a circle subtend equal angles at the centre]
In ΔOBD and ΔOCD,
∠DOB = ∠DOC [From (i)]
OB = OC [Radii of the same circle]
OD = OD (Common)
∴ ΔOBD ≅ ΔOCD [By SAS]
∠ODB = ∠ODC …(ii) (By CPCT)
And BD = CD ……..(iii) [By CPCT]
∴ ∠ODB + ∠ODC = 180° [Linear pair]
⇒ ∠ODB + ∠ODB = 180°
[From equation (ii)]
⇒ 2∠ODB = 180°
⇒ ∠ODB = 90°
∴ ∠ODB = ∠ODC=90°….(iv) [From(ii)]
So, by (iii) and (iv), OA is the perpendicular bisector of BC. Hence, proved.

Question 3.
Prove that the line joining the midpoints of the two parallel chords of a circle passes through the centre of the circle.

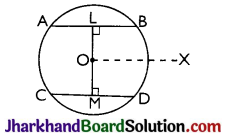
Solution :
Let AB and CD be two parallel chords of a circle whose centre is O.
Let L and M be the mid-points of the chords AB and CD respectively. Join OL and OM. Draw OX || AB or CD.
As L is the mid-point of the chord AB and O is the centre of the circle
∴ ∠OLB = 90°
But, OX || AB
∴ ∠LOX = 90° ………….(i)
[∵ Sum of the consecutive interior angles on the same side of a transversal is 180°]
As, M is the mid-point of the chord CD and O is the centre of the circle.
∴ ∠OMD = 90° [∵ The perpendicular drawn from the centre of a circle to a chord bisects the chord]
But OX || CD ………….(ii)
[∵ Sum of the consecutive interior angles on the same side of a transversal is 180°]
∴ ∠MOX = 90°
From above equations, we get
∠LOX + ∠MOX = 90° + 90° = 180°
⇒ ∠LOM = 180°
⇒ LM is a straight line passing through the centre of the circle.
Hence, proved.

Question 4.
PQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ = 16 cm and RS = 12 cm, find the distance between PQ and RS, if they lie
(i) on the same side of the centre O.
(ii) on opposite sides of the centre O.

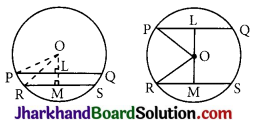
Solution :
(i) Draw the perpendicular bisectors OL and OM of PQ and RS respectively.
∵ PQ || RS
∴ OL and OM are in the same line.
⇒ O, L and M are collinear.
Join OP and OR
In right triangle OLP,
OP² = OL² + PL²
[By Pythagoras Theorem]
⇒ (10)² = OL² + (\(\frac {1}{2}\) × PQ)²
[∵ The perpendicular drawn from the centre of a circle to a chord bisects the chord]
⇒ 100 = OL² + (\(\frac {1}{2}\) × 16)²
⇒ 100 = OL² + (8)²
⇒ 100 = OL² + 64
⇒ OL² = 100 – 64 = 36 = (6)²
⇒ OL = 6 cm
In right triangle OMR,
OR² = OM² + RM²
[By Pythagoras Theorem]
⇒ OR² = OM² + (\(\frac {1}{2}\)× RS)²
[∵ The perpendicular drawn from the centre of a circle to a chord bisects the chord]
⇒ (10)² = OM² + (\(\frac {1}{2}\) × 12)²
⇒ (10)² = OM² + (6)²
⇒ OM² = (10)² – (6)² = 100 – 36 = 64
⇒ OM = 8 cm
∴ LM = OM – OL = 8 – 6 = 2 cm
Hence, the distance between PO and RS, if they lie on the same side of the centre O, is 2 cm.

(ii) Draw the perpendicular bisectors OL and OM to PQ and RS respectively,
∵ PQ || RS
∴ OL and OM are in the same line
⇒ L, O and M are collinear. Join OP and OR.
In right triangle OLP,
OP² = OL² + PL²
[By Pythagoras Theorem]
⇒ OP² = OL² + (\(\frac {1}{2}\) × PQ)²
[∵ The perpendicular drawn from the centre of a circle to a chord bisects the chord]
⇒ (10)² = OL² + (\(\frac {1}{2}\) × 16)²
⇒ 100 = OL² + (8)²
⇒ 100 = OL² + 64
⇒ OL² = 100 – 64
⇒ OL² = 36 = (6)²
⇒ OL = 6 cm
In right triangle OMR,
OR² = OM² + RM²
[By Pythagoras Theorem]
⇒ OR² = OM² + (\(\frac {1}{2}\) × 12)²
[∵ The perpendicular drawn from the centre of a circle to a chord bisects the chord]
⇒ (10)² = OM² + (6)²
⇒ OM² = (10)² – (6)² = (10 – 6)(10 + 6)
⇒ (4)(16) = 64 = (8)²
⇒ OM = 8 cm
∴ LM = OL + OM = 6 + 8 = 14 cm
Hence, the distance between PQ and RS, if they lie on the opposite sides of the centre O, is 14 cm.

Question 5.
Bisector AD of ∠BAC of ΔABC passed through the centre of the circumcircle of ΔABC. Prove that AB = AC.

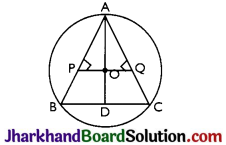
Solution :
Given: Bisector AD of ∠BAC of ΔABC passed through the centre of the circumcircle of ΔABC,
To Prove: AB = AC.
Construction: Draw OP ⊥ AB and OQ ⊥ AC.
Proof: In ΔAPO and ΔAQO,
∠OPA = ∠OQA
[Each = 90° (by construction)]
∠OAP = ∠OAQ
[Given]
OA = OA (Common)
∴ ΔAPO ≅ ΔAQO
(By AAS congruence crieterion)
∴ OP = OQ [By CPCT]
∴ AB = AC. [∵ Chords equidistant from the centre are equal] Hence, proved.

Question 6.
In figure, ∠ABC = 79°, ∠ACB = 41°, find ∠BDC.

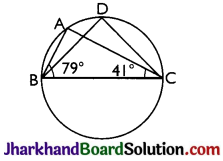
Solution :
In ΔABC.
∠BAC + ∠ABC + ∠ACB = 180°
[Sum of all the angles of a triangle is 180°]
⇒ ∠BAC + 79° + 41° = 180°
⇒ ∠BAC + 120° = 180°
⇒ ∠BAC = 180° – 120° = 60°
Now, ∠BDC = ∠BAC = 60°
[Angles in the same segment of a circle are equal]

Question 7.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 80°, ∠BAC = 40°, find ∠BCD. Further, if AB = BC, find ∠ECD.

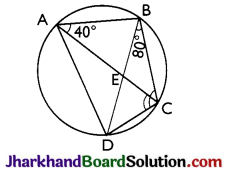
Solution :
∠CDB = ∠BAC = 40° ………….(i)
[Angles in the same segment of a circle are equal]
∠DBC = 80° ………….(ii)
In ΔBCD
∠BCD + ∠DBC + ∠CDB = 180°
[Sum of all the angles of a triangle is 180°]
⇒ ∠BCD + 80° + 40° = 180°
[Using (i) and (ii)]
⇒ ∠BCD + 120° = 180°
⇒ ∠BCD = 180° – 120°
⇒ ∠BCD = 60° ………………(ii)
In ΔABC,
AB = BC
∴ ∠BCA = ∠BAC = 40° …(iv)
[Angles opposite to equal sides of a triangle are equal]
Now, ∠BCD = 60° [From (iii)]
⇒ ∠BCA + ∠ECD = 60°
⇒ 40° + ∠ECD = 60°
⇒ ∠ECD = 60° – 40°
⇒ ∠ECD = 20°

Question 8.
Find the area of a triangle, the radius of whose circumcircle is 3 cm and the length of the altitude drawn from the opposite vertex to the hypotenuse is 2 cm.
Solution :
We know that the hypotenuse of a right-angled triangle is the diameter of its circumcircle.
∴ BC = 2(OB) = 2 × 3 = 6 cm
Let, AD ⊥ BC
AD = 2 cm [Given]

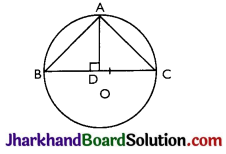
∴ Area of ΔABC = \(\frac {1}{2}\)(BC)(AD)
= \(\frac {1}{2}\)(6)(2) = 6 cm².

Question 9.
In figure, PQ is a diameter of a circle with centre O. If ∠PQR = 65°, ∠SPR = 40°, ∠PQM = 50°, find ∠QPR, ∠PRS and ∠QPM.

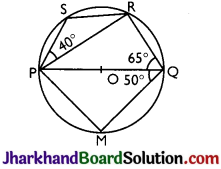
Solution :
(i) ∵ PQ is a diameter
∴ ∠PRQ = 90°
[Angle in a semi-circle is 90°]
In ΔPQR,
∠QPR + ∠PRQ + ∠PQR = 180°
[Angle sum property of a triangle]
⇒ ∠QPR + 90° + 65° = 180°
⇒ ∠QPR = 180° – 155° = 25°

(ii) PQRS is a cyclic quadrilateral
∴ ∠PSR + ∠PQR = 180°
[∵ Opposite angles of a cyclic quadrilateral are supplementary]
⇒ ∠PSR + 65° = 180°
⇒ ∠PSR = 180° – 65°
⇒ ∠PSR = 115°
In ΔPSR
∠PSR + ∠SPR + ∠PRS = 180°
[Angle sum property of a triangle]
⇒ 115° + 40° + ∠PRS = 180°
⇒ 155° + ∠PRS = 180°
⇒ ∠PRS = 180° – 155°
⇒ ∠PRS = 25°

(iii) PQ is a diameter
∴ ∠PMQ = 90°
[∵ Angle in a semi-circle is 90°]
In ΔPMQ,
∠PMQ + ∠PQM + ∠QPM = 180°
[Angle sum property of a triangle]
⇒ 90° + 50° + ∠QPM = 180°
⇒ 140° + ∠QPM = 180°
⇒ ∠QPM = 180° – 140°
⇒ ∠QPM = 40°

Multiple Choice Questions

Question 1.
If two circular wheels rotate on a horizontal road then locus of their centres will be
(a) Circles
(b) Rectangle
(c) Two straight lines
(d) Parallelogram
Solution :
(c) Two straight lines

Question 2.
In a circle of radius 10 cm, the length of chord whose distance is 6 cm from the centre is
(a) 4 cm
(b) 5 cm
(c) 8 cm
(d) 16 cm
Solution :
(d) 16 cm

Question 3.
If a chord a length 8 cm is situated at a distance of 3 cm form centre, then the diameter of circle is:
(a) 11 cm
(b) 10 cm
(c) 12 cm
(d) 15 cm
Solution :
(b) 10 cm

Question 4.
In a circle the lengths of chords which are situated at a equal distance from centre are :
(a) double
(b) four times
(c) equal
(d) three times
Solution :
(c) equal

Question 5.
In the given figure, O is the centre of the circle and ∠BDC = 42°. The ∠ACB is equal to:

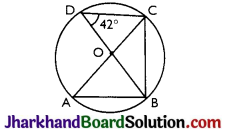
(a) 48°
(b) 45°
(c) 42°
(d) 60°
Solution :
(a) 48°

Question 6.
In the given figure, ∠CAB = 80°, ∠ABC = 40°. The sum of ∠DAB and ∠ABD is equal to:

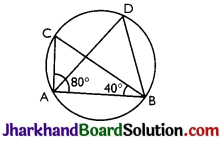
(a) 80°
(b) 100°
(c) 120°
(d) 140°
Solution :
(c) 120°

Question 7.
In the given figure, if C is the centre of the circle and ∠PQC = 25° and ∠PRC = 15°, then ∠QCR is equal to:

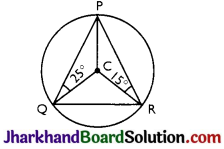
(a) 40°
(b) 60°
(c) 80°
(d) 120°
Solution :
(c) 80°

Question 8.
In a cyclic quadrilateral if ∠B – ∠D = 60°, then the smaller of the angles B and D is:
(a) 30°
(b) 45°
(c) 60°
(d) 75°
Solution :
(c) 60°

Question 9.
Three wires of length l₁, l₂, l₃, form a triangle surmounted by another circular wire. If l₃ is the diameter and l₃ = 2l₁, then the angle between l₁ and l₃ will be
(a) 30°
(b) 60°
(c) 45°
(d) 90°
Solution :
(b) 60°

Question 10.
In a circle with centre O, OD ⊥ chord AB. If BC is the diameter, then:
(a) AC = BC
(b) OD = BC
(c) AC = 2OD
(d) None of these
Solution :
(c) AC = 2OD

Question 11.
The sides AB and DC of cyclic quadrilateral ABCD are produced to meet at P, the sides AD and BC are produced to meet at Q. If ∠ADC = 85° and ∠BPC = 40°, then ∠CQD equals:
(a) 30°
(b) 45°
(c) 60°
(d) 75°
Solution :
(a) 30°

Question 12.
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, then ∠CBD is equal to

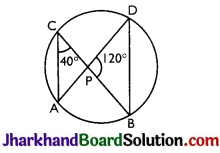
(a) 40°
(b) 20°
(c) 0°
(d) 60°
Solution :
(a) 40°

Question 13.
Any cyclic parallelogram is a:
(a) rectangle
(b) rhombus
(c) trapezium
(d) square
Solution :
(a) rectangle

Question 14.
The locus of the centre of all circles of given radius r, in the same plane, passing through a fixed point is:
(a) A point
(b) A circle
(c) A straight line
(d) Two straight lines
Solution :
(b) A circle

Question 15.
In a cyclic quadrilateral if ∠A – ∠C = 70°, then the greater of the angles A and C is equal to:
(a) 95°
(b) 105°
(c) 125°
(d) 115°
Solution :
(c) 125°

Question 16.
The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends on the longer segment of the circle is equal to :
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution :
(a) 30°

Question 17.
If a trapezium is cyclic then,
(a) Its parallel sides are equal.
(b) Its non-parallel sides are equal.
(c) Its diagonals are not equal.
(d) None of these
Solution :
(b) Its non-parallel sides are equal.