Students should go through these JAC Class 9 Maths Notes Chapter 11 Constructions will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 11 Constructions
To Construct The Bisector Of A Line Segment
Example 1.
Draw a line segment of length 7.8 cm and draw the perpendicular bisector of this line segment.
Solution:
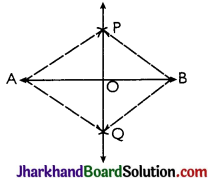
Given: Let the given line segment be AB = 7.8 cm
Steps:
- Draw the line segment AB = 7.8 cm,
- With point A as centre and a suitable radius, more than half the length of AB, draw arcs on both the sides of AB.
- With point B as centre and with the same radius draw arcs on both the sides of AB. Let these arcs cut at points P and Q as shown in the figure.
- Draw a line through the points P and Q. The line so obtained is the required perpendicular bisector of given line segment AB.
Line PQ is perpendicular bisector of AB.
(A) PQ bisects AB i.e., OA = OB.
(B) PQ is perpendicular to AB ie, ∠POA = ∠POB = 90°
Proof: In ΔAPQ and ΔBPQ,
AP = AQ [By construction]
BP = BQ [By construction]
PQ = PQ [Common]
⇒ ΔAPQ ≅ ΔBPQ [By SSS]
⇒ ∠APQ = ∠BPQ [By CPCT]
Now, in ΔAPO and ΔBPO,
AP = BP [By construction]
OP = OP [Common side]
∠APO = ∠BPO [Proved above]
⇒ ΔAPO ≅ ΔBPO [By SAS]
∠POA = ∠POB [CPCT]
and OA = OB
⇒ ∠POA = ∠POB = \(\frac{180^{\circ}}{2}\) = 90°
[∵∠POA + ∠POB = 180°]
⇒ PQ is perpendicular bisector of AB.
![]()
To Construct The Bisector Of A Given Angle
Let ABC be the given angle to be bisected.
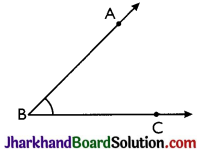
Steps:
- With Bas centre and a suitable radius, draw an arc which cuts ray BA at point D and ray BC at point E.
- Taking D and E as centres and with equal radii draw arcs which intersect each other at point E In this step, each equal radius must be more than half the length of arc DE.
- Join B and F and produce to get the ray BF. Ray BF is the required bisector of the given angle ABC.
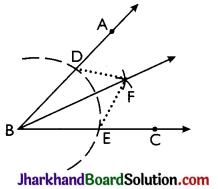
Proof:
Join DF and EF.
In ΔBDF and ΔBEF
BD = BE [Radii of the same arc]
DF = EF [Radii of the equal arcs]
BF = BF [Common]
⇒ ΔBDF ≅ ΔBEF [By SSS]
⇒ ∠DBF = ∠EBF [By CPCT]
i.e., ∠ABF = ∠CBF
⇒ BF bisects ∠ABC. Hence, proved.
To Construct The Required Angles
→ To Construct the Required Angle of 60°:
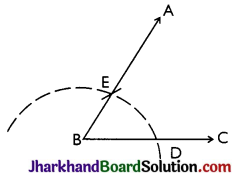
Steps:
- Draw the ray BC.
- With B as centre and any suitable radius. draw an arc which cuts BC at point D.
- With D as centre and same radius, as taken in step (ii), draw one more arc which cuts previous arc at point E.
- Join BE and produce up to any point A.
Then, ∠ABC = 60°.
→ To Construct an Angle of 120°:
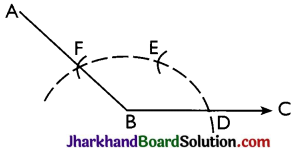
Steps:
- Draw the ray BC.
- Taking B as centre and with any suitable radius, draw an arc which cuts BC at point D.
- Taking Das centre, draw an arc of the same radius, as taken in step (ii), which cuts the first arc at point E.
- Taking E as centre and same radius, as taken in step (ii), draw one more arc which cuts the first arc at point E.
- Join BF and produce up to any suitable point A. Then, ∠ABC = 120°.
→ To Construct an Angle of 30°:
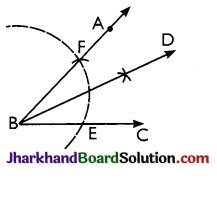
Steps:
- Construct angle ABC = 60° by compass.
- Draw BD, the bisector of angle ABC.
Then, ∠DBC = 30°
→ To Construct an Angle of 90°:
Steps:
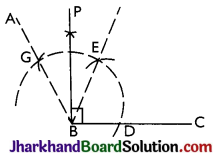
- Construct angle ABC = 120° by using compass.
- Draw BP, the bisector of angle EBG.
Then, ∠PBC = 90°
→ To Construct an Angle of 45°:
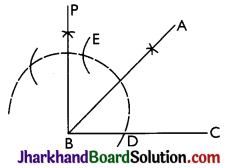
Steps:
- Draw ∠PBC = 90° by compass.
- Draw BA which bisects angle PBC,
Then, ∠ABC = 45°.
→ To Construct an Angle of 105°:
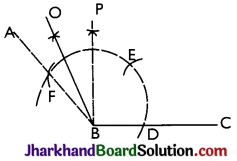
Steps:
- Construct ∠ABC = 120° and ∠PBC = 90° by compass.
- Draw BO, the bisector of ∠ABP.
Then, ∠OBC = 105°
→ To Construct an Angle of 150°:
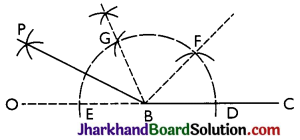
Steps:
- Draw the ray BC. Produce CB towards B up to any point.
With B as centre, draw an arc (with any suitable radius) which cuts OC at points D and E. - With D as centre, draw an arc of the same radius, as taken in step (ii), which cuts the first arc at point E.
- With F as centre, draw one more arc of the same radius, taken in step (ii), which cuts the first arc at point G.
- Draw BP, the bisector of angle EBG.
Now ∠FBD = ∠GBF = ∠EBG = 60° and
∠GBP = ∠PBE = 30°
Then, ∠PBC = 150°
→ To Construct an Angle of 135°:
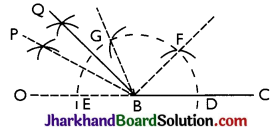
Steps:
- Construct ∠PBC = 150° and ∠GBC = 120° by compass.
- Construct BQ, the bisector of angle PBG.
Then, ∠QBC = 135°
![]()
To Construct A Triangle
Case (i) To construct an equilateral triangle when its one side is given.
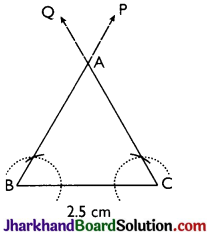
Example 2.
Draw an equilateral triangle having each side of 2.5 cm.
Solution:
Given one side of the equilateral triangle be 2.5 cm.
Steps:
- Draw a line segment BC = 2.5 cm.
- Through B, construct ray BP making angle 60° with BC. i.e. ∠PBC = 60°
- Through C, construct ray CQ making angle 60° with BC
i.e., ∠QCB = 60° - Let BP and CQ intersect each other at point A. Then, AABC is the required equilateral triangle.
Proof:
Since, ∠ABC = ∠ACB = 60°
∠BAC = 180° – (60° +60°) = 60°
⇒ All the angles of the AABC are equal.
⇒ ΔABC is the required equilateral triangle. Hence, proved.
Case (ii) When the base of the triangle, one base angle and the sum of other two sides are given.

Example 3.
Construct a triangle with 3 cm base and sum of other two sides is 8 cm and one base angle is 60°.
Solution:
Given the base BC of the triangle ABC be 3 cm, one base angle ∠B = 60° and the sum of the other two sides be 8 cm
i.e, AB + AC = 8 cm.
Steps:
- Draw BC = 3 cm.
- At point B, draw ray BP so that ∠PBC = 60°.
- From BP, cut BD = 8 cm.
- Join D and C.
- Draw perpendicular bisector of CD, which meets BD at point A.
- Join A and C.
Thus, ABC is the required triangle
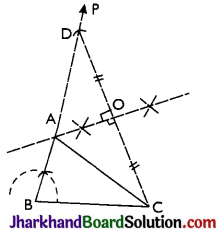
Proof: Since, OA is perpendicular bisector of CD
⇒ OC = OD
∠AOC = ∠AOD = 90°
Also, OA = OA [Common]
∴ ΔAOC ≅ ΔAOD [By SAS]
⇒ AC = AD [CPCT]
∴ BA + AC = BA + AD = BD = 8cm.
Example 4.
Construct a right triangle, when one side is 3.8 cm and the sum of the other side and hypotenuse is 6 cm.
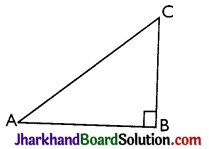
Solution:
Here, consider the ΔABC, as shown in figure.
Clearly, AB = 3.8 cm, ∠B = 90° and BC + AC = 6 cm.
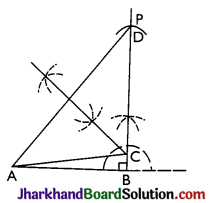
Steps:
- Draw AB = 3.8 cm.
- Through B. draw ray BP so that ∠ABP = 90°.
- From BP, cut BD = 6 cm.
- Join A and D.
- Draw perpendicular bisector of AD, which meets BD at point C.
Thus, ABC is the required triangle.
Case (iii) When the base of the triangle, one base angle and the difference of the other two sides are given.
Example 5.
Construct a triangle with base of 8 cm and difference between the length of other two sides is 3 cm and one base angle is 60°.
Solution:
Given the base BC of the required triangle ABC be 8 cm i.e., BC = 8 m, base angle B = 60° and the difference between the lengths of other two sides AB and AC be 3 cm.
i.e, AB – AC = 3 cm or AC – AB = 3 cm.
(a) When AB – AC = 3 cm i.e., AB > AC:
Steps:
- Draw BC = 8 cm.
- Through point B, draw BP so that ∠PBC = 60°.
- From BP cut BD = 3 cm.
- Join D and C.
- Draw perpendicular bisector of DC; which meets BP at point A.
- Join A and C.
Thus, ΔABC is the required triangle.
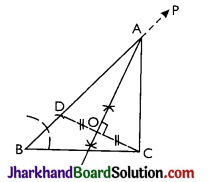
Proof:
Since OA is perpendicular bisector of CD.
⇒ OD = OC
∠AOD = ∠AOC = 90°
And, OA = OA [Common]
∴ ΔAOD ≅ ΔAOC [By SAS]
⇒ AD = AC [By CPCT]
Now, AB – AC = AB – AD = BD = 3 cm
(b) When AC – AB = 3 cm i.e, AB < AC:
Steps:
- Draw BC = 8 cm
- Through B, draw line BP so that ∠PBC = 60°
- Produce BP backward up to a suitable point Q.
- From BQ, cut BD = 3 cm.
- Join D and C.
- Draw perpendicular bisector of DC, which meets BP at point A.
- Join A and C.
Thus, ΔABC is the required triangle
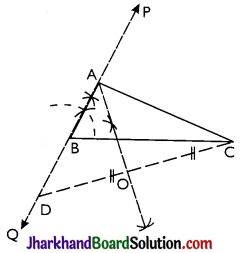
Proof:
Since, OA is perpendicular bisector of CD
⇒ OD = OC
∠AOD = ∠AOC = 90°
And OA = OA [Common]
∴ ΔAOD ≅ ΔAOC [By SAS]
⇒ AD = AC [By CPCT]
Now, AC – AB = AD – AB = BD = 3cm
Case (iv) When the perimeter of the triangle and both the base angles are given.
![]()
Example 6.
Construct a triangle ABC with AB + BC + CA = 12 cm; ∠B = 45° and ∠C = 60°.
Solution:
Given the perimeter of the triangle ABC be 12 cm i.e., AB + BC + CA = 12 cm and both the base angles be 45° and 60° i.e., ∠B = 45° and ∠C = 60°
Steps:
- Draw a line segment PQ = 12 cm.
- At P, construct ray PR so that ∠RPQ = 45° and at Q. construct ray QS so that ∠SQP = 60°.
- Draw bisector of angles RPQ and SQP which meet each other at point A.
- Draw perpendicular bisector of AP, which meets PQ at point B.
- Draw perpendicular bisector of AQ, which meets PQ at point C.
- Join AB and AC.
Thus, ABC is the required triangle
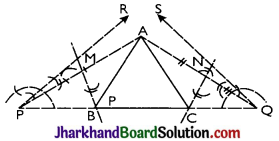
Proof:
Since, MB is perpendicular bisector of AP.
⇒ AM = PM
∠AMB = ∠PMB = 90°
BM = BM
⇒ ΔAMB ≅ ΔPMB [By SAS]
PB = AB [By CPCT]
Similarly, NC is perpendicular bisector of AQ.
⇒ ΔQNC ≅ ΔANC [By SAS]
⇒ CQ = AC [By CPCT]
Now, PQ = PB + BC + CQ = AB + BC + AC
= Given perimeter of the AABC drawn.
Also, ∠BPA = ∠BAP [AS ΔPMB ≅ ΔMB]
∴ ∠ABC = ∠BPA + ∠BAP
[Ext. angle of a triangle = sum of two interior opposite angles]
∠ABC = 2∠BPA = ∠RPB = 45°
∠ACB= ∠CQA + ∠CAQ = 2∠CQA
[∵ ΔQNC ≅ ΔANC ∴ ∠CQA = ∠CAQ]
= ∠SQC = 60°