Jharkhand Board JAC Class 9 Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण
प्रश्न 1.
समीकरण x + 3y – 10 को सन्तुष्ट करने वाला बिन्दु है :
(A) (4, 2)
(B) (-4, 2)
(C) (4, – 1)
(D) (2, 4).
हल :
समीकरण x + 3y = 10 में करते हैं।
x = 4 और y = 2 रखने पर,
4 + 3 × 2 = 10
अतः विकल्प ‘A’ के दोनों मान समीकरण को सन्तुष्ट
∴ सही विकल्प ‘A’ है।
![]()
प्रश्न 2.
रैखिक समीकरण x + 40 = 0 है
(A) एकचरीय समीकरण
(B) द्विचरीय समीकरण
(C) द्विघात समीकरण
(D) उपर्युक्त में से कोई नहीं।
हल :
x + 4 y = 0
इस समीकरण में और y दो चर हैं।
∴ यह दो चरों वाला रैखिक समीकरण है।
अतः सही विकल्प ‘B’ है।
प्रश्न 3.
समीकरण 4x + 5y = k में यदि x = 2, y = 1 हो, तो k का मान होगा :
(A) 9
(B) – 12
(C) – 13
(D) 13.
हल :
समीकरण 4x + 5y = k में x = 2 और y = 1
रखने पर,
4 × 2 + 5 × 1 = k
⇒ 8 + 5 = k ⇒ 13 = k
अतः सही विकल्प ‘D’ है।
प्रश्न 4.
रैखिक समीकरण y – 2 = 0 का आलेख खींचने पर प्राप्त होगा :
(A) X- अक्ष के समान्तर सरल रेखा
(B) मूलबिन्दु से गुजरती हुई सरल रेखा
(C) Y-अक्ष के समान्तर सरल रेखा
(D) आलेख नहीं खींचा जा सकता।
हल :
समीकरण y – 2 = 0 को निम्न प्रकार लिख सकते हैं : 0x + y = 2
x के विभिन्न मानों के लिए y का मान 2 प्राप्त होगा । अतः सरल रेखा X- अक्ष के समान्तर प्राप्त होगी।
∴ सही विकल्प ‘A’ है।
![]()
प्रश्न 5.
दो चर वाले रैखिक समीकरण के हल होंगे:
(A) एक अद्वितीय
(B) केवल अपरिमित रूप से अनेक
(C) दो
(D) चार हल।
हल :
दो चर वाले रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं।
अतः सही विकल्प ‘B’ है।
प्रश्न 6.
रैखिक समीकरण y = 3x से व्यक्त रेखा पर स्थित बिन्दु होगा :
(A) (2, 3)
(B) (3, 1)
(C) (1, 3)
(D) (1, -3).
हल :
समीकरण y = 3x
समीकरण में x = 1 रखने पर y = 3 प्राप्त होता है
अतः सही विकल्प ‘C’ है।
प्रश्न 7.
किसी रैखिक समीकरण में घरों की बात होती है
(A) कोई भी
(B) 0
(C) 2
(D) 1.
हल :
रैखिक समीकरण की घात होती है।
अतः सही विकल्प ‘D’ है।
प्रश्न 8.
रैखिक समीकरण के बिन्दु (2, 5) से गुजरने वाली रेखाओं की संख्या होगी :
(A) 2
(B) 5
(C) अनन्त
(D) 7.
हल :
किसी बिन्दु से गुजरने वाली रेखाओं की संख्या अनन्त होती है।
अतः सही विकल्प ‘C’ है।
प्रश्न 9.
यदि दो अंकों वाली संख्या में इकाई का अंक b तथा दहाई का अंक a हो तो संख्या लिखिए।
हल :
संख्या (10a + b).
![]()
प्रश्न 10.
यदि आपके लिए कोई रैखिक समीकरण दिया गया है, तो उसे कैसे पहचानोगे? उदाहरण दीजिए।
हल :
रैखिक समीकरण में चर की अधिकतम घात एक होती है।
जैसे: 2x + y – 10 = 0, y + 3x = 0 आदि रैखिक समीकरण के उदाहरण हैं।
प्रश्न 11.
y = mx प्रकार के समीकरण की रेखा किस बिन्दु से गुजरती है ?
हल :
मूलबिन्दु (0, 0) से ।
प्रश्न 12.
यदि x = 3y समीकरण में y = 0 हो तो उक्त समीकरण किस अक्ष का होगा ?
हल :
दिया गया समीकरण है :
x = 3y, x = 3 (0) = 0
⇒ x = 0, Y अक्ष का समीकरण है।
![]()
प्रश्न 13.
समीकरण 230 का आलेख किस प्रकार का होगा ? समझाइए ।
हल :
समीकरण
2y – 3 = 0 ⇒ 2y = 3
∴ y = \(\frac {3}{2}\)
अतः x के सभी मानों के लिए रैखिक समीकरण
0.x + 2y – 3 = 0 से y का मान \(\frac {3}{2}\) प्राप्त होगा।
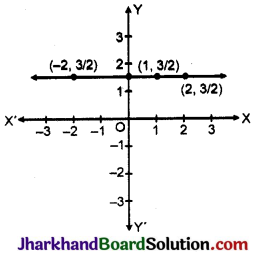
∴ बिन्दु (1, \(\frac {3}{2}\)), (2, \(\frac {3}{2}\)), (-2, \(\frac {3}{2}\))………… से प्राप्त आलेख मूल बिन्दु से \(\frac {3}{2}\) इकाई दूर X- अक्ष के समान्तर होगा।
प्रश्न 14.
फारेनहाइट को सेल्सियस में परिवर्तित करने वाला रैखिक समीकरण लिखिए ।
हल :
रैखिक समीकरण F = (\(\frac {9}{5}\))C + 32.
![]()
प्रश्न 15.
निम्नलिखित सेल्सियस को फारेनहाइट में रूपांतरित कीजिए :
(i) 25°C
(ii) 35°C
(iii) 0°C.
हल :
(i) 25°C.
F = \(\frac {9}{5}\) × 25 + 32 = 9 × 5 + 32 = 45 + 32 = 77
अतः 25°C = 77°E.
(ii) 35°C.
F = \(\frac {9}{5}\) × 35 + 32 = 9 × 7 + 32 = 63 + 32 = 95
अतः 35°C = 95°F.
(iii) 0°C.
F = \(\frac {9}{5}\) × 0 + 32 = 32
अतः 0°C = 32°F.
प्रश्न 16.
यदि x = 1 हो तो समीकरण \(\frac{4}{x}+\frac{3}{y}\) = 5 में y का मान बताइए।
हल :
समीकरण \(\frac{4}{x}+\frac{3}{y}\) = 5 में x = 1 रखने पर,
\(\frac{4}{1}+\frac{3}{y}\) = 5
⇒ \(\frac {3}{y}\) = 5 – 4 = 1
⇒ \(\frac {3}{y}\) = 1
∴ y = 3.
![]()
प्रश्न 17.
निम्नलिखित समीकरणों को ax + by + c = 0 के रूप में व्यक्त करने पर a, b और c के मान ज्ञात कीजिए:
(i) 3 + 5y = πx
(ii) 2x + \(\frac {3}{2}\) = 1.4y.
हल :
(i) समीकरण
3 + 5y = πx
⇒ πx – 5y – 3 = 0 की तुलना ax + by + c = 0 से करने पर, a = π, b = – 5 और c = – 3.
(ii) समीकरण 2x + \(\frac {3}{2}\) = 1.4y
⇒ 2x – 14y + \(\frac {3}{2}\) = 0 की तुलना ax + by + c = 0
से करने पर, a = 2, b = – 1.4 और c = \(\frac {3}{2}\)
प्रश्न 18.
निम्नलिखित समीकरणों में से प्रत्येक के दो संगत हल ज्ञात कीजिए :
(i) 4x + 3y = 12
(ii) 2x + 5y = 0
(iii) 3y + 4 = 0.
हल :
(i) x = 0 लेने पर,
4(0) + 3y = 12 ∴ y = 4
अत: (0, 4) समीकरण का हल है।
y = 0 लेने पर,
4x + 3(0) = 12 ⇒ 4x = 12 ∴ x = 3
अतः (3, 0) समीकरण का हल है।
अत: समीकरण 4x + 3y = 12 के दो हल (0, 4) और (3, 0) होंगे।
(ii) x = 0 लेने पर 2(0) + 5y = 0 ⇒ y = 0
अतः (0, 0) समीकरण का हल है।
x = 1 लेने पर,
2 × 1 + 5y = 0 ⇒ 5y = -2 ∴ y = \(\frac {-2}{5}\)
अतः (1, \(\frac {-2}{5}\)) समीकरण का हल हैं।
अतः दिये गये समीकरण के दो हल (0, 0) और (1, \(\frac {-2}{5}\)) होंगे।
(iii) समीकरण 3y + 4 = 0 को 0x + 3y + 4 = 0 के रूप में लिखने पर x के सभी मानों के लिए y = \(\frac {-4}{3}\) प्राप्त होगा ।
अतः दिये गये समीकरण के दो हल (0, \(\frac {-4}{3}\)) और (1, \(\frac {-4}{3}\)) हैं।
![]()
प्रश्न 19.
निम्नलिखित कथनों को समीकरण के रूप में लिखिए :
(i) यदि किसी संख्या में 9 जोड़ दिया जाए, तो वह 25 के बराबर होती है।
(ii) यदि किसी संख्या में से 15 घटा दिए जाये, तो वह 5 के बराबर हो जाती है।
(iii) किसी संख्या का 7 गुना, 42 के बराबर होता है।
(iv) किसी संख्या में 5 का भाग देने पर वह 6 बन जाती है।
(v) यदि किसी संख्या के 3 गुने में 6 जोड़ा जाये, तो वह 15 के बराबर हो जाती है।
हल :
सभी प्रश्नों में अज्ञात संख्या को x मानने पर,
(i) x + 9 = 25
(ii) x – 15 = -5
(iii) x × 7 = 42 ⇒ 7x = 42
(iv) \(\frac {x}{5}\) = 6
(v) x × 3 + 6 = 15 ⇒ 3x + 6 = 15.
प्रश्न 20.
समीकरण 2x – 3y + 4 = 0 का आलेख खींचिए ।
हल :
दिया गया समीकरण 2x – 3y + 4 = 0
या 2x = 3y – 4
या x = \(\frac{3 y-4}{2}\)
यदि y = 0, हों, तो x = \(\frac{3 \times 0-4}{2}\) = – 2
यदि y = 2, हों, तो x = \(\frac{3 \times 2-4}{2}\) = 1
यदि y = 4, हों, तो x = \(\frac{3 \times 4-4}{2}\) = 4
सारणी :
| x | – 2 | 1 | 4 |
| y | 0 | 2 | 4 |
आलेख खींचना : माना पैमाना X- अक्ष पर 1 सेमी 1 इकाई, Y- अक्ष पर 1 सेमी = 1 इकाई ।
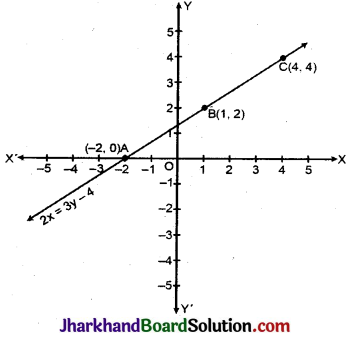
बिन्दु A(-2, 0) B (1, 2) और C(4, 4) दो चर रैखिक समीकरण 2x = 3y – 4 के हल हैं।
![]()
प्रश्न 21.
पिता की आयु पुत्र की आयु से 25 वर्ष अधिक है। 10 वर्ष पूर्व पिता की आयु पुत्र की आयु से दुगुनी थी। दोनों की वर्तमान आयु ज्ञात करो ।
हल :
माना, पिता की आयु = x वर्ष
पुत्र की आयु = y वर्ष
प्रश्नानुसार, x = y +25 ……..(i)
तथा 10 वर्ष पूर्व दोनों की आयु (x – 10) वर्ष तथा (y – 10) वर्ष होगी।
अतः (x – 10) = 2(y – 10)
⇒ x – 10 = 2y – 20
⇒ x = 2y – 20 +10
⇒ x = 2y – 10 ……..(ii)
समी. (ii) में (i) से x का मान रखने पर
y + 25 = 2y – 10
⇒ 25 + 10 = 2y – y
⇒ y = 35
समी. (i) में y का मान रखने पर,
x = 35 + 25 = 60
∴ पिता की आयु 60 वर्ष तथा पुत्र की आयु 35 वर्ष।