Students should go through these JAC Class 9 Maths Notes Chapter 9 Areas of Parallelograms and Triangles will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 9 Areas of Parallelograms and Triangles
Polygonal Region
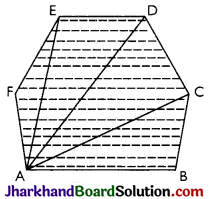
Polygon region can be expressed as the union of a finite number of triangular regions in a plane such that if two of these intersect, their intersection is either a point or a line segment. It is the shaded portion including its sides as shown in the figure.
Parallelogram
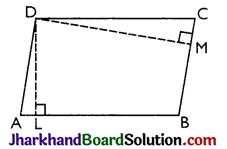
(a) Base and Altitude of a Parallelogram:
→ Base: Any side of parallelogram can be called its base.
→ Altitude: The perpendicular to the base from the opposite side is called the altitude of the parallelogram corresponding to the given base.
In the given Figure
→ DL is the altitude of ||gm ABCD corresponding to the base AB.
→ DM is the altitude of ||gm ABCD, corresponding to the base BC.
![]()
Theorem 1.
A diagonal of parallelogram divides it into two triangles of equal area.
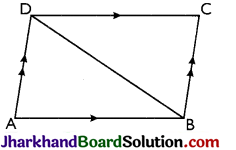
Proof:
Given: A parallelogram ABCD whose one of the diagonals is BD.
To prove: ar(ΔABD) = ar(ΔCDB).
Proof: In ΔABD and ΔCDB;
AB = DC [Opp sides of a ||gm]
AD = BC [Opp. sides of a ||gm]
BD = BD [Common side]
∴ ΔΑΒD ≅ ΔCDB [By SSS]
ar(ΔABD) = ar (ΔCDB) [Areas of two congruent triangles are equal]
Hence, proved.
Theorem 2.
Parallelograms on the same base or equal base and between the same parallels are equal in area.
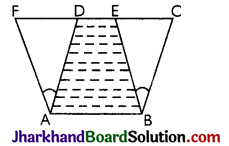
Proof:
Given: Two Parallelograms ABCD and ABEF are on the same base AB and between the same parallels AB and FC.
To Prove: ar(||gm ABCD) = ar(||gm ABEF)
Proof: In ΔADF and ΔBCE, we have
AD = BC [Opposite sides of a ||gm]
and AF = BE [Opposite sides of a ||gm]
AD || BC (Opposite sides of a parallelogram)
⇒ ∠ADF = ∠BCE (Alternate interior angles)
∴ ΔADF ≅ ΔBCE [By AAS]
∴ ar(ΔADF) = ar(ΔBCE) …..(i)
[Congruent triangles have equal area]
∴ ar (||gm ABCD) = ar(ABED) + ar(ΔBCE)
= ar (ABED) + ar(ΔADF) [Using (1)]
= ar(||gm ABEF).
Hence, ar(||gm ABCD) = ar(||gm ABEF).
Hence, proved.
![]()
Theorem 3.
The area of parallelogram is the product of its base and the corresponding altitude.
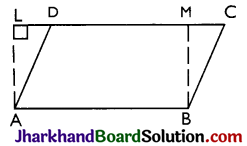
Proof:
Given: A ||gm ABCD in which AB is the base and AL is the corresponding height.
To prove: Area (||gm ABCD) = AB × AL.
Construction: Draw BM ⊥ DC so that rectangle ABML is formed.
Proof: ||gm ABCD and rectangle ABML are on the same base AB and between the same parallel lines AB and LC.
∴ ar(||gm ABCD) = ar(rectangle ABML)
= AB × AL
∴ area of a ||gm = base × height.
Hence, proved.
Area Of A Triangle
Theorem 4.
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
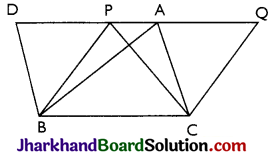
Proof:
Given: Two triangles ABC and PCB on the same base BC and between the same parallel lines BC and AP.
To prove: ar(ΔABC) = ar(ΔPBC)
Construction: Through B, draw BD || CA intersecting PA produced in D and through C, draw CQ || BP, intersecting line AP produced in Q.
Proof: We have, BD || CA (By construction) And, BC || DA [Given]
∴ Quad. BCAD is a parallelogram.
Similarly, Quad. BCQP is a parallelogram.
Now, parallelogram BOQP and BCAD are on the same base BC, and between the same parallels.
∴ ar (||gm BCQP) = ar (||gm BCAD)….(i)
We know that the diagonals of a parallelogram divides it into two triangles of equal area.
∴ ar(ΔPBC) = \(\frac{1}{2}\)(||gm BCQP) …..(ii)
And ar (ΔABC) = \(\frac{1}{2}\)(||gm BCAD)….(iii)
Now, ar (||gm BCQP) = ar(||gm BCAD) [From (i)]
\(\frac{1}{2}\)ar(||gm BCAD) = \(\frac{1}{2}\)ar(||gm BCQP)
Hence, \(\frac{1}{2}\)ar(ABC) = ar(APBC) (Using (ii) and (iii) Hence, proved.
Theorem 5.
The area of a trapezium is half the product of its height and the sum of the parallel sides.
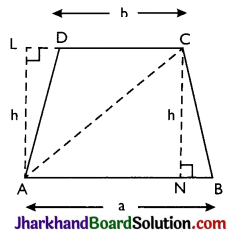
Proof:
Given: Trapezium ABCD in which AB || DC, AL ⊥ DC, CN ⊥ AB and AL = CN = h (say). AB = a, DC = b.
To prove: ar(trap. ABCD) = \(\frac{1}{2}\)h × (a + b).
Construction: Join AC.
Proof: AC is a diagonal of quad. ABCD.
∴ ar(trap. ABCD) = ar(ΔABC) + ar(ΔACD)
= \(\frac{1}{2}\)h × a+\(\frac{1}{2}\)h × b= \(\frac{1}{2}\)h(a + b).
Hence, proved.
![]()
Theorem 6.
Triangles having equal areas and having one side of the triangle equal to corresponding side of the other, have their corresponding altitudes equal.
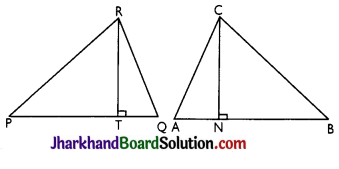
Proof:
Given: Two triangles ABC and PQR such that
(i) ar(ΔABC) = ar(ΔPQR) and
(ii) AB = PQ.
CN and RT and the altitudes corresponding to AB and PQ respectively of the two triangles.
To prove: CN = RT.
Proof: In ΔABC, CN is the altitude corresponding to the side AB
ar(ΔABC) = \(\frac{1}{2}\)AB × CN ……(i)
Similarly, ar(ΔPQR) = \(\frac{1}{2}\)PQ × RT ……(ii)
Since, ar(ΔABC) = ar(ΔPQR) [Given]
∴ \(\frac{1}{2}\)AB × CN = PQ × RT
Also, AB = PQ [Given]
∴ CN = RT Hence, proved.