Jharkhand Board JAC Class 9 Maths Solutions Chapter 11 रचनाएँ Ex 11.2 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 11 रचनाएँ Exercise 11.2
प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 7 सेमी, ∠B = 75° और AB + AC = 13 सेमी हो।
हल:
रचना (1) रेखाखण्ड BC = 7 सेमी खींचा।
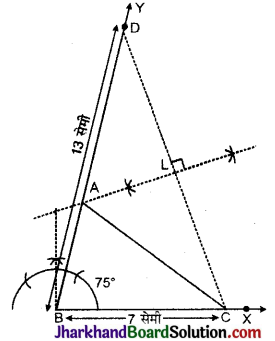
(2) ∠XBY = 75° बनाती हुयी रेखा BY खींची।
(3) BY से BD = 13 सेमी काटा।
(4) CD को मिलाया।
(5) CD का लम्ब समद्विभाजक खींचा जो BD को A बिन्दु पर काटता है।
(6) AC को मिलाया।
इस प्रकार प्राप्त ΔABC अभीष्ट त्रिभुज है।
![]()
प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 8 सेमी, ∠B = 45° और AB – AC = 3.5 सेमी हो।
हल:
रचना: (1) रेखाखण्ड BC = 8 सेमी खींचा।
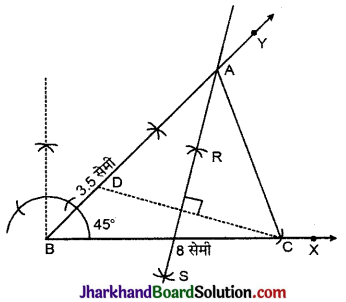
(2) ∠YBC = 45° बनाती हुयी रेखा BY खींची।
(3) BY से BD = 3.5 सेमी का रेखाखण्ड काटा।
(4) CD को मिलाया।
(5) CD का लम्ब समद्विभाजक खींचा जो BY को A बिन्दु पर काटता है।
(6) AC को मिलाया।
इस प्रकार ΔABC ही अभीष्ट त्रिभुज है।
प्रश्न 3.
एक त्रिभुज PQR की रचना कीजिए, जिसमें QR = 6 सेमी, ∠Q = 60° और PR – PQ = 2 सेमी हो।
हल:
रचना: (1) रेखाखण्ड RQ = 6 सेमी खींचा।
(2) 60° का कोण बनाते हुए QR के साथ किरण QY खींची और YQ को YQY’ तक विपरीत दिशा में बढ़ाया।
(3) QY’ से एक रेखाखण्ड QS = 2 सेमी काटा।
(4) RS को मिलाया।
(5) RS का लम्बसम द्विभाजक खींचा जो SY को P बिन्दु पर काटता है।
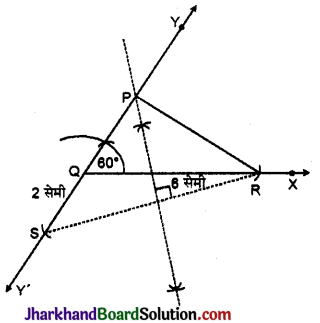
(6) PR को मिलाया।
इस प्रकार, ΔPQR एक अभीष्ट त्रिभुज है।
![]()
प्रश्न 4.
एक त्रिभुज XYZ की रचना कीजिए, जिसमें ∠Y = 30°, ∠Z = 90° और XY + YZ + ZX = 11 सेमी हो।
हल:
रचना: (1) रेखाखण्ड AB = 11 सेमी खींचा।
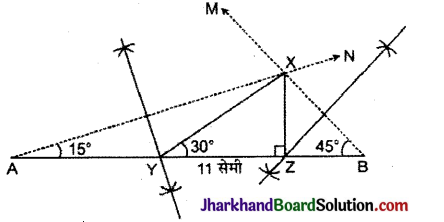
(2) बिन्दु 4 पर 15° का कोण बनाती हुयी एक किरण AN खींची।
∠NAB = \(\frac{1}{2}\) × 30° = 150
(3) B बिन्दु पर \(\frac{1}{2}\) × 90° = 45° का कोण बनाती हुयी BM खींची जो एक-दूसरे को X बिन्दु पर काटती हैं।
(4) XA और XB के लम्ब समद्विभाजक खाँचे, जो AB को क्रमश: Y और Z बिन्दुओं पर काटते हैं।
(5) XY और XZ को मिलाया।
इस प्रकार, ΔXYZ अभीष्ट त्रिभुज है।
![]()
प्रश्न 5.
एक समकोण त्रिभुज की रचना कीजिए, जिसका आधार 12 सेमी और कर्ण तथा अन्य भुजा का योग 18 सेमी है।
हल:
रचना: (1) रेखाखण्ड BC = 12 सेमी खींचा।
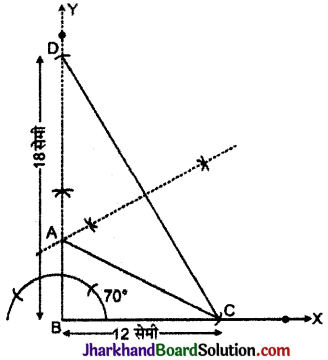
(2) ∠XBY = 90° बनाती हुयी रेखा BY खींची।
(3) इसमें से BD = 18 सेमी का एक रेखाखण्ड काया ।
(4) CD को मिलाया।
(5) CD को समद्विभाजित करते हुए एक लम्ब समद्विभाजक खींचा जो BD को A बिन्दु पर काटता है।
(6) AC को मिलाया।
इस प्रकार, ΔABC ही अभीष्ट समकोण त्रिभुज है।