Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 त्रिभुज Ex 7.1 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 7 त्रिभुज Exercise 7.1
प्रश्न 1.
चतुर्भुज ACBD में, AC = AD है और AB कोण को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि ΔABC ≅ ΔABD है।
BC और BD के बारे में आप क्या कह सकते हैं ?
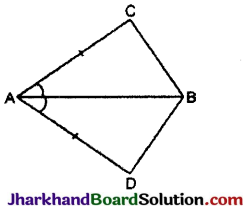
हल:
ΔABC और ΔABD में,
AC = AD [दिया है]
∠CAB = ∠BAD [दिया है]
और AB = AB [उभयनिष्ठ]
ΔABC ≅ ΔABD [SAS नियम]
⇒ BC = BD
[∵ सर्वागसम त्रिभुजों के संगत भाग बराबर होते हैं]
![]()
प्रश्न 2.
ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA है (आकृति देखें) सिद्ध कीजिए कि
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
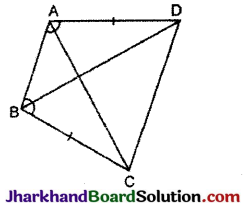
हल:
AD = BC [दिया है]
(i) ΔABD तथा ΔBAC में,
∠DAB = ∠CBA [दिया है]
व AB = AB [उभयनिष्ठ]
∴ भुजा कोण-भुजा सर्वांगसमता गुणधर्म से,
ΔABD ≅ ΔBAC इति सिद्धम्।
(ii) ∵ ΔABD ≅ ΔBAC
⇒ BD = AC
(∵ सर्वागसम त्रिभुजों के संगत भाग बराबर होते हैं)
(iii) ΔABD तथा ΔBAC में,
AD = BC [दिया है]
∠DAB = ∠CBA [दिया है]
AB = AB [उभयनिष्ठ]
∴ भुजा कोण भुजा सर्वागसमता गुणधर्म से,
ΔABD ≅ ΔBAC
⇒ BD = AC
और ∠ABD = ∠BAC
[∵ सर्वागसम त्रिभुजों के संगत भाग बराबर होते हैं]
इति सिद्धम्।
प्रश्न 3.
एक रेखाखण्ड AB पर AD और BC दो बराबर लम्ब रेखाखण्ड हैं (देखिए आकृति)। दर्शाइए कि CD, रेखाखण्ड AB को समद्विभाजित करता है।
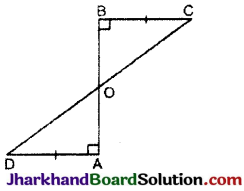
हल:
चित्रानुसार
ΔAOD और ΔBOC मैं, ∠AOD = ∠BOC [शीर्षाभिमुख कोण]
∠DAO = ∠OBC [प्रत्येक 90°]
और AD = BC [दिया है]
∴ ΔAOD ≅ ΔBOC (AAS नियम)
∴ OA = OB
अत: CD, रेखाखण्ड AB को समद्विभाजित करती है।
इति सिद्धम्।
![]()
प्रश्न 4.
l और m दो समान्तर रेखाएँ हैं जिन्हें समान्तर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति)। दर्शाइए कि ΔABC ≅ ΔCDA है।
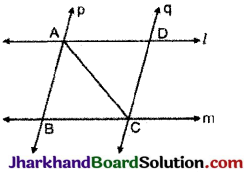
हल:
चूंकि l तथा m समान्तर रेखाएँ दूसरी समान्तर रेखाओं P और q द्वारा प्रतिच्छेदित की जाती हैं। अतः AD || BC तथा AB || CD.
अत: ABCD समान्तर चतुर्भुज है व AB = CD और BC = AD
अब ΔABC और ΔCDA में,
∵ AB = CD [ऊपर सिद्ध किया है]
BC = AD [ऊपर सिद्ध किया है]
व AC = AC [उभयनिष्ठ]
∴ भुजा भुजा भुजा सर्वागममता गुणधर्म से,
ΔABC ≅ ΔCDA, इति सिद्धम्।
अन्य विधि: AD || BC तथा तिर्यक रेखा A उन्हें प्रतिच्छेदित करती है।
∴ ∠ACB = ∠CAD (एकान्तर कोण)
तथा ∠CAB = ∠ACD (एकान्तर कोण)
अब ΔABC तथा ΔCDA में
∠ACB = ∠CAD (एकान्तर कोण)
AC = CA (उभयनिष्ट)
∴ ΔABC ≅ ΔCDA इति सिद्धम|
प्रश्न 5.
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिन्दु है BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं (देखिए आकृति)| दर्शाइए कि :
(i) ΔAPB ≅ ΔAQB,
(ii) BP = BQ है अर्थात् बिन्दु B कोण A की भुजाओं से समदूरस्थ है।
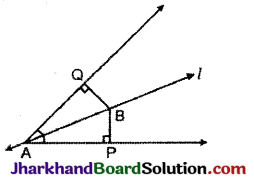
हल:
(i) ΔAPB तथा ΔAQB में,
∠APB = ∠AQB [∵ प्रत्येक = 90°]
∠PAB = ∠QAB
[∵ AB, ∠PAQ का समद्विभाजक है]
व AB = AB [उभयनिष्ठ]
ΔAPB ≅ ΔAQB (AAS नियम)
और (ii) BP = PQ,
[सर्वांगसम त्रिभुजों के संगत भाग]
अतः बिन्दु B, ∠A की भुजाओं से समदूरस्थ है।
इति सिद्धम्।
![]()
प्रश्न 6.
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
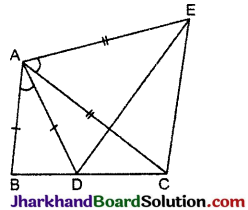
हल:
ΔABC तथा ΔADE में.
AB = AD [दिया है]
∠BAD = ∠DAC [दिया है]
दोनों ओर ∠DAC जोड़ने पर
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠DAE
और AC = AE [दिया है]
ΔABC ≅ ΔADE [SAS नियम]
⇒ BC = DE इति सिद्धम्।
प्रश्न 7.
AB एक रेखाखण्ड है और इसका मध्य-बिन्दु है D और E रेखाखण्ड AB के एक ही ओर स्थित दो
बिन्दु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB हैं (देखिए आकृति)। दर्शाइए कि
(i) ΔDAP ≅ ΔEBP, (ii) AD = BE.
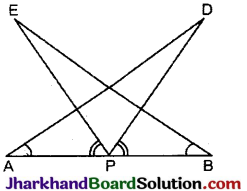
हल:
(i) ∠EPA = ∠DPB [दिया है]
दोनों ओर ∠DPE जोड़ने पर,
∠EPA + ∠DPE = ∠DPB + ∠DPE
⇒ ∠DPA = ∠EPB
अब, ΔDAP तथा ΔEBP में.
∠EPB = ∠DPA [सिद्ध किया है]
BP = AP [∵ P, AB का मध्य-बिन्दु है]
∠EBP =∠DAP [दिया है]
∴ ΔDAP ≅ ΔEBP [ASA नियम]
इति सिद्धम्।
और (ii) ∴ AD = BE
[∵ सर्वागसम त्रिभुजों के संगत भाग] इति सिद्धम् ।
![]()
प्रश्न 8.
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिन्दु है। C को M से मिलाकर बिन्दु D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिन्दु D को बिन्दु B से मिला दिया जाता है (देखिए आकृति) । दर्शाइए कि :
(i) ΔAMC ≅ ΔBMD,
(ii) ∠DBC एक समकोण है,
(iii) ΔDBC ≅ ΔACB
(iv) CM = \(\frac{1}{2}\)AB
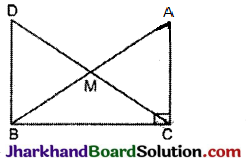
हल:
(i) ΔAMC तथा ΔBMD में,
AM = BM [∵ M, AB का मध्य-बिन्दु है]
∠AMC = ∠BMD [शीर्षाभिमुख कोण]
व CM = MD [दिया है]
∴ ΔAMC ≅ ΔBMD. [SAS नियम]
इति सिद्धम् ।
(ii) ∵ ΔAMC ≅ ΔBMD
∴ BD = CA
व ∠BDM = ∠ACM
[सर्वागसम त्रिभुजों के संगत भाग]
इसलिए तिर्यक रेखा CD, CA तथा BD को क्रमश: C तथा D पर बिन्दुओं पर इस प्रकार काटती है कि एकान्तर कोण
∠BDM = ∠ACM । अत: BD || CA.
⇒ ∠CBD + ∠BCA = 180°
[∵ तिर्यक रेखा के एक ही ओर के आन्तरिक कोण]
⇒ ∠CBD + 90° = 180° [∵ ∠BCA = 90°]
⇒ ∠DBC = 90°. इति सिद्धम्।
(iii) अब ΔDBC तथा ΔACB में,
BD = CA [भाग (i) से]
∠DBC = ∠ACB [प्रत्येक 90°]
BC = BC. [उभयनिष्ठ]
ΔDBC ≅ ΔACB. [SAS नियम ]
इति सिद्धम्।
(iv) CD = AB
[सर्वागसम त्रिभुजों के संगत भाग]
या \(\frac{1}{2}\)CD = \(\frac{1}{2}\)AB
या CM = \(\frac{1}{2}\)AB.
इति सिद्धम्।