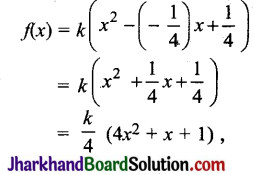Month: October 2024

Jharkhand Board JAC Class 9 Science Important Questions Chapter 10 गुरुत्वाकर्षण Important Questions and Answers.

JAC Board Class 9 Science Important Questions Chapter 10 गुरुत्वाकर्षण

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सूत्र F = G \(\frac{m_1 m_2}{r^2}\) से ज्ञात किया जा सकता है-
(a) गुरुत्वाकर्षण बल
(b) पृथ्वी द्वारा आरोपित गुरुत्वीय बल
(c) गुरुत्वीय त्वरण
(d) पृथ्वी तथा चन्द्रमा के बीच लगने वाला आकर्षण बल।
उत्तर:
(a) गुरुत्वाकर्षण बल।

प्रश्न 2.
दो पिण्डों के मध्य गुरुत्वाकर्षण बल निम्न से किस पर निर्भर नहीं करता?
(a) उनके मध्य की दूरी पर
(b) उनके द्रव्यमानों के गुणनफल पर
(c) गुरुत्वाकर्षण नियतांक पर
(d) द्रव्यमानों के योग पर।
उत्तर:
(d) द्रव्यमानों के योग पर।

प्रश्न 3.
निर्वात् में स्वतन्त्रतापूर्वक गिरते हुए पिण्डों का-
(a) वेग समान होता है
(b) त्वरण समान होता है
(c) बल समान होता है
(d) जड़त्व समान होता है।
उत्तर:
(b) त्वरण समान होता है

प्रश्न 4.
यदि किसी मीनार से मुक्त रूप से गिरते हुए पिण्ड को पृथ्वी तक पहुँचने में 6 सेकण्ड का समय लगता है तो मीनार की ऊँचाई होगी-
(a) 176.4 मीटर
(c) 100 मीटर
(b) 175 मीटर
(d) 600 मीटर।
उत्तर:
(a) 176.4 मीटर।

प्रश्न 5.
पृथ्वी पर रखी दो वस्तुओं के मध्य गुरुत्वाकर्षण बल F है। यदि उनमें से प्रत्येक का द्रव्यमान 1/4 कर दिया जाय तो गुरुत्वाकर्षण बल होगा-
(a) F
(b) \(\frac { F }{ 16 }\)
(c) \(\frac { F }{ 4 }\)
(d) 4F.
उत्तर:
(b) \(\frac { F }{ 16 }\)

प्रश्न 6.
सार्वत्रिक गुरुत्वाकर्षण नियतांक G का मात्रक होता है-
(a) न्यूटन / किग्रा
(b) मीटर/सेकण्डर
(c) न्यूटन मीटर²- किग्रा²
(d) न्यूटन मीटर² / किग्रा²।
उत्तर:
(d) न्यूटन मीटर² / किग्रा²।

प्रश्न 7.
किसी मकान की छत से पिण्ड गिराया जाता है। 50 मीटर गिरने के बाद पिण्ड की चाल होगी-
(a) 9.8 मीटर/सेकण्ड
(b) 31.30 मीटर / सेकण्ड
(c) 3.13मीटर / सेकण्ड
(d) उपर्युक्त में से कोई नहीं।
उत्तर:
(b) 31.30 मीटर / सेकण्ड।

प्रश्न 8.
गुरुत्वजनित त्वरण g का सही सूत्र है-
(a) g = \(\frac { GM }{ R }\)
(b) g = \(\frac{\mathrm{GM}}{r^2}\)
(c) g = \(\frac{G M^2}{\mathrm{R}}\)
(d) g = \(\frac{G M^2}{\mathrm{R}^2}\)
उत्तर:
(b) g = \(\frac{\mathrm{GM}}{r^2}\)

प्रश्न 9.
गुरुत्वीय त्वरण का मान-
(a) सभी ग्रहों पर समान होता है।
(b) पृथ्वी के सभी स्थानों पर समान होता है
(c) ध्रुवों पर अधिक, भूमध्य रेखा पर कम होता है
(d) उपर्युक्त में कोई सत्य नहीं है।
उत्तर:
(c) ध्रुवों पर अधिक, भूमध्य रेखा पर कम होता है।

प्रश्न 10.
ऊर्ध्वाधर ऊपर फेंके गये पिण्ड का महत्तम ऊँचाई पर वेग-
(a) शून्य होता है
(b) अधिकतम होता है
(c) न्यूनतम होता है
(d) 9.8 मी / सेकण्ड होता है।
उत्तर:
(a) शून्य होता है।

प्रश्न 11.
दो पत्थर 2: 3 के अनुपात के वेगों से फेंके जाते हैं तो उनके द्वारा तय महत्तम ऊँचाइयों का अनुपात होगा-
(a) 2:3
(b) 3:2
(c) 9:1
(d) 4:91
उत्तर:
(d) 4:91

प्रश्न 12.
पृथ्वी पर किसी वस्तु का भार 120 किग्रा है तो चन्द्रमा पर उसका भार होगा-
(a) 120 किग्रा
(b) 60 किग्रा
(c) 20 किग्रा
(d) 10 किग्रा ।
उत्तर:
(c) 20 किग्रा।

प्रश्न 13.
चन्द्रमा पर गुरुत्वीय त्वरण का मान होता है-
(a) 9.8m/s²
(b) 1.57m/g²
(c) 6.67m/s²
(d) 0.98m/s².
उत्तर:
(b) 1.57m/s².

प्रश्न 14.
आपेक्षिक घनत्व का मात्रक है-
(a) मी.
(b) किग्रा
(c) सेकण्ड
(d) कोई मात्रक नहीं होता।
उत्तर:
(d) कोई मात्रक नहीं होता।

प्रश्न 15.
दाब का मात्रक है-
(a) न्यूटन²
(b) न्यूटन / मीर²
(c) न्यूटन मीटर²
(d) न्यूटन मीटर
उत्तर:
(b) न्यूटन / मी²

रिक्त स्थान भरो

1. गुरुत्वीय त्वरण का मान भिन्न-भिन्न स्थानों पर ……………… होता है।
2. गुरुत्वीय स्थिरांक का मान सदैव ……………… होता है।
3. उत्प्लावन बल सदैव ……………… की ओर आरोपित होता है।
4. किसी पदार्थ का एकांक आयतन द्रव्यमान ……………… कहलाता है।

उत्तर:

1. भिन्न
2. स्थिर
3. ऊपर
4. घनत्व।

सुमेलन कीजिए

उत्तर:
1. (ख) mg
2. (घ) \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
3.
4. (ख) mg

सत्य / असत्य

1. दो वस्तुओं के बीच उनकी बीच दूरी के वर्ग के अनुक्रमानुपाती होता है।
2. G का मान भिन्न स्थानों पर भिन्न होता है।
3. g की दिशा सदैव पृथ्वी के केन्द्र की ओर होती है।
4. भार का SI मात्रक kg होता है।

उत्तर:

1. असत्य
2. असत्य
3. सत्य
4. असत्य।

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
वस्तुओं का पृथ्वी की ओर मुक्त रूप से गिरना किस बल के कारण होता है?
उत्तर:
पृथ्वी के गुरुत्व बल के कारण।

प्रश्न 2.
क्या ‘g’ का मान वस्तु के द्रव्यमान पर निर्भर करता है?
उत्तर:
नहीं, ‘g’ का मान वस्तु के द्रव्यमान पर निर्भर नहीं करता।

प्रश्न 3.
यदि दो भिन्न-भिन्न द्रव्यमान की वस्तुओं को एक ऊँचाई से एक साथ मुक्त रूप से गिराया जाए तो वे एक ही साथ पृथ्वी पर पहुंचेंगी या अलग-अलग समय पर?
उत्तर:
एक ही साथ।

प्रश्न 4.
किन्हीं दो वस्तुओं के बीच अन्य कोई द्रव्य रखा जाए तो उनके बीच लगने वाला गुरुत्व बल समान रहता है या बदल जाता है।
उत्तर:
गुरुत्व बल का मान समान रहता है।

प्रश्न 5.
‘g’ व G में क्या सम्बन्ध है?
उत्तर:
g = G\(\frac{\mathrm{M}}{\mathrm{R}^2}\)

प्रश्न 6.
पृथ्वी तल से ऊपर जाने पर g के मान पर क्या प्रभाव पड़ता है?
उत्तर:
पृथ्वी तल से ऊपर जाने पर 8 का मान घटता है।

प्रश्न 7.
चन्द्रमा पर गुरुत्वीय त्वरण कितना होता है?
उत्तर:
चन्द्रमा पर गुरुत्वीय त्वरण का मान, पृथ्वी पर गुरुत्वीय त्वरण के मान का 1/6 भाग होता है।

प्रश्न 8.
क्या g तथा G दोनों सार्वत्रिक नियतांक हैं?
उत्तर:
नहीं, केवल G सार्वत्रिक नियतांक है।

प्रश्न 9.
क्या गुरुत्वीय त्वरण एक सदिश राशि है अथवा अदिश? इसका SI मात्रक लिखिए।
उत्तर:
यह एक सदिश राशि है जिसकी दिशा सदैव पृथ्वी के केन्द्र की ओर होती है। इसका SI मात्रक मीटर / सेकण्ड² है।

प्रश्न 10.
यदि कोई पत्थर का टुकड़ा पृथ्वी की ओर मुक्त रूप से गिरता है तो पृथ्वी उस पर गुरुत्व बल लगाती है जिसके कारण पत्थर का टुकड़ा पृथ्वी की ओर त्वरित होता है क्या पत्थर भी पृथ्वी को अपनी ओर आकर्षित करता है?
उत्तर:
पत्थर भी पृथ्वी को गुरुत्व बल के बराबर बल से अपनी ओर आकर्षित करता है।

प्रश्न 11.
किसी वस्तु पर लगा गुरुत्व बल किस दिशा में कार्य करता है?
उत्तर:
वस्तु से पृथ्वी के केन्द्र को मिलाने वाली रेखा के अनुदिश कार्य करता है।

प्रश्न 12.
गुरुत्वीय त्वरण का मान कितना है और इसके मात्रक क्या हैं?
उत्तर:
गुरुत्वीय त्वरण g का मान = 9.8 m/s² तथा मात्रक m/s² है।

प्रश्न 13.
ध्रुवों तथा भूमध्य रेखा में से किस स्थान पर गुरुत्वीय त्वरण का मान अधिक होता है?
उत्तर:
ध्रुवों पर।

प्रश्न 14.
किसी द्रव पर तैरती वस्तु पर कार्य करने वाले दो बलों के नाम बताइए।
उत्तर:

1. वस्तु का भार
2. द्रव का उत्क्षेप।

प्रश्न 15.
किसी द्रव में डुबोने पर कोई वस्तु हल्की क्यों प्रतीत होती है?
उत्तर:
द्रव द्वारा वस्तु पर लगाए गए उत्प्लावन बल के कारण।

प्रश्न 16.
कुएँ के पानी में डूबी हुई जल से भरी हुई बाल्टी क्यों हल्की प्रतीत होती है?
उत्तर:
कुएँ के पानी के उत्क्षेप के कारण।

प्रश्न 17.
जब किसी तैरती हुई वस्तु को थोड़ा नीचे की ओर दबाया जाता है तो दोनों में से कौन सी राशि बढ़ती है, वस्तु का भार या द्रव का उत्प्लावन बल?
उत्तर:
द्रव का उत्प्लावन बल।

प्रश्न 18.
सबसे पहले किस वैज्ञानिक ने यह अनुमान लगाया कि पृथ्वी की ओर गिरते हुए पिण्डों का त्वरण उनके द्रव्यमान पर निर्भर नहीं करता?
उत्तर:
गैलीलियो ने।

प्रश्न 19.
उस वैज्ञानिक का नाम बताओ जिसने सबसे पहले प्रयोग द्वारा सिद्ध किया कि भिन्न-भिन्न वस्तुओं का त्वरण पृथ्वी की ओर गिरते हुए, द्रव्यमान पर निर्भर नहीं करता अर्थात् सभी पिण्ड पृथ्वी की ओर समान त्वरण से गिरते हैं।
उत्तर:
राबर्ट बॉयल।

प्रश्न 20.
गुरुत्वाकर्षण स्थिरांक G का मान विभिन्न ग्रहों पर अलग-अलग होगा या समान।
उत्तर:
विभिन्न ग्रहों पर G का मान समान रहेगा।

प्रश्न 21.
एक वस्तु का वायु में भार W₁ तथा जल में डुबोने पर भार W₂ है। वस्तु का आपेक्षिक घनत्व क्या होगा?
उत्तर:
वस्तु का आपेक्षिक घनत्व

प्रश्न 22.
6.5 आपेक्षिक घनत्व तथा 0.7 आपेक्षिक घनत्व वाले दो पिण्डों में से कौन-सा पिण्ड जल पर तैरेगा और क्यों?
उत्तर:
0.7 आपेक्षिक घनत्व वाला पिण्ड जल पर तैरेगा क्योंकि इसका आपेक्षिक घनत्व 1 से कम है।

प्रश्न 23.
एक ही ऊँचाई से एक पत्थर का टुकड़ा तथा एक कागज का टुकड़ा गिराने पर वे एक साथ पृथ्वी पर क्यों नहीं आते?
उत्तर:
वायु के घर्षण के कारण।

प्रश्न 24.
वस्तु के आभासी भार का क्या अर्थ है?
उत्तर:
किसी वस्तु का द्रव में डूबी हुई अवस्था में भार, वस्तु का ‘आभासी भार’ कहलाता है।

प्रश्न 25.
यदि विभिन्न प्रक्षेप्य पृथ्वी के समांतर एक ही ऊँचाई से तथा विभिन्न चाल से एक ही समय फेंके जाएँ तो वे पृथ्वी पर एक साथ पहुँचेंगे या अलग-अलग समय पर?
उत्तर:
एक साथ।

प्रश्न 26.
द्रव्यमान या संहति का SI मात्रक क्या है?
उत्तर:
किलोग्राम (kg)।

प्रश्न 27.
भार का SI मात्रक क्या है?
उत्तर:
न्यूटन (N)।

प्रश्न 28.
1 किलोग्राम भार (kg wt) में कितने न्यूटन होते हैं?
उत्तर:
1 किलोग्राम भार 9.8 न्यूटन (यदि g = 9.8 m/s²)।

प्रश्न 29.
एक पिण्ड द्वारा दूसरे पिण्ड पर लगाए गए गुरुत्वाकर्षण बल तथा दूसरे पिण्ड द्वारा पहले पर लगाए गए गुरुत्वाकर्षण बल के बीच क्या अनुपात होगा?
उत्तर:
दोनों एक-दूसरे पर समान परिमाण का बल लगाते हैं; अतः यह अनुपात 1 : 1 होगा।

प्रश्न 30.
उस वैज्ञानिक का नाम बताइए जिसने सार्वत्रिक गुरुत्वाकर्षण नियतांक G का मान ज्ञात किया था?
उत्तर:
हेनरी कैवेन्डिश।

प्रश्न 31.
कोई वस्तु ऊपर से नीचे की ओर गिर रही है तो गति के समीकरण का स्वरूप बताइए।
उत्तर:

1. v = u + gt
2. h = ut + \(\frac { 1 }{ 2 }\) gt²
3. v² = u² + 2gh.

प्रश्न 32.
दाब का सूत्र लिखिए।
उत्तर:

प्रश्न 33.
क्या दाब एक सदिश राशि है?
उत्तर:
नहीं, दाब एक सदिश राशि नहीं है।

प्रश्न 34.
किसी वस्तु को नीचे से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है तो गति के समीकरणों के स्वरूप बताइए।
उत्तर:

1. v = u – gt.
2. h = ut – \(\frac { 1 }{ 2 }\) gt²
3. v² = u² – 2gh

लघुत्तरात्मक एवं दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
प्लवन अथवा उत्प्लवन के नियम लिखिए।
उत्तर:
जब किसी वस्तु को किसी द्रव में छोड़ा जाता है, तो उस पर दो बल कार्य करते हैं-

• वस्तु का भार W नीचे की ओर,
• वस्तु पर द्रव का उछाल बल F ऊपर की ओर।

इन दोनों बलों का परिणामी बल जिस दिशा में होगा, वस्तु का तैरना या डूबना इन्हीं बलों के मान पर निर्भर करता है; इसमें निम्नलिखित तीन स्थितियाँ सम्भव हैं-
स्थिति 1.
यदि वस्तु का भार W, उत्क्षेप बल F से अधिक है। इस स्थिति में वस्तु का परिणामी (WF) नीचे की ओर कार्य करता है तथा वस्तु द्रव में डूब जाएगी (चित्र 10.9. (a)) I

स्थिति 2.
यदि W = F अर्थात् वस्तु का भार उत्क्षेप बल के बराबर है। इस अवस्था में वस्तु पर परिणामी बल शून्य होगा। अतः वस्तु द्रव में पूरी तरह डूबकर तैरेगी। इसे वस्तु की प्लवन या तैरने की अवस्था कहते हैं ऐसा तब होता है जब वस्तु का घनत्व, द्रव के घनत्व के बराबर होता है (चित्र 10.9. (b))।

स्थिति 3.
जब W < F, इस अवस्था में वस्तु पर परिणामी बल (F- W) ऊपर की ओर लगेगा। अतः वस्तु द्रव में आंशिक रूप से डूबी रहकर तैरेगी सन्तुलन की अवस्था में वस्तु का आभासी भार शून्य होगा। यह भी वस्तु के प्लवन अथवा तैरने की अवस्था है। इस अवस्था में वस्तु का घनत्व, द्रव के घनत्व से कम होता है (चित्र 10.9 (c))।

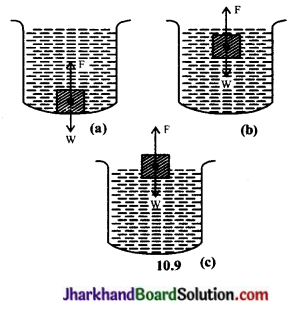
इस प्रकार हम देखते हैं “कि जब कोई वस्तु द्रव में पूर्णतः या आंशिक रूप से डूबी रहकर तैरती है, तो वस्तु का भार, उसके डूबे हुए भाग द्वारा हटाए गए द्रव के भार के बराबर होता है।” यही प्लवन का नियम हैं।

वस्तु का भार तथा वस्तु पर उत्क्षेप परस्पर विपरीत दिशाओं में लगते हैं। वस्तु के सन्तुलन में तैरने के लिए किसी भी प्रकार का बल आघूर्ण नहीं होना चाहिए। इसके लिए वस्तु का भार व उत्क्षेप बल एक ही ऊर्ध्वाधर रेखा में होने चाहिए अतः सन्तुलन में वस्तु के तैरने के लिए निम्नलिखित दो शर्तें हैं-

• वस्तु का भार उसके द्वारा विस्थापित द्रव के भार के बराबर होना चाहिए।
• वस्तु का गुरुत्व केन्द्र तथा विस्थापित द्रव का उत्प्लवन केन्द्र एक ही ऊर्ध्वाधर रेखा में होने चाहिए।

प्रश्न 2.
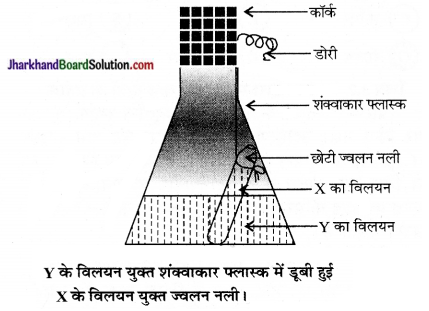
आर्किमिडीज के सिद्धान्त के सत्यापन को लिखिए।
उत्तर:
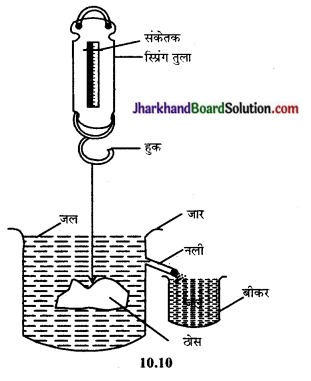
इसे चित्र 10.10 के अनुसार प्रदर्शित उपकरण द्वारा सत्यापित किया जाता है। इसमें काँच का एक जार होता है। इसके मुँह के पास नली लगी होती है। जार में नली की सतह तक जल भर दिया जाता है। अब ठोस का भार वायु में ज्ञात कर लेते हैं। इसके लिए एक स्प्रिंग से लटके हुए ठोस को पानी से भरे जार में डुबोते हैं।

जैसे-जैसे ठोस पानी में डूबता जाता है उसके भार में कमी होती जाती है; स्प्रिंग तुला द्वारा इसके भार में कमी को नोट कर लेते हैं तथा विस्थापित द्रव एक बीकर में एकत्रित होता जाता है। बीकर में एकत्रित हुए जल का भार ज्ञात कर लिया जाता है। ठोस के भार में कमी, उसके द्वारा हटाए गए पानी के भार के बराबर हो जाती है। अतः आर्किमिडीज के सिद्धान्त का सत्यापन हो जाता है।

प्रश्न 3.
किसी पदार्थ के आपेक्षिक घनत्व से आप क्या समझते हैं? स्पष्ट कीजिए।
उत्तर:
आपेक्षिक घनत्व किसी पदार्थ के घनत्व तथा जल के घनत्व के अनुपात को उस पदार्थ का आपेक्षिक घनत्व कहते हैं।

चूँकि आपेक्षिक घनत्व एक अनुपात है; अतः इसका कोई मात्रक नहीं होता है।
किसी पदार्थ का आपेक्षिक घनत्व से कम होने पर वह पदार्थ जल में तैरेगा। यदि किसी पदार्थ का आपेक्षिक घनत्व से अधिक है तो वह पदार्थ जल में डूब जाएगा।
माना किसी वस्तु का आयतन V तथा घनत्व d₁ है, जबकि जल का घनत्व d₂ है।
तब वस्तु का वायु में भार
W₁ = वस्तु का आयतन x घनत्व x g = Vd₁ g
तथा जल में डुबोने पर, वस्तु के भार में कमी – वस्तु द्वारा हटाए गए पानी का भार
= वस्तु का आयतन × जल का घनत्व x g = Vd₂ g

प्रश्न 4.
भारी वाहनों के पहियों के टायर काफी चौड़े क्यों बनाए जाते हैं?
उत्तर:
भारी वाहनों के टायर काफी बड़े बनाना भारी वाहनों के टायर चौड़े होने से (क्षेत्रफल A अधिक है) सड़क अथवा जमीन पर लगने वाला दाब (PF/A) कम हो जाता है, क्योंकि वाहन का भार अधिक क्षेत्रफल पर लगता है, इसलिए वाहन के पहिये सड़क में धँसने से बच जाते हैं।

प्रश्न 5.
लोहे से बना जहाज समुद्र में तैरता है, परन्तु लोहे का ठोस टुकड़ा (कील) डूब जाता है, क्यों? सम्बन्धित नियम देते हुए इस कथन की व्याख्या कीजिये।
उत्तर:
लोहे से बने जहाज का जल पर तैरना – लोहे की कील की बनावट इस प्रकार की होती है कि उसका भार, उसके द्वारा हटाए गए जल के भार से बहुत अधिक होता है। इसी कारण वह जल में डूब जाती है।

इसके विपरीत लोहे का जहाज तैरता है। इसका कारण यह है कि जहाज का ढाँचा अवतल होता है तथा अन्दर से खोखला बनाया जाता है। जैसे ही जहाज समुद्र में प्रवेश करता है तो उसके द्वारा (उसकी बनावट के कारण) इतना जल हटा दिया जाता है कि उसके द्वारा हटाए गए जल का भार, जहाज (जहाज व उसके समस्त सामान सहित) के कुल भार के बराबर हो जाता है। इसी कारण प्लवन के सिद्धान्त के अनुसार जहाज जल में तैरता रहता है।

प्रश्न 6.
उत्प्लवन बल तथा उत्प्लवन केन्द्र से क्या तात्पर्य हैं?
उत्तर:
उत्प्लवन बल अथवा उत्क्षेप तथा उत्प्लवन केन्द्र- प्रत्येक द्रव अपने अन्दर पूर्ण अथवा आंशिक रूप से डूबी वस्तु पर ऊपर की ओर एक बल लगाता है। इस बल को उत्प्लवन बल अथवा उत्क्षेप कहते हैं यह बल वस्तु द्वारा हटाए गए द्रव के गुरुत्व केन्द्र पर कार्य करता है, इसे उत्प्लवन केन्द्र कहते हैं। उत्प्लवन बल के कारण ही द्रव में डूबी वस्तुएँ अपने वास्तविक भार से हल्की लगती हैं।

प्रश्न 7.
प्लवन (तैरने के नियम लिखिए।
अथवा
किसी वस्तु के सन्तुलन में तैरने के लिए क्या आवश्यक शर्तें हैं?
अथवा
कोई वस्तु किसी द्रव में कब तक तैरती है?
उत्तर:
प्लवन (तैरने) के नियम- किसी वस्तु के सन्तुलन में तैरने की दो शर्तें हैं-

• तैरने वाली वस्तु का भार वस्तु द्वारा हटाए गए द्रव के भार के बराबर होना चाहिए।
• वस्तु का गुरुत्व केन्द्र तथा हटाए गए द्रव का उत्प्लावन केन्द्र एक ही ऊर्ध्वाधर रेखा में होने चाहिए।

उपर्युक्त दोनों शर्तों के पूर्ण होने पर ही वस्तु द्रव में तैरती हैं।

प्रश्न 8.
रेलगाड़ी की पटरियों के नीचे लकड़ी अथवा लोहे के चौड़े स्लीपर क्यों लगाए जाते हैं?
उत्तर:
यदि रेलगाड़ी की पटरियों के नीचे चौड़े स्लीपर न लगाए जाएँ तो रेल की पटरियाँ अधिक दबाव के कारण जमीन में भैंस सकती हैं। पटरियों के नीचे स्लीपर लगाने से क्षेत्रफल अधिक हो जाता है, जिसके कारण दाब कम पड़ता है (P = F/A); अत: रेल की पटरियाँ जमीन में नहीं भैंस सकती।

प्रश्न 9.
एक तख्ते पर कुछ पुस्तकें फैलाकर रखने की अपेक्षा वही पुस्तकें एक जगह पर ऊपर-नीचे रखने पर तख्ता अधिक नीचे को झुक जाता है, ऐसा क्यों?
उत्तर:
तख्ते पर पुस्तकों को फैलाकर रखने से, उनके द्वारा घिरा क्षेत्रफल (A) अधिक होगा, जिसके कारण तख्ते पर दाब (PF / A) कम लगेगा। पुस्तकों को एक ही स्थान पर ऊपर नीचे रखने से उनके द्वारा घिरा क्षेत्रफल (A) कम होगा, इस कारण तख्ते पर दाब बढ़ जाएगा और तख्ता झुक जाएगा।

प्रश्न 10.
विशाल बाँधों की दीवारें नीचे मोटी व ऊपर पतली क्यों बनाई जाती हैं ?
उत्तर:
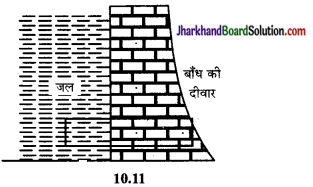
बाँध की दीवारों का नीचे मोटी व ऊपर पतली होना – विशाल बाँधों की गहराई बहुत अधिक होती है, चूँकि द्रव के अन्दर किसी बिन्दु पर दाब उस बिन्दु की मुक्त तल से गहराई के अनुक्रमानुपाती होता है; अतः बाँध की तली में जल का दाब सर्वाधिक होता है दाब क्योंकि एक ही क्षैतिज तल में सब बिन्दुओं पर सभी दिशाओं में समान होता है; अतः बाँध की दीवार पर सबसे अधिक दाब नीचे होता है; जैसे-जैसे ऊपर आते हैं दाब भी घटता जाता है; अतः बाँध की दीवार नीचे से मोटी बनाई जाती है, जिससे वह अधिक दाब बल को सहन कर सके। ऊपर जाने पर, क्योंकि दाब घटता जाता है अतः दीवारों की मोटाई भी कम करते जाते हैं, जैसा कि चित्र 10.11 में दिखाया गया है।

प्रश्न 11.
समान बल लगाने पर मोटी कील की अपेक्षा नुकीली कील दीवार में शीघ्र क्यों गढ़ जाती है?
उत्तर:
मोटी तथा नुकीली कीलों पर दाब – नुकीली कील के सिरे का क्षेत्रफल, मोटी कील के सिरे के क्षेत्रफल की अपेक्षा बहुत कम होती है; अतः दोनों कीलों पर एकसमान – बल लगाने से नुकीली कील द्वारा दीवार पर मोटी कील की अपेक्षा अधिक दाब (P = F/A) लगता है, जिससे नुकीली कील दीवार में आसानी से गढ़ जाती है।

प्रश्न 12.
कुएँ से जल खींचते समय जल से भरी बाल्टी जल की सतह से ऊपर आने पर धीरे-धीरे भारी क्यों प्रतीत होने लगती है?
उत्तर:
जब बाल्टी जल में डूबी होती है, तब उस पर उसके द्वारा हटाए गए जल के भार के बराबर उत्क्षेप बल लगता है जैसे-जैसे बाल्टी को जल से बाहर निकालते हैं, उस पर लगने वाले उत्क्षेप बल का मान कम होने लगता है। और बाल्टी भारी लगने लगती है।

आंकिक प्रश्न

प्रश्न 1.
किसी कक्षा में बैठे दो छात्रों के मध्य कितना आकर्षण बल लगेगा यदि इनके द्रव्यमान क्रमश: 20 किग्रा, 30 किग्रा है तथा इनके मध्य की दूरी 2 मीटर है।
हल:
प्रश्नानुसार ms₁ = 20 किग्रा, m₂ = 30 किग्रा, d = 2 मीटर G = 6.7 x 10^-11 न्यूटन मीटर 2 / किग्रा, F = ?
∵ गुरुत्वाकर्षण बल F = G\(\frac{m_1 m_2}{d^2}\)
= 6.67 × 10^-11 x \(\frac{20 \times 30}{(2)^2}=\frac{6.67 \times 10^{-11} \times 20 \times 30}{4}\)
= 1000.5 x 10^-11 न्यूटन
= 1.0 × 10^-8 न्यूटन (लगभग) उत्तर

प्रश्न 2.
यदि पृथ्वी का द्रव्यमान 5.97 x 10²⁴ किग्रा, पृथ्वी की त्रिज्या 6.38 x 10⁶ मीटर तथा एक व्यक्ति का द्रव्यमान 60 किग्रा है यदि गुरुत्वाकर्षण नियतांक 6.67 x 10^-11 न्यूटन मीटर²/किग्रा² हो, तो पृथ्वी एवं व्यक्ति के मध्य गुरुत्वाकर्षण बल की गणना कीजिए।
हल:
प्रश्नानुसार,
पृथ्वी का द्रव्यमान M = 5.97 x 10²⁴ किग्रा
पृथ्वी की त्रिज्या R = 6.38 x 10⁶ मीटर
व्यक्ति का द्रव्यमान m = 60 किग्रा
गुरुत्वाकर्षण नियतांक
G = 6.67 x 10^-11 न्यूटन मी² / किग्रार
गुरुत्वाकर्षण बल F = ?

प्रश्न 3.
पृथ्वी का द्रव्यमान 6 x 10²⁴ किग्रा, चन्द्रमा का द्रव्यमान 7.4 x 10²² किग्रा तथा दोनों के मध्य की दूरी 3.84 x 10⁸ मीटर है। पृथ्वी तथा चन्द्रमा के मध्य लगने वाले आकर्षण बल की गणना कीजिए।
हल:
प्रश्नानुसार,
पृथ्वी का द्रव्यमान M = 6 × 10²⁴ किग्रा
चन्द्रमा का द्रव्यमान m = 7.4 x 10²² किग्रा
पृथ्वी तथा चन्द्रमा के मध्य दूरी d = 3.84 x 10⁸ मीटर
गुरुत्वाकर्षण नियतांक
G = 6.67 x 10^-11 न्यूटन मी²/ किग्रा²

प्रश्न 4.
यदि पृथ्वी की त्रिज्या 6.67 x 10^-11 न्यूटन – मी² / किग्रा² तथा 89.8 मीटर/सेकण्ड² हो तो पृथ्वी के द्रव्यमान की गणना कीजिए।
हल:
पृथ्वी की त्रिज्या R = 6.38 x 10⁶ मीटर
गुरुत्वाकर्षण नियतांक G = 6.67 x 10^-11 न्यूटन मी²./किग्रा
गुरुत्वीय त्वरण g = 9.8 मीटर/सेकण्ड²
पृथ्वी का द्रव्यमान M = ?
समीकरण g = \(\frac{g \mathrm{R}^2}{G}\) से M
= \(\frac{9.8 \times\left(6.38 \times 10^6\right)^2}{6.67 \times 10^{-11}}=\frac{398.90312 \times 10^{12}}{6.67 \times 10^{-11}}\)
= 59.81 × 10²³ = 5.98 × 10²⁴ किग्रा

प्रश्न 5.
एक व्यक्ति का पृथ्वी की सतह पर भार 60 किग्रा है। यदि मंगल ग्रह का द्रव्यमान, पृथ्वी की अपेक्षा \(\frac { 1 }{ 9 }\) तथा त्रिज्या पृथ्वी की अपेक्षा \(\frac { 1 }{ 2 }\) है तो मंगल ग्रह पर व्यक्ति का भार ज्ञात कीजिए।
हल:
∵ F = G x \(\frac{\mathrm{M} \times m}{\mathrm{R}^2}\)
पृथ्वी का द्रव्यमान M तथा त्रिज्या R है।
प्रश्नानुसार, F = 60 किग्रा भार = 60 x 9.8 न्यूटन
60 × 9.8 = G\(\frac{\mathrm{M} \times m}{\mathrm{R}^2}\) … (i)
मंगल का द्रव्यमान = \(\frac {M }{ 9 }\), मंगल ग्रह की त्रिज्या = \(\frac { R }{ 2 }\) यदि मंगल ग्रह पर व्यक्ति का भार ‘m’ किग्रा हो तो
m’g = \(\frac{\mathrm{G} \times \frac{\mathrm{M}}{9} \times m}{\left(\frac{\mathrm{R}}{2}\right)^2}\) … (ii)
समीकरण (ii) को (i) से भाग देने पर
\(\frac{m^{\prime} g}{60 \times 9.8}=\frac{4}{9} ; m^{\prime} g=\frac{60 \times 9.8 \times 4}{9}=\frac{2352}{9}\)
m’g – 261.34 न्यूटन = \(\frac { 261.34 }{ 9.8 }\)
m’ = 26:67 किग्रा

प्रश्न 6.
एक ग्रह का द्रव्यमान पृथ्वी से 6 गुना है। इसका व्यास पृथ्वी के व्यास का 6 गुना है। यदि पृथ्वी पर g का मान 9.8 मीटर / से² हो तो ग्रह पर गुरुत्वीय त्वरण g’ का मान ज्ञात कीजिए।
हल:
पृथ्वी पर गुरुत्वीय त्वरण
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) … (i)
इसी प्रकार ग्रह पर गुरुत्वीय त्वरण
g’ = \(\frac{\mathrm{GM}^{\prime}}{\mathrm{R}^{\prime 2}}\) … (ii)
समीकरण (ii) को समीकरण (i) से भाग देने पर
\(\frac{g^{\prime}}{g}=\frac{\frac{\mathrm{GM}^{\prime}}{\mathrm{R}^{\prime 2}}}{\frac{\mathrm{GM}}{\mathrm{R}^2}} \Rightarrow \frac{g^{\prime}}{g}=\left(\frac{\mathrm{M}^{\prime}}{\mathrm{M}}\right)\left(\frac{\mathrm{R}}{\mathrm{R}^{\prime}}\right)^2\)
प्रश्नानुसार, M’ = 6M अथवा \(\frac {M’ }{ M }\) = 6
R’ = 6R अथवा \(\frac {R }{ R’ }\) = \(\frac { 1 }{ 6 }\)
अतः \(\frac { g’ }{ g }\) = 6 x (\(\frac { 1 }{ 6 }\))² = \(\frac { 1 }{ 6 }\)
अतः ग्रह पर गुरुत्वीय त्वरण
g’ = g x \(\frac { 1 }{ 6 }\) = 9.8 x \(\frac { 1 }{ 6 }\)
= 1.63 मीटर / सेकण्डर²

प्रश्न 7.
दो पिण्डों के मध्य गुरुत्वाकर्षण F है। यदि पिण्डों के मध्य दूरी आधी कर दी जाय तो उनके मध्य गुरुत्वाकर्षण बल कितना हो जायेगा?
हल:
माना कि पिण्डों के द्रव्यमान m₁ एवं m₂ हैं तथा उनके बीच की पहली दूरी है तो-
F = G \(\frac { 1 }{ 6 }\) … (i)
बीच की दूरी आधा कर देने पर बल
F’ = \(\frac{\mathrm{G} m_1 m_2}{(r / 2)^2}=\frac{4 \mathrm{G} m_1 m_2}{r^2}\)
\(\frac{\mathrm{F}^{\prime}}{\mathrm{F}}=\frac{4 \mathrm{G} m_1 m_2}{r^2} / \frac{\mathrm{G} m_1 m_2}{r^2}\) = 4 … (ii)
∴ F’ = 4F
अतः गुरुत्वाकर्षण बल 4 गुना हो जायेगा।0

प्रश्न 8.
एक पिण्ड को पृथ्वी तल से h ऊँचाई से गिराने पर वह पृथ्वी पर 10 सेकण्ड में पहुँचता है, तो / का मान ज्ञात कीजिए। (g = 9.8 मीटर/सेकण्ड²)
हल:
प्रश्नानुसार u = 0 मीटर / सेकण्ड
= 10 सेकण्ड
h = ?
∵ h = ut + \(\frac { 1 }{ 2 }\) gt²
∴ h = (0 × 10) + \(\frac { 1 }{ 2 }\) × 9.8 × (10)²
h = \(\frac { 1 }{ 2 }\) × 9.8 × 10 × 10
= 490 मीटर

प्रश्न 9.
यदि किसी पिण्ड का भार 98 न्यूटन है तो वस्तु का द्रव्यमान कितना होगा? (g = 9.8 मीटर / सेकण्ड²)
हल:
प्रश्नानुसार, W = 98 न्यूटन
8 = 9.8 मीटर/सेकण्डर²
m = ?
∵ भार (W) = द्रव्यमान (m) x गुरुत्वीय त्वरण (g)
∴ द्रव्यमान (m) = \(\frac { W }{ g }\) = \(\frac { 9.8 }{ 9.8 }\)
= 10 किलोग्राम उत्तर

प्रश्न 10.
एक पिण्ड को ऊर्ध्वाधरतः ऊपर की ओर किस वेग से फेंकें कि वह 150 मीटर ऊँचाई तक जाये। (g = 9.8 मीटर/सेकण्ड²)
हल:
प्रश्नानुसार,
अन्तिम वेग v = 0
प्रारम्भिक वेग u = ?
गुरुत्वीय त्वरण g = 9.8 मीटर/सेकण्डर²
∵ v² = u² – 2gh
∴ (0)² = u² – 2gh या u² = 2gh
या u = \(\sqrt{2gh}\)
या u = \(\sqrt{2 \times 9.8 \times 150}\)
= 54.22 मीटर / सेकण्ड उत्तर

प्रश्न 11.
60 मीटर ऊँचाई की मीनार से एक लड़का किसी पत्थर के टुकड़े को नीचे गिराता है। पुनः 1 सेकण्ड पश्चात् वही लड़का दूसरे पत्थर के टुकड़े को मीनार से फेंकता है। यदि दोनों पत्थर के टुकड़े पृथ्वी पर एक साथ पहुँचते हैं तो लड़के ने दूसरे पत्थर को किस वेग से फेंका?
हल:
पहले पत्थर के लिए-
प्रश्नानुसार, u = 0, h = 60 मीटर, t = ?
∵ h = ut + \(\frac { 1 }{ 2 }\) gt² से
60 = 0 + \(\frac { 1 }{ 2 }\) x 9.8 x t²
60 = 4.9 x t²
t² = \(\frac { 60 }{ 4.9 }\)
= 12.24
∴ t = \(\sqrt{12.24}\) = 3.49 सेकण्ड
दूसरे पत्थर के लिए-
प्रश्नानुसार,
h = 60 मीटर
t = 349 – 1 = 2.49 सेकण्ड
g = 9.8 मीटर/सेकण्ड², u = ?
समीकरण
h = ut + \(\frac { 1 }{ 2 }\) gt² से
60 = u × 2.49 + \(\frac { 1 }{ 2 }\) x 9.8 (2.49)²
60 = 2.49 u + 30.38
2.49 u = 60 – 30.38
2.49 u = 29.61
u = \(\frac { 29.61 }{ 2.49 }\)
= 11.89 मीटर / सेकण्ड
अतः दूसरे पत्थर का वेग 11.89 मीटर / सेकण्ड होगा।

प्रश्न 12.
किसी व्यक्ति का पृथ्वी पर द्रव्यमान 60 किग्रा है इसका चन्द्रमा पर भार तथा द्रव्यमान कितना होगा ? जबकि चन्द्रमा पर गुरुत्वीय त्वरण, पृथ्वी पर गुरुत्वीय त्वरण g का \(\frac { 1 }{ 6 }\) है।
हल:
प्रश्नानुसार,
चन्द्रमा पर गुरुत्वीय त्वरण
= पृथ्वी पर गुरुत्वीय त्वरण x \(\frac { 1 }{ 6 }\)
= 9.8 × \(\frac { 1 }{ 6 }\)
= 1.63 मीटर/सेकण्डर²
∴ चन्द्रमा पर व्यक्ति का भार (W) = द्रव्यमान (m) x गुरुत्वीय त्वरण (g)
= 60 × 1.63 = 97.8 किग्रा.
∵ द्रव्यमान प्रत्येक स्थान पर नियत रहता है।
अतः चन्द्रमा पर व्यक्ति का द्रव्यमान 60 किग्रा.

प्रश्न 13.
दो वस्तुएँ एक साथ ऊपर फेंकी जाती हैं। यदि उनके प्रारम्भिक वेग का अनुपात 2:3 है तो उनके द्वारा प्राप्त ऊँचाइयों में अनुपात ज्ञात कीजिए।
हल:
माना पहली वस्तु का प्रारम्भिक वेग u तथा प्राप्त ऊँचाई है।
तब वस्तु का अन्तिम वेग शून्य होगा।
अत: समीकरण v² = u² – 2gh से
(0)² = u² – 2gh
∴ h = \(\frac{u^2}{2 g}\) … (i)
इसी प्रकार दूसरी वस्तु का प्रारम्भिक वेग u’ तथा प्राप्त ऊँचाई h’ है।
तब 0 = u² – 2gh’
h’ = \(\frac{u^{\prime 2}}{2 g}\) … (ii)
समीकरण (i) को (ii) से भाग देने पर
\(\frac{h}{h^{\prime}}=\frac{u^2}{u^{\prime 2}}=\left(\frac{u}{u^{\prime}}\right)^2\)
प्रश्नानुसार \(\frac { u }{ u’ }\) = \(\frac { 2 }{ 3 }\)
∴ ऊँचाइयों का अनुपात \(\frac { h }{ h’ }\) = (\(\frac { u }{ u’ }\))² = \(\frac { 4 }{ 9 }\)
अतः प्राप्त ऊँचाइयों का अनुपात 49 होगा।

प्रश्न 14.
दो वस्तुएँ क्रमशः h₁ व h₂ ऊँचाई से एक साथ गिराई जाती हैं। सिद्ध कीजिए कि उनके पृथ्वी पर पहुँचने के समय में \(\sqrt{\frac{h_1}{h_2}}\) का अनुपात होगा।
हल:
दोनों वस्तुएँ एक साथ गिरायी जाती हैं। अतः उनके प्रारम्भिक वेग शून्य होंगे। यदि उनके पृथ्वी पर पहुँचने के समय t₁ व h₂ हाँ तो-
h = ut + \(\frac { 1 }{ 2 }\) gt² से
प्रथम वस्तु के लिए
h₁ = \(\frac { 1 }{ 2 }\) gt₁² (∵ u = 0)
इसी प्रकार द्वितीय वस्तु के लिए
h₂ = \(\frac { 1 }{ 2 }\) gt₁² (∵ u = 0)
∴ \(\frac{h_1}{h_2}=\frac{t_1^2}{t_2^2}\)
अतः \(\frac{t_1}{t_2}=\sqrt{\frac{h_1}{h_2}}\) इति सिद्धम्

प्रश्न 15.
किसी पिण्ड को मीनार की छत के किनारे से गिराया गया है-
(i) 10 मीटर दूरी तय करने में पिण्ड को कितना समय लगेगा?
(ii) उस समय पिण्ड की चाल क्या होगी?
(iii) 16 मीटर दूरी तय करने के बाद उसकी चाल क्या होगी?
(iv) गिरने के 2 सेकण्ड तथा 5 सेकण्ड बाद वस्तु का त्वरण क्या होगा?
हल:
(i) प्रारम्भिक चाल u = 0, ऊँचाई 60 मीटर गुरुत्वीय त्वरण g = 19.8 मीटर/सेकण्ड² समय t = ?
समीकरण h = ut + \(\frac { 1 }{ 2 }\) gt² से
10 = 0 × \(\frac { 1 }{ 2 }\) x 9.8 x t²
10 = 4.9 x t²
t² = 2.04
t = \(\sqrt{2.04}\) = 1.43 सेकण्ड
∴ पत्थर को 10 मीटर तय करने में लगा समय
= 1.43 सेकण्ड

(ii) समीकरण
v = u + gt से
v = 0 + 9.8 × 1.43
= 14 मीटर / सेकण्ड

(iii) ∵ u = 0, h = 16 मीटर, v = ?
समीकरण v² = u² + 2gh
v² = (0)² + 2 × 9.8 × 16
या v² = 313.6
∴ v = 17.71 मीटर/सेकण्ड

(iv) ∵ पत्थर अचर गुरुत्वीय त्वरण के अधीन गति कर रहा है। इसलिए
2 सेकण्ड बाद गुरुत्वीय त्वरण = 9.8 मीटर/सेकण्डर²
5 सेकण्ड बाद गुरुत्वीय त्वरण = 9.8 मीटर/सेकण्डर²

प्रश्न 16.
यदि बल को चार गुना तथा क्षेत्रफल को आधा कर दिया जाए, तो दाब, प्रारम्भिक दाब को कितने गुना हो जाएगा?
हल:

अतः दाब, प्रारम्भिक दाब का आठ गुना हो जाएगा।

प्रश्न 17.
एक व्यक्ति अधिक से अधिक 35 किग्रा भार उठा सकता है। उस पिण्ड का वायु में अधिकतम भार ज्ञात कीजिए जिसे वह व्यक्ति जल में उठा सकता है। (पिण्ड का घनत्व = 3 x 10³ किग्रा / मीटर³, जल का घनत्व = 1 x 10³ किग्रा / मी.³)
हल:
दिया है, जल में पिण्ड का भार = 35 किग्रा
यदि पिण्ड का वायु में भार W किग्रा हो, तो
जल में डुबोने पर पिण्ड के भार में कमी = (W – 35) किग्रा
पुनः पिण्ड का आपेक्षिक घनत्व

अतः पिण्ड का वायु में भार W 52.5 किग्रा।

प्रश्न 18.
75 ग्राम भार के एक पिण्ड को द्रव में डुबोने पर उस पर दूब का उछाल 45 ग्राम भार के बराबर है। यदि पिण्ड के पदार्थ का आपेक्षिक घनत्व 2.5 हो, तो द्रव का आपेक्षिक घनत्व ज्ञात कीजिए।
हल:
दिया है, पिण्ड का वास्तविक भार = 75 ग्राम-भार
पिण्ड पर द्रव का उत्क्षेप = 45 ग्राम भार
पिण्ड के पदार्थ का आपेक्षिक घनत्व = 2.5
द्रव का आपेक्षिक घनत्व = ?
जब पिण्ड द्रव में पूर्णतः डूबता है, तब

प्रश्न 19.
180 ग्राम द्रव्यमान की लकड़ी का एक टुकड़ा एल्कोहॉल में तैर रहा है। टुकड़े द्वारा विस्थापित एल्कोहॉल का आयतन ज्ञात कीजिए । एल्कोहॉल का घनत्व 0.90 ग्राम / सेमी³ है।
हल:
दिया है, m 180 ग्राम, 0.90 ग्राम / सेमी³, V = ?
∴ लकड़ी का टुकड़ा एल्कोहॉल पर तैर रहा है अतः टुकड़े का भार = विस्थापित एल्कोहॉल का भार
180 x g = विस्थापित एल्कोहॉल का आयतन x एल्कोहॉल का घनत्व x g
∴ विस्थापित एल्कोहॉल का आयतन

प्रश्न 20.
पानी से पूरे भरे गिलास में बर्फ का एक टुकड़ा तैर रहा है। थोड़े समय बाद जब बर्फ का टुकड़ा पूरा पिघल जाता है, तो गिलास के पानी के तल पर क्या प्रभाव पड़ेगा? कितना पानी बाहर निकल जाएगा? गणना द्वारा समझाइए। [बर्फ का आपेक्षिक घनत्व = 0.9]
हल:
माना बर्फ का द्रव्यमान M₁, उसका पानी में डूबा आयतन तथा जल का घनत्व d है, जब तैरने के नियम से,
बर्फ का भार बर्फ द्वारा हटाए गए जल का भार
Mg = V x d x g
अतः V = \(\frac { M }{ d }\) … (i)
बर्फ के पिघलने पर जल बनता है M किग्रा बर्फ के पिघलने पर बने जल का आयतन
V’ = \(\frac { M }{ d }\) … (ii)
समीकरण (i) व समीकरण (ii) से स्पष्ट है कि V = V’
अर्थात् पानी में डूबी बर्फ का आयतन = बर्फ से बने जल का आयतन
अतः बर्फ पिघलने पर जल के तल में कोई परिवर्तन नहीं होगा अर्थात् पानी बाहर नहीं निकलेगा।

प्रश्न 21.
किसी लकड़ी के टुकड़े का 2/3 भाग पानी में डूबता है। यदि उसे पूरा डुबाने के लिए उस पर कम से कम 200 ग्राम भार रखने की आवश्यकता हो, तो लकड़ी के टुकड़े का भार ज्ञात कीजिए।
हल:
माना लकड़ी के टुकड़े का भार W तथा आयतन V है। चूँकि तैरते समय टुकड़े के आयतन का 2/3 भाग पानी में डूबता है, अतः
लकड़ी के टुकड़े का भार W= हटाए गए जल का भार
W = \(\frac { 2 }{ 3 }\) V x d x g … (i)
200 ग्राम भार और रख देने पर लकड़ी का टुकड़ा पूरा डूब जाता है, अतः
W + 200 = V x d x g … (ii)
समीकरण (ii) को समीकरण (i) से भाग देने पर
\(\frac{W+200}{W}=\frac{3}{2}\)
अथवा
2W + 400 = 3 W
अतः लकड़ी के टुकड़े का भार W = 400 ग्राम

Students must go through these JAC Class 10 Science Notes Chapter 3 धातु एवं अधातु to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 3 धातु एवं अधातु

→ धातुओं का स्त्रोत- धातुएँ मुक्त व संयुक्त दोनों अवस्थाओं में पायी जाती हैं। पृथ्वी में सबसे अधिक पायी जाने वाली धातु A1 है।

→ धातुएँ – वे तत्त्व जो अपने स्वतन्त्र इलेक्ट्रॉन त्यागकर धनायन बनाते हैं।

→ खनिज – पृथ्वी में पाये जाने वाले धातुओं के ऐसे यौगिक जिनमें रेत आदि की अशुद्धियाँ पाई जाती हैं।

→ अयस्क – वे खनिज जिससे धातु का निष्कर्षण, सुविधाजनक व लाभदायक हो।

→ अधात्री – अयस्क में उपस्थित मिट्टी, कंकड़, पत्थर आदि की अशुद्धियाँ।

→ भर्जन – वायु की उपस्थिति में अयस्क को गर्म करने की प्रक्रिया को भर्जन कहते हैं।

→ प्रगलन – धातु ऑक्साइडों को उच्च ताप पर अपचयित करके धातु प्राप्त करने की प्रक्रिया जिसमें धातु पिघली हुई अवस्था में प्राप्त होती है।

→ गालक – धातुकर्म की प्रक्रिया में प्रयुक्त होने वाला वह पदार्थ है जो अयस्क में उपस्थित अगलनीय अशुद्धियों से संयोग करके एक गलनीय धातुमल बनाता है जो हल्का होने के कारण उस पर तैरता है जिसे आसानी से अलग कर लिया जाता है।

→ धातुमल – अधात्री और गालक के साथ बना हुआ वह गलनीय पदार्थ जो धातु के ऊपर एक पृथक सतह बनाता है।

→ अम्लीय गालक- अम्लीय ऑक्साइड जैसे SiO₂ जो क्षारीय अधात्री, जैसे- FeO, CaO आदि से क्रिया करके धातुमल (FeSiOg) बनाता है।

→ क्षारीय गालक – क्षारीय ऑक्साइड जैसे CaO जो अम्लीय अधात्री, जैसे- SiO₂ आदि से संयोग करके धातुमल (CaSiO₃) बनाता है।

→ ऐलुमिनोतापी विधि – Al का अपचायक के रूप में प्रयोग करके धात्विक ऑक्साइड के अपचयन से धातु प्राप्त करना।

→ धातुओं का शोधन – अशुद्ध धातु से शुद्ध धातु प्राप्त करना।

→ बेसमरीकरण – पिघले हुए अशुद्ध लोहे में वायु तेज प्रवाह से अशुद्धियों का ऑक्सीकरण।
अमलगमन – अशुद्ध धातु को पारे के साथ घोंटकर पारे का मिश्रधातु (अमलगम) बनाकर उसमें से शुद्ध धातु को पृथक करना। अमलगम का वाष्पन करने पर शुद्ध पारा दूर हो जाता है और अशुद्ध धातु शेष रह जाती है।

→ विद्युत अपघटनी शोधन – अशुद्ध धातु का एनोड तथा शुद्ध धातु का कैथोड लेकर इन्हें इसी धातु आयन के विलयन में डुबोकर विद्युत अपघटन करना, जिसमें एनोड में से शुद्ध धातु घुलकर विलयन में जाती है और विलयन से शुद्ध धातु कैथोड पर एकत्रित होती है।

→ एलुमिनियम के प्रमुख अयस्क – बॉक्साइट (Al₂O₃.2H₂O), क्रायोलाइट (Na₂AlF₆।
आयरन के प्रमुख अयस्क – मैग्नेटाइट (Fe₃O₄ हेमेटाइट (Fe₂O₃), सिडेराइट (FeCO₃), आयरन पाइराइट (FeS₂)।

→ Al का धातुकर्म-

→ Fe का धातुकर्म

→ उभयधर्मी ऑक्साइड-
ऑक्सीजन के साथ संयुक्त होकर धातुएँ क्षारकीय ऑक्साइड बनाती हैं। ऐलुमिनियम ऑक्साइड एवं जिंक ऑक्साइड, क्षारकीय ऑक्साइड तथा अम्लीय ऑक्साइड, दोनों के गुणधर्म प्रदर्शित करती हैं। इन ऑक्साइड को उभयधर्मी ऑक्साइड कहते हैं।

→ जल एवं तनु अम्लों के साथ विभिन्न धातुओं की अभिक्रियाशीलता भिन्न-भिन्न होती है।

→ सक्रियता श्रेणी- अभिक्रियाशीलता के आधार पर अवरोही क्रम में व्यवस्थित सामान्य धातुओं की सूची को सक्रियता श्रेणी कहते हैं।

→ सक्रियता श्रेणी में हाइड्रोजन के ऊपर स्थित धातुएँ तनु अम्ल से हाइड्रोजन को विस्थापित कर सकती हैं।

→ अधिक अभिक्रियाशील धातुएँ अपने से कम अभिक्रिया- शील धातुओं को उसके लवण विलयन से विस्थापित कर सकती हैं।

→ प्रकृति में धातुएँ स्वतंत्र अवस्था में या अपने यौगिकों के रूप में पाई जाती हैं।

→ धातुकर्म – अयस्क से धातु का निष्कर्षण तथा उसका परिष्करण कर उपयोगी बनाने के प्रक्रम को धातुकर्म कहते हैं।

→ मिश्रधातु – दो या दो से अधिक धातुओं अथवा एक धातु या एक अधातु के समांगी मिश्रण को मिश्रधातु कहते हैं।

→ संक्षारण-लंबे समय तक आई वायु के संपर्क में रखने से लोहा जैसे कुछ धातुओं की सतह संक्षारित हो जाती है। इस परिघटना को संक्षारण कहते हैं।

→ अधातुओं के गुणधर्म धातुओं के विपरीत होते हैं। यह न तो आघातवर्ध्य तथा न ही तन्य होते हैं। ग्रैफाइट के अलावा सभी अधातुएँ ऊष्मा एवं विद्युत की कुचालक होती हैं। ग्रेफाइट विद्युत का चालक होता है।

→ अधातुएँ विद्युत ऋणात्मक तत्त्व होती हैं क्योंकि धातुओं के साथ अभिक्रिया में इलेक्ट्रॉन ग्रहण कर ऋण आवेशित आयन बनाती हैं।

→ अधातुएँ ऑक्साइड बनाती हैं जो अम्लीय या उदासीन होती हैं।

→ अधातुएँ तनु अम्लों में से हाइड्रोजन का विस्थापन नहीं करती हैं। यह हाइड्रोजन के साथ अभिक्रिया कर हाइड्राइड बनाती हैं।

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 2 बहुपद Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 2 बहुपद

प्रश्न 1.
बहुपद p(x) = 5x² – 3x +7 में x 1 रखने पर बहुपद का मान होगा :
(A) 9
(B) 11
(C) 12
(D) 3
हल :
p(x) = 5x² – 3x +7
x = 1 रखने पर,
P( 1 ) = 5 (1)² – 3 ( 1 ) + 7
= 5 – 3 + 7 = 9
अतः सही विकल्प ‘A’ है।

प्रश्न 2.
p(x) = 2x + 1 का एक शून्यक होगा :
(A) \(\frac {1}{2}\)
(B) 3
(C) –\(\frac {1}{2}\)
(D) 1
हल :
p(x) = 2x + 1
शून्यक होने के लिए p(x) = 0 होगा।
∴ 0 = 2x + 1 ⇒ x = – \(\frac {1}{2}\)
अतः सही विकल्प ‘C’ है।

प्रश्न 3.
x⁴ + x³ – 2x² + x + 1 को x – 1 से भाग देने पर प्राप्त शेषफल होगा :
(A) 0
(B) 2
(C) 1
(D) – 2
हल :
p(x) = x⁴ + x³ – 2x² + x + 1 को (x – 1) से शेषफल p (1) का मान (1) होता है।
∵ x – 1 = 0 ⇒ x = 1
p(1) = 1⁴ + 1³ – 2 (1)² + 1 + 1
= 1 + 1 – 2 + 1 +1 = 2
अतः सही विकल्प ‘B’ है।

प्रश्न 4.
व्यंजक (x – 3) बहुपद
p(x) = x³ + x² – 17x + 15
का गुणनखण्ड होगा, यदि :
(A) p(3) = 0
(B) p(-3) = 0
(C) P(-3) = 0
(D) p(-3) = – 3
हल :
p(x) = x³ + x² – 17x + 15
(x – 3), p(x) का एक गुणनखण्ड है, तो
x – 3 = 0, x = 3
अत: सही विकल्प ‘A’ है।

प्रश्न 5.
x³ – y³ का एक गुणनखण्ड है:
(A) x + y
(B) x² + y²
(C) x² – xy + y²
(D) x – y
हल :
x³ – y³ के गुणनखण्ड
= (x – y) (x² + xy + y²)
एक गुणनखण्ड (x – y) है। अतः सही विकल्प ‘D’ है।

प्रश्न 6.
x⁴ + 8x का एक गुणनखण्ड है:
(A) x + 2
(B) x – 2
(C) x + 8
(D) x² + 2x + 2
हल :
x⁴ + 8x = x(x³ + 8)
= x[(x)³ + (2)³]
= x(x + 2) (x² – 2x + 4)
एक गुणनखण्ड (x + 2) है अतः सही विकल्प ‘A’ है।

प्रश्न 7.
x³ – 8 का एक गुणनखण्ड है:
(A) x + 2
(B) x – 4
(C) x² + 2x + 4
(D) x² – 2x – 4
हल :
x³ – 8 = (x)³ – (2)³
= (x – 2) (x² + 2x + 4)
एक गुणनखण्ड (x² + 2x + 4 ) है अतः सही विकल्प ‘C’ है |

प्रश्न 8.
3y³ + 8y² – 1 का पूर्णांक शून्य है :
(A) 1
(B) – 1
(C) 0
(D) विद्यमान नहीं
हल :
3y³ + 8y² – 1 का पूर्णांक शून्य है।
y = 1 रखने पर, 3(1)³ + 8(1)² – 1
= 3 + 8 – 1 = 10 ≠ 0
y = – 1 रखने पर, 3(-1)³ + 8(-1)² – 1
= – 3 + 8 – 1 = 4 ≠ 0
y = 0 रखने पर, 3(0)³ + 8 × (0)² – 1
= – 1 ≠ 0
अतः व्यंजक में के स्थान पर 1, – 1 और 0 रखने पर शून्य नहीं आता है।
अतः सही विकल्प ‘D’ है।

प्रश्न 9.
सत्यापित कीजिए कि 2 और 0 बहुपद x² – 2x के शून्यक हैं।
हल:
p(x) = x² – 2x
p(2) = 2² – 2(2)
p(2) = 4 – 4 = 0
एवं p(0) = 0 – 0 = 0
अतः 2 और 0 दोनों ही बहुपद x² – 2x के शून्यक हैं। इति सिद्धम्

प्रश्न 10.
जाँच कीजिए कि बहुपद
q(t) = 4t³ + 4t² – t – 1, 2t + 1 का एक गुणज है।
हल :
बहुपद q(t), 2t + 1 का गुणज केवल तब होगा जब 2t + 1 से q(t) को भाग देने पर शेषफल शून्य आता हो ।
∴ 2t + 1 = 0
t = – \(\frac {1}{2}\)
\(q\left(-\frac{1}{2}\right)=4\left(-\frac{1}{2}\right)^3+4\left(-\frac{1}{2}\right)^2-\left(-\frac{1}{2}\right)\) – 1
= – 4 × \(\frac {1}{8}\) + 4 × \(\frac {1}{4}\) + \(\frac {1}{2}\) – 1
= – \(\frac {1}{2}\) + 1 + \(\frac {1}{2}\) – 1 = 0
अतः 2t + 1 दिए गये बहुपद q(t) का एक गुणज है।

प्रश्न 11.
सिद्ध कीजिए कि 5, बहुपद 2x³ – 7x² – 16x + 5 का शून्यक है।
हल :
5 बहुपद 2x³ – 7x² – 16x + 5 का शून्यांक है। बहुपद में x = 5 रखने पर,
2x³ – 7x² – 16x + 5 = 2(5)³ – 7(5)³ – 16(5) + 5
= 2 × 125 – 7(25) – 80 + 5
= 250 – 175 – 80 + 5
= 255 – 255 = 0
∵ x = 5 रखने पर बहुपद का मान शून्यक प्राप्त होता है।
अतः 5 बहुपद का पूर्णांक शून्यक होगा। इति सिद्धम्

प्रश्न 12.
a के किस मान के लिए बहुपद x³ + 2x² – 3ax – 8 में व्यंजक (x – 4) का पूरा-पूरा भाग जाता है?
हल :
बहुपद में x – 4 का भाग देने पर शेषफल f(4) प्राप्त होगा।
f(x) = x³ + 2x² – 3ax – 8 में x के स्थान पर 4 रखने पर
f(4) = (4)³ + 2(4)² – 3a(4) – 8 = 0
= 64 + 2 × 16 – 12a – 8 = 0
= 64 + 32 – 12a – 8 = 0
= 96 – 12a – 8 = 88 – 12a = 0
⇒ 12a = 88
∴ a = \(\frac {88}{12}\) = \(\frac {22}{3}\)
अतः a = \(\frac {22}{3}\)

प्रश्न 13.
यदि x² + \(\frac{1}{x^2}\) = 48 हो तब (x + \(\frac {1}{x}\)) का मान ज्ञात करो ।
हल :
सूत्र से,

प्रश्न 14.
यदि x³ + a³ में x + a का भाग दिया जाए, तो शेषफल ज्ञात कीजिए ।
हल:

∴ शेषफल = 0

प्रश्न 15.
(2x + 3)³ + (3x – 2)³ – (5x + 1)³ क गुणनखण्ड कीजिए।
हल :
माना
2x + 3 = a
3x – 2 = b
– (5x + 1) = c
अब a + b + c = (2x + 3) + (3x – 2 ) – (5x + 1)
= 2x + 3 + 3x – 2 – 5x – 1
= 5x – 5x + 3 – 3 = 0
सर्वसमिका a³ + b³ + c³ = 3abc
a, b तथा c के मान रखने पर
(2x + 3 )³ + (3x – 2)³ – (5x + 1 )³
= 3 × (2x + 3) × (3x – 2) × [- (5x + 1) ]
= – 3 (2x + 3) (3x – 2) (5x + 1).

प्रश्न 16.
सिद्ध कीजिए कि x² + 6x + 15 का कोई शून्य नहीं होता।
हल :
माना कि f(x) = x² + 6x + 15
∴ f(x) = {x2 + 2 (3)x + 9} + 6
= (x + 3)² + 6
यहाँ x के प्रत्येक वास्तविक मान के लिए (x + 3)² का मान कभी भी ऋणात्मक नहीं हो सकता। अतः (x + 3)² का मान सदैव शून्य से बड़ा ही रहेगा। परिणामस्वरूप f(x) का मान भी 6 या उससे अधिक होगा।
इसलिए (x) का कोई शून्य विद्यमान नहीं है।

प्रश्न 17.
गुणनखण्ड कीजिए:
(i) x³ – 64
(ii) (2x – 1)³ – (x – 1)³
हल :
(i) x³ – 64 = (x)³ – (4)³
∵ a³ – b³ = (a – b) (a² + ab + b²)
∴ (x – 4) [(x)² + (x)(4) + (4)²]
= (x – 4) (x² + 4x + 16)

(ii) (2x – 1)³ – (x – 1)³
= [(2x – 1) – (x – 1)] [(2x – 1)² + (2x – 1) (x – 1) + (x – 1)³]
= x[4x² – 4x + 1 + 2x² – 3x + 1 + x² – 2x + 1]
= x(7x² – 9x+3).

प्रश्न 18.
(3a + 4b + 5c)² को प्रसारित रूप में लिखिए।
हल :
सर्वसमिका (x + y + z)² = x² + y² + z² + 2xy + 2yz +2zx
(3a + 4b + 5c)² = (3a)² + (4b)² + (5c)² + 2(3a)(4b) + 2 (4b) (5c) + 2 (5c) (3a)
= 9a² + 16b² + 25c² + 24ab + 40bc + 30ac.

प्रश्न 19.
4x² + y² + z² – 4xy – 2yz + 4xz को गुणनखण्ड कीजिए।
हल :
(2x)² + (y)² + (z)² + 2(2x)(-y) + 2(- y)(z) + 2(2x)(z)
सर्वसमिका (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
= [2x + (-y) + z]²
= (2x – y + z)²
= (2x – y + z) (2x – y + z).

प्रश्न 20.
उपयुक्त सर्वसमिकाएँ प्रयोग करके, निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए :
(i) (104)³
(ii) (999)³
हल :
(i) यहाँ (104)³ = ( 100 + 4)³
=(100)³ + (4)³ + 3(100)(4)(100 + 4)
[सर्वसमिका (a + b)³ = a³ + b³ + 3ab (a + b)]
= 1000000 + 64 + 124800 = 1124864.

(ii) यहाँ (999)³ = ( 1000 – 1)³
= (1000)³ – (1)³ – 3(1000)(1)(1000 – 1)
[सर्वसमिका a³ – b³ = a³ – b³ – 3ab (a + b)]
= 1000000000 – 1 – 2997000
= 997002999.

प्रश्न 21.
8x³ + 27y³ + 36x²y + 54xy – 2 के गुणनखण्डन कीजिए।
हल :
दिए हुए व्यंजक को इस प्रकार लिखा जा सकता है:
(2x)³ + (3y)³ + 3(4x²)(3y) + 3(2x)(9y²)
[सर्वसमिका (a + b)³ = a³ + b³ + 3a²b + 3ab²)
= (2x)³ + (3y)³ + 3(2x)²(3y) + 3(2x)(3y)²
= (2x + 3y)³
= (2x + 3y) (2x + 3y) (2x + 3y).

प्रश्न 22.
(4a – 2b – 3c)² का प्रसार कीजिए।
हल :
सर्वसमिका
(x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
∴ (4a – 2b – 3c)² = [4a + (-2b) + (- 3c)]²
= (4a)² + (-2b)² + (- 3c)² + 2(4a)(-2b) + 2(-2b) (- 3c) + 2 (-3c) (4a)
= 16a² + 4b² + 9c² – 16ab + 12bc – 24ac.

प्रश्न 23.
यदि (x – \(\frac {1}{x}\))² = 5 तो(x² – \(\frac{1}{x^2}\)) का मान ज्ञात करो ।
हल :
सूत्र,
(a – b)² = a² + 2ab – b²
(x – \(\frac {1}{x}\))² = x² + \(\frac{1}{x^2}\) – 2.x.\(\frac {1}{x}\)
5 = (x² + \(\frac{1}{x^2}\)) – 2
∴ x² + \(\frac{1}{x^2}\) = 7

प्रश्न 24.
प्रदर्शित कीजिए कि बहुपद x¹⁰ – 1 और x¹¹ – 1 का एक गुणनखण्ड (x – 1) है ।
हल :
माना
p(x) = x¹⁰ – 1
तथा
q(x) = x¹¹ – 1
(x – 1) गुणनखण्ड प्रदर्शित करने के लिए p(x) = 0, q(x) = 0 दिखाना पड़ेगा।
∴ p(x) = x¹⁰ – 1
p(1) = (1)¹⁰ – 1
P(1) = 1 – 1
P(1) = 0

तथा q(x) = x¹¹ – 1
q (1) = (1)¹¹ – 1
q (1) = 1 – 1
q(1) = 0
अत: (x – 1), बहुपद (x¹⁰ – 1) तथा (x¹¹ – 1) का एक गुणनखण्ड है।

प्रश्न 25.
व्यंजक x⁸ – y⁸ के गुणनखण्ड कीजिए।
हल :
सर्वसमिका a² + b² = (a + b) (a – b) से, (x⁴)² – (y⁴)²
= (x⁴ – y⁴) (x⁴ + y⁴)
= [(x²)² – (y²)²] [x⁴ + y⁴]
(x² – y²) (x² + y²) (x⁴ + y⁴)
पुनः (x – y) (x + y) (x² + y²) (x⁴ + y⁴)

प्रश्न 26.
यदि (x² + \(\frac{1}{x^2}\)) = 83 तो (x³ – \(\frac{1}{x^3}\)) का मान ज्ञात करो ।
हल :

प्रश्न 27.
व्यंजक (x¹² – y¹²) के गुणनखण्ड कीजिए।
हल :
x¹² – y¹² = (x⁶)² – (y⁶)²,
सर्वसमिका a² – b² = (a – b)(a + b)
= (x⁶ + y⁶)(x⁶ – y⁶)
= (x⁶ + y⁶) [(x³)² – (y³)²]
= (x⁶ + y⁶) [x³ + y³] [x³ – y³]
सर्वसमिका a³ + b³ = (a + b) (a² – ab + b²)
तथा a³ – b³ = (a – b) (a² + ab + b²)
= (x⁶ + y⁶) [(x + y) (x² – xy + y²) (x – y) (x² + xy + y²)]
= [(x²)³ + (y²)³] [(x + y) (x – y) (x² – xy + y²) (x² + xy + y²)]
= (x² + y²) (x⁴ – x²y² + y⁴) (x + y) (x – y)(x² – xy + y²)(x² + xy + y²)
अतः x¹² – y¹² = (x + y) (x – y)(x² + y²) (x⁴ – x²y² + y⁴)(x² – xy + y²)(x² + xy + y²)

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय

प्रश्न 1.
यदि दो रेखाएँ परस्पर लम्बवत् हों, तो उनके मध्य कोण होगा :
(A) 180°
(B) 80°
(C) 90°
(D) 360°
हल :
दो लम्बवत् रेखाओं के मध्य कोण 90° होता है।
अतः सही विकल्प ‘C’ है।

प्रश्न 2.
रेखाखण्ड की लम्बाई होती है :
(A) अनिश्चित दूरी
(B) निश्चित दूरी
(C) अपनी इच्छा के अनुरूप
(D) किन्हीं दो बिन्दुओं के मध्य दूरी।
हल :
किन्हीं दो बिन्दुओं के मध्य की दूरी को रेखाखण्ड द्वारा व्यक्त किया जाता है। होगी:
अतः सही विकल्प ‘D’ है।

प्रश्न 3.
दो बिन्दुओं से गुजरने वाली रेखाओं की संख्या
(A) एक
(B) तीन
(C) अनन्त
(D) दो।
हल :
दो बिन्दुओं से होकर केवल एक रेखा गुजर सकती है।
अतः सही विकल्प ‘A’ है।

प्रश्न 4.
यदि रेखाखण्ड AB तथा CD बराबर तथा संपाती हैं और यदि CD = 3 सेमी हो, तो AB की दूरी दोगुनी हो जाने पर CD की दूरी हो जायेगी :
(A) 1.5 सेमी
(B) 6 सेमी
(C) 5 सेमी
(D) 9 सेमी।
हल :
AB = CD (दिया है)
CD = 3 सेमी
यदि AB दोगुनी कर दी जाय, तो CD भुजा भी दोगुनी होगी।
∴ CD = 3 × 2 = 6 सेमी ।
अतः सही विकल्प ‘B’ है।

प्रश्न 5.
यदि एक रेखा दो समान्तर रेखाओं को काटती है तो उसके एक ही ओर बने दो अन्तः कोणों का योग होगा :
(A) 180° से कम
(B) 2 समकोण
(C) 180° से अधिक
(D) 180° < 90°.
हल :
दो समान्तर रेखाओं को कोई एक तिर्यक रेखा काटती है, तो उससे बने अन्तः कोणों का योग 2 समकोण अर्थात् 180° होता है।
अतः सही विकल्प ‘B’ है।

प्रश्न 6.
यूक्लिड ने सांत रेखा किसे कहा था ?
(A) किरण को
(B) रेखा को
(C) रेखाखण्ड को
(D) त्रिज्या को।
हल :
यूक्लिड ने रेखाखण्ड को सांत रेखा कहा था।
अतः सही विकल्प ‘C’ है।

प्रश्न 7.
अथर्ववेद में दिये गये ‘श्रीयंत्र’ में एक-दूसरे से जुड़े कितने समद्विबाहु त्रिभुज अन्तर्निहित हैं :
(A) आठ
(B) छ:
(C) नौ
(D) पन्द्रह ।
हल :
‘श्रीयन्त्र’ में एक-दूसरे से जुड़े ‘नौ’ समद्विबाहु त्रिभुज अन्तर्निहित हैं।
अतः सही विकल्प ‘C’ है।

प्रश्न 8.
एलीमेन्ट्स (Elements) नामक प्रसिद्ध ग्रन्थ के लेखक हैं :
(A) गणितज्ञ थेल्स
(B) गणितज्ञ यूक्लिड
(C) गणितज्ञ पाइथागोरस
(D) गणितज्ञ आर्यभट्ट |
हल :
एलीमेन्ट्स नामक प्रसिद्ध ग्रन्थ के लेखक गणितज्ञ यूक्लिड थे।
अतः सही विकल्प ‘B’ है।

प्रश्न 9.
ज्यामितीय विधि से \(\sqrt{3}\), \(\sqrt{5}\) ………. आदि को अपरिमेय सिद्ध करने वाले गणितज्ञ थे :
(A) थिरोडोरस
(B) बोधायन
(C) आर्काइटस
(D) बेल्स
हल :
ज्यामितीय विधि से \(\sqrt{3}\), \(\sqrt{5}\) ………. आदि को अपरिमेय सिद्ध करने वाले गणितज्ञ थिरोडोरस थे ।
अतः सही विकल्प ‘A’ है।

प्रश्न 10.
यूनानियों ने ज्यामिति का ज्ञान प्राप्त किया था :
(A) भारत से
(B) अमेरिका से
(C) मिस्त्र से
(D) इंग्लैण्ड से
हल :
यूनानियों ने ज्यामिति का ज्ञान मिस्त्र से प्राप्त किया था।
अतः सही विकल्प ‘C’ है।

प्रश्न 11.
वे वस्तुएँ जो एक ही वस्तु के बराबर हों, एक दूसरे के ………….. ‘होती हैं।
हल :
बराबर ।

प्रश्न 12.
एक सांत रेखा को …………….. रूप से बढ़ाया जा सकता है।
हल :
अनिश्चित ।

प्रश्न 13.
उस भारतीय गणितज्ञ का नाम बताइए जो पाइथागोरस प्रमेय की खोज पहले ही कर चुके थे।
हल :
पाइथागोरस प्रमेय की खोज करने वाले सर्वप्रथम गणितज्ञ बोधायन थे।

प्रश्न 14.
क्या समान्तर रेखाएँ, किसी बिन्दु पर प्रतिच्छेद करती हैं ? यदि नहीं तो क्यों ?
हल :
नहीं, क्योंकि समान्तर रेखाओं के मध्य की दूरी सदैव समान होती है, इसलिए वे प्रतिच्छेद नहीं कर सकती।

प्रश्न 15.
यूक्लिड ने ज्यामिति के कौन-कौन से मुख्य बिन्दुओं को अपने शब्दों में परिभाषित किया है ?
हल :
यूक्लिड ने बिन्दु, रेखा और तल को अपने शब्दों में परिभाषित किया है।

प्रश्न 16.
ज्यामिति में गणितज्ञों ने कौन-कौन से पदों को अपरिभाषित माना है?
हल :

1. बिन्दु – इसका कोई परिमाण नहीं होता है।
2. रेखा – सीधी रेखा को दोनों ओर कितना भी बढ़ाया जा सकता है।
3. तल – दीवार का समतल पृष्ठ, समतल भूमि, कागज का पृष्ठ तल आदि ।

प्रश्न 17.
दो बिन्दुओं से कितनी रेखाएँ गुजर सकती हैं ?
हल :
दो बिन्दुओं से केवल एक रेखा गुजर सकती है।

प्रश्न 18.
यूक्लिड द्वारा दी गई अभिधारणाओं में से कोई दो अभिधारणाएँ लिखिए।
हल :
अभिधारणा (1) – एक बिन्दु से अन्य बिन्दु तक एक सीधी रेखा खींची जा सकती है।
अभिधारणा (2) – किसी बिन्दु को केन्द्र मानकर भिन्न त्रिज्याओं वाले अनन्त वृत्त खींचे जा सकते हैं।

प्रश्न 19.
सिद्ध कीजिए कि एक दिये हुए रेखाखण्ड पर एक समबाहु त्रिभुज की रचना की जा सकती है।.
हल :
प्रश्नानुसार,
(i) बिन्दु A को केन्द्र मानकर AB त्रिज्या का वृत्त खींचते हैं।
(ii) इसी प्रकार बिन्दु B को केन्द्र मानकर BA त्रिज्या लेकर दूसरा वृत्त खींचते हैं ये दोनों वृत्त C बिन्दु पर मिलते हैं।
(iii) बिन्दु C से A और B बिन्दु को मिलाते हैं।

इस प्रकार ΔABC की चना हुई।
जहाँ AB = AC, क्योंकि ये एक ही वृत्त की त्रिज्याएँ हैं।
इस प्रकार, AB = BC (एक ही वृत्त की त्रिज्याएँ)
⇒ AB = BC = AC
अत: ΔABC समबाहु त्रिभुज है।

प्रश्न 20.
यदि A, B और C एक रेखा पर स्थित तीन बिन्दु हैं और B बिन्दुओं A और C के बीच स्थित है, तो सिद्ध कीजिए कि AB + BC = AC.

हल :
चित्र में, AB + BC के साथ AC सम्पाती है।
हम जानते हैं कि वे वस्तुएँ जो परस्पर संपाती हों एक- दूसरे के बराबर होती हैं।
अतः AB + BC = AC.
अतः दो बिन्दुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।

प्रश्न 21.
यूक्लिड ने ज्यामिति के बिन्दु, रेखा और तल (पृष्ठ) के बारे में क्या परिभाषाएँ दीं हैं, लिखिए।
हल :

1. बिन्दु ऐसी आकृति होती है, जिसका कोई भाग नहीं होता।
2. रेखा की केवल लम्बाई होती है, चौड़ाई नहीं
3. एक सीधी रेखा ऐसी रेखा है जो स्वयं पर बिन्दुओं के साथ सपाट रूप में स्थित होती है।
4. एक पृष्ठ वह है जिसकी लम्बाई चौड़ाई होती है।
5. किसी पृष्ठ के किनारे रेखाएँ होती हैं।
6. एक समतल पृष्ठ ऐसा पृष्ठ है जो स्वयं पर सीधी रेखाओं के साथ सपाट रूप से स्थित होता है।

Jharkhand Board JAC Class 9 Science Solutions Chapter 3 परमाणु एवं अणु Textbook Exercise Questions and Answers.

JAC Board Class 9 Science Solutions Chapter 3 परमाणु एवं अणु

Jharkhand Board Class 9 Science परमाणु एवं अणु Textbook Questions and Answers

प्रश्न 1.
0.24 g ऑक्सीजन एवं बोरॉन युक्त यौगिक के नमूने में विश्लेषण द्वारा यह पाया गया कि उसमें 0.096g बोरॉन एवं 0.144g ऑक्सीजन है। उस यौगिक के प्रतिशत संघटन का भारात्मक रूप में परिकलन कीजिए।
हल:
0.24 ग्राम यौगिक में बोरॉन = 0.096 ग्राम
∴ 100 ग्राम यौगिक में बोरॉन

प्रश्न 2.
3.0g कार्बन 8.00g ऑक्सीजन में जलकर 11.00g कार्बन डाइऑक्साइड निर्मित करता है। जब 3.00g कार्बन को 50.00g ऑक्सीजन में जलाएँगे तो कितने ग्राम कार्बन डाइऑक्साइड का निर्माण होगा? आपका उत्तर रासायनिक संयोजन के किस नियम पर आधारित होगा?
उत्तर:
C + O₂ → CO₂
कार्बन का द्रव्यमान = 3g
ऑक्सीजन का द्रव्यमान = 8g
अभिकारकों का कुल द्रव्यमान = 3 + 8 = 11g
उत्पाद (CO₂) का द्रव्यमान = 11 g
अतः अभिकारकों का कुल द्रव्यमान = उत्पाद का कुल द्रव्यमान
प्रश्नानुसार, कार्बन का द्रव्यमान = 3g
ऑक्सीजन का द्रव्यमान = 50g
अभिकारकों का कुल द्रव्यमान = 3 + 50 = 53 g
द्रव्यमान संरक्षण के नियमानुसार
अभिकारकों का कुल द्रव्यमान = उत्पाद का कुल द्रव्यमान
∴ उत्पाद का कुल द्रव्यमान = 53 g
यह रासायनिक संयोग ‘द्रव्यमान संरक्षण नियम’ पर आधारित है।

प्रश्न 3.
बहु परमाणुक आयन क्या होते हैं? उदाहरण दीजिए।
उत्तर:
परमाणुओं के समूह जिन पर नेट आवेश विद्यमान है उसे बहुपरमाणुक आयन कहते हैं। जैसे अमोनियम (NH₄)⁺ सल्फेट (SO₄)^2- आदि।

प्रश्न 4.
निम्नलिखित के रासायनिक सूत्र लिखिए-
(a) मैग्नीशियम क्लोराइड
(b) कैल्सियम क्लोराइड
(c) कॉपर नाइट्रेट
(d) ऐलुमिनियम क्लोराइड
(e) कैल्सियम कार्बोनेट
उत्तर:
(a) मैग्नीशियम क्लोराइड का सूत्र

मैग्नीशियम क्लोराइड MgCl₂

(b) कैल्सियम क्लोराइड का सूत्र

कैल्सियम क्लोराइड = CaCl₂

(c) कॉपर नाइट्रेट का सूत्र कॉपर

कॉपर नाइट्रेट = Cu(NO₃)₂

(d) एलुमिनियम क्लोराइड का सूत्र ऐलुमिनियम

एलुमिनियम क्लोराइड AlCl₃

(e) कैल्सियम कार्बोनेट का सूत्र

कैल्सियम कार्बोनेट = CaCO₃

प्रश्न 5.
निम्नलिखित यौगिकों में विद्यमान तत्वों का नाम लिखिए-
(a) बुझा हुआ चूना
(b) हाइड्रोजन ब्रोमाइड
(c) बेकिंग पाउडर (खाने वाला सोडा)
(d) पोटैशियम सल्फेट
उत्तर:

यौगिक का नाम	रासायनिक	उपस्थित तत्व
(a) बुझा हुआ चूना	Ca(OH)2	कैल्सियम, ऑक्सीजन व हाइड्रोजन
(d) हाइड्रोजन ब्रोमाइड	HBr	हाइड्रोजन, ब्रोमीन
(c) बेकिंग पाउडर	NaHCO3	सोडियम, हाइड्रोजन, कार्बन, ऑक्सीजन
(d) पोटैशियम	K2SO4	पोटैशियम, सल्फर, ऑक्सीजन

प्रश्न 6.
निम्नलिखित पदार्थों में मोलर द्रव्यमान का परिकलन कीजिए-
(a) एथाइन, C₂H₂
(b) सल्फर अणु, S₈
(c) फॉस्फोरस अणु, P₄ (फॉस्फोरस का परमाणु द्रव्यमान – 31)
(d) हाइड्रोक्लोरिक अम्ल, HCl
(e) नाइट्रिक अम्ल HNO₃
उत्तर:
किसी पदार्थ के एक मोल अणु के द्रव्यमान को उसका मोलर द्रव्यमान कहते हैं।
(a) कार्बन का परमाणु द्रव्यमान = 12 u
हाइड्रोजन का परमाणु द्रव्यमान = 1 u
C₂H₂ का
अणु द्रव्यमान = 2 × C का
परमाणु द्रव्यमान (परमाणु द्रव्यमान ) + 2 × H का परमाणु द्रव्यमान = 2 × 12 + 2 + 1
= 24 + 2
= 26u.
∴ C₂H₂ का मोलर द्रव्यमान = 26g

(b) सल्फर का परमाणु द्रव्यमान = 32
S₈ का अणु द्रव्यमान = 8 x 32
= 256 g
∴ S₈ का मोलर द्रव्यमान = 256 g

(c) फास्फोरस का परमाणु द्रव्यमान = 31 u
P₄ का अणु द्रव्यमान = 4 × 31 = 124 u
∴ P₄ का मोलर द्रव्यमान = 124 g

(d) हाइड्रोजन का परमाणु द्रव्यमान = 1 u
क्लोरीन का परमाणु द्रव्यमान = 35.5u
HCl का अणु द्रव्यमान = H का परमाणु द्रव्यमान + Cl का परमाणु द्रव्यमान
∴ HCI का मोलर द्रव्यमान = 36.5 g

(e) हाइड्रोजन का परमाणु द्रव्यमान = 1 u
नाइट्रोजन का परमाणु द्रव्यमान = 14u
ऑक्सीजन का परमाणु द्रव्यमान = 16u
HNO₃ का अणु द्रव्यमान H का परमाणु द्रव्यमान + N का परमाणु द्रव्यमान + 3 x O का परमाणु द्रव्यमान
= 1 + 14 + 3 × 16
= 1 + 14 + 48
= 63 g
∴ HNO₃ का मोलर द्रव्यमान = 63g

प्रश्न 7.
निम्न का द्रव्यमान क्या होगा?
(a) 1 मोल नाइट्रोजन परमाणु
(b) 4 मोल ऐलुमिनियम का परमाणु (ऐलुमिनियम का परमाणु द्रव्यमान = 27 )
(c) 10 मोल सोडियम सल्फाइट (Na₂ SO₃)
उत्तर:
मोलर द्रव्यमान आयन के परमाणु द्रव्यमान के बराबर होता है।
(a) मोल संख्या (n) = 1
N परमाणुओं का मोलर द्रव्यमान (M) = 14g
द्रव्यमान = मोलर द्रव्यमान मोल संख्या
द्रव्यमान = 14 × 1 = 14 g

(b) मोल संख्या (n) = 4
ऐलुमिनियम आयनों का मोलर द्रव्यमान (M) = 27 ग्रा.
(समान तत्व के एक आयन का द्रव्यमान उसके परमाणु के द्रव्यमान के बराबर होता है।)
द्रव्यमान = मोलर द्रव्यमान x मोल संख्या
m = 27 x 4 = 108 g

(c) मोल संख्या (n) = 10
Na₂SO₃ का मोलर द्रव्यमान (M)
= 2 × 23 + 32 + 3 × 16
= 46 + 32 + 48 = 126
द्रव्यमान मोलर द्रव्यमान मोल संख्या
m = 126 × 10 = 1260 g

प्रश्न 8.
मोल में परिवर्तित कीजिए-
(a) 12 g ऑक्सीजन गैस
(b) 20g जल
(c) 22 g कार्बन डाइऑक्साइड
उत्तर:
(a) ऑक्सीजन गैस का परमाणु द्रव्यमान = 32 u
∴ O₂ का मोलर द्रव्यमान (m) = 32 g
ऑक्सीजन का दिया गया द्रव्यमान (m) = 12 g

मोलों की संख्या = \(\frac { 12 }{ 32 }\) = 0.375 मोल

(b) जल का अणु द्रव्यमान = 18 u
जल का मोलर द्रव्यमन = 18 u
जल का दिया गया द्रव्यमान = 20 g

मोलों की संख्या = \(\frac { 20 }{ 18 }\) = 1.11 मोल

(c) 22 ग्राम CO₂ में मोलों की संख्या = \(\frac { 22 }{ 44 }\)
= 0.5 मोल

प्रश्न 9.
निम्न का द्रव्यमान क्या होगा?
(a) 0.2 मोल ऑक्सीजन परमाणु
(b) 0.5 मोल जल अणु
उत्तर:
(a) मोल ऑक्सीजन संख्या (n) = 0.2
ऑक्सीजन का परमाणु द्रव्यमान = 16u
ऑक्सीजन का मोलर द्रव्यमान (M) = 16g
द्रव्यमान = मोलर द्रव्यमान x मोल संख्या
द्रव्यमान = 16 x 0.2 = 3.2 g

(b) मोल जल अणु (n) = 0.5
जल का अणु द्रव्यमान = 18 u
जल का मोलर द्रव्यमान = 18 u
द्रव्यमान = मोलर द्रव्यमान × मोल संख्या
द्रव्यमान = 18 x 0.5 = 9 g

प्रश्न 10.
16 g ठोस सल्फर में सल्फर (S₈) के अणुओं की संख्या का परिकलन कीजिए।
उत्तर:
सल्फर का परमाणु द्रव्यमान = 32 u
S₈ अणु का मोलर द्रव्यमान = 32 x 8 = 256 u
S₈ अणु का प्रदत्त द्रव्यमान (m) = 16 g
आवोगाद्रो स्थिरांक (N_A) = 6.022 × 10²³
कणों (अणुओं) की संख्या

प्रश्न 11.
0.051g ऐलुमिनियम ऑक्साइड (Al₂O₃) में ऐलुमिनियम आयन की संख्या का परिकलन कीजिए।
संकेत-किसी आयन का द्रव्यमान उतना ही होता है जितना कि उस तत्व के परमाणु का द्रव्यमान होता है। ऐलुमिनियम का परमाणु द्रव्यमान 27 u है।
उत्तर:
ऐलुमिनियम ऑक्साइड (Al₂ O₃) का अणु द्रव्यमान
= 2 × 27 + 3 x 16
= 54 + 48 = 102 u
Al₂O₃ का मोलर द्रव्यमान (M) = 102 g
Al₂O₃ का प्रदत्त द्रव्यमान (m) = 0.051 g
आवोगाद्रो स्थिरांक (N_A) = 6.022 × 10²³
कणों (आयनों) की संख्या (N)

N = \(\frac { m }{ M }\) × N_A
N = \(\frac { 0.051 }{ 102 }\) × 6.022 × 10²³
N = 0.003011 × 10²³
चूँकि Al₂ O₃ का प्रत्येक अणु दो ऐलुमिनियम आयन धारण किए हुए है,
अतः ऐलुमिनियम तत्वों की संख्या
= 2 x 0.003011 × 10²³
= 0.006022 × 10²³
= 6.022 × 10²⁰

Jharkhand Board Class 9 Science परमाणु एवं अणुं InText Questions and Answers

क्रियाकलाप 1.
निम्न X तथा Y रसायनों का एक युगल लीजिए-

X	Y
(i) कॉपर सल्फेट	सोडियम कार्बोनेट
(ii) बेरियम क्लोराइड	सोडियम सल्फेट
(iii) लेड नाइट्रेट	सोडियम क्लोराइड

X तथा Y युगलों की सूची में से किसी एक युगल के रसायनों के अलग-अलग 5% विलयन जल में तैयार करंके Y के विलयन की कुछ मात्रा को एक शंक्वाकार फ्लास्क में लेकर X के विलयन की कुछ मात्रा को एक ज्वलन नली में लीजिए।

ज्वलन नली को विलेय युक्त फ्लास्क में इस प्रकार लटकाना है कि दोनों विलयन आपस में मिश्रित न हों तथा फ्लास्क के मुख पर कॉर्क चित्र की भाँति लगाइए-

• अन्दर समाहित वस्तु सहित फ्लास्क को सावधानी पूर्वक तोला।
• अब फ्लास्क को झुकाकर इस प्रकार घुमायें कि X व Y के विलयन परस्पर मिश्रित हो जाएँ।
• इस फ्लास्क को पुनः तौलकर देखें कि क्या कोई रासायनिक अभिक्रिया हुई?
• क्या फ्लास्क के द्रव्यमान एवं अंतर्वस्तुओं में कोई परिवर्तन हुआ?

द्रव्यमान संरक्षण के नियमानुसार “किसी रासायनिक अभिक्रिया में द्रव्यमान का न तो सृजन किया जा सकता है और न ही विनाश। ”

खंड 3.1 पर आधारित पाठ्य पुस्तक के प्रश्न (पा. पु. पू. सं. 36)

प्रश्न 1.
एक अभिक्रिया में 5.3g सोडियम कार्बोनेट एवं 6.0g एसीटिक अम्ल अभिकृत होते हैं। 2.2g कार्बन डाइऑक्साइड, 8.2g सोडियम एसीटेट एवं 0.9g जल उत्पाद के रूप में प्राप्त होते हैं। इस अभिक्रिया द्वारा दिखाइए कि यह परीक्षण द्रव्यमान संरक्षण के नियम के अनुरूप है।
सोडियम कार्बोनेट + एसीटिक अम्ल → सोडियम एसीटेट + कार्बन डाइऑक्साइड + जल
उत्तर:

अभिकारकों का द्रव्यमान = 5.3 + 6.0 = 11.3 g
उत्पादों का द्रव्यमान = 8.2g + 2.2g + 0.9g = 11.3 g
इस अभिक्रया में अभिकारकों तथा उत्पादों का द्रव्यमान समान है अतः यह द्रव्यमान संरक्षण के नियम के अनुसार है।

प्रश्न 2.
हाइड्रोजन एवं ऑक्सीजन द्रव्यमान के अनुसार 18 के अनुपात में संयोग करके जल निर्मित करते हैं। 3g हाइड्रोजन गैस के साथ पूर्ण रूप से संयोग करने के लिए कितने ऑक्सीजन गैस के द्रव्यमान की आवश्यकता होगी?
उत्तर:

1g हाइड्रोजन 8g ऑक्सीजन के साथ संयोग करके 9gm जल बनाती है।
∵ 1g हाइड्रोजन के लिए आवश्यक ऑक्सीजन 8g
∴ 3g हाइड्रोजन के लिए आवश्यक ऑक्सीजन
= \(\frac { 1 }{ 8 }\) x 3 = 24g
अतः 3g हाइड्रोजन गैस के साथ पूर्ण रूप से संयोग करने के लिए 24g ऑक्सीजन गैस की आवश्यकता होगी।
अतः द्रव्यमान अनुपात = 3 : 24 ⇒ 18
अत: यह अभिक्रिया स्थिर अनुपात के नियम का अनुसरण करती है।

प्रश्न 3.
डाल्टन के परमाणु सिद्धान्त का कौन-सा अभिग्रहीत द्रव्यमान के संरक्षण के नियम का परिणाम है?
उत्तर:
डाल्टन के सिद्धान्त का दूसरा अभिग्रहीत “परमाणु अविभाज्य सूक्ष्मतम कण होते हैं जो रासायनिक क्रिया में न तो सृजित होते हैं और न ही उनका विनाश होता है।”

प्रश्न 4.
डाल्टन के परमाणु सिद्धान्त का कौन-सा अभिग्रहीत निश्चित अनुपात के नियम की व्याख्या करता है?
उत्तर:
भिन्न-भिन्न तत्वों के परमाणु परस्पर छोटी पूर्ण संख्या के अनुपात में संयोग कर यौगिक निर्मित करते हैं तथा किसी भी यौगिक में परमाणु की सापेक्ष संख्या एवं प्रकार निश्चित होते हैं। परमाणु सिद्धान्त का यह अभिग्रहीत निश्चित अनुपात नियम की व्याख्या करता है।

खण्ड-3 पर आधारित पाठ्य पुस्तक के प्रश्न (पा. पु. पृ. सं. – 40)

प्रश्न 1.
परमाणु द्रव्यमान इकाई को परिभाषित कीजिए।
उत्तर:

1. कार्बन – 12 समस्थानिक को मानक सन्दर्भ के रूप में सार्वभौमिक रूप से स्वीकार किया गया था।
2. कार्बन – 12 समस्थानिक के एक परमाणु द्रव्यमान के 1/12 वें भाग को मानक परमाणु द्रव्यमान इकाई कहते हैं।

प्रश्न 2.
एक परमाणु को आँखों द्वारा देखना क्यों सम्भव नहीं होता है?
उत्तर:
परमाणु का आकार अत्यन्त सूक्ष्म होता है। अतः परमाणु का आँखों द्वारा देखना संभव नहीं होता है।

क्रियाकलाप 2.
सारणी 3.5 अणुओं में विद्यमान परमाणुओं के द्रव्यमान अनुपातों तथा सारणी 3.3 को परमाणु द्रव्यमान के लिए देखें।
सारणी 3.5 में दिए गए यौगिकों के अणुओं में प्रयुक्त तत्वों के परमाणुओं की संख्या के अनुपातों को ज्ञात कीजिए। जल के अणु में प्रयुक्त परमाणुओं की संख्याओं का अनुपात निम्न प्रकार से प्राप्त किया जा सकता है।

तत्व	द्रव्यमान अनुपात	परमाणु द्रव्यमान (u)	द्रव्यमान अनुपात/ परमाणु द्रव्यमान	सरलतम अनुपात
H	1	1	\(\frac { 1 }{ 1 }\) = 1	2
O	8	16	\(\frac { 8 }{ 16 }\) = \(\frac { 1 }{ 2 }\)	1

अतः जल के अणु में प्रयुक्त परमाणुओं की संख्याओं का अनुपात H : O = 2 : 1 है।

खण्ड 3.4 से सम्बन्धित पाठ्य पुस्तक के प्रश्न (पा. पु. पृ. सं. -44)

प्रश्न 1.
निम्न के सूत्र लिखिए-
(i) सोडियम ऑक्साइड
(ii) ऐलुमिनियम क्लोराइड
(iii) सोडियम सल्फाइड
(iv) मैग्नीशियम हाइड्रॉक्साइड
उत्तर:
(i) सोडियम ऑक्साइड

सूत्र Na₂O

(ii) ऐलुमिनियम क्लोराइड

सूत्र AlCl₃

(iii) सोडियम सल्फाइड

सूत्र Na₂S

(iv) मैग्नीशियम हाइड्रॉक्साइड

सूत्र Mg(OH)₂

प्रश्न 2.
निम्नलिखित सूत्रों द्वारा प्रदर्शित यौगिकों के नाम लिखिए-

1. Al₂(SO₄)₃
2. CaCl₂
3. K₂SO₄
4. KNO₃
5. CaCO₃

उत्तर:

1. ऐलुमिनियम सल्फेट
2. कैल्सियम क्लोराइड
3. पोटैशियम सल्फेट
4. पोटैशियम नाइट्रेट
5. कैल्सियम कार्बोनेट

प्रश्न 3.
रासायनिक सूत्र का क्या तात्पर्य है?
उत्तर:
किसी यौगिक के संघटक तत्वों तथा संयोग करने वाले सभी तत्वों की परमाणु संख्या के प्रतीकात्मक निरूपण को रासायनिक सूत्र कहते हैं।

प्रश्न 4.
निम्नलिखित में कितने परमाणु विद्यमान हैं?
(i) H₂S अणु एवं
(ii) PO₄^3- आयन?
उत्तर:
(i) H₂S अणु-इसमें तीन परमाणु (दो परमाणु हाइड्रोजन तथा एक परमाणु सल्फर) विद्यमान हैं।
(ii) PO₄^3- आयन-इसमें पाँच परमाणु (एक परमाणु फॉस्फोरस तथा चार परमाणु ऑक्सीजन के विद्यमान हैं।

खण्ड 3.5 से सम्बन्धित पाठ्य पुस्तक के प्रश्न (पा. पु. पृ. सं. -46)

प्रश्न 1.
निम्नलिखित यौगिकों के आण्विक द्रव्यमान का परिकलन कीजिए-H₂, O₂, Cl₂, CO₂, CH₄, C₂H₆, C₂H₄, NH₃ एवं CH₃OH
हल:

• H₂ का आण्विक द्रव्यमान = 2 x 1 = 2 u
• O₂ का आण्विक द्रव्यमान = 2 x 16 = 32 u
• Cl₂ का आण्विक द्रव्यमान = 2 x 35.5 = 71 u
• CO₂ का आण्विक द्रव्यमान = 1 x 12 + 2 x 16 = 44 u
• CH₄ का आण्विक द्रव्यमान = 1 x 12 + 4 x 1 = 16 u
• C₂H₆ का आण्विक द्रव्यमान = 2 x 12 + 6 + 1 = 30 u
• NH₃ का आण्विक द्रव्यमान = 2 x 12 + 4 x 1 = 28 u
• CH₃OH का आण्विक द्रव्यमान = 1 x 12 + 3 x 1 + 1 x 16 + 1 x 1 = 32 u

प्रश्न 2.
निम्नलिखित यौगिकों के सूत्र इकाई द्रव्यमान का परिकलन कीजिए- ZnO, Na₂O एवं K₂CO₃ दिया गया है-
Zn का परमाणु द्रव्यमान = 65 u,
Na का परमाणु द्रव्यमान = 23 u
K का परमाणु द्रव्यमान = 39 u,
C का परमाणु द्रव्यमान = 12 u एवं
O का परमाणु द्रव्यमान = 16 u है।
हल:
(i) ZnO का सूत्र इकाई द्रव्यमान =(1 × 65 + 1 × 16) u
= (65 + 16) u
= 81u

(ii) Na₂O का सूत्र इकाई द्रव्यमान
=(2 × 23 + 1 × 16) u
= (46 + 16) u = 62 u

(iii) K₂CO₃ का सूत्र इकाई द्रव्यमान
= (2 × 39 + 1 × 12 + 3 x 16 ) u
= (78 + 12 + 48) u
= 138 u

खण्ड 3.5 से सम्बन्धित पाठ्य पुस्तक के प्रश्न (पा. पु. पृ. सं. -48)

प्रश्न 1.
यदि कार्बन परमाणुओं के एक मोल का द्रव्यमान 12 ग्राम है तो कार्बन के एक परमाणु का द्रव्यमान क्या होगा?
हल:
कार्बन के एक मोल परमाणुओं अर्थात् 6.022 x 10²³ परमाणुओं का द्रव्यमान = 12 ग्राम
अतः कार्बन के 1 परमाणु का द्रव्यमान होगा
= \(\frac{12}{6.022 \times 10^{23}}\) ग्राम
= 1.99 x 10^-23 ग्राम

प्रश्न 2.
किसमें अधिक परमाणु होंगे – 100g सोडियम अथवा 100g लोहा (Fe)? (Na का परमाणु द्रव्यमान = 23 u Fe का परमाणु द्रव्यमान = 56 u)
हल:
सोडियम (Na) का परमाणु द्रव्यमान = 23 u
सोडियम (Na) का मोलर द्रव्यमान = 23 ग्राम
मोलों की संख्या n = \(\frac { n }{ M }\) = \(\frac { 100 g }{ 23 g }\) = 4.35 मोल
इसी प्रकार Fe के मोलों की संख्या = \(\frac { 100 }{ 56 }\) = 1.78 मोल
चूँकि सोडियम के मोलों की संख्या, Fe से अधिक है;
अत: Na के 100 ग्राम में अधिक परमाणु हैं।

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 7 त्रिभुज Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 7 त्रिभुज

प्रश्न 1.
समकोण त्रिभुज ABC में कोण C समकोण हो, तो बड़ी भुजा होगी:

(A) AB
(B) BC
(C) CA
(D) कोई नहीं।
हल :
समकोण के सामने वाली भुजा AB (कर्ण) सबसे बड़ी होगी।
अत: सही विकल्प ‘A’ है।

प्रश्न 2.
किसी त्रिभुज की किन्हीं दो भुजाओं का अन्तर उसकी तीसरी भुजा से होता है:
(A) अधिक
(B) समान
(C) कम
(D) आधा।
हल :
किसी त्रिभुज की किन्हीं दो भुजाओं का अन्तर उसकी तीसरी भुजा से कम होता है।
अतः सही विकल्प ‘C’ है।

प्रश्न 3.
त्रिभुज के तीनों शीर्ष लम्बों का योग उसके परिमाप से होता है:
(A) अधिक
(B) समान
(C) आधा
(D) कम।
हल :
त्रिभुज के तीनों शीर्ष लम्बों का योग, त्रिभुज के परिमाप से कम होता है।
अतः सही विकल्प ‘D’ है।

प्रश्न 4.
चित्र में, ∠A का मान होगा : यदि AB = BC एवं ∠B = 70°।

(A) 70°
(B) 40°
(C) 55°
(D) 90°.
हल :
चित्र में, ΔABC एक समद्विबाहु 4 है।
AB = BC
∴ ∠C = ∠A
हम जानते हैं कि
∠A + ∠B + ∠C = 180°
⇒ ∠A + 70° + ∠A = 180°
⇒ 2∠A = 180° – 70°
⇒ 2∠A = 110°
⇒ ∠A = \(\frac {110°}{2}\)
∴ ∠A = 55°
अतः सही विकल्प ‘C’ है।

प्रश्न 5.
एक समद्विबाहु त्रिभुज ABC में, AB = AC तथा ∠B = 45° है, एवं भुजा BA को D तक इस प्रकार बढ़ाया कि AB = AD हो, तो ∠BCD की माप होगी :

(A) 70°
(B) 90°
(C) 60°
(D) 45°
हल :
AB = AC ……………(i)
∠ACB = ∠B
(समान भुजाओं के सम्मुख कोण समान होते हैं)
∠ACB = 45°
∠A + ∠B + ∠CAB = 180°
(त्रिभुज के अन्तः कोणों का योग )
45° + 45° + ∠CAB = 180°
∠CAB = 180° – 90° = 90°
तथा ∠CAD = ∠CAB = 90°
अब AB = AD (दिया है)
तब AD = AC (∵ AC = AB)
ΔACD समकोण समद्विबाहु D में, (माना)
∴ ∠C = ∠D = x°
तब
∠A + ∠C + ∠D = 180°
90° + x + x° = 180°
2x = 180 – 90° = 90°
x° = 45°
∴ ∠BCD = 45° + 45° = 90°
अतः सही विकल्प ‘B’ है।

प्रश्न 6.
चित्र में, AB = AC एवं ∠ABD = ∠ACD हो, तो ΔBDC होगा :

(A) समबाहु त्रिभुज
(B) समद्विबाहु त्रिभुज
(C) समानकोणिक त्रिभुज
(D) विषमबाहु त्रिभुज ।
हल :
AB = AC (दिया है)
∴ ∠ABC = ∠ACB …….(i)
(समान भुजाओं के सामने के कोण)
∠ABD = ∠ACD (दिया है) …(ii)
(i) व (ii) को जोड़ने पर,
∠ABC + ∠ABD = ∠ACB + ∠ACD
∠DBC = ∠DCB
∴ BD = DC
(समान कोणों की सम्मुख भुजाएँ )
अत: ΔBCD एक समद्विबाहु 4 है।
अतः सही विकल्प ‘B’ है।

प्रश्न 7.
चित्र में ΔABC में, AB = AC एवं AD ⊥ BC हो, न्तो भुजा AD समद्विभाजक होगी :

(A) कोण 4 की
(B) भुजा BC की
(C) कोण A एवं भुजा BC की
(D) किसी की नहीं।
हल :
चित्र में, AB = AC (दिया है)
AD ⊥ BC (दिया है)
ΔABD तथा ΔADC में,
AB = AC (दिया है)
∠ADB = ∠ADC (समकोण)
∠ABD = ∠ACD (समान कोणों के सम्मुख कोण)
∴ ΔABD ≅ ΔADC (ASA)
∴ ∠BAD = ∠CAD
तथा BC = DC
अतः भुजा AD, ∠A और भुजा BC की समद्विभाजक है।
अतः सही विकल्प ‘C’ है।

प्रश्न 8.
किसी त्रिभुज की बराबर भुजाओं के सम्मुख कोण …………… होते हैं।
हल :
बराबर।

प्रश्न 9.
चित्र में, भुजा AB एवं AC में सम्बन्ध लिखिए।

हल :
यहाँ बहिष्कोण B = 135°
∴ ∠ABC + 135° = 180°
∴ ∠ABC = 180° – 135° = 45°
और बहिष्कोण C = 115°
∠ACB + 115° = 180°
∴ ∠ACB = 180° – 115° = 65°
अब ∠ACB > ∠ABC
AB > AC
(बड़े कोण की सम्मुख भुजा बड़ी होती है)

प्रश्न 10.
यदि ΔABC में, AB = AC तथा ∠A < 60° हो, भुजा BC एवं AC में सम्बन्ध लिखिए।

हल :
ΔABC में दियां, ∠A < 60° ……..(i)
∵ AB = AC
∴ ∠B = ∠C (समान भुजाओं के सम्मुख कोण)
हम जानते हैं कि ΔABC में, किसी त्रिभुज के तीनों कोणों का योग 180° होता है।
∠A + ∠B + ∠C = 180°
∵ ∠A < 60° और ∠B = ∠C
∴ ∠B = ∠C > 60° और ∠A < 60° (दिया है)
अब ∠B = ∠C > ∠A
⇒ ∠B > ∠A (सम्मुख भुजाओं के कोण)
⇒ AC > BC
⇒ BC < AC

प्रश्न 11.
चित्र में, चतुर्भुज ABCD के ∠ABC = ∠ABD एवं AC = BD हो, तो सिद्ध कीजिए कि ΔABC ≅ ΔABD.

हल :
दिया है चतुर्भुज ABCD में
∠ABC = ∠ABD, AC = BD.
सिद्ध करना है: ΔABC ≅ ΔABD
उपपत्ति: ΔABC और ΔABD में.
BC = BD (दिया हैं)
∠ABC = ∠ABD (दिया है)
AB = AB (उभयनिष्ठ)
अतः भुजा कोण-भुजा
ΔABC ≅ ΔABD (SAS नियम) इति सिद्धम् ।

प्रश्न 12.
चित्र में त्रिभुज में कोई अन्तःबिन्दु O हो, तो सिद्ध कीजिए कि
(BC + AB + AC) < 2 (OA + OB + OC).

हल :
दिया है ΔABC में, O अन्त: बिन्दु है।
सिद्ध करना है
(BC + AB + AC) < 2 (OA + OB + OC).
उपपत्ति ΔAOB में, AO + BO > AB …(i) (Δ की दो भुजाओं का योग )
इसी प्रकार ΔBOC में, OB + OC > BC ….(ii)
इसी प्रकार ΔAOC में, OC + OA > AC ….(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर
(AO + BO) + (OB + OC) + (OC + OA) > AB + BC + AC
2(OA + OB + OC) > AB + BC + AC
या AB + BC + AC < 2(OA + OB + OC) इति सिद्धम् ।

प्रश्न 13.
निम्नांकित आकृति में PQRS एक चतुर्भुज है जिसके विकर्ण PR और Q5 बिन्दु पर प्रतिच्छेदित करते है। दिखाइये कि
(i) PQ + QR + RS + SP > PR + QS तथा
(ii) PQ + QR + RS + SP < 2 (PR + QS)
हल :
दिया है: चतुर्भुज PQRS में विकर्ण PR तथा QS एक दूसरे को O पर काटते हैं। सिद्ध करना है
(i) PQ + QR + RS + SP > PR + QS तथा
(ii) PQ + QR + RS + SP < 2(PR + QS)

उपपत्ति : चूँकि त्रिभुज में किन्हीं दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
∴ ΔPQR से, PQ + QR > PR ……….(i)
ΔRSP में RS + SP > PR ………. (ii)
ΔQRS में OR + RS > QS ………. (iii)
ΔPQS में PQ + SP > QS …………(iv)

(i), (ii), (iii) और (iv) को जोड़ने पर,
2PQ + 2QR + 2RS + 2SP > 2(PR + QS)
⇒ PQ + QR + RS + SP > PR + QS इति सिद्धम् ।
पुन: ΔOPQ में
OP + OQ > PQ ………(v)
ΔOQR में OQ + OR > QR ……(vi)
ΔORS में OR + OS > RS ………(vii)
ΔOSP में OS + OP > SP ……..(viii)
(v), (vi), (vii) और (viii) को जोड़ने पर
2OP + 2OR + 2OQ + 2OS > PQ + QR + RS + SP
2(OP + OR + OQ + OS) > PQ + QR + RS + SP
2(PR+ QS) > PQ+QR + RS + SP
PQ + QR + RS + SP < 2 (PR + QS) इति सिद्धम् ।

प्रश्न 14.
सिद्ध कीजिए कि त्रिभुज की तीनों भुजाओं का योग उसकी तीनों माध्यिकाओं के योग से अधिक होता है।
हल :

दिया है ABC में, माध्यिकाए AD BE और सिद्ध करना है AB + BC + AC > AD + BE + CE
उपपत्ति: हम जानते हैं कि किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा पर खींची गई माध्यिका के दुगुने से अधिक होता है। चित्र में 4 शीर्ष से
खींची गई भुजा BC पर AD माध्यिका है।
⇒ AB + AC > 2AD ……….(i)
B शीर्ष से खींची गई भुजा CA पर BE माध्यिका है।
⇒ BC + AB > 2BE …….(ii)
C शीर्ष से खींची गई भुजा AB पर CF माध्यिका है।
⇒ AC + BC > 2CF …………. (iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर,
(AB + AC) + (BC + AB) + (AC + BC) > 2AD + 2BE + 2CF
⇒ 2(AB + BC + AC) > 2 (AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF इति सिद्धम् ।

प्रश्न 15.
शलभ दो वस्तुओं के मध्य की दूरी मालूम करना चाहता है, परन्तु इन दोनों वस्तुओं के मध्य एक रुकावट है (जैसा कि चित्र में दिखाया गया है।), जिसके कारण वह यह दूरी सीधे नाप कर ज्ञात नहीं कर सकता।

इस कठिनाई को दूर करने के लिए वह दिमाग लड़ाता है। पहले वह एक बिन्दु O ऐसा लेता है जिससे A और B दोनों दिखाई दें और वह एक खम्भा स्थापित करता है। फिर रेखा AO की सीध में एक बिन्दु पर खम्भा इस प्रकार स्थापित करता है कि AO = OD इसी प्रकार वह एक तीसरा खम्भा C पर स्थापित करता है, जिससे BO = CO। तब वह CD को नापता है और देखता हैकि CD = 170 मी. सिद्ध कीजिए कि A तथा B के मध्य की दूरी भी 170 मीटर है।
हल :
दिया है AD = OD, BO = CO व CD = 170
सिद्ध करना है: AB = CD = 170 मीटर

उपपत्ति: ΔAOB व ΔDOC में,
∠AOB = ∠COD (शीर्षाभिमुख कोण)
OA = OD (दिया है)
OB = OC (दिया है)
∴ ΔAOB ≅ ΔDOC (ASS)
∴ AB = CD
∴ AB = 170 मीटर इति सिद्धम् ।

प्रश्न 16.
निम्नांकित आकृति में AC = BC, ∠DCA = ∠ECB तथा ∠DBC = ∠EAC सिद्ध कीजिए कि ΔDBC और ΔEAC सर्वांगसम हैं और DC = EC
हल :
दिया है : AB = BC, ∠DCA = ∠ECB
तथा ∠DBC = ∠EAC,
सिद्ध करना है ΔDBC ≅ ΔEAC
तथा DC = EC

उपपत्ति:
∠ECB = ∠DCA (दिया है)
⇒ ∠ECB + ∠ECD = ∠DCA + ∠ECD
(दोनों पक्षों में ∠ECD जोड़ने पर )
⇒ ∠DCB = ∠ECA ………….(i)
अब, ΔDBC व ΔEAC में
∠DCA = ∠ECA ((i) से)
BC = AC (दिया है)
∠DBC = ∠EAC (दिया है)
∴ ΔDBC ≅ ΔEAC (ASA)
∴ DC = EC इति सिद्ध ।

प्रश्न 17.
निम्न आकृति में, ΔABC में, AB = AC और CF क्रमश: ∠B और ∠C के समद्विभाजक हैं। सिद्ध कीजिए कि ΔEBC ≅ ΔFCB.

हल :
दिया है ΔABC में, AB = AC व BF तथा CF
क्रमश: ∠B और ∠C के समद्विभाजक हैं।
सिद्ध करना है:
ΔEBC ≅ ΔFCB.
उपपत्ति
ΔMBC में, ΔBAC
∴ ∠B = ∠C (समान भुजओं के सम्मुख कोण)
⇒ ∠ABC = ∠ACB
⇒ \(\frac {1}{2}\)∠ABC = \(\frac {1}{2}\)∠ACB
⇒ ∠EBC = ∠FCB ……..(i)
अब ΔEBC और ΔFCB में,
∠EBC = ∠FCB [समीकरण (i) से]
BC = BC (उभयनिष्ठ भुजा)
∠ECB = ∠FBC [∵ ∠ABC = ∠ACB ]
ΔEBC ≅ ΔFCB. (ASA से) इति सिद्धम् ।

प्रश्न 18.
यदि त्रिभुज के किसी कोण का समद्विभाजक सम्मुख भुजा को भी समद्विभाजित करता है, तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु है ।
हल :
दिया हुआ माना त्रिभुज ABC में
कोण ∠BAC का समद्विभाजक, सम्मुख भुजा BC को समद्विभाजित करता है।
सिद्ध करना है : AB = AC
रचना : भुजा AD, ∠A
तथा भुजा BC को समद्विभाजित करती है। AD को E तक इस प्रकार बढ़ाया कि AD = DE।
E और C को मिलाया।
उपपत्ति :
ΔADB और ΔEDC में,
BD = DC (दिया है)
AD = DE (रचना से)
∠ADB = ∠EDC (शीर्षाभिमुख कोण)
∴ ΔADB ≅ ΔEDC (SSA)
⇒ AB = EC ………….(i)
और ∠BAD = ∠CED (एकान्तर कोण)
लेकिन ∠BAD = ∠CAD (दिया है)
∴ ∠CAD = ∠CED
⇒ AC = EC [∵ समान भुजाओं के सम्मुख कोण]
⇒ AC = AB [समीकरण (i) से]
अत: ΔABC एक समद्विबाहु त्रिभुज है। इति सिद्धम् ।

प्रश्न 19.
सम्मुख आकृति में, ΔABC समद्विबाहु में AB = AC हैं तथा दो माध्यिकाएँ BD तथा CE सिद्ध कीजिए कि BD = CE.

हल :
दिया है : समद्विबाहु त्रिभुज ABC में, AB = AC और BD तथा CE शीर्षों B तथा C से खींची गयी माध्यिकाएँ है।
सिद्ध करना है : BD = CE.
उपपत्ति : ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∴ ∠ABC = ∠ACB (समान भुजाओं के सम्मुख कोण)
∴ ∠EBC = ∠DCB ……..(1)
∵ BD, भुजा AC की माध्यिका है
∴ CD = \(\frac {1}{2}\)AC या AC = 2CD
इसी प्रकार
∴ BE = \(\frac {1}{2}\) AB या AB = 2BE
∵ ΔABC समद्विबाहु त्रिभुज है जिसमें भुजा AC = AB
∴ 2CD = 2BE ⇒ CD = BE
अब ΔBCE तथा ΔBCD में,
भुजा BE = भुजा CD, अभी सिद्ध किया है
∠EBC = ∠DCB, समीकरण (1) से
BC = BC, दोनों त्रिभुजों में उभयनिष्ठ भुजा है
ΔBCE ≅ ΔBCD (SAS) इति सिद्धम् ।

प्रश्न 20.
निम्न आकृति में यदि AB = EF, BC = DE, AB ⊥ BD तथा FE ⊥ CE, तो सिद्ध कीजिए कि ΔABD = ΔFEC

हल :
BC = DE (दिया है)
∴ BC + CD = CD + DE
(दोनों पक्षों में CD जोड़ने पर)
⇒ BD = CE …(i)
अब ΔMBD और ΔFEC में
AB = EF (दिया है)
∠ABD =∠FEC = 90° (∵ AB ⊥ BD और FE ⊥ CE)
BD = CE …(i) से]
अतः ΔABD ≅ ΔFEC इति सिद्धम्

प्रश्न 21.
ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA को D तक इस प्रकार बढ़ाया गया है कि AB = AD सिद्ध कीजिए कि ∠BCD समकोण है।
हल :
त्रिभुज ABC में
AB = BC (दिया है) …….(i)
∠ABC = ∠ACB …….(ii)
(समान भुजाओं के सम्मुख कोण)
AB = AD (दिया है ) … (iii)
∠ADC = ∠DCA ….(iv)
(समान भुजाओं के सम्मुख कोण)
(ii) और (iii) को जोड़ने पर
∠ABC +∠ADC = ∠ACB + ∠DCA
∠ABC + ∠ADC = ∠BCD ……(v)
∠ABC + ∠ADC + ∠BCD = 180°
(त्रिभुज के अन्त कोणों का योग)

∠BCD + ∠BCD = 180° [(v) से]
2 ∠BCD = \(\frac {180°}{2}\)
∠BCD = 90° इति सिद्धम् ।

प्रश्न 22.
सिद्ध कीजिए कि त्रिभुज के तीनों शीर्ष लम्बों का योग उस त्रिभुज के परिमाप से कम होता है।

हल :
दिया है ΔABC में शीर्षों A, B तथा C से क्रमशः सम्मुख भुजाओं पर डाले गए लम्ब AD, BE तथा CF
सिद्ध करना है :
AD + BE + CF < AB + BC + CA
उपत्ति : ΔABD में, ∠ADB = 90°
∴ AD < AB ………..(i)
ΔBEC में, BE ⊥ AC
∴ BE < BC …..(ii)
इसी प्रकार, ΔACF में,
CF ⊥ AB
∴ CF < AC …(iii)
(i), (ii) और (iii) को जोड़ने पर,
AD + BE + CF < AB + BC + AC इति सिद्धम्

प्रश्न 23.
रिक्त स्थानों की पूर्ति कीजिए :
(i) यदि कोई बिन्दु दो बिन्दुओं को मिलाने वाले रेखाखण्ड के लम्ब समद्विभाजक पर स्थित हो, तो वह दिए हुए बिन्दुओं से …………… होता है।
(ii) बिन्दुओं का ऐसा समुच्चय जो कुछ दिए हुए प्रतिबन्धों को संतुष्ट करता है, …………… कहलाता है।
(iii) किसी ऐसे बिन्दु का बिन्दु पथ जो स्थिर बिन्दुओं से समदूरस्थ है, दोनों बिन्दुओं को मिलाने वाले रेखाखण्ड का ……… होता है।
(iv) यदि कोई बिन्दु दो प्रतिच्छेदी रेखाओं के मध्य बने कोण के समद्विभाजक पर स्थित हो, तो वह दोनों रेखाओं से ………….. होता है।
(v) किसी त्रिभुज के शीर्ष और सम्मुख भुजा के मध्य बिन्दु को मिलाने वाली रेखाखण्ड ……………. कहलाती है।
हल :
(i) समदूरस्थ
(ii) बिन्दुपथ,
(iii) लम्ब समद्विभाजक,
(iv) समदूरस्थ
(v) माध्यिका

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण

प्रश्न 1.
समीकरण x + 3y – 10 को सन्तुष्ट करने वाला बिन्दु है :
(A) (4, 2)
(B) (-4, 2)
(C) (4, – 1)
(D) (2, 4).
हल :
समीकरण x + 3y = 10 में करते हैं।
x = 4 और y = 2 रखने पर,
4 + 3 × 2 = 10
अतः विकल्प ‘A’ के दोनों मान समीकरण को सन्तुष्ट
∴ सही विकल्प ‘A’ है।

प्रश्न 2.
रैखिक समीकरण x + 40 = 0 है
(A) एकचरीय समीकरण
(B) द्विचरीय समीकरण
(C) द्विघात समीकरण
(D) उपर्युक्त में से कोई नहीं।
हल :
x + 4 y = 0
इस समीकरण में और y दो चर हैं।
∴ यह दो चरों वाला रैखिक समीकरण है।
अतः सही विकल्प ‘B’ है।

प्रश्न 3.
समीकरण 4x + 5y = k में यदि x = 2, y = 1 हो, तो k का मान होगा :
(A) 9
(B) – 12
(C) – 13
(D) 13.
हल :
समीकरण 4x + 5y = k में x = 2 और y = 1
रखने पर,
4 × 2 + 5 × 1 = k
⇒ 8 + 5 = k ⇒ 13 = k
अतः सही विकल्प ‘D’ है।

प्रश्न 4.
रैखिक समीकरण y – 2 = 0 का आलेख खींचने पर प्राप्त होगा :
(A) X- अक्ष के समान्तर सरल रेखा
(B) मूलबिन्दु से गुजरती हुई सरल रेखा
(C) Y-अक्ष के समान्तर सरल रेखा
(D) आलेख नहीं खींचा जा सकता।
हल :
समीकरण y – 2 = 0 को निम्न प्रकार लिख सकते हैं : 0x + y = 2
x के विभिन्न मानों के लिए y का मान 2 प्राप्त होगा । अतः सरल रेखा X- अक्ष के समान्तर प्राप्त होगी।
∴ सही विकल्प ‘A’ है।

प्रश्न 5.
दो चर वाले रैखिक समीकरण के हल होंगे:
(A) एक अद्वितीय
(B) केवल अपरिमित रूप से अनेक
(C) दो
(D) चार हल।
हल :
दो चर वाले रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं।
अतः सही विकल्प ‘B’ है।

प्रश्न 6.
रैखिक समीकरण y = 3x से व्यक्त रेखा पर स्थित बिन्दु होगा :
(A) (2, 3)
(B) (3, 1)
(C) (1, 3)
(D) (1, -3).
हल :
समीकरण y = 3x
समीकरण में x = 1 रखने पर y = 3 प्राप्त होता है
अतः सही विकल्प ‘C’ है।

प्रश्न 7.
किसी रैखिक समीकरण में घरों की बात होती है
(A) कोई भी
(B) 0
(C) 2
(D) 1.
हल :
रैखिक समीकरण की घात होती है।
अतः सही विकल्प ‘D’ है।

प्रश्न 8.
रैखिक समीकरण के बिन्दु (2, 5) से गुजरने वाली रेखाओं की संख्या होगी :
(A) 2
(B) 5
(C) अनन्त
(D) 7.
हल :
किसी बिन्दु से गुजरने वाली रेखाओं की संख्या अनन्त होती है।
अतः सही विकल्प ‘C’ है।

प्रश्न 9.
यदि दो अंकों वाली संख्या में इकाई का अंक b तथा दहाई का अंक a हो तो संख्या लिखिए।
हल :
संख्या (10a + b).

प्रश्न 10.
यदि आपके लिए कोई रैखिक समीकरण दिया गया है, तो उसे कैसे पहचानोगे? उदाहरण दीजिए।
हल :
रैखिक समीकरण में चर की अधिकतम घात एक होती है।
जैसे: 2x + y – 10 = 0, y + 3x = 0 आदि रैखिक समीकरण के उदाहरण हैं।

प्रश्न 11.
y = mx प्रकार के समीकरण की रेखा किस बिन्दु से गुजरती है ?
हल :
मूलबिन्दु (0, 0) से ।

प्रश्न 12.
यदि x = 3y समीकरण में y = 0 हो तो उक्त समीकरण किस अक्ष का होगा ?
हल :
दिया गया समीकरण है :
x = 3y, x = 3 (0) = 0
⇒ x = 0, Y अक्ष का समीकरण है।

प्रश्न 13.
समीकरण 230 का आलेख किस प्रकार का होगा ? समझाइए ।
हल :
समीकरण
2y – 3 = 0 ⇒ 2y = 3
∴ y = \(\frac {3}{2}\)
अतः x के सभी मानों के लिए रैखिक समीकरण
0.x + 2y – 3 = 0 से y का मान \(\frac {3}{2}\) प्राप्त होगा।

∴ बिन्दु (1, \(\frac {3}{2}\)), (2, \(\frac {3}{2}\)), (-2, \(\frac {3}{2}\))………… से प्राप्त आलेख मूल बिन्दु से \(\frac {3}{2}\) इकाई दूर X- अक्ष के समान्तर होगा।

प्रश्न 14.
फारेनहाइट को सेल्सियस में परिवर्तित करने वाला रैखिक समीकरण लिखिए ।
हल :
रैखिक समीकरण F = (\(\frac {9}{5}\))C + 32.

प्रश्न 15.
निम्नलिखित सेल्सियस को फारेनहाइट में रूपांतरित कीजिए :
(i) 25°C
(ii) 35°C
(iii) 0°C.
हल :
(i) 25°C.
F = \(\frac {9}{5}\) × 25 + 32 = 9 × 5 + 32 = 45 + 32 = 77
अतः 25°C = 77°E.

(ii) 35°C.
F = \(\frac {9}{5}\) × 35 + 32 = 9 × 7 + 32 = 63 + 32 = 95
अतः 35°C = 95°F.

(iii) 0°C.
F = \(\frac {9}{5}\) × 0 + 32 = 32
अतः 0°C = 32°F.

प्रश्न 16.
यदि x = 1 हो तो समीकरण \(\frac{4}{x}+\frac{3}{y}\) = 5 में y का मान बताइए।
हल :
समीकरण \(\frac{4}{x}+\frac{3}{y}\) = 5 में x = 1 रखने पर,
\(\frac{4}{1}+\frac{3}{y}\) = 5
⇒ \(\frac {3}{y}\) = 5 – 4 = 1
⇒ \(\frac {3}{y}\) = 1
∴ y = 3.

प्रश्न 17.
निम्नलिखित समीकरणों को ax + by + c = 0 के रूप में व्यक्त करने पर a, b और c के मान ज्ञात कीजिए:
(i) 3 + 5y = πx
(ii) 2x + \(\frac {3}{2}\) = 1.4y.
हल :
(i) समीकरण
3 + 5y = πx
⇒ πx – 5y – 3 = 0 की तुलना ax + by + c = 0 से करने पर, a = π, b = – 5 और c = – 3.

(ii) समीकरण 2x + \(\frac {3}{2}\) = 1.4y
⇒ 2x – 14y + \(\frac {3}{2}\) = 0 की तुलना ax + by + c = 0
से करने पर, a = 2, b = – 1.4 और c = \(\frac {3}{2}\)

प्रश्न 18.
निम्नलिखित समीकरणों में से प्रत्येक के दो संगत हल ज्ञात कीजिए :
(i) 4x + 3y = 12
(ii) 2x + 5y = 0
(iii) 3y + 4 = 0.
हल :
(i) x = 0 लेने पर,
4(0) + 3y = 12 ∴ y = 4
अत: (0, 4) समीकरण का हल है।
y = 0 लेने पर,
4x + 3(0) = 12 ⇒ 4x = 12 ∴ x = 3
अतः (3, 0) समीकरण का हल है।
अत: समीकरण 4x + 3y = 12 के दो हल (0, 4) और (3, 0) होंगे।

(ii) x = 0 लेने पर 2(0) + 5y = 0 ⇒ y = 0
अतः (0, 0) समीकरण का हल है।
x = 1 लेने पर,
2 × 1 + 5y = 0 ⇒ 5y = -2 ∴ y = \(\frac {-2}{5}\)
अतः (1, \(\frac {-2}{5}\)) समीकरण का हल हैं।
अतः दिये गये समीकरण के दो हल (0, 0) और (1, \(\frac {-2}{5}\)) होंगे।

(iii) समीकरण 3y + 4 = 0 को 0x + 3y + 4 = 0 के रूप में लिखने पर x के सभी मानों के लिए y = \(\frac {-4}{3}\) प्राप्त होगा ।
अतः दिये गये समीकरण के दो हल (0, \(\frac {-4}{3}\)) और (1, \(\frac {-4}{3}\)) हैं।

प्रश्न 19.
निम्नलिखित कथनों को समीकरण के रूप में लिखिए :
(i) यदि किसी संख्या में 9 जोड़ दिया जाए, तो वह 25 के बराबर होती है।
(ii) यदि किसी संख्या में से 15 घटा दिए जाये, तो वह 5 के बराबर हो जाती है।
(iii) किसी संख्या का 7 गुना, 42 के बराबर होता है।
(iv) किसी संख्या में 5 का भाग देने पर वह 6 बन जाती है।
(v) यदि किसी संख्या के 3 गुने में 6 जोड़ा जाये, तो वह 15 के बराबर हो जाती है।
हल :
सभी प्रश्नों में अज्ञात संख्या को x मानने पर,
(i) x + 9 = 25
(ii) x – 15 = -5
(iii) x × 7 = 42 ⇒ 7x = 42
(iv) \(\frac {x}{5}\) = 6
(v) x × 3 + 6 = 15 ⇒ 3x + 6 = 15.

प्रश्न 20.
समीकरण 2x – 3y + 4 = 0 का आलेख खींचिए ।
हल :
दिया गया समीकरण 2x – 3y + 4 = 0
या 2x = 3y – 4
या x = \(\frac{3 y-4}{2}\)
यदि y = 0, हों, तो x = \(\frac{3 \times 0-4}{2}\) = – 2
यदि y = 2, हों, तो x = \(\frac{3 \times 2-4}{2}\) = 1
यदि y = 4, हों, तो x = \(\frac{3 \times 4-4}{2}\) = 4
सारणी :

x	– 2	1	4
y	0	2	4

आलेख खींचना : माना पैमाना X- अक्ष पर 1 सेमी 1 इकाई, Y- अक्ष पर 1 सेमी = 1 इकाई ।

बिन्दु A(-2, 0) B (1, 2) और C(4, 4) दो चर रैखिक समीकरण 2x = 3y – 4 के हल हैं।

प्रश्न 21.
पिता की आयु पुत्र की आयु से 25 वर्ष अधिक है। 10 वर्ष पूर्व पिता की आयु पुत्र की आयु से दुगुनी थी। दोनों की वर्तमान आयु ज्ञात करो ।
हल :
माना, पिता की आयु = x वर्ष
पुत्र की आयु = y वर्ष
प्रश्नानुसार, x = y +25 ……..(i)
तथा 10 वर्ष पूर्व दोनों की आयु (x – 10) वर्ष तथा (y – 10) वर्ष होगी।
अतः (x – 10) = 2(y – 10)
⇒ x – 10 = 2y – 20
⇒ x = 2y – 20 +10
⇒ x = 2y – 10 ……..(ii)
समी. (ii) में (i) से x का मान रखने पर
y + 25 = 2y – 10
⇒ 25 + 10 = 2y – y
⇒ y = 35
समी. (i) में y का मान रखने पर,
x = 35 + 25 = 60
∴ पिता की आयु 60 वर्ष तथा पुत्र की आयु 35 वर्ष।

Jharkhand Board JAC Class 9 Science Solutions Chapter 11 कार्य तथा ऊर्जा Textbook Exercise Questions and Answers.

JAC Board Class 9 Science Solutions Chapter 11 कार्य तथा ऊर्जा

Jharkhand Board Class 9 Science कार्य तथा ऊर्जा Textbook Questions and Answers

प्रश्न 1.
निम्न सूचीबद्ध क्रियाकलापों को ध्यान से देखिए। अपनी कार्य शब्द की व्याख्या के आधार पर तर्क दीजिए कि इनमें कार्य हो रहा है अथवा नहीं।

1. सूमा एक तालाब में तैर रही है।
2. एक गधे ने अपनी पीठ पर बोझा उठा रखा है।
3. एक पवन चक्की (विंड मिल) कुएँ से पानी उठा रही है।
4. एक हरे पौधे में प्रकाश संश्लेषण की प्रक्रिया हो रही है।
5. एक इंजन ट्रेन को खींच रहा है।
6. अनाज के दाने सूर्य की धूप में सूख रहे हैं।
7. एक पाल नाव पवन ऊर्जा के कारण गतिशील है।

उत्तर:

1. हाँ, इस स्थिति में कार्य हो रहा है, किन्तु किया जा रहा कार्य ऋणात्मक है, क्योंकि बल पीछे की ओर लगाया जा रहा है, जबकि विस्थापन आगे की दिशा में हो रहा है।
2. इस स्थिति में कोई कार्य नहीं हो पा रहा है, क्योंकि बल नीचे की ओर लग रहा है, परंतु कोई विस्थापन नहीं हो रहा है।
3. हाँ, इस स्थिति में कार्य हो रहा है, क्योंकि बल ऊपर की ओर आरोपित किया जा रहा है तथा पानी भी ऊपर की ओर उठाया जा रहा है।
4. इस स्थिति में कोई कार्य नहीं हो रहा है, क्योंकि न तो कोई बल आरोपित किया जा रहा है और न ही वस्तु विस्थापित हो रही है।
5. हाँ, इस स्थिति में कार्य हो रहा है, क्योंकि इंजन द्वारा रेलगाड़ी पर बल आरोपित किया जा रहा है तथा रेलगाड़ी आरोपित बल की दिशा में विस्थापित हो रही है।
6. नहीं, इसमें कोई कार्य नहीं हो रहा है, क्योंकि यहाँ न तो कोई बल आरोपित हो रहा है और न कोई विस्थापन उत्पन्न हो रहा है।
7. हाँ, इस स्थिति में कार्य हो रहा है, क्योंकि पवन ऊर्जा द्वारा नाव पर बल आरोपित हो रहा है तथा नाव भी आरोपित बल की दिशा में गति कर रही है।

प्रश्न 2.
एक पिण्ड को धरती से किसी कोण पर फेंका जाता है। यह एक वक्र पथ पर चलता है और वापस धरती पर आ गिरता है। पिण्ड के पथ के प्रारम्भिक तथा अंतिम बिन्दु एक ही क्षैतिज रेखा पर स्थित हैं। पिण्ड पर गुरुत्व बल द्वारा कितना कार्य किया गया?
उत्तर:
गुरुत्वाकर्षण बल द्वारा वस्तु पर किए गए कार्य की मात्रा शून्य होगी, क्योंकि गुरुत्व बल के विरुद्ध किया गया कार्य mgh वस्तु का द्रव्यमान तथा गुरुत्वीय त्वरण तो स्थिर रहते हैं, किन्तु उसकी ऊँचाई शून्य हो जाती है। ऐसा पथ के आरंभिक तथा अंतिम बिन्दुओं के एक ही क्षैतिज तल में स्थित होने के कारण होता है।

प्रश्न 3.
एक बैटरी बल्ब जलाती है। इस प्रक्रम में होने वाले ऊर्जा परिवर्तनों का वर्णन कीजिए।
उत्तर:
बैटरी की रासायनिक ऊर्जा, विद्युत ऊर्जा में परिवर्तित होती है। विद्युत ऊर्जा, ताप एवं प्रकाश ऊर्जा में परिवर्तित होती है।

प्रश्न 4.
20 kg द्रव्यमान पर लगने वाला कोई बल इसके वेग को 5ms^-1 से 2ms^-1 में परिवर्तित कर देता है। बल द्वारा किए गए कार्य का परिकलन कीजिए।
हल:
वस्तु का द्रव्यमान m = 20 kg
आरंभिक वेग u = 5 m/s
अंतिम वेग v = 2m/s
समय t = 1 s
गति के पहले समीकरण से v = u + at
या, a = \(\frac{v-u}{t}=\frac{2 \mathrm{~m} / \mathrm{s}-5 \mathrm{~m} / \mathrm{s}}{1 \mathrm{~s}}\)
या, a = – 3 m/s²
गति के तीसरे समीकरण से,
v² – u² = 2as
(2m/s)² – (5m/s)² = 2 × (-3m/s²) x s
– 21 m²/s² = – 6m/s².s
s = \(\frac { -21 }{ -6 }\) = \(\frac { 7 }{ 2 }\) m
किया गया कार्य = F x s
W = m x a x s
= 20 kg × (- 3m/s²) x \(\frac { 7 }{ 2 }\)
= – 210 J

प्रश्न 5.
10 kg द्रव्यमान का एक पिण्ड मेज पर A बिन्दु पर रखा है। इसे B बिन्दु तक लाया जाता है। यदि A तथा B को मिलाने वाली रेखा क्षैतिज है तो पिण्ड पर गुरुत्व बल द्वारा किया गया कार्य कितना होगा। अपने उत्तर की व्याख्या कीजिए।
उत्तर:
द्रव्यमान m = 10 kg
गुरुत्वीय त्वरण g = 10m/s²
गुरुत्वाकर्षण बल द्वारा किया गया कार्य = m x g x h
इस स्थिति में, गुरुत्वाकर्षण बल द्वारा वस्तु पर किए गए कार्य की मात्रा शून्य होगी, क्योंकि बिन्दु A तथा B को जोड़ने वाली रेखा एक ही क्षैतिज तल अर्थात् वस्तु द्वारा प्राप्त ऊँचाई शून्य है। साथ ही, गुरुत्वाकर्षण बल का कोई भी घटक वस्तु के विस्थापन की दिशा में कार्य नहीं करता है।

प्रश्न 6.
मुक्त रूप से गिरते एक पिण्ड की स्थितिज ऊर्जा लगातार कम होती जाती है। क्या यह ऊर्जा संरक्षण नियम का उल्लंघन करती है? कारण बताओ।
उत्तर:
यह ऊर्जा संरक्षण सिद्धान्त की उल्लंघन नहीं करती है, क्योंकि जिस अनुपात में वस्तु की स्थितिज ऊर्जा में कमी आती है, उसी अनुपात में उसकी गतिज ऊर्जा में वृद्धि भी होती है अर्थात्, वस्तु की कुल ऊर्जा हमेशा संरक्षित रहती है।

प्रश्न 7.
जब आप साइकिल चलाते हैं तो कौन-कौन से ऊर्जा रूपांतरण होते हैं?
उत्तर:
स्थितिज ऊर्जा से पेशीय ऊर्जा तथा पेशीय ऊर्जा से यान्त्रिक ऊर्जा में ऊर्जा का रूपान्तरण होता है।

प्रश्न 8.
जब आप अपनी सारी शक्ति लगाकर एक बड़ी चट्टान को धकेलना चाहते हैं और इसे हिलाने में असफल हो जाते हैं तो क्या इस अवस्था में ऊर्जा का स्थानांतरण होता है? आपके द्वारा व्यय की गई ऊर्जा कहाँ चली जाती है?
उत्तर:
नहीं, जब हम अपनी पूरी शक्ति से बड़ी चट्टान को धकेलने पर उसे हिला नहीं पाते हैं, तो ऊर्जा का स्थानांतरण नहीं होता है। जब हम चट्टान को धक्का लगाते हैं तो हमारी पेशियाँ तन जाती हैं तथा इन पेशियों की ओर रक्त बहुत तेजी से विस्थापित होता है और ऊष्मीय ऊर्जा उत्पन्न होती है। इन परिवर्तनों में ऊर्जा खपत होती है तथा हम थका हुआ अनुभव करते हैं।

प्रश्न 9.
किसी घर में एक महीने में ऊर्जा की 250 यूनिटें व्यय हुई। यह ऊर्जा जूल में कितनी होगी?
हल:
पूरे महीने के दौरान कुल ऊर्जा खपत = 250 यूनिट
1 यूनिट = 1 kWh
∴ 250 यूनिट = 250kWh
पुन:, 1kWh = 36,00,0003
∴ 250kWh = 250 × 36,00,000 J
= 90,00,00,000 J
= 9 x 10⁸ J

प्रश्न 10.
40 kg द्रव्यमान का एक पिण्ड धरती से 5 m की ऊँचाई तक उठाया जाता है। इसकी स्थितिज ऊर्जा कितनी है? यदि पिण्ड मुक्त रूप से गिरने दिया जाए तो जब पिण्ड ठीक आधे रास्ते पर है, उस समय इसकी गतिज ऊर्जा का परिकलन कीजिए। (g = 10ms^-2)
हल:
वस्तु का द्रव्यमान m = 40 kg
ऊँचाई h = 5m
गुरुत्वीय त्वरण g = 10 ms^-2
स्थितिज ऊर्जा = m x g x h
= 40kg x 10ms^-2 x 5m
= 2000 J
जब वस्तु आधी ऊँचाई पर होती है
वस्तु का द्रव्यमान = 40kg
ऊँचाई h = 2.5m
गुरुत्वीय त्वरण g = 10ms^-2
आरंभिक वेग u = 0 m/s
तृतीय समीकरण के अनुसार,
v² – u² = 2as
v² = u² + 2as
v² = 0 + 2 × 10 ms^-2 x s = 20.s
गतिज ऊर्जा = \(\frac { 1 }{ 2 }\) mv²
= \(\frac { 1 }{ 2 }\) x 40 kg x 20 x 2.5 m²/s²
= 1000 J

प्रश्न 11.
पृथ्वी के चारों ओर घूमते हुए किसी उपग्रह पर गुरुत्व बल द्वारा कितना कार्य किया जाएगा? अपने उत्तर को तर्कसंगत बनाइए।
उत्तर:
पृथ्वी के चारों ओर घूमते हुए उपग्रह पर किये जाने वाले कार्य की मात्रा शून्य है।
उपग्रह अपनी वृत्तीय कक्षा में घूमता है, तो उसकी कक्षा की त्रिज्या के केन्द्र की ओर एक अभिकेन्द्रीय बल बल कार्य करता है तथा उपग्रह की दिशा कक्षा के लंबवत् होती है। इस तरह, बल तथा विस्थापन की दिशा एक-दूसरे के लंबवत् होती है।

किया गया कार्य = F x s x cos θ
W = Fs cos 90° = 0
एकसमान वृत्तीय गति की स्थिति में किया गया कुल कार्य शून्य होगा।

प्रश्न 12.
क्या किसी पिण्ड पर लगने वाले किसी भी बल की अनुपस्थिति में इसका विस्थापन हो सकता है? सोचिए। इस प्रश्न के बारे में अपने मित्रों तथा अध्यापकों से विचार-विमर्श कीजिए।
उत्तर:
जब वस्तु विरामावस्था में होती है, तो न्यूटन के गति के नियम के अनुसार, यह तब तक विरामावस्था में रहती है जब तक कि उस पर लगा बल उसकी इस अवस्था में परिवर्तन न ला दे। जब वस्तु गति अवस्था में होती है, जैसे चलती हुई बस, तो इसे रोकने के लिए बल की आवश्यकता होती है। अतः इस स्थिति में किसी कार्यकारी बल की अनुपस्थिति में भी बस में विस्थापन संभव है।

प्रश्न 13.
कोई मनुष्य भूसे के एक गट्ठर को अपने सिर पर 30 मिनट तक रखे रहता है और थक जाता है। क्या उसने कुछ कार्य किया या नहीं? अपने उत्तर को तर्कसंगत बनाइए।
उत्तर:
नहीं, व्यक्ति ने भूसे के गट्ठर पर कोई कार्य नहीं किया, क्योंकि गट्ठर में कोई विस्थापन नहीं होता है।

प्रश्न 14.
एक विद्युत्-हीटर (उष्मक) की घोषित शक्ति 1500 W है। 10 घंटे में यह कितनी ऊर्जा उपयोग करेगा?
हल:

प्रश्न 15.
जब हम किसी सरल लोलक के गोलक को एक ओर ले जाकर छोड़ते हैं तो यह दोलन करने लगता है। इसमें होने वाले ऊर्जा परिवर्तनों की चर्चा करते हुए ऊर्जा संरक्षण के नियम को स्पष्ट कीजिए। गोलक कुछ समय पश्चात् विराम अवस्था में क्यों आ जाता है? अंततः इसकी ऊर्जा का क्या होता है? क्या यह ऊर्जा संरक्षण के नियम का उल्लंघन है?
उत्तर:
(i) लोलक के गोलक की स्थितिज ऊर्जा उस समय सर्वाधिक होती है जब इसे एक तरफ खींचा जाता है। जब इसे दोलन के लिए छोड़ा जाता है, तो प्रत्येक अधिकतम विस्थापन की स्थिति में स्थितिज ऊर्जा अधिकतम तथा गतिज ऊर्जा शून्य होती है और माध्य की स्थिति में गतिज ऊर्जा अधिकतम हो जाती है जबकि स्थितिज ऊर्जा शून्य होती है। किन्तु कुल ऊर्जा हमेशा संरक्षित रहती है।

(ii) लोलक का गोलक अंत में रुक जाता है। ऐसा इसलिए होता है कि लोलक जिस बिन्दु से बंधा रहता है, उसके साथ घर्षण के कारण तथा दोलन करते हुए गोलक का हवा के साथ घर्षण के कारण होता है। इस घर्षण के कारण दोलन करते हुए गोलक की यांत्रिक ऊर्जा धीरे-धीरे ऊष्मा या ताप ऊर्जा में परिवर्तित हो जाती है।

(iii) अंत में यह ताप ऊर्जा वातावरण में खो जाती है।

(iv) नहीं, यह ऊर्जा संरक्षण के सिद्धान्त का उल्लंघन नहीं है।

प्रश्न 16.
m द्रव्यमान का एक पिंड एक नियत वेग से गतिशील है। पिण्ड पर कितना कार्य करना चाहिए कि वह विराम अवस्था में आ जाए?
हल:
द्रव्यमान = m, स्थिर वेग = v
वस्तु की ऊर्जा = \(\frac { 1 }{ 2 }\) mv² (चूँकि वस्तु गति में है)
अतः वस्तु को विराम में लाने के लिए समान मात्रा में कार्य करने की आवश्यकता होगी।
अतः वस्तु पर किया जाने वाला कार्य = \(\frac { 1 }{ 2 }\) mv²

प्रश्न 17.
1500 kg द्रव्यमान की कार को जो 60 km/b के वेग से चल रही है, रोकने के लिए किए गए कार्य का परिकलन कीजिए।
हल:
द्रव्यमान m = 1500 kg
वेग v = 60 km/h
= \(\frac { 60×1000m }{ 3600s }\) = 16.67 m/s
गतिज ऊर्जा = \(\frac { 1 }{ 2 }\) mv²
= \(\frac { 1 }{ 2 }\) x 1500 kg x (16.67m/s)²
= 208416.67 J

प्रश्न 18.
निम्न में से प्रत्येक स्थिति में m द्रव्यमान के एक पिण्ड पर एक बल F लग रहा है। विस्थापन की दिशा पश्चिम से पूर्व की ओर है जो एक लंबे तीर से प्रदर्शित की गई है। चित्रों को ध्यानपूर्वक देखिए और बताइए कि किया गया कार्य ऋणात्मक है, धनात्मक है या शून्य है।

उत्तर:
स्थिति (i) में किए गए कार्य की मात्रा शून्य है, क्योंकि बल विस्थापन के लम्बवत् कार्य कर रहा है।
θ कोण पर किया गया कार्य = F x s x cos θ
W = F x s x cos 90°
W = F × s × 0 = 0 J

स्थिति (ii) में किया गया कार्य धनात्मक है, क्योंकि वस्तु का विस्थापन आरोपित बल की दिशा में हो रहा है।

स्थिति (iii) में किया गया कार्य ऋणात्मक है, क्योंकि आरोपित बल की विपरीत दिशा में वस्तु का विस्थापन हो रहा है।

प्रश्न 19.
सोनी कहती है कि किसी वस्तु का त्वरण शून्य हो सकता है चाहे उस पर कई बल कार्य कर रहे हों। क्या आप उससे सहमत हैं? बताइए क्यों?
उत्तर:
हाँ, सोनी का कहना ठीक है, क्योंकि जब कोई वस्तु विरामावस्था में होती है तथा उसकी गति शून्य होती है, तब उसमें त्वरण भी शून्य होता है जब किसी वस्तु में एक साथ कई बल लगते हैं, तो वे एक-दूसरे को अप्रभावी कर देते हैं। जब वस्तु एकसमान वेग से गति में होती है, उसका त्वरण शून्य होता है। हाँ, क्योंकि इस स्थिति में भी वस्तु पर एक साथ कई संतुलनकारी बल कार्य कर सकते हैं।

प्रश्न 20.
चार युक्तियाँ, जिनमें प्रत्येक की शक्ति 500 W है 10 घंटे तक उपयोग में लाई जाती हैं इनके द्वारा व्यय की गई ऊर्जा kWh में परिकलित कीजिए।
हल:
कुल युक्तियाँ = 5
1 युक्ति की शक्ति = 500W
समय = 10 घंटे
कुल शक्ति = कुल युक्तियाँ – युक्ति की शक्ति
= 4 x 500 वाट = 2000 वाट 2kW
व्यय ऊर्जा = शक्ति x समय
= 2kW x 10 घंटे
= 20 kWh

प्रश्न 21.
मुक्त रूप से गिरता एक पिण्ड अंतत: धरती तक पहुँचने पर रुक जाता है इसकी गतिज ऊर्जा का क्या होती है?
उत्तर:
मुक्त रूप से गिरते हुए पिण्ड की स्थितिज ऊर्जा धीरे-धीरे गतिज ऊर्जा में बदलने लगती है। लेकिन जैसे ही पिण्ड पृथ्वी पर पहुँचता है तो यह रुक जाता है, जिससे इसका वेग शून्य हो जाता है।
अत: सूत्र गतिज ऊर्जा = \(\frac { 1 }{ 2 }\) mv² के अनुसार वेग शून्य हो जाने पर गतिज ऊर्जा भी शून्य हो जाएगी।
K.E. = \(\frac { 1 }{ 2 }\) mv²
= \(\frac { 1 }{ 2 }\) x m x 0² = 0
यह गतिज ऊर्जा ऊष्मीय ऊर्जा, ध्वनि ऊर्जा आदि में रूपान्तरित हो जाती है।

Jharkhand Board Class 9 Science कार्य तथा ऊर्जा InText Questions and Answers

क्रियाकलाप 11.1. (पा. प. पृ. सं. 163)
उपर्युक्त उदाहरणों में दैनिक जीवन के क्रियाकलाप पर चर्चा हुई है। इनमें से प्रत्येक कार्यकलाप के लिए निम्नलिखित प्रश्नों का उत्तर दें-
(i) किस वस्तु पर कार्य किया गया?
(ii) वस्तु पर क्या घटित हो रहा है?
(iii) कार्य कौन (क्या) कर रहा है?
नोट: छात्र अध्यापक की सहायता से स्वयं करें।

क्रियाकलाप 11.2. (पा. पु. पृ. सं. 163 )
अपने दैनिक जीवन की कुछ स्थितियों पर विचार करके उन्हें सूचीबद्ध कीजिए जिनमें कार्य सम्मिलित हो। अपने मित्रों से विचार-विमर्श करके किए गए कार्य के बारे में जानिए।

क्रियाकलाप 11.3. (पा. पु. पृ. सं, 164)
कुछ ऐसी स्थितियों पर विचार करें जब वस्तु पर बल लगने के बावजूद भी उसमें विस्थापन न हो। इसी प्रकार ऐसी स्थिति पर भी विचार करें जब कोई वस्तु बल लगे बिना ही विस्थापित हो जाए। इन स्थितियों को सूचीबद्ध करें तथा मित्रों से विचार-विमर्श करें कि कार्य हुआ या नहीं।

क्रियाकलाप 11.4. (पा. पु. पृ. सं. 165)
किसी वस्तु को ऊपर उठाइए। आपके द्वारा वस्तु पर लगाए गए बल के द्वारा कार्य किया गया तथा आपके द्वारा आरोपित बल, विस्थापन की दिशा में है। इसके अतिरिक्त वस्तु पर गुरुत्वीय बल भी कार्यरत है। इनमें से कौन सा बल धनात्मक तथा कौन सा ऋणात्मक है? कारण सहित बताइए।

उदाहरण 11.2.
एक कुली 15k g का बोझ धरती से 1.5 m ऊपर उठाकर अपने सिर पर रखता है। उसके द्वारा बोझे पर किए गए कार्य का परिकलन कीजिए।
हल:
बोझ का द्रव्यमान m = 15kg तथा
विस्थापन s = 1.5 m
किया गया कार्य W = F x s = mg x s
∵ F = mg
= 15 × 10 × 1.5
= 225 N m
= 225 J
कुली द्वारा बोझे पर किया गया कार्य 225 J है।

खण्ड 11.1 से सम्बन्धित पाठ्य पुस्तक के प्रश्नोत्तर (पा.पु. पृ. सं. 165)

प्रश्न 1.
हम कब कहते हैं कि कार्य किया गया है?
उत्तर:
किसी वस्तु पर बल लगाने पर वस्तु विस्थापित हो जाती है तो कहा जाता है कि कार्य किया गया है।

प्रश्न 2
जब किसी वस्तु पर लगने वाला बल इसके विस्थापन की दिशा में हो तो किए गए कार्य का व्यंजक लिखिए।
उत्तर:
जब बल विस्थापन की दिशा में ही लगता है तो कार्य = बल x बल की दिशा में विस्थापन।

प्रश्न 3.
1 J कार्य को परिभाषित कीजिए।
उत्तर:
जब किसी वस्तु पर एक न्यूटन का बल लगाने पर वस्तु में बल की दिशा में 1 मीटर का विस्थापन हो जाता है तो किया गया कार्य 1 J कहलाता है।
1 J = 1 N × 1 m

प्रश्न 4.
बैलों की एक जोड़ी खेत जोतते समय किसी हल पर 140 न्यूटन का बल लगाती है। जोता गया खेत 15 m लंबा है। खेत की लंबाई को जोतने में कितना कार्य किया गया?
हल:
बैलों द्वारा लगाया गया बल = 140 N
जोता गया खेत = 15 m
किया गया कार्य = बल x विस्थापन
= 140 N x 15 m
= 21000 N m या 2100 जूल

क्रियाकलाप 11.5. (पा. पु. पृ. सं. 166)
ऊर्जा के कुछ स्रोतों की सूची बनाइए। छोटे समूह में विचार-विमर्श कीजिए कि किस प्रकार ऊर्जा के कुछ स्रोत सूर्य के कारण हैं।

क्रियाकलाप 11.6. (पा.पु. पृ. सं. 167)
एक भारी गेंद लेकर इसे गीले रेत की मोटी परत पर गिराइए। गेंद को लगभग 30 सेमी की ऊँचाई से गिराकर हम पाते हैं कि रेत में एक गड्ढा हो जाता है । इसी क्रियाकलाप को 50 cm, 1 m तथा 1.5 m की ऊँचाइयों से गिराकर बने गड्ढों की तुलना करके सूचीबद्ध करें तथा देखें कि किसके कारण बड़ा गड्ढा बना।

अब उत्तर दें-

प्रश्न-
कौन सा गड्ढा सबसे अधिक गहरा है, क्यों?
उत्तर:
सबसे अधिक ऊँचाई (1.5 m) से गिरने पर बना गड्ढा सबसे अधिक गहरा होगा, क्योंकि अधिक ऊँचाई से गिरने के कारण उस गेंद में गतिज ऊर्जा अधिक होगी।

क्रियाकलाप 11.7. (पा.पु. पृ. सं. 167)
चित्र 11.4 के अनुसार एक ज्ञात द्रव्यमान के लकड़ी के गुटके को ट्रॉली के सामने किसी सुविधाजनक निश्चित दूरी पर रखकर पलड़े पर एक साथ ज्ञात द्रव्यमान रखा जिससे कि ट्राली गतिमान हो जाए। गतिमान ट्रॉली लकड़ी के गुटके से टकराती है। मेज पर एक अवरोधक इस प्रकार लगाया जाए कि गुटके से टकराकर ट्राली वहीं रुक जाए, गुटका विस्थापित हो जाता है तथा गुटके के विस्थापन को मापकर सारणी में लिखिए। पलड़े के द्रव्यमान को बढ़ाकर इस प्रयोग को दोहराकर विस्थापन का मापन किया तथा उसे सारणीबद्ध किया।

अब उत्तर दें-

प्रश्न 1.
गतिशील ट्राली किस प्रकार कार्य करती है?
उत्तर:
गतिशील ट्राली में गतिज ऊर्जा निहित होती है जो कि लकड़ी के गुटके से टकराने पर उसमें स्थानान्तरित हो जाती है जिससे गुटका विस्थापित हो जाता है। ट्राली से बँधे पलड़े पर अधिक द्रव्यमान लटकाने पर उसमें अधिक गतिज ऊर्जा संचित हो जाती है जिसके कारण गुटका और अधिक विस्थापित हो जाता है।

अतः किसी वस्तु में उसकी गति के कारण जो ऊर्जा निहित रहती है उसे उस वस्तु की गतिज ऊर्जा कहते हैं। उदाहरण के लिए चलती हुई कार, फेंकी हुई गेंद, गिरता हुआ कोई पिण्ड तथा बन्दूक से निकली गोली इन सभी में गतिज ऊर्जा निहित रहती है।.

गतिज ऊर्जा की माप (Measurement of Kinetic Energy) – किसी गतिमान पिण्ड की गतिज ऊर्जा की माप कार्य की उस मात्रा से की जाती है, जो वह पिण्ड उसकी वर्तमान अवस्था से विरामावस्था तक लाए जाने में कर सकता है।
यदि m द्रव्यमान की किसी वस्तु पर जो कि विरामावस्था में है, एक बल F लगाया जाता है तब न्यूटन के गति विषयक द्वितीय नियम से
F = ma अत: a = \(\frac { F }{ m }\) … (i)
यदि वस्तु द्वारा चली गई दूरी हो तब वस्तु पर कृत
कार्य W = F x s … (ii)
गति के तृतीय समीकरण के अनुसार
v² = u² + 2 as [∵ u = 0)
v² = 0 + 2 as … (iii)
समीकरण (i) व (iii) से
v² = 2 x (\(\frac { F }{ m }\)) x s
या mv² = 2Fs या Fs = \(\frac { F }{ m }\) mv² … (iv)
समीकरण (ii) व (iv) की तुलना करने पर
W = Fs = \(\frac { 1 }{ 2 }\) mv²
यदि गतिज ऊर्जा को E_K से प्रदर्शित करें तब
वस्तु की गतिज ऊर्जा
W = E_K = Fs = \(\frac { 1 }{ 2 }\) mv²
अतः वस्तु की गतिज ऊर्जा
E_K = \(\frac { 1 }{ 2 }\) mv² x द्रव्यमान x (वेग)²
अतः वस्तु की गतिज ऊर्जा वस्तु के द्रव्यमान समानुपाती व वस्तु के वेग के वर्ग के समानुपाती होती है।

खंड 11.2 से सम्बन्धित पाठ्य पुस्तक के प्रश्नोत्तर (पा. पु. पू. सं. 169)

प्रश्न 1.
किसी वस्तु की गतिज ऊर्जा क्या होती है?
उत्तर:
गतिज ऊर्जा- किसी वस्तु में उसकी गति के कारण जो ऊर्जा निहित होती है, उसे वस्तु की गतिज ऊर्जा कहते हैं। किसी वस्तु की गतिज ऊर्जा, उसे विरामावस्था से वर्तमान गति की अवस्था तक लाने में वस्तु पर किए गए कार्य के बराबर होती है।

प्रश्न 2.
किसी वस्तु की गतिज ऊर्जा के लिए व्यंजक लिखिए।
उत्तर:
यदि द्रव्यमान की कोई वस्तु वेग से गतिमान है तो वस्तु की गतिज ऊर्जा E_K = \(\frac { 1 }{ 2 }\) mv² होगी।

प्रश्न 3.
5 मीटर प्रति सेकण्ड के वेग से गतिशील किसी m द्रव्यमान की वस्तु की गतिज ऊर्जा 25 जूल है। यदि इसके वेग को दोगुना कर दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी? यदि इसके वेग को तीन गुना बढ़ा दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी?
हल:
प्रश्नानुसार, वेग v = 5 मीटर / सेकण्ड,
E_K = 25 जूल
सूत्र ∴ E_K = \(\frac { 1 }{ 2 }\) से
25 = \(\frac { 1 }{ 2 }\) x (5)² या 2 x 25 = m x 25
∵ वस्तु का द्रव्यमान m = 2 किग्रा
प्रथम दशा – जबकि वेग दुगना अर्थात् v₂ = 2 × 5 = 10
मीटर / सेकण्ड कर दिया जाता है तो
गतिज ऊर्जा E_K = \(\frac { 1 }{ 2 }\)mv_v²
= \(\frac { 1 }{ 2 }\) x 2 x (10)²
= 100 जूल।
दूसरी दशा- जबकि वेग तीन गुना अर्थात् v₃ = 3 x 5 = 15 मीटर / सेकण्ड कर दिया जाता है तो
गतिज ऊर्जा E_k = \(\frac { 1 }{ 2 }\)mv₃²
= \(\frac { 1 }{ 2 }\) x 2 किग्रा (15 मीटर / सेकण्ड )²
= 225 जूल

क्रियाकलाप 11.8. (पा.पु. पू. सं. 169)
एक रबड़ बैंड लेकर इसके एक सिरे को पकड़कर दूसरे सिरे से खींचने पर छल्ला खिंच जाता है तथा सिरे को छोड़ देने पर यह अपनी प्रारम्भिक लम्बाई को प्राप्त करने का प्रयत्न करता है। स्पष्ट है कि स्थिति विशेष के कारण रबड़ के छल्ले ने ऊर्जा संचित कर ली थी।

क्रियाकलाप 11.9. (पा.पु. पू. सं. 169)
चित्र 11.5 के अनुसार एक स्लिंकी (स्प्रिंग) लेकर इसके एक सिरे को पकड़िए तथा दूसरे सिरे को अपने मित्र से पकड़वाकर थोड़ा सा खींचिए। अब स्लिंकी को छोड़ दीजिए।

स्लिंकी ने किस प्रकार की ऊर्जा उपार्जित की तथा संपीडित करने पर भी क्या स्लिंकी ऊर्जा उपार्जित करेगी?

क्रियाकलाप 11.10. (पा.पु. पू. सं. 169)
एक खिलौना कार लेकर उसमें चाबी भरकर कार को जमीन पर रखिए यह चलने लगेगी। इसमें ऊर्जा कहाँ से आयी, सोचिए।

क्रियाकलाप 11.11. (पा.पु. पू. सं. 169)
किसी वस्तु को एक निश्चित ऊँचाई तक उठाकर इसे छोड़ने पर यह नीचे गिरने लगती है, और अधिक ऊँचा उठाने पर यह और अधिक कार्य कर सकती है। इसमें ऊर्जा कहाँ से आई? सोचिए तथा विचार-विमर्श कीजिए।

क्रियाकलाप 11.12. (पा.पु. पृ. सं. 170)
बाँस की खपच्ची लेकर इसका धनुष बनाकर एक हल्की डंडी लेकर इसका तीर बनाइए, डोरी को चित्रानुसार खींचिए और तीर को मुक्त कीजिए। तीर को धनुष दूर जाते देखिए।

धनुष की आकृति में परिवर्तन को नोट कीजिए धनुष की आकृति में परिवर्तन के से कारण उसमें संचित स्थितिज ऊर्जा तीर को गतिज ऊर्जा प्रदान करती है जिससे तीर गतिमान होकर दूर तक जाता है।

अब उत्तर दें-

प्रश्न 1.
क्रियाकलाप 11.8 में रबड़ का छल्ला खींचने पर ऊर्जा किस प्रकार उपार्जित करता है?
उत्तर:
रबर बैंड में स्थितिज ऊर्जा संचित हो जाती है।

प्रश्न 2.
खींचने पर स्लिंकी ऊर्जा उपार्जित करती है। क्या संपीड़ित करने पर भी स्लिंकी ऊर्जा उपार्जित करेगी?
उत्तर:
छोड़ने पर स्लिंकी अपनी मूल अवस्था प्राप्त कर लेती है। खींचने के दौरान किए गए कार्य के कारण स्लिंकी ऊर्जा उपार्जित करती है। हाँ, स्लिंकी संपीडित करने पर भी स्थितिज ऊर्जा उपार्जित करेगी।

प्रश्न 3.
फर्श पर चाबी भरकर खिलौने को रखने पर यह चलता है। क्या उपार्जित ऊर्जा, चाबी द्वारा भरे गए लपेटनों की संख्या पर निर्भर है?
उत्तर:
कृत कार्य लपेटनों में, स्थितिज ऊर्जा के रूप में संचित होती है। उपार्जित ऊर्जा, चाबी द्वारा भरे गए लपेटनों पर निर्भर करती है। लपेटनों की संख्या अधिक होने पर अधिक ऊर्जा संचित हो जाती है।

प्रश्न 4.
किसी वस्तु को अधिक ऊँचाई तक उठाने पर उसमें अधिक ऊर्जा समाहित हो जाती है। यह ऊर्जा कहाँ से प्राप्त होती है? विचार विमर्श कीजिए।
उत्तर:
निश्चित ऊँचाई तक उठाने में किसी वस्तु को गुरुत्वीय बल के विरुद्ध कार्य करना पड़ता है। यह कार्य वस्तु में स्थितिज ऊर्जा के रूप में संचित रहता है। वस्तु की पृथ्वी तल से ऊँचाई बढ़ने पर उसमें समाहित ऊर्जा बढ़ती जाती है।

प्रश्न 5.
बाँस की एक खपच्ची से बने धनुष और हल्की डंडी से बने तीर को धनुष की डोरी पर रखकर और डोरी को खींचकर तीर को छोड़िए तीर धनुष से दूर क्यों जा गिरता है?
उत्तर:
धनुष की आकृति में परिवर्तन के कारण उसमें संचित स्थितिज ऊर्जा तीर की गतिज ऊर्जा में परिवर्तित हो जाती है जिससे तीर गतिशील होकर दूर तक जाता है।

क्रियाकलाप 11.13.
छोटे समूहों में बैठकर प्रकृति में ऊर्जा रूपान्तरण की विभिन्न विधियों पर विचार करें तथा निम्नलिखित प्रश्नों पर विचार-विमर्श करें –

• हरे पौधे खाना कैसे बनाते हैं?
• उन्हें ऊर्जा कहाँ से मिलती है?
• वायु एक स्थान से दूसरे स्थान को क्यों बहती है?
• कोयला तथा पेट्रोलियम कैसे बने?
• किस प्रकार के ऊर्जा रूपान्तरण जल चक्र को बनाए रखते हैं?

नोट:

• जब हमने गमले में लगे पौधे को अंधेरे कमरे में रखकर उसे पानी नहीं दिया तो वह सूख गया। इससे निष्कर्ष निकलता है कि हरे पौधे अपना भोजन प्रकाश एवं जल से बनाते हैं।
• उन्हें ऊर्जा सूर्य के प्रकाश (सौर ऊर्जा) से मिलती है।
• वायुदाब में अन्तर के कारण वायु के कणों पर बल आरोपित होता है जिससे वायु एक स्थान से दूसरे स्थान की ओर बहती है।
• करोड़ों वर्ष पूर्व पृथ्वी की गहराई में हरे पेड़-पौधे एवं जीव-जन्तुओं हलचल के कारण दब गए जो कालान्तर में आज  कोयला तथा पैट्रोलियम में बदल गए।
• रासायनिक ऊर्जा का ऊष्मीय ऊर्जा में रूपान्तरण।

क्रियाकलाप 11.14. (पा.पु. पृ. सं. 172)
अनेक मानव क्रियाकलापों तथा हमारे द्वारा उपयोग में लाए जाने वाले जुगतों में ऊर्जा रूपान्तरण सम्मिलित है। इस प्रकार के क्रियाकलापों तथा जुगतों की एक सूची बनाइए तथा पहचानिए कि किस प्रकार का ऊर्जा रूपान्तरण हो रहा है।

क्रियाकलाप 11.15. (पा.पु. पृ. सं. 172)
20 kg द्रव्यमान का कोई पिण्ड 4m की ऊँचाई से मुक्त रूप से गिराया जाता है। दी गई सारणी के अनुसार प्रत्येक स्थिति में स्थितिज ऊर्जा तथा गतिज ऊर्जा की गणना करके, सारणी में रिक्त स्थानों को भरिए। (g = 10ms^-2)
सारणी 11.2

ऊँचाई जहाँ पर पिण्ड स्थित है	स्थितिज ऊर्जा Ep = mgh (जूल में)	गतिज ऊर्जा (जूल में)	Ep + Ek Ek = \(\frac { 1 }{ 2 }\) mv² (जूल में)
4m
3m
2m
1m
भूमि से ठीक ऊपर

संकेत-
h = 4m पर, E_p = mgh = 20 x 10 x 4800 J
v = 0, E_k = \(\frac { 1 }{ 2 }\) mv² = 0
h = 3m पर, E_p = 20 x 10 x 3 = 600 J
तय की गई दूरी s = 4 – 3 = 1m
v² = u² + 2gs = 0 + 2gs = 2gs
E_k = \(\frac { 1 }{ 2 }\)mv² = \(\frac { 1 }{ 2 }\) m x 2gs = mgs
= 20 x 10 x 1 = 200 J
h = 2m पर, s = 4 – 2 = 2m
E_p = mgh = 20 × 10 × 2 = 400 J
E_p = mgs = 20 x 10 × 2 = 400 J
h = 1 m पर, h = 1 m, s = 4 -1 = 3 m
E_p = mgh = 20 x 10 × 1 = 200 J
E_k= mgs = 20 x 10 × 3 = 600 J
भूमि से ठीक ऊपर,
h = 0, s = 4 – 0 = 4m
E_p = mg x 0 = 0
E_k= 20 x 10 × 4800 J

सारणी 11.3

ऊँचाई जहाँ पर पिण्ड स्थित है	स्थितिज ऊर्जा Ep = mgh	गतिज ऊर्जा (जूल में) Ek  = \(\frac { 1 }{ 2 }\) mv²	Ep + Ek
4m	800 J	0	800 J
3m	600 J	200 J	800 J
2m	400 J	400 J	800 J
1m	200 J	600 J	800 J
भूमि से ठीक ऊपर	0	800 J	800 J

इससे स्पष्ट है कि प्रत्येक ऊँचाई पर कुल यान्त्रिक ऊर्जा अचर रहती है, अर्थात् ऊर्जा संरक्षित है।

क्रियाकलाप 11.16. (पा. पु. पू. सं. 173)
A तथा B दो बच्चों का द्रव्यमान समान है। दोनों रस्से पर अलग-अलग चढ़ना प्रारंभ करते हैं। दोनों 8 m की ऊँचाई तक पहुँचते हैं। मान लीजिए इस कार्य को करने में A 15s तथा B 20s लेता है।
प्रत्येक बच्चे द्वारा किया गया कार्य कितना है ? किया गया कार्य समान है तथापि A ने कार्य करने के लिए B की अपेक्षा कम समय लिया।
किस बच्चे ने दिए हुए समय मान लो 1 में अधिक कार्य किया ?
संकेत माना कि प्रत्येक बच्चे का भार mg प्रत्येक बच्चे द्वारा किया गया कार्यmgh
किया गया कार्य समान है। परन्तु A 15s लेता है जबकि B 20s लेता है
समान कार्य करने के लिए इसलिए 1s में A ने अधिक कार्य किया। हम कहते हैं कि B से A ने अधिक काम किया।

खंड 11.3 से सम्बन्धित पाठ्य-पुस्तक के प्रश्नोत्तर (पा.पु. पू. सं. 174)

प्रश्न 1.
शक्ति क्या है?
उत्तर:
किसी कारक के कार्य करने की दर को शक्ति कहते हैं। यदि कोई कारक W कार्य करने में t समय लगाता हैं तो,

प्रश्न 2.
1 बाट शक्ति को
उत्तर:
जब 1 सेकण्ड में कार्य करने की दर को 1 वाट कहते हैं।

प्रश्न 3.
एक लैंप 1000 J विद्युत ऊर्जा 10 में व्यय करता है। इसकी शक्ति कितनी है?
उत्तर:
दिया है:
W = 1000 J, t = 10s, P = ?
P = \(\frac { W }{ t }\) = \(\frac { 1000 }{ 10 }\)
= 100 वॉट

प्रश्न 4.
औसत शक्ति को परिभाषित कीजिए।
उत्तर:
कुल उपयोग की गई ऊर्जा को कुल लिए गए समय से भाग देकर निकाली गई शक्ति को औसत शक्ति कहते हैं।

क्रियाकलाप 11.17. (पा.पु. पू. सं. 175)
अपने घर में विद्युत मीटर में प्रतिदिन प्रातः तथा सायं 6:00 बजे मीटर का पाठ्यांक नोट करें।
दिन के समय कितनी ‘यूनिट’ व्यय होती है?
रात के समय कितनी ‘यूनिट’ व्यय होती है?
इस क्रिया को लगभग एक सप्ताह तक कीजिए।
अपने प्रेक्षणों को सारणीबद्ध कीजिए।
अपने आँकड़ों से निष्कर्ष निकालिए।
अपने प्रेक्षणों की तुलना विद्युत् के मासिक बिल में दिए गए विवरणों से कीजिए।
संकेत-
हम मीटर का पाठ्यांक महीने के शुरू में तथा अंत में ले सकते हैं। दोनों पाठ्यांकों का अंतर हमें कुल व्यय हुई विद्युत के बारे में बताता है। इसकी हम मासिक बिल में दी गई यूनिटों से तुलना कर सकते हैं।

Students must go through these JAC Class 10 Science Notes Chapter 2 अम्ल, क्षारक एवं लवण to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 2 अम्ल, क्षारक एवं लवण

→ अम्ल-वह यौगिक जो अत्यधिक क्रियाशील धातु से अभिक्रिया करके हाइड्रोजन गैस बनाते हों, उन्हें अम्ल कहते हैं।

→ क्षार-जल में घुलनशील क्षारक को क्षार कहते हैं। इनका स्पर्श साबुन की तरह, स्वाद कड़वा तथा प्रकृति संक्षारक होती है।

→ लवण-जब अम्लों से हाइड्रोजन धातु द्वारा विस्थापित होते हैं, तब लवण बनता है। दूसरे शब्दों में, जब अम्ल एवं क्षारक उदासीनीकरण अभिक्रिया करते हैं, तब लवण एवं जल बनता है।

→ अम्ल-क्षारक सूचक रंजक या रंजकों के मिश्रण होते हैं जिनका उपयोग अम्ल एवं क्षारक की उपस्थिति को सूचित करने के लिए किया जाता है।

→ विलयन में H⁺(aq) आयन के निर्माण के कारण ही पदार्थ की प्रकृति अम्लीय होती है। विलयन में OH^– आयन के निर्माण से पदार्थ की प्रकृति क्षारकीय होती है।

→ जब कोई अम्ल किसी धातु के साथ अभिक्रिया करता है तो हाइड्रोजन गैस का उत्सर्जन होता है। साथ ही संगत लवण का निर्माण होता है।

→ जब क्षारक किसी धातु से अभिक्रिया करता है तो हाइड्रोजन गैस के उत्सर्जन के साथ एक लवण का निर्माण होता है जिसका ऋणआयन एक धातु एवं ऑक्सीजन के परमाणुओं से संयुक्त रूप से
निर्मित होता है।

→ जय अम्ल किसी धातु कार्बोनेट या धातु हाइड्रोजन कार्बोनेट से अभिक्रिया करता है तो यह संगत लवण उसके यौगिक में से हटाकर स्वयं उसका स्थान ले लेता है, विस्थापन अभिक्रिया कहलाती है।

→ द्विविस्थापन अभिक्रिया में दो अलग-अलग परमाणु या परमाणुओं के समूह (आयन) का आपस में आदान-प्रदान होता है।

→ अवक्षेपण अभिक्रिया से अविलेय लवण प्राप्त होता है।

→ सह-संयोजक अभिक्रिया जब रासायनिक अभिक्रिया में अभिकारकों एवं क्रियाफलों के मध्य सह-संयोजक बन्ध टूटकर नये सह-संयोजक बन्ध बनाते हैं तो इसे सह-संयोजक अभिक्रिया कहते हैं।

→ उत्क्रमणीय अभिक्रियाएँ ऐसी अभिक्रियाएँ जो समान परिस्थितियों में अग्र एवं पश्च दोनों दिशाओं में होती हैं और किसी भी दिशा में पूर्णता को नहीं पहुँचतीं उत्क्रमणीय अभिक्रियाएँ कहलाती हैं।

→ अनुत्क्रमणीय अभिक्रियाएँ-वे अभिक्रियाएँ जो केवल एक ही दिशा में चलती हैं तथा पूर्णता को प्राप्त होती हैं, अनुत्क्रमणीय अभिक्रियाएँ कहलाती हैं।

→ अभिक्रिया दर- अभिकारकों की वह मात्रा जो इकाई समय में उत्पादों में परिवर्तित होती हैं, उस अभिक्रिया की दर कहलाती है।

→ मंद अभिक्रियाएँ वे अभिक्रियाएँ जो धीरे-धीरे होती हैं व जिनके पूर्ण होने में अत्यधिक समय लगता है, मंद अभिक्रियाएँ कहलाती हैं।

→ तीव्र अभिक्रियाएँ वे अभिक्रियाएँ जो अतिशीघ्रता (लगभग 10 सेकण्ड) में पूर्ण होती हैं तीव्र अभिक्रियाएँ कहलाती हैं।

→ रासायनिक साम्यावस्था किसी उत्क्रमणीय अभिक्रिया की वह अवस्था जिसमें अग्र व विपरीत दोनों अभिक्रियाओं के वेग बराबर हो जाते हैं, रासायनिक साम्यावस्था कहलाती हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 बहुपद Exercise 2.2

प्रश्न 1.
निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x.
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4
हल:
(i) दिया गया बहुपद f(x) = x² – 2x – 8
= x² – (4 – 2) x – 8 = x² – 4x + 2x – 8
= x(x – 4) + 2(x – 4) = (x – 4) (x + 2)
∴ x² – 2x – 8 = (x – 4) (x + 2)
बहुपद f(x) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ f(x) = 0
अतः यदि x – 4 = 0 हो, तो x = 4
या फिर x + 2 = 0 हो, तो x = -2
अत: बहुपद x² – 2x – 8 के शून्यक = 4 और -2
बहुपद के गुणांकों और शून्यकों में सम्बन्ध :
शून्यकों का योग = 4 + (-2) = 2

अत: बहुपद के गुणांकों और शून्यकों के बीच सम्बन्ध सत्य है।

(ii) दिया हुआ बहुपद = 4s² – 4s + 1
= (28)² – 2 (2s). 1 + (1)²
= (2s – 1)²
बहुपद f(x) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ (2s – 1)² = 0
यदि (2s – 1)² = 0 ⇒ 2s – 1 = 0 ⇒ s = \(\frac{1}{2}\)
यहाँ बहुपद के शून्यक समान हैं।
अतः बहुपद के शून्यक \(\frac{1}{2}\) और \(\frac{1}{2}\) हैं।

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के शून्यकों और गुणांकों के मध्य सम्बन्ध सही है।

(iii) दिया गया बहुपद f(x)
= 6x² – 3 – 7x = 6x² – 7x – 3
= 6x² – (9 – 2) x – 3
= 6x² – 9x + 2x – 3
= 3x (2x – 3) + 1(2x – 3)
= (2x – 3) (3x + 1)
∴ बहुपद 6x² – 3 – 7x = (2x – 3 ) (3x + 1)
बहुपद 6x² – 7x – 3 के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ f(x) = 0
यदि 2x – 3 = 0 हो, तो 2x = 3 ⇒ x = \(\frac{3}{2}\)
और यदि 3x + 1 = 0 हो, तो 3x = -1 ⇒ x = –\(\frac{1}{3}\)
अत: बहुपद के शून्यक \(\frac{3}{2},-\frac{1}{3}\)

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के गुणांकों और के बीच सम्बन्ध सत्य है।

(iv) दिया गया बहुपद f(u) = 4u² + 8u
⇒ f(u) = 4u(u + 2)
बहुपद f(u) के शून्यक ज्ञात करने के लिए f(u) शून्य होगा।
∴ f(u) = 0 ⇒ 4u(u + 2) = 0
u = 0 या u + 2 = 0 ⇒ u = 0 या u = -2
अतः f(u) के शून्यक 0 और -2 है।

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के गुणांकों और शून्यकों के बीच सम्बन्ध सत्य है।

(v) दिया गया बहुपद f(t) = t² – 15 है।
बहुपद f(t) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
t² = 15 या t = ±\(\sqrt{15}\)
अत: बहुपद t² – 15 के शून्यक = +\(\sqrt{15}\), –\(\sqrt{15}\)

बहुपद के गुणांकों और शून्यकों के मध्य सम्बन्ध :

अतः बहुपद के गुणांकों और शून्यकों के मध्य सम्बन्ध सत्य है।

(vi) दिया गया बहुपद f(x) = 3x² – x – 4
= 3x² – (4 – 3)x – 4
= 3x² – 4x + 3x – 4
= x(3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)
∴ 3x² – x – 4 = (3x – 4) (x + 1)
बहुपद f(x) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ f(x) = 0
(3x – 4 ) (x + 1) = 0
यदि 3x – 4 = 0 हो, तो 3x = 4 ⇒ x = \(\frac{4}{3}\)
या फिर x + 1 = 0 हो, तो x = -1
अत: बहुपद के शून्यक \(\frac{4}{3}\) और -1 हैं।

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के गुणांकों और शून्यकों के बीच सम्बन्ध सत्य है।

प्रश्न 2.
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों का योग तथा गुणनफल क्रमश: हैं:
(i) \(\frac{1}{4}\) और -1
(ii) \(\sqrt{2}\) और \(\frac{1}{3}\)
(iii) 0 और \(\sqrt{5}\)
(iv) 1 और 1
(v) –\(\frac{1}{4}\) और \(\frac{1}{4}\)
(vi) 4 और 1
हल:
यदि द्विघात बहुपद f(x) के शून्यक ज्ञात हो तो निम्न सूत्र द्वारा अभीष्ट बहुपद ज्ञात करते है
f(x) = k{x² – (शून्यकों का योग) x + शून्यकों का गुणनफल},
जहाँ k = एक वास्तविक संख्या
(i) माना f(x) वह बहुपद है जिसके शून्यकों का योग \(\frac{1}{4}\) और गुणनफल – 1 हैं।

अतः अभीष्ट बहुपद 4x² – x – 4 या K(4x² – x – 4) हैं।

(ii) माना f(x) वह द्विघात बहुपद है, जिसके शून्यकों का योग \(\sqrt{2}\) और गुणनफल \(\frac{1}{3}\) हैं।
f(x) = \(k\left(x^2-\sqrt{2} x+\frac{1}{3}\right)\)
= \(k\left(\frac{3 x^2-3 \sqrt{2} x+1}{3}\right)\)
= \(\frac{k}{3}\left(3 x^2-3 \sqrt{2} x+1\right)\)
= K(3x² – 3\(\sqrt{2}\)x + 1)
जहाँ \(\frac{k}{3}\) एक अचर पद है/ वास्तविक संख्या है।
अत: अभीष्ट बहुपद 3x² – 3\(\sqrt{2}\)x + 1
या K (3x² – 3\(\sqrt{2}\)x + 1 ) है।

(iii) माना f(x) वह द्विघात बहुपद है जिसके शून्यकों का योग 0 और गुणनफल \(\sqrt{5}\) हैं।
∴ f(x) = k[x² – 0, x + \(\sqrt{5}\) = k[x² + \(\sqrt{5}\)]
(जहाँ k अचर पद है)
अतः अभीष्ट बहुपद x² + \(\sqrt{5}\) है।

(iv) माना f(x) वह द्विघात बहुपद है जिसके शून्यकों का योगफल 1 और गुणनफल 1 हैं।
∴ f(x) = k (x² – 1x + 1)
= k(x² – x + 1), जहाँ k अचर पद है।
अतः अभीष्ट बहुपद x² – x + 1 है।

(v) माना f(x) वह द्विघात बहुपद है जिसके शून्यकों का योग –\(\frac{1}{4}\) औरगुणनफल \(\frac{1}{4}\) हैं।

(जहाँ \(\frac{k}{4}\) एक अचर पद है)
अतः अभीष्ट बहुपद 4x² + x + 1 है।

(vi) माना f(x) वह द्विघात बहुपद है जिसके शून्यक का योग 4 और गुणनफल 1 हैं।
∴ f(x) = k[x² – 4x + 1], (जहाँ k अचर पद है)
अत: अभीष्ट बहुपद x² – 4x + 1 है।

Students must go through these JAC Class 10 Science Notes Chapter 1 रासायनिक अभिक्रियाएँ एवं समीकरण to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 1 रासायनिक अभिक्रियाएँ एवं समीकरण

→ रासायनिक अभिक्रिया – जब एक या एक से अधिक पदार्थ आपस में क्रिया करके नये पदार्थ का निर्माण करते हैं तो ऐसी अभिक्रिया रासायनिक अभिक्रिया कहलाती है।

→ आयनिक अभिक्रिया – जब अभिकारकों एवं क्रियाफलों के मध्य आयनिक बन्ध टूटकर नये आयनिक बन्ध बनाते हैं तो आयनिक अभिक्रिया होती है। ये मुख्यत: तीन प्रकार की होती हैं- संयोजन, वियोजन एवं विस्थापन अभिक्रिया।

→ विद्युत या आयनिक वियोजन अभिक्रिया- कुछ यौगिक जल में घोलने पर या विद्युत धारा प्रवाहित करने पर अपने ऋण एवं धन आयनों में टूट जाते हैं तो इसे विद्युत अथवा आयनिक वियोजन कहते हैं।

→ रासायनिक समीकरण – किसी रासायनिक अभिक्रिया को अभिकारकों तथा उत्पादों के प्रतीक व रासायनिक सूत्रों का प्रयोग करके प्रदर्शित करना, रासायनिक समीकरण कहलाता है।

→ संयोजन अभिक्रिया जब दो या दो से अधिक पदार्थ मिलकर एक नया पदार्थ बनाते हैं, उसे संयोजन अभिक्रिया कहते हैं।

→ वियोजन अभिक्रिया – वियोजन अभिक्रिया संयोजन अभिक्रिया के विपरीत होती है। वियोजन अभिक्रिया में एकल पदार्थ वियोजित होकर दो या दो से अधिक पदार्थ बनते हैं।

→ ऊष्माक्षेपी अभिक्रियाएँ-वे अभिक्रियाएँ जिसमें ऊष्मा उत्पन्न होती है, ऊष्माक्षेपी अभिक्रियाएँ कहलाती हैं।

→ ऊष्माशोषी अभिक्रियाएँ – वे अभिक्रियाएँ जिनमें ऊष्मा अवशोषित होती है, ऊष्माशोषी अभिक्रियाएँ कहलाती हैं।

→ विस्थापन अभिक्रिया- वह अभिक्रिया जिसमें एक तत्त्व (या पदार्थ) किसी दूसरे तत्त्व (या पदार्थ) को उसके यौगिक में से हटाकर स्वयं उसका स्थान ले लेता है, विस्थापन अभिक्रिया कहलाती है।

→ द्विविस्थापन अभिक्रिया में दो अलग-अलग परमाणु या परमाणुओं के समूह (आयन) का आपस में आदान-प्रदान होता है।

→ अवक्षेपण अभिक्रिया से अविलेय लवण प्राप्त होता है।

→ सह-संयोजक अभिक्रिया जब रासायनिक अभिक्रिया में अभिकारकों एवं क्रियाफलों के मध्य सह-संयोजक बन्ध टूटकर नये सह-संयोजक बन्ध बनाते हैं तो इसे सह-संयोजक अभिक्रिया कहते हैं।

→ उत्क्रमणीय अभिक्रियाएँ ऐसी अभिक्रियाएँ जो समान परिस्थितियों में अग्र एवं पश्च दोनों दिशाओं में होती हैं और किसी भी दिशा में पूर्णता को नहीं पहुँचतीं उत्क्रमणीय अभिक्रियाएँ कहलाती हैं।

→ अनुत्क्रमणीय अभिक्रियाएँ-वे अभिक्रियाएँ जो केवल एक ही दिशा में चलती हैं तथा पूर्णता को प्राप्त होती हैं, अनुत्क्रमणीय अभिक्रियाएँ कहलाती हैं।

→ अभिक्रिया दर- अभिकारकों की वह मात्रा जो इकाई समय में उत्पादों में परिवर्तित होती हैं, उस अभिक्रिया की दर कहलाती है।

→ मंद अभिक्रियाएँ वे अभिक्रियाएँ जो धीरे-धीरे होती हैं व जिनके पूर्ण होने में अत्यधिक समय लगता है, मंद अभिक्रियाएँ कहलाती हैं।

→ तीव्र अभिक्रियाएँ वे अभिक्रियाएँ जो अतिशीघ्रता (लगभग 10 सेकण्ड ) में पूर्ण होती हैं तीव्र अभिक्रियाएँ कहलाती हैं।

→ रासायनिक साम्यावस्था किसी उत्क्रमणीय अभिक्रिया की वह अवस्था जिसमें अग्र व विपरीत दोनों अभिक्रियाओं के वेग बराबर हो जाते हैं, रासायनिक साम्यावस्था कहलाती हैं।

→ आयनिक साम्य-आयनिक अभिक्रियाओं की वह अवस्था जिसमें आयनिक क्रियाकारकों तथा उत्पादों का सान्द्रण परिवर्तित नहीं होता, आयनिक साम्य कहलाता है।

→ विकृतगंधिता-ऐसी प्रक्रिया जिसमें वसायुक्त सामग्री खराब होने लगती है तथा स्वाद व गंध में परिवर्तन होने लगता है, खाद्य पदार्थों का ऑक्सीजन से अभिक्रिया करके ऑक्सीकरण कर देते हैं विकृतगंधिता कहलाती है।