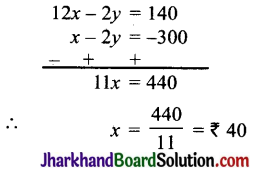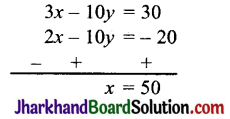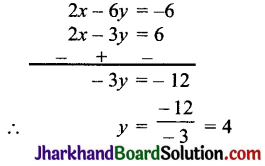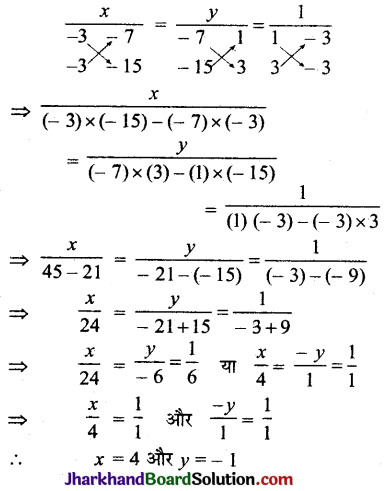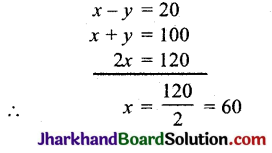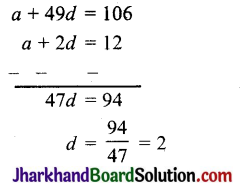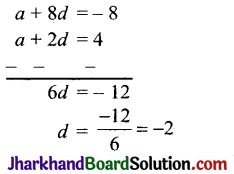Bhagya

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.6 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Exercise 3.6

प्रश्न 1.
निम्नलिखित समीकरणों के युग्मों को रैखिक समीकरणों के युग्म में परिवर्तित करके हल कीजिए:


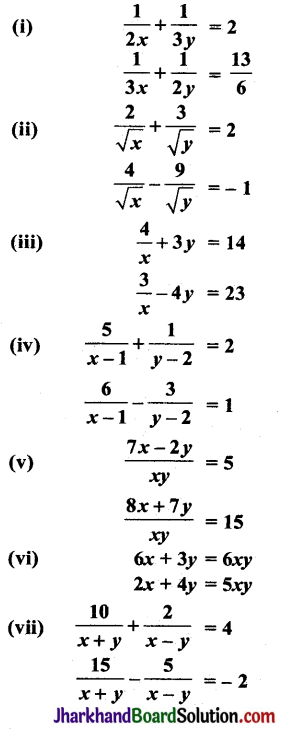
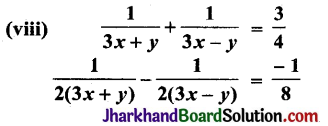
हल:
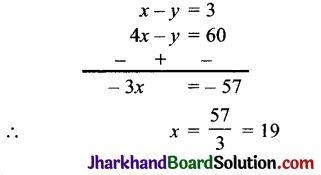
(i) दिया गया रैखिक समीकरण युग्म हैं:

समीकरण (i) को 2 से और (ii) को 3 से गुणा करके घटाने पर,

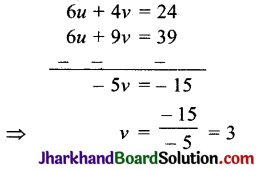
y के इस मान को समीकरण (1) में प्रतिस्थापित करने
3u + 2 × 3 = 12
⇒ 3u + 6 = 12
⇒ 3u = 12 – 6
⇒ 3u = 6
⇒ u = \(\frac{6}{3}\) = 2
क्योंकि u = \(\frac{1}{x}\)
इसलिए x = \(\frac{1}{2}\)
क्योंकि ν = \(\frac{1}{y}\)
इसलिए y = \(\frac{1}{3}\)
अतः x = \(\frac{1}{2}\) और y = \(\frac{1}{3}\)

(ii) दिया गया रैखिक समीकरण युग्म है:

2u + 3ν = 2 …..(i)
4u – 9ν = -1 …..(ii)
समीकरण (i) को 2 से गुणा करने पर,
4u + 6ν = 4 …..(iii)
समीकरण (iii) में से समी. (ii) को घटाने पर,

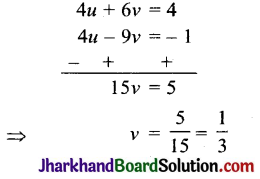
ν के इस मान को समीकरण (i) में रखने पर,
2u + 3 × \(\frac{1}{3}\) = 2
2u + 1 = 2
2u = 2 – 1
2u = 1
u = \(\frac{1}{2}\)

⇒ \(\sqrt{y}\) = 3
दोनों पक्षों का वर्ग करने पर
⇒ \((\sqrt{y})^2=(3)^2\) ⇒ y = 9
अतः x = 4 और y = 9

(iii) दिया गया रैखिक युग्म समीकरण है
\(\frac{4}{x}+3 y\) = 14
और \(\frac{3}{x}-4 y\)
माना \(\frac{1}{x}\) = u है, तब
4u + 3y = 14 …..(i)
3u – 4y = 23 …..(ii)
समीकरण (i) को 3 से और समीकरण (ii) को 4 से गुणा करके घटाने पर,

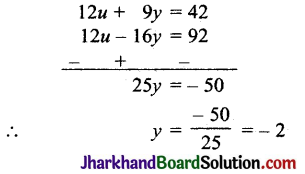
y का मान समीकरण (i) में रखने पर,
4u + 3 × – 2 = 14
⇒ 4u – 6 = 14
⇒ 4u = 14 + 6 = 20

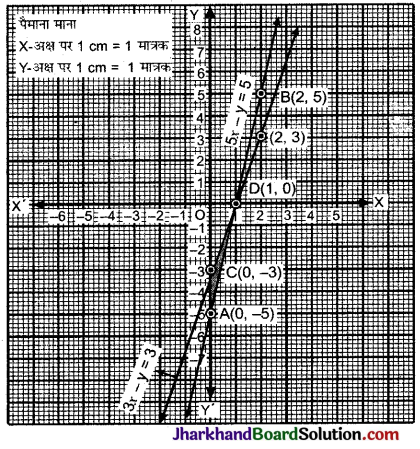
तब 5u + ν =2 …..(i)
6u – 3ν = 1 …..(ii)
समीकरण (i) को 3 से गुणा करने पर,
15u + 3ν = 6
समीकरण (ii) व (iii) को जोड़ने पर,
6u – 3ν = 1
15u + 3ν = 6
21u = 7
u = \(\frac{7}{21}=\frac{1}{3}\)
u के इस मान को समीकरण (i) में रखने पर

⇒ y – 2 = 3
y = 3 + 2 = 5
अंत: x = 4 और y = 5

(v) दिया गया रैखिक समीकरण युग्म है:

माना \(\frac{1}{x}\) = P और \(\frac{1}{y}\) = q रखने पर,
7q – 2p = 5 …..(i)
8q + 7p = 15 …..(ii)
समीकरण (i) को 7 से तथा समीकरण (ii) को 2 से गुणा करने पर,
49q – 14p = 35 …..(iii)
16g + 14p = 30 …..(iv)
समीकरण (iii) व (iv) को जोड़ने पर,

q के इस मान को समीकरण (i) में प्रतिस्थापित करने पर,
7 × 1 – 2p = 5
⇒ 7 – 2p = 5
⇒ – 2p = 5 – 7 = -2
⇒ p = 1
⇒ \(\frac{1}{x}\) = 1 (∵ p = \(\frac{1}{2}\))
⇒ x = 1
अब q = 1
⇒ \(\frac{1}{y}\) = 1 (∵ q = \(\frac{1}{y}\))
⇒ y = 1
अतः x = 1 और y = 1

(vi) दिया हुआ समीकरण युग्म है :
6x + 3y = 6xy और 2x + 4y = 5xy
दोनों समीकरणों में xy का भाग देने पर,

माना \(\frac{1}{x}\) = q और \(\frac{1}{y}\) = p रखने पर,
6p + 3q = 6 …..(1)
और 2p + 4q = 5 …..(2)
समीकरण (2) में 3 से गुणा करने पर
6p + 12g = 15 …..(3)
समीकरण (3) में से समीकरण (1) को घटाने पर,

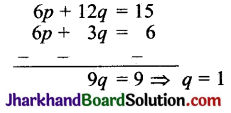
समीकरण (2) में q = 1 रखने पर,
⇒ 2p + 4 × 1 = 5
⇒ 2p = 5 – 4
⇒ 2p = 1
⇒ p = \(\frac{1}{2}\)
⇒ \(\frac{1}{y}=\frac{1}{2}\) (∵ p = \(\frac{1}{y}\))
⇒ y = 2
अब q = 1
⇒ \(\frac{1}{x}\) = 1 (∵ q = \(\frac{1}{x}\))
⇒ x = 1
अतः समीकरण युग्म के हल x = 1 और y = 2

(vii) दिया गया समीकरण युग्म है :
\(\frac{10}{x+y}+\frac{2}{x-y}=4\)
\(\frac{15}{x+y}-\frac{5}{x-y}=-2\)
माना \(\frac{1}{x+y}\) = u और \(\frac{1}{x-y}\) = ν को प्रतिस्थापित करने पर,
10u + 2ν = 4
⇒ 2(5u + ν) = 4
⇒ 5u + ν = 2 …..(1)
तथा 15u – 5ν = -2 …..(2)
समीकरण (1) में 5 से गुणा करने पर,
25u + 5ν = 10 …..(3)
समीकरण (3) तथा समीकरण (2) को जोड़ने पर,
25u + 5ν = 10
15u – 5ν = -2
40u = 8
u = \(\frac{8}{40}=\frac{1}{5}\)
u के इस मान को समीकरण (1) में प्रतिस्थापित करने पर,
5(\(\frac{1}{5}\)) + ν = 2 ⇒ 1 + ν = 2
⇒ ν = 2 – 1 ⇒ ν = 1

x के इस मान को समीकरण (4) में रखने पर
3 + y = 5 ⇒ y = 5 – 3 ⇒ y = 2
अतः x = 3 तथा y = 2

(viii) दिया हुआ समीकरण युग्म

समीकरण (1) मैं A = \(\frac{1}{4}\) रखने पर,

x = 1 समीकरण (5) में रखने पर
3 × 1 – y = 2
⇒ 3 – y = 2
⇒ – y = 2 – 3 = -1
∴ y = 1
अतः दिए गए समीकरण के अभीष्ट हल :
x = 1 और y = 1

प्रश्न 2.
निम्नलिखित समस्याओं को रैखिक समीकरण युग्म में परिवर्तित कीजिए और उनके हल ज्ञात कीजिए :
(i) रितु धारा के अनुकूल 2 घंटे में 20 किमी तैर सकती है और धारा के प्रतिकूल 2 घंटे में 4 किमी तैर सकती है। उसकी स्थिर जल में तैरने की चाल और धारा की चाल ज्ञात कीजिए।
(ii) 2 महिलाएँ एवं 5 पुरुष एक कसीदें के काम को साथ-साथ 4 दिन में पूरा कर सकते हैं, जबकि 3 महिलाएँ एवं 6 पुरुष इसे 3 दिन में पूरा कर सकते हैं। 1 महिला अकेले उस काम को कितने दिन में करेगी और 1 पुरुष अकेले उस काम को कितने दिन में करेगा ?
(iii) रितु अपने घर के लिए 300 किमी यात्रा कुछ दूरी रेलगाड़ी से और कुछ दूरी बस से तय करती है। यदि वह 60 किमी यात्रा रेलगाड़ी से और शेष बस द्वारा करे तो उसे 4 घंटे लगते हैं। यदि वह 100 किमी रेलगाड़ी से और शेष बस से यात्रा करे तो उसे 10 मिनट अधिक लगते हैं। रेलगाड़ी और बस की पृथक् पृथक् चाल ज्ञात कीजिए।
हल:
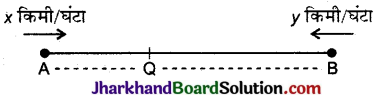
(i) माना कि स्थिर जल में रितु की चाल
= x किमी / घण्टा
तथा धारा की चाल = y किमी / घण्टा
नदी में रितु की धारा के विरुद्ध चाल = (x – y) किमी / घण्टा
तथा नदी में रितु की धारा की दिशा में चाल = (x + y) किमी / घण्टा
रितु द्वारा धारा की दिशा में 2 घण्टे में तय की गई दूरी = चाल × समय
= (x + y) × 2 किमी
पहली शर्त के अनुसार,
2 (x + y) = 20
⇒ x + y = 10 …..(1)
रितु द्वारा धारा के विरुद्ध 2 घण्टे में तय की गई दूरी = चाल × समय
= (x – y) × 2 किमी
दूसरी शर्त के अनुसार,
2 (x – y) = 4
⇒ x – y = 2 …..(2)
समीकरण (1) व (2) को जोड़ने पर,

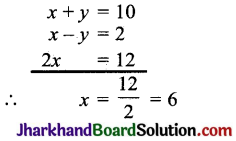
अब x = 6 समीकरण (1) में रखने पर,
6 + y = 10
⇒ y = 10 – 6 ⇒ y = 4
अतः स्थिर जल में रितु के तैरने की चाल = 6 किमी / घण्टा
तथा धारा की चाल = 4 किमी / घण्टा

(ii) माना उस काम को 1 महिला x दिन में तथा 1 पुरुष y दिन में पूरा करता है।
महिला की दिन की कार्यक्षमता = \(\frac{1}{x}\) भाग
और पुरुष की 1 दिन की कार्यक्षमता = \(\frac{1}{y}\) भाग
अब 2 महिलाओं द्वारा 4 दिन में किया गया कार्य = \(\frac{8}{x}\)
और 5 पुष्पों द्वारा 4 दिन में किया गया कार्य = \(\frac{20}{y}\)
∴ 2 महिलाओं और 5 पुरूषों द्वारा 4 दिन में किया गया कुल कार्य = \(\left(\frac{8}{x}+\frac{20}{y}\right)\)
प्रश्नानुसार, \(\frac{8}{x}+\frac{20}{y}=1\) …..(1)
इसी प्रकार,
3 महिलाओं द्वारा 3 दिन में किया गया कार्य = \(\frac{9}{x}\)
और 6 पुरुषों द्वारा 3 दिन में किया गया कार्य = \(\frac{18}{x}\)
∴ 3 महिलाओं और 6 पुरुषों द्वारा 3 दिन में किया गया कुल कार्य = \(\left(\frac{9}{x}+\frac{18}{y}\right)\)
प्रश्नानुसार, \(\frac{9}{x}+\frac{18}{y}=1\) …..(2)
माना \(\frac{1}{x}\) = u तथा \(\frac{1}{y}\) = ν समीकरण (1) व (2) मैं प्रतिस्थापित करने पर
8u + 20ν = 1 …..(3)
तथा 9u + 18ν = 1 …..(4)
समीकरण (3) में 9 से तथा समीकरण (4) में 8 से गुणा करके घटाने पर

\(\frac{1}{x}=\frac{1}{18}\) (∵ u = \(\frac{1}{x}\))
x = 18
अब ν = \(\frac{1}{36}\)
\(\frac{1}{y}=\frac{1}{36}\) (∵ ν = \(\frac{1}{4}\))
y = 36
अतः एक महिला अकेले उस काम को 18 दिन में तथा एक पुरूष अकेला उसे 36 दिन में पूरा कर सकता है।
(iii) मान लीजिए रेलगाड़ी की चाल = x किमी / घण्टा
तथा बस की चाल = y किमी / घण्टा
कुल दूरी = 300 किमी
स्थिति I:
रेलगाड़ी द्वारा 60 किमी दूरी तय करने में लगा समय

शेष दूरी = 300 – 60 = 240 किमी
बस द्वारा 240 किमी दूरी तय करने में लगा समय = \(\frac{240}{y}\) घण्टे
कुल समय = \(\left(\frac{60}{x}+\frac{240}{y}\right)\) घण्टे
पहली शर्त के अनुसार,
\(\frac{60}{x}+\frac{240}{y}=4\)
⇒ \(\frac{15}{x}+\frac{60}{y}=1\) …..(1)

स्थिति II:
रेलगाड़ी द्वारा 100 किमी दूरी तय करने में लगा समय = \(\frac{100}{x}\) घण्टे
शेष दूरी = 300 – 100 = 200 किमी
बस द्वारा 200 किमी दूरी तय करने में लगा समय = \(\frac{200}{y}\) घण्टे
∴ कुल समय = \(\left(\frac{100}{x}+\frac{200}{y}\right)\) घण्टे
दूसरी शर्त के अनुसार,
\(\frac{100}{x}+\frac{200}{y}\) = 4 घण्टे 10 मिनट

माना \(\frac{1}{x}\) = u और \(\frac{1}{y}\) = ν समीकरण (1) व (2) में रखने पर,
15u + 60ν = 1
15u + 60ν – 1 = 0 …..(3)
तथा 24u + 48ν = 1
24u + 48ν – 1 = 0 …..(4)
समीकरण (3) व (4) को बज्रगुणन विधि से हल करने पर

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.7 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Exercise 3.7

प्रश्न 1.
दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अन्तर है। अनी के पिता धरम की आयु अनी की आयु की दुगनी और बीजू की आयु अपनी बहन कैथी की आयु की दुगनी है। कैथी और धरम की आयु में अन्तर 30 वर्ष है। अनी और बीजू की आयु ज्ञात कीजिए।
हल:
माना अनी की आयु = x वर्ष
तथा बीजू की आयु = y वर्ष
प्रश्नानुसार,
x – y = 3 …..(i)
या y – x = 3
⇒ -x + y = 3 …..(ii)
और अनी के पिता की आयु = 2 × अनी की आयु
= 2x वर्ष
बीजू की आयु = कैथी की आयु का दुगना

प्रश्नानुसार, धरम, कैथी से 30 वर्ष बड़ा है।
∴ \(2 x-\frac{y}{2}=30\)
⇒ \(\frac{4 x-y}{2}=30\)
⇒ 4x – y = 60 …..(iii)
समीकरण (i) में से समीकरण (iii) को घटाने पर,

x का यह मान समीकरण (ii) में रखने पर,
19 – y = 3
⇒ -y = 3 – 19
⇒ -y = – 16 ∴ y = 16
पुन: समीकरण (2) तथा समीकरण (3) को जोड़ने पर
-x + y = 3
4x – y = 60
3x = 63
⇒ x = \(\frac{63}{3}\) = 21
x का मान समी. (2) में रखने पर,
– 21 + y = 3 ⇒ y= 3 + 21 = 24
अनी की आयु 19 वर्ष और बीजू की आयु 16 वर्ष है या अनी की आयु 21 वर्ष तथा बीजू की आयु 24 वर्ष है।

प्रश्न 2.
एक मित्र दूसरे से कहता है कि ‘यदि मुझे एक सौ रुपये दे दो, तो मैं आपसे दो गुना धनी बन जाऊँगा।’ दूसरा उत्तर देता है, ‘यदि आप मुझे दस रुपये दे दें, तो मैं आपसे छः गुना धनी बन जाऊँगा। बताइए कि उनकी क्रमशः क्या सम्पत्तियाँ हैं ?
हल:
माना A और B दो दोस्त हैं। A के पास ₹ x तथा B के पास रु. हैं।
का धन ₹ (x + 100)
प्रथम शर्तानुसार A का धन = ₹(x + 100)
B का धन = ₹(y – 100)
∵ A का धन = 2 × B का धन
x + 100 = 2 × (y – 100)
⇒ x + 100 = 2y – 200
⇒ x – 2y = – 300 …..(i)
तथा द्वितीय शर्तानुसार,
B का धन = ₹ (y + 10),
A का धन = ₹ (x – 10)
B का धन = 6 × A का धन
y + 10 = 6 × (x – 10)
y + 10 = 6x – 60
6x – y = 60 + 10
6x – y = 70 …..(ii)
समीकरण (ii) में 2 से गुणा करने पर,
12x – 2y = 140 …..(iii)
समीकरण (iii) में से समी. (i) को घटाने पर,

x का यह मान समीकरण (i) में रखने पर
40 – 2y = -300
– 2y = – 300 – 40
– 2y = – 340
2y = 340
y = \(\frac{340}{2}\) = ₹ 170
अतः पहले मित्र के पास धन = ₹ 40
और दूसरे मित्र के पास धन = ₹ 170

प्रश्न 3.
एक रेलगाड़ी एक समान चाल से एक निश्चित दूरी तय करती है। यदि गाड़ी 10 किमी/घण्टा अधिक तेज चलती होती, तो इसे नियत समय से 2 घण्टे कम लगते और यदि रेलगाड़ी 10 किमी/ घण्टा धीमी चलती होती, तो इसे नियत समय से 3 घण्टे अधिक लगते। रेलगाड़ी द्वारा तय की गई दूरी ज्ञात कीजिए।
हल:
माना कि रेलगाड़ी की चाल = x किमी / घण्टा
और रेलगाड़ी द्वारा लिया गया = y घण्टा
रेलगाड़ी द्वारा तय की गई दूरी = चाल × समय
= x × y
= xy किमी
रेलगाड़ी के तेज चलने पर चाल = (x + 10 ) किमी / घण्टा
रेलगाड़ी द्वारा लिया गया समय = (y – 2) घण्टे
दूरी = (x + 10 ) (y – 2)
⇒ xy = xy – 2x + 10y – 20
⇒ 2x – 10y = – 20 …..(i)
रेलगाड़ी के धीमी गति से चलने पर चाल = (x – 10) किमी / घण्टा
समय = (y + 3) घण्टे
दूरी = चाल × समय
⇒ xy = (x – 10) × (y + 3)
⇒ xy = xy + 3x – 10y – 30
⇒ 3x – 10y = 30 …..(ii)
समीकरण (ii) में से (i) को घटाने पर,

∴ x = 50
समीकरण (i) में x का मान रखने पर,
2 × 50 – 10y = -20
100 – 10y = – 20
-10y = -20 – 100
– 10y = -120
y = \(\frac{-120}{-10}\) = 12
अतः रेलगाड़ी की चाल = 50 किमी / घण्टा
रेलगाड़ी द्वारा लिया गया समय = 12 घण्टे
∴ रेलगाड़ी द्वारा तय की गई दूरी = चाल × समय
= 50 × 12
= 600 किमी।

प्रश्न 4.
एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा होना है। यदि प्रत्येक पंक्ति में 3 विद्यार्थी अधिक होते तो 1 पंक्ति कम होती। यदि पंक्ति में 3 विद्यार्थी कम होते तो 2 पंक्तियाँ अधिक बनतीं कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।
हल:
माना प्रत्येक पंक्ति में विद्यार्थियों की संख्या x है
तथा कुल पंक्तियों की संख्या y है
∴ कुल विद्यार्थियों की संख्या = xy
स्थिति I: यदि प्रत्येक पंक्ति में 3 विद्यार्थी अधिक हैं
तब इस स्थिति में पंक्तियों की संख्या (y – 1) हो जाती है।
xy = (x + 3) (y – 1)
⇒ xy = xy – x + 3y – 3
⇒ x – 3y = – 3 …..(i)
स्थिति II: यदि प्रत्येक पंक्ति में 3 विद्यार्थी कम हैं तब इस स्थिति में पंक्तियों की संख्या (y + 2) हो जाती है।
xy = (x – 3) (y + 2)
⇒ xy = xy + 2x – 3y – 6
⇒ 2x – 3y = 6 …..(ii)
समीकरण (i) में 2 से गुणा करने पर,
2x – 6y = – 6 …..(iii)
समीकरण (iii) में से (ii) को घटाने पर,

y का मान समीकरण (i) में रखने पर,
⇒ x – 3y = – 3
⇒ x – 3 × 4 = -3
⇒ x – 12 = – 3
x = – 3 + 12
∴ x = 9
अतः कक्षा में विद्यार्थियों की कुल संख्या = 9 × 4 = 36

प्रश्न 5.
एक ΔABC में, ∠C = 3 ∠B = 2 (∠A + ∠B) है। त्रिभुज के तीनों कोण ज्ञात कीजिए।
हल:
माना त्रिभुज के कोण A, B तथा C हैं।
तब ∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠B = 180° – ∠C
∠C = 3∠B = 2 (∠A + ∠B)
∠C = 2 (∠A + ∠B)
⇒ ∠C = 2 (180° – ∠C)
[क्योंकि ∠A + ∠B = 180° – ∠C]
⇒ ∠C = 360° – 2∠C
⇒ ∠C + 2∠C = 360°
⇒ 3∠C = 360°
∴ C = \(\frac{360^{\circ}}{3}\) = 120°
अब ∠C = 3∠B
⇒ 3∠B = 120°
∴ ∠B = \(\frac{120^{\circ}}{3}\) = 40°
परन्तु ∠A + ∠B + ∠C = 180°
⇒ ∠A + 40° + 120° = 180°
⇒ ∠A = 180° – 160°
∠A = 20°
अतः Δ के कोण ∠A = 20°
∠B = 40°
∠C = 120°

प्रश्न 6.
समीकरणों 5x – y = 5 और 3x – y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष पर बने त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
हल:
दिया गया समीकरण युग्म है
5x – y = 5 …..(i)
3x – y = 3 …..(ii)
समीकरण (i) से,
⇒ y = 5x – 5
x = 0 रखने पर, y = 5 × 0 – 5 = 0 – 5 = -5
x = 1 रखने पर, y = 5 × 1 – 5 = 0
x = 2 रखने पर, y = 5 × 2 – 5
= 10 – 5 = 5
x के विभिन्न मानों के लिए सारणी :

x	0	1	2
y	-5	0	5

समीकरण (ii) से,
⇒ y = 3x – 3
x = 0 रखने पर, y = 3 × 0 – 3 = -3
x = 1 रखने पर, y = 3 × 1 – 3 = 0
x= 2 रखने पर, y = 3 × 2 – 3 = 3
x के विभिन्न मानों के लिए सारणी:

x	0	1	2
y	-3	0	3

बिन्दुओं (0, -5), (1, 0) तथा (2, 5) को ग्राफ पेपर पर आलेखित करने पर समीकरण 5x – y = 5 की एक सरल रेखा प्राप्त होती है।
इसी प्रकार बिन्दुओं (0, -3), (1, 0) और (2, 3) को ग्राफ पेपर पर आलेखित करने पर समीकरण 3xy – 3 की सरल रेखा प्राप्त होती है।
इन रेखाओं से y-अक्ष पर बना छायांकित त्रिभुज ACD है जिसके निर्देशांक A(0, -5), C(0, -3) और D(1, 0) हैं।
माना x₁ = 0, y₁ = -5, x₂ = 0, y₂ = – 3
तथा x₃ = 1, y₃ = 0
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\) [0(- 3 – 0) + 0{0 – (-5)} + 1 {-5 – (-3)}]
= \(\frac{1}{2}\) [0 + 0 + 1(- 5 + 3)]
= \(\frac{1}{2}\) (-2) = -1 वर्ग मात्रक
त्रिभुज के शीषों के निर्देशांक (1, 0), (0, -3), (0, -5) है।
∵ क्षेत्रफल ऋणात्मक नहीं हो सकता। अतः त्रिभुज का क्षेत्रफल 1 वर्ग मात्रक होगा।

प्रश्न 7.
निम्नलिखित रैखिक समीकरणों के युग्मों को हल कीजिए-
(i) px + qy = p – q
qx – py = p + q
(ii) ax + by = c
bx + ay = 1 + c
(iii) \(\frac{x}{a}-\frac{y}{b}=0\)
ax + by = a² + b²
(iv) (a – b)x + (a + b)y = a² – 2ab – b²
(a + b) (x + y) = a² + b²
(v) 152x – 378y = -74
-378x + 152y = -604
हल:
(i) दिया गया रैखिक समीकरण युग्म
px + qy = p – q …(1)
और qx – py = p + q …(2)

समीकरण (1) को से और समीकरण (2) को p से गुणा करने पर,

घटाने पर,
y के इस मान को समीकरण (1) में रखने पर,
px + q(-1) = p – q
⇒ px – q = p – q
⇒ px= p – q + q
⇒ px = p
∴ x = 1
अतः x = 1 और y = -1

(ii) दिया गया रैखिक समीकरण युग्म
ax + by = c
⇒ ax + by – c = 0 …..(i)
तथा bx + ay = 1 + c
⇒ bx + ay – (1 + c) = 0 …..(ii)
वज्रगुणन विधि से समी. (i) एवं (ii) को हल करने पर

(iii) दिया गया रैखिक समीकरण युग्म
\(\frac{x}{a}-\frac{y}{b}=0\)
⇒ \(\frac{b x-a y}{a b}\) = 0
⇒ bx – ay = 0 …..(i)
और ax + by = a² + b²
⇒ ax + by – (a² + b²) = 0 …..(ii)
वज्रगुणन विधि से हल करने पर,

अतः समीकरण के अभीष्ट हल x = a और y = b हैं।

(iv) दिया गया रैखिक समीकरण युग्म
(a – b)x + (a + b)y = a² – 2ab – b²
ax – bx + ay + by = a² – 2ab – b² …..(i)
और (a + b) (x + y) = a² + b²
⇒ ax + bx + ay + by = a² + b² …..(ii)
समीकरण (i) में से (ii) को घटाने पर,

x के इस मान को समीकरण (i) में रखने पर,
(a – b) (a + b) + (a + b)y = a² – 2ab – b²
⇒ a² – b² + (a + b)y = a² – 2ab – b²
⇒ (a + b)y = a² – 2ab – b² – a² + b²
⇒ (a + b)y = -2ab
∴ y = \(\frac{-2 a b}{a+b}\)
अतः x = (a + b)
और y = \(-\frac{2 a b}{a+b}\)

(v) दिया गया समीकरण युग्म
152x – 378y = -74 …..(1)
-378x + 152y = -604 …..(2)
समीकरण (1) व समीकरण (2) को जोड़ने पर,
-226x – 226y = -678
⇒ -226(x + y) = -678
⇒ x + y = \(\frac{-678}{-226}\)
∴ x + y = 3 …..(3)
समीकरण (1) मैं से समीकरण (2) को घटाने पर,
(152x – 378y) – (-378x + 152y) = – 74 – (-604)
⇒ 152x – 378y + 378x – 152y = – 74 + 604
⇒ 530x – 530y = 530
⇒ 530(x – y) = 530
∴ x – y = 1 …..(4)
समीकरण (3) व समीकरण (4) को जोड़ने पर,
x + y + x – y = 3 + 1
⇒ 2x = 4
⇒ x = \(\frac{4}{2}\)
∴ x = 2
x = 2 समीकरण (3) में रखने पर,
⇒ 2 + y = 3
⇒ y = 3 – 2 ⇒ y = 1
अत: समीकरण के अभीष्ट हल x = 2 और y = 1 हैं।

प्रश्न 8.
ABCD एक चक्रीय चतुर्भुज है। इस चक्रीय चतुर्भुज के कोण ज्ञात कीजिए।

हल:
∵ ABCD एक चक्रीय चतुर्भुज है।
∴ ∠A + ∠C = 180°
⇒ 4y + 20 + (- 4x ) = 180°
या – 4x + 4y = 180° – 20° = 160°
या x – y = – 40° …..(1)
और ∠B + ∠D = 180°
तो -7x + 5 + 3y – 5 = 180°
या -7x + 3y = 180°
या 7x – 3y = – 180° …..(2)
समीकरण (1) से y = x + 40 समीकरण (2) में प्रतिस्थापित करने पर,
7x – 3(x + 40) = – 180
⇒ 7x – 3x – 120 = -180
⇒ 4x = – 180 + 120
⇒ 4x = -60
∴ x = \(\frac{-60}{4}\) = -15
x का यह मान समीकरण (1) में रखने पर,
– 15 – y = – 40
⇒ – y = -40 + 15
⇒ – y = – 25 ⇒ y = 25
तब ∠A = 4y + 20 = 4 × 25 + 20 = 120°
∠B = – 7x + 5 = (-7) × (-15) + 5
= 110°
∠C = – 4x = – 4 × – 15 = 60°
∠D = 3y – 5 = 3 × 25 – 5 = 70°

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 निर्देशांक ज्यामिति Exercise 7.1

प्रश्न 1.
बिन्दुओं के निम्नलिखित युग्मों के बीच की दूरियाँ ज्ञात कीजिए:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (1, 3)
(iii) (a, b ), (-a, -b)
हल:
(i) दिए गए बिन्दु: (2, 3), (4, 1)
दो बिन्दुओं के बीच की दूरी

प्रश्न 2.
बिन्दुओं (0, 0) और (36, 15) के बीच की दूरी ज्ञात कीजिए। क्या अब आप अनुच्छेद 7.2 में दिए दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं?
हल:
दिए गए बिन्दु हैं :
A (0, 0) और B (36, 15)
अभीष्ट दूरी AB = \(\sqrt{(0-36)^2+(0-15)^2}\)
= \(\sqrt{1296+225}\)
= \(\sqrt{1521}\)
= 39 मात्रक
अनुच्छेद 7.2 के अनुसार,
दिए गए शहरों के कार्तीय निर्देशांक A(0, 0) और B(36, 15)

अतः बिन्दुओं के बीच की अभीष्ट दूरी 39 km है।

प्रश्न 3.
निर्धारित कीजिए कि क्या बिन्दु (1, 5), (2, 3) और (-2, 11) संरेखी हैं?
हल:
माना दिए गए बिन्दु क्रमानुसार A(1, 5), B(2, 3) और C (-2, -11)

उपर्युक्त दूरियों से स्पष्ट है कि किन्हीं दो का योगफल तीसरे के बराबर नहीं है। अतः दिए गए बिन्दु संरेखी नहीं हैं।

प्रश्न 4.
जाँच कीजिए कि क्या बिन्दु (5, -2), (6, 4) और (7, -2) एक समद्विबाहु त्रिभुज के शीर्ष हैं?
हल:
माना दिए गए बिन्दु क्रमानुसार A(5, -2), B(6, 4) और C(7, -2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।

उपर्युक्त दूरियों से स्पष्ट है कि AB = BC = \(\sqrt{37}\)
अत: दिए गए बिन्दु समद्विबाहु त्रिभुज के शीर्ष हैं।

प्रश्न 5.
किसी कक्षा में, चार मित्र बिन्दुओं A, B, C और D पर बैठे हुए हैं, जैसा कि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अन्दर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, ‘क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है ? ‘चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके बताइए कि इनमें कौन सही है।

हल:
दी गई आकृति में बिन्दुओं A, B, C व D के निर्देशांक क्रमश: (3, 4), (6, 7), (9, 4) और (6, 1) हैं।


उपर्युक्त दूरियों से स्पष्ट है कि
AB = BC = CD = DA = 3\(\sqrt{2}\) मात्रक
AC = BD = 65 मात्रक
अत: चतुर्भुज ABCD एक वर्ग है तथा चंपा की सोच सही है।

प्रश्न 6.
निम्नलिखित बिन्दुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(1) (-1, -2), (1, 0), (1, 2), (3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
हल:
(i) दिए गए बिन्दु A(-1, 2), B(1, 0), C (-1, 2) और D(-3, 0) हैं।

यहाँ हम देखते हैं कि,
AB = BC = CA = DA
अब, AC = \(\sqrt{[-1-(-1)]^2+[2-(-2)]^2}\)
= \(\sqrt{(-1+1)^2+(4)^2}\)
= \(\sqrt{0+(4)^2}\) = 4 मात्रक
∵ AB² + BC² = (2\(\sqrt{2}\))² + (2\(\sqrt{2}\))²
8 + 8 = 16 = (4)² = AC²
∴ ∠B समकोण है।
अतः दिए गये बिन्दुओं से बना चतुर्भुज ABCD एक वर्ग है।

(ii) दिए गए बिन्दु A(-3, 5), B(3, 1), C(0, 3), और D(-1, -4) हैं।

अर्थात् A, B, C संरेखी हैं। अतः दिए गए बिन्दु चतुर्भुज नहीं बनाते हैं।

(iii) दिए गए बिन्दु A(4, 5), B(7, 6), C(4, 3) और D(1, 2) हैं।

= \(\sqrt{0+4}=\sqrt{4}\) = 2 मात्रक
BD = \(\sqrt{(1-7)^2+(2-6)^2}\)
= \(\sqrt{36+16}=\sqrt{52}=2 \sqrt{13}\) मात्रक
उपर्युक्त दूरियों से स्पष्ट है कि
AB = CD, BC = DA और AC ≠ BD अर्थात् दिए गए बिन्दुओं से बने चतुर्भुज की सम्मुख भुजाएँ बराबर हैं तथा वकर्ण AC ≠ BD हैं।
अतः चतुर्भुज ABCD एक समान्तर चतुर्भुज है।

प्रश्न 7.
x-अक्ष पर वह बिन्दु ज्ञात कीजिए जो (2, -5) और (-2, 9) से समदूरस्थ है।
हल:
माना x-अक्ष पर स्थित किसी बिन्दु के निर्देशांक (x, 0) हैं क्योंकि x-अक्ष के लिए y-निर्देशांक शून्य होता है।
(x, 0) और (2, -5) के बीच की दूरी

(दोनों पक्षों का वर्ग करने पर)
⇒ x² – 4x + 29 = x² + 4x + 85
⇒ -8x = 85 – 29
⇒ -8x = 56
⇒ x = \(\frac{56}{-8}\)
∴ x = -7
अतः अभीष्ट बिन्दु के निर्देशांक (-7, 0) हैं।

प्रश्न 8.
y का वह मान ज्ञात कीजिए, जिसके लिए बिन्दु P(2, -3) और Q(10, y) के बीच की दूरी 10 मात्रक है।
हल:
दिए हुए बिन्दु P(2, -3) तथा Q(10, y) है।
तब PQ = \(\sqrt{(10-2)^2+[y-(-3)]^2}\)
= \(\sqrt{(8)^2+(y+3)^2}\)
∵ दोनों बिन्दुओं के बीच की दूरी (PQ) = 10 मात्रक (दिया है)
∴ \(\sqrt{8^2+(y+3)^2}\) = 10
(दोनों पक्षों का वर्ग करने पर)
8² + (y + 3)² = 10²
(y + 3)² = 10² – 8²
(y + 3)² = 100 – 64
(y + 3)² = 36
(y + 3) = ±\(\sqrt{36}\)
(y + 3) = ±6
‘+’ चिहन् लेने पर,
y + 3 = 6
∴ y = 6 – 3 = 3
‘-‘ चिहन लेने पर,
y + 3 = – 6
y = – 6 – 3 = -9
अतः y के अभीष्ट मान 3 और -9 हैं।

प्रश्न 9.
यदि Q (0, 1); बिन्दुओं P(5, -3) और R (x, 6) से समदूरस्थ है तो x के मान ज्ञात कीजिए। दूरियाँ QR और PR भी ज्ञात कीजिए ।
हल:
∵ Q(0, 1), P(5, -3) और R (x, 6)
∵ Q, P तथा R से समदूरस्थ है।
∴ PQ = QR
∴ \(\sqrt{(5-0)^2+(-3-1)^2}\)
= \(\sqrt{(0-x)^2+(1-6)^2}\)
\(\sqrt{(5)^2+(-4)^2}\)
⇒ \(\sqrt{x^2+(-5)^2}\)
दोनों पक्षों का वर्ग करने पर,
⇒ (5)² + (-4)² = x² + (-5)²
⇒ 25 + 16 = x² + 25
⇒ x² = 25 + 16 – 25
⇒ x² = 16
⇒ x = ±4
जब x = 4 हो, तो बिन्दु R के निर्देशांक (4, 6) होंगे।

PR = \(\sqrt{(-4-5)^2+(6+3)^2}\)
= \(\sqrt{81+81}=\sqrt{162}\)
= \(9 \sqrt{2}\)
अत: x = ±4, QR = \(\sqrt{41}\) और PR = \(\sqrt{82}\) या 9\(\sqrt{2}\)

प्रश्न 10.
x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिन्दु (x, y) बिन्दुओं (3, 6) और (-3, 4) से समदूरस्थ हो।
अथवा
यदि बिन्दु A(x, y), B(3, 6) तथा C(-3, 4) संरेखी है, तो दर्शाइए कि x – 3y + 15 = 0.
हल:
माना अभीष्ट बिन्दु P (x, y) है, जो कि दिए गए बिन्दु A(3, 6) और B(-3, 4) से समदूरस्थ है।
PA = PB
⇒ PA² = PB²
(x – 3)² + (y – 6)² = [x – (-3)]² + (y – 4)²
⇒ x² – 6x + 9 + y² – 12y + 36 = (x + 3)² + (y – 4)²
⇒ x² – y² – 6x – 12 y + 45 = x² + 6x + 9 + y² – 8y + 16
⇒ x² + y – 6x – 12y + 45 = x² + y² + 6x – 8y + 25
⇒ – 6x – 12y = 6x – 8y + 25 – 45
⇒ – 6x – 12y – 6x + 8y = -20
⇒ – 12x – 4y = -20
⇒ 3x + y = 5
[(-4) से दोनों पक्षों में भाग देने पर]
अत: अभीष्ट सम्बन्ध 3x + y – 5 = 0 है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.5 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Exercise 3.5

प्रश्न 1.
निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं हैं या किसके अपरिमित रूप से अनेक हल हैं? अद्वितीय हल की स्थिति में, उसे वज्रगुणन विधि से ज्ञात कीजिए :
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii) 2x + y = 5
3x + 2y = 8
(iii) 3x – 5y = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
हल:
(i) दिए गए रैखिक समीकरणों का युग्म है
x – 3y – 3 = 0 …..(1)
तथा 3x – 9y – 2 = 0 …..(2)
उक्त समीकरण युग्म की तुलना व्यापक रैखिक समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर,

अंत: दिये गये समीकरण युग्म का कोई हल नहीं है।

(ii) दिए गए रैखिक समीकरणों का युग्म है।
2x + y = 5 ⇒ 2x + y – 5 = 0
3x + 2y = 8 ⇒ 3x + 2y – 8 = 0
उक्त समीकरण युग्म की तुलना व्यापक रैखिक समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर,
a₁ = 2, b₁ = 1, c₁ = -5
a₂ = 3, b₂ = 2, c₂ = -8

अतः दिए गए समीकरणों का एक अद्वितीय हल है।
अब वज्रगुणन विधि से,

अतः समीकरण युग्म का हल x = 2 और y = 1 है।

(iii) दिए हुए समीकरण युग्म :
3x – 5y = 20.
6x – 10y = 40
इन समीकरणों को निम्न प्रकार लिख सकते हैं :
3x – 5y – 20 = 0
6x – 10y – 40 = 0
उक्त समीकरणों की तुलना व्यापक रैखिक समीकरण युग्म् a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर,
a₁ = 3, b₁ = -5, c₁ = -20
a₂ = 6, b₂ = -10, c₂ = 40

अतः समीकरण युग्म के अपरिमित रूप से अनेक हल होंगे।

(iv) दिया गया समीकरण युग्म :
x – 3y – 7 = 0 …..(i)
3x – 3y – 15 = 0 …..(ii)
उक्त समीकरणों की तुलना व्यापक रैखिक समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर,
a₁ = 1, b₁ = -3, c₁ = – 7
a₂ = 3, b₂ = – 3, c₂ = – 15

अतः दिया गया समीकरण युग्म का एक अद्वितीय हल है।
अब बज्रगुणन विधि से,

अतः दिए गए समीकरण के हल x = 4 और y = -1 है।

प्रश्न 2.
(i) a और 6 के किन मानों के लिए, निम्न रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हाल होंगे ?
(i) 2x + 3y = 7
(a – b)x + (a + b)y = 3a + b – 2
(ii) k के किस मान के लिए, निम्न रैखिक समीकरणों के युग्म का कोई हल नहीं है ?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k +1
हल:
(i) दिया गया समीकरण युग्म है:
2x + 3y = 7
या 2x + 3y – 7 = 0 …..(i)
(a – b)x + (a + b)y = 3a + b – 2
या (a – b)x + (a + b)y – (3a + b – 2) = 0 …..(ii)
उक्त समीकरण युग्म की तुलना व्यापक रैखिक समीकरण
a₁x + b₁y + c₁ =0 तथा a₂x + b₂y + c₂ = 0 से करने पर,
a₁ = 2, b₁ = 3, c₁ = -7
a₂ = (a – b), b₂ = (a+b), c₂ = -(3a + b – 2)
अपरिमित रूप से अनेक हल के लिए शर्त

⇒ 7(a – b) = 2(3a + b – 2)
⇒ 7a – 7b = 6a + 2b – 4
⇒ 7a – 6a – 7b – 2b = -4
⇒ a – 9b = -4 …..(iii)
और \(\frac{3}{a+b}=\frac{7}{3 a+b-2}\)
⇒ 7(a + b) = 3(3a + b – 2)
⇒ 7a + 7b = 9a + 3b – 6
⇒ 9a + 3b – 6 – 7a – 7b = 0
⇒ 2a – 4b = 6
⇒ 2(a – 2b) = 6
⇒ a – 2b = 3
⇒ a = 3 + 2b …..(iv)
समीकरण (iv) से a = 3 + 2b समीकरण (iii) में रखने पर,
⇒ 3 + 2b – 9b = -4
⇒ -7b = – 4 – 3
⇒ -7b = -7
b = \(\frac{-7}{-7}\) = 1
b के इस मान को समीकरण (iv) में प्रतिस्थापित करने पर,
a = 3 + 2 × 1
= 3 + 2 = 5
अतः रैखिक समीकरण युग्म के अभीष्ट हल a = 5 तथा b = 1 हैं।

(ii) दिया गया रैखिक समीकरण युग्म है:
3x + y = 1 ⇒ 3x + y -1 = 0 …..(i)
(2k – 1)x + (k – 1)y = 2k + 1
⇒ (2k – 1)x + (k – 1)y – (2k + 1) = 0 … (ii)
उक्त समीकरण युग्म की तुलना व्यापक रैखिक समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂x + c₂ = 0 से करने पर,
a₁ = 3, b₁ = 1, c₁ = -1
a₂ = (2k – 1), b₂ = (k – 1), c₂ = – (2k + 1)
कोई हल नहीं है के लिए शर्त

⇒ 6k + 3 ≠ 2k – 1
⇒ 6k – 2k ≠ – 1 – 3
⇒ 4k ≠ -4
⇒ k ≠ -1
और \(\frac{3}{2 k-1}=\frac{1}{k-1}\)
3(k – 1) = 2k – 1
3k – 3 = 2k – 1
3k – 2k = – 1 + 3
∴ k = 2
अतः k = 2 और k ≠ -1

प्रश्न 3.
निम्नलिखित रैखिक समीकरणों के युग्म को प्रतिस्थापन विधि और वज्रगुणन विधि द्वारा हल कीजिए।
8x + 5y = 9
3x + 2y = 4
हल:
दिया गया समीकरण युग्म है:
8x + 5y = 9 …..(i)
3x + 2y = 4 …..(ii)
प्रतिस्थापन विधि से : समीकरण (ii) से,
2y = 4 – 3x
⇒ y = \(\frac{4-3 x}{2}\) …..(iii)
y के इस मान को समीकरण (i) में प्रतिस्थापित करने पर,

x + 20 = 18
⇒ x = 18 – 20
∴ x = – 2
x का यह मान समीकरण (3) में रखने पर,
y = \(\frac{4-3 \times-2}{2}=\frac{4+6}{2}\)
∴ y = \(\frac{10}{2}\) = 5
अत: x = – 2 और y = 5
वज्रगुणन विधि से-रैखिक युग्म समीकरण है-
8x + 5y – 9 = 0
और 3x + 2y – 4 = 0

अतः दिए गए रैखिक समीकरण युग्म के हल x = -2 तथा y = 5 होंगे।

प्रश्न 4.
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) किसी बीजगणितीय विधि से ज्ञात कीजिए :
(i) एक छात्रावास के मासिक व्यय का एक भाग नियत है तथा शेष इस पर निर्भर करता है कि छात्र ने कितने दिन भोजन लिया है जब एक विद्यार्थी 4 को, जो 20 दिन भोजन करता है, ₹ 1000 छात्रावास के व्यय के लिए अदा करने पड़ते हैं, जबकि एक विद्यार्थी B को, जो 26 दिन भोजन करता है छात्रावास के व्यय के लिए ₹ 1180 अदा करने पड़ते हैं। नियत व्यय और प्रतिदिन के भोजन का मूल्य ज्ञात कीजिए।
(ii) एक भिन्न
हो जाती \(\frac{1}{3}\) है जब उसके अंश से 1 घटाया जाता है और वह \(\frac{1}{4}\) हो जाती है जब हर में 8 जोड़ दिया जाता है। वह भिन्न ज्ञात कीजिए।
(iii) यश ने एक टेस्ट में 40 अंक अर्जित किए, जबकि उसे प्रत्येक सही उत्तर पर 3 अंक मिले तथा गलत उत्तर पर 1 अंक की कटौती की गई। यदि उसे सही उत्तर पर 4 अंक मिलते और गलत उत्तर पर 2 अंक कटते, तो यश 50 अंक अर्जित करता। टेस्ट में कितने प्रश्न थे ?
(iv) एक राजमार्ग पर दो स्थान A और B, 100 किमी की दूरी पर हैं। एक कार A से तथा दूसरी कार B से एक ही समय चलना प्रारम्भ करती है। यदि ये कारें भिन्न-भिन्न चालों से एक ही दिशा में चलती हैं तो वे 5 घण्टे पश्चात् मिलती हैं। यदि वे विपरीत दिशाओं में चलना प्रारम्भ करती हैं तो वे 1 घण्टे पश्चात् मिलती हैं। दोनों कारों की चाल ज्ञात कीजिए।
(v) एक आयत का क्षेत्रफल 9 वर्ग इकाई कम हो जाता है, यदि उसकी लम्बाई 5 इकाई कम कर दी जाती है और चौड़ाई 3 इकाई बढ़ा दी जाती है। यदि हम लम्बाई को 3 इकाई और चौड़ाई को 2 इकाई बढ़ा दें, तो क्षेत्रफल 67 वर्ग इकाई बढ़ जाता है। आयत की विमाएँ ज्ञात कीजिए।
हल:
(i) माना कि छात्रावास में भोजन करने वाले छात्र के नियत व्यय = ₹ x तथा प्रतिदिन के भोजन का मूल्य ₹ y है।
20 दिन के भोजन के लिए किया गया भुगतान = नियत व्यय + 20 दिन के भोजन का मूल्य
= ₹ (x + 20y)
परन्तु विद्यार्थी A 20 दिन भोजन करने के ₹ 1000 चुकाता है।
∴ x + 20y = 1000 …..(i)
इसी प्रकार, 26 दिन के भोजन के लिए किया गया भुगतान = नियत व्यय + 26 दिन के भोजन का मूल्य
= ₹ (x + 26y)
परन्तु विद्यार्थी B 26 दिन भोजन करने के ₹ 1180 चुकाता है।
x + 26y = 1180 …..(ii)
∴ समीकरण (ii) मैं से समीकरण (i) को घटाने पर,

समीकरण (i) में y = 30 रखने पर
x + 20 (30) = 1000
⇒ x + 600 = 1000
⇒ x = 1000 – 600
∴ x = 400
समीकरण युग्म के अभीष्ट हल x = 400 और y = 30 है।
अत: छात्रावास का नियत व्यय = ₹ 400
तथा प्रतिदिन भोजन का व्यय = ₹ 30

(ii) माना कि भिन्न का अंश x तथा हर y है।
भिन्न = \(\frac{x}{y}\)
जब भिन्न के अंश में से 1 घटाया जाता है तो वह \(\frac{x-1}{y}\) हो जाती है।
प्रश्नानुसार, \(\frac{x-1}{y}=\frac{1}{3}\)
⇒ 3(x – 1) = y
⇒ y = 3x – 3 …..(i)
इसी प्रकार जब भिन्न के हर में 8 जोड़ा जाता है तो वह \(\frac{x}{y+8}\) हो जाती है।
प्रश्नानुसार, \(\frac{x}{y+8}=\frac{1}{4}\)
⇒ x = (y + 8) × 1 = x × 4
⇒ y + 8 = 4x …..(ii)
समीकरण (i) से समीकरण (ii) में y का मान प्रतिस्थापित करने पर,
⇒ 3x – 3 + 8 = 4x
⇒ – 3 + 8 = 4x – 3x
⇒ 5 = x
∴ x = 5
x का यह मान समीकरण (i) में रखने पर,
y = 3x – 3
= 3 × 5 – 3
= 15 – 3 = 12
y = 12
अत: x = 5, y = 12
∴ अभीष्ट भिन्न = \(\frac{5}{12}\)

(iii) माना कि यश द्वारा हल किए गये सही प्रश्नों की संख्या x है और गलत हल किए गये प्रश्नों की संख्या y है।
पहली शर्त के अनुसार,
3x – y = 40
⇒ 3x – y – 40 = 0 …..(1)
दूसरी शर्त के अनुसार,
4x – 2y = 50
⇒ 4x – 2y – 50 = 0 …..(2)
वज्रगुणन विधि से हल करने पर,

सही प्रश्नों की संख्या = 15
तथा गलत प्रश्नों की संख्या = 5
अत: प्रश्नों की कुल संख्या = [सही प्रश्नों की संख्या] + [गलत प्रश्नों की संख्या]
= 15 + 5
= 20

(iv) माना कि स्थान A से चलने वाली कार की चाल = x किमी./ घण्टा
और स्थान B से चलने वाली कार की चाल = y कि.मी./ घण्टा
स्थान A व स्थान B के बीच की दूरी = 100 किमी
जब कारें एक ही दिशा में स्थान A तथा B से चलती हैं तो 5 घण्टे बाद P स्थान पर मिलती हैं।

∴ 5 घण्टे में स्थान A से चली दूरी – 5 घण्टे में स्थान B से चली दूरी = 100 किमी.
⇒ 5x – 5y = 100 [दूरी = चाल × समय]
⇒ x – y = 20 …..(1)
जब कारें विपरीत दिशा में स्थान A तथा B से चलकर Q स्थान पर मिलती हैं तो उन्हें 1 घण्टे में 100 किमी चलना होगा।

∴ 1 घण्टे में स्थान A से चली दूरी + 1 घण्टे में स्थान B से चली दूरी = 100 किमी
⇒ x + y = 100 ……(2)
समीकरण (1) व (2) को जोड़ने पर

x का यह मान समीकरण (1) में रखने पर,
60 – y = 20 ⇒ y = 40
अतः कारों की चाल 60 किमी./ घण्टा और 40 किमी./ घण्टा है।

(v) माना कि आयत की लम्बाई = x मात्रक
और आयत की चौड़ाई = y मात्रक
∴ आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= x × y
= xy वर्ग मात्रक
पहली शर्त के अनुसार,

अतः आयत की लम्बाई = 17 मात्रक
तथा आयत की चौड़ाई = 9 मात्रक

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.5

प्रश्न 1.
माचिस की डिब्बी की माप 4 सेमी × 2.5 सेमी × 1.5 सेमी है। ऐसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा ?
हल:
माचिस की डिब्बी की माप
∴ l = 4 सेमी, b = 2.5 सेमी तथा h = 1.5 सेमी
∴ माचिस की डिब्बी का आयतन = lbh
= 4 × 2.5 × 1.5 घन सेमी
= 15 घन सेमी
अतः 12 माचिसों के पैकेट का आयतन = 15 × 12
= 180 घन सेमी।

प्रश्न 2.
एक घनाभाकार पानी की टंकी 6 मीटर लम्बी, 5 मीटर चौड़ी और 4.5 मीटर गहरी है। इसमें कितने लीटर पानी आ सकता है? (1 घन मीटर = 1000 लीटर)
हल:
घनाभाकार टंकी की लम्बाई (l) = 6 मीटर,
चौड़ाई (b) = 5 मीटर और गहराई (h) = 4.5 मीटर।
∴ टंकी का आयतन = lbh
= 6 × 5 × 4.5 घन मीटर
= 135 घन मीटर
∴ टंकी में समाहित हो सकने वाले पानी का आयतन
= 135 घन मीटर
= 135 × 1000 लीटर
= 1,35,000 लीटर
अतः टंकी में 1,35,000 लीटर पानी आ सकता है।

प्रश्न 3.
एक घनाभाकार बर्तन 10 मीटर लम्बा और 8 मीटर चौड़ा है। इसको कितना ऊँचा बनाया जाए कि इसमें 380 घन मीटर द्रव आ सके ?
हल:
लम्बाई (l) = 10 मीटर, चौड़ाई (b) = 8 मीटर और आयतन = 380 मीटर³
माना बर्तन की ऊँचाई = h
बर्तन का आयतन = लम्बाई × चौड़ाई × ऊँचाई

प्रश्न 4.
8 मीटर लम्बा, 6 मीटर चौड़ा और 3 मीटर गहरा एक घनाभाकार गड्ढा खुदवाने में 30 रुपये प्रति घन मीटर की दर से होने वाला व्यय ज्ञात कीजिए।
हल:
घनाभाकार गड्ढे की लम्बाई (l) = 8 मीटर.
चौड़ाई (b) = 6 मीटर तथा गहराई (h) = 3 मीटर
∴ गड्ढे का आयतन = lbh
= 8 × 6 × 3 घन मीटर
= 144 घन मीटर
घनाभाकार गड्ढे को खुदवाने का व्यय = गड्डे का आयतन × दर = 30 × 144 = ₹ 4,320
अतः गड्ढा खुदवाने में होने वाला व्यय = ₹ 4,320

प्रश्न 5.
एक घनाभाकार पानी की टंकी की धारिता 50,000 लीटर है। यदि इस टंकी की लम्बाई और गहराई क्रमश: 2.5 मीटर और 10 मीटर है तो इसकी चौड़ाई ज्ञात कीजिए।
हल:
माना टंकी की चौड़ाई b मीटर है।
∵ टंकी की लम्बाई (l) = 2.5 मीटर और टंकी की गहराई (h) = 10 मीटर।
∴ घनाभाकार टंकी का आयतन = lbh
= 2.5 × b × 10 घन मीटर
= 256 घन मीटर
∴ टंकी की धारिता = 25b घन मीटर
= 25b × 1000 लीटर [∵ 1 घन मीटर 1000 लीटर]
प्रश्नानुसार
टंकी का आयतन = टंकी की धारिता
= 50,000 लीटर
∴ 25,000b = 50,000
∴ b = \(\frac{50,000}{25 \times 1000}\) = 2 मीटर
अतः टंकी की चौड़ाई 2 मीटर।

प्रश्न 6.
एक गाँव जिसकी जनसंख्या 4000 है, को प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। इस गाँव में 20 मीटर × 15 मीटर × 6 मीटर मापों वाली एक टंकी बनी हुई है। इस टंकी का पानी वहाँ कितने दिन के लिए पर्याप्त होगा ?
हल:
गाँव की जनसंख्या = 4000
प्रति व्यक्ति प्रतिदिन पानी की आवश्यकता = 150 लीटर
∴ प्रतिदिन गाँव के लिए आवश्यक पानी की मात्रा = 4000 × 150 लीटर
= 6,00,000 लीटर
= 600 घन मीटर
(∵ 1000 लीटर = 1 घन मीटर)
टंकी का आयतन = 20 × 15 × 6 घन मीटर
= 1800 घन मीटर
जल की पर्याप्तता (दिनों में)

अतः टंकी का जल 3 दिन के लिए पर्याप्त होगा।

प्रश्न 7.
किसी गोदाम की माप 40 मीटर × 25 मीटर × 15 मीटर है। इस गोदाम में 1.5 मीटर × 1.25 मीटर × 0.5 मीटर माप वाले लकड़ी के कितने अधिकतम क्रेट (crate) रखे जा सकते हैं?
हल:
गोदाम का आयतन (40 × 25 × 15) मीटर³
1 क्रेट का आयतन = (1.5 × 1.25 × 0.5 ) मीटर³
गोदाम में रखे जा सकने वाले क्रेटों की संख्या

प्रश्न 8.
12 सेमी भुजा वाले एक ठोस घन को बराबर आयतन वाले 8 घनों में काटा जाता है। नये घन की क्या भुजा होगी? साथ ही, इन दोनों घनों के पृष्ठीय क्षेत्रफलों का अनुपात भी ज्ञात कीजिए।
हल:
बड़े घन की भुजा = 12 सेमी
∴ आयतन = (भुजा)³ = (12)³ सेमी³
= 12 × 12 × 12 सेमी³
यह घन 8 बराबर आयतन के घनों में काटा जाता है।

अतः नये घन की भुजा \(\sqrt[3]{6 \times 6 \times 6}\) सेमी
= 6 सेमी।
बड़े घन का पृष्ठीय क्षेत्रफल = 6 × (भुजा)²
= 6 × (12)² वर्ग सेमी
= 864 वर्ग सेमी
छोटे प्रत्येक घन का पृष्ठीय क्षेत्रफल = 6 × (भुजा)²
= 6 × (6)² वर्ग सेमी
= 6 × 6 × 6 वर्ग सेमी
= 216 वर्ग सेमी
∴ दोनों घनों के पृष्ठीय क्षेत्रफल का अनुपात = 864 : 216 = 4 : 1
अतः नये घन की भुजा 6 सेमी और दोनों घनों के पृष्ठीय क्षेत्रफल का अनुपात = 4 : 1.

प्रश्न 9.
3 मीटर गहरी और 40 मीटर चौड़ी एक नदी 2 किमी प्रति घण्टा की चाल से बहकर समुद्र में गिरती है। एक मिनट में समुद्र में कितना पानी गिरेगा ?
हल:
नदी की गहराई (h) = 3 मीटर और चौड़ाई (b) = 40 मीटर
∴ नदी का परिच्छेद क्षेत्रफल = लम्बाई × चौडाई
= 3 × 40
= 120 वर्ग मीटर
∵ नदी के पानी की चाल 2 किमी प्रति घण्टा है।
∴ 1 मिनट में नदी के विस्थापित पानी की लम्बाई = \(\frac{2 \times 1000}{60}\) मीटर
= \(\frac{100}{3}\) घन मीटर
∴ 1 मिनट में बहने वाले पानी का आयतन = नदी के परिच्छेद का क्षेत्रफल × नदी की प्रति मिनट चाल
= 120 × \(\frac{100}{3}\) घन मीटर
= 4000 घन मीटर।
अतः 1 मिनट में समुद्र में 4000 घन मीटर पानी गिरेगा।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Exercise 4.4

प्रश्न 1.
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का अस्तित्व हो, तो उन्हें ज्ञात कीजिए:
(i) 2x² – 3x + 5 = 0
(ii) 3x² – 4\(\sqrt{3}\)x + 4 = 0
(iii) 2x² – 6x + 3 = 0
हल:
(i) दिया गया समीकरण है:
2x² – 3x + 5 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = – 3 तथा c = 5
विविक्तकर (D) = b² – 4ac
= (- 3)² – 4 × 2 × 5
= 9 – 40
= -31 < 0
अतः दी गई द्विघात समीकरण का कोई वास्तविक मूल नहीं है।

(ii) दिया गया द्विघात समीकरण है:
3x² – 4\(\sqrt{3}\)x + 4 = 0
इसकी तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 3, b = – 4\(\sqrt{3}\), c = 4
∴ विविक्तकर (D) = b² – 4ac
= (-4\(\sqrt{3}\))² – 4 × 3 × 4
= 48 – 48 = 0
अतः दी गई द्विघात समीकरण के मूल वास्तविक और बराबर होंगे।
अब श्रीधराचार्य सूत्र से,
x = \(\frac{-b \pm 4 \sqrt{D}}{2 a}\)
= \(\frac{-(-4 \sqrt{3}) \pm \sqrt{0}}{2 \times 3}=\frac{4 \sqrt{3}}{6}\)
= \(\frac{2 \sqrt{3}}{3} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{2 \times 3}{3 \times \sqrt{3}}=\frac{2}{\sqrt{3}}\)
अतः द्विघात समीकरण के मूल \(\frac{2}{\sqrt{3}}\) और \(\frac{2}{\sqrt{3}}\)

(iii) दिया गया द्विघात समीकरण है : 2x² – 6x + 3 = 0 है।
इसकी तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
∴ विविक्तकर (D) = b² – 4ac
a = 2, b = – 6, c =3
= (- 6)² – 4 × 2 × 3
= 36 – 24 = 12 > 0
∴ दी गई द्विघात समीकरण के मूल वास्तविक और भिन्न-भिन्न होंगे।
अब श्रीधराचार्य सूत्र से समीकरण के मूल

प्रश्न 2.
निम्न प्रत्येक द्विघात समीकरण में k का ऐसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों :
(i) 2x² + kx + 3 = 0
(ii) kx(x – 2) + 6 = 0
हल:
(i) दिया गया समीकरण है:
2x² +kx +3 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = k तथा c = 3
विविक्तकर D = b² – 4ac
= k² – 4 × 2 × 3
= k² – 24
समीकरण के मूल बराबर तब होंगे, जब विविक्तकर
D = 0 हो
अर्थात् k² – 24 = 0
⇒ k² = 24
⇒ k = ±\(\sqrt{24}\) = ±2\(\sqrt{6}\)
अतः मूल बराबर होने के लिए ±2\(\sqrt{6}\) होना चाहिए।

(ii) दिया गया समीकरण
kx(x – 2) + 6 = 0
या kx² – 2kx + 6 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = k, b = -2k तथा c = 6
विविक्तकर D =b² – 4ac
= (-2k)² – 4 × k × 6
= 4k² – 24k
= 4k(k – 6)
समीकरण के मूल बराबर तब होंगे, जब विविक्तकर
D = 0 हो
अर्थात् 4k(k – 6) = 0
⇒ k = 0 या k – 6 = 0
⇒ k = 0 या k = 6
अतः समीकरण के बराबर होने के लिए k = 6 होना चाहिए क्योंकि k = 0 प्रतिबन्धित होता है।

प्रश्न 3.
क्या एक ऐसी आम की बगिया बनाना सम्भव है जिसकी लम्बाई, चौड़ाई से दुगनी हो और उसका क्षेत्रफल 800 मी’ हो ? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल:
माना कि एक आयताकार बगिया की चौड़ाई = x मी
आयताकार बगिया की लम्बाई = 2x मी
आयताकार बगिया का क्षेत्रफल = लम्बाई × चौड़ाई
= [2x × x] मी²
= 2x² मी²
प्रश्नानुसार, 2x² = 800
⇒ x² = \(\frac{800}{2}\) = 400
⇒ x = ±\(\sqrt{400}\)
⇒ x = ±20
∵ आयताकार बगिया की लम्बाई ऋणात्मक नहीं हो सकती इसलिए हम x = – 20 को छोड़ देते हैं।
∴ x = 20
∴ आयताकार बगिया की चौड़ाई = 20 मी
और आयताकार बगिया की लम्बाई = (2 × 20) मी
= 40 मी

प्रश्न 4.
क्या निम्न स्थिति सम्भव है ? यदि है, तो उनकी वर्तमान आयु ज्ञात कीजिए। दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पूर्व उनकी आयु (वर्षो में) का गुणनफल 48 था।
हल:
माना कि पहले मित्र की आयु = x वर्ष
∵ दोनों की आयु का योग 20 वर्ष है।
दूसरे मित्र की आयु = (20 – x) वर्ष
चार वर्ष पूर्व,
पहले मित्र की आयु = (x – 4) वर्ष
दूसरे मित्र की आयु = (20 – x – 4) वर्ष
= (16 – x) वर्ष
और उनका गुणनफल = (x – 4) (16 – x)
= 16x – x² – 64 + 4x
= – x + 20x – 64
प्रश्नानुसार,
-x² + 20x – 64 = 48
⇒ -x² + 20x – 64 – 48 = 0
⇒ -x² + 20x – 112 = 0 …..(1)
इसकी मानक समीकरण ax² + bx + c = 0 से तुलना करने पर,
a = -1, b = 20, c = -112
∴ विविक्तकर (D) = b² – 4ac
= (20)² – 4 × (1) × (-112)
=400 – 448 = -48 < 0
∵ मूल वास्तविक नहीं होंगे।
इसलिए x का कोई भी मान द्विघात समीकरण (1) को सन्तुष्ट नहीं कर सकता है।
अतः दी गई स्थिति सम्भव नहीं है।

प्रश्न 5.
क्या परिमाप 80 मी तथा क्षेत्रफल 400 मी² के एक पार्क को बनाना सम्भव है? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल:
माना आयताकार पार्क की लम्बाई = x मी
एवं चौड़ाई = y मी
∴ आयताकार पार्क का परिमाप = 2(x + y) मी
और आयताकार पार्क का क्षेत्रफल = xy मी²
प्रश्न की प्रथम शर्त के अनुसार,
2 (x + y) = 80
⇒ x + y = \(\frac{80}{2}\)
⇒ x + y = 40
⇒ y = 40 – x …..(1)
प्रश्न की दूसरी शर्त के अनुसार,
xy = 400
समीकरण (1) से y का मान रखने पर,
x(40 – x) = 400
⇒ 40x – x² = 400
⇒ x² – 40x + 400 = 0
इसकी तुलना मानक समीकरण ax² + bx + c = 0 से करने पर,
a = 1, b = – 40, c = 400
विविक्तकर (D) = b² – 4ac
= (-40)² – 4 × 1 × 400
= 1600 – 1600 = 0
अतः इस द्विघात समीकरण के मूल वास्तविक और बराबर होंगे।
अब श्रीधराचार्य सूत्र से, x = \(\frac{1}{2}\)
= \(\frac{1}{2}\)
∴ x = 20 मी
तथा y = 40 मी – 20 मी = 20 मी
∴ आयताकार पार्क की लम्बाई और चौड़ाई की माप बराबर अर्थात् 20 मीटर है।
अतः दिया गया आयताकार पार्क का अस्तित्व सम्भव है और यह एक वर्ग है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.1

प्रश्न 1.
कोष्ठकों में दिए गए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिए:
(i) सभी वृत्त ……… होते हैं। (सर्वांगसम, समरूप)
(ii) सभी वर्ग ………. होते हैं। (समरूप, सर्वांगसम)
(iii) सभी……… त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (a) उनके संगत कोण ………….. हों तथा (b) उनकी संगत भुजाएँ ………. हों । (बराबर, समानुपाती)
हल:
(i) समरूप,
(ii) समरूप,
(iii) समबाहु,
(iv) (a) बराबर (b) समानुपाती।

प्रश्न 2.
निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ।
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।
हल:
(i) 1. समबाहु त्रिभुजों का युग्म समरूप आकृतियाँ हैं।
2. वर्गों का युग्म समरूप आकृतियाँ हैं।

(ii) 1. एक त्रिभुज और एक चतुर्भुज ऐसी आकृतियों का युग्म बनाती हैं जो समरूप नहीं हैं।
2. एक वर्ग और एक समचतुर्भुज ऐसी आकृतियों का युग्म बनाती हैं जो समरूप नहीं हैं।

प्रश्न 3.
बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं :

हल:
दोनों चतुर्भुज समरूप हैं क्योंकि उनके संगत कोण बराबर हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Exercise 4.1

प्रश्न 1.
जाँच कीजिए कि क्या निम्न द्विघात समीकरण है:
(i) (x + 1)² = 2(x – 3 )
(ii) x² – 2x = (-2) (3 – x)
(iii) (x – 2) (x + 1) = (x – 1) (x + 3)
(iv) (x – 3) (2x + 1) = x (x + 5)
(v) (2x – 1) (x – 3) = (x + 5)
(vi) x² + 3x + 1 = (x – 2)²
(vii) (x + 2)³ = 2x(x² – 1)
(viii) x³ – 4x² – x + 1 = (x – 2)³
हल:
(i) दिया गया समीकरण है:
(x + 1)² = 2(x – 3)
[सूत्र (a + b)² = a² + 2ab + b² से]
⇒ x² + 2x + 1 = 2x – 6
⇒ x² + 2x + 1 – 2x + 6 = 0
⇒ x² + 7 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

(ii) दिया गया समीकरण है:
x² – 2x = (- 2) (3 – x)
⇒ x² – 2x = – 6 + 2x
⇒ x² – 2x – 2x + 6 = 0
⇒ x² – 4x + 6 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

(iii) दिया गया समीकरण
(x – 2) (x + 1) = (x – 1) (x + 3)
⇒ x(x + 1) – 2 (x + 1) = x (x + 3) – 1 (x + 3)
⇒ x² + x – 2x – 2 = x² + 3x – x – 3
⇒ x² + x – 2x – 2 – x² – 3x + x + 3 = 0
⇒ 3x + 1 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 1 है।
अतः समीकरण, द्विघात समीकरण नहीं है।

(iv) दिया गया समीकरण
(x – 3) (2x + 1) = x(x + 5)
⇒ 2x² + x – 6x – 3 = x² + 5x
⇒ 2x² – 5x – 3 – x² – 5x = 0
⇒ x² – 10x – 3 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः समीकरण द्विघात समीकरण है।

(v) दिया गया समीकरण
(2x – 1) (x – 3) = (x + 5) (x – 1)
2x² – 6x – x + 3 = x² – x + 5x – 5
2x² – 7x + 3 = x² + 4x – 5
2x² – 7x + 3 – x² – 4x + 5 = 0
x² – 11x + 8 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

(vi) दिया गया समीकरण
x² + 3x + = (x – 2)²
⇒ x² + 3x + 1 = x² + 4 – 4x
⇒ x² + 3x + 1 – x² – 4 + 4x = 0
⇒ 7x – 3 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 1 है।
अतः दिया गया समीकरण द्विघात समीकरण नहीं है।

(vii) दिया गया समीकरण
(x + 2)³ = 2x(x² – 1)
⇒ x³ + (2)³ + 3 × x × 2 (x + 2) = 2x³ – 2x
⇒ x³ + 8 + 6x² + 12x = 2x³ – 2x = 0
⇒ x³ + 8 + 6x² + 12x – 2x³ + 2x = 0
⇒ -x³ + 6x² + 14x + 8 = 0
∵ यहाँ x की उच्चतम घात 3 है।
अतः यह एक द्विघात समीकरण नहीं है।

(viii) दिया गया समीकरण
x³ – 4x² – x + 1 = (x – 2)³
⇒ x³ – 4x² – x + 1 = x³ – (2)³ – 3 × x × 2 (x – 2)
⇒ x³ – 4x² – x + 1 = x³ – 8 – 6x² + 12x = 0
⇒ x³ – 4x² – x + 1 – x³ + 8 + 6x² – 12x = 0
⇒ 2x² – 13x + 9 = 0
∵ उक्त समीकरण में चर x की अधिकतम घात 2 है।
अतः दिया गया समीकरण द्विघात समीकरण है।

प्रश्न 2.
निम्नलिखित स्थितियों को द्विघात समीकरणों के रूप में निरूपित कीजिए :
(i) एक आयताकार भूखण्ड का क्षेत्रफल 528 मीटर 2 है। क्षेत्र की लम्बाई (मीटरों में) चौड़ाई के दुगने से एक अधिक है। हमें भूखण्ड की लम्बाई और चौड़ाई ज्ञात करनी हैं।
(ii) दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 306 है। हमें पूर्णांकों को ज्ञात करना है।
(iii) रोहन की माँ उससे 26 वर्ष बड़ी है। उनकी आयु (वर्षो में) का गुणनफल अब से तीन वर्ष पश्चात् 360 हो जाएगा। हमें रोहन की वर्तमान आयु ज्ञात करनी है।
(iv) एक रेलगाड़ी 480 किमी की दूरी समान चाल से तय करती है। यदि इसकी चाल 8 किमी/घण्टा कम होती, तो वह उसी दूरी को तय करने में 3 घण्टे अधिक लेती। हमें रेलगाड़ी की चाल ज्ञात करनी है।
हल:
(i) माना भूखण्ड की चौड़ाई x मीटर है।
∵ भूखण्ड की लम्बाई, उसकी चौड़ाई के दुगुने से 1 मीटर अधिक है।
∴ भूखण्ड की लम्बाई = (2 × चौड़ाई) + 1
= (2 × x + 1)
= (2x + 1) मीटर
∵ आयताकार भूखण्ड का क्षेत्रफल = ल. × चौ.
= (2x + 1) × x
= (2x² + x) वर्ग मीटर
दिया है भूखण्ड का क्षेत्रफल = 528 वर्ग मीटर
∴ 2x² + x = 528
या 2x² + x – 528 = 0
अतः अभीष्ट द्विघात समीकरण :
2x² + x – 528 = 0

(ii) माना पहला धन पूर्णांक है तथा दूसरा क्रमागत धन पूर्णांक x + 1 है,
∴ पूर्णांकों का गुणनफल = x × (x + 1) = x² + x
प्रश्नानुसार, x² + x = 306
x² + x – 306 = 0
अतः अभीष्ट द्विघात समीकरण:
x² + x – 306 = 0

(iii) माना रोहन की वर्तमान आयु = x वर्ष तथा उसकी माँ उससे 26 वर्ष बड़ी है।
∴ रोहन की माँ की वर्तमान आयु = (x + 26) वर्ष
तीन वर्ष बाद रोहन की आयु = (x + 3) वर्ष
तथा तीन वर्ष बाद रोहन की माँ की आयु = (x + 26) + 3 = (x + 29) वर्ष
∴ रोहन और उसकी माँ की आयु का गुणनफल = (x + 3) (x + 29 ) वर्ष
प्रश्नानुसार,
⇒ (x + 3) (x + 29) = 360
⇒ x² + 29x + 3x + 87 = 360
⇒ x² + 32x + 87 – 360 = 0
⇒ x² + 32x – 273 = 0
अतः अभीष्ट द्विघात समीकरण :
x² + 32x – 273 = 0

(iv) माना रेलगाड़ी की चाल x किमी/घण्टा है।
निर्धारित दूरी = 480 किमी
रेलगाड़ी द्वारा लिया गया समय

यदि रेलगाड़ी की चाल 8 किमी / घण्टा कम हो अर्थात् चाल (x – 8) किमी / घण्टा होती तो रेलगाड़ी द्वारा 480 किमी दूरी चलने में लगा समय

⇒ 3x² – 24x = 3840
⇒ 3x² – 24x – 3840 = 0
⇒ 3(x² – 8x – 1280) = 0
⇒ x² – 8x – 1280 = 0
अतः अभीष्ट द्विघात समीकरण : x² – 8x – 1280 = 0

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.4

प्रश्न 1.
A. P. 121, 117, 113, का कौन-सा पद सबसे पहला ऋणात्मक पद होगा ?
हल:
दी गई A. P. है : 121 117, 113, …
प्रथम पद a = a₁ = 121; a₂ = 117; a₃ = 113
सार्वन्तर d = a₂ – a₁ = 117 – 121 = – 4
सूत्र a_n = a + (n – 1)d का प्रयोग करने पर,
⇒ a_n = 121 + (n – 1 ) (- 4)
= 121 – 4n + 4
= 125 – 4n
प्रश्नानुसार,
a_n < 0
⇒ 125 – 4n < 0
⇒ 4n > 125
⇒ n > \(\frac{125}{4}\)
⇒ n > 31\(\frac{1}{4}\)
⇒ n > 31.25
⇒ n < 32
क्योंकि n एक पूर्णांक है।
अत: 32वाँ पद पहला ऋणात्मक पद होगा।

प्रश्न 2.
किसी AP के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है। इस A. P. के प्रथम 16 पदों का योग ज्ञात कीजिए।
हल:
माना दी गई A.P का प्रथम पद a तथा सार्वअन्तर d है।
तीसरा पद a₃ = a + (3 – 1)d = a + 2d
सातवाँ पद a₇ = a + (7 – 1)d = a + 6d
प्रश्नानुसार,
तीसरे और सातवें पदों का योग = 6
या a₃ + a₇ = 6
⇒ a + 2d + a + 6d = 6
⇒ 2a + 8d = 6
⇒ a + 4d = 3 …(1)
पुन: प्रश्नानुसार, a₃ × a₇ = 8
⇒ (a + 2d)(a + 6d) = 8
⇒ a² + 8ad + 12d² = 8 …(2)
समीकरण (1) के वर्ग में से समीकरण (2) को घटाने पर,
(a + 4d)² – (a² + 8ad + 12d²) = (3)² – 8
⇒ a² + 8ad + 16d² – a² – 8ad – 12d² = 9 – 8
4d² = 1
∴ d = ±\(\frac{1}{2}\)
तव a + 4d = 3 में d = \(\frac{1}{2}\) रखने पर,
a + 4 × \(\frac{1}{2}\) = 2
⇒ a + 2 = 3
∴ a = 1
पुन: a + 4d = 3 में d = –\(\frac{1}{2}\) रखने पर,
a + 4 × (-\(\frac{1}{2}\)) = 3
⇒ a – 2 = 3
∴ a = 5

स्थिति I. a = 1, d = \(\frac{1}{2}\)
प्रथम 16 पदों का योग
S₁₆ = \(\frac{16}{2}\) [2a + (16 – 1)d]
= 8[2 + 15 × \(\frac{1}{2}\)]
= 8 × \(\frac{19}{2}\) = 4 × 19 = 76
अतः 16 पदों का योग = 76

स्थिति II. a = 5, d = –\(\frac{1}{2}\)
∴ प्रथम 16 पदों का योग

अतः 16 पर्दों का योगफल = 20.

प्रश्न 3.
एक सीणी के क्रमागत डण्डे परस्पर 25 सेमी की दूरी पर हैं (देखिए आकृति)। डण्डों की लम्बाई एकसमान रूप से घटती जाती है तथा सबसे निचले डंडे की लम्बाई 45 सेमी है और सबसे ऊपर वाले डण्डे की लम्बाई 25 सेमी है। यदि ऊपरी और निचले डण्डे के बीच की दूरी 2\(\frac{1}{2}\) मीटर है, तो डण्डों को बनाने के लिए लकड़ी की कितनी लम्बाई की आवश्यकता होगी ?

हल:
प्रथम व अन्तिम डण्डे के बीच की दूरी
= 2\(\frac{1}{2}\) मीटर = 250 सेमी
और दो क्रमागत डण्डों के बीच की दूरी = 25 सेमी
∴ सीणी में डण्डों की संख्या

∵ प्रथम डण्डे की लम्बाई (a) = 25 सेमी और अन्तिम डण्डे की लम्बाई (l) = 45 सेमी
∴ 11 डण्डों में प्रयुक्त लकड़ी की कुल माप
= 2\(\frac{1}{2}\)(a + l) = \(\frac{1}{2}\)(25 + 4)
\(\frac{11}{2}\) × 70 = 11 × 35
= 385 सेमी = 3.85 मीटर
अतः सीणी के डण्डों में प्रयुक्त लकड़ी की लम्बाई = 385 सेमी या 3.85 मीटर।

प्रश्न 4.
एक पंक्ति के मकानों को क्रमागत रूप से संख्या 1 से 49 तक अंकित किया गया है। दर्शाइए कि x का एक ऐसा मान है किx से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। x का मान ज्ञात कीजिए।
हल:
मकानों पर क्रमागत रूप से अंकित संख्याएँ :
1, 2, 3, 4, 5, 6, …… 47, 48, 49 है।
x एक ऐसी संख्या है कि x के एक ओर की संख्याओं का योग = x के दूसरी ओर की संख्याओं का योग
अर्थात् 1 से x – 1 तक की संख्याओं का योग
= x + 1 से 49 तक की संख्याओं का योग
अनुक्रम की सभी संख्याओं में सार्वअन्तर d = 1 है।
तब से x – 1 तक की संख्याओं का योग, a = 1, n = x – 1

और x + 1 से 49 तक की संख्याओं का योग
= S₄₉ – S_x
(∵ S_x+1 नहीं होगा क्योंकि x के बाद ही x + 1 प्रारम्भ होगा)

अतः x का मान 35 है।

प्रश्न 5.
एक फुटबाल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीणियाँ बनी हुई हैं। इन सीणियों में से प्रत्येक की लम्बाई 50 मीटर है और वह ठोस कंक्रीट (concrete) की बनी हैं। प्रत्येक सीणी में \(\frac{1}{4}\) मीटर की बनाई है और \(\frac{1}{2}\) मीटर का फैलाव (चौड़ाई) है। (देखिए आकृति)। इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।

हल:
प्रत्येक सौणी की लम्बाई 50 मीटर और चौड़ाई \(\frac{1}{2}\) मीटर है सीणियों की संख्या 15 है। प्रत्येक सीणी की जमीन से ऊँचाई एक समान्तर श्रेढी (A.P.) का अनुक्रम है-
\(\frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}, \frac{5}{4}, \frac{6}{4}, \ldots, \frac{15}{4}\)
अतः पहली सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{1}{4}=\frac{50}{8}\) घन मीटर
दूसरी सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{2}{4}=\frac{100}{8}\) घन मीटर
तीसरी सीणी में लगी कंक्रीट का आयतन
\(=50 \times \frac{1}{2} \times \frac{3}{4}=\frac{150}{8}\) घन मीटर
चौथी सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{4}{4}=\frac{200}{8}\) घन मीटर
अतः चबूतरा बनाने में लगे कंक्रीट का कुल आयतन

अतः चबूतरे में लगी कंक्रीट का कुल आयतन = 750 घन मीटर

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.2

प्रश्न 1.
निम्नलिखित सारणी में रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a सार्वअन्तर d और nवाँ पद a_n है-

हल:
(i) a = 7, d = 3, n = 8
∵ a_n = a + (n – 1)d
∴ a₈ = 7 + (8 – 1)3
= 7 + 21 = 28
अत: a₈ = 28

(ii) a = – 18, a = 10, a_n = 0
∵ a_n = a + (n – 1)d
∴ a₁₀ = -18 + (10 – 1)d
⇒ 0 = -18 + 9d
⇒ 9d = 18
∴ d = \(\frac{18}{9}\) = 2
अत: d = 2

(iii) d = -3, n = 18, a_n = -5
∵ a_n = a + (n – 1)d
∴ a₁₈ = a + (18 – 1) (-3)
⇒ -5 = a – 51
∴ a = – 5 + 51 = 46

(iv) a = – 18.9, d = 2.5, a_n = 3.6
∵ a_n = a + (n – 1)d
∴ 3.6 = -18.9 + (n – 1) 2.5
⇒ 3.6 + 18.9 = (n – 1) 2.5
⇒ (n – 1)2.5 = 22.5
⇒ n – 1 = \(\frac{22.5}{2.5}\) = 9
∴ n = 9 + 1 = 10

(v) a = 3.5, d = 0, n = 105
∵ a_n = a + (n – 1)d
∴ a_n = 43.5 + (105 – 1)0
a_n = 3.5 + 0 = 3.5

प्रश्न 2.
निम्नलिखित में सही उत्तर चुनिए और उसका औचित्य दीजिए-
(i) A.P. : 10, 7, 4, … का 30वीं पद है-
(A) 97 (B) 77 (C) – 77 (D) – 87
(ii) A.P. : -3, –\(\frac{1}{2}\), 2, … का 11वाँ पद है-
(A) 28 (B) 22 (C) -38 (D) -48\(\frac{1}{2}\)
हल:
(i) A.P. : 10, 7, 4, … का 30वाँ पद
यहाँ a = 10, d = 7 – 10 = -3 तथा n = 30
∵ a_n = a + (n – 1)d
∴ a₃₀ = 10 + (30 – 1) × -3
= 10 + 29 × -3 = 10 – 87 = -77
अतः विकल्प (C) सही है।

(ii) A.P.: -3, –\(\frac{1}{2}\), 2, … का 11वाँ पद
यहाँ a = – 3, d = –\(\frac{1}{2}\) – (-3) = –\(\frac{1}{2}\) + 3 = \(\frac{5}{2}\)
n = 11
a_n = a + (n – 1)d
a₁₁ = -3 + (11 – 1) × \(\frac{5}{2}\)
= – 3 + 10 × \(\frac{5}{2}\)
= -3 + 25 = 22
अतः विकल्प (B) सही है।

प्रश्न 3.
निम्नलिखित समान्तर श्रेढियों में रिक्त खानों (boxes) के पदों को ज्ञात कीजिए :

हल:
(i) पहला पद a = 2 तीसरा पद a₃ = 26,
दूसरा पद a₂ = ?
माना सार्वअन्तर है।
अब a₃ = a + 2d
⇒ 26 = 2 + 2d
⇒ 2d = 26 – 2 = 24
⇒ d = 12
∴ दूसरा पद a₂ = a + d = 2 + 12 = 14
अतः रिक्त बॉक्स का पद a₂ = 14

(ii) पहला पद a = ?, दूसरा पद a₂ = 13, तीसरा पद a₃ = ?, चौथा पद d₄ = 3
माना सार्वअन्तर d है a₂ = a + d
⇒ 13 = a + d …(1)
तथा a₄ = a + 3d
⇒ 3 = a + 3d …(2)
समीकरण (2) में से (1) को घटाने पर,
2d = – 10 ⇒ d = -5
समीकरण (1) से, 13 = a + d
⇒ 13 = a – 5 ⇒ a = 18
∴ तीसरा पद a₃ = a + 2d
= 18 + 2 × (-5)
⇒ a₃ = 8
अतः रिक्त बॉक्सों के पद क्रमश: 18 व 8 हैं।

(iii) पहला पद a = 5, चौथा पद a₄ = 9\(\frac{1}{2}\), दूसरा पद a₂ = ? तीसरा पद a₃ = ?
माना सार्वअन्तर d है।

अतः रिक्त बाक्सों के पद क्रमशः 6\(\frac{1}{2}\) और 8 हैं।

∵ पहला पद a = -4 और माना सार्वअन्तर d है।
6वाँ पद = a + (6 – 1)d
= a + 5d
∵ a + 5d = 6
⇒ – 4 + 5d = 6
⇒ 5d = 6 + 4 = 10
⇒ 5d = 10
∴ d = \(\frac{10}{5}\) = 2
तब दूसरा पद a₂ = a + d = – 4 + 2 = – 2
तीसरा पद a₃ = a₂ + d = – 2 + 2 = 0
चौथा पद a₄ = a₃ + d = 0 + 2 = 2
पाँचवाँ पद a₅ = a₄ + d = 2 + 2 = 4

माना पहला पद a और सार्वअन्तर d है।
दूसरा पद = a + d = 38 …(i)
और छठवाँ पद = a + (6 – 1)d
⇒ a + 5d = -22 …(ii)
समीकरण (ii) में से (i) को घटाने पर,
(a + 5d) – (a + d) = – 22 – 38
⇒ 5d – d = 60
⇒ 4d = 60
∴ d = \(\frac{-60}{4}\) = -15
∴ समीकरण (i) से,
a + d = 38
⇒ a + (-15) = 38
∴ a = 38 + 15 = 53
तब पहला पद a₁ = 53
तीसरा पद a₃ = a₂ + d = 38 – 15 = 23
चौथा पद a₄ = a₃ + d = 23 – 15 = 8
पाँचवाँ पद a₅ = a₄ + d = 8 – 15 = – 7
अतः रिक्त बॉक्सों में क्रमिक प्रविष्टियाँ

प्रश्न 4.
A.P. 3, 8, 13, 18, … का कौन-सा पद 78 है ?
हल:
दी गई A. P. : 3, 8, 13, 18, ….
यहाँ a = 3
d = 8 – 3 = 5
माना पद 78 है।
∴ a_n = 78
∵ a_n = a + (n – 1)d
⇒ 78 = 3+ (n – 1)5
⇒ 78 = 3 + 5n – 5
⇒ 78 = 5n – 2
⇒ 5n = 78 – 2
⇒ 5n = 80
∴ n = \(\frac{80}{5}\) = 16
अतः 16वाँ पद 78 है।

प्रश्न 5.
निम्नलिखित समान्तर श्रेढियों में से प्रत्येक श्रेठी में कितने पद हैं ?
(i) 7, 13, 19, …., 205
(ii) 18, 15, 13, …., -47
हल:
(i) दी गई समान्तर श्रेढी (A.P.) : 7, 13, 19, ….., 205
यहाँ a = 7 तथा d = 13 – 7 = 6
माना दी गई A. P. में n पद हैं
nवाँ पद a_n = 205
a_n = 205
⇒ a + (n – 1)d = 205
⇒ 7 + (n – 1)6 = 205
⇒ 7 + 6n – 6 = 205
⇒ 1 + 6n = 205
⇒ 6n = 205 – 1 = 204
∴ n = \(\frac{204}{6}\) = 34
अतः दी गई A. P. में 34 पद हैं।

(ii) दी गई समान्तर श्रेढी (A.P.):
18, 15\(\frac{1}{2}\), 13, …, – 47
यहाँ पहला पद a = 18
तथा सार्वअन्तर d = 15\(\frac{1}{2}\) – 18
= \(\frac{31}{2}-18=\frac{31-36}{2}\)
= \(-\frac{5}{2}\)
माना दी गई श्रेढी में पद हैं।
n पद a_n = -47
a + (n – 1)d = -47
⇒ 18 + (n – 1) × \(\left(-\frac{5}{2}\right)\) = -47
\(-\frac{5(n-1)}{2}\) = -47 – 18 = -65
(n – 1) \(\frac{(-65) \times 2}{-5}\) = 26
n = 26 + 1 = 27
अतः दी गई श्रेढी (A.P.) में 27 पद हैं।

प्रश्न 6.
क्या A.P. : 11, 8, 5, 2… का एक पद -150 है ? क्यों ?
हल:
दी गई A. P. : 11, 8, 5, 2 …
यहाँ पहला पद a = 11 तथा सार्वअन्तर d = 8 – 11
= -3
माना nवाँ पद (a_n) = -150 है।
⇒ a_n = -150
⇒ a + (n – 1)d = -150
⇒ 11 + (n – 1) × (-3) = -150
⇒ -3(n – 1) = -150 – 11 = -161
⇒ (n – 1) = \(\frac{-161}{-3}\)
= 53.6 (लगभग)
∴ n = 53.6 + 1 = 54.6
⇒ n का मान एक पूर्ण संख्या नहीं है।
अतः दी गई A.P का कोई पद -150 नहीं है।

प्रश्न 7.
उस A. P. का 31वाँ पद ज्ञात कीजिए, जिसका 11वाँ पद 38 है और 16वाँ पद 73 है।
हल:
माना A.P का प्रथम पद a तथा सार्वअन्तर d है।
तब 11वाँ पद a₁₁ = 38
a + (11 – 1)d = 38
a + 10d = 38 …(i)
और 16वाँ पद a₁₆ = 73
⇒ a + (16 – 1)d = 73
⇒ a + 15d = 73 …(ii)
समीकरण (ii) में से (i) को घटाने पर,
(a + 15d) – (a + 10d) = 73 – 383
⇒ a + 15d – a – 10d = 35
⇒ 5d = 35
∴ d = \(\frac{35}{5}\) = 7
समीकरण (i) में d का मान रखने पर,
⇒ a + 10 × 7 = 38
⇒ a + 70 = 38
∴ a = 38 – 70 = -32
श्रेढी का 31वाँ पद
a₃₁ = a + (31 – 1)d
= – 32 + 30 × 7
= – 32 + 210 = 178
अत: A.P का 31वाँ पद = 178

प्रश्न 8.
एक A.P में 50 पद हैं, जिसका तीसरा पद 12 है और अन्तिम पद 106 है। इसका 29वाँ पद ज्ञात कीजिए।
हल:
माना कि A.P का प्रथम पद ‘a’ और सार्वअन्तर ‘d’ है। दिया है कि,
तीसरा पद a₃ = 12
a + (3 – 1)d = 12 [∵ a_n = a + (n – 1)d]
⇒ a + 2d = 12 ….(1)
और अन्तिम पद = a50 = 106
a + (50 – 1)d = 106
⇒ a + 49d = 106 …(2)
समीकरण (2) में से (1) को घटाने पर,

d का यह मान समीकरण (1) में प्रतिस्थापित करने पर,
a + 2 × 2 = 12
⇒ a + 4 = 12
∴ a = 12 – 4 = 8
अब श्रेढी का 29वीं पद
a₂₉ = a + (29 – 1)d
= 8 + 28 × 2 = 8 + 56 = 64
अत: A.P का 29वाँ पद = 64

प्रश्न 9.
यदि किसी A. P. के तीसरे और नौवें पद क्रमशः 4 और -8 हैं, तो इसका कौन-सा पद शून्य होगा ?
हल:
माना कि A.P का प्रथम पद ‘a’ और सार्वअन्तर ‘d’ है।
दिया है, तीसरा पद a₃ = 4
a + (3 – 1)d = 4 [a_n = a + (n – 1)d से]
⇒ a + 2d = 4 ….(1)
और a₉ = – 8
a + (9 – 1)d = -8
a + 8d = -8 ….(2)
समीकरण (2) मैं से (1) को घटाने पर,

d का यह मान समीकरण (1) में प्रतिस्थापित करने पर,
a + 2 (-2) = 4
या a – 4 = 4
∴ a = 4 + 4 = 8
अब माना कि श्रेढी का व पद शून्य होगा, तब
nवाँ पद a_n = 0
∴ a + (n – 1)d = 0
⇒ 8 + (n – 1) × (-2) = 0
⇒ – 2 (n – 1) = – 8
⇒ (n – 1) = 4
∴ n = 5
अत: दी गई A. P. का 5वाँ पद शून्य होगा।

प्रश्न 10.
किसी A.P. का 17वाँ पद उसके 10वें पद से 7 अधिक है। इसका सार्वअन्तर ज्ञात कीजिए।
हल:
माना A.P. का प्रथम पद a तथा सार्वअन्तर d है।
तब 17वाँ पद a₁₇ = a + (17 – 1)d
= a + 16d
10वाँ पद a₁₀ = a + (10 – 1)d
= a + 9d
∵17वाँ पद, 10 वें पद से 7 अधिक है।
a₁₇ – a₁₀ = 7
⇒ (a + 16d) – (a + 9d) = 7
⇒ 7d = 7
∴ d = 1
अतः श्रेढी का सार्वअन्तर = 1

प्रश्न 11.
A. P. : 3, 15, 27, 39, … का कौन-सा पद उसके 54वें पद से 132 अधिक होगा ?
हल:
माना अभीष्ट पद व पद है।
दी गई A. P.: 3, 15, 27, 39, …
प्रथम पद a = 3 तथा सार्वअन्तर d = 15 – 3 = 12
तब श्रेढी का 54वाँ पद a₅₄ = a + (54 – 1)d
= 3 + 53 × 12
=3 + 636 = 639
⇒ nवाँ पद = 54वें पद से 132 अधिक
= 639 + 132 = 771
nवाँ पद a_n = 771
⇒ a + (n – 1)d = 771
⇒ 3 + (n – 1) 12 = 771
⇒ (n – 1)12 = 771 – 3 = 768
n – 1 = \(\frac{768}{12}\) = 64
∴ n = 64 + 1 = 65
अतः श्रेढी का 65वाँ पद 54वें पद से 132 अधिक है।

प्रश्न 12.
दो समान्तर श्रेडियों का सार्वअन्तर समान है। यदि इनके 100वें पदों का अन्तर 100 है, तो इनके 1000 वें पदों का अन्तर क्या होगा ?
हल:
माना पहली A.P का प्रथम पद तथा सार्वअन्तर d है और दूसरी A. P. का प्रथम पद 4 तथा सार्वअन्तर है क्योंकि सार्वअन्तर समान हैं।
पहली श्रेढी का 100वाँ पद = a + (100 – 1)d
= a + 99d
दूसरी श्री का 100वाँ पद = A + (100 – 1) d
= A + 99d
∴ दोनों श्रेढियों के 100वें पदों का अन्तर = (A + 99d) – (a + 99d)
= A – a
प्रश्नानुसार, A – a = 100 …(1)
पहली श्रेढी का 1000वाँ पद = a +(1000 – 1)d = a + 999d
दूसरी श्रेढी का 1000वाँ पद = A + (1000 – 1)d = A + 999d
∴ दोनों श्रेढियों के 1000 वें पदों का अन्तर = (A + 999d) – (a + 999d) = A – a
∴ दोनों श्रेढियों के 1000वें पदों का अन्तर A – a = 100 (समी. 1 से)
अतः 1000वें पदों का अन्तर = 100

प्रश्न 13.
तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं ?
हल:
तीन अंकों की संख्याओं की सूची 100, 101, 102, ….., 999,
3 अंकों की 7 से विभाज्य प्रथम संख्या = 105 और अन्तिम संख्या = 994
तब 7 से विभाज्य 3 अंकीय संख्याओं की सूची-
105, (105 + 7), (105 + 7 + 7),… 994 = 105, 112, 119, …, 994
माना ऐसी कुल संख्याएँ n हैं।
प्रथम संख्या a = 105, सार्वअन्तर d = 7,
∴ nवाँ पद a_n = 994
⇒ a + (n – 1)d = 994
⇒ 105 + (n – 1) × 7 = 994
⇒ (n – 1) × 7 = 994 – 105 = 889
⇒ (n – 1) = \(\frac{889}{7}\) = 127
∴ n = 127 + 1 = 128
अतः 7 से विभाव्य तीन अंकों वाली संख्याएँ = 128

प्रश्न 14.
10 और 250 के बीच में 4 के कितने गुणज हैं ?
हल:
10 से बड़ा 4 का पहला गुणज = 12
250 से छोटा 4 का पहला गुणज = 248
∵ 10 और 250 के बीच 4 के गुणजों की श्रेढी निम्न होगी :
12, 16, 20, 24, ….., 248
माना गुणजों की संख्या n है।
पहला पद a = 12, सार्वअन्तर d = 16 – 12 = 4
तब nवाँ पद, a_n = 248
a + (n – 1)d = 248
12 + (n – 1)4 = 248
12 + 4n – 4 = 248
4n = 248 + 4 – 12= 240
n = \(\frac{240}{4}\) = 60
अतः 10 और 250 के बीच 4 के गुणजों की संख्या 60 है।

प्रश्न 15.
n के किस मान के लिए, दोनों समान्तर श्रेतियों 63, 65, 67,… और 3, 10, 17, … के वें पद बराबर होंगे ?
हल:
पहली समान्तर श्रेढी 63, 65, 67, ….
प्रथम पद a = 63, सार्वअन्तर d = 65 – 63 = 2
∴ श्रेढ़ी का nवाँ पद a_n = a + (n – 1)d
= 63 + (n – 1)2
= 63 + 2n – 2
= 61 + 2n
दूसरी समान्तर श्रेढी = 3, 10, 17, …..
प्रथम पद a’ = 3, सार्वअन्तर d’ = 10 – 3 = -7
इस श्रेढी का nवाँ पद a_n‘ = a’ + (n – 1)d’
= 3 + (n – 1)7
-= 3 + 7n – 7 = 7n – 4
प्रश्नानुसार,
पहली A.P का nवाँ पद = दूसरी A.P का nवाँ पद
⇒ 61 + 2n = 7n – 4
⇒ 2n – 7n = – 4 – 61
⇒ – 5n = -65
n = \(\frac{-65}{-5}\) = 13
अतः दोनों समान्तर श्रेढियों के 13वें पद बराबर होंगे।

प्रश्न 16.
वह A. P. ज्ञात कीजिए जिसका तीसरा पद 16 है और 7वाँ पद 5वें पद से 12 अधिक है।
हल:
माना कि A.P का प्रथम पद a और सार्वअन्तर d है।
दिया है a₃ = 16
a + (3 – 1)d = 16
⇒ a + 2d = 16 …(1)
प्रश्न के अनुसार, a₇ – a₅ = 12
[a + (7 – 1)d] – [a + (5 – 1) d] = 12
⇒ a + 6d – a – 4d = 12
⇒ 2d = 12
∴ d = \(\frac{12}{2}\) = 6
d का यह मानं समीकरण (1) में प्रतिस्थापित करने पर,
a + 2(6) = 16
∴ a = 16 – 12 = 4
A.P. = a, a + d, a + 2d,…
= 4, 4 + 6, 4 + 2 × 6,…
= 4, 10, 16,…
अतः वाँछित A. P. है, 4, 10, 16, 22….

प्रश्न 17.
A. P. : 3, 8, 13, …, 253 में अन्तिम पद से 20वाँ पद ज्ञात कीजिए।
हल:
दी गई A. P.: 3, 8, 13, …., 253
प्रथम पद a = 3
सार्वअन्तर d = 8 – 3 = 5
अन्तिम पद a_n = 253
समान्तर श्रेढी का nवाँ पद
an = a + (n – 1)d
253 = 3 + (n – 1) × 5
253 = 3 + 5n – 5
5n = 253 + 2
5n = 255
∴ n = \(\frac{255}{5}\) = 51
समान्तर श्रेढी के अन्तिम पद से 20वाँ पद
= (पदों की संख्या) – 20 + 1
= 51 – 20 + 1 = 32वाँ पद
∴ A.P के अन्तिम पद से 20वाँ पद = आरम्भ से 32वाँ पद
∵ a_n = a + (n – 1)d
a₃₂ = 3 + (32 – 1) × 5
= 3 + 31 × 5
= 3 + 155 = 158
अत: A.P के अन्तिम पद से 20वाँ पद = 158

द्वितीय विधि :
यहाँ प्रथम पद a = 3, सार्वअन्तर d = 8 – 3 = 5
अन्तिम पद a_n = 253
सूत्र: अन्त rवाँ पद = a_n – (r – 1)d
अन्त से 20वाँ पद = 253 – (20 – 1)5
= 253 – 19 × 5
= 253 – 95 = 158
अत: A. P. के अन्तिम पद से 20वाँ पद 158 है।

प्रश्न 18.
किसी A. P. के चौथे और 8वें पदों का योग 24 है तथा छठे और 10वें पदों का योग 44 है। इस A. P. के ‘प्रथम तीन पद ज्ञात कीजिए।
हल:
माना A.P का प्रथम पद a और सार्वअन्तर d है।
∵ चौथा पद a₄ + 8वाँ पद a₈ = 24
⇒ [a + (4 – 1)d] + [a + (8 – 1)d] = 24
⇒ a + 3d + a + 7d = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 …(1)
∵ 6वाँ पद a₆ + दसवाँ पद a₁₀ = 44
⇒ [a + (6 – 1)d] + [a + (10 – 1)d] = 44
⇒ a + 5d + a + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22 … (2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(a + 7d) – (a + 5d) = 22 – 12
⇒ a + 7d – a – 5d = 10
⇒ 2d = 10 ⇒ d = 5
d का मान समीकरण (1) में रखने पर,
a + 5 × 5 = 12
⇒ a + 25 = 12
∴ a = -13
अब श्रेढी का पहला पद a = -13
दूसरा पद a₂ = a + d = -13 + 5 = -8
तीसरा पद a₃ = a₂ + d = – 8 + 5= -3
अतः वांछित A.P. के प्रथम तीन पद = -13, – 8, -3

प्रश्न 19.
सुब्बाराव ने 1995 में ₹ 5000 के मासिक वेतन पर कार्य आरम्भ किया और प्रत्येक वर्ष ₹ 200 की वेतन वृद्धि प्राप्त की। किस वर्ष में उसका वेतन ₹ 7000 हो गया ?
हल:
पहले वर्ष में प्रारम्भिक वेतन = ₹ 5000 प्रति मास
दूसरे वर्ष में वेतन = ₹ 5000 + ₹ 200
= ₹ 5200 प्रति मास
तीसरे वर्ष में वेतन = ₹ 5200 + ₹ 200
= ₹ 5400 प्रति मास
इस प्रकार प्रत्येक वर्ष के वेतन (रु. में) 5000, 5200, 5400…… एक समान्तर श्रेढी बनाते हैं,
जिसका प्रथम पद a = 5000 तथा सार्वअन्तर d = 200
माना n वर्ष बाद वेतन ₹ 7000 होगा।
तब nवाँ पद = 7000
⇒ a + (n – 1)d = 7000
⇒ 5000 + (n – 1)200 = 7000
⇒ (n – 1) × 200 = 7000 – 5000
⇒ (n – 1) × 200 = 2000
⇒ (n – 1) = \(\frac{2000}{200}\) = 10
∴ n = 10 + 1 = 11
अतः 11 वें वर्ष में अर्थात 2006 में सुब्बाराव का वेतन ₹ 7000 होगा।

प्रश्न 20.
रामकली ने किसी वर्ष के प्रथम सप्ताह में ₹ 5 की बचत की और फिर अपनी साप्ताहिक बचत ₹ 1.75 बणाती गई। यदि वें सप्ताह में उसकी साप्ताहिक बचत ₹ 20.75 हो जाती है, तो n ज्ञात कीजिए।
हल:
माना प्रथम पद a तथा सार्वअन्तर d है
प्रथम सप्ताह की बचत = ₹ 5
प्रति सप्ताह बचत में वृद्धि = ₹ 1.75
यह स्पष्ट है कि यह एक A.P. है
प्रथम पद a = 5, d = 1.75
nवें सप्ताह में उसकी बचत a_n = 20.75
∵ a_n = a + (n – 1)d
⇒ 20.75 = 5 + (n – 1) × 1.75
⇒ 20.75 = 5 + 1.75n – 1.75
⇒ 1.75n = 20.75 – 5 + 1.75
⇒ 1.75n = 17.5
n = \(\frac{17.5}{1.75}\) ⇒ n = 0
अतः 10वें सप्ताह में रामकली की बचत ₹ 20.75

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.1

प्रश्न 1.
निम्नलिखित स्थितियों में से किन स्थितियों में सम्बद्ध संख्याओं की सूची A. P. है और क्यों ?
(i) प्रत्येक किलोमीटर के बाद का टैक्सी का किराया, जबकि प्रथम किलोमीटर के लिए किराया ₹ 15 है और प्रत्येक अतिरिक्त किलोमीटर के लिए किराया ₹ 8 है।
(ii) किसी बेलन (cylinder) में उपस्थित हवा की मात्रा, जबकि वायु निकालने वाला पम्प प्रत्येक बार बेलन की शेष हवा का \(\frac{1}{4}\) भाग बाहर निकाल देता है।
(iii) प्रत्येक मीटर की खुदाई के बाद, एक कुआँ खोदने में आई लागत, जबकि प्रथम मीटर खुदाई की लागत ₹ 150 है और बाद में प्रत्येक मीटर खुदाई की लागत ₹ 50 बणती जाती है।
(iv) खाते में प्रत्येक वर्ष का मिश्रधन, जबकि ₹ 10000 की राशि 8% वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है।
हल:
(i) यदि टैक्सी का पहले किमी का किराया a₁, दूसरे किमी का किराया a₂ तथा वें किमी का किराया a_n से व्यक्त किया जाए तो
प्रश्नानुसार,
a₁ = 15
a₂ = 15 + 8 = 23
a₃ = 23 + 8 = 31
अब सार्वअन्तर (d) = a₂ – a₁ = 23 – 15 = 8
और a₃ – a₂ = 31 – 23 = 8
∵ a₃ – a₂ = a₂ – a₁
अर्थात् सार्वअन्तर समान हैं।
∴ दी गई स्थिति A.P. (समान्तर श्रेढी) के रूप की है।

(ii) माना कि एक बेलन में उपस्थित हवा की मात्रा को x मात्रक से तथा प्रत्येक पम्प के बाद हवा की शेष मात्रा को a₂, a₃, a₄ से व्यक्त किया जाता है।
प्रश्न के अनुसार,

और आगे भी इसी प्रकार से….
अब सार्वअन्तर,

यहाँ a₃ – a₂ ≠ a₂ – a₁
∵ सार्वअन्तर समान नहीं है।
∴ दी गई स्थिति A.P का रूप नहीं है।

(iii) माना कि एक कुआँ खोदने के nवें मीटर की लागत को a_n से व्यक्त किया जाए तो.
प्रश्न के अनुसार, a₁ = ₹ 150
a₂ = ₹ (150 + 50) = ₹ 200
a₃ = ₹ (200 + 50) = ₹ 250
और आगे भी इसी प्रकार से…..
अब सार्वअन्तर
a₃ – a₂ = ₹ (250 – 200) = ₹ 50
a₂ – a₁ = ₹ (200 – 150) = ₹ 50
यहाँ a₃ – a₂ = a₂ – a₁ = ₹ 50
सार्वअन्तर समान हैं।
अतः दी गई स्थिति A. P. (समान्तर श्रेढी) के रूप की है।

(iv) खाते में जमा किए गए धन के लिए भिन्न वर्षों के मिश्रधन:
मूलधन P = ₹ 10000
ब्याज की दर R% = 8%


निरीक्षण से ही स्पष्ट है कि
A₂ – A₁ ≠ A₃ – A₂
अतः मिश्रधन A.P. (समान्तर श्रेढी) में नहीं हैं।

प्रश्न 2.
दी हुई A. P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्वअन्तर d निम्नलिखित हैं:
(i) a = 10, d = 10,
(ii) a = -2, d = 0
(iii) a = 4, d = – 3,
(iv) a = -1, d = \(\frac{1}{2}\)
(v) a = -1.25, d = -0.25
हल:
(i) दिया है, प्रथम पद (a) = 10
और सार्व अन्तर (d) = 10
∴ a₁ = प्रथम पद (a) = 10
a₂ = a + d = 10 + 10 = 20
a₃ = a + 2d = 10 + 2 × 10 = 30
a₄ = a + 3d = 10 + 3 × 10 = 40
अत: A.P के प्रथम चार पद 10, 20, 30, 40 हैं।

(ii) दिया हुआ है कि प्रथम पद (a) = 22
और सार्वअन्तर (d) = 0
∴ a₁ = a = -2
a₂ = a + d = 2 + 0 = 2
a₃ = a + 2d = -2 + 2 × 0 = -2
a₄ = a + 3d = 2 + 3 × 0 = -2
अत: A.P. के प्रथम चार पद -2, -2, -2, -2, हैं ।

(iii) दिया हुआ है, प्रथम पद (a) = 4
और सार्वअन्तर (d) = -3
∴ a₁ = a = 4
a₂ = a + d = 4 + (-3) = 1
a₃ = a + 2d = 4 + 2 × (-3) = -2
a₄ = a + 3d = 4 + 3 × (-3) = – 5
अत: A.P. के प्रथम चार पद 4, 1, 2, 5 हैं।

(iv) दिया है कि प्रथम पद a = -1
और सार्वअन्तर d = \(\frac{1}{2}\)
∴ a₁ = a = -1
a₂ = a + d
= \(-1+\frac{1}{2}=\frac{-1}{2}\)
a₃ = a + 2d
= \(-1+2\left(\frac{1}{2}\right)\)
– 1 + 1 = 0
a₄ = a + 3d
= \(-1+3\left(\frac{1}{2}\right)\)
= \(\frac{-2+3}{2}=\frac{1}{2}\)
अत: A.P. के प्रथम चार पद -1, –\(\frac{1}{2}\), 0, \(\frac{1}{2}\) हैं।

(v) दिया हैं कि प्रथम पद = a = -1.25
और सार्वअन्तर (d) = -0.25
∴ a₁ = a = – 1.25
a₂ = a + d = – 1.25 – 0.25 = -1.50
a₃ = a + 2d = – 1.25 + 2(-0.25)
= -1.25 – 0.50 = -1.75
a₄ = a + 3d = – 1.25 + 3(-0.25)
= – 1.25 – 0.75 = -2
अत: A.P. के प्रथम चार पद -1.25, -1.50, 1.75, – 2. हैं।

प्रश्न 3.
निम्नलिखित में से प्रत्येक A. P. के लिए प्रथम पद तथा सार्वअन्तर लिखिए:
(i) 3, 1, -1, -3,…
(ii) -5, 1, 3, 7,…
(iii) \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots\)
(iv) 0.6, 1.7, 2.8, 3.9,…
हल:
(i) दी गई A.P. = 3, 1, -1, -3, …
यहाँ a₁ = 3, a₂ = 1
a₃ = -1, a₄ = -3
प्रथम पद a = a₁ = 3
सार्वअन्तर d = a₂ – a₁ = 1 – 3 = -2
अत: प्रथम पद 3 तथा सार्वअन्तर = -2

(ii) दी गई A. P. = -5, -1, 3, 7, …
यहाँ a₁ = -5
a₂ = -1
a₃ = 3
a₄ = 7
प्रथम पद a₁ = -5
सार्वन्तर d = a₂ – a₁ = – 1 – (-5) = – 1 + 5 = 4
अतः प्रथम पद = -5 तथा सार्वन्तर = 4

(iii) दी गई A.P. = \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots \ldots\)
यहाँ a₁ = \(\frac{1}{3}\),
a₂ = \(\frac{5}{3}\),
a₃ = \(\frac{9}{3}\),
a₄ = \(\frac{13}{3}\)
प्रथम पद a = a₁ = \(\frac{1}{3}\)
सार्वन्तर d = a₂ – a₁ = \(\left(\frac{5}{3}-\frac{1}{3}\right)\)
= \(\frac{5-1}{3}=\frac{4}{3}\)
अतः प्रथम पद = \(\frac{1}{3}\) तथा सार्वअन्तर = \(\frac{4}{3}\)

(iv) दी गई A.P. = 0.6, 1.7, 2.8, 3.9, …
a₁ = 0.6, a₂ = 1.7
a₃ = 2.8, a₄ = 3.9
प्रथम पद a = a₁ = 0.6
सार्वअन्तर d = a₂ – a₁ = 1.7 – 0.6 = 1.1
अत: प्रथम पद = 0.6 तथा सार्वअन्तर = 1.1

प्रश्न 4.
निम्नलिखित में से कौन-कौन A.P. हैं ? यदि कोई A.P. है, तो इसका सार्वअन्तर ज्ञात कीजिए और इनके तीन और पद लिखिए:
(i) 2, 4, 8, 16, …
(ii) 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …
(iii) -1.2, -3.2, -5.2, -7.2,
(iv) -10, -6, -2, 2,…
(v) 3, 3 + \(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\),…
(vi) 0.2, 0.22, 0.222, 0.2222,
(vii) 0, -4, -8, -12,…
(viii) \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \ldots\)
(ix) 1, 3, 9, 27, …
(x) a, 2a, 3a, 4a, …
(xi) a, a², a³, a⁴, …
(xii) \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\),…
(xiii) \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\),…
(xiv) 1², 3², 5², 7², …
(xv) 1², 5², 7², 7³, …
हल:
(i) दिया हुआ अनुक्रम 2, 4, 8, 16, …
यहाँ a₁ = 2, a₂ = 4, a₃ = 8, a₄ = 16
दो क्रमागत पदों का अन्तर (सार्वअन्तर)
d = a₂ – a₁ = 4 – 2 = 2
a₃ – a₂ = 8 – 4 = 4
a₄ – a₃ = 16 – 8 = 8
∵ दो क्रमागत पदों का अन्तर समान नहीं है,
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A.P. नहीं है।

(ii) दिया गया अनुक्रम 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …
यहाँ a₁ = 2, a₂ = \(\frac{5}{2}\), a₃ = 3, a₄ = \(\frac{7}{2}\)
∵ दो क्रमागत पदों का अन्तर (सार्वअन्तर)

दो क्रमागत पदों का अन्तर समान है। सार्वअन्तर = \(\frac{1}{2}\) हैं।
∴ दिया गया अनुक्रम A.P. है।
अगले तीन पद

अत: दिये गये अनुक्रम के अगले तीन पद 4, \(\frac{9}{2}\) और 5 हैं।

(iii) दिया गया अनुक्रम -1.2, -3.2, -5.2, -7.2, …
यहाँ a₁ = -1.2, a₂ = -3.2, a₃ = -5.2, a₄ = -7.2
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = – 3.2 – (-1.2) = – 2.0
a₃ – a₂ = -5.2 – (-3.2) = -2.0
a₄ – a₃ = -7.2 – (-5.2) = -2.0
∵ दो क्रमागत पदों का अन्तर समान (-2.0) है।
∴ सार्वन्तर d = -2.0 और दिया गया अनुक्रम एक A.P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= -7.2 + (-2) = -9.2
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= -9.2 + (-2) = -11.2
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
-11.2 + (-2) = -13.2
अतः दिए गए अनुक्रम के अगले तीन पद -9.2, -11.2, -13.2 हैं।

(iv) दिया हुआ अनुक्रम -10, 6, – 2, 2,…
यहाँ a₁ = -10, a₂ = -6, a₃ = -2, a₄ = 2
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = -6 – (-10) = – 6 + 10 = 4
a₃ – a₂ = – 2 – (-6) = – 2 + 6 = 4
a₄ – a₃ = 2 – (-2) = 2 + 2 = 4
∵ दो क्रमागत पदों का अन्तर समान (4) है।
∴ सार्वअन्तर d = 4 और दिया गया अनुक्रम एक A.P. हैं।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= 2 + 4 = 6
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= 6 + 4 = 10
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= 10 + 4 = 14
अतः दिए गए अनुक्रम के अगले तीन पद 6, 10, 14 हैं।

(v) दिया हुआ अनुक्रम 3, 3 + \(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\),…
यहाँ a₁ = 3, a₂ = 3 + \(\sqrt{2}\), a₃ = 3 + 2\(\sqrt{2}\), a₄ = 3 + 3\(\sqrt{2}\)
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = (3+ \(\sqrt{2}\)) – 3 = \(\sqrt{2}\)
a₃ – a₂ = (3 + 2\(\sqrt{2}\)) – (3 + \(\sqrt{2}\)) = \(\sqrt{2}\)
a₄ – a₃ = (3 + 3\(\sqrt{2}\)) – (3 + 2\(\sqrt{2}\))= \(\sqrt{2}\)
∵ दो क्रमागत पद का अन्तर समान (\(\sqrt{2}\)) है।
∴ सार्वअन्तर d = \(\sqrt{2}\) और दिया गया अनुक्रम एक A. P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
3 + 3\(\sqrt{2}\) + \(\sqrt{2}\)
= 3 + \(\sqrt{2}\)(3 + 1) = 3 + 4\(\sqrt{2}\)
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= 3 + 4\(\sqrt{2}\) + \(\sqrt{2}\)
= 3 + \(\sqrt{2}\)(4 + 1) = 3 + 5\(\sqrt{2}\)
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= 3 + 5\(\sqrt{2}\) + \(\sqrt{2}\)
= 3 + \(\sqrt{2}\)(5 + 1) = 3 + 6\(\sqrt{2}\)
अतः दिए गए अनुक्रम के अगले तीन पद
3 + 4\(\sqrt{2}\), 3 + 5\(\sqrt{2}\), 3 + 6\(\sqrt{2}\) है।

(vi) दिया हुआ अनुक्रम
0.2, 0.22, 0.222, 0.2222, …
यहाँ a₁ = 0.2, a₂ = 0.22, a₃ = 0.222, a₄ = 0.2222,
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = 0.22 – 0.2 = 0.02
a₃ – a₂ = 0.222 – 0.22 = 0.002
a₄ – a₃ = 0.2222 – 0.222 = 0.0002
दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A. P. नहीं है।

(vii) दिया हुआ अनुक्रम 0, -4, -8, -12, ….
यहाँ a₁ = 0, a₂ = -4, a₃ = -8, a₄ = -12
दो क्रमागत पदों का अन्तर :
a₂ – a₁ = – 4 – 0 = -4
a₃ – a₂ = – 8 – (-4)
= – 8 + 4 = -4
a₄ – a₃ = – 12 – (-8)
= – 12 + 8 = -4
दो क्रमागत पदों का अन्तर समान है सार्वअन्तर = -4 है। अतः दिया गया अनुक्रम A.P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= – 12 + (-4) = -16
पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= – 16 + (-4) = -20
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= -20 + (-4) = -24
अतः दिए गये अनुक्रम के अगले तीन पद -16, -20 और -24 हैं।

(viii) दिया हुआ अनुक्रम \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \ldots\)

a₄ – a₃ = \(-\frac{1}{2}-\left(-\frac{1}{2}\right)\)
= \(-\frac{1}{2}+\frac{1}{2}\) = 0
दो क्रमागत पदों का अन्तर समान है। सार्वअन्तर = 0 है अतः दिया गया अनुक्रम एक A.P. है।
पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= \(-\frac{1}{2}+0=-\frac{1}{2}\)
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= \(-\frac{1}{2}+0=-\frac{1}{2} \)
सातवाँ पद a₇ = छठा पद a₆ + सार्वअन्तर d
= \(-\frac{1}{2}+0=-\frac{1}{2}\)
दिए गए अनुक्रम के अगले तीन पद \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\) है।

(ix) दिया हुआ अनुक्रम 1, 3, 9, 27,…
यहाँ a₁ = 1, a₂ = 3, a₃ = 9, a₄ = 27
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = 3 – 1 = 2
a₃ – a₂ = 9 – 3 = 6
a₄ – a₃ = 27 – 9 = 18
दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A.P. में नहीं है।

(x) दिया हुआ अनुक्रम a, 2a, 3a, 4a…..
यहाँ a₁ = a, a₂ = 2a, a₃ = 3a, a₄ = 4a
दो क्रमागत पद का अन्तर d:
a₂ – a₁ = 2a – a = a
a₃ – a₂ = 3a – 2a = a
a₄ – a₃ = 4a – 3a = a
∵ दो क्रमागत पर्दों का अन्तर समान (a) है।
अतः सार्वन्तर d = a तथा दिया गया अनुक्रम एक A. P. है।
तब पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर d
= 4a + a = 5a
छठा पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर d
= 5a + a = 6a
सातवाँ पद a₇ = छटा पद a₇ + सार्वअन्तर d
= 6a + a = 7a
अतः दिए गए अनुक्रम के अगले तीन पद 5a, 6a, 7a है।

(xi) दिया हुआ अनुक्रम यहाँ a, a², a³, a⁴, ….
यहाँ a₁ = a, a₂ = a², a₃ = a³‚ a₄ = a⁴
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = a² – a = a(a – 1)
a₃ – a₂ = a³ – a² = a²(a – 1)
∵ दो क्रमागत पद का अन्तर समान नहीं है।
अर्थात a₂ – a₁ ≠ a₃ – a₂
अतः दिया गया अनुक्रम एक A. P. नहीं है।

(xii) दिया हुआ अनुक्रम \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\)……
यहाँ a₁ = \(\sqrt{2}\), a₂ = \(\sqrt{8}\), a₃ = \(\sqrt{18}\), a₄ = \(\sqrt{32}\)
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = \(\sqrt{8}\) – \(\sqrt{2}\) = \(\sqrt{2}\)(\(\sqrt{4}\) – 1)
= \(\sqrt{2}\) (2 – 1) = \(\sqrt{2}\)
a₃ – a₂ = \(\sqrt{18}\) – \(\sqrt{8}\) = \(\sqrt{2}\)(\(\sqrt{9}\) – \(\sqrt{4}\))
= \(\sqrt{2}\)(3 – 2) = \(\sqrt{2}\)
a₄ – a₃ = \(\sqrt{32}\) – \(\sqrt{18}\) = \(\sqrt{2}\)(\(\sqrt{19}\) – \(\sqrt{9}\))
= \(\sqrt{2}\)(4 – 3) = \(\sqrt{2}\)
दो क्रमागत पदों का अन्तर समान (\(\sqrt{2}\)) है।
अतः सार्वअन्तर d = \(\sqrt{2}\) तथा दिया गया अनुक्रम एक A.P. है।
तब 5वाँ पद a₅ = 4वाँ पद + सार्वअन्तर d.
= \(\sqrt{32}\) + \(\sqrt{2}\)
= \(\sqrt{2}\)(\(\sqrt{16}\) + 1) = \(\sqrt{2}\)(4 + 1)
= 5\(\sqrt{2}\) = \(\sqrt{25}\) × \(\sqrt{2}\) = \(\sqrt{50}\)
6वाँ पद a₆ = 5वाँ पद + सार्वअन्तर d
= \(\sqrt{50}\) + \(\sqrt{2}\) = \(\sqrt{2}\)(\(\sqrt{25}\) + 1)
= \(\sqrt{2}\)(5 + 1) = 6\(\sqrt{2}\)
= \(\sqrt{36}\) × \(\sqrt{2}\) = \(\sqrt{72}\)
7वाँ पद a₇ = 6वीं पद + सार्वअन्तर d
= \(\sqrt{72}\) + \(\sqrt{2}\) = \(\sqrt{2}\)(\(\sqrt{36}\) + 1)
= \(\sqrt{2}\)(6 + 1) = 7\(\sqrt{2}\)
= \(\sqrt{49}\) × \(\sqrt{2}\) = \(\sqrt{98}\)
अतः दिए गए अनुक्रम के अगले तीन पद \(\sqrt{50}\), \(\sqrt{72}\), \(\sqrt{98}\) हैं।

(xiii) दिया हुआ अनुक्रम \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\), …
a₁ = \(\sqrt{3}\), a₂ = \(\sqrt{6}\), a₃ = \(\sqrt{9}\), a₄ = \(\sqrt{12}\)
दो क्रमागत पदों का अन्तर d
a₂ – a₁ = \(\sqrt{6}\) – \(\sqrt{3}\) = \(\sqrt{3}\) (\(\sqrt{2}\) – 1) = 0.717
a₃ – a₂ = \(\sqrt{9}\) – \(\sqrt{6}\) = \(\sqrt{3}\)(\(\sqrt{3}\) – \(\sqrt{2}\)) = 0.530
∵ दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात a₂ – a₁ ≠ a₃ – a₂
अतः दिया गया अनुक्रम एक A.P. नहीं है।

(xiv) दिया हुआ अनुक्रम 1², 3², 5², 7², ….
a₁ = 1², a₂ = 3², a₃ = 5², a₄ = 7²
दो क्रमागत पदों का अन्तर d:
a₂ – a₁ = 3² – 1² = 9 – 1 = 8
a₃ – a₂ = 5² – 3² = 25 – 9 = 16
a₄ – a₃ = 7² – 5² = 49 – 25 = 24
∵ दो क्रमागत पदों का अन्तर समान नहीं है।
अर्थात् a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃
अतः दिया गया अनुक्रम A.P. नहीं है।

(xv) दिया गया अनुक्रम 1², 5², 7², 7³, ….
यहाँ a₁ = 1², a₂ = 5², a₃ = 7², a₄ = 7³
दो क्रमागत पर्दों का अन्तर d:
a₂ – a₁ = 5² – 1² = 25 – 1 = 24
a₃ – a₂ = 7² – 5² = 49 – 25 = 24
a₄ – a₃ = 7³ – 7² = 73 – 49 = 24
चूँकि दो क्रमागत पदों का अन्तर समान है।
अतः सार्वअन्तर d = 24
तथा दिया गया अनुक्रम A.P. है।
पाँचवाँ पद a₅ = चौथा पद a₄ + सार्वअन्तर
= 73 + 24 = 97
छठवाँ पद a₆ = पाँचवाँ पद a₅ + सार्वअन्तर
= 97 + 24 = 121
छठवाँ पद a₇ = छठवाँ पद a₆ + सार्वअन्तर
= 121 + 24 = 145
अत: दिये गये अनुक्रम के अगले तीन पद 97, 121 और 145 हैं।