Bhagya

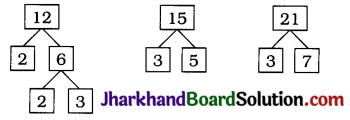
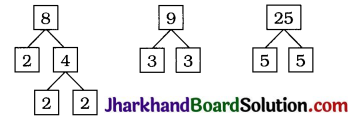
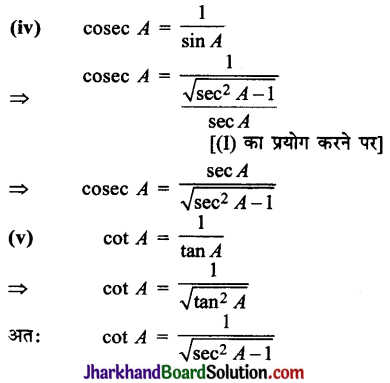
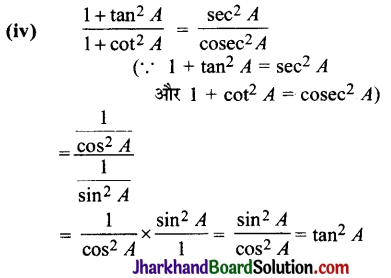
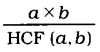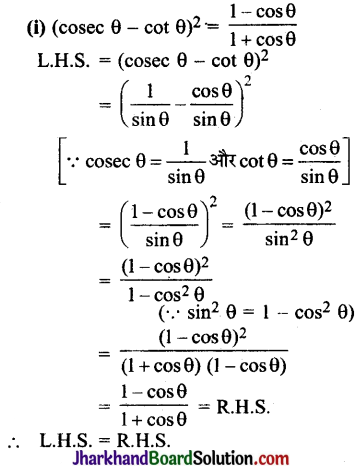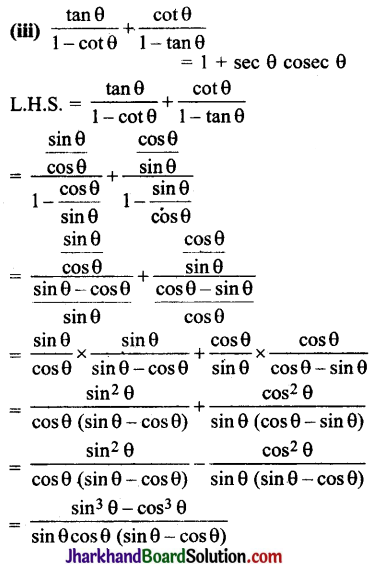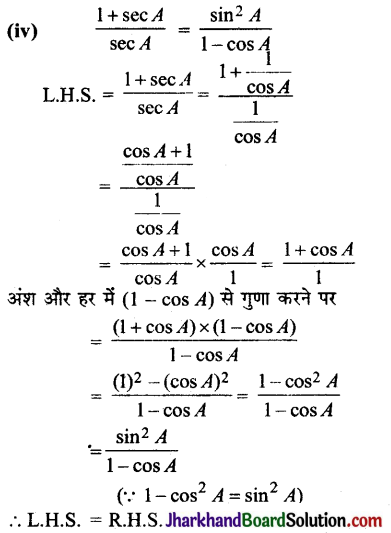Students should go through these JAC Class 10 Maths Notes Chapter 5 समांतर श्रेढ़ियाँ will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 5 समांतर श्रेढ़ियाँ

भूमिका :
इस अध्याय में, हम कुछ प्रतिरूपों का अध्ययन करेंगे जिनमें उत्तरोत्तर पद अपने पहले पदों में एक स्थिर संख्या जोड़ने पर प्राप्त किए जाते हैं। हम यह भी देखेंगे कि किस प्रकार उनके n वें पद और n पदों का योग ज्ञात किया जाता है और इस ज्ञान का उपयोग दैनिक जीवन की समस्याओं को हल करने में किया जा सकता है।
(1) पद (Terms) : अनुक्रम में उपस्थित विभिन्न संख्याएँ इसके पद कहलाती हैं।
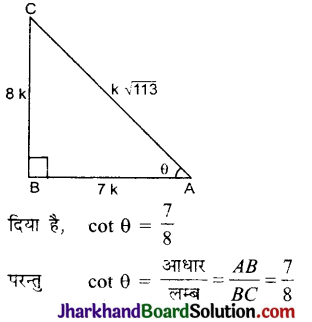
(2) सार्वअन्तर (Common difference) : समान्तर श्रेढी के किन्हीं दो क्रमागत पदों का अन्तर सार्वअन्तर कहलाता है।
(3) सीमित समान्तर श्रेढी (Finite A. P.) : एक समान्तर श्रेढी जिसमें पदों की संख्या सीमित हो, सीमित समान्तर श्रेढी कहलाती हैं।
(4) असीमित समान्तर श्रेढी (Infinite A. P.) : एक समान्तर श्रेढी जिसमें पदों की संख्या असीमित हो, असीमित समान्तर श्रेढी कहलाती है।
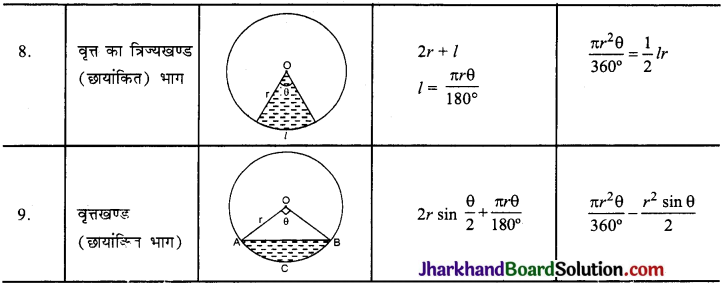
(5) व्यापक पद (General Term) : प्रथम पद a और सार्वअन्तर d वाली A. P का nवाँ पद व्यापक पद कहलाता a_n या l से निरूपित किया जाता है।
सूत्र a_n = a + (n – 1)d

अनुक्रम (Sequence)- संख्याओं (राशियों) के एक निश्चित नियमानुसार क्रम को अनुक्रम कहते हैं।
जैसे: (i) 2, 4, 6, 8, 10, ……….. इस क्रम में प्रत्येक संख्या (पहली संख्या को छोड़कर) अपनी पूर्व की संख्या से 2 अधिक है।
(ii) -3, -2, -1, 0, ……….. इस क्रम में प्रत्येक पद, अपने पिछले पद से 1 अधिक है।
(iii) 3, 3, 3, 3, 3, ……….. इस क्रम में प्रत्येक पद, अपने पिछले पद से 0 अधिक या 0 कम है।
(iv) 5, 7, 2, 9, 15, ……….. इस क्रम में कोई निश्चित क्रम नहीं है जिससे कि उसकी आगे की संख्याएँ ज्ञात की जा सकें।

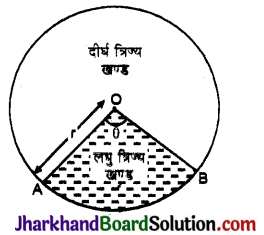
समान्तर श्रेढ़ियाँ :
समान्तर श्रेढी संख्याओं का एक ऐसा क्रम होता है जिसमें पहले पद के अतिरिक्त प्रत्येक पद पिछली संख्या में एक स्थिर संख्या जोड़ने पर प्राप्त किया जाता है। इस स्थिर संख्या को समान्तर श्रेढी का सार्वअन्तर कहते हैं। यह संख्या धनात्मक, ऋणात्मक या शून्य हो सकती है।
समान्तर श्रेढी के पहले पद को a₁ से, दूसरे पद को a₂ से, ……., nवें पद को a_n से और सार्वअन्तर को d से व्यक्त करते हैं, तब श्रेढी a₁, a₂, a₃, ………. , a_n हो जाती है।
अब, a₂ – a₁ = a₃ – a₂ = ………. = a_n – a_{n – 1} = d
⇒ a, a + d, a + 2d, a + 3d, ………..
यह अनुक्रम एक समान्तर श्रेढी (A.P.) को निरूपित करता है जिसमें प्रथम पद ‘a’ और सार्वअन्तर d है। इसे समान्तर शेष का व्यापक रूप कहते हैं।
सामान्यतः, प्रथम पद को a₁, t₁, x₁ आदि से प्रकट किया जाता है, दूसरे पद को a₂, t₂, x₂ आदि से प्रकट किया जाता है। व्यापक रूप से n वें पद को a_n, t_n, x_n आदि से प्रकट किया जाता है।

समान्तर श्रेढी का nवाँ पद :
माना कि a₁, a₂, a₃, …….., a_n एक समान्तर श्रेढी है जिसका प्रथम पद a₁ = a, और सार्वअन्तर d है।
⇒ a₁ = a + (1 – 1)d
तब दूसरा पद a₂ = a + d
⇒ a₂ = a + (2 – 1) d
इसी प्रकार, तीसरा पद a₃ = a₂ + d
⇒ a₃ = (a + d) + d
= a + 2d = a + (3 – 1)d
चौथा पद a₄ = a₃ + d = (a + 2d) + d
= a + 3d = a + (4 – 1)d
इस प्रतिरूप को देखते हुए हम कह सकते हैं कि nवाँ पद (a_n) = a + (n – 1) d होगा। अर्थात्
समान्तर श्रेढी का व्यापक पद = प्रथम पद + (पदों की संख्या – 1) × सार्वअन्तर
a_n को A.P का व्यापक पद भी कहते हैं। यदि किसी A. P. में m पद हों तो a_m इसके अन्तिम पद निरूपित करता है जिसे कभी-कभी l द्वारा भी व्यक्त किया जाता है।

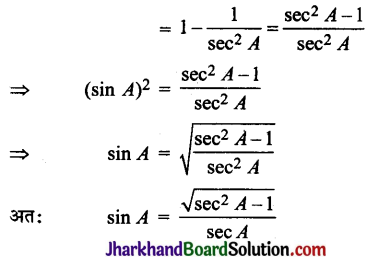
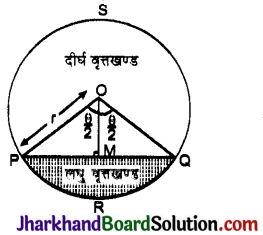
समान्तर श्रेढी के n पदों का योगफल :
प्रमेय : यदि एक समान्तर श्रेढी का प्रथम पद a, सार्वअन्तर d तथा पदों का योगफल S_n है, तो
S_n = \(\frac{n}{2}\){2a + (n – 1) d}
या S_n = \(\frac{n}{2}\) (a + 1)
जहाँ l = अन्तिम पद = a + (n – 1)d
प्रमाण : माना कि A.P. के n पद हैं:
a, a + d, a + 2d, …… a + (n – 1)d
इस A. P. का nवाँ पद a + (n – 1)d है तथा A. P. के प्रथम n पदों के योग को S_n द्वारा व्यक्त करते हैं।
S_n = a + (a + d) + (a + 2d) + [a + (- 1)d] …. (1)
पदों को विपरीत क्रम में लिखने पर, हम प्राप्त करते हैं:
S_n = [a + (n – 1)d] + [a + (n – 2)d] + …….. + (a + d) + a …… (2)
समीकरण (1) और (2) को जोड़ने पर हमें प्राप्त होता हैं:
2S_n = {2a + (n – 1)d} + {2a + (n – 1)d} + …… + {2a + (n – 1)d }
⇒ 2S_n = n[2a + (n – 1)d]
⇒ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
इसे हम इस रूप में भी लिख सकते हैं:
S_n = \(\frac{n}{2}\)[a + a + (n – 1)d]
अर्थात् S_n = \(\frac{n}{2}\)(a + a_n) …..(3)
∵ a_n = l, अन्तिम पद है।
समीकरण (3), से S_n = \(\frac{n}{2}\)(a + l) …..(4)
इस सूत्र की सहायता से जब प्रथम पद और अन्तिम पद दिया हो और सार्वअन्तर नहीं दिया हो, तो S_n का मान ज्ञात कर सकते हैं।

टिप्पणी 1. सूत्र S_n = \(\frac{n}{2}\)[2a + (n – 1)d ] में चार राशियाँ S_n, a, n और d हैं। यदि इनमें से कोई भी तीन ज्ञात हों तो शेष चौथी राशि को उपर्युक्त सूत्र से ज्ञात किया जा सकता है।
कभी-कभी इनमें से दो राशियाँ ज्ञात होती हैं ऐसी स्थिति में शेष दोनों राशियाँ किसी दूसरे सम्बन्ध से ज्ञात की जा सकती हैं।
टिप्पणी 2. यदि किसी अनुक्रम के n पदों का योग S_n दिया हो तो निम्नलिखित सूत्र से अनुक्रम का nवाँ पद (a_n) ज्ञात किया जा सकता है:
a_n = S_n – S_{n – 1}

Jharkhand Board JAC Class 10 Maths Solutions Chapter 1 Real Numbers Ex 1.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 1 Real Numbers Exercise 1.4

Question 1.
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
1. \(\frac{13}{3125}\)
2. \(\frac{17}{8}\)
3. \(\frac{64}{455}\)
4. \(\frac{15}{1600}\)
5. \(\frac{29}{343}\)
6. \(\frac{23}{2^3 5^2}\)
7. \(\frac{129}{2^2 5^7 7^5}\)
8. \(\frac{6}{15}\)
9. \(\frac{35}{50}\)
10. \(\frac{77}{210}\)
Solution:
1. \(\frac{13}{3125}\)
Here, the denominator q(5⁵) is of the form 2ⁿ5^m with n = 0 and m = 5.
Hence, the decimal expansion of \(\frac{13}{3125}\) is terminating.

2. \(\frac{17}{8}\) = \(\frac{17}{2^3}\)
Here, the denominator q(2³) is of the form 2ⁿ5^m with n = 3 and m = 0.
Hence, the decimal expansion of \(\frac{17}{8}\) terminating.

3. \(\frac{64}{455}=\frac{64}{5 \times 7 \times 13}\)
Here, the denominator q(5 × 7 × 13) is not of the form 2ⁿ5^m, where n and m are non-negative integers.
Hence, the decimal expansion of \(\frac{64}{455}\) is non-terminating repeating.

4. \(\frac{15}{1600}=\frac{3}{320}=\frac{3}{2^6 \times 5^1}\)
Here, the denominator q(2⁶ × 5¹) is of the form 2ⁿ5^m with n = 6 and m = 1.
Hence, the decimal expansion of \(\frac{15}{1600}\) is terminating.

5. \(\frac{29}{343}=\frac{29}{7^3}\)
Here, the denominator q(7³) is not of the form 2ⁿ5^m, where n and m are non-negative integers.
Hence, the decimal expansion of \(\frac{29}{343}\) is non-terminating repeating.

6. \(\frac{23}{2^3 5^2}\)
Here, the denominator q(2³5²) is of the form 2ⁿ5^m with n = 3 and m = 2.
Hence, the decimal expansion of \(\frac{23}{2^3 5^2}\) is terminating.

7. \(\frac{129}{2^2 5^7 7^5}\)
Here, the denominator q (2² × 5⁷ × 7⁵) is not of the form 2ⁿ5^m, where n and m are non-negative integers. Hence, the decimal expansion of \(\frac{129}{2^2 5^7 7^5}\) is non-terminating repeating.

8. \(\frac{6}{15}=\frac{2 \times 3}{3 \times 5}=\frac{2}{5^1}\)
Here, the denominator q(5¹) is of the form 2ⁿ5^m with n = 0 and m = 1.
Hence, the decimal expansion of \(\frac{6}{15}\) is terminating.

9. \(\frac{35}{50}=\frac{5 \times 7}{2 \times 5 \times 5}=\frac{7}{2^1 \times 5^1}\)
Here, the denominator q(2¹ × 5¹) is of the form 2ⁿ5^m with n = 1 and m = 1.
Hence, the decimal expansion of \(\frac{35}{50}\) is terminating.

10. \(\frac{77}{210}=\frac{7 \times 11}{2 \times 3 \times 5 \times 7}=\frac{11}{2 \times 3 \times 5}\)
Here, the denominator q(2 × 3 × 5) is not of the form 2²ⁿ5^m, where n and m are non-negative integers.
Hence, the decimal expansion of \(\frac{77}{210}\) is non-terminating repeating.

Question 2.
Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solution:

Question 3.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form \(\frac{p}{q}\), what can you say about the prime factors of q?
1. 43.123456789
2. 0.120120012000120000…
3. \(43 . \overline{123456789}\)
Solution:
1. The given number 43.123456789 is a rational number as its decimal expansion is terminating
Since the decimal expansion of the given number is terminating, in the \(\frac{p}{q}\) form of the number, the prime factors of q will only be 2 or 5 or both. (Theorem 1.5)

2. The given number 0.120120012000120000…. is an irrational number as its decimal expansion is non-terminating non-repeating.

3. The given number \(43 . \overline{123456789}\) is a rational number as its decimal expansion is an non-terminating repeating.
Since the decimal expansion of the given number is non-terminating repeating, in the \(\frac{p}{q}\) form of the number, the prime factors of q will contain at least one prime other than 2 and 5. (Converse of Theorem 1.7)

Jharkhand Board JAC Class 10 Maths Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 1 Real Numbers Exercise 1.3

Question 1.
Prove that \(\sqrt{5}\) is irrational.
Solution:
Let us assume that \(\sqrt{5}\) is rational.
So, we can find co-prime integers a and b such that \(\sqrt{5}\) = \(\frac{a}{b}\)
Then, squaring on both the sides, we get
5 = \(\frac{a^2}{b^2}\)
∴ a² = 5b²
This suggests that 5 is a factor of a².
Since 5 is a prime number, by theorem 1.3, 5 is also a factor of a.
Let a = 5c, where c is an integer.
∴ a² = 25c²
∴ 25c² = 5b²
∴ b² = 5c²
This suggests that 5 is a factor of b². Since 5 is a prime number, by theorem 1.3, 5 is also a factor of b.
Thus, a and b have a common factor 5.
But, this contradicts the fact that a and b are co-prime.
Hence, our assumption that \(\sqrt{5}\) is rational is incorrect.
So, we conclude that \(\sqrt{5}\) is irrational.

Question 2.
Prove that 3 + 2\(\sqrt{5}\) is irrational.
Solution:
Suppose 3 + 2\(\sqrt{5}\) is rational.
Then, 3 + 2\(\sqrt{5}\) = \(\frac{a}{b}\); where a and b are co-prime integers.
Now, 3 + 2\(\sqrt{5}\) = \(\frac{a}{b}\)
∴ 2\(\sqrt{5}\) = \(\frac{a}{b}\) – 3
∴ 2\(\sqrt{5}\) = \(\frac{a-3 b}{b}\)
∴ \(\sqrt{5}\) = \(\frac{a-3 b}{2 b}\)
As a and b are integers, \(\frac{a-3 b}{2 b}\) is a rational number and so is \(\sqrt{5}\).
This contradicts the fact that \(\sqrt{5}\) is irrational.
Hence, our assumption is incorrect.
So, we conclude that 3 + 2\(\sqrt{5}\) is irrational.

Question 3.
Prove that the following are irrationals:
1. \(\frac{1}{\sqrt{2}}\)
2. 7\(\sqrt{5}\)
3. 6 + \(\sqrt{2}\)
Solution:
1. \(\frac{1}{\sqrt{2}}\)
Suppose \(\frac{1}{\sqrt{2}}\) is rational.
Then, \(\frac{1}{\sqrt{2}}=\frac{a}{b}\) where a and b are co-prime integers.
Squaring on both the sides, we get
\(\frac{1}{2}=\frac{a^2}{b^2}\)
∴ b² = 2a²
Hence, 2 is a factor of b².
Since 2 is a prime number, by theorem 1.3, 2 is also a factor of b.
Let b = 2c, where c is an integer.
∴ b² = 4c²
∴ 4c² = 2a²
∴ a² = 2c²
Hence, 2 is a factor of a².

Since 2 is a prime number, by theorem 1.3, 2 is also a factor of a.
Thus, a and b have a common factor 2. which contradicts our assumption that a and b are co-prime integers.
Hence, our assumption that \(\frac{1}{\sqrt{2}}\) is rational is incorrect.
So, we conclude that \(\frac{1}{\sqrt{2}}\) is irrational.

2. 7\(\sqrt{5}\)
Suppose 7\(\sqrt{5}\) is rational.
Then, 7\(\sqrt{5}\) = \(\frac{a}{b}\) where a and b are co-prime integers.
This gives, \(\sqrt{5}\) = \(\frac{a}{7 b}\)
As a and b are integers, \(\frac{a}{7 b}\) is a rational number and so is \(\sqrt{5}\).
This contradicts the fact that \(\sqrt{5}\) is irrational.
Hence, our assumption is incorrect.
So, we conclude that 7\(\sqrt{5}\) is irrational.

3. 6 + \(\sqrt{2}\)
Suppose 6 + \(\sqrt{2}\) is rational.
Then, 6 + \(\sqrt{2}\) = \(\frac{a}{b}\) where a and b are co-prime integers.
This gives, \(\sqrt{2}\) = \(\frac{a}{b}\) – 6
As a and b are integers, \(\frac{a}{b}\) – 6 is a rational number and so is \(\sqrt{2}\).
This contradicts the fact that \(\sqrt{2}\) is irrational.
Hence, our assumption is incorrect. So, we conclude that 6 + \(\sqrt{2}\) is irrational.

Students should go through these JAC Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल

भूमिका :
पिछली कक्षाओं में हमने समान्तर चतुर्भुअत : समचतुर्भुज तथा वर्ग के परिमाप तथा क्षेत्रफल के बारे में पढ़ा था। इस अध्याय में हम प्रारम्भ में वृत्त के परिमाप तथा क्षेत्रफल का पुनरावलोकन करेंगे तथा त्रिज्यखण्ड, वृत्तखण्ड का क्षेत्रफल ज्ञात करने के बारे में सीखेंगे। हम वृत्तों के भागों तथा वृत्तों से सम्बद्ध समतल आकृतियों के कुछ संयाजनों के क्षेत्रफलों के बारे में भी अध्ययन करेंगे।
→ वृत्त (Circle) : वृत्त एक ऐसे बिन्दु का बिन्दु पथ है जो एक समतल में एक नियत बिन्दु से सदैव समान (अचर) दूरी पर गति करता है।
→ केन्द्र (Centre) : निश्चित बिन्दु को वृत्त का केन्द्र (O) कहते हैं।
→ त्रिज्या (Radius) : एक रेखाखण्ड जो वृत्त पर एक बिन्दु तथा इसके केन्द्र को जोड़ती है. त्रिज्या कहलाती है।
→ व्यास (Diameter) : केन्द्र से होकर गुजरने वाली जीवा जिसके अन्तः बिन्दु वृत्त पर होते हैं, वृत्त का व्यास कहलाता है।
व्यास = 2 × त्रिज्या
→ जीवा (Chord) : वृत्त पर दो बिन्दुओं को जोड़ने वाले रेखाखण्ड को वृत्त की जीवा कहते हैं।
→ चाप (Arc) : वृत्त पर दो बिन्दुओं के बीच की दूरी को वृत्त का चाप कहते हैं।
→ वृत्तीय क्षेत्र (Circular region) : वह क्षेत्र जिसमें सभी बिन्दु या तो वृत्त पर या वृत्त के अन्दर स्थित होते हैं वृत्तीय क्षेत्र कहलाता है।
→ अर्द्धवृत्तीय क्षेत्र (Semi circular region) : जब दो चाप बराबर होते हैं तब प्रत्येक एक अर्द्धवृत्त होता है तथा दोनों वृत्तखण्ड व त्रिज्यखण्ड बराबर होते हैं और प्रत्येक को अर्द्धवृत्तीय क्षेत्र से जाना जाता है।
→ संकेन्द्रीय वृत्त (Concentric Circles) : ऐसे दो या दो से ज्यादा वृत्त जिनका केन्द्र समान हो तथा त्रिज्याएँ विभिन्न हों, संकेन्द्रीय वृत्त कहलाते हैं।

वृत्त का परिमाप और क्षेत्रफल – एक समीक्षा
वृत्त की परिधि (Circumference of Circle) :
वृत्त का एक चक्कर लगाने पर तय की गई दूरी को वृत्त का परिमाप या परिधि कहते हैं। किसी भी वृत्त की परिधि और व्यास का अनुपात एक निश्चित अचर राशि होती है। इस अनुपात की अचर राशि को ग्रीक अक्षर π द्वारा प्रदिर्शित करते हैं।

अतः π = परिधि / व्यास
परिधि = π × व्यास
= π × 2 = 2πr
वृत्त की परिधि = 2πr
व्यवहार में π का मान प्रायः \(\frac{22}{7}\) अथवा 3.14 लिया जाता है परन्तु π एक अपरिमेय संख्या है जिससे इसका दशमलव अनावर्ती और असान्त है। आर्यभट्ट ने इसका मान 3.1416 ज्ञात किया था जो दशमलव के 4 स्थानों तक शुद्ध है।

वृत्त का क्षेत्रफल (Area of Circle) :

वृत्त का क्षेत्रफल = \(\frac{1}{2}\) × r × (वृत्त की परिधि)
= \(\frac{1}{2}\) × r × (2πr) = πr²
अतः वृत्त का क्षेत्रफल = π(त्रिज्या)²
वृत्त का व्यास वृत्त को दो समान भागों में विभाजित करता है। अतः
अर्द्धवृत्त का परिमाप = πr + 2r
अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr²

वलयिका का क्षेत्रफल (Area of an Annullus) :

चित्र में, एक वलयिका का केन्द्र O है और जिसकी बाह्य और अन्तः त्रिज्याएँ क्रमशः r₁ और r₂ (r₁ > r₂) हैं।
वलयिका का क्षेत्रफल = दोनों वृत्तों के बीच का क्षेत्रफल
= बड़े वृत्त का क्षेत्रफल – छोटे वृत्त का क्षेत्रफल
= πr₁² – πr₂²
= π(r₁² – r₂²)
= π × (त्रिज्याओं के वर्गों का अन्तर)
अतः वलयिका का क्षेत्रफल = π(r₁² – r₂²)

त्रिज्यरखण्ड और वृत्तरखण्ड के क्षेत्रफल :
वृत्त के त्रिज्यखण्ड का क्षेत्रफल (Area of a Sector of a Circle) :
किसी भी वृत्त की दो त्रिज्याओं और एक चाप से घिरे हुए क्षेत्र को वृत्त का त्रिज्यखण्ड (Sector) कहते हैं।
चित्र में, वृत्त का एक त्रिज्यखण्ड AOB है। माना कि ∠AOB = θ है और θ < 180° जब कोण 6 का मान बढ़ता है तो चाप AB की लम्बाई भी उसी अनुपात में बढ़ती है। जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो

चाप की लम्बाई = अर्द्धवृत्त के चाप की लम्बाई
= πr
∵ केन्द्र पर 180° कोण अन्तरित करने वाले चाप की लम्बाई = πr
∴ केन्द्र पर θ कोण अन्तरित करने वाले चाप की लम्बाई = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
इसी प्रकार, जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो उसके संगत त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi r^2}{2}\)
∴ वृत्त के केन्द्र पर θ कोण अन्तरित करने पर बने त्रिज्यखण्ड का क्षेत्रफल
= \(\frac{\pi r^2 \theta}{2 \times 180^{\circ}}\)
= \(\frac{\pi r^2 \theta}{360^{\circ}}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
यदि r त्रिज्या के वृत्त में कोण θ के त्रिज्यखण्ड के चाप की लम्बाई L और क्षेत्रफल A है, तो
L = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
और A = \(\frac{\pi r^2 \theta}{360}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
चाप की लम्बाई (L) और त्रिज्यखण्ड के क्षेत्रफल (A) में सम्बन्ध :
A = \(\frac{1}{2}\)Lr
यहाँ कोण θ को डिग्री में लेते हैं।

वृत्तखण्ड का क्षेत्रफल (Area of Segment of a Circle) :
वृत्त की प्रत्येक जीवा वृत्त को दो भागों में विभाजित करती है। इससे बने प्रत्येक भाग को वृत्तखण्ड कहते हैं। छोटे भाग को लघु वृत्तखण्ड तथा बड़े भाग को दीर्घ वृत्तखण्ड कहते हैं।
चित्र में, वृत्त का केन्द्र O हैं और इसकी त्रिज्या r है। जीवा PQ वृत्त को दो भागों में विभाजित करती है। हमें लघु वृत खण्ड PRQ का क्षेत्रफल ज्ञात करना है।

माना ∠POQ = θ
ΔΡΟΜ ≅ ΔQΟΜ (RHS सर्वांगसमता नियम से)
∠POM = ∠QOM = \(\frac{\theta}{2}\)
त्रिज्यखण्ड OPRQ का क्षेत्रफल = लघु वृत्तखण्ड PRQ का क्षेत्रफल + ΔPOQ का क्षेत्रफल
∴ लघु वृत्तखण्ड PRQ का क्षेत्रफल = त्रिज्यखण्ड OPRQ का क्षेत्रफल – ΔPOQ का क्षेत्रफल

यदि हम दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात करना चाहें, तो वृत्त के क्षेत्रफल में से लघु वृत्तखण्ड का क्षेत्रफल घटाकर ज्ञात कर सकते हैं।
अतः दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड PRQ का क्षेत्रफल
= πr² – \(\left[\frac{\pi r^2 \theta}{360^{\circ}}-\frac{r^2}{2} \sin \theta\right]\)
∴ दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = πr² – \(\frac{r^2}{2}\left[\frac{\pi \theta}{180^{\circ}}-\sin \theta\right]\)

समतल आकृतियों के संयोजन के क्षेत्रफल (Areas of Combinations of Plane Figures) :
समतल आकृतियों के छायांकित भाग का क्षेत्रफल ज्ञात करने के लिए निम्न सूत्रों की आवश्यकता होगी :

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Exercise 8.1

प्रश्न 1.
ΔABC में, जिसका कोण B समकोण है, AB = 24 सेमी और BC = 7 सेमी है। निम्नलिखित का मान ज्ञात कीजिए :
(i) sin A, cos A,
(ii) sin C, cos C
हल:
समकोण ΔABC में,
∠B = 90°
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (24)² + (7)²
= 576 + 49 = 625
AC = 25 सेमी

(i) समकोण ΔABC में,
sin A = \(\frac{A B}{A C}=\frac{7}{25}\)
और cos A = \(\frac{B C}{A C}=\frac{24}{25}\)

(ii) समकोण ΔABC में,
sin C = \(\frac{A B}{A C}=\frac{24}{25}\)
और cos C = \(\frac{B C}{A C}=\frac{7}{25}\)

प्रश्न 2.
चित्र में, tan P – cot R का मान ज्ञात कीजिए।

हल:
समकोण ΔPQR में, पाइथागोरस प्रमेय से,
PR² = QR² + PQ²
⇒ (13)² = QR² + (12)²
⇒ 169 = QR² + 144
⇒ QR² = 169 – 144
⇒ QR² = 25
⇒ QR = 5
tan P = \(\frac{Q R}{P Q}=\frac{5}{12}\)
और cot R = \(\frac{Q R}{P Q}=\frac{5}{12}\)
तब tan P – cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0

प्रश्न 3.
sin A = \(\frac{3}{4}\) तो cos A और tan A के मान परिकलित कीजिए।
हल:
माना कि ABC एक समकोण Δ है जिसमें
∠B = 90°

∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC

माना कि BC = 3k तथा AC = 4k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ (4k)² = AB² + (3k)²
⇒ 16k² = AB² + 9k²
⇒ AB² = 16k² – 9k²
⇒ AB² = 7k²
AB² = 7k²
AB = k\(\sqrt{7}\)


अतः cos A = \(\frac{\sqrt{7}}{4}\) तथा tan A = \(\frac{3}{\sqrt{7}}\)

प्रश्न 4.
यदि 15 cot A = 8 हो, तो sin A और sec A के मान ज्ञात कीजिए।
हल:
माना कि ABC एक समकोण Δ है, जिसमें ∠B = 90°.

∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC
15 cot A = 8 (दिया है)
⇒ cot A = \(\frac{8}{15}\)

माना कि AB = 8k
तथा BC = 15k
समकोण ΔABC में,
AC² = AB² + BC²
= (8k)² + (15k)²
= 64k² + 225k²
= 289k²
AC = \(\sqrt{289 k^2}\)
∴ AC = 17k

प्रश्न 5.
यदि sec θ = \(\frac{13}{12}\) हो, तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
हल:
माना कि ABC एक समकोण Δ है, जिसमें ∠B = 90° और ∠A = θ है।
∠θ के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC

माना कि AC = 13k और AB = 12k
समकोण ΔABC में,
AC² = AB² + BC²
(13k)² = (12k)² + BC²
BC² = (13k)² – (12k)²
= 169k² – 144k² = 25k²
∴ BC = 5k

प्रश्न 6.
यदि ∠A और ∠B न्यूनकोण हैं, जहाँ cos A = cos B, तो दिखाइए कि ∠A = ∠B.
हल:
माना कि ABC एक समकोण Δ है, जिसमें कोण C = 90°, तब ∠A तथा ∠B न्यूनकोण होंगे।

दिया है : cos A = cos B
⇒ \(\frac{A C}{A B}=\frac{B C}{A B}\)
⇒ AC = BC
ABC में, AC = BC
∵ ΔABC एक समद्विबाहु Δ है और बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
∴ ∠A = ∠B

प्रश्न 7.
यदि cot θ = \(\frac{7}{8}\), तो
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ का मान निकालिए।
हल:
माना कि ABC एक समकोण त्रिभुज है, जिसमें ∠B = 90° और ∠A = θ है।
आधार = AB, लम्ब = BC तथा कर्ण = AC

माना कि AB = 7k तथा BC = 8k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (7k)² + (8k)²
= 49k² + 64k² = 113k²
AC = ±\(\sqrt{113 k^2}\)
∴ AC = k\(\sqrt{113}\)
(∵ AC ≠ k\(\sqrt{113}\), क्योंकि भुजा ऋणात्मक नहीं हो सकती है)

[सूत्रः (a + b) (a – b) = a² – b² से]

प्रश्न 8.
यदि 3 cot = A, तो जाँच कीजिए कि \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A है या नहीं।
हल:
माना कि ABC एक समकोण Δ है, जिसमें कोण B समकोण है।
∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC
दिया है, 3 cot A = 4
cot A = \(\frac{4}{3}\)

माना कि AB = 4k, BC = 3k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (4k)² + (3k)²
= 16k² + 9k² = 25k²
⇒ AC = ±\(\sqrt{25 k^2}\)
∴ AC = 5k
[∵ AC ≠ -5k, क्योंकि भुजा ऋणात्मक नहीं हो सकती है]

R.H.S. = cos² A – sin² A
= \(\left(\frac{4}{5}\right)^2-\left(\frac{3}{5}\right)^2\)
= \(\frac{16}{25}-\frac{9}{25}\)
= \(\frac{16-9}{25}=\frac{7}{25}\) …(2)
L.H.S. = R.H.S.
अर्थात् \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A

प्रश्न 9.
त्रिभुज ABC में, जिसका कोण B समकोण है, यदि tan A = \(\frac{1}{\sqrt{3}}\) तो निम्नलिखित के मान ज्ञात कीजिए:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
हल:
दिया है, एक ΔABC, जिसका कोण B समकोण

माना कि AB = \(\sqrt{3}\)k तथा BC = k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (\(\sqrt{3}\)k)² + (k)²
= 3k² + k² = 4k²
⇒ AC = ±2k
∴ AC = 2k
(AC ≠ -2k, क्योंकि दूरी ऋणात्मक नहीं हो सकती)
∠A के लिए,
आधार = AB, लम्ब = BC, कर्ण = AC

प्रश्न 10.
ΔPQR में, जिसका कोण Q समकोण है, PR + QR = 25 सेमी और PQ = 5 सेमी है। sin P, cos P और tan P के मान ज्ञात कीजिए।
हल:
दिया है, ΔPQR में कोण Q समकोण है।

तथा PR + QR = 25 सेमी
PQ = 5 सेमी
माना कि QR = x सेमी
∴ PR = (25 – x) सेमी
अब समकोण ΔPQR में, पाइथागोरस प्रमेय से,
PR² = QR² + PQ²
(25 – x)² = (x)² + (5)²
625 – 50x + x² = x² + 25
– 50x = -600
x = \(\frac{-600}{-50}\) = 12 सेमी
∴ QR = 12 सेमी
PR = 25 – 12 = 13 सेमी

प्रश्न 11.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए:
(i) tan A का मान सदैव 1 से कम होता है।
(ii) कोण A के किसी मान के लिए sec A = \(\frac{12}{5}\)
(iii) cos A, कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) cot A, cot और A का गुणनफल होता है।
(v) किसी भी कोण θ के लिए sin θ = \(\frac{4}{3}\)
हल:
(I) ∵ tan A = लम्ब / आधार
tan A का मान 1 से कम तभी हो सकता है, जब लम्ब, आधार से छोटा हो।
परन्तु ऐसा सदैव होना आवश्यक नहीं है।
अतः कथन असत्य है।

(ii) sec A = कर्ण / आधार = \(\frac{12}{5}\)
चूँकि sec A का मान सदैव 1 के बराबर या 1 से बड़ा होता है।
अतः कथन सत्य है।

(iii) ∵ cos A कोण A की cosine का संक्षिप्त रूप होता है, जबकि cosecant का अर्थ cosec A है।
अतः दिया हुआ कथन असत्य है।

(iv) cot A का अर्थ ∠A के cotangent से है।
स्वतन्त्र रूप में cot का कोई अस्तित्व ही नहीं है। अतः cot और A का गुणनफल कभी भी cot A नहीं हो सकता है।
अतः दिया हुआ कथन असत्य है।

(v) किसी समकोण त्रिभुज में कोण θ के लिए, यदि sin θ = \(\frac{4}{3}\), तो इसका अर्थ है कि θ की सम्मुख भुजा
और कर्ण का अनुपात 4 : 3 है।
परन्तु कर्ण, समकोण त्रिभुज की सबसे बड़ी भुजा होती है।
अतः दिया गया कथन असत्य है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 1 Real Numbers Ex 1.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 1 Real Numbers Exercise 1.2

Question 1.
Express each number as a product of its prime factors:
1. 140
2. 156
3. 3825
4. 5005
5. 7429
Solution:
1. Using factor tree method, we have

Thus, 140 = 2 × 2 × 5 × 7
= 2² × 5 × 7

2. Using factor tree method, we have

Thus, 156 = 2 × 2 × 3 × 13
= 2² × 3 × 13

3. Using factor tree method, we have

Thus, 3825 = 3 × 3 × 5 × 5 × 17
= 3² × 5² × 17

4. Using factor tree method, we have

Thus, 5005 = 5 × 7 × 11 × 13

5. Using factor tree method, we have

Thus, 7429 = 17 × 19 × 23

Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers:
1. 26 and 91
2. 510 and 92
3. 336 and 54
Solution:
1. Using factor tree method, we have

∴ 26 = 2 × 13 and 91 = 7 × 13
Then, LCM (26, 91) = 2 × 7 × 13 = 182 and HCF (26, 91) = 13
Now, LCM × HCF = 182 × 13 = 2366 and 26 × 91 = 2366.
Hence, LCM × HCF = product of the two numbers.

2. Using factor tree method, we have

∴ 510 = 2 × 3 × 5 × 17 and
92 = 2 × 2 × 23 = 2² × 23
Then,
LCM (510, 92) = 2² × 3 × 5 × 17 × 23
= 23,460
and HCF (510, 92) = 2
Now, LCM × HCF = 23,460 × 2 = 46,920
and 510 × 92 = 46,920
Hence, LCM × HCF = product of the two numbers.

3. Using factor tree method, we have

∴ 336 = 2 × 2 × 2 × 2 × 3 × 7
= 2⁴ × 3 × 7 and
54 = 2 × 3 × 3 × 3 = 2 × 3³
Then, LCM (336, 54) = 2⁴ × 3³ × 7 = 3024
and HCF (336, 54) = 2 × 3 = 6
Now, LCM × HCF = 3024 × 6 = 18,144 and
336 × 54 = 18,144.
Hence, LCM × HCF = product of the two numbers.

Question 3.
Find the LCM and HCF of the following integers by applying the prime factorisation method:
1. 12, 15 and 21
2. 17, 23 and 29
3. 8, 9 and 25
Solution:
1. Using factor tree method, we have

∴ 12 = 2 × 2 × 3 = 2² × 3, 15 = 3 × 5 and 21 = 3 × 7
Then,
LCM (12, 15, 21) = 2² × 3 × 5 × 7 = 420 and HCF (12, 15, 21) = 3.

2. 17 = 17 × 1, 23 = 23 × 1 and 29 = 29 × 1 as each of the given numbers is a prime.
Then, LCM (17, 23, 29) = 17 × 23 × 29
= 11,339
and HCF (17, 23, 29) = 1.

3. Using factor tree method, we have

∴ 8 = 2 × 2 × 2 = 2³, 9 = 3 × 3 = 3²
and 25 = 5 × 5 = 5²
Then, LCM (8, 9, 25) = 2³ × 3² × 5²
= 1800
and HCF (8, 9, 25) = 1.

Question 4.
Given that HCF (306, 657) = 9 find LCM (306, 657).
Solution:
We know, LCM (a, b) =

Taking a = 306 and b = 657, we get
LCM (306, 657) = \(\frac{306 \times 657}{\mathrm{HCF}(306,657)}\)
= \(\frac{306 \times 657}{9}\)
= 34 × 657
= 22,338
Thus, LCM (306, 657) = 22,338.

Question 5.
Check whether 6ⁿ can end with the digit 0 for any natural number n.
Solution:
If a number ends with digit 0, it would be divisible by 5 as well as 2. Hence, any number ending with digit 0, must have 2 and 5 both in its prime factorisation.
Now, 6ⁿ = (2 × 3)ⁿ = 2ⁿ × 3ⁿ for any natural number n. Thus, 6n has only two prime factors 2 and 3. So, the prime factorisation of 6ⁿ does not include 5 and hence 6ⁿ cannot end with digit 0 for any natural number n.

Question 6.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
7 × 11 × 13 + 13 = 13 (7 × 11 + 1)
= 13 (77 + 1)
= 13 (78)
= 13 × 2 × 3 × 13
(∵ 78 = 2 × 3 × 13)
= 2 × 3 × 13²
Thus, 7 × 11 × 13 + 13 can be expressed as a product of primes. Hence, 7 × 11 × 13 + 13 is a composite number.
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5(7 × 6 × 4 × 3 × 2 × 1 + 1)
= 5 (1008 + 1)
= 5 × 1009
Thus, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 can be expressed as a product of primes. Hence, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 is a composite number.

Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
Here, the LCM of the timings (in minutes) taken by Sonia and Ravi will answer the question satisfying all the conditions as mentioned in the question.
Now, 12 = 2 × 2 × 3 = 2² × 3 and
18 = 2 × 3 × 3 = 2 × 3².
Then, LCM (12, 18) = 2² × 3² = 36
Hence, after 36 minutes, Sonia and Ravi meet again at the starting point if they both start at the same point and at the same time and go in the same direction.

Students should go through these JAC Class 10 Maths Notes Chapter 11 रचनाएँ will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 11 रचनाएँ

भूमिका :
कक्षा IX में, हमने कुछ रचनाओं के बारे में सीखा था जैसे कि किसी रेखाखण्ड का लम्ब समभाजक खींचना, किसी कोण का समद्विभाजक खींचना, त्रिभुजों की रचनाएँ करना इत्यादि और उनका औचित्य भी दिया था। इस अध्याय में पिछली रचनाओं के ज्ञान का उपयोग करते हुए कुछ और रचनाओं के बारे में अध्ययन करेंगे। जैसे एक रेखाखण्ड का विभाजन, किसी त्रिभुज के समरूप दूसरे त्रिभुज की रचना, वृत्त पर स्पर्श रेखा की रचना इत्यादि।

→ रचना (Construction) : कल्पना करने और बनाने की कला।

→ समरूप आकृतियाँ (Similar figures) : ऐसी ज्यामितीय आकृतियाँ जिनका रूप (shape) समान है, परन्तु जरूरी नहीं कि आकार भी समान हो, समरूप आकृतियाँ कहलाती हैं।

→ चाप (Arc) : वक्र रेखा पर दो बिन्दुओं के बीच की दूरी चाप कहलाता है।

→ स्पर्श रेखा (Tangent) : एक सीधी रेखा जो वृत्त को सिर्फ एक बिन्दु पर स्पर्श करती है, स्पर्श रेखा कहलाती है।

→ स्पर्श बिन्दु (Point of Contact) : वह बिन्दु जिस पर स्पर्श रेखा वृत्त को स्पर्श करती है, स्पर्श बिन्दु कहलाता है।

→ संकेन्द्रीय वृत्त (Concentric circles) : यदि दो वृत्तों का केन्द्र एक हो तथा विभिन्न त्रिज्याएँ हो, संकेन्द्रीय वृत्त कहलाते हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Exercise 8.4

प्रश्न 1.
त्रिकोणमितीय अनुपातों sin A, sec A और tan A को cot A के पदों में व्यक्त कीजिए।
हल:

प्रश्न 2.
∠A के अन्य सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।
हल:
(i) ∵ sin² A + cos² A = 1
⇒ sin² A = 1 – cos² A

(ii) cos A = \(\frac{1}{\sec A}\)
(iii) 1 + tan² = sec² A
⇒ tan²A = sec² A – 1
⇒ (tan A)² = sec² A – 1
अत: tan A = \(\sqrt{\sec ^2 A-1}\)

प्रश्न 3.
मान निकालिए:
(i) \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)
(ii) sin 25° cos 65° + cos 25° sin 65°
हल:

= \(\frac{\cos ^2 27^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\sin ^2 17^{\circ}}\)
{∵ sin (90° – θ) = cos θ
और a cos (90° – θ) = sin θ}
= \(\frac{1}{1}\) = 1 = (∵ sin² θ + cos² θ = 1)

(ii) sin 25° cos 65° + cos 25° sin 65° = sin 25° cos (90° – 25°) + cos 25° sin (90° – 25°)
= sin 25°.sin 25° + cos 25°.cos 25°
[∵ cos (90° – 25°) = sin 25°
और sin (90° – 25°) = cos 25°]
= sin² 25° + cos² 25°
= 1

प्रश्न 4.
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए:
(i) 9 sec² A – 9 tan² A बराबर है:
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 + tan θ + see θ) (1 + cot θ – cosec θ) बराबर है:
(A) 0
(B) 1
(C) 2
(D) -1
(iii) (sec A + tan A) (1 – sin A) बराबर है:
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(iv) \(\frac{1+\tan ^2 A}{1+\cot ^2 A}\) बराबर है:
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A
हल:
(i) 9 sec² A – 9 tan² A
= 9(sec² A – tan² A)
(∵ sec² A = 1 + tan² A)
= 9(1 + tan² A – tan² A)
= 9 × (1) = 9
अत: सही विकल्प (B) है।

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)


(∵ sin² θ + cos² θ = 1)
अत: सही विकल्प (C) है।

(iii) (sec A + tan A) (1 – sin A)

अत: सही विकल्प (D) है।

अत: सही विकल्प (D) है।

प्रश्न 5.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यूनकोण हैं:

हल:

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A
L.H.S.
= (sin A + cosec A)² + (cos A + sec A)²
= (sin² A + cosec² A + 2 sin A cosec A) + (cos² A + sec² A + 2 cos A sec A)
= (sin² A + cosec² A + 2 sin A × \(\frac{1}{\sin A}\)) + (cos² A + sec² A + 2 × cos A × \(\frac{1}{\cos A}\))
= (sin² A + cosec² A + 2) + (cos² A + sec² A + 2)
= sin² A + cosec² A + cos² A + sec² A + 4
= sin² A + cos² A + cosec² A + sec² A + 4
= 1 + cosec² A + sec² A + 4 [∵ sin² θ + cos² θ = 1]
= cosec² A + sec² A + 5
= (1 + cot² A) + (1 + tan² A) + 5
[∵ cosec² θ = 1 + cot² θ]
sec² θ = 1 + tan² θ]
= tan² A + cot² A + 7 = R.H.S.
∴ L.H.S. = R.H.S.

(ix) (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)

Students should go through these JAC Class 10 Maths Notes Chapter 1 वास्तविक संख्याएँ will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 1 वास्तविक संख्याएँ

भूमिका :
हमने पिछली कक्षाओं में प्राकृतिक संख्याओं, पूर्ण संख्याओं, परिमेय संख्याओं अपरिमेय संख्याओं व वास्तविक संख्याओं के विषय में पढ़ा है। हमने इनके गुणों के विषय में भी पढ़ा है स्मरण करें कि वास्तविक संख्याएँ परिमेय संख्याओं और अपरिमेय संख्याओं का समूह होती हैं।

इस अध्याय में हम \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\) आदि की अपरिमेयता सिद्ध करने, परिमेय संख्याओं का दशमलव प्रसार, सांत आवर्ती दशमलवं प्रसार, यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग, अंकगणित की आधारभूत प्रमेव यूक्लिड विभाजन प्रमेविका आदि के विषय में अध्ययन करेंगे।
→ वास्तविक संख्याएँ (Real Numbers) : परिमेय संख्या और अपरिमेय संख्याओं के समूह को वास्तविक संख्याएँ कहते हैं।
जैसे 3, 5, \(\sqrt{7}\), \(\frac{-\sqrt{3}}{2}\) आदि।

→ परिमेय संख्याएँ (Rational numbers): वे संख्याएँ जिनका दशमलव प्रसार सांत अथवा असांत आवर्ती होता परिमेय संख्याएँ कहलाती हैं। इन्हें \(\frac{p}{q}\) (जहाँ q ≠ 0) के रूप में लिखा जा सकता है।
जैसे- \(\frac{2}{4}\), 3, \(\frac{1}{3}\) आदि।

→ अपरिमेय संख्याएँ (Irrational numbers): वे संख्याएँ जिनका दशमलव प्रसार असांत तथा अनावर्ती होता है. अपरिमेय संख्याएँ कहलाती हैं।
जैसे- \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt[3]{4}\), π आदि ।

→ पूर्णांक (Integers): शून्य प्राकृतिक संख्याओं एवम् ऋणात्मक प्राकृतिक संख्याओं के समूह की पूणांक कहते हैं।
जैसे- -9, -8, 0, 5, 4, आदि।

→ सम संख्याएँ (Even numbers): वे संख्याएँ जो 2 से विभाजित होती हैं, सम संख्याएँ कहलाती है।
जैसे- 2, 4, 6, 8, 10 ….. (सम संख्याओं में इकाई का अंक 0, 2, 4, 6, 8 होता है।)

→ विषम संख्याएँ (Odd numbers): वे संख्याएँ जो 2 से विभाजित नहीं होती हैं, विषम संख्याएँ कहलाती हैं।
जैसे- 1, 3, 5, 7, 9, …. (विषम संख्याओं में इकाई का अंक 1, 3, 5, 9 होता है।)

→ अभाज्य संख्याएँ (Prime numbers): वे संख्याएँ जिनके सिर्फ दो गुणनखंड (1 व स्वयं) होते हैं, अभाज्य संख्याएँ कहलाती हैं अथवा वे संख्याएँ जो या स्वयं से विभाजित होती हैं, अभाज्य संख्या कहलाती हैं।
जैसे- 2, 5, 7, 11, 13, ….. ( सबसे छोटी अभाज्य संख्या 2 होती है।)

→ भाज्य संख्याएँ (Composite numbers): वे संख्याएँ जिनके और स्वयं के अलावा कम से कम एक और “गुणनखण्ड हो, भाज्य संख्याएँ कहलाती हैं।
जैसे- 4, 6, 8, 9, 10, 12, …
महत्वपूर्ण बिन्दु: 1 न तो अभाज्य संख्या है और न ही भाज्य संख्या।

→ सांत दशमलव प्रसार (Terminating decimal expansion): जिन परिमेय संख्याओं के हर 2ⁿ × 5^m के रूप में होते हैं, उनके दशमलव प्रसार सांत होते हैं।
जैसे \(\frac{2}{4}\) = 0.5, \(\frac{1}{5}\), 0.2, \(\frac{10}{25}=\frac{2}{5}\) = 0·4

→ असांत आवर्ती दशमलव प्रसार (Non-terminating recurring decimal expansion): जिन परिमेय संख्याओं के हर 2ⁿ × 5^m के रूप में नहीं होते हैं, उन परिमेय संख्याओं के दशमलव प्रसार असांत आवर्ती होते हैं।
जैसे \(\frac{1}{3}\) = 0.333, …. \(\frac{17}{6}\) = 2.8333…

→ लघुत्तम समापवर्त्य (LCM): दी गयी संख्याओं के छोटे से छोटे सार्वगुणज को लघुत्तम समापवर्त्य कहते हैं।

→ महत्तम समापवर्त्य (HCF): दी गयी संख्याओं के बड़े से बड़े सार्व गुणनखंड को महत्तम समापवर्तक कहते हैं।

पूर्णांकों की भाजकता तथा धनात्मक पूर्णांकों के दो महत्वपूर्ण गुण-
(i) यूक्लिड विभाजन एल्गोरिथ्म ( कलन विधि) (Euclid’s Division Algorithm ): यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग इस अध्याय में दो धनात्मक पूर्णांकों के महत्तम समापवर्तक (HCF) परिकलित करने में करेंगे।
(ii) अंकगणित की आधारभूत प्रमेय (Fundamental Theorem of Arithmetic ): अंकगणित की आधारभूत प्रमेय का प्रयोग दो अनुप्रयोगों में करेंगे:
(i) प्रथम अनुप्रयोग में कुछ संख्याओं जैसे \(\sqrt{2}\), \(\sqrt{3}\) और \(\sqrt{5}\) आदि की अपरिमेयता सिद्ध करने में करेंगे। (ii) किसी दी गई संख्या के अभाज्य गुणनखण्ड ज्ञात करने में करेंगे।

यूक्लिड विभाजन प्रमेविका :
यूक्लिड प्रथम यूनानी गणितज्ञ थे, जिन्होंने समतल ज्यामिति के अध्ययन हेतु एक नई विचारधारा को प्रारम्भ किया जिसमें से एक यूक्लिड विभाजन प्रमेयिका है। इसके अनुसार एक धनात्मक पूर्णांक a को किसी अन्य धनात्मक पूर्णांक b से विभाजित करने पर भागफल q और शेषफल r प्राप्त होता है तथा शेषफल r या तो शून्य होता है या भाजक b से छोटा होता है अर्थात् 0 ≤ r < b होता है।

यही यूक्लिड की विभाजन प्रमेयिका है।
इसे औपचारिक रूप से निम्न प्रकार व्यक्त कर सकते हैं:
यदि a और b दो धनात्मक पूर्णांक हैं तो दो ऐसे अद्वितीय पूर्णांक q और r विद्यमान होते हैं कि
a = bq + r, जहाँ 0 ≤ r < b
ध्यान रहे कि या शून्य भी हो सकते हैं।
साधारण शब्दों में, भाज्य (a) = भाजक (b) × भागफल (q) + शेषफल (r)

अंकगणित की आधारभूत प्रमेय :
प्रत्येक भाज्य संख्या को अभाज्य संख्याओं के एक गुणनफल के रूप में व्यक्त (गुणनखंडित) किया जा सकता है तथा यह गुणनखंडन अभाज्य गुणनखंडों के आने वाले क्रम के बिना अद्वितीय होता है अर्थात् इस पर कोई ध्यान दिए बिना कि अभाज्य गुणनखंड किस क्रम में आ रहे हैं।

उदाहरण के लिए :
44 एक भाज्य संख्या है। इसे 2 × 2 × 11 अथवा 11 × 2 × 2 के रूप में लिखा जा सकता है। यदि हम 2 × 2 × 11 अथवा 11 × 2 × 2 के क्रम पर ध्यान नहीं देते अर्थात् यदि 2 × 2 × 11 और 11 × 2 × 2 में कोई अन्तर नहीं है, तो यह गुणनखण्ड अद्वितीय भी है।
दो संख्याओं के म. स. तथा ल.स. में सम्बन्ध- दो संख्याओं के म. स. तथा ल.स. का गुणनफल उन संख्याओं के गुणनफल के बराबर होता है। अर्थात्
म.स. (H.C.F.) × ल.स. (L.C.M.) = एक संख्या (a) × दूसरी संख्या (b)
यदि दो संख्याएँ a और b हों, तो
H.C.F. × L.C.M. = a × b
इस मुख्य सम्बन्ध की सहायता से निम्नांकित सम्बन्ध भी लिखे जा सकते हैं-
(i) H.C.F. = \(\frac{a \times b}{\text { L.C.M }}\)
(ii) L.C.M. = \(\frac{a \times b}{\text { H.C.F. }}\)
(iii) a = \(\frac{\text { H.C.F. } \times \text { L.C.M. }}{b}\)
(iv) b = \(\frac{\text { H.C.F. } \times \text { L.C.M. }}{a}\)

अपरिमेय संख्याओं का पुनभ्रमण :
अपरिमेय संख्याएँ: वे संख्याएँ जिनका दशमलव प्रसार असान्त (Non-terminating) और अनावर्ती (Non-repeating) हो, अपरिमेय संख्याएँ कहलाती हैं। इन संख्याओं को \(\frac{p}{q}\) के रूप में व्यक्त नहीं किया जा सकता; जहाँ p और q पूर्णांक है और q ≠ 0.
उदाहरण : \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{15}\), π, \(\frac{-\sqrt{2}}{\sqrt{3}}\), 0.10110111011110…….. इत्यादि।
हम विरोधाभास विधि द्वारा संख्याओं की अपरिमेयता को सिद्ध करते हैं।

परिमेय संख्याओं और उनके दशमलव प्रसारों का पुनभ्रमण :
कोई भी परिमेय संख्या जिसका दशमलव प्रसार सांत है, उसे हम एक ऐसी परिमेय संख्या के रूप में लिख सकते हैं जिसका हर 10 की कोई घात होती है अर्थात् कोई भी 10 की धनात्मक घात को 2 और 5 की घातों के गुणनफल के रूप में व्यक्त कर सकते हैं।
जैसे 10ⁿ = (2 × 5)ⁿ ⇒ 2ⁿ × 5ⁿ
10² = 2² × 5²
10³ = 2³ × 5³ इत्यादि
अतः जिन परिमेय संख्याओं के दशमलव प्रसार सांत होते हैं, उनके हर 2ⁿ × 5^m के रूप में होते हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.2

प्रश्न 1.
आकृति (i) और (ii) में DE || BC है। (i) में, EC और (ii) में AD ज्ञात कीजिए।

अथवा
यदि ΔABC में DE || BC है, AD = 1.5 सेमी, BD = 3 सेमी तथा AE = 1 सेमी हो, तो EC ज्ञात कीजिए।
हल:
(i) ΔABC में,
DE || BC (दिया है)
(आधारभूत समानुपातिक प्रमेय से)
\(\frac{A D}{D B}=\frac{A E}{E C}\)
⇒ \(\frac{1.5}{3}=\frac{1}{E C}\)
⇒ EC = \(\frac{3}{1.5}\)
∴ EC = 2 सेमी

(ii) ΔABC में,
DE || BC (आधारभूत समानुपातिक प्रमेय से)

प्रश्न 2.
किसी ΔPQR की भुजाओं PQ और PR पर क्रमशः बिन्दु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
(i) PE = 3.9 सेमी, EQ = 3 सेमी, PF = 3.6 सेमी और FR = 2.4 सेमी।
(ii) PE = 4 सेमी, QE = 4.5 सेमी, PF = 8 सेमी और RF = 9 सेमी।
(iii) PQ = 1.28 सेमी, PR = 2.56 सेमी, PE = 0.18 सेमी और PF = 0.36 सेमी।
हल:
ΔPQR में दो बिन्दु E और F क्रमश: PQ और PR भुजाओं पर स्थित हैं।

(i) PE = 3.9 सेमी, EQ = 3 सेमी, PF = 3.6 सेमी और FR = 2.4 सेमी,

अत: EF, QR के समान्तर नहीं है।

(ii) PE = 4 सेमी, QE = 4.5 सेमी, PF = 8 सेमी और RF = 9 सेमी,
\(\frac{P E}{Q E}=\frac{4}{4.5}=\frac{40}{45}=\frac{8}{9}\) …(1)
तथा \(\frac{P F}{R F}=\frac{8}{9}\) …(2)
समीकरण (1) व (2) से,
\(\frac{P E}{Q E}=\frac{P F}{R F}\)
(आधारभूत आनुपातिकता प्रमेय के विलोम से)
अत: EF || QR

(iii) PQ = 1.28 सेमी, PR = 2.56 सेमी, PE = 0.18 सेमी, PF = 0.36 सेमी
EQ = PQ – PE
= 1.28 – 0.18 = 1.10 सेमी
FR = PR – PF
= 2.56 – 0.36 = 2.20 सेमी

समीकरण (1) व (2) से,
\(\frac{P E}{E Q}=\frac{P F}{F R}\)
(आधारभूत आनुपातिकता प्रमेय के विलोम से)
अत: EF || QR

प्रश्न 3.
निम्न आकृति में, यदि LM || CB और LN || CD हो, तो सिद्ध कीजिए कि \(\frac{A M}{A B}=\frac{A N}{A D}\) है।

हल:
ΔABC में,
ML || BC (दिया है)
∴ \(\frac{A M}{M B}=\frac{A L}{L C}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
∴ पुन: ΔADC में,
LN || DC (दिया है)
\(\frac{A N}{N D}=\frac{A L}{L C}\) …(ii)
(आधारभूत आनुपातिकता प्रमेय से)

प्रश्न 4.
निम्न चित्र में, DE || AC और DF || AE है। सिद्ध कीजिए कि \(\frac{B F}{F E}=\frac{B E}{E C}\) है।

हल:
दिया है : ΔABC में भुजा AB पर एक बिन्दु D हैं और भुजा BC पर दो बिन्दु E व F हैं। रेखाखण्ड DF, DE व AE खींचे गये हैं।
सिद्ध करना है : \(\frac{B F}{F E}=\frac{B E}{E C}\)
उपपत्ति : ΔBCA में, DE || AC (दिया है)
∴ \(\frac{B E}{E C}=\frac{B D}{D A}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
पुन: ΔBEA में, DF || AE (दिया है)
∴ \(\frac{B F}{F E}=\frac{B D}{D A}\) …(ii)
(आधारभूत समानुपातिक प्रमेय से)
समीकरण (i) व (ii) से,
\(\frac{B F}{F E}=\frac{B E}{E C}\) इति सिद्धम्।

प्रश्न 5.
निम्न चित्र में, DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।

हल:
दिया है दी गई आकृति में DE || OQ तथा DF || OR है।
सिद्ध करना है : EF || QR
उपपत्ति : ΔPOQ में,
DE || OQ
\(\frac{P E}{E Q}=\frac{P D}{D O}\) …(i)
(आधारभूत आनुपातिकता प्रमेव से)
पुन: ΔPOR में,
DF || OR
\(\frac{P F}{F R}=\frac{P D}{D O}\) …(ii)
(आधारभूत आनुपातिकता प्रमेव से)
समीकरण (i) व (ii) से,
\(\frac{P E}{E Q}=\frac{P F}{F R}\)
अब ΔPQR में,
\(\frac{P E}{E Q}=\frac{P F}{F R}\)
(आधारभूत अनुपातिकता प्रमेय के विलोम से)
∴ EF || QR इति सिद्धम्।

प्रश्न 6.
निम्न चित्र में क्रमश: OP, OQ और OR पर स्थित बिन्दु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।

हल:
दिया है : ΔPQR में बिन्दु A, B और C क्रमश: OP, OQ और OR पर इस प्रकार स्थित हैं कि AB || PQ और AC || PR
सिद्ध करना है : BC || QR
उपपत्ति : ΔPQO में,
AB || PQ (दिया है)
\(\frac{O A}{A P}=\frac{O B}{B Q}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
पुन: ΔPRO में,
AC || PR
\(\frac{O A}{A P}=\frac{O C}{C R}\) …(ii)
(आधारभूत समानुपातिक प्रमेय से)
समीकरण (i) व (ii) से,
\(\frac{O B}{B Q}=\frac{O C}{C R}\)
(आधारभूत समानुपातिक प्रमेय के विलोम से)
ΔCQR में, BC || QR. इति सिद्धम्।

प्रश्न 7.
प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य बिन्दु से होकर दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
हल:
दिया है : ΔABC में; D, AB का मध्य- बिन्दु है अर्थात् AD = DB है।
BC के समान्तर रेखा l, AB व AC को क्रमश: D तथा E बिन्दु पर प्रतिच्छेद करती है।
सिद्ध करना है : E, AC का मध्य- बिन्दु है।

उपपत्ति: ∵ D, AB का मध्य बिन्दु है (दिया है)
∴ AD = DB
\(\frac{A D}{B D}=1\) …(i)
ΔABC में DE || BC
\(\frac{A D}{D B}=\frac{A E}{E C}\)
(आधारभूत समानुपातिक प्रमेय से)
\(1=\frac{A E}{E C}\)
[समी. (i) के प्रयोग से]
AE = EC
∴ E, AC का मध्यबिन्दु है। इति सिद्धम्।

प्रश्न 8.
प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं।)
हल:
दिया है ΔABC में, AB तथा AC के मध्य-बिन्दु क्रमश: D और E हैं अर्थात् AD = BD और AE = EC हैं। D को E से मिलाया।

सिद्ध करना है: DE || BC
उपपत्ति D, AB का मध्य बिन्दु है
∴ AD = BD (दिया है)
⇒ \(\frac{A D}{B D}=1\) …(i)
E, AC का मध्य- बिन्दु है।
∴ AE = EC
⇒ \(\frac{A E}{E C}=1\) …(ii)
समीकरण (i) व (ii) से,
⇒ \(\frac{A D}{B D}=\frac{A E}{E C}\)
(आधारभूत समानुपातिकता प्रमेय के विलोम से)
∴ DE || BC इति सिद्धम्।

प्रश्न 9.
ABCD एक समलम्ब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। दर्शाइए कि \(\frac{A O}{B O}=\frac{C O}{D O}\) हैं।

हल:
दिया है : समलम्ब चतुर्भुज ABCD है जिसमें AC और BD दो विकर्ण हैं, जो परस्पर O बिन्दु पर काटते हैं।
सिद्ध करना है : \(\frac{A O}{B O}=\frac{C O}{D O}\)
रचना : O से जाती हुई OE || CD खींची।
उपपत्ति: ΔADC में,
OE || DC
\(\frac{A E}{E D}=\frac{A O}{C O}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
समलम्ब चतुर्भुज ABCD में,
AB || CD
∴ OE || CD (रचना से)
OE || AB
अब ΔADB में,
OE || AB
\(\frac{E D}{A E}=\frac{D O}{B O}\)
⇒ \(\frac{A E}{E D}=\frac{B O}{D O}\) …(ii)
समीकरण (i) व समीकरण (ii) से,
\(\frac{A O}{C O}=\frac{B O}{D O}\)
⇒ AO × DO = BO × CO
⇒ \(\frac{A O}{B O}=\frac{C O}{D O}\) इति सिद्धम्।

प्रश्न 10.
एक चतुर्भुज ABCD के विकर्ण परस्पर हिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि \(\frac{A O}{B O}=\frac{C O}{D O}\) है। दर्शाइए कि ABCD एक समलम्ब है।

हल:
दिया है ABCD एक चतुर्भुज है जिसके विकर्णं AC तथा BD बिन्दु O पर एक दूसरे को इस प्रकार प्रतिच्छेद करते हैं कि
\(\frac{A O}{B O}=\frac{C O}{D O}\)
सिद्ध करना है : ABCD एक समलम्ब है।
रचना : O से OE || DC खींची।
उपपत्ति: ΔBDC में,
OE || DC
\(\frac{B O}{D O}=\frac{B E}{E C}\) …(i)
परन्तु दिया है, \(\frac{A O}{B O}=\frac{C O}{D O}\)
⇒ \(\frac{A O}{C O}=\frac{B O}{D O}\) … (ii)
समीकरण (i) व (ii) से,
\(\frac{A O}{C O}=\frac{B E}{E C}\)
⇒ \(\frac{C O}{A O}=\frac{E C}{B E}\)
∴ OE || AB
(आधारभूत आनुपातिक प्रमेय के विलोम से)
इसी प्रकार, OE || CD
⇒ AB || CD
अत: ABCD एक समलम्ब है। इति सिद्धम्।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 10 वृत्त Ex 10.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 10 वृत्त Exercise 10.2

प्रश्न सं. 1, 2, 3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।

प्रश्न 1.
एक बिन्दु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 सेमी तथा 2 की केन्द्र से दूरी 25 सेमी है। वृत्त की त्रिज्या है :
(A) 7 सेमी
(B) 12 सेमी
(C) 15 सेमी
(D) 24.5 सेमी
हल:
एक वृत्त जिसका केन्द्र O है। बाह्य बिन्दु Q से स्पर्श रेखा PQ की लम्बाई 24 सेमी तथा Q की केन्द्र O से दूरी 25 सेमी है।
∴ ∠QPO = 90° [प्रमेय 10.1 से]

समकोण ΔQPO में,
OQ² = PQ² + OP²
⇒ (25)² = (24)² + OP²
⇒ OP² = (25)² – (24)²
⇒ OP² = 625 – 576
⇒ OP² = 49
⇒ OP = \(\sqrt{49}\)
∴ OP = 7 सेमी
अतः सही विकल्प (A) है।

प्रश्न 2.
चित्र में, यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110, तो ∠PTQ बराबर है:

(A) 60°
(B) 70°
(C) 80°
(D) 90°
हल:
हम जानते हैं कि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्बवत् होती है।
∴ ∠OPT = 90°
तथा ∠OQT = 90°
अब चतुर्भुज POQT में,
∠POQ + ∠OQT + ∠PTQ + ∠TPO = 360°
⇒ 110° + 90° + ZPTO + 90° = 360°
⇒ ∠PTQ = 360° – 290°
∴ ∠PTQ = 70°
अतः सही विकल्प (B) है।

प्रश्न 3.
यदि एक बिन्दु से 0 केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ∠POA है:
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हल:
वृत्त का केन्द्र O है और बिन्दु P से PA व PB वृत्त पर स्पर्श रेखाएँ हैं जिनके बीच ∠APB = 80° है।

OA तथा OB वृत्त की त्रिज्याएँ हैं।
चूँकि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∠A = 90° और ∠B = 90°
∴ ∠AOB व ∠APB सम्पूरक हैं।
∠AOB + ∠APB = 180°
⇒ ∠AOB = 180° – ∠APB
⇒ ∠AOB = 180° – 80°
∴ ∠AOB = 100°
हम जानते हैं कि OP रेखा, ∠AOB को समद्विभाजित करती है।
∠POA = \(\frac{1}{2}\)∠AOB
= \(\frac{1}{2}\) × 100° = 50°
∠POA = 50°
अतः सही विकल्प (A) है।

प्रश्न 4.
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
हल:
दिया है एक वृत्त जिसका केन्द्र O तथा व्यास AB हैं। PQ और RS बिन्दु A व B पर स्पर्श रेखाएँ हैं।

सिद्ध करना है: PQ || RS
उपपत्ति: ∵ OA त्रिज्या है और PQ स्पर्श रेखा, OA त्रिज्या पर लम्ब है।
[प्रमेय 10.1 से ]
∴ ∠1 = 90°
इसी प्रकार,
RS ⊥ OB
∴ ∠2 = 90°
अब ∴ ∠1 = ∠2
परन्तु यह दो समान्तर रेखाओं के एकान्तर कोण हैं, जब एक तिर्यक रेखा उन्हें काटती है।
∴ PQ || RS
अतः किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर समान्तर होती हैं।

प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
हल:
दिया है: एक वृत्त जिसका केन्द्र O है। AB इसकी स्पर्श रेखा है जो वृत्त को P पर स्पर्श करती है।
सिद्ध करना है: लम्ब PQ वृत्त के केन्द्र O से जाता है।
उपपत्ति: यदि सम्भव हो, तो माना PQ, AB के लम्बवत् है, जो O से नहीं गुजरती है।
OP को मिलाया।

∵ वृत्त के बिन्दु पर स्पर्श रेखा, स्पर्श बिन्दु पर त्रिज्या के लम्बवत् होती है, इसलिए
AB ⊥ OP अर्थात् ∠OPB = 90°
तथा ∠QPB = 90° (रचना से)
∴ ∠QPB = ∠OPB, जो सम्भव नहीं है क्योंकि रेखाखण्ड OP रेखा PQ के बराबर नहीं हो सकता है।
यह हमारी कल्पना के विपरीत है।
अतः स्पर्श रेखा AB के स्पर्श बिन्दु P पर खींचा गया लम्ब PQ, वृत्त के केन्द्र से होकर जाता है।

प्रश्न 6.
एक बिन्दु A से, जो एक वृत्त के केन्द्र से 5 सेमी दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई 4 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
एक वृत्त जिसका केन्द्र ‘O’ है। वृत्त के बाहर इसके केन्द्र से 5 सेमी की दूरी पर कोई बिन्दु A है।
स्पर्श रेखा की लम्बाई = PA = 4 सेमी
∵ हम जानते हैं कि वृत्त पर स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∴ ∠OPA = 90°

समकोण ΔOPA में, पाइथागोरस प्रमेय से,
OA² = OP² + PA²
(5)² = OP² + (4)²
⇒ OP² = 25 – 16
⇒ OP² = 9
⇒ OP = \(\sqrt{9}\) ⇒ OP = 3 सेमी
अतः वृत्त की त्रिज्या 3 सेमी है।

प्रश्न 7.
दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 सेमी तथा 3 सेमी हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल:
माना O केन्द्र वाले दो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ OA तथा OP क्रमश: 5 सेमी व 3 सेमी हैं।
बड़े वृत्त की एक जीवा AB है जो छोटे वृत्त को बिन्दु P पर स्पर्श करती है।
∠OP ⊥ AB (प्रमेय 10.1 से)
∠OPA = 90°

∴ समकोण ΔOPA में, पाइथागोरस प्रमेय से,
AP² + OP² = OA²
⇒ AP² + (3)² = (5)²
⇒ AP² = (5)² – (3)²
= 25 – 9 = 16
∴ AP = 4 सेमी
परन्तु बड़े वृत्त में, जीवा AB पर केन्द्र O से OP लम्ब है।
∴ बिन्दु P, जीवा AB को समद्विभाजित करता है।
AP = BP = 4 सेमी
जीवा AB की लम्बाई = AP + BP
= 4 + 4
= 8 सेमी
अतः बड़े वृत्त की जीवा की लम्बाई 8 सेमी।

प्रश्न 8.
एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है। सिद्ध कीजिए:
AB + CD = AD + BC
हल:
दिया है: O केन्द्र वाले वृत्त के परिगत एक चतुर्भुज ABCD जिसकी भुजाएँ AB, BC, CD तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R और S पर स्पर्श करती हैं।

सिद्ध करना है: AB + CD = AD + BC
उपपत्ति: हम जानते हैं कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई बराबर होती है।
अब B, वृत्त के बाहर स्थित कोई बिन्दु है और BP, BQ वृत्त पर स्पर्श रेखाएँ हैं।
∴ BP = BQ …..(1)
इसी प्रकार, AP = AS …..(2)
और DR = DS …..(3)
और CR = CQ …..(4)
समीकरण (1), (2), (3) व (4) को जोड़ने पर,
BP + AP + DR+ CR = BQ + AS + DS + CQ
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC

प्रश्न 9.
आकृति में, XY तथा XY’ 0 केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A पर तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB = 90° है।

हल:
दिया है: XY तथा X’Y’, O केन्द्र वाले वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर एक अन्य स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है। OA तथा OB को मिलाया।

सिद्ध करना है: ∠AOB = 90°
रचना: OC मिलाया।
उपपत्ति: XY और X’Y’ वृत्त की दो स्पर्श रेखाएँ हैं, जो वृत्त को P और Q पर स्पर्श करती हैं। बिन्दु C से वृत्त की स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर काटती है।
∴ बिन्दु A से वृत्त पर AP व AC स्पर्श रेखाएँ हैं।
∴ AP = AC
ΔOPA तथा ΔOCA में,
OP = OC (वृत्त की त्रिज्याएँ)
AP = AC (बाह्य बिन्दु से वृत्त की स्पर्श रेखाएँ)
OA = OA (उभयनिष्ठ भुजा)
∴ ΔOPA ≅ ΔOCA (SSS सर्वांगसमता गुणधर्म से )
सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं।
∠POA = ∠AOC …..(1)
इसी प्रकार बिन्दु B से वृत्त पर BQ और BC स्पर्श रेखाएँ हैं।
अतः BQ = BC
ΔOQB तथा ΔOBC में,
OQ = OC (वृत्त की त्रिज्याएँ)
BQ = BC (बिन्दु B से वृत्त पर स्पर्श रेखाएँ)
OB = OB (उभयनिष्ठ भुजा)
∴ ΔOQB ≅ ΔOCB
⇒ ∠BOQ = ∠COB …..(2)
∵ ∠POA + ∠AOC + ∠COB + ∠BOQ = 180°
समीकरण (1) व (2) से,
⇒ ∠AOC + ∠AOC + ∠COB + ∠COB = 180°
⇒ 2(∠AOC + ∠COB) = 180°
⇒ ∠AOC + ∠COB = \(\frac{180^{\circ}}{2}\) = 90°
∴ ∠AOB = 90°

प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है।
हल:
दिया है: एक वृत्त जिसका केन्द्र O है। वृत्त के बाहर स्थित किसी बिन्दु P से PQ और PR दिए गए वृत्त पर स्पर्श रेखाएँ हैं।

सिद्ध करना है: ∠ROQ + ∠QPR = 180°
उपपत्ति : OQ त्रिज्या है तथा बिन्दु P से PQ स्पर्श रेखा है जो वृत्त को बिन्दु Q पर स्पर्श करती है।
∠OQP = 90°
[∵ स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है]
इसी प्रकार, ∠ORP = 90°
अब चतुर्भुज ROQP में,
∠ROQ + ∠PRO + ∠OQP + ∠QPR = 360°
⇒ ∠ROQ + 90° + 90° + ∠QPR = 360°
⇒ ∠ROQ + ∠QPR = 360° – 180°
⇒ ∠ROQ + ∠QPR = 180°
अत: ∠QPR, ∠ROQ का सम्पूरक है।

प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है।
हल:
दिया है: केन्द्र O वाले वृत्त के परिगत एक समान्तर चतुर्भुज ABCD खींचा जिसकी भुजाएँ वृत्त को क्रमश: E, F, G, H बिन्दुओं पर स्पर्श करती हैं।

सिद्ध करना है: ABCD एक समचतुर्भुज है।
उपपत्ति: ∵ बाहरी बिन्दु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लम्बाई समान होती है।
अब वृत्त के बाहर स्थित बिन्दु B से BE और BF वृत्त पर दो स्पर्श रेखाएँ हैं।
∴ BE = BF …..(1)
इसी प्रकार, AE = AH …..(2)
CG = CF …..(3)
तथा DG = DH …..(4)
समीकरण (1), (2), (3) व (4) को जोड़ने पर,
(BE + AE) + (CG + DG) = (BF + CF) + (AH+DH)
⇒ AB + CD = BC + AD …..(5)
∵ दिया है, ABCD एक समान्तर चतुर्भुज है।
∴ AB = CD
और BC = AD …..(6)
समान्तर चतुर्भुज की सम्मुख भुजाएँ
समीकरण (5) व (6) से,
AB + AB = BC + BC
⇒ 2AB = 2BC
⇒ AB = BC
∴ AB = BC = CD = AD
अत: ABCD एक समचतुर्भुज है।

प्रश्न 12.
4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाइयाँ क्रमशः 8 सेमी और 6 सेमी हैं। भुजाएँ AB और AC ज्ञात कीजिए।

हल:
4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक ΔABC खींचा गया है। त्रिभुज की भुजाएँ BC, CA, AB वृत्त को क्रमश: D, E F बिन्दुओं पर स्पर्श करती हैं।
∵ किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई समान होती है।
∴ AE = AF = x सेमी (माना)
CE = CD = 6 सेमी
और BF = BD = 8 सेमी
OF, OE, OA, OB तथा OC को मिलाया।

हम जानते हैं कि वृत्त की स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∴ OD ⊥ BC, OE ⊥ AC और OF ⊥ AB
ΔABC में, b = AC = (x + 6) सेमी
a = CB
= (6 + 8) सेमी = 14 सेमी
c = BA(8 + x) सेमी

ΔOBC का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × 14 × 4
= 28 सेमी² …..(2)
ΔBOA का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × (8 + x) × 4
= ( 16 + 2x ) सेमी² …..(3)
ΔAOC का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × (6 + x) × 4
= (12 + 2x) सोमी² …(4)
ΔABC का क्षेत्रफल = ΔOBC का क्षेत्रफल + ΔBOA का क्षेत्रफल + ΔAOC का क्षेत्रफल
\(\sqrt{48 x^2+672 x}\) = 28 + 16 + 2x + 12 + 2x
⇒ \(\sqrt{48 x^2+672 x}\) = 4x + 56
⇒ \(\sqrt{48 x^2+672 x}\) = 4(x + 14)
दोनों पक्षों का वर्ग करने पर
48x² + 672x = 16(x + 14)²
⇒ 48x(x + 14 ) = 16(x + 14)²
⇒ 3x = x + 14
⇒ 2x = 14
⇒ x = \(\frac{14}{2}\) = 7
∴ AC = (x + 6) सेमी
= (7 + 6) = 13 सेमी
और AB = (x + 8 ) सेमी
= (7 + 8) = 15 सेमी
अतः AB = 15 सेमी
और AC = 13 सेमी।

प्रश्न 13.
सिद्ध कीजिए कि वृत्त के परिगत बने चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
हल:
दिया है: केन्द्र O वाले वृत्त के परिगत बना चतुर्भुज PQRS जिसकी भुजाएँ PQ, QR, RS और SP वृत्त को क्रमश: L, M, N, T बिन्दुओं पर स्पर्श करती हैं।

सिद्ध करना है: ∠POQ + ∠SOR = 180°
और ∠SOP + ∠ROQ = 180°
रचना: वृत्त के केन्द्र O से P, Q, R, S, L, M, N तथा T को मिलाया।
उपपत्ति: OL, OM, ON तथा OT वृत्त की त्रिज्याएँ हैं तथा QL, MQ, RN तथा ST वृत्त पर स्पर्श रेखाएँ हैं।
QL ⊥ OL, QM ⊥ OM, RN ⊥ ON तथा ST ⊥ OT (प्रमेय 10.1 से)।
अब समकोण ΔOMQ तथा समकोण ΔOLQ में
∠OMQ = ∠OLQ (प्रत्येक 90° है)
कर्ण OQ = कर्ण OQ (उभयनिष्ठ भुजा)
तथा OM = OL (वृत्त की समान त्रिज्याएँ)
∴ ΔΟΜQ ≅ ΔΟLQ (RHS सर्वागसमता गुणधर्म से)
⇒ ∠3 = ∠2 (CPCT)
इसी प्रकार, ∠4 = ∠5
∠6 = ∠7 तथा ∠8 = ∠1
∵ वृत्त के केन्द्र बिन्दु पर बने सभी कोणों का योग 360° होता है।
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
⇒ ∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
⇒ 2(∠1 + ∠2 + ∠5 + ∠6) = 360°
⇒ (∠1 + ∠2) + (∠5 + ∠6) = 180°
∠POQ + ∠SOR = 180°
[∵ ∠1 + ∠2 = ∠POQ तथा ∠5 + ∠6 = ∠SOR]
इसी प्रकार ∠SOP + ∠ROQ = 180°
अतः वृत्त के परिगत बने चतुर्भुज के आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।