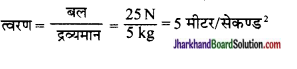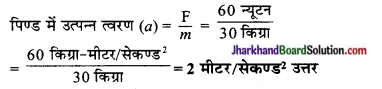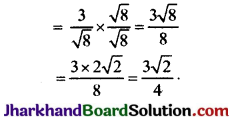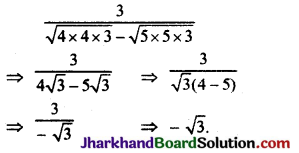Class 9

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 15 प्रायिकता Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 15 प्रायिकता

प्रश्न 1.
एक पाँसे को फेंकने पर 2 का अंक आने की प्रायिकता होगी:
(A) \(\frac {1}{6}\)
(B) \(\frac {2}{3}\)
(C) \(\frac {5}{6}\)
(D) \(\frac {1}{3}\)
हल :
पाँसे में 1, 2, 3, 4, 5 और 6 अंक होते हैं।
कुल सम्भव परिणाम = 6
अंक 2 केवल 1 बार है।
∴ 2 अंक आने की अनुकूल परिणाम = 1
2 का अंक आने की प्रायिकता P(E) = \(\frac {1}{6}\)
अतः विकल्प (A) सही है।

प्रश्न 2.
दो पाँसों को फेंकने पर अंकों का योग 5 आने की प्रायिकता होगी:
(A) \(\frac {1}{7}\)
(B) \(\frac {1}{6}\)
(C) \(\frac {1}{9}\)
(D) \(\frac {2}{9}\)
हल :
पाँसे में 1, 2, 3, 4, 5 और 6 अंक होते हैं।
योग 5 आने के लिए अनुकूल परिणाम (1, 4), (2, 3), (4, 1), (3, 2) = 4
दो पाँसे एकसाथ फेंकने पर सम्भावित परिणाम = 6 × 6 = 36
अतः योग 5 आने की प्रायिकता P(E) = \(\frac {4}{36}\)
= \(\frac {1}{9}\)
अत: विकल्प (C) सही है।

प्रश्न 3.
ताश की एक गड्डी में से एक लाल पत्ता खींचने की प्रायिकता होगी :
(A) \(\frac {1}{52}\)
(B) \(\frac {1}{2}\)
(C) \(\frac {1}{26}\)
(D) \(\frac {25}{26}\)
हल :
कुल सम्भावित परिणाम = ताश की गड्डी में कुल पत्तों की संख्या = 52
अनुकूल परिणाम = लाल रंग के पत्तों की संख्या = 26
अत: P(एक लाल रंग का पत्ता खींचने) की प्रायिकता = \(\frac{26}{52}=\frac{1}{2}\)
अतः विकल्प (B) सही है।

प्रश्न 4.
बारह टिकटों पर एक-एक संख्या 1 से 12 तक लिखी गई है। उनमें से एक टिकट का यादृच्छिक चयन किया जाए, तो इस पर लिखी गई संख्या के 3 के गुणज होने की प्रायिकता ज्ञात करो :
(A) \(\frac {2}{3}\)
(B) \(\frac {1}{12}\)
(C) \(\frac {1}{2}\)
(D) \(\frac {1}{3}\)
हल :
1 से 12 तक की संख्याओं में 3 के गुणज वाली संख्याएँ 3, 6, 9, 12 हैं।
∴ संख्या 3 के गुणज की अनुकूल परिणाम = 4
कुल सम्भावित परिणाम = 12
अतः संख्या 3 के गुणज होने की प्रायिकता
P(E) = \(\frac{4}{12}=\frac{1}{3}\)
अतः विकल्प (D) सही है।

प्रश्न 5.
एक सिक्के को 1000 बार उछालने पर निम्न- लिखित बारम्बारताएँ प्राप्त होती हैं चित : 455 ; पट : 545 प्रत्येक घटना की प्रायिकता अभिकलित कीजिए ।
हल :
अभिप्रयोगों की कुल संख्या = 1000
चित आने की संख्या = 455

प्रश्न 6.
एक पाँसे के फेंकने पर सम अंक आने की प्रायिकता ज्ञात कीजिए ।
हल :
एक पाँसे को फेंकने पर 6 अंक
(1, 2, 3, 4, 5, 6) आ सकते हैं।
सम अंकों की संख्या = 3 है।
∴ घटना के लिए अनुकूल स्थितियाँ = 3
सम अंक आने की प्रायिकता,
P(E) = अनुकूल स्थितियाँ / कुल संख्या
= \(\frac{3}{6}=\frac{1}{2}\)

प्रश्न 7.
एक ताश की गड्डी से एक पत्ता निकाला जाता है। इसके इक्का होने की प्रायिकता ज्ञात करो ।
हल :
ताश की गड्डी में कुल पत्तों की संख्या = 52
तथा ताश की गड्डी में इक्कों की संख्या = 4
∴ इक्का होने की अनुकूल परिस्थितियाँ = 4 होंगी।
∴ इक्का होने की प्रायिकता,
P(E) = \(\frac{4}{52}=\frac{1}{13}\)

प्रश्न 8.
दो सिक्कों को एक साथ 500 बार उछालने पर हमें यह प्राप्त होता है:
दो खित : 105 बार
एक चित : 275 बार
कोई भी चित नहीं : 120 बार
उनमें से प्रत्येक घटना के घटने की प्रायिकता ज्ञात कीजिए ।
हल :
माना दो चित आने की घटना को E₁ से, एक चित आने की घटना को E₂ से और कोई भी चित न आने की घटना को E₃ से व्यक्त करें, तो
दो चित आने की प्रायिकता, P(E₁) = \(\frac {105}{500}\) = 0.21
एक चित आने की प्रायिकता, P(E₂) = \(\frac {275}{500}\) = 0·55
कोई भी चित न आने की प्रायिकता P(E₃) = \(\frac {120}{500}\) = 0·24

प्रश्न 9.
एक पाँसे को फेंकने पर 4 से बड़ा अंक आने की प्रायिकता ज्ञात कीजिए ।
हल :
पाँसे में 1, 2, 3, 4, 5 और 6 अंक होते हैं जिनमें 5 तथा 6 दोनों 4 से बड़े अंक हैं।
∴ कुल सम्भावित परिणाम = 6
4 से बड़ा अंक आने की अनुकूल परिस्थितियाँ = 2 हैं।
अतः 4 से बड़ा अंक आने की प्रायिकता = \(\frac{2}{6}=\frac{1}{3}\)

प्रश्न 10.
PEACE शब्द के अक्षरों से बनने वाले शब्दों में दोनों E के साथ न आने की प्रायिकता ज्ञात कीजिए।
हल :
PEACE में कुल वर्ण = 5 हैं।
∴ कुल सम्भव स्थितियाँ = 5 होंगी।
PEACE में E अक्षर दो बार प्रयुक्त हुआ है।
∴ E अक्षर आने की अनुकूल स्थितियाँ = 2
दोनों E अक्षर एक साथ आने की प्रायिकता,
P(E) = \(\frac {2}{5}\)
अतः अक्षर न आने की प्रायिकता = 1 – P(E)
= 1 – \(\frac {2}{5}\) = \(\frac {3}{5}\)

प्रश्न 11.
एक पौसे को 1000 बार फेंकने पर प्राप्त परिणाम निम्न प्रकार हैं:

परिणाम	बारम्बारता
1 2 3 4 5 6	179 150 157 149 175 190

प्रत्येक परिणाम के प्राप्त होने की प्रायिकता ज्ञात कीजिए ।
हल :
पाँसा फेंकने की कुल संख्या = 1000
माना परिणाम 1, 2, 3, 4, 5 और 6 से घटना के घटित होने की प्रायिकता E₁, E₂, E₃, E₄, E₅ और E₆ है, तब

प्रश्न 12.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गये अंकों का प्रतिशत निम्न प्रकार है :

मिट परीक्षा	प्राप्त अंकों का %
I II III IV V	69 71 73 68 74

इन आंकड़ों के आधार पर 70% से अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
हल :
ली गई यूनिट परिक्षाओं की कुल संख्या = 5
विद्यार्थी द्वारा 70% से अधिक अंक प्राप्त करने वाली यूनिट परिक्षाओं की संख्या = 3
∴ 70% से अधिक अंक प्राप्त करने की अनुकूल स्थितियाँ = 3
अतः 70% से अधिक अंक प्राप्त होने की प्रायिकता,
P(E) = अनुकूल स्थितियाँ / कुल यूनिट परीक्षाओं की संख्या
= \(\frac {3}{5}\)
= 0.6

प्रश्न 13.
बीजों के 5 थैलों में से प्रत्येक थैले से पचास बीज यदृच्छया चुने और उन्हें ऐसी मानवीकृत अवस्थाओं में रखा गया जो अंकुरण के अनुकूल हैं। 20 दिन बाद प्रत्येक संग्रह में अंकुरित हुए बीजों की संख्या नीचे दर्शाए अनुसार सारणी में लिखी गई हैं:

थैला	अंकुरित बीजों की संख्या
1 2 3 4 5	40 48 42 39 41

निम्नलिखित बीजों के अंकुरण की प्रायिकता क्या होगी ?
(i) एक थैले में 40 से अधिक बीज,
(ii) एक थैले में 49 बीज,
(iii) एक थैले में 35 से अधिक बीज हैं।
हल :
पैलों की कुल संख्या = 5
(i) 50 बीजों में से 40 बीज से अधिक बीज अंकुरित होने की अनुकूल स्थितियाँ = 3
अत: P (एक थैले में 40 से अधिक बीजों का अंकुरण )
= \(\frac {3}{5}\)
= 0.6

(ii) 49 बीज अंकुरित होने वाले थैलों की संख्या = 0
अत: P (एक थैले में 49 बीजों का अंकुरण) = \(\frac {0}{5}\)
= 0

(iii) उन बैलों की संख्या, जिनमें 35 से अधिक बीज अंकुरित हुए हैं, 5 है।
अतः अपेक्षित प्रायिकता = \(\frac {5}{5}\)
= 1.

प्रश्न 14.
एक टेलीफोन निर्देशिका के एक पृष्ठ पर 200 टेलीफोन नम्बर हैं। उनके इकाई स्थान वाले अंक का बारम्बारता बंटन निम्न सारणी में दिया गया है :

अंक (इकाई)	बारम्बारता
0 1 2 3 4 5 6 7 8 9	22 26 22 20 10 25 14 22 20 19

इकाई के स्थान पर 6 अंक आने की प्रायिकता ज्ञात कीजिए ।
टेलीफोन नम्बरों की कुल संख्या = 200
हल :
इकाई के स्थान पर अंक 6 के होने की प्रायिकता,
P(E) = अंक 6 की बारम्बारता / टेलीफोन नम्बरों की कुल संख्या
= \(\frac {14}{200}\)
= 0.07.

प्रश्न 15.
एक पिता के तीन बच्चों में से कम से कम एक लड़का है। उसके दो लड़के तथा एक लड़की होने की प्रायिकता ज्ञात कीजिए।
हल :
लड़का और लड़की की संख्या की 3 निःशेष स्थितियाँ सम्भव हैं
एक लड़का व दो लड़कियाँ
एक लड़की व दो लड़के
तीनों लड़के व कोई लड़की नहीं
इनमें एक ही स्थिति अनुकूल है।
प्रायिकता (P) = \(\frac {1}{3}\)

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

प्रश्न 1.
यदि एक बेलन का वक्रपृष्ठ सिरों के क्षेत्रफल से दोगुना है तो उसकी ऊंचाई और त्रिज्या का अनुपात होगा :
(A) 1 : 2
(B) 1 : 1
(C) 2 : 1
(D) 2 : 3
हल :
माना बेलन की त्रिज्या r तथा ऊँचाई h है, तब वक्रपृष्ठ = 2 × सिरों का क्षेत्रफल
2πrh = 2 × 2πr²
h = 2r
\(\frac{h}{r}=\frac{2}{1}\) = 2 : 1
अत: विकल्प (C) सही है।

प्रश्न 2.
एक गोले का आयतन 36π घन सेमी है, तो उसकी त्रिज्या है:
(A) 3 सेमी
(B) 6 सेमी
(C) 2 सेमी
(D) 9 सेमी।
हल :
\(\frac {4}{3}\)πr³ = 36π
r³ = \(\frac{36 \times 3}{4}\) = 9 × 3
r = \(\sqrt{3 \times 3 \times 3}\) = 3 सेमी
अत: विकल्प (A) सही है।

प्रश्न 3.
किसी समकोण त्रिभुज की समकोण बनाने वाली किसी एक भुजा के परितः घुमाने पर निर्मित आकृति होगी
(A) बेलन
(B) प्रिज्म
(C) गोला
(D) शंकु
हल :
अत: विकल्प (D) सही है।

प्रश्न 4.
यदि दो शंकुओं की ऊंचाइयाँ बराबर हो तथा उनकी त्रिज्याओं का अनुपातः 4 : 7 हो तो उनके आयतनों का अनुपात होगा :
(A) 16 : 49
(B) 49 : 16
(C) 14 : 17
(D) 4 : 7
हल :
माना दोनों शंकुओं का त्रिज्याएँ क्रमशः 4x तथा 7x हैं:

= \(\frac {16}{49}\)
अतः सही विकल्प (A) है।

प्रश्न 5.
एक बेलनाकार बोतल का व्यास 10 सेमी है। यदि उसमें 14 सेमी ऊंचाई तक द्रव भरा हो, तो द्रव का आयतन है :
(A) 1200 घन सेमी
(B) 1100 घन सेमी
(C) 1500 घन सेमी
(D) 1150 घन सेमी।
हल :
बेलनाकार बोतल का व्यास = 10 सेमी
अतः बोतल की त्रिज्या (r) = व्यास / 2 = \(\frac {10}{2}\) = 5 सेमी
द्रव की ऊँचाई (h) = 14 सेमी
द्रव का आयतन = πr²h
= \(\frac {22}{7}\) × (5)² × 14 = \(\frac {22}{7}\) × 25 × 14
= 22 × 25 × 2 = 22 × 50
= 1100 घन सेमी
अत: सही विकल्प (B) है।

प्रश्न 6.
9 सेमी त्रिज्या के धातु के गोले को पिघलाकर 3 सेमी त्रिज्या और 6 सेमी ऊंचाई के शंकु बनाये जा सकने वाले शंकुओं की संख्या है :
(A) 54
(B) 45
(C) 55
(D) 44
हल :
9 सेमी त्रिज्या वाले गोले का आयतन
= \(\frac {4}{3}\)πr³ = \(\frac {4}{3}\) × π × (9)³
= \(\frac {4}{3}\) × π × 9 × 9 × 9
= 4 × π × 3 × 81 घन सेमी
अब 3 सेमी त्रिज्या और 6 सेमी ऊँचाई वाले शंकु का आयतन
= \(\frac {1}{3}\)πr²h = \(\frac {1}{3}\) × π × (3)² × 6
= \(\frac {1}{3}\) × π × 9 × 6
= π × 3 × 6 = 18π घन सेमी
शंकुओं की संख्या = गोले का आयतन / शंकु का आयतन
= \(\frac{4 \times \pi \times 3 \times 81}{\pi \times 3 \times 6}\) = 54
= \(\frac {972π}{18π}\) = 54
अत: (A) विकल्प सही है।

प्रश्न 7.
यदि दो गोलों की त्रिज्याओं का अनुपात 2 : 3 है, तो उनके आयतन का अनुपात है:
(A) 7 : 8
(B) 8 : 27
(C) 4 : 9
(D) 1 : 27
हल :
माना दोनों गोलों की त्रिज्याएँ क्रमश: r₁ और r₂ है।
दिया है, दोनों गोलों की त्रिज्याओं का अनुपात = r₁ : r₂ = 2 : 3
⇒ \(\frac{r_1}{r_2}=\frac{2}{3}\)
दोनों गोलों के आयतनों का अनुपात

अतः दोनों गोलों के आयतनों का अनुपात 8 : 27 होगा।
अत: सही विकल्प (B) है।

प्रश्न 8.
एक तार का व्यास 5% कम कर दिया जाए तो उसकी लम्बाई कितने प्रतिशत बढ़ा दी जाए कि आयतन न बदले ?
(A) 10%
(B) 10.8%
(C) 4%
(D) 2.5%
हल :
माना तार का व्यास = x सेमी
व्यास में कमी = 5%
नया व्यास \(\frac{95 x}{100}=\frac{19}{20}\)
तथा त्रिज्या = \(\frac {19}{40}\)x
माना त्रिज्याओं की कमी होने पर ऊँचाई h से बढ़कर h’ हो जाती है।
प्रश्नानुसार – π(\(\frac {19}{40}\)x)² h’ = π(\(\frac {x}{2}\))² h

प्रश्न 9.
एक लम्बवृत्तीय बेलन का आयतन 175π घन सेमी और ऊँचाई 7 सेमी है, तो उसका व्यास होगा।
(A) 5 सेमी
(B) 25 सेमी
(C) 10 सेमी
(D) 7 सेमी
हल :
बेलन का आयतन = πr²h
= 175π
r² × 7 = 175
r² = \(\frac {175}{7}\) = 25
r = \(\sqrt{25}\) = 25 सेमी
व्यास = 2 × r = 2 × 5 = 10 सेमी
अतः विकल्प (C) सही है।

प्रश्न 10.
यदि नल का बाहरी व्यास तथा भीतरी व्यास क्रमशः 4 सेमी तथा 3 सेमी और ऊंचाई 20 सेमी है, तो आयतन होगा। नल का आयतन = π(r₁r² – r₂r²)h
(A) π(4² – 3²) 20
(B) π[(2)² – (1.5)²]20
(C) π(4 – 3) 20
(D) π(2 – 1.5) 20.
हल :
नल का बाहरी व्यास तथा भीतरी व्यास क्रमश: 4 सेमी तथा 3 सेमी है।
∴ उसकी बाहरी तथा भीतरी त्रिज्याएँ क्रमशः \(\frac {4}{2}\) = 2
सेमी और \(\frac {3}{2}\) = 1.5 है।
अत: विकल्प (B) सही है।

प्रश्न 11.
14 सेमी भुजा के एक घन में से एक बड़े से बड़ा शंकु काटा जाता है। शंकु का आयतन होगा :

(A) 766.18 घन सेमी
(B) 817.54 घन सेमी
(C) 1232 घन सेमी
(D) 718.66 घन सेमी।
हल :
14 सेमी भुजा के घन से बड़े से बड़ा शंकु काटा जाता है।
अतः शंकु की ऊँचाई (h) = 14 सेमी
शंकु के आधार का व्यास = 14 सेमी
अतः शंकु की त्रिज्या = व्यास / 2 = \(\frac {14}{2}\) = 7 सेमी
शंकु का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × (7)² × 14
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × 7 × 7 × 14
= \(\frac {22}{3}\) × 7 × 14
= \(\frac{22 \times 98}{3}=\frac{2156}{3}\)
= 718.66 घन सेमी
अत: सही विकल्प (D) है।

प्रश्न 12.
एक लम्बवृत्तीय बन्द बेलन के आधार की त्रिज्या r और ऊँचाई h हो, तो उसके सभी पृष्ठों पर रंग कराने के लिए क्षेत्रफल होगा:
(A) 2πrh
(B) 2π(h + r)r
(C) πr²h
(D) 2πrh + πr².
हल :
बेलन के सभी पृष्ठों पर रंग कराने के लिए सम्पूर्ण पृष्ठीय क्षेत्रफल = 2π(h + r) r
अंत: सही विकल्प (B) है।

प्रश्न 13.
एक बेलन का आधार 625 वर्ग सेमी उसकी ऊँचाई 10 सेमी है, तो बेलन का आयतन होगा :
(A) 62.5 सेमी³
(B) 1320 सेमी³
(C) 6250 सेमी³
(D) 125 सेमी।³
हल :
बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई
= 625 × 10 = 6250 सेमी³
अत: सही विकल्प (C) है।

प्रश्न 14.
एक शंकु के आधार की त्रिज्या 7 सेमी और ऊंचाई 24 सेमी है। शंकु का पृष्ठीय क्षेत्रफल होगा :
(A) 25 सेमी²
(B) 550 सेमी²
(C) 189.6 सेमी²
(D) 134.09 सेमी²
हल :
दिया है,
शंकु के आधार की त्रिज्या (r) = 7 सेमी
और शंकु की ऊँचाई (h) = 24 सेमी
शंकु की तिर्यक ऊँचाई (l) = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(24)^2+(7)^2}\) = \(\sqrt{576+49}\)
= \(\sqrt{625}\)
शंकु की तिर्यक ऊँचाई (l) = 25 सेमी।
शंकु के वक्रपृष्ठ का क्षेत्रफल = πrl
= \(\frac {22}{7}\) x 7 x 25 = 22 × 25 550 वर्ग सेमी
अत: विकल्प (B) सही है।

प्रश्न 15.
यदि एक गोले का पृष्ठीय क्षेत्रफल 616 वर्ग सेमी हो तो उसकी त्रिज्या होगी :
(A) 7 सेमी
(B) 6 सेमी
(C) 4.5 सेमी
(D) 7.2 सेमी
हल
माना गोले की त्रिज्या r है।
गोले का पृष्ठीय क्षेत्रफल 616 वर्ग सेमी
4πr² = 616
⇒ r² = \(\frac{616}{4 \pi}=\frac{616 \times 7}{4 \times 22}\) = 7 × 7
⇒ r = \(\sqrt{7 \times 7}\)
∴ r = 7 सेमी।
अत: सही विकल्प (A) है

प्रश्न 16.
एक शंकु, अर्द्धगोला और बेलन एक ही आधार और समान ऊँचाई पर बने हैं। उनके आयतनों का अनुपात होगा :
(A) 2 : 1 : 3
(B) 1 : 2 : 3
(C) 3 : 1 : 2
(D) 1 : 3 : 2
हल :
माना शंकु, अर्द्ध त्रिज्या तथा बेलन की समान (एक ही आधार) r है गोला तथा ऊँचाई h है।
तब शंकु का आयतन V₁ = \(\frac {1}{3}\)πr²h
अर्द्ध गोले का आयतन V₂ = \(\frac {2}{3}\)πr³ = \(\frac {2}{3}\)πr²(h)
[∵ अर्द्ध-गोले में r = h]
= \(\frac {2}{3}\)πr²h
बेलन का आयतन V₃ = πr²h
V₁ : V₂ : V₃ = \(\frac {1}{3}\)πr²h : \(\frac {2}{3}\)πr²h : πr²h
= \(\frac {1}{3}\) : \(\frac {2}{3}\) : 1 = \(\frac {1}{3}\) × 3 : \(\frac {2}{3}\) × 3 : 1 × 3
V₁ : V₂ : V₃ = 1 : 2 : 3
अतः सही विकल्प (B) हैं।

प्रश्न 17.
सीसे के एक घन की कोर 11 सेमी है। घन को पिघलाकर 1 सेमी व्यास की गोलियाँ बनाई जा सकती हैं:
(A) 2541
(B) 2154
(C) 5245
(D) 1245.
हल :
घन का आयतन = (कोर)³
= (11)³ = 1331 घन सेमी
1 सेमी व्यास की गोली की त्रिज्या = व्यास / 2
गोली की त्रिज्या = \(\frac {1}{2}\) = 0.5 सेमी

प्रश्न 18.
एक लोहे के पाइप की लम्बाई 20 सेमी तथा बाह्य व्यास 25 सेमी है। यदि पाइप की मोटाई 1 सेमी हो, तो पाइप का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हल :
माना पाइप की बाह्य और अन्तः त्रिज्याएँ क्रमशः व हैं।
बाह्य त्रिज्या (r₁) = 12.5 सेमी
अन्तः त्रिज्या (r₂) = (बाह्य त्रिज्या – मोटाई)
= (12.5 – 1) = 11.5 सेमी
पाइप की लम्बाई (h) = 20 सेमी
अतः पाइप का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2π(r₁ + r₂) (h + r₁ – r₂)
= 2 × \(\frac {22}{7}\) × (12.5 + 11.5) × (20 + 12.5 – 11.5) वर्ग सेमी
= 2 × \(\frac {22}{7}\) × 24 × 21 वर्ग सेमी
= 3168 वर्ग सेमी।

प्रश्न 19.
एक बेलन की त्रिज्या और ऊँचाई का अनुपात 5 : 7 तथा इसका आयतन 550 घन सेमी है। बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
बेलन की त्रिज्या ऊँचाई = 5 : 7
माना बेलन की त्रिज्या 5r तथा ऊँचाई 7r है।
बेलन का आयतन = 550 घन सेमी
⇒ πr²h = 550
⇒ \(\frac {22}{7}\) × (5r)² × 7r = 550
⇒ 22 × 25r³ = 550
⇒ 550r³ = 550
⇒ r³ = 1
∴ r = 1 सेमी
बेलन की त्रिज्या (r) = 5 सेमी और ऊँचाई (h) = 7
∴ बेलन का सम्पूर्ण पृष्ठ = 2r (h+r) r
= 2 × \(\frac {22}{7}\) × (7 + 5) × 5
= 2 × \(\frac {22}{7}\) × 12 × 5
= \(\frac {2640}{7}\) वर्ग सेमी
= 377.14 वर्ग सेमी।

प्रश्न 20.
एक हॉल 15 मीटर लम्बा और 12 मीटर चौड़ा है। यदि हाल के फर्श तथा छत के क्षेत्रफलों का योग उसकी चारों दीवारों के क्षेत्रफलों के योग के बराबर हो तो उस हॉल का आयतन ज्ञात कीजिए।
हल :
हाल के फर्श की लम्बाई (l) = 15 मीटर
तथा चौड़ाई (h) = 12 मीटर
फर्श का क्षेत्रफल = l × b = 15 × 12 = 180 मीटर²
क्योंकि छत का क्षेत्रफल = फर्श का क्षेत्रफल
∴ हॉल के फर्श का क्षेत्रफल + छत का क्षेत्रफल
= 180 + 180 = 360 मीटर
माना हॉल की ऊँचाई = h मीटर
चारों दीवारों का क्षेत्रफल = 2 (l + b) h मी²
= 2 (15 + 12) × h
= 54 h मी²
मौ प्रश्नानुसार, फर्श और छत के क्षेत्रफलों का योग = चारों भुजाओं के क्षेत्रफलों का योग
⇒ 360 मी² = 54 h मी²
h = \(\frac {360}{54}\)
हाल का आयतन = lbh
= 15 × 12 × \(\frac {20}{3}\)मी³
= 1200 घन मीटर

प्रश्न 21.
यदि शंकु के आधार की त्रिज्या 21 सेमी तथा ऊंचाई 28 सेमी हो, तो शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए।
हल :
शंकु के आधार की त्रिज्या (r) = 21 सेमी
ऊँचाई (h) = 28 सेमी
माना शंकु की तिर्यक ऊँचाई l सेमी है, तब
l² = h² + r²
∴ l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(28)^2+(21)^2}\) सेमी
= \(\sqrt{784+441}\) सेमी
= \(\sqrt{1225}\) = 35 सेमी

(i) अत: शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = π(l + r)r
= \(\frac {22}{7}\)(35 + 21) × 21 वर्ग सेमी
= \(\frac {22}{7}\) × 56 × 21 वर्ग सेमी ।
= 3696 वर्ग सेमी

(ii) शंकु का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × (21)² × 28 घन सेमी
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × 21 × 21 × 28 घन सेमी
= 12936 घन सेमी।

प्रश्न 22.
एक टेन्ट शंकु के आकार का है, जिसके आधार की त्रिज्या 7 मीटर तथा ऊंचाई 5 मीटर है। टेन्ट में लगने वाले कपड़े का क्षेत्रफल ज्ञात कीजिए।
हल :
टेन्ट के आधार की त्रिज्या (r) = 7 मीटर
ऊँचाई (h) = 5 मीटर
∴ टेन्ट की तिर्यक ऊँचाई (l) = \(\sqrt{h^2+r^2}\)
l = \(\sqrt{(5)^2+(7)^2}\) मीटर
= \(\sqrt{25+49}\) = \(\sqrt{74}\) = 8.6 मीटर (लगभग).
अतः टेन्ट में लगने वाले कपड़े का क्षेत्रफल = πrl
= \(\frac {22}{7}\) × 7 × 8.6 वर्ग मीटर
= 189.2 वर्ग मीटर ।

प्रश्न 23.
एक धातु के गोले की त्रिज्या 14 सेमी है। इसका पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए ।
हल :
गोले की त्रिज्या (r) = 14 सेमी
अतः गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac {22}{7}\) × 14 × 14
= 2464 वर्ग सेमी
∴ गोले का आयतन = \(\frac {4}{3}\)πr³
= \(\frac {4}{3}\) × \(\frac {22}{7}\) × 14 × 14 × 14
= 11498.67 घन सेमी

प्रश्न 24.
12 सेमी त्रिज्या वाला एक धातु का गोला पिघलाकर तीन छोटे गोले बनाए गए हैं। यदि उनमें से दो छोटे गोलों की त्रिज्याऐं 6 सेमी तथा 8 सेमी हों तो तीसरे गोले की त्रिज्या ज्ञात कीजिए।
हल :
बड़े गोले की त्रिज्या = 12 सेमी
∴ आयतन = \(\frac {4}{3}\)πr³ = \(\frac {4}{3}\) × π × 12 × 12 × 12
= 2304π घन सेमी
नवनिर्मित तीन गोलियों में से एक की त्रिज्या = 8 सेमी
आयतन = \(\frac {4}{3}\)π × 8 × 8 × 8
= \(\frac {2048}{3}\)π घन सेमी
नवनिर्मित दूसरी गोली की त्रिज्या = 6 सेमी
आयतन = \(\frac {4}{3}\)π × 6 × 6 × 6
= 288π घन सेमी
इन दोनों गोलियों के आयतनों का योग = \(\frac {2048}{3}\)π + 288π
= \(\frac{2048 \pi+864 \pi}{3}\)
= \(\frac {2912}{3}\)π घन सेमी
तीसरी गोली का आयतन = बड़ी गोली का आयतन – दो गोलियों के आयतन का योग
= 2304π – \(\frac {2912}{3}\)π घन सेमी
= \(\frac {4000}{3}\)π घन सेमी
माना इस गोली की त्रिज्या = R
तब \(\frac {4}{3}\)πR³ = \(\frac {4000}{3}\)π
R³ = \(\frac {4000}{4}\) = 1000
R = \(\sqrt{1000}\) = 10
अतः तीसरी गोली की त्रिज्या = 10 सेमी

प्रश्न 25.
त्रिज्या 21 सेमी वाले एक अर्द्ध-गोले के लिए, ज्ञात कीजिए :
(i) चक्र पृष्ठीय क्षेत्रफल
(ii) कुल पृष्ठीय क्षेत्रफल ।
हल :
(i) त्रिज्या = 21 सेमी
अर्द्ध-गोले का वक्र पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac {22}{7}\) × 21 × 21 सेमी²
= 2772 सेमी² ।

(ii) अर्द्ध-गोले का कुल पृष्ठीय क्षेत्रफल = 3πr²
= 3 × \(\frac {22}{7}\) × 21 × 21 सेमी²
= 4158 सेमी² ।

प्रश्न 26.
किसी गोले की त्रिज्या 10 सेमी है। यदि त्रिज्या को 5% बढ़ा दिया जाए तो आयतन में कितने प्रतिशत की वृद्धि होगी ?
हल :
गोले की त्रिज्या = 10 सेमी
त्रिज्या में 5% की वृद्धि होने पर नयी त्रिज्या
= \(\frac {105}{100}\) × 10 = 10.5 सेमी
जब त्रिज्या 10 सेमी तो आयतन = \(\frac {4}{3}\)π(10)³
= \(\frac {88000}{21}\)घन सेमी

प्रश्न 27.
24 सेमी ऊँचे और 7 सेमी आधार की त्रिज्या के बेलन में उसी ऊँचाई और उसी आधार त्रिज्या का एक शंक्वाकार छिद्र किया जाता है। बचे हुए बेलनाकार सम्पूर्ण पृष्ठ और आयतन ज्ञात कीजिए ।

हल :
ठोस बेलन का आयतन = πr²h
= π(7)² × 24 घन सेमी
= π × 49 × 24 घन सेमी
= 1176π घन सेमी
शंक्वाकार छिद्र का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × π(7)² × 24
= π × 49 × 8 घन सेमी
= 392 π घन सेमी

शेष बेलन का आयतन = (1176π – 392π)
= 784π घन सेमी
= 784 × \(\frac {22}{7}\)घन सेमी
= 112 × 22
= 2464 घन सेमी

ठोस बेलन का वक्रपृष्ठ = 2πrh
= 2 × \(\frac {22}{7}\) × 7 × 24 वर्ग सेमी
= 44 × 24 वर्ग सेमी
= 1056 वर्ग सेमी
शंक्वाकार छिद्र के कारण ठोस का वक्रपृष्ठ उतना ही बढ़ जाएगा जितना कि छिद्र का वक्र पृष्ठ है।
∴ शंक्वाकार छिद्र की तिरछी ऊँचाई
l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{24^2+7^2}\)
= \(\sqrt{576+49}\)
= \(\sqrt{625}\)
l = 25 सेमी
शंक्वाकार छिंद्र का वक्र पृष्ठ = πrl
= \(\frac {22}{7}\) × 7 × 25
= 22 × 25 = 550 वर्ग सेमी

बेलन का सम्पूर्ण पृष्ठ = 1056 + 550 + πr²
= 1056 + 550 + \(\frac {22}{7}\) × 7 × 7 वर्ग सेमी
= 1056 + 550 + 154 वर्ग सेमी
= 1760 वर्ग सेमी
अतः बेलन का सम्पूर्ण पृष्ठ = 1760 वर्ग सेमी
आयतन = 2464 घन सेमी

प्रश्न 28.
एक समद्विबाहू समकोण त्रिभुज में कर्ण 4 सेमी लम्बा है। यदि त्रिभुज के कर्ण को अक्ष मानकर उसके परितः घुमाया जाए, तो निर्मित आकृति का वक्र आयतन ज्ञात कीजिए।
हल :

4 सेमी कर्ण वाले समद्विबाहु समकोण त्रिभुज ABC को कर्ण AC के परितः घुमाने से एक उभयनिष्ठ आधार वाला द्विशंकु बनेगा। प्रत्येक शंकु की ऊँचाई कर्ण की आधी \(\frac {4}{2}\) = 2
सेमी होगी। हम जानते हैं कि समकोण त्रिभुज में समकोण वाले शीर्ष को कर्ण के मध्य बिन्दु से मिलाने वाली रेखा की आधी होती है।
यह समकोण समद्विबाहु त्रिभुज है।
यह रेखा कर्ण पर भी होगी। यह रेखा ही शंकु की त्रिज्या है।
अतः त्रिज्या r = 2 सेमी
तिर्यक ऊँचाई l = \(\sqrt{2^2+2^2}\) = \(\sqrt{8}\)
= 2\(\sqrt{2}\) सेमी
वक्र पृष्ठ = 2 × एक शंकु का वक्रपृष्ठ
= 2 × πrl
= 2 × π × 2 × 2\(\sqrt{2}\)
= 8\(\sqrt{2}\)π वर्ग सेमी
ठोस का आयतन = 2 × एक शंकु का आयतन
= 2 × \(\frac {1}{3}\)πr²h
= 2 × \(\frac {1}{3}\) × π × 2 × 2\(\sqrt{2}\)
= \(\frac {16}{3}\)π घन सेमी

प्रश्न 29.
एक शंकु के आकार के बर्तन की त्रिज्या 10 सेमी और ऊंचाई 18 सेमी है, पानी से पूरा भरा हुआ है। इसे 5 सेमी त्रिज्या के एक बेलनाकार बर्तन में उड़ेला जाता है। बेलनाकार बर्तन में पानी की ऊंचाई ज्ञात कीजिए।
हल :
शंकु के आकार के बर्तन की त्रिज्या (r) = 10 सेमी
बर्तन की ऊँचाई (h) = 18 सेमी
शंकु के आकार के बर्तन का आयतन = \(\frac {1}{3}\) × πr²h
= \(\frac {1}{3}\) × π × (10)² × 18
= \(\frac {1}{3}\) × π × 100 × 18
= π × 100 × 6 = 600π घन सेमी
माना बेलनाकार बर्तन में पानी की ऊँचाई H सेमी है।
बेलनाकार बर्तन की त्रिज्या (R) = 5 सेमी
अब प्रश्नानुसार,
बेलनाकार बर्तन का आयतन = शंकु के आकार के बर्तन का आयतन
⇒ πR²H = 600π
⇒ π(5)² × H = 600π
⇒ 25π × H = 600π
∴ H = \(\frac {600π}{25π}\)
= 24 सेमी।
अतः बेलनाकार बर्तन में पानी की ऊँचाई 24 सेमी है।

प्रश्न 30.
एक गोले की त्रिज्या 4.2 सेमी है। गोले का वक्रपृष्ठ और आयतन ज्ञात कीजिए।
हल :
दिया है, गोले की त्रिज्या (r) = 4.2 सेमी
अतः गोले का वक्रपृष्ठ = 4πr² = 4 × \(\frac {22}{7}\) × (4.2)²
= 4 × \(\frac {22}{7}\) × 4.2 × 4.2 = 44 × 22 × 0.6 × 4.2
= 88 × 2.52 = 221.76 वर्ग सेमी।
और गोले का आयतन = \(\frac {4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × (4.2)³
= \(\ frac{4}{3} \times \frac{22}{7}\) × 4.2 × 4.2 × 4.2
= 4 × 22 × 1.4 × 0.6 × 4.2
= 88 × 0.84 × 4.2 = 88 × 3.528
= 310.464 = 310.46 घन सेमी
अतः गोले का वक्रपृष्ठ 221.76 वर्ग सेमी
और आयतन 310.46 घन सेमी है।

प्रश्न 31.
एक अर्द्ध-गोले की त्रिज्या 3.5 सेमी है, तो इसका आयतन और सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
दिया है,
अर्द्ध-गोले की त्रिज्या (r) = 3.5 सेमी
अर्द्ध-गोले का आयतन = \(\frac {2}{3}\)πr³
= \(\frac{2}{3} \times \frac{22}{7}\) × (3.5)³
= \(\frac{2}{3} \times \frac{22}{7}\) × 3.5 × 3.5 × 3.5
= \(\frac {2}{3}\) × 22 × 0.5 × 12.25
= \(\frac {2}{3}\) × 11 × 12.25
= \(\frac {269.5}{3}\) = 89.83 घन सेमी
अर्द्ध-गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 3πr² = 3 × \(\frac {22}{7}\) × (3.5)²
= 3 × \(\frac {22}{7}\) × 3.5 × 3.5 = 3 × 22 × 0.5 × 3.5
= 3 × 11 × 3.5 = 115.5 वर्ग सेमी
अतः अर्द्ध-गोले का आयतन 89.83 घन सेमी
और सम्पूर्ण पृष्ठीय क्षेत्रफल 115.5 वर्ग सेमी है।

प्रश्न 32.
एक रोलर की लम्बाई 2 मीटर और व्यास 1.4 मीटर है। ज्ञात कीजिए कि 5 चक्कर लगाने में रोलर कितना क्षेत्र समतल करेगा ?
हल :
रोलर की लम्बाई (h) = 2 मीटर
और रोलर का व्यास = 1.4 मीटर
अतः रोलर की त्रिज्या r = व्यास / 2 = \(\frac {1.4}{2}\) = 0.7 मीटर
1 चक्कर लगाने में तय क्षेत्रफल = वक्र पृष्ठीय का क्षेत्रफल
= 2πrh ⇒ 2 × \(\frac {22}{7}\) × 0.7 × 2
= 2 × 22 × \(\frac {1}{10}\) × 2 = \(\frac {88}{10}\) = 88 वर्ग मीटर
∴ 5 चक्कर में समतल किया क्षेत्र
= 8.8 × 5 = 44.0 वर्ग मीटर।

प्रश्न 33.
एक सन्दूक की माप 50 सेमी x 36 सेमी x 25 सेमी है। इस सन्दूक का कवर बनाने में कितने वर्ग सेमी कपड़े की आवश्यकता होगी?
हल :
सन्दूक की लम्बाई (l) = 50 सेमी
सन्दूक की चौड़ाई (b) = 36 सेमी
सन्दूक की ऊँचाई (h) = 25 सेमी
सन्दूक का कवर बनाने के लिए उसके सम्पूर्ण पृष्ठीय क्षेत्रफल के बराबर कपड़े की आवश्यकता होगी।
सन्दूक का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (50 × 36 + 36 × 25 + 25 × 50)
= 2 (1800 + 900 + 1250)
= 2 (3950) वर्ग सेमी
= 7900 वर्ग सेमी।
अतः सन्दूक के कवर के लिए आवश्यक कपड़ा 7900 वर्ग सेमी।

प्रश्न 34.
सीसे के एक गोले की त्रिज्या 5 सेमी है। इससे 5 मिमी त्रिज्या की कितनी गोलियाँ बनायी जा सकती हैं ?
हल :
सीसे के बड़े गोले की त्रिज्या (R) = 5 सेमी
इस गोले का आयतन (V) = \(\frac {4}{3}\)πR³ = \(\frac {4}{3}\)π(5)³
= \(\frac {4}{3}\) × π × 5 × 5 × 5 घन सेमी
इस सीसे से निर्मित प्रत्येक गोली की त्रिज्या (r) = 5 मिमी
= \(\frac {5}{10}\) सेमी = 0.5 सेमी
निर्मित प्रत्येक छोटी गोली का आयतन = \(\frac {4}{3}\)πr³
= \(\frac {4}{3}\) × π × (0.5)³
= \(\frac {4}{3}\) × π × 0.5 × 0.5 × 0.5 घन सेमी

प्रश्न 35.
एक घनाभ के तीन आसन्न फलकों का क्षेत्रफल क्रमश: xy और 2 हैं। सिद्ध कीजिए कि घनाभ का आयतन \(\sqrt{xyz}\) है।
हल :
माना घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमशः
l, b और h है।
प्रश्नानुसार,
l × b = x …………..(i)
b × h =y …………..(ii)
और h × l = z …………..(iii)
समीकरण (i), (ii) और (iii) का गुणा करने पर,
l × b × b × h × h × l = x × y × z
⇒ l²b²h² = xyz
⇒ (lbh)² = xyz
⇒ lbh = \(\sqrt{xyz}\)
∴ घनाभ का आयतन = \(\sqrt{xyz}\) . इति सिद्धम्

प्रश्न 36.
एक शंकु, जिसकी ऊँचाई 24 सेमी और आधार की त्रिज्या 6 सेमी है, प्रतिमा बनाने वाली चिकनी मिट्टी से बनाया गया है। एक बच्चा उसको पुनः गोले का आकार देता है। गोले की त्रिज्या ज्ञात कीजिए ।
हल :
माना गोले की त्रिज्या R सेमी है।
शंकु की ऊँचाई (h) = 24 सेमी तथा शंकु के आधार की त्रिज्या (r) = 6 सेमी।
शंकु का आयतन = \(\frac {1}{3}\)πr²h = \(\frac {1}{3}\) × π × (6)² × 24
= π × 12 × 24 = 288π घन सेमी
निर्मित गोले का आयतन = शंकु का आयतन
⇒ \(\frac {4}{3}\)πR³ = 288π
⇒ \(\frac {4}{3}\) × R³ = 288
⇒ R³ = \(\frac{288 \times 3}{4}\) = 72 × 3 = 216
⇒ R³ = \(\sqrt[3]{216}\)सेमी
= \(\sqrt[3]{6 \times 6 \times 6}\) = 6
अतः गोले की त्रिज्या 6 सेमी है।

प्रश्न 37.
यदि एक गोले का आयतन 38808 घन सेमी है, तो गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
गोले का आयतन = 38808 घन सेमी
माना गोले की त्रिज्या = r
अतः गोले का आयतन
\(\frac {4}{3}\)πr³ = 38808
या r³ = \(\frac{38808 \times 3}{4 \pi}\)
= \(\frac{38808 \times 3 \times 7}{4 \times 22}\) = 9261 घन सेमी
= (21)³ घन सेमी
∴ r = 21 सेमी
अब गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac {22}{7}\) × 21 × 21 वर्ग सेमी
= 5544 वर्ग सेमी।

प्रश्न 38.
2 सेमी त्रिज्या वाले एक बेलनाकार गिलास की ऊंचाई \(\frac {6}{π}\) सेमी है, तो उसमें कितना पानी आयेगा ?
हल :
बेलनाकार गिलास की त्रिज्या (r) = 2 सेमी
ऊँचाई (h) = \(\frac {6}{π}\)सेमी
गिलास में पानी का आयतन = बेलनाकार गिलास का आयतन
= πr²h
= π × (2)² × \(\frac {6}{π}\)
= π × 4 × \(\frac {6}{π}\)
= 24 घन सेमी.

प्रश्न 39.
50 सेमी × 36 सेमी माप की एक धातु की आयताकार चादर है। इसके प्रत्येक कोने से 8 सेमी भुजा का वर्ग काट कर निकाल दिया गया है। शेष चादर से खुला हुआ डिब्बा बनाया गया है। डिब्बे का आयतन ज्ञात कीजिए।
हल :
चादर की लम्बाई = 50 सेमी
तथा चौड़ाई = 36 सेमी

इस प्रकार चादर के प्रत्येक कोने से 8 सेमी भुजा के वर्ग काटे गये हैं तो
सन्दूक की लम्बाई (l) = 50 – 16 = 34 सेमी
सन्दूक की चौड़ाई (b) = 36 – 16 = 20 सेमी.
सन्दूक की ऊँचाई (h) = काटे गये वर्ग की भुजा
= 8 सेमी
∴ सन्दूक का आयतन ल. × चौ. × ऊ.
= 34 × 20 × 8
= 3.4 × 160
∴ आयतन = 5440 घन सेमी।

प्रश्न 40.
12 सेमी व्यास का एक गोलाकार भाग जल से अंशत: भरा हुआ है। यदि उसमें 6 सेमी व्यास का एक गोला पूर्णतः डुबो दिया जाता है। ज्ञात कीजिए कि बेलनाकार बर्तन में जल की सतह कितनी ऊंचाई तक उठ जायेगी।
हल :

गोले का व्यास 6 सेमी
∴ गोले की त्रिज्या (r) = 3 सेमी
गोले का आयतन = \(\frac {4}{3}\)³
= \(\frac {4}{3}\) × π × 3 × 3 × 3
= 36π³
∴ गोले का आयतन = 36π घन सेमी
गोला डूबने पर अपने आयतन के बराबर पानी हटायेगा।
∴ हटे पानी का आयतन = 36π सेमी³
हटा पानी एक छोटा बेलनाकार भाग होगा, जैसा कि चित्र में दिखाया गया है।
बेलन की त्रिज्या (R) = \(\frac {12}{2}\) = 6
अतः R = 6 सेमी
माना हटाए गए पानी की ऊँचाई = h सेमी
अतः हटे पानी का आयतन = πR²h
अथवा πR²h = 36π
π(6)² × h = 36n
36h = 36
∴ h = \(\frac {36}{36}\) = 1 सेमी
अतः बडी ऊँचाई h = 1 सेमी. ।

Jharkhand Board JAC Class 9 Science Important Questions Chapter 9 बल तथा गति के नियम Important Questions and Answers.

JAC Board Class 9 Science Important Questions Chapter 9 बल तथा गति के नियम

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
बन्दूक से गोली निकलने पर पीछे की ओर धक्का लगता है क्योंकि
(a) बन्दूक से गोली छूटने की क्रिया के कारण पीछे की ओर प्रतिक्रिया होती है।
(b) बन्दूक चलाने वाला बन्दूक को पीछे खींचता है।
(c) बारूद से बनने वाली गैस पीछे की ओर दाब डालती है।
(d) उपर्युक्त तीनों में से कोई नहीं।
उत्तर:
(a) बन्दूक से गोली छूटने की क्रिया के कारण पीछे की ओर प्रतिक्रिया होती है।

प्रश्न 2.
न्यूटन के गति के तीसरे नियम के अनुसार क्रिया तथा प्रतिक्रिया से सम्बन्ध बल
(a) सदैव एक ही वस्तु पर लगे होने चाहिए
(b) भिन्न-भिन्न वस्तुओं पर लगे हो सकते हैं।
(c) सदैव भिन्न-भिन्न वस्तुओं पर ही लगे होने चाहिए
(d) का परिमाण बराबर होना आवश्यक नहीं है परन्तु दिशा एक समान होनी चाहिए।
उत्तर:
(c) सदैव भिन्न-भिन्न वस्तुओं पर ही लगे होने चाहिए।

प्रश्न 3.
बल (\(\overrightarrow{\mathbf{F}}\)) द्रव्यमान (mm) तथा त्वरण (\(\overrightarrow{\mathbf{a}} \)) सम्बन्धित समीकरण है-
(a) F = ma
(b) m = a F
(c) a = mF
(d) ma = \(\frac { 1 }{ F }\)
उत्तर:
(a) F ma.

प्रश्न 4.
बल का मात्रक है-
(a) किग्रा मीटर सेकण्ड
(b) किग्रा मीटर सेकण्ड?
(c) किग्रा मीटर / सेकण्डर
(d) किग्रा मीटर/सेकण्ड
उत्तर:
(b) किग्रा मीटर / सेकण्डर

प्रश्न 5.
संवेग का मात्रक है-
(a) मीटर/सेकण्ड
(b) किग्रा मीटर / सेकण्डर
(c) किग्रा भार
(d) किग्रा मीटर / सेकण्ड।
उत्तर:
(d) किग्रा मीटर/सेकण्ड।

प्रश्न 6.
संवेग परिवर्तन की दर बराबर होती है-
(a) त्वरण के
(b) वेग के
(c) बल के
(d) बल के आवेग के।
उत्तर:
(c) बल के।

प्रश्न 7.
यदि कोई पिण्ड संवेग से सीधी रेखा में गतिमान है। यदि उस पर कोई बाह्य बल न लगे तो-
(a) इसके वेग में वृद्धि होगी
(b) वेग नियत रहेगा
(c) थोड़ी देर पश्चात् पिण्ड रुक जायेगा
(d) चाल में वृद्धि होगी।
उत्तर:
(b) वेग नियत रहेगा।

प्रश्न 8.
किसी वस्तु का जड़त्व निर्भर करता है-
(a) वस्तु के गुरुत्व केन्द्र पर
(b) वस्तु के द्रव्यमान पर
(c) गुरुत्वीय त्वरण पर
(d) वस्तु के आकार पर।
उत्तर:
(b) वस्तु के द्रव्यमान पर।

प्रश्न 9.
जब किसी वस्तु की गति त्वरित होती है तो-
(a) उसकी चाल में सदैव वृद्धि होती है।
(b) उसके वेग में सदैव वृद्धि होती है
(c) वह सदैव पृथ्वी की ओर गिरती है।
(d) उस पर सदैव कोई बल कार्य करता है।
उत्तर:
(d) उस पर सदैव कोई बल कार्य करता है।

प्रश्न 10.
5 किग्रा का एक पिण्ड 10 मीटर/सेक² के त्वरण से सरल रेखा में गतिमान है। पिण्ड पर कार्यरत परिणामी बल होगा-
(a) 50 न्यूटन
(b) 0.5 न्यूटन
(c) शून्य
(d) 2 न्यूटन।
उत्तर:
(a) 50 न्यूटन।

प्रश्न 11.
यदि पिण्ड A (5 किग्रा), पिण्ड B (10 किग्रा) पर यदि 5 न्यूटन बल लगाता हो तो इसके फलस्वरूप पिण्ड B द्वारा पिण्ड A पर लगने वाली प्रतिक्रिया का परिमाण कितना होगा-
(a) 5 न्यूटन
(b) 10 न्यूटन
(c) 2 न्यूटन
(d) शून्य।
उत्तर:
(a) 5 न्यूटन

प्रश्न 12.
किसी पिण्ड का द्रव्यमान 5 किग्रा हो और उस 15 न्यूटन का बल आरोपित किया जाय तो उसमें उत्पन्न त्वरण होगा-
(a) 5 मीटर / सेकण्ड
(b) 4 मीटर/सेकण्डर
(c) 3 मीटर/सेकण्ड 2
(d) 2 मीटर / सेकण्ड।
उत्तर:
(c) 3 मीटर / सेकण्ड।

प्रश्न 13.
जब नेट बल किसी वस्तु पर कार्य करता है, वस्तु निम्नलिखित के आनुपातिक त्वरण से बल की दिशा में त्वरित होगा-
(a) वस्तु के ऊपर बल
(b) वस्तु के वेग
(c) वस्तु का द्रव्यमान
(d) वस्तु का जड़त्व
उत्तर:
(a) वस्तु के ऊपर बल

प्रश्न 14.
यदि दो वस्तुओं A तथा B का द्रव्यमान क्रमशः
16 kg तथा 40 kg हो तो-
(a) A का जड़त्व B से अधिक होगा
(b) B का जड़त्व A से अधिक होगा
(c) A तथा B का जड़त्व बराबर होगा
(d) A तथा B का जड़त्व शून्य होगा।
उत्तर:
(b) B का जड़त्व A से अधिक होगा।

प्रश्न 15.
यदि किसी वस्तु पर कोई बाह्य बल लग रहा है तो वह बल की दिशा में त्वरित हो जाती है। इस प्रकार उत्पन्न त्वरण वस्तु-
(a) पर लगे बल के समानुपाती होता है।
(b) के वेग के समानुपाती होता है
(c) के द्रव्यमान के समानुपाती होता है
(d) के ‘जड़त्व के समानुपाती होता है।
उत्तर:
(a) पर लगे बल के समानुपाती होता है।

रिक्त स्थान भरो-

1. जड़त्व का माप किसी वस्तु के …………………….. से होता है।
2. अधिक द्रव्यमान वाली वस्तु का ……………………. भी अधिक होता है।
3. संवेग का SI मात्रक ……………………. है।
4. संवेग किसी वस्तु के द्रव्यमान और ……………………. गुणनफल होता है।

उत्तर:

1. द्रव्यमान
2. जड़त्व
3. kgm/s
4. वेग।

सुमेलन कीजिए-

कौलम ‘कं	कॉलम ‘ख’
1. संवेग	(क) kg m/s
2. बल	(ख) N
3. बल का S.I. मात्रक	(ग) ma
4. संवेग का S.I मात्रक	(घ) mv

उत्तर:
1. (घ) mv
2. (ग) ma
3. (ख) N
4. (क) kg m/s

सत्य / असत्य –

1. किसी वस्तु में समाहित गति की कुल मात्रा को संवेग कहते हैं।
2. संतुलित बल किसी स्थिर वस्तु को गतिशील कर देता है।
3. यदि किसी वस्तु का द्रव्यमान अधिक है तो उसका जड़त्व भी अधिक होगा।
4. बल ऋणात्मक भी हो सकता है।

उत्तर:

1. सत्य
2. असत्य
3. सत्य
4. सत्य।

अतिलघुत्तरात्मक प्रश्न

प्रश्न 1.
एक न्यूटन बल क्या है?
उत्तर:
F = ma से यदि m = 1 किग्रा, a = 1 मी/सेकण्डर² तब F = 1 न्यूटन। अतः एक न्यूटन बल वह बल है जो एक किलो ग्राम द्रव्यमान की किसी वस्तु में का त्वरण उत्पन्न कर दे।

प्रश्न 2.
जड़त्व क्या है?
उत्तर:
वस्तुओं की इस प्रवृत्ति को कि वे स्वतः (बिना बाह्य बल लगाये) अपनी विराम या गति की अवस्था को नहीं बदल सकतीं, जड़त्व कहते हैं।

प्रश्न 3.
ब्रेक लगाने से चलती हुई गाड़ी रुक जाती है। इस प्रक्रिया में गाड़ी के संवेग का क्या होता है?
उत्तर:
गाड़ी के संवेग का अधिकांश भाग पृथ्वी को तथा शेष भाग वायु के अणुओं को हस्तांतरित हो जाता है।

प्रश्न 4.
संवेग की परिभाषा दो।
उत्तर:
किसी वस्तु के द्रव्यमान तथा वेग के गुणनफल को उस वस्तु का संवेग कहते हैं।
संवेग = द्रव्यमान × वेग

प्रश्न 5.
संवेग का S.I. मात्रक क्या है?
उत्तर:
संवेग का S.I. मात्रक किग्रा मी./सेकण्ड है।

प्रश्न 6.
संवेग के संरक्षण का नियम लिखिए।
उत्तर:
जब दो (अथवा अधिक) वस्तुएँ एक-दूसरे के ऊपर कार्य करती हैं, उनका सम्पूर्ण संवेग स्थिर ( अथवा संरक्षित) बना रहता है, बशर्ते कोई बाहरी बल न कार्य कर रहा हो।

प्रश्न 7.
क्रिया और प्रतिक्रिया बराबर तथा विपरीत होती है, क्यों वे एक-दूसरे को खत्म नहीं करतीं?
उत्तर:
क्योंकि क्रिया तथा प्रतिक्रिया बल विभिन्न वस्तुओं पर कार्य करते हैं।

प्रश्न 8.
न्यूटन के गति का प्रथम नियम बताओ।
उत्तर:
न्यूटन के गति का पहला नियम- यदि कोई वस्तु विराम अवस्था में है तो वह विरामावस्था में ही रहेगी और यदि वह एक समान चाल में सीधी रेखा से चल रही है तो वैसे ही चलती रहेगी जब तक कि उस पर कोई बाह्य बल न लगाया जाये। इसे गैलीलियो का नियम भी कहते हैं।

प्रश्न 9.
जब कई बल किसी वस्तु पर एक साथ लगते हैं, और उनका परिणामी बल शून्य हो, तो उन बलों को क्या कहते हैं?
उत्तर:
सन्तुलित बल।

प्रश्न 10.
बन्दूक से गोली छोड़ने से पहले बन्दूक तथा गोली का संवेग कितना होता है?
उत्तर:
शून्य।

प्रश्न 11.
जिस गुण के कारण कोई वस्तु अपनी विरामावस्था या गति परिवर्तन का विरोध करती है उसे क्या कहते हैं?
उत्तर:
जड़त्व।

प्रश्न 12.
साइकिल के पैडल मारने बन्द करने के बाद भी साइकिल चलती रहती है। क्यों?
उत्तर:
जड़त्व के कारण।

प्रश्न 13.
यदि एक जैसी गोलियों को हल्की रायफल तथा भारी राइफल से छोड़ा जाये, तो हल्की रायफल भारी रायफल की अपेक्षा बड़ा झटका देती है क्यों?
उत्तर:
प्रतिक्षेप बेग रायफल के द्रव्यमान के व्युत्क्र- मानुपाती होता है अतः हल्की रायफल बड़ा झटका देती है।

प्रश्न 14.
5 किग्रा द्रव्यमान की एक गतिशील वस्तु का संवेग 20 किग्रा मी/सेकण्ड है। वस्तु का वेग क्या होगा?
उत्तर:

प्रश्न 15.
5kg द्रव्यमान की वस्तु पर 25 N का बल लगता है। वस्तु में उत्पन्न त्वरण कितना होगा?
उत्तर:

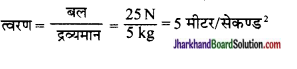
प्रश्न 16.
एक से दो टूक सड़क पर समान वेग से चल रहे हैं। उनमें से एक खाली है और दूसरा बोझ से लदा हुआ है। किस ट्रक को रोकने के लिए अधिक बल की आवश्यकता होगी?
उत्तर:
भरे ट्रक का द्रव्यमान अधिक होने के कारण इसका संवेग अधिक होगा। अतः भरे ट्रक को रोकने के लिए अधिक बल की आवश्यकता होगी।

प्रश्न 17.
चलती हुई रेलगाड़ी में बैठे व्यक्ति द्वारा कवांधर दिशा में फेंकी गेंद लौटकर उसके हाथ में वापस क्यों आ जाती है?
उत्तर:
जड़त्व के कारण व्यक्ति एवं गेंद दोनों बराबर गाड़ी के साथ उसी वेग से क्षैतिज दिशा में चलते रहते हैं। इसलिए यदि गेंद उछालने के पश्चात् व्यक्ति का हाथ गेंद के नीचे ही रहता है तो गेंद उसके हाथ में आ जाती है।

प्रश्न 18.
एक बास्केटबाल तथा उसी आकार की धातु की बनी वस्तु में किसका जड़त्व अधिक होता है?
उत्तर:
धातु की बनी वस्तु का।

प्रश्न 19.
संवेग संरक्षण के लिये कौन-सा प्रतिबन्ध आवश्यक है?
उत्तर:
पिण्डों पर कोई बाह्य असन्तुलित बल नहीं लगा होना चाहिए।

प्रश्न 20.
रॉकेट का क्रिया-सिद्धान्त, न्यूटन के गति के किस नियम पर आधारित है?
उत्तर:
रॉकेट का क्रिया- सिद्धान्त, न्यूटन के गति के तृतीय नियम (क्रिया-प्रतिक्रिया नियम) पर आधारित है।

प्रश्न 21.
गोली छोड़ते समय बन्दूक पीछे की ओर क्यों प्रतिक्षेपित होती है?
उत्तर:
क्रिया-प्रतिक्रिया के नियम से बन्दूक गोली पर आगे की ओर बल लगाती है और गोली बन्दूक पर पीछे की ओर बल लगाती है, इसी बल के कारण बन्दूक प्रतिक्षेपित होती है।

प्रश्न 22.
यदि किसी गतिमान पिण्ड पर कोई असन्तुलित बल नहीं लगा है तो उसके संवेग का क्या होगा?
उत्तर:
संवेग संरक्षित रहेगा।

प्रश्न 23.
फर्श पर लुढ़क रही गेंद कुछ देर पश्चात् स्वयं ही रुक जाती है, इसके लिए कौन-सा बल उत्तरदायी है?
उत्तर:
फर्श पर लुढ़क रही गेंद के स्वयं रुकने के लिए घर्षण बल उत्तरदायी है।

प्रश्न 24.
एक गाड़ी को 500 न्यूटन के बल से सड़क पर खींचने से वह एक नियत वेग से चलती है। गाड़ी व पृथ्वी के बीच कितना घर्षण बल कार्य कर रहा है?
उत्तर:
500 न्यूटन; गाड़ी के चलने की विपरीत दिशा में।

प्रश्न 25.
घर्षण बल को कम करने का एक उपाय बताइए।
उत्तर:
दो सतहों के मध्य स्नेहक जैसे- तेल, ग्रीस आदि का प्रयोग करके घर्षण कम किया जा सकता है।

प्रश्न 26.
एक ही आकार के पत्थर व फुटबाल में किसका जड़त्व अधिक होगा?
उत्तर:
पत्थर का जड़त्व अधिक होगा।

प्रश्न 27.
पदार्थ का वह कौन-सा गुण है, जो पदार्थ की अवस्था परिवर्तन का विरोध करता है?
उत्तर:
जड़त्व का गुण।

प्रश्न 28.
किसी पिण्ड का भार 15 न्यूटन है। पृथ्वी उस पिण्ड को कितने बल से अपनी ओर खींच रही है?
उत्तर:
15 न्यूटन के बल से।

प्रश्न 29.
बिजली का पंखा स्विच बन्द होने के बाद भी कुछ समय तक किस कारण से चलता है?
उत्तर:
अपने गति – जड़त्व के गुण के कारण पंखा स्विच बन्द होने के बाद भी कुछ समय तक गति में रहता है।

प्रश्न 30.
चलती कार के एकाएक रुकने पर उसमें बैठे यात्री किस दिशा में गिरेंगे?
उत्तर:
आगे की ओर गिरेंगे।

प्रश्न 31.
किसी वस्तु का द्रव्यमान तथा वेग का गुणनफल किस भौतिक राशि को प्रदर्शित करता है?
उत्तर:
इन दोनों का गुणनफल संवेग को प्रदर्शित करता है।

प्रश्न 32.
सभी वस्तुएँ किसका विरोध करती हैं?
उत्तर:
अपनी गति की अवस्था में परिवर्तन का विरोध।

प्रश्न 33.
संवेग परिवर्तन की दर किस भौतिक राशि को प्रदर्शित करती है?
उत्तर:
यह बल को प्रदर्शित करती है।

प्रश्न 34.
बल तथा संवेग परिवर्तन की दर में क्या सम्बन्ध है?
उत्तर:
बल (F) = संवेग परिवर्तन की दर \(\left(\frac{\Delta p}{\Delta t}\right)\)

प्रश्न 35.
एक मनुष्य पृथ्वी पर खड़ा है, इस दशा में क्रिया तथा प्रतिक्रिया की व्याख्या कीजिए।
उत्तर:
मनुष्य अपने भार के बराबर बल पृथ्वी तल पर लगाता है (क्रिया); पृथ्वी भी उतना ही बल मनुष्य पर ऊपर की ओर लगाती है (प्रतिक्रिया)।

प्रश्न 36.
स्पष्ट कीजिए कि जूतों के तले क्यों घिस जाते हैं?
उत्तर:
जब हम सड़क पर चलते हैं तो जूतों के तलों तथा सड़क के बीच घर्षण बल कार्य करता है जिससे जूतों के तले घिस जाते हैं।

प्रश्न 37.
टायरों को लहरदार तथा खुरदरा क्यों बनाया जाता है?
उत्तर:
सड़क की सतह तथा टायर के मध्य घर्षण बल बढ़ाने के लिए वाहनों के टायरों की ऊपरी सतह को लहरदार तथा खुरदरा बनाया जाता है, जिससे तीव्र गति पर वाहन अनियन्त्रित होकर अथवा ब्रेक लगाने पर फिसले नहीं।

प्रश्न 38.
गति के नियमों के आधार पर तैरने की क्रिया को समझाइए ।
उत्तर:
तैरने की क्रिया में तैराक बल लगाकर पानी को पीछे की ओर धकेलता है और पानी प्रतिक्रिया के रूप में तैराक पर आगे की ओर बल लगाता है, जिससे तैराक आगे बढ़ जाता है।

प्रश्न 39.
बन्दूक की गोली शरीर में क्यों घुस जाती है?
उत्तर:
बन्दूक की गोली शरीर में घुस जाती है-इसका कारण यह है कि बन्दूक से निकली गोली का वेग बहुत अधिक होता है तथा शरीर से टकराने पर यह बहुत कम समय में शून्य हो जाता है अतः गोली में वेग परिवर्तन की दर (अर्थात् मन्दन) a एवं बल (F=ma) बहुत अधिक होता है। परिणामस्वरूप गोली शरीर में घुस जाती है।

प्रश्न 40.
साइकिल के पहिये में तेल क्यों दिया जाता है?
उत्तर:
पहिये तथा धुरी के बीच घर्षण बल कार्य करता है इन दोनों के बीच खुरदरापन आने से घर्षण बल अधिक हो जाता है जिसके कारण पहिये को घुमाने के लिए अधिक बल लगाना पड़ता है। अतः घर्षण बल कम करने के लिए साइकिल के पहिये में तेल दिया जाता है।

प्रश्न 41.
तीव्र गति से गतिशील, किसी कंकड़ के लगने से खिड़की का काँच टूट जाता है, क्यों?
उत्तर:
वेग कम होने के कारण कंकड़ शीशे से टकराकर पार निकलने में पर्याप्त समय ले लेता है। इतने समय में सम्पूर्ण शीशे में गति उत्पन्न हो जाती है और शीशा चटखकर टूट जाता है।

प्रश्न 42.
दीवार पर किसी स्पंज के टुकड़े पर लगभग बराबर बल से हाथ से मारकर उन्हें पीटने का प्रयास कीजिए। इसमें से किस स्थिति में अधिक चोट लगेगी?
उत्तर:
दीवार को पीटने में हमारा हाथ अति शीघ्र विराम में आ जाएगा अर्थात् इस दशा में संवेग परिवर्तन की दर अधिक होगी। अतः इस दशा में अधिक चोट लगेगी।

लघुत्तरात्मक एवं दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
क्या होता है जब किसी गीले कपड़े को झटकते हैं? अपने प्रेक्षण को स्पष्ट कीजिए।
उत्तर:
जब गीले कपड़े को झटकते हैं तो कपड़े से पानी की बूँदें बाहर आ जाती हैं। इसका कारण यह है कि कपड़ा झटकने पर वह तो गति की अवस्था में आ जाता है, परन्तु कपड़े के भीतर उपस्थित पानी की बूँदें जड़त्व के कारण अपनी विरामावस्था में बनी रहती हैं और कपड़े से अलग होकर बाहर निकल जाती हैं। इससे कपड़ा जल्दी सूख जाता है।

प्रश्न 2.
जैवलिन थ्रो में यदि खिलाड़ी किसी निश्चित रेखा को पार कर लेता है तो यह फाउल माना जाता है, किन्तु खिलाड़ी इस रेखा पर रुकने में प्रायः असफल रहते हैं। स्पष्ट कीजिए, क्यों?
उत्तर:
जैवलिन थ्रो (भाला फेंक) में तीव्र गति से भाला फेंकने के लिए खिलाड़ी तीव्र गति से आगे की ओर भागता है, इसलिये निश्चित रेखा तक पहुँचते समय खिलाड़ी गति की अवस्था में होता है। अतः शरीर के गति जड़त्व के कारण प्रायः वह निश्चित रेखा तक अपने को रोकने में असफल रहता है।

प्रश्न 3.
बन्दूक से गोली छोड़ने पर पीछे की ओर धक्का लगता है, क्यों?
उत्तर:
बन्दूक से गोली छोड़ने पर पीछे की ओर धक्का लगता है। इसका कारण यह है कि बन्दूक से गोली छूटने पर, बारूद की एकदम गैस बन जाती है जो कि फैलने के कारण गोली को बहुत जोर से आगे की ओर फेंक देती है। गोली भी गैस पर उतना ही, परन्तु विपरीत दिशा में प्रतिक्रिया बल लगाती है जिससे कि बन्दूक चलाने वाले को पीछे की ओर धक्का लगता है।

प्रश्न 4.
कुएं से जल खींचते समय यकायक रस्सी टूट जाने पर पानी खींचने वाला व्यक्ति पीछे की ओर क्यों गिर पड़ता है?
उत्तर:
कुएँ से जल खींचते समय यकायक रस्सी टूट जाने पर पानी खींचने वाला व्यक्ति पीछे की ओर गिर पड़ता है। इसका कारण यह है कि जब कोई व्यक्ति रस्सी द्वारा जल से भरी बाल्टी को अपनी ओर खींचता है तो बाल्टी भी उस बल से व्यक्ति को अपनी ओर खींचती है। यदि रस्सी यकायक (अचानक ) टूट जाए तो बाल्टी द्वारा व्यक्ति पर लगाया गया बल समाप्त हो जाता है तथा व्यक्ति अपने द्वारा लगाए गए बल के कारण पीछे की ओर गिर पड़ता है।

प्रश्न 5.
क्रिकेट की गेंद लपकते समय खिलाड़ी गेंद की गति की दिशा में अपने हाथ पीछे क्यों खींच लेता है?
उत्तर:
क्रिकेट की गेंद पकड़ते समय खिलाड़ी अपने हाथ पीछे की ओर खींच लेता है। इसका कारण यह है कि यदि खिलाड़ी हाथ को स्थिर रखकर गेंद पकड़ता है तो गेंद को रुकने में बहुत कम समय लगता है जिससे वेग परिवर्तन की दर (अर्थात् मन्दन) अधिक रहता है। अत: खिलाड़ी की हथेली को गेंद रोकने में अधिक बल (F= ma) लगाना होता है जिससे खिलाड़ी की हथेली में चोट लग सकती है। इसलिए खिलाड़ी गेंद को अधिक समय में रोकने के लिए हाथ को गेंद की गति की दिशा में पीछे खींचता है जिससे कि वेग परिवर्तन की दर (अर्थात् मन्दन) कम हो तथा उसे कम बल लगाना पड़े। इससे खिलाड़ी के हाथ ‘चोट लगने की सम्भावना घट जाती है।

प्रश्न 6.
“प्रत्येक क्रिया की उसके समान परन्तु विपरीत दिशा में प्रतिक्रिया होती है।” इसको स्पष्ट करने के दो उदाहरण दीजिए।
उत्तर:
उदाहरण 1-जब कोई व्यक्ति नाव से कूदता है तो वह अपने पैरों से बल लगाकर नाव को पीछे की ओर धकेलता है अर्थात् नाव पीछे की ओर जाती है। उसकी प्रतिक्रिया के फलस्वरूप नाव व्यक्ति पर आगे की ओर बल लगाती है और मनुष्य किनारे पर कूद जाता है।

उदाहरण 2-घोड़ा, गाड़ी को खींचते समय अपनी पिछली टाँगों से पृथ्वी को पीछे की ओर धकेलता है, जिससे प्रतिक्रिया के रूप में पृथ्वी घोड़े पर आगे की ओर बल लगाती है और गाड़ी आगे बढ़ जाती है।

प्रश्न 7.
यदि कोई व्यक्ति नाव से किनारे पर कूदे तो नाव विपरीत दिशा में चली जाती है, क्यों? स्पष्ट कीजिए।
उत्तर:
जब कोई व्यक्ति नाव से कूदता है तो वह अपने पैरों से बल लगाकार नाव को पीछे की ओर धकेलता है। इस क्रिया बल के कारण नाव पीछे की ओर हट जाती है। नाव द्वारा बराबर व विपरीत बल ( प्रतिक्रिया बल) मनुष्य पर आगे की ओर लगता है जिससे वह किनारे पर कूद जाता है।

प्रश्न 8.
रेत की दलदल अथवा बालूपंक बहुत चिकने व छोटे रेत के कणों से बनता है। यदि कोई व्यक्ति अथवा भारी जन्तु रेगिस्तान में ऐसे स्थान पर चला जाए तो क्या हो सकता है?
उत्तर:
यदि कोई व्यक्ति अथवा भारी जन्तु रेत की दलदल या बालूपंक वाले स्थान पर चलने की कोशिश करता है, तो उसे आगे बढ़ने के लिए आवश्यक प्रतिक्रिया बल नहीं मिल पाता। इसके विपरीत, दलदल पीछे की ओर तथा नीचे की ओर खिसकती जाती है। इस प्रकार, व्यक्ति ( भारी जन्तु) आगे बढ़ने में असमर्थ रहता है, जितना ही वह आगे बढ़ने की कोशिश करता है उतना ही वह दलदल में भैंसता जाता |

प्रश्न 9.
जब कभी अचानक हमारा पैर केले के छिलके पर पड़ जाता है तो हमारे लिए अपने शरीर का सन्तुलन बनाए रखना कठिन क्यों हो जाता है?
उत्तर:
जब हम सड़क पर चलते हैं तो सड़क और हमारे पैरों के बीच कार्यरत बल हमारे शरीर का सन्तुलन बनाए रखने में हमारी मदद करता है। ऐसे में जब कभी हमारा पैर केले के छिलके पर पड़ता है तो हमारे पैरों और सड़क के बीच घर्षण बल एकाएक कम हो जाता है जिसके कारण शरीर का सन्तुलन बनाए रखना कठिन हो जाता है और हम गिर पड़ते हैं।

प्रश्न 10.
चलती हुई गाड़ी से अचानक उतरने पर यात्री आगे की ओर गिर पड़ता है, क्यों? स्पष्ट कीजिए।
उत्तर:
चलती हुई गाड़ी से अचानक उतर जाने पर यात्री गिर पड़ता है- इसका कारण यह है कि यात्री अचानक चलती हुई गाड़ी से उतरता है तो उसके पैर तो जमीन के सम्पर्क में आते ही विरामावस्था में आ जाते हैं, परन्तु शरीर का ऊपरी भाग उसी वेग से चलता रहता है। अतः यात्री गाड़ी के चलने की दिशा में गिर पड़ता है। यदि यात्री गाड़ी से उतरते समय थोड़ी दूर गाड़ी के साथ-साथ दौड़े तो वह गिरने से बच सकता है।

प्रश्न 11.
यदि हथौड़े का हत्या ढीला हो तो हत्थे को पृथ्वी पर ऊर्ध्वाधर पटखने से हथौड़ा हत्थे में क्यों कस जाता है?
उत्तर:
हथौड़े को हत्थे में कसने के लिए हत्थे को तेजी से जमीन पर मारते हैं- जब हथौड़े के हत्थे को जमीन पर मारने के लिए तेजी से नीचे की ओर लाते हैं तो हथौड़ा तथा हत्था दोनों गति की अवस्था में होते हैं। हत्थे का सिरा जमीन पर लगते ही विरामावस्था में आ जाता है, जबकि हथौड़ा जड़त्व के कारण गति की अवस्था में रहता है अतः हथौड़ा नीचे आकर हत्थे में कस जाता है।

प्रश्न 12.
स्पष्ट कीजिए कि गति विषयक द्वितीय नियम F = ma में न्यूटन का गतिविषयक प्रथम नियम स्वतः निहित है।
उत्तर:
न्यूटन के गति के द्वितीय नियम से, F = ma
यदि F = 0 हो तो a = 0 अर्थात् यदि वस्तु पर बाह्य बल न लगाया जाए तो वस्तु में त्वरण भी उत्पन्न नहीं होगा। त्वरण के शून्य होने पर या तो वस्तु विरामावस्था में ही रहेगी या एकसमान वेग से गतिमान रहेगी । यही न्यूटन का गति विषयक प्रथम नियम है। अतः न्यूटन के गति के द्वितीय नियम में प्रथम नियम स्वतः निहित है।

प्रश्न 13.
गिलास पर रखे पत्ते को अचानक हटा देने पर उस पर रखा सिक्का गिलास में क्यों गिर जाता है?
उत्तर:
गिलास पर रखे पत्ते को अचानक हटा देने पर उस पर रखा सिक्का गिलास में जा गिरता है-इसका कारण यह है कि प्रारम्भ में पत्ता तथा सिक्का दोनों विरामावस्था में थे। पत्ते को क्षैतिज दिशा में ऊँगली से तीव्रता से धक्का देने पर उसमें गति उत्पन्न हो जाती है, जबकि सिक्का जड़त्व के कारण उसी स्थान पर स्थिर रहता है अतः पत्ता हटकर आगे बढ़ जाता है तथा सिक्का (पत्ता हटने के कारण) गिलास में गिर जाता है।

प्रश्न 14.
चलती हुई गाड़ी को अचानक रोक देने पर यात्री का शरीर आगे क्यों झुक जाता है?
उत्तर:
चलती हुई गाड़ी के अचानक रुकने पर उसमें बैठे यात्री आगे की आगे झुक जाते हैं-इसका कारण यह है कि गाड़ी के अचानक रुकने पर उसका फर्श तथा उस पर रखे हुए यात्रियों के पैर तो विरामावस्था में आ जाते हैं, परन्तु उनके शरीर का ऊपरी भाग जड़त्व के कारण उसी वेग से आगे की ओर चलने का प्रयास करता है। इसलिए यात्री आगे की ओर झुक जाते हैं।

प्रश्न 15.
रेलगाड़ी के अचानक चलने पर उसमें खड़ा यात्री पीछे की ओर क्यों गिर पड़ता है?
उत्तर:
रेलगाड़ी के अचानक चलने पर उसमें खड़ा यात्री पीछे की ओर गिर पड़ता है-इसका कारण यह है कि यात्री के शरीर का निचला भाग तो गाड़ी के सम्पर्क में होने के कारण गाड़ी के चलने पर तुरन्त गति में आ जाता है, परन्तु उसका ऊपरी भाग विराम जड़त्व के कारण विरामावस्था में ही बना रहता है। इस कारणवश यात्री के शरीर के ऊपरी भाग को पीछे की ओर धक्का लगता है तथा यात्री पीछे की ओर गिर पड़ता है।

प्रश्न 16.
न्यूटन के गतिविषयक नियमों को उदाहरण देकर समझाइए।
अथवा
गैलीलियो (जड़त्व) का नियम उदाहरण देकर समझाइए।
अथवा
न्यूटन के गतिविषयक द्वितीय नियम की सहायता से सिद्ध कीजिए-
बल = द्रव्यमान × त्वरण
अथवा
न्यूटन का गति-विषयक तृतीय नियम उदाहरण देकर स्पष्ट कीजिए।
अथवा
क्रिया-प्रतिक्रिया नियम लिखिए तथा इसका उदाहरण
देकर व्याख्या कीजिए।
अथवा
गति के तृतीय नियम का उल्लेख कीजिए। इसे क्रिया-प्रतिक्रिया नियम भी कहा जाता है, क्यों? स्पष्ट कीजिए।
उत्तर:
(1) न्यूटन का गति-विषयक प्रथम नियम इस नियम के अनुसार, “यदि कोई वस्तु विरामावस्था में है तो विरामावस्था में ही बनी रहेगी और यदि वह एक सरल रेखा में एकसमान वेग से चल रही है तो वह उसी प्रकार चलती रहेगी, जब तक कि उस पर कोई बाह्य बल लगाकर उसकी वर्तमान अवस्था में परिवर्तन न किया जाए।” इसे गैलीलियो का नियम अथवा जड़त्व का नियम भी कहते हैं।
उदाहरण 1- यदि कोई पुस्तक मेज पर रखी है तो वह तब तक उसी अवस्था में रहेगी, जब तक कि उस पर बाहर से कोई बल लगाकर उसे वहाँ से हटा न दिया जाए।

उदाहरण 2- चलती बस का इंजन बन्द करने के बाद भी बस कुछ दूर चलकर रुक जाती है यह घर्षण बल के कारण होता है। यदि घर्षण बल न हो तो बस चलती रहेगी।

(2) न्यूटन का गतिविषयक द्वितीय नियम इस नियम के अनुसार, “किसी वस्तु पर बाहर से लगाया गया बल, उस वस्तु के द्रव्यमान तथा उस वस्तु में बल की दिशा में उत्पन्न त्वरण के गुणनफल के अनुक्रमानुपाती होता है।”
बल (F) ∝ द्रव्यमान (m) x त्वरण (a)
अथवा बल (F) = K x m x a … (1)
(जहाँ K एक नियतांक है।)
यदि हम बल F के मात्रक इस प्रकार चुनें कि एकांक बल, एकांक द्रव्यमान की वस्तु में एकांक त्वरण उत्पन्न कर सके, तब
समीकरण (1) मैं F = 1, m = 1 तथा a = 1 रखने पर,
1 = K × 1 × 1
अथवा K = 1
अत: समीकरण (1) से,
F = m x a
अर्थात्
बल = द्रव्यमान x त्वरण
इसे ही न्यूटन का गतिविषयक द्वितीय नियम कहते हैं।
उदाहरण 1- क्रिकेट की गेंद पकड़ते समय खिलाड़ी अपने हाथ पीछे की ओर खींचता है।
उदाहरण 2- बन्दूक की गोली शरीर में ‘घुस जाती है।

(3) न्यूटन का गति-विषयक तृतीय नियम- इस नियम के अनुसार, जब दो वस्तुओं में आपस में अन्योन्य क्रिया होती है तो पहली वस्तु द्वारा दूसरी वस्तु पर लगाया गया बल, दूसरी वस्तु द्वारा पहली वस्तु पर लगाए गए बल के बराबर और विपरीत दिशा में होता है अथवा क्रिया व उसकी प्रतिक्रिया बराबर तथा विपरीत दिशा में होती है।

उदाहरण- तैरते समय मनुष्य पानी को पीछे धकेलता है (क्रिया); परिणामस्वरूप जल मनुष्य को आगे की ओर धकेलता है (प्रतिक्रिया)।

(i) इन दो बलों में से एक को क्रिया तथा दूसरे को प्रतिक्रिया कहते हैं अतः इसे क्रिया-प्रतिक्रिया का नियम भी कहते हैं। इस नियम के अनुसार, “प्रत्येक क्रिया की उसके बराबर, परन्तु विपरीत दिशा में प्रतिक्रिया होती है।”
(ii) बन्दूक से गोली छोड़ने पर गोली क्रिया बल के कारण आगे बढ़ती है परन्तु गोली भी बन्दूक पर विपरीत दिशा में इतना ही प्रतिक्रिया बल लगाती है; अतः बन्दूक स्वयं पीछे की ओर हटती है तथा बन्दूक चलाने वाले को पीछे की ओर धक्का मारती है।

आंकिक प्रश्न

प्रश्न 1.
9.8 kg द्रव्यमान की एक वस्तु पर 4kg wt का बल लगता है। वस्तु में उत्पन्न त्वरण ज्ञात कीजिए। (gm 9.8N/kg)
हल:
F = 4kg wt = 4 × 9.8N, m = 9.8 kg
परन्तु F = ma से
वस्तु में उत्पन्न त्वरण
a = \(\frac { F }{ m }\)
= \(\frac{4 \times 9.8 \mathrm{~N}}{9.8 \mathrm{~kg}}\)
= 4m/s² उत्तर

प्रश्न 2.
घर्षण रहित क्षैतिज तल पर रखी किसी वस्तु में 10 N का बल लगाने पर 5m/s² का त्वरण उत्पन्न होता है। वस्तु का द्रव्यमान कितना होगा?
हल:
F = 10 N, a = 5m/s², m = ?
हम जानते हैं कि F = ma
∴ m = \(\frac { F }{ a }\)
= \(\frac{10 \mathrm{~N}}{5 \mathrm{~m} / \mathrm{s}^2}\)
= 2 kg

प्रश्न 3.
1500kg की एक कार को विरामावस्था से 10 5 में 30 m/s का वेग प्रदान करने के लिए कितने बल की आवश्यकता होगी?
हल:
= 30m/s, t = 10s
हम जानते हैं
a = \(\frac{v-u}{t}=\frac{(30-0)}{10 s}\) = 3 ms²
अब m = 1500 kg, a = 3 m/s²
तो F = m x a = 1,500 kg x a = 3 ms² = 4500N उत्तर

प्रश्न 4.
0.5 kg द्रव्यमान का एक ठोस मेज पर रखा है। बताइए उस पर कितना बल लगाया जाए कि उसमें 4 सेकण्ड में 2 m/s का वेग उत्पन्न हो जाए?
हल:
u = 0 m/s, v = 2 m/s, t = 4s, F = ?
त्वरण a के लिए
a = \(\frac{v-u}{t}=\frac{2 \mathrm{~m} / \mathrm{s}-0 \mathrm{~m} / \mathrm{s}}{4 \mathrm{~s}}\) = 0.5m/s²
अब बल
F = m.a = 0.5 kg x 0.5 m/s²
= 0.25 kg m/s² अथवा 0.25N उत्तर

प्रश्न 5.
एक 5 किग्रा. की रायफल 500 मीटर / सेकण्ड के वेग से 10 ग्राम की गोली छोड़ती है। रायफल का गोली छोड़ने का वेग ज्ञात करो।
हल:
रायफल का द्रव्यमान (m₁) = 5 किग्रा.
गोली का द्रव्यमान (m₂) = 10 ग्रा. = 10 x 10^-3 किग्रा.
गोली का वेग u₂ = 500 मीटर प्रति सेकण्ड
मान लो रायफल की गोली का वेग u₂ = u₁
संवेग संरक्षण के नियम का उपयोग करके
m₁u₁ = m₂u₂ या 5 x u₁ = 10 x 10^-3 x 500
u₁ = \(\frac{10 \times 10^{-3} \times 500}{5}\)
u₁ = 1 मीटर प्रति सेकण्ड।

प्रश्न 6.
एक वस्तु जिसका द्रव्यमान 10 kg है; 100 cm/ 8 के वेग से चल रही है। इसको 10 सेकण्ड में स्थिर दशा में लाने के लिए कितना बल लगेगा?
हल:
वस्तु का द्रव्यमान m = 10kg
वस्तु का प्रारम्भिक वेग u = 100 cm/s
वस्तु का अन्तिम वेग v = 0
समय t = 10 s
अब त्वरण a = \(\frac{v-u}{t}=\frac{0 \times 100}{10}\)
= – 10 cm/s²
= \(\frac { -10 }{ 100 }\)m/s²
= – 0.01 m/s²
F = ma = 10 x \(\frac { 10 }{ 100 }\) उत्तर

प्रश्न 7.
दो गोले 20 kg तथा 80 kg द्रव्यमान के क्रमशः 40 m/s तथा 10 m/s के वेग से एक-दूसरे की ओर आ रहे हैं। यदि वे टकराकर जुड़ जायें तो संयुक्त गोला किस वेग से गति करेगा?
हल:
प्रश्नानुसार, m₁ = 20 kg, m₂ = 80kg
u₁ = 40m/s; u₂ = 10 m/s (-)
टक्कर से पूर्व संवेग m₁u₁ + m₂u₂
= 20 × 40 – 80 x 10 = 800 – 800 = 0
टक्कर के बाद संयुक्त गोले का द्रव्यमान 20 + 80 = 100 kg, माना टक्कर के बाद वेग v है तब
टक्कर के बाद संवेग = mv = 100v
संवेग संरक्षण के नियम से,
टक्कर के पूर्व संवेग टक्कर के बाद संवेग 100 v या v = 0
अतः टक्कर के बाद दोनों गोले जुड़कर स्थिर हो जायेंगे।

प्रश्न 8.
6 किग्रा का एक पिण्ड स्थिर अवस्था में रखा है उस पर कितना बल लगाया जाए कि उसमें 4 सेकण्ड में 4 मीटर / सेकण्ड का वेग उत्पन्न हो जाए।
हल:
दिया है प्रारम्भिक वेग (u) = 0, अन्तिम वेग (v) = 4 मीटर / सेकण्ड समय (t) = 4 सेकण्ड
द्रव्यमान (m) = 6 किग्रा, बल (F) = ?
गति के प्रथम समीकरण
v = u + at से, 4 = 0 + a × 4
∴ पिण्ड में उत्पन्न त्वरण (a) = \(\frac { 4 }{ 4 }\) = 1 मीटर / सेकण्डर
पिण्ड पर लगाया गया बल (F) = m xa
= 6 किग्रा 1 मीटर/सेकण्डर²
= 6 किग्रा मीटर / सेकण्ड² = 6 न्यूटन।

प्रश्न 9.
30 न्यूटन का बल 5 किग्रा के पिण्ड पर कितनी देर तक कार्य करे कि उसका वेग 2 मीटर/सेकण्ड हो जाए?
हल:
दिया है बल (F) = 30 न्यूटन, द्रव्यमान (m) = 5 किग्रा, प्रारम्भिक वेग (u) = 0
अन्तिम वेग (v) = 12 मीटर / सेकण्ड समय (t) = ?
सूत्र F = m x a से,
पिण्ड में उत्पन्न त्वरण (a)

प्रश्न 10.
किसी राइफल का द्रव्यमान 3 kg है। उससे 0.03 kg द्रव्यमान की गोली चलाई जाती है। गोली राइफल से 100 m/s के वेग से बाहर निकलती है। यदि गोली नाल से होकर बाहर निकलने में 0.003 सेकण्ड का समय लेती है, तो राइफल पर प्रतिक्षेप के कारण लगने वाले बल की गणना कीजिए।
हल:
m₁ = 3kg, m₂ = 0.03kg
u₁ = u₂ = 0, v₁ = ?, v₂ = 100n/s
संवेग संरक्षण के नियम के अनुसार
m₁ u₁ + m₁v₁ = m₁v₁ + m₂v₂
अथवा 0 + 0 = 3 x v₁ + 100(0.03)
या v₁ = \(\frac{100 \mathrm{~m} / \mathrm{s} \times 0.03 \mathrm{~kg}}{3 \mathrm{~kg}}\) = – 1m/s
F = \(\frac{-3 \mathrm{~kg} \mathrm{~m} / \mathrm{s}}{0.003 \mathrm{~s}}\) = – 1000 kg m/s² = – 1000 N
अतः राइफल से गोली चलाने वाले व्यक्ति पर 1000 N के बल का धक्का पीछे की ओर लगेगा।

प्रश्न 11.
रायफल से 50g की गोली 400 m/s के बेग से निकलती है। रायफल 4 m/s के वेग से पीछे हटती है। रायफल का द्रव्यमान ज्ञात कीजिए।
हल:
गोली के छूटने से पहले संवेग = 0
गोली के छूटने के बाद संवेग = 50 × 10^-3 kg × 400m/s
माना रायफल का द्रव्यमान m है अतः इसका संवेग
= – 4m ( पीछे हटती है।)
इसलिए गोली तथा रायफल का संयुक्त संवेग
= 20 – 4m
अतः गोली छूटने के बाद संयुक्त संवेग = गोली छूटने से पहले संयुक्त संवेग
20 – 4m = 0
अथवा m = \(\frac { 20 }{ 4 }\) = 5 kg

प्रश्न 12.
1000 kg की एक मोटर कार 4 m/s के वेग से जा रही है। 10,000 kg का एक ट्रक विपरीत दिशा से आता है तथा कार से टकरा जाता है। दोनों गाड़ियाँ तुरन्त रुक जाती हैं। दूक का वेग ज्ञात कीजिए।
हल:
टकराने से पहले कार का संवेग p = mv
= 10³ × 4 = 4 x 10³ kg m/s
माना टकराने से पहले ट्रक का वेग v m/s है।
इसलिए, टकराने से पहले ट्रक का संवेग
= 10⁴ x v kg m/s
कुल संवेग = 4 x 10³ + 10⁴ x v
टकराने के बाद कुल संवेग = 0
इसलिए, टकराने से पहले कुल संवेग = टकराने के बाद कुल संवेग
4 x 10³ + 10⁴ x v = 0 या v = \(\frac{4 \times 10^3}{10^4}\) = 0.4m/s

प्रश्न 13.
20 kg का विस्फोटक गोला जो कि 12 m/s के वेग से गतिमान है, अचानक फटकर दो टुकड़ों में टूट जाता है, जिनके द्रव्यमान 14 kg तथा 6 kg हैं। यदि बड़े टुकड़े का वेग शून्य हो तो छोटे टुकड़े का वेग क्या होगा? हल:
गोले के फटने से पहले संवेग = m x v
= 20 x 12 = 240 kgm/s
माना छोटे गोले का वेग है। फटने के बाद दोनों का संयुक्त संवेग
= 14 × 0 + 6 × v = 6v kg m/s
चूँकि फटने के बाद संवेग = फटने के पहले संवेग
6v = 240 या v = \(\frac { 240 }{ 6 }\) = 40 m/s

प्रश्न 14.
एक पिण्ड का द्रव्यमान 30 किग्रा है। उस पर 60 न्यूटन का बल आरोपित किया जाता है। ज्ञात कीजिए कि पिण्ड में कितना त्वरण उत्पन्न होगा?
हल:
दिया है पिण्ड का द्रव्यमान (m) 30 किग्रा, बल (F) = 60 न्यूटन, त्वरण (a) = ?
सूत्र F = m x a से,

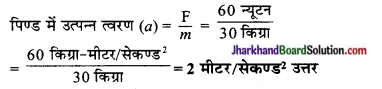
प्रश्न 15.
10 न्यूटन का एक बल 0.2 किग्रा के एक पिण्ड पर कार्य कर रहा है। पिण्ड में उत्पन्न त्वरण की गणना कीजिए।
हल:
दिया है बल (F) = 10 न्यूटन = 10 किग्रा मीटर / सेकण्ड², द्रव्यमान (m) = 0.2 किग्रा, त्वरण (a) = ?
सूत्र F= m x a से,
पिण्ड में उत्पन्न त्वरण (a) = \(\frac{\mathrm{F}}{m}=\frac{10 \mathrm{~N}}{0.2 \mathrm{~kg} .}=\frac{100}{2}\)ms²
= 50 मीटर / सेकण्ड²।

प्रश्न 16.
किसी 10 ग्राम के द्रव्यमान में 5 मीटर / सेकण्ड का त्वरण उत्पन्न करने में अधिक बल की आवश्यकता होगी अथवा 20 ग्राम के द्रव्यमान में 5 मीटर/सेकण्ड का त्वरण उत्पन्न करने में?
हल:
पहली अवस्था में,
दिया है द्रव्यमान (m₁) = 10 ग्राम = 10 x 10^-3 किग्रा,
त्वरण (a₁) = 5 मीटर/सेकण्डर²
∴ बल (F₁) = m₁ x a₁
= (10 × 10^-3 किग्रा) x (5 मीटर / सेकण्ड)
= 5 × 10^-2 न्यूटन
= 0.05 न्यूटन
दूसरी अवस्था में,
दिया है द्रव्यमान (m₁) = 20 ग्राम 20 x 10^-3 किग्रा, त्वरण (a) = 5 मीटर/सेकण्ड 2 बल (F₂) = m₂ x a₂
= (20 x 10^-3 किग्रा) x (5 मीटर / सेकण्ड²)
= (10 x 10^-2 किग्रा – मीटर/सेकण्ड²)
= 10 × 10^-2 न्यूटन = 0.1 न्यूटन
क्योंकि F₂ का परिमाण F₁ से अधिक है; अतः दूसरी अवस्था में अर्थात् 20 ग्राम द्रव्यमान में 5 मीटर / सेकण्ड² का त्वरण उत्पन्न करने के लिए अधिक बल की आवश्यकता होगी।

प्रश्न 17.
यदि 5 किग्रा द्रव्यमान की वस्तु पर 200 न्यूटन का बल लगाया जाए तो वस्तु में उत्पन्न त्वरण कितना होगा?
हल:
दिया है वस्तु का द्रव्यमान = 5 किग्रा, वस्तु पर
बल F = 200 न्यूटन, वस्तु का त्वरण a = ?
सूत्र F = ma से,
वस्तु का त्वरण a = \(\frac { F }{ m }\)
= \(\frac { 200 }{ 5 }\)
= 40 मीटर/सेकण्ड²।

प्रश्न 18.
दो पिण्डों पर समान बल लगाने पर उसमें त्वरणों का अनुपात 1: 2 है। पहले पिण्ड का द्रव्यमान 5 किग्रा है। दूसरे पिण्ड का द्रव्यमान क्या होगा?
हल:
दिया है त्वरणों \(\left(\frac{a_1}{a_2}\right)\) का अनुपात = \(\frac { 1 }{ 2 }\), m₁ = 2 किग्रा, m₂ = ?
माना दोनों पिण्डों के द्रव्यमान क्रमश: m₁ व m₂ तथा उनमें उत्पन्न त्वरण a₁ व a₂ हैं।
सूत्र F = m x a से, m₁ x a₁ = m₂ × a₂
अत: दूसरे पिण्ड का द्रव्यमान
(m₂) = \(\frac{m_1 \times a_1}{a_2}\)
= \(\frac { 2×1 }{ 2 }\) = 1 किया।

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 10 वृत्त Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 10 वृत्त

प्रश्न 1.
चित्र में, ∠BAC का मान होगा :

(A) 80°
(B) 160°
(C) 90°
(D) 200°
हल :
∠BOC + ∠BOA + ∠COA = 360° (बिन्दु O पर बने कोणों का योग )
⇒ ∠BOC + 85° + 115° = 360°
⇒ ∠BOC + 200° = 360°
∠BOC = 360° – 200° = 160°.
केन्द्र पर अन्तरित कोण वृत्त की परिधि पर बने कोण का दोगुना होता है।
∴ ∠BOC = 2∠BAC
⇒ ∠BAC = \(\frac {∠BOC}{2}\) = \(\frac {160°}{2}\)
∴ ∠BAC = 80°
अतः सही विकल्प ‘A’ है।

प्रश्न 2.
चित्र में, यदि वृत्त का केन्द्र O हो, तो ∠AOB का मान होगा :

(A) 70°
(B) 110°
(C) 120°
(D) 140°.
हल :
C को O से मिलाने पर
ΔAOC में, AO = OC (समान वृत्त की त्रिज्याएँ)
⇒ ∠OAC = ∠OCA
∴ ∠OCA = 30°
इसी प्रकार OB = OC
∠OBC = ∠OCB = 40°
∠ACB = ∠OCA + ∠OCB = 30° + 40° = 70°
∠AOB = 2ACB (वृत्त के केन्द्र पर अन्तरित कोण)
∠AOB = 2 × 70° = 140°
अत: सही विकल्प ‘D’ है।

प्रश्न 3.
चित्र में, यदि वृत्त का केन्द्र O हो और ∠AOC = 160° हो, तो ∠ABC का मान होगा :

(A) 160°
(B) 80°
(C) 200°
(D) 100°.
हल :
दिया है,
लघु ∠AOC = 160°
दीर्घ ∠AOC = 360°- लघु ∠AOC
= 360° – 160° = 200°
दीर्घ ∠AOC = 2∠ABC (वृत्त के केन्द्र पर अन्तरित कोण)
⇒ ∠ABC = \(\frac {दीर्घ ∠AOC}{2}\)
∴ ∠ABC = \(\frac {200°}{2}\) = 100°
अत: सही विकल्प ‘D’ है।

प्रश्न 4.
चित्र में, यदि ∠ABC = 75° और ∠BAC = 35° हो, तो ∠ADB होगा :

(A) 40°
(B) 110°
(C) 70°
(D) 75°.
हल :
ΔABC में,
∠ABC + ∠BAC + ∠BCA = 180°, (Δ के अन्तः कोणों का योग)
⇒ 75° + 35° + ∠BCA = 180°
⇒ 110° + ∠BCA = 180°
∴ ∠BCA = 180° – 110° = 70°
∴ ∠ADB = ∠BCA (एक ही वृत्तखण्ड के कोण)
∠ADB = 70°
अत: सही विकल्प ‘C’ है।

प्रश्न 5.
चित्र में x का मान होगा :

(A) 40°
(B) 70°
(C) 110°
(D) 90°
हल :
⇒ ∠ADB = ∠ACB = 40°
(एक ही वृत्तखण्ड के कोण)
∴ ∠ACB = 40°
[∵ ∠ADB = 40° दिया है ] (Δ के अन्तः कोणों का योग)
अब ΔABC में,
∠ABC + ∠ACB + ∠BAC = 180°
⇒ x° + 40° + 70° = 180°
⇒ x° + 110° = 180°
x° = 180° – 110° = 70°
अतः सही विकल्प ‘B’ है।

प्रश्न 6.
चित्र में, ABCD एक चक्रीय चतुर्भुज है। यदि ∠D = 120° हो, तो ∠CBE होगा :

(A) 120°
(B) 60°
(C) 180°
(D) 90°.
हल :
∵ चक्रीय चतुर्भुज का बहिष्कोण उसके अन्तराभिमुख कोण के बराबर होता है।
∴ ∠CBE = ∠ADC = 120°
अत: सही विकल्प ‘A’ है।

प्रश्न 7.
चित्र में, यदि A, B, C और D एक चक्रीय चतुर्भुज के शीर्ष हों, तो ∠x का मान होगा :

(A) 70°
(B) 35°
(C) 110°
(D) 100°.
हल :
∵ ∠CBA + 70° = 180°, (रैखिक युग्म कोण)
∴ ∠CBA = 180° – 70° = 110°
∵ ABCD चक्रीय चतुर्भुज है।
हम जानते हैं कि चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है।
अतः ∠CBA + ∠CDA = 180°
⇒ 110° + ∠CDA = 180°
∴ ∠CDA = 180° – 110° = 70°
परन्तु ∠x + ∠CDA = 180° (रैखिक युग्म कोण)
⇒ ∠x + 70° = 180°
∴ ∠x = 180° – 70° = 110°
‘अतः सही विकल्प ‘C’ है।

प्रश्न 8.
यदि वृत्त का व्यास दो जीवाओं में से प्रत्येक समद्विभाजित करे तो जीवाएँ होंगी :
(A) समान्तर
(B) लम्बवत्
(C) प्रतिच्छेदी
(D) इन में से कोई नहीं।
हल :
सही विकल्प ‘A’ है।

प्रश्न 9.
यदि सर्वांगसम वृत्तों में दो चाप सर्वांगसम हों, तो उनकी संगत जीवाएँ होंगी :
(A) समान्तर
(B) बराबर
(C) लम्बवत्
(D) प्रतिच्छेदी ।
हल :
सही विकल्प ‘B’ है।

प्रश्न 10.
एक वृत्त में केन्द्र से समान दूरी पर स्थित जीवाएँ एक-दूसरे की होती हैं :
(A) दोगुनी
(B) तिगुनी
(C) आधी
(D) बराबर ।
हल :
सही विकल्प ‘D’ है।

प्रश्न 11.
एक वृत्त के किसी चाप का डिग्री माप 180° है, वह चाप है :
(A) दीर्घ चाप
(B) लघु चाप
(C) वृत्त
(D) अर्द्धवृत्त ।
हल :
सही विकल्प ‘D’ है।

प्रश्न 12.
तीन संरेखीय बिन्दुओं से गुजरने वाले वृत्तों की संख्या है :
(A) एक
(B) दो
(C) शून्य
(D) अनन्त ।
हल :
सही विकल्प ‘C’ है।

प्रश्न 13.
यदि किसी वृत्त में चाप AB = चाप BA हो, तो
(A) दीर्घ चाप
(B) लघु चाप
(C) अर्द्ध वृत्त
(D) वृत्त ।
हल :
सही विकल्प ‘C’ है।

प्रश्न 14.
आकृति में, AB वृत्त का एक व्यास है और CD त्रिज्या के बराबर एक जीवा है। AC और BD बढ़ाये जाने पर बिन्दु E पर मिलती हैं। सिद्ध कीजिए कि ∠AEB = 60° है।

हल :
OC, OD और BC को मिलाया। त्रिभुज ODC एक समबाहु त्रिभुज है।
[क्योंकि OC = OD त्रिज्याएँ हैं तथा CD = त्रिज्या (दिया है)]
∴ ∠COD = 60°
अब ∠CBD = \(\frac {1}{2}\)∠COD
=  \(\frac {1}{2}\) × 60°
∴ ∠CBD = 30° ……(i)
∵ AB वृत्त का व्यास है तथा ∠ACB अर्द्धवृत्त में बना कोण है।
∴ ∠ACB = 90°
∴ ∠BCE = 180° – ∠ACB
= 180° – 90°
∴ ∠BCE = 90° ……(ii)
हम जानते हैं ΔBCE से,
∠CBD + ∠BCE + ∠CEB = 180°
∴ ∠CEB = 180° – ∠CBD – ∠BCE
समीकरण (i) व (ii) से मान रखने पर,
∠CEB = 180° – 30° – 90°
∴ ∠CEB = 60°
अर्थात् ∠AEB = 60°
इति सिद्धम् ।

प्रश्न 15.
दो वृत्त दो बिन्दुओं A और B पर प्रतिच्छेद करते हैं। AD और AC दोनों वृत्तों के व्यास हैं। सिद्ध कीजिए कि बिन्दु B, रेखाखण्ड DC पर स्थित हैं।
हल :
AB को मिलाया।
∠ABD = 90°
(अर्द्धवृत्त में बना कोण) …………..(i)
∠ABC = 90°
(अर्द्धवृत्त में बना कोण) ………(ii)

समीकरण (i) व (ii) को जोड़ने पर,
∠ABD + ∠ABC = 90° + 90°
∴ ∠ABD + ∠ABC = 180°
अत: DBC एक सरल रेखा है।
अत: B, रेखाखण्ड DC पर स्थित है । इति सिद्धम् ।

प्रश्न 16.
सिद्ध कीजिए कि किसी चक्रीय चतुर्भुज के अन्तः कोणों के समद्विभाजकों से बना चतुर्भुज (यदि सम्भव हो) चक्रीय होता है।
हल :

दिया है : ABCD एक चक्रिय चतुर्भुज है, जिसके अन्तः कोण A, B, C और D समद्विभाजक क्रमशः AH, BF, CF और DH
चतुर्भुज EFGH बनाते हैं।
∠ABE = ∠AEB + ∠EAB = 180°
∠AEB = 180°- (∠ABE + ∠EAB) ………..(i)
सिद्ध करना है : EFGH चक्रीय चतुर्भुज है।
उपपत्ति : ΔABE में,
∵ ∠ABE = \(\frac {1}{2}\)∠B (दिया है) … (ii)
∠EAB = \(\frac {1}{2}\)∠A (दिया है) … (iii)
∠AEB = ∠FEH
(शीर्षाभिमुख कोण) …(iv)
समीकरण (i) मैं (ii), (iii) व (iv) से मान रखने पर,
∠FEH = 180° – \(\frac {1}{2}\)(∠A + ∠B)
इसी प्रकार,
∠FGH = 180° – \(\frac {1}{2}\)(∠C + ∠D)
अतः
∠FEH + ∠FGH = 180° – \(\frac {1}{2}\)(∠A + ∠B) + 180° – \(\frac {1}{2}\)(∠C + ∠D)
= 360° – \(\frac {1}{2}\)(∠A + ∠B + ∠C + ∠D)
= 360° – \(\frac {1}{2}\) × 360°
= 360° – 180°= 180°
अतः ∠FEH + ∠FGH = 180°
[चतुर्भुज के सम्मुख कोण]
इसी प्रकार ∠EFG + ∠EHG = 180°
[चतुर्भुज के सम्मुख कोण]
अतः EFGH एक चक्रीय चतुर्भुज है । इति सिद्धम् ।

प्रश्न 17.
सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज की किसी भी समान भुजा को व्यास मानकर खींचा गया वृत्त, आधार को समद्विभाजित करता है।
हल :

दिया है : समद्विबाहु ΔABC में AB = AC और व्यास AC पर खींचा गया वृत्त आधार BC को D बिन्दु पर प्रतिच्छेदित है।
सिद्ध करना है : BD = CD.
उपपत्ति : AC को व्यास मानकर वृत्त खींचा गया है और ∠ADC अर्द्धवृत्त का कोण है,
अत: ∠ADC = 90°
अब ΔABD और ΔACD से,
AB = AC (दिया है)
AD = AD (उभयनिष्ठ)
∠ADB = ∠ADC (समकोण)
∴ ΔABD ≅ ΔACD (SAS नियम से)
∴ BD = CD. इति सिद्धम् ।

प्रश्न 18.
चित्र में, वृत्त का केन्द्र O एवं त्रिज्या 5 सेमी है। यदि OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 सेमी और CD = 6 सेमी हो, तो PQ ज्ञात कीजिए।

हल :
दिया है, OP ⊥ AB एवं OQ ⊥ CD
चूँकि जीवा पर केन्द्र से डाला गया लम्ब जीवा को समद्विभाजित करता है।
अत: AP = PB = \(\frac {1}{2}\)AB = 4 सेमी
तथा CQ = QD = \(\frac {1}{2}\)CD = 3 सेमी
और OA = OC = 5 सेमी (त्रिज्याएँ)
ΔOPA में, बौधायन प्रमेय से,
या OP² = OA² – AP²
OP² = 5² – 4² = 25 – 16 = 9
∴ OP = 3 सेमी
इसी प्रकार ΔOQC में,
OQ² = OC² – CQ²
OQ² = 5² – 3²
= 25 – 9 = 16
∴ OQ = 4 सेमी
अतः PQ = OP + OQ
= 3 + 4 = 7 सेमी।

प्रश्न 19.
सिद्ध कीजिए कि किसी समपंचभुज के कोई से चार शीर्ष एक वृत्त पर स्थित होते हैं।

हल :
दिया है समपंचभुज ABCDE
∴ AB = BC = CD = DE = AE.
सिद्ध करना है: कोई चार शीर्ष वृत्त पर स्थित हैं।
रचना : AC तथा BE को मिलाया।
उपपत्ति: ΔABE और ΔABC में,
AB = AB (उभयनिष्ठ)
∠BAE = ∠ABC (समपंचभुज के अन्त:कोण)
AE = BC (दिया है)
ΔABE ≅ ΔABC (SAS नियम से)
अत: ∠AEB = ∠ACB
परन्तु ये कोण भुजा AB द्वारा भुजा के एक ही ओर बनाये गये हैं।
अतः बिन्दु A, B, C और E एक वृत्त पर स्थित हैं। इति सिद्धम् ।

प्रश्न 20.
दिये गये चित्र में ‘O’ वृत्त का केन्द्र है। यदि ∠APB = 40° है, तो ∠AQB का मान ज्ञात करो ।
हल :

जीवा AB द्वारा ∠APB तथा ∠AQB एक ही वृत्तखण्ड में अन्तरित हैं।
अतः ∠APB = ∠AQB
= 40° (एक ही वृत्तखण्ड के कोण)
∴ ∠AQB =40°.

प्रश्न 21.
दिये गये चित्र में, ∠BOC = 75° तो ∠ACO का मान ज्ञात करो ।
हल :

∵ AOB वृत्त का व्यास है।
∴ ∠AOB = 180°
तथा ∠AOC + ∠BOC = 180° (रैखिक कोण युग्म)
⇒ ∠AOC + 75° = 180°
⇒ ∠AOC = 180°- 75° = 105°
अब ΔAOC में
AO = CO (एक ही वृत्त ही त्रिज्याएँ)
∴ ∠OAC = ∠OCA (समान भुजाओं के सम्मुख कोण)
∠AOC + ∠OAC + ∠OCA = 180°
(त्रिभुज के अन्तः कोणों का योग )
105° + ∠OCA + ∠OCA = 180°
2∠OCA = 180° – 105° = 75°
∠OCA = \(\frac {75}{2}\)
∠OCA = 37.5°

प्रश्न 22.
दिये गये चित्र में ABCD एक चक्रीय चतुर्भुज है। यदि ∠PCB = 70° तो ∠BOD का मान बताइए।
हल :

हम जानते हैं कि वृत्त के अन्तर्गत बने चक्रीय चतुर्भुज के बहिष्कोण का मान उस चतुर्भुज के सम्मुख कोण के बराबर होता है।
अतः ∠BAD = 70°
∠BOD = 2∠BAD (वृत्त केन्द्र पर अन्तरित कोण)
अतः ∠BOD = 70° × 2
∴ ∠BOD = 140°

प्रश्न 23.
दिये गये चित्र में वृत्त की जीवाएँ AB = CD तथा ∠OBA = 40° तो ∠COD का मान बताइए।

हल :
दिया है AB = CD
तथा OB = OD
∴ ∠OBA = ∠ODC = 40°
ΔOCD एक समद्विबाहु त्रिभुज है।
∴ ∠OCD = ∠ODC = 40°
ΔOCD में
∠ODC + ∠OCD + ∠COD = 180°
⇒ 40° + 40° + ∠COD = 180°
∴ ∠COD (x) = 180° – 40° – 40° = 180° – 80
∴ ∠COD = 100°

प्रश्न 24.
एक वृत्त की दो जीवाएँ AB तथा CD जिनकी लम्बाइयाँ क्रमशः 6 सेमी तथा 12 सेमी है, एक-दूसरे के समान्तर तथा वृत्त के केन्द्र के एक ही ओर स्थित हैं। यदि दोनों जीवाओं के बीच की दूरी 3 सेमी है तो वृत्त की त्रिज्या ज्ञात करो ।

हल :
दिया है AB = 6 सेमी
AQ = \(\frac {1}{2}\)AB = \(\frac {1}{2}\) × 6
AQ = 3 सेमी
CD = 12 सेमी
CP = \(\frac {1}{2}\)CD
= \(\frac {1}{2}\) × 12
CP = 6 सेमी
PQ = 3 सेमी
माना वृत्त की त्रिज्या = x सेमी है।
तथा OP = y सेमी है।
समकोण त्रिभुज CPO में,
अतः CO² = CP² + OP²
⇒ x² = (6)² + y²
⇒ x² = 36 + y² …………….(i)
अब, समकोण त्रिभुज, QOA में,
AQ² = OQ² + AQ²
⇒ x² = (3 + y)² + (3)
⇒ x² = (3 + y)² + 9 …………….(ii)
समी. (i) तथा (ii) की तुलना करने पर,
36 + y² = (3 + y)² + 9
या 36 + y² = 9 + y² + 6y + 9
या 36 – 9 – 9 = 6y
या 18 = 6y
∴ y = \(\frac {18}{6}\) = 3 सेमी
y का मान समीकरण (i) में रखने पर,
∴ x² = 36 + y²
⇒ x² = 36 + (3)²
⇒ x² = 36 + 9 = 45
⇒ x = \(\sqrt{45}\) = \(\sqrt{9 \times 5}\)
∴ x = 3\(\sqrt{5}\)
अतः वृत्त की त्रिज्या = 3\(\sqrt{5}\) सेमी

Jharkhand Board JAC Class 9 Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.4 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Exercise 9.4

प्रश्न 1.
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
हल:
दिया है एक समान्तर चतुर्भुज ABCD और एक आयत ABEF समान आधार पर स्थित हैं और उनके क्षेत्रफल भी समान हैं।

सिद्ध करना है: समान्तर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप।
उपपत्ति: ∵ समान्तर चतुर्भुज और आयत की सम्मुख भुजाएँ बराबर होती हैं।
∴ AB = DC …..(i)
[∵ ABCD एक समान्तर चतुर्भुज है]
तथा AB = EF …..(ii)
समीकरण (i) व (ii) से,
DC = EF [∵ ABEF एक आयत है।]
दोनों ओर AB को जोड़ने पर,
AB + DC = AB + EF ….. (iii)
∵ दी गई रेखा के किसी बिन्दु से खींचे जा सकने वाले सभी रेखा खण्ड इस पर स्थित नहीं है, अतः लम्ब खण्ड सबसे छोटा है।
∴ BE < BC तथा AF < AD
⇒ BC > BE तथा AD > AF
⇒ BC + AD > BE + AF …..(iv)
समीकरण (iii) व (iv) को जोड़ने पर
AB + DC + BC + AD > AB + EF + BE + AF
⇒ AB + BC + CD + DA > AB + BE + EF + FA
अत: समान्तर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप।
इति सिद्धम्।

प्रश्न 2.
आकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित हैं कि BD = DE = EC है दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है। क्या आप अब उस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि “क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है ?”

हल:
माना AL रेखा BC पर लम्ब है, अत: AL, ΔABD, ΔADE और ΔAEC की ऊँचाई है।

∴ ar (ΔABD) = \(\frac{1}{2}\) × BD × AL
ar (ΔADE) = \(\frac{1}{2}\) × DE × AL
और ar (ΔAEC) = \(\frac{1}{2}\) × EC × AL
⇒ BD = DE = EC
∴ ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
हाँ, सभी त्रिभुजों की ऊँचाई समान है। बुधिया इस उत्तर द्वारा अपने खेत को तीन बराबर भागों में बाँट सकती है।

प्रश्न 3.
आकृति में ABCD, DCFE और ABFE समान्तर चतुर्भुज हैं। दर्शाइए कि ar (ΔADE) = ar (ΔBCF)।

हल:
चूँकि समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं। और ☐ABCD, ☐DCEF तथा ☐ABFE समान्तर चतुर्भुज हैं।
∴ AD = BC
इसी प्रकार, DE = CF
और AE = BF
ΔADE ≅ ΔBCF (SSS नियम)
या ar (ΔADE) = ar (ΔBCF). इति सिद्धम्।

प्रश्न 4.
आकृति में, ABCD एक समान्तर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि
ar (ΔBPC) = ar (ΔDPQ).

हल:
A और C को मिलाया।
∵ ΔAPC और ΔBPC एक ही आधार PC पर तथा समान समान्तर रेखाओं PC और AB के मध्य स्थित हैं।

∴ ar (ΔAPC) = ar (ΔBPC) …..(i)
∵ AD = CQ (दिया है)
∵ AD || BC (∵ ABCD समान्तर चतुर्भुज है)
तथा AD || CQ
∴ चतुर्भुज ADQC में, सम्मुख भुजाओं का एक युग्म बराबर और समान्तर है।
∴ ADQC एक समान्तर चतुर्भुज है।
⇒ AP = PQ और CP = DP
[∵ समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं]
ΔAPC और ΔDPQ में,
∵ AP = PQ
∠APC = ∠DPQ [ऊर्ध्वाधर सम्मुख कोण हैं]
PC = PD [सिद्ध किया है]
∴ ΔAPC ≅ ΔDPQ (SAS नियम)
⇒ ar (ΔAPC) = ar (ΔDPQ)
∴ ar (ΔBPC) = ar (ΔDPQ), [∵ ar (ΔAPC) = ar (ΔBPC)] इति सिद्धम्।

प्रश्न 5.
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेदित करती है, तो दर्शाइए कि
(i) ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
(ii) ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE)
(iii) ar (ΔABC) = 2ar(ΔBEC)
(iv) ar (ΔBFE) = ar (ΔAFD)

(v) ar (ΔBFE) = 2 ar (ΔFED).
(vi) ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC).
हल:
दिया है दी गई आकृति ABC और ABDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्यबिन्दु है। रेखाखण्ड AE खींचा गया है जो BC को F पर प्रतिच्छेदित करता है।

सिद्ध करना है:
(i) ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
(ii) ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE)
(iii) ar (ΔABC) = 2ar(ΔBEC)
(iv) ar (ΔBFE) = ar (ΔAFD)
(v) ar (ΔBFE) = 2 ar (ΔFED).
(vi) ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC).
रचना: रेखाखण्ड EC और AD खींचे।
उपपत्ति: (i) ∵ D, BC का मध्य- बिन्दु है।
∴ BD = DC या BD = \(\frac{1}{2}\)BC

तब समीकरण (1) व (2) से,
ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC).

(ii) ∵ ΔABC समबाहु त्रिभुज है।
∴ ∠ACB = 60°
और ΔBDE समबाहु त्रिभुज है।
∴ ∠DBE = 60° या ∠CBE = 60°
∴ ∠ACB और ∠CBE एकान्तर कोण हैं जो BE तथा AC को BC द्वारा काटने से बने हैं।
∴ BE || AC
∵ ΔBAE और ΔBEC समान आधार BE पर और समान समान्तर रेखाओं BE AC के मध्य स्थित हैं।
∴ ar (ΔBAE) = ar (ΔBEC) ……(3)
∵ D, BC का मध्यबिन्दु है।
∴ DE, ΔBEC की माध्यिका है।
∴ ar (ΔBDE) = ar (ΔDEC)
⇒ ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBEC)
⇒ 2ar (ΔBDE) = ar (ΔBEC) ……(4)
समीकरण (3) व (4) से,
2 ar (ΔBDE) = ar (ΔBAE)
अतः ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE).

(iii) समीकरण (4) से,
2 ar (ΔBDE) = ar (ΔBEC)
परन्तु परिणाम (i) से,
ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
∴ 2 · \(\frac{1}{4}\) ar (ΔABC) = ar (ΔBEC)
या \(\frac{1}{2}\) ar (ΔABC) = ar (ΔBEC)
अत: \(\frac{1}{2}\) ar (ΔABC) = 2 ar (ΔBEC)

(iv) ∵ ΔBDE समबाहु त्रिभुज है।
∴ ∠BDE = 60°
और ΔABC समबाहु त्रिभुज है।
∴ ∠ABC = 60° या ∠ABD = 60°
∵ ∠BDE और ∠ABD एकान्तर कोण हैं जो AB और DE को BD के काटने से बने हैं।
∴ AB || DE
∵ ΔBDE और ΔADE एक ही आधार DE पर और समान समान्तर रेखाओं AB और DE के बीच बने हैं।
∴ ar (ΔBDE) = ar (ΔADE)
ar (ΔBFE) + ar (ΔFED) = ar (ΔFED) + ar (ΔAFD)
या ar (ΔBFE) = ar (ΔAFD).

(v) ∵ ΔABC की भुजा ΔBDE की भुजा से दो गुनी है।
∴ ΔABC की ऊँचाई भी ΔBDE की ऊँचाई से दो गुनी होगी।
∴ GE : AD = 1 : 2
यही अनुपात GF और FD में भी होगा, अत:
GF : FD = 1 : 2
परन्तु GD = BG = \(\frac{1}{4}\)BC
परन्तु GD = GF + FD
यदि GF = a तो FD = 2a होगा।
तब GD = a + 2a = 3a
तब BC = 2BD = 2(2BG)
= 4GB = 4GD = 4 × 3a = 12a
BG = GD = 3a ⇒ BD = 6a

(vi) ∵ परिणाम (iv) से,
ar (ΔAFD) = ar (ΔBFE)
और परिणाम (v) से,
ar (ΔBFE) = 2 ar (ΔFED)
∴ ar (ΔAFD) = 2ar (ΔFED) ……(5)
∵ ar (ΔACD)= \(\frac{1}{2}\)ar (ΔABC)
= \(\frac{1}{2}\) · 4 ar (ΔBDE), परिणाम (i) से
= 2 ar (ΔBDE)
∴ ar (ΔACD) = 2 ar (ΔBDE) …..(6)
∵ ar (ΔBFE) = 2ar (ΔFED), परिणाम (v) से
दोनों ओर ar (ΔFED) जोड़ने पर,
ar (ΔBFE) + ar (ΔFED) = 3 ar (ΔFED)
या ar (ΔBDE) = 3 ar (ΔFED) …..(7)
समीकरण (6) व (7) से,
ar (ΔACD) = 2[3 ar (ΔFED)]
∴ ar (ΔACD) = 6ar (ΔFED) …..(8)
समीकरण (5) व (8) को जोड़ने पर,
ar (ΔAFD) + ar (ΔACD) = 8 ar (ΔFED)
∴ ar (ΔAFC) = 8 ar (ΔFED)
अतः ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC).
इति सिद्धम्।

प्रश्न 6.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु पर प्रतिच्छेदित करते हैं दर्शाइए कि
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC) है।
हल:
दिया है: ☐ABCD के विकर्ण AC और BD परस्पर बिन्दु पर प्रतिच्छेदित करते हैं।

सिद्ध करना है:
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC)
रचना : A तथा C से BD पर क्रमश: AM तथा CN लम्ब डालें।
उपपत्ति: ar (ΔAPB) = \(\frac{1}{2}\)AM × BP …..(1)
ar (ΔAPD) = \(\frac{1}{2}\)AM × DP …..(2)
ar (ΔBPC) = \(\frac{1}{2}\)CN × BP …(3)
ar (ΔCPD) = \(\frac{1}{2}\)CN × DP ….. (4)
समीकरण (1) को (2) से भाग देने पर,

वज्रगुणन से,
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC). इति सिद्धम्।

प्रश्न 7.
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिन्दु हैं तथा R रेखाखण्ड AP का मध्य-बिन्दु है। दर्शाइए कि

(i) ar (ΔPRQ) = \(\frac{1}{2}\)ar (ΔARC)
(ii) ar (ΔRQC) = \(\frac{3}{8}\)ar (ΔABC)
(iii) ar (ΔPBQ) = ar (ΔARC).
हल:
P और Q क्रमश: त्रिभुज ABC की भुजाओं AB और BC के मध्य बिन्दु हैं। AQ और PC को मिलाया।
(i) ∵ ar (ΔPQR) = \(\frac{1}{2}\)ar (ΔAPQ),
[∵ QR, त्रिभुज APQ की माध्यिका है जो इसे समान क्षेत्रफलों वाले त्रिभुजों में बाँटती है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABQ)
[∵ QP, त्रिभुज ABQ की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABQ)
= \(\frac{1}{4} \times \frac{1}{2}\)ar (ΔABC)
[∵ AQ, त्रिभुज ABC की माध्यिका है]
= \(\frac{1}{8}\)ar (ΔABC) …..(i)
पुन:, ar (ΔARC) = \(\frac{1}{2}\)ar (ΔAPC)
[∵ CR, त्रिभुज APC की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABC)
[∵ CP त्रिभुज ABC की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABC) ……(ii)
समीकरण (i) और (ii) से,
ar (ΔPQR) = \(\frac{1}{8}\)ar (ΔABC)
= \(\frac{1}{2} \times \frac{1}{4}\)ar (ΔABC)
[∵ \(\frac{1}{4}\)ar (ΔABC) = ar (ΔARC)]
= \(\frac{1}{2}\)ar (ΔARC). इति सिद्धम्।

(ii) ar (ΔRQC) = ar (ΔRQA) + ar (ΔAQC) – ar (ΔARC) …..(iii)
अब ar (ΔRQA) = \(\frac{1}{2}\)ar (ΔPQA)
[∵ RQ, ΔPQA की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔAQB)
[∵ AQ, ΔAQB की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔAQB)
= \(\frac{1}{4} \times \frac{1}{2}\)ar (ΔABC)
[∵ AQ, ΔABC की माध्यिका है]
= \(\frac{1}{8}\)ar (ΔABC) …..(iv)
अतः ar (ΔAQC) = \(\frac{1}{2}\)ar (ΔABC) …..(v)
[∵ AQ, ΔABC की माध्यिका है]
⇒ ar(ΔARC) = \(\frac{1}{2}\)ar (ΔAPC)
[∵ CR, ΔAPC की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar(ΔABC)
[∵ CP, ΔABC की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABC) …..(vi)
समीकरण (iii), (iv), (v) और (vi) से,
ar (ΔRQC) = \(\frac{1}{8}\)ar (ΔABC) + \(\frac{1}{2}\)ar (ΔABC) – \(\frac{1}{4}\)ar (ΔABC)
= \(\left(\frac{1}{8}+\frac{1}{2}-\frac{1}{4}\right)\)ar (ΔABC)
= \(\frac{3}{8}\)ar (ABC).
इति सिद्धम्।

(iii) ∵ ar (ΔPBQ) = ar (ΔABQ)
[∵ PQ, ΔABQ की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABC)
[∵ AQ, ΔABC की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABC)
= ar (ΔARC) [समीकरण (vi) से]
इति सिद्धम्।

प्रश्न 8.
आकृति में, ABC एक समकोण त्रिभुज है, जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखण्ड AX ⊥ DE भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि
(i) ΔMBC ≅ ΔABD
(ii) ar (☐BYXD) = 2 ar (ΔMBC)
(iii) ar (☐BYXD) = ar (☐ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar (☐CYXE) = 2 ar (ΔFCB)
(vi) ar (☐CYXE) = ar (☐ACFG)
(vii) ar (☐BCED) = ar (☐ABMN) + ar (ACFG).

हल:
(i) ΔMBC और ΔABD में,
∵ BC = BD [वर्ग BCED की भुजाएँ]
MB = AB [वर्ग ABMN की भुजाएँ]
∠MBC = ∠ABD
[∵ प्रत्येक कोण = 90° + ∠ABC] (SAS नियम)
ΔMBC ≅ ΔABD. इति सिद्धम्।

(ii) ΔABD और आयत BYXD समान आधार BD पर और समान समान्तर रेखाओं BD और XY के मध्य स्थित हैं।
∴ ar (ΔABD) = \(\frac{1}{2}\)ar (☐BYXD)
लेकिन ΔMBC = ΔABD [भाग (i) से]
⇒ ar (ΔMBC) = ar (ΔABD)
∴ ar (ΔMBC) = ar (ΔABD)
= \(\frac{1}{2}\)ar (☐BYXD)
⇒ ar (☐BYXD) = 2ar (ΔMBC). इति सिद्धम्।

(iii) वर्ग ABMN और ΔMBC समान आधार MB पर और समान समान्तर रेखाओं MB और NAC के बीच स्थित हैं।
∴ ar (ΔMBC) = \(\frac{1}{2}\)ar(☐ABMN)
ar (☐ABMN) = 2 ar (ΔMBC)
ar (☐ABMN) = ar (☐BYXD). [भाग (ii) से]
इति सिद्धम्।

(iv) ΔACE और ΔBCF में,
CE = BC [वर्ग BCED की भुजाएँ]
AC = CF [वर्ग ACFG की भुजाएँ]
और ∠ACE = ∠BCF [∵ प्रत्येक 90° + ∠BCA]
∴ ΔACE ≅ ΔBCF. (SAS नियम) इति सिद्धम्।

(v) ΔACE और आयत CYXE समान आधार CE पर और समान समान्तर रेखाओं CE और AYX के बीच स्थित हैं।
ar (ΔACE) = \(\frac{1}{2}\)ar (☐CYXE)
⇒ ar (ΔFCB) = \(\frac{1}{2}\)ar (☐CYXE)
[∵ ΔACE ≅ ΔBCF, भाग (iv) से]
⇒ ar (☐CYXE) = 2ar (ΔFCB). इति सिद्धम्।

(vi) वर्ग ACFG और ΔBCF समान आधार CF पर और समान समान्तर रेखाओं CF और BAG के मध्य स्थित हैं।
∴ ar (ΔBCF) = \(\frac{1}{2}\)ar (☐ACFG)
⇒ \(\frac{1}{2}\)ar (☐CYXE) = \(\frac{1}{2}\)ar (☐ACFG) [भाग (v) से]
⇒ ar (☐CYXE) = ar (☐ACFG). इति सिद्धम्।

(vii) भाग (iii) और (vi) से,
ar (☐BYXD) = ar (☐AMBN)
और ar (☐CYXE) = ar (☐ACFG)
जोड़ने पर,
ar (☐BYXD) + ar (☐CYXE) = ar (☐ABMN) + ar (ACFG)
या ar (☐BCED) = ar (☐ABMN) + ar (☐ACFG).
इति सिद्धम्।

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

प्रश्न 1.
यदि किसी समलम्ब की समान्तर भुजाएँ a व b हैं तथा उनके बीच की लम्बवत दूरी h है तो उसके क्षेत्रफल का सूत्र होगा :
(A) 2h(\(\frac {a}{b}\))
(B) 2h(a + b) h
(C) a.b.h
(D) \(\frac {1}{2}\)(a + b)h.
हल :
विकल्प ‘D’ सही है।

प्रश्न 2.
किसी त्रिभुज का क्षेत्रफल उसकी भुजा और संगत शीर्षलम्ब के गुणन का होता है।
(A) दो गुना
(B) बराबर का
(C) एक तिहाई
(D) आधा
हल :
विकल्प ‘D’ सही है।

प्रश्न 3.
समान्तर चतुर्भुज का प्रत्येक विकर्ण उसको समान क्षेत्रफल वाले जिन दो प्रान्तों में विभाजित करता हैं, उनका आकार होता है :
(A) समचतुर्भुजाकार
(B) त्रिभुजाकार
(C) समान्तर चतुर्भुजाकार
(D) विषमबाहु चतुर्भुजाकार
हल :
विकल्प ‘B’ सही है।

प्रश्न 4.
एक त्रिभुज का आधार 6 सेमी और ऊँचाई 5 सेमी है, तो क्षेत्रफल होगा :
(A) 15 सेमी²
(B) 25 सेमी²
(C) 30 सेमी²
(D) 36 सेमी²
हल :
Δ का क्षेत्रफल = \(\frac {1}{2}\) × आधार × ऊँचाई
= \(\frac {1}{2}\) × 6 × 5 सेमी²
= 3 × 5 सेमी² = 15 सेमी²
सही विकल्प ‘A’ है।

प्रश्न 5.
एक समान्तर चतुर्भुज का आधार 5 सेमी और ऊंचाई 4 सेमी है, तो क्षेत्रफल होगा :
(A) 10 वर्ग सेमी
(B) 20 वर्ग सेमी
(C) 18 वर्ग सेमी
(D) 40 वर्ग सेमी।
हल :
समान्तर चतुर्भुज का क्षेत्रफल आधार × ऊंचाई
= 5 × 4 सेमी² = 20 सेमी²
सही विकल्प ‘B’ है।

प्रश्न 6.
एक समान्तर चतुर्भुज और त्रिभुज क्षेत्रफल में समान हैं और एक ही आधार पर स्थित हैं। यदि समान्तर चतुर्भुज की ऊंचाई 2 सेमी हो, तो त्रिभुज की ऊँचाई है:
(A) 4 सेमी
(B) 1 सेमी
(C) 2 सेमी
(D) 3 सेमी।
हल :
Δ का क्षेत्रफल = समान्तर चतुर्भुज का क्षेत्रफल (दिया है)
\(\frac {1}{2}\) × आ. × ॐ. = आ. × स. च. की ऊँचाई
∴ त्रिभुज की ऊँ. = 2 × स. च. की ऊँचाई
= 2 × 2 = 4 सेमी
अतः विकल्प ‘A’ सही है।

प्रश्न 7.
ABCD एक समान्तर चतुर्भुज है, जिसमें AB = 10 सेमी है। AB और AD भुजाओं के शीर्षलम्ब 7 सेमी व 8 सेमी है। AD की लम्बाई है:
(A) 8.75 सेमी
(B) 8.25 सेमी
(C) 7.75 सेमी
(D) 9 सेमी
हल :
समान्तर चतुर्भुज का क्षेत्रफल = आधार × संगत शीर्षलम्ब
पुन:
= AB × DM
= 10 × 7 = 70 सेमी² …….(i)
ar (|| ABCD) = AD × BN
= AD × 8 …….(ii)
(i) और (ii) से
AD × 8 = 70
AD = \(\frac {70}{8}\) = 8.75 सेमी
अतः विकल्प ‘A’ सही है।

प्रश्न 8.
चित्र में ABCD का क्षेत्रफल होगा :
(A) 12 सेमी²
(B) 8 सेमी²
(C) 10 सेमी²
(D) 9 सेमी²

हल :
☐ABCD का क्षेत्रफल
= ar (ΔABC) + ar (ΔADC)
= \(\frac {1}{2}\) × 4 × 3 + \(\frac {1}{2}\) × 4 × 2
= 6 + 4 = 10 सेमी²
अतः विकल्प ‘C’ सही है।

प्रश्न 9.
एक समान्तर चतुर्भुज की दो क्रमागत लम्बाई 15 सेमी तथा 12 सेमी है। यदि 15 सेमी भुजाकी भुजाओं की भुजाओं के दूरी 6 सेमी हो तो 12 सेमी भुजाओं की दूरी होगी :
(A) 8 सेमी
(B) 7.5 सेमी
(C) 12 सेमी
(D) 6 सेमी.
हल :
समान्तर चतुर्भुज का क्षेत्रफल = आधार × संगत शीर्ष लम्ब
= 15 × 6 = 90 सेमी²
पुनः माना 12 सेमी भुजाओं के मध्य की दूरी = x
∴ 12 × x = 90
x = \(\frac {90}{12}\) = 7.5 सेमी
अतः विकल्प ‘B’ सही है।

प्रश्न 10.
यदि किसी Δ की तीनों भुजाएँ क्रमशः a, b तथा c हैं तो उसकी अर्द्धमाप होगी :
(A) abc
(B) \(\frac {a + b + c}{2}\)
(C) \(\frac {abc}{2}\)
(D) a + b + c
हल :
त्रिभुज का परिमाप = a + b + c
त्रिभुज का अर्द्धमाप = \(\frac {a + b + c}{2}\)
अतः विकल्प ‘B’ सही है।

11. रिक्त स्थानों की पूर्ति करो :

प्रश्न (i)
त्रिभुज का क्षेत्रफल समान्तर चतुर्भुज के क्षेत्रफल का ………………. कल होता है।
हल :
आधा

प्रश्न (ii)
किसी आकृति का तलीय क्षेत्र का परिमाण या माप उस आकृति का ………. कहलाता है।
हल :
क्षेत्रफल ।

प्रश्न (iii)
एक ही आधार और बराबर क्षेत्रफल वाले त्रिभुज समान ………… के बीच स्थित होते हैं।
हल :
समान्तर रेखाओं ।

प्रश्न (iv)
त्रिभुज की माध्यिका, त्रिभुज को ………………………. वाले दो त्रिभुजों में विभाजित करती है।
हल :
बराबर क्षेत्रफल ।

प्रश्न (v)
समातर चतुर्भुज की कोई भी भुजा इसका ……………….. हो सकती है।
हल :
आधार।

प्रश्न (vi)
4 सेमी भुजा वाले वर्ग का क्षेत्रफल ………………….. भुजाओं वाले आयत के क्षेत्रफल के बराबर होता है।
हल :
8 सेमी तथा 2 सेमी।

प्रश्न (vii)
किसी समबाहु त्रिभुज की भुजाओं के मध्य-बिन्दुओं को मिलाने से बने त्रिभुज का क्षेत्रफल मूल त्रिभुज के क्षेत्रफल का …………. होता है।
हल :
एक चौथाई।

प्रश्न (viii)
ऐसी आकृति जिसकी चारों भुजाएँ तो बराबर होती हैं किन्तु कोण नहीं ………………… कहलाता है।
हल :
समचतुर्भुज ।

प्रश्न (ix)
किसी समकोण त्रिभुज का परिगत केन्द्र, उसके …………… भुजा पर स्थित होता है।
हल :
कर्ण।

प्रश्न (x)
समान आधार तथा समान समान्तर रेखाओं के मध्य बने समचतुर्भुज तथा आयत के क्षेत्रफलों में आयत का क्षेत्रफल ………………….. होता है।
हल :
कम।

प्रश्न 12.
सिद्ध करो कि यदि एक त्रिभुज और एक समान्तर चतुर्भुज, एक ही आधार पर और उन्हीं दो समान्तर रेखाओं के बीच में हों, तो त्रिभुज का क्षेत्रफल, समान्तर चतुर्भुज के क्षेत्रफल का आधा होता है।
हल :
दिया है ΔVAB और ||^gm ABCD, इस प्रकार हैं कि V, D और C संरेख हैं।

सिद्ध करना है : ar (ΔVAB) = \(\frac {1}{2}\)ar (||^gm ABCD).
रचना : CL ⊥ AB खींचा जो बढ़ी हुई रेखा AB के बिन्दु L पर मिलती है, और VM ⊥ AB, जो रेखा AB को M बिन्दु पर मिलती है।
उपपत्ति : V, D और C संरेख हैं और DC || AB,
∴ VM = CL, …….(1)
(समान्तर रेखाओं के बीच की दूरी )
अब ar (ΔVAB) = \(\frac {1}{2}\)VM × AB …….. (2)
ar (||^gm ABCD) = CL × AB ………..(3)
समीकरण (2) से,
ar (ΔVAB) = \(\frac {1}{2}\) × VM × AB
ar (ΔVAB) = \(\frac {1}{2}\) × CL × AB …………(4) [∵ VM = CL]
समीकरण (3) एवं (4) से,
ar (ΔVAB) = \(\frac {1}{2}\)ar (||^gm ABCD).
इति सिद्धम् ।

प्रश्न 13.
सिद्ध करो कि समलम्ब चतुर्भुज का क्षेत्रफल, उसकी समान्तर भुजाओं के मध्य लम्बवत दूरी और समान्तर भुजाओं के योगफल के गुणनफल का आधा होता है।
हल :
दिया है समलम्ब चतुर्भुज ABCD, जिसमें AB || CD
AL ⊥ DC और CN ⊥ AB है।
AB = a, DC = b, AL = CN = h (माना)
सिद्ध करना है :
ar (समलम्ब चतुर्भुज ABCD) = \(\frac {1}{2}\)h × (a + b).

रचना : A और C को मिलाया।
उपपत्ति : AC, चतुर्भुज ABCD का विकर्ण है।
∴ ar (समलम्ब चतुर्भुज ABCD)
= ar (ΔABC) + ar (ΔACD)
अब, ar (ΔABC) = \(\frac {1}{2}\)h × a …….(i)
ar (ΔACD) = \(\frac {1}{2}\)h × b ………….(ii)
समीकरण (i) और (ii) को जोड़ने पर,
∵ ar (ΔABC) + ar (ΔACD)
= \(\frac {1}{2}\)h × a + \(\frac {1}{2}\)h × b
= \(\frac {1}{2}\)h × (a + b)
इति सिद्धम् ।

प्रश्न 14.
एक समबाहु त्रिभुज के शीर्षलम्ब की लम्बाई और क्षेत्रफल ज्ञात कीजिए जिसकी भुजा की लम्बाई a है।
हल :
एक समबाहु त्रिभुज जिसकी भुजा की लम्बाई a है।

अतः
AB = BC = CA = a
त्रिभुज का शीर्षलम्ब AD है।
BD = \(\frac {1}{2}\)BC
[समबाहु Δ में प्रत्येक शीर्षलम्ब सम्मुख भुजा को समद्विभाजित करता है।]
∴ BD = \(\frac {1}{2}\) × a = \(\frac {a}{2}\)
ΔABD में, ∠D समकोण है, अत: पाइथागोरस प्रमेय से,

प्रश्न 15.
चित्र में यदि ΔABC एवं ΔDBC एक ही आधार BC पर स्थित हैं, तो सिद्ध कीजिए कि

हल :
दिया है ΔABC और ΔDBC का आधार BC है।

रचना : A तथा D से AL ⊥ BC तथा DM ⊥ BC डालें।
ΔALO और ΔDMO में,
∠ALO = ∠DMO (प्रत्येक 90°)
∠AOL = ∠DOM (शीर्षाभिमुख कोण)
ΔALO ~ ΔDMO (AAA नियम)

प्रश्न 16.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफल संगत माध्यिकाओं के वर्गों के अनुपात में होते हैं।
हल :
दिया है : समरूप त्रिभुज ABC और DEF में AP और DQ माध्यिकाएँ हैं।

उपपत्ति: हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के समान होता है (मूलभूत समानुपातिक प्रमेय)

प्रश्न 17.
दो त्रिभुज के आधार क्रमशः 8 सेमी व 6 सेमी हैं। यदि उनकी ऊंचाई क्रमशः 6 सेमी व 8 सेमी हो, तो उनके क्षेत्रफल का अनुपात ज्ञात कीजिए।
हल :
पहले त्रिभुज का क्षेत्रफल = \(\frac {1}{2}\)आधार × ऊँचाई
= \(\frac {1}{2}\) × 8 × 6
= 24 वर्ग सेमी
दूसरे त्रिभुज का क्षेत्रफल = \(\frac {1}{2}\) × 6 × 8
= 24 वर्ग सेमी
अतः अनुपात = पहले त्रिभुज का क्षेत्रफल / दूसरे त्रिभुज का क्षेत्रफल
= \(\frac{24}{24}=\frac{1}{1}\)
अतः दोनों त्रिभुजों के क्षेत्रफल का अनुपात = 1 : 1

प्रश्न 18.
दो त्रिभुज एक ही आधार पर एवं समान समान्तर रेखाओं के बीच स्थित हैं। एक त्रिभुज की ऊंचाई 5 सेमी तथा क्षेत्रफल 18 वर्ग सेमी. है। दूसरे त्रिभुज की ऊँचाई ज्ञात कीजिए।
हल :
दो त्रिभुज ABC तथा त्रिभुज DBC एक ही आधार BC पर तथा एक ही समान्तर रेखाओं BR तथा PQ के मध्य स्थित हैं। अतः दोनों त्रिभुजों का क्षेत्रफल समान होगा।

अत: त्रिभुज ABC का क्षे. = \(\frac {1}{2}\) × आधार × ऊँचाई
18 = \(\frac {1}{2}\) × आधार × 5
∴ आधार = \(\frac{2 \times 18}{5}=\frac{36}{5}\)
∴ आधार (y) = 7.2 सेमी
दूसरे त्रिभुज का क्षे. = \(\frac {1}{2}\) × आधार × ऊँचाई
18 = \(\frac {1}{2}\) × y × x
18 = \(\frac {1}{2}\) × 7.2 × x
∴ x = \(\frac{18 \times 2}{7.2}\)
= \(\frac{18 \times 20}{72}\) = 5
∴ दूसरे त्रिभुज DBC की ऊँचाई (x) = 5 सेमी
अतः ऊंचाई: = 5 सेमी।

प्रश्न 19.
एक समचतुर्भुज का एक विकर्ण दूसरे विकर्ण से दोगुना है। यदि उस समचतुर्भुज का क्षेत्रफल 80 वर्ग सेमी हो तो उसकी भुजा की लम्बाई ज्ञात कीजिए।
हल :
माना, सम चतुर्भुज ABCD की प्रत्येक भुजा की लम्बाई = a सेमी
माना, समचतुर्भुज के एक विकर्ण की लम्बाई = x सेमी
समचतुर्भुज का क्षेत्रफल = \(\frac {1}{2}\) × (x × 2x)
= x² वर्ग सेमी

चूंकि समचतुर्भुज के विकर्ण एक दूसरे को समकोण पर समद्विभाजिक करते हैं। अतः ∠AOD एक समकोण त्रिभुज है, जिसका ΔAOD = 90°

अतः समचतुर्भुज की भुजा की लम्बाई = 10 सेमी

प्रश्न 20.
एक नहर की अनुप्रस्थ काट का आकार समलम्ब है। यदि नहर के ऊपरी सिरे की चौड़ाई 10 मी, तली की 6 मी तथा अनुप्रस्थ काट का क्षेत्रफल 72 वर्ग मीटर हो तो उसकी गहराई ज्ञात कीजिए। समलम्ब की अन्य भुजाओं की लम्बाई भी बताइए।

हल :
माना अनुप्रस्थ काट की गहराई = d मीटर की दूरी = d मीटर समलम्ब ABCD का क्षेत्रफल = \(\frac {1}{2}\)(AB + BC) × d
72 = \(\frac {1}{2}\)(10 + 6) × d
72 × 2 = 16 d
d = \(\frac{72 \times 2}{16}\) = 9
नहर की गहराई = 9 मीटर
समलम्ब की अन्य दो भुजाएँ AD = BC
ΔAFD में, ∠AFD = 90°
AF = \(\frac{10-6}{2}\) = 2, DF = d = 9
AD = \(\sqrt{2^2+9^2}=\sqrt{4+81}=\sqrt{85}\)मीटर

Jharkhand Board JAC Class 9 Maths Solutions Chapter 14 सांख्यिकी Ex 14.2 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 14 सांख्यिकी Exercise 14.2

प्रश्न 1.
आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैं :
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O इन आँकड़ों को एक बारम्बारता बंटन सारणी के रूप में प्रस्तुत कीजिए। बताइए कि इन विद्यार्थियों में कौन-स रक्त समूह अधिक सामान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है।
हल:

सारणी से स्पष्ट है कि रक्त समूह O की बारम्बारता सर्वाधिक है अतः यह अधिक सामान्य है और रक्त समूह AB की बारम्बारता सबसे कम है, अतः यह विरलतम (कम) है।

प्रश्न 2.
40 इंजीनियरों की उनके आवास से कार्य स्थल की (किलोमीटर में) दूरियाँ ये हैं :

0-5 को (जिसमें 5 सम्मिलित नहीं है) पहला अन्तराल लेकर ऊपर दिए हुए आँकड़ों से वर्ग-माप 5 वाली एक वर्गीकृत बारम्बारता बंटन सारणी बनाइए। इस सारणीबद्ध निरूपण में आपको कौन-से मुख्य लक्षण देखने को मिलते हैं?
हल:
इन आँकड़ों में न्यूनतम तथा अधिकतम दूरियाँ (किमी) क्रमशः 2 और 32 हैं। प्रश्न से स्पष्ट है कि प्रथम वर्ग अन्तराल 0-5 है और विस्तार समान है अतः समान आकार के वर्ग निम्न प्रकार से प्राप्त होते हैं:
0 – 5, 5 – 10, 10 – 15, 15 – 20, 20 – 25, 25 – 20 और 30 – 35
अतः बारम्बारता सारणी निम्नवत् है:

आँकड़ों की उच्चतम सीमा 35 इस वर्ग तालिका में शामिल नहीं है। इसी प्रकार तालिका से स्पष्ट हैं कि न्यूनतम दूरी भी आँकड़ों में सम्मिलित नहीं है अतः कोई भी इन्जीनियर कार्य स्थल पर निवास नहीं करता। अत: 0-5 किमी वर्ग में अपने काम पर जाने के लिए 5 किमी चली दूरी इस वर्ग में नहीं आयेगी। वह अपने वर्ग 5-10 में आयेगी। अतः निष्कर्ष यह निकलता है कि 40 में 27 इंजीनियरों का कार्यस्थल उनके घर से 15 किमी से अधिक नहीं है।

प्रश्न 3.
30 दिन वाले महीने में एक नगर की सापेक्ष आर्द्रता (% में) यह रही है:

(i) वर्ग 84-86, 86-88 आदि लेकर एक वर्गीकृत बारम्बारता बंटन सारणी बनाइए।
(ii) क्या आप बता सकते हैं कि ये आँकड़े किस महीने या ऋतु से सम्बन्धित हैं ?
(iii) इन आँकड़ों का परिसर क्या है?
हल:
(i) इन आँकड़ों में न्यूनतम और अधिकतम सापेक्षिक आर्द्रता (% में) 84.9 और 99.2 है और वर्ग 84-86, 86-88,…. आदि समान आकार के हैं।
अतः बारम्बारता सारणी :

(ii) सापेक्षिक आर्द्रता अधिक है। अतः ये आँकड़े वर्षा ऋतु के हैं।
(iii) परिसर = अधिकतम आर्द्रता – न्यूनतम सापेक्ष आर्द्रता
= 99.2 – 84.9 = 14.3

प्रश्न 4.
निकटतम सेण्टीमीटरों में मापी गई 50 विद्यार्थियों की लम्बाइयाँ ये हैं:

(i) 160 – 165, 165 – 170 आदि का वर्ग अंतराल लेकर ऊपर दिए गए आँकड़ों को एक वर्गीकृत बारम्बारता बंटन सारणी के रूप में निरूपित कीजिए।
(ii) इस सारणी की सहायता से आप विद्यार्थियों की लम्बाइयों के सम्बन्ध में क्या निष्कर्ष निकाल सकते हैं?
हल:
(i) इन आँकड़ों में अधिकतम और न्यूनतम लम्बाई क्रमशः 150 सेमी और 173 सेमी दी गयी हैं। दो वर्गअन्तराल 160 – 165 एवं 165 – 170
दिए गए है जिनकी समान वर्ग माप 165 – 160 = 170 – 165 = 5 है।
अतः समान आकार के वर्ग 150 – 155,155 – 160,…… 170 – 175 हैं अतः बारम्बारता सारणी निम्न है :

(ii) इस सारणी से यह निष्कर्ष निकलता है कि 50% से अधिक छात्रों की लम्बाई 165 सेमी से कम है।

प्रश्न 5.
एक नगर में वायु में सल्फर डाइऑक्साइड का सान्द्रण भाग प्रति मिलियन [parts per million (ppm)] में ज्ञात करने के लिए एक अध्ययन किया गया। 30 दिनों के प्राप्त किए गए आँकड़े ये हैं :.

(i) 0.00 – 0.04, 0.04 – 0.08 आदि का वर्ग अन्तराल लेकर इन आँकड़ों की एक वर्गीकृत बारम्बारता बंटन सारणी बनाइए।
(ii) सल्फर डाइऑक्साइड की सान्दता कितने दिन 0.11 भाग प्रति मिलियन से अधिक रही?
हल:
(i) इन आँकड़ों में न्यूनतम और अधिकतम सल्फर डाइऑक्साइड की सान्द्रता क्रमशः 0.01 और 0.22 है। वर्गमाप समान दी है तथा एक वर्ग 0.00 – 0.04 ज्ञात है।
अतः वर्ग समान आकार के होंगे जो निम्न हैं:
0.00 – 0.04, 0.04 – 0.08,……, 0.20 – 0.24
अतः बारम्बारता सारणी निम्न है:

(ii) सल्फर डाइ-ऑक्साइड का सान्द्रण 0.11 भाग प्रति मिलियन से अधिक सीमा वाले वर्ग और उनकी बारम्बारता :

अत: सल्फर डाइऑक्साइड का वायु में सान्द्रण 0.11 भाग प्रति मिलियन से अधिक 8 दिनों तक रहा।

प्रश्न 6.
तीन सिक्कों को एक साथ 30 बार उछाला गया। प्रत्येक बार चित (Head) आने की संख्या निम्न प्रकार है:

ऊपर दिए गए आंकड़ों के लिए एक बारम्बारता बंटन सारणी बनाइए।
हल:
चित आने की न्यूनतम संख्या = 0 और अधिकतम संख्या = 3
बारम्बारता सारणी निम्न है :

प्रश्न 7.
50 दशमलव स्थान तक शुद्ध का मान नीचे दिया गया है:
3.14159265358979323846264338327950288419716939937510
(i) दशमलव बिन्दु के बाद आने वाले 0 से 9 तक के अंकों का एक बारम्बारता बंटन बनाइए ।
(ii) सबसे अधिक बार और सबसे कम बार आने वाले अंक कौन-कौन से हैं?
हल:
(i) 0 से 9 तक के अंकों की बारम्बारता बंटन सारणी

(ii) सारणी से स्पष्ट है कि सबसे कम बार शून्य का अंक और सबसे अधिक बार 3 और 9 का अंक आया है।

प्रश्न 8.
तीस बच्चों से यह पूछा गया कि पिछले सप्ताह उन्होंने कितने घण्टों तक टी. वी. प्रोग्राम देखे। प्राप्त परिणाम ये रहे हैं:

(i) वर्ग-चौड़ाई 5 लेकर और एक वर्ग अन्तराल को 5-10 लेकर इन आँकड़ों की एक वर्गीकृत बारम्बारता बंटन सारणी बनाइए।
(ii) कितने बच्चों ने सप्ताह में 15 या अधिक घण्टों तक टेलीविजन देखा?
हल:
(i) सबसे कम तथा अधिक टी. वी. देखने का समय क्रमश: 1 घण्टा और 17 घण्टे हैं। वर्ग अन्तराल 5-10 ज्ञात है। अत: समान आकार के वर्ग अन्तराल होंगे : 0-5, 5-10, 10-15 और 15-20.
अतः वर्ग बारम्बारता सारणी निम्न है:

(ii) 2 बच्चे सप्ताह में 15 या अधिक घण्टे टी. वी. देखते हैं।

प्रश्न 9.
एक कम्पनी एक विशेष प्रकार की कार बैटरी बनाती है। इस प्रकार की 40 बैटरियों के जीवन काल (वर्षो में) ये रहे हैं:

0.5 माप के वर्ग अन्तराल लेकर तथा अन्तराल 2-2.5 से प्रारम्भ करके इन आँकड़ों की एक वर्गीकृत बारम्बारता बंटन सारणी बनाइए।
हल:
बैटरी का न्यूनतम तथा अधिकतम जीवन काल क्रमशः 2.2 वर्ष तथा 4.6 वर्ष है।
वर्गमाप 0.5 है अतः वर्ग-अन्तराल है 2.0-2.5, 2.5-3.0 3.0-3.5,….., 4.5-5.0
अतः बारंबारता सारणी निम्न है :

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.7 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.7

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
उस लम्बवृत्तीय शंकु का आयतन ज्ञात कीजिए, जिसकी :
(i) त्रिज्या 6 सेमी और ऊँचाई 7 सेमी है।
(ii) त्रिज्या 3.5 सेमी और ऊँचाई 12 सेमी है।
हल:
(i) लंम्बवृत्तीय शंकु की त्रिज्या (r) = 6 सेमी तथा ऊँचाई (h) = 7 सेमी।
∴ शंकु का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times(6)^2 \times 7\) घन सेमी
= 264 घन सेमी।
अतः लम्बवृत्तीय शंकु का आयतन 264 घन सेमी।

(ii) लम्बवृत्तीय शंकु की त्रिज्या (r) = 3.5 सेमी
= \(\frac{7}{2}\) सेमी
शंकु की ऊँचाई (h) = 12 सेमी
∴ शंकु का आयतन = \(\frac{1}{3}\) × πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 12\) घन सेमी
= 154 घन सेमी
अतः लम्बवृत्तीय शंकु का आयतन = 154 घन सेमी।

प्रश्न 2.
शंकु के आकार के उस बर्तन की लीटरों में धारिता ज्ञात कीजिए, जिसकी:
(i) त्रिज्या 7 सेमी और तिर्यक ऊंचाई 25 सेमी है।
(ii) ऊंचाई 12 सेमी और तिर्यक ऊंचाई 13 सेमी है।
हल:
(i) यहाँ, r = 7 सेमी और l = 25 सेमी
माना शंकु की ऊँचाई h सेमी है, तब
∴ l² = h² + r²
h² = l² – r² = 25² – 7²
= 625 – 49
= 576
∴ h = \(\sqrt{576}\) = 24 सेमी
शंक्वाकार बर्तन का आयतन = \(\frac{1}{3}\) πr²h
= \(\left(\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 24\right)\) सेमी³
= 1232 सेमी³
∴ बर्तन की धारिता (लीटर में)
= \(\left(\frac{1232}{1000}\right)\) लीटर = 1.232 लीटर।

(ii) यहाँ h= 12 सेमी और l = 13 सेमी
माना शंकु के आधार की त्रिज्या सेमी है।
तब, r² = l² – h² = 13² – 12²
= 169 – 144 = 25
⇒ r = \(\sqrt{25}\) = 5 सेमी
शंक्वाकार बर्तन का आयतन = \(\frac{1}{3}\) πr²h
= \(\left(\frac{1}{3} \times \frac{22}{7} \times 5 \times 5 \times 12\right)\) सेमी³
= \(\frac{2200}{7}\) सेमी³
∴ लीटर में बर्तन की धारिता (आयतन) = \(\left(\frac{2200}{7} \times \frac{1}{1000}\right)\) लीटर
(∵ 1000 घन सेमी = 1 लीटर)
= \(\frac{11}{35}\) लीटर।

प्रश्न 3.
एक शंकु की ऊंचाई 15 सेमी है। यदि इसका आयतन 1570 सेमी³ है, तो इसके आधार की त्रिज्या ज्ञात कीजिए।
(π = 3.14 प्रयोग कीजिए।)
हल:
यहाँ, h = 15 सेमी और आयतन = 1570 सेमी³
माना शंकु के आधार की त्रिज्या सेमी है।
आयतन = 1570 सेमी³
\(\frac{1}{3}\) πr²h = 1570
\(\frac{1}{3}\) × 3.14 × r² × 15 = 1570
r² = \(\frac{1570}{3.14 \times 5}\) = 100
∴ r = \(\sqrt{100}\) = 10
अतः शंकु के आधार की त्रिज्या 10 सेमी है।

प्रश्न 4.
यदि 9 सेमी ऊँचाई वाले एक लम्बवृत्तीय शंकु का आयतन 48π सेमी है। इसके आधार का व्यास ज्ञात कीजिए।
हल:
शंकु की ऊँचाई (h) = 9 सेमी
शंकु का आयतन = 48π सेमी³
\(\left(\frac{1}{3} \pi r^2 h\right)\) = 48π सेमी³
\(\frac{1}{3}\) × πr² × 9 = 48π
r² = \(\frac{48 \pi \times 3}{\pi \times 9}\) सेमी²
= 16 सेमी²
∴ r = \(\sqrt{16}\) सेमी = 4 सेमी
⇒ 2r = 2 × 4 सेमी = 8 सेमी
अंतः शंकु के आधार का व्यास 8 सेमी।

प्रश्न 5.
ऊपरी व्यास 3.5 मीटर वाले शंकु के आकार का एक गड्डा 12 मीटर गहरा है। इसकी धारिता किलोलीटर में कितनी है ?
हल:
गड्ढे का ऊपरी व्यास = 3.5 मीटर
∴ गड्ढे की त्रिज्या (r) = \(\frac{3.5}{2}\) मीटर
= \(\frac{35}{2 \times 10}\) मीटर = \(\frac{7}{4}\) मीटर
गड्ढे की ऊँचाई (h) = 12 मीटर
∴ गड्ढे का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times 12\) मीटर³ = \(\frac{154}{4}\) मीटर³
∵ 1 मी = 1000 लीटर = 1 किलो लीटर
∴ 38.5 मी³ = 38.5 किलो लीटर
अतः गढ्ढे की धारिता = 38.5 किलो लीटर

प्रश्न 6.
एक लम्बवृत्तीय शंकु का आयतन 9856 सेमी³ है। यदि इसके आधार का व्यास 28 सेमी है, तो ज्ञात कीजिए:
(i) शंकु की ऊंचाई
(ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल।
हल:
(i) शंकु के आधार का व्यास 28 सेमी
∴ त्रिज्या = r = \(\frac{28}{2}\) सेमी
= 14 सेमी
शंकु का आयतन = 9856 सेमी³
⇒ \(\frac{1}{3}\) πr²h = 9856 सेमी³
⇒ \(\frac{1}{3} \times \frac{22}{7}\) × 14 × 14 × h = 9856
⇒ h = \(\frac{9856 \times 3 \times 7}{22 \times 14 \times 14}\)
= 48 सेमी
अतः शंकु की ऊँचाई = 48 सेमी।

(ii) माना शंकु की तिर्यक ऊँचाई l है, तब
l² = h² + r²
= 48² + 14²
= 2304 + 196 = 2500
∴ l = \(\sqrt{2500}\) = 50 सेमी
अतः शंकु की तिर्यक् ऊँचाई = 50 सेमी

(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 14 × 50
= 2,200 सेमी²।

प्रश्न 7.
भुजाओं 5 सेमी, 12 सेमी और 13 सेमी वाले एक समकोण त्रिभुज ABC को भुजा 12 सेमी के परितः घुमाया जाता है। इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए।
हल:
∵ ΔABC को 12 सेमी वाली भुजा AB के परित: घुमाए जाने पर प्राप्त निम्नलिखित शंक्वाकार ठोस आकृति प्राप्त होती हैं जिसमें

∴ शंकु की ऊँचाई AB = 12 सेमी
और शंकु की त्रिज्या CB = शंकु की दूसरी भुजा
= 5 सेमी
∴ शंकु का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × π × (5)² × 12
= 100π घन सेमी।
अतः प्राप्त शंकु का आयतन = 100π घन सेमी।

प्रश्न 8.
यदि प्रश्न 7 के त्रिभुज ABC को यदि भुजा 5 सेमी के परितः घुमाया जाए, तो इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए। प्रश्न 7 और 8 में प्राप्त किए गए दोनों ठोसों के आयतनों का अनुपात भी ज्ञात कीजिए।
हल:
…. ΔABC को 5 सेमी वाले भुजा के परितः घुमाए जाने पर निम्नांकित शंक्वाकार आकृति प्राप्त होती है जिसमें

∴ शंकु की ऊँचाई (h) = 5 सेमी
और आधार की त्रिज्या (r) = दूसरी भुजा
= 12 सेमी
∴ शंकु का आयतन = \(\frac{1}{3}\) πr²h
\(\frac{1}{3}\) × π × (12)² × 5 घन सेमी
= 240π घन सेमी
अतः प्राप्त शंकु का आयतन = 240π घन सेमी।
तब प्रश्न 7 व प्रश्न 8 से प्राप्त ठोसों के आयतनों का अनुपात
= 100π : 240π
= 5 : 12.

प्रश्न 9.
गेहूँ की एक ढेरी 10.5 मीटर व्यास और 3 मीटर ऊँचाई वाले एक शंकु के आकार की है इसका ‘आयतन ज्ञात कीजिए। इस बेरी को वर्षा से बचाने के लिए केनवास से ढका जाता है। वांछित केनवास का क्षेत्रफल ज्ञात कीजिए।
हल:
गेहूँ की ढेरी से बने शंकु की ऊँचाई (h) = = 3 मीटर
तथा आधार का व्यास = 10.5 मीटर = \(\frac{21}{2}\) मीटर
∴ आधार की त्रिज्या (r) = \(\frac{21}{2 \times 2}=\frac{21}{4}\) मीटर
∴ गेहूँ की ढेरी (शंकु) का आयतन = \(\frac{1}{3}\) πr2h
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{21}{4} \times \frac{21}{4} \times 3\) घन मीटर
= \(\frac{693}{8}\) घन मीटर
= 86.625 घन मीटर।

∴ ढेरी को ढकने के लिए आवश्यक केनवास = गेहूँ की ढेरी का वक्र पृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7} \times \frac{21}{4} \times 6.05\)
= 99.825 वर्ग मीटर
अत: गेहूँ की ढेरी (शंकु) को ढकने के लिए आवश्यक केनवास का क्षेत्रफल
= 99.825 वर्ग मीटर।

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 8 चतुर्भुज Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 8 चतुर्भुज

प्रश्न 1.
यदि किसी चतुर्भुज की चारों भुजाएँ और कोण परस्पर बराबर हों, तब चतुर्भुज होगा :
(A) आयत
(B) समचतुर्भुज
(C) वर्ग
(D) समान्तर चतुर्भुज ।
हल :
विकल्प (C) सही है।

प्रश्न 2.
यदि समान्तर चतुर्भुज के दो विकर्ण समान हों, तो यह होगा :
(A) चतुर्भुज
(B) आयत
(C) समचतुर्भुज
(D) समलम्ब चतुर्भुज ।
हल :
विकल्प (B) सही है।

प्रश्न 3.
चित्र में ABCD एक समचतुर्भुज है। यदि AC = 8 सेमी और DB = 6 सेमी हो, तो BC का मान होगा :

(A) 5 सेमी
(B) 4 सेमी
(C) 7 सेमी
(D) 3.5 सेमी
हल :
हम जानते हैं कि समचतुर्भुज के विकर्ण एक दूसरे को 90° पर समद्विभाजित करते हैं, तब ΔOBC में,
OC = \(\frac {1}{2}\)AC = \(\frac {1}{2}\) × 8 = 4 सेमी
OB = \(\frac {1}{2}\) × BD = \(\frac {1}{2}\) × 6 = 3 सेमी
पाइथागोरस प्रमेय से,
BC² = OB² + OC² = 3² + 4²
= 9 + 16 = 25
BC = 5 सेमी।
अतः विकल्प ‘A’ सही है।

प्रश्न 4.
त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर तथा लम्बाई में उसका होता है
(A) आधा
(B) बराबर
(C) एक-तिहाई
(D) एक-चौथाई
हल :
विकल्प (A) सही है।

प्रश्न 5.
किसी चतुर्भुज में सम्मुख भुजाओं का एक युग्म परस्पर समान्तर है, चतुर्भुज होगा :
(A) समलम्ब
(B) आयत
(C) वर्ग
(D) समचतुर्भुज
हल :
विकल्प (B) सही है।

प्रश्न 6.
यदि किसी चतुर्भुज के विकर्ण बराबर हो तथा एक दूसरे को समकोण पर प्रतिच्छेदित करते हों, तो वह होगा :
(A) आयत
(B) वर्ग
(C) समचतुर्भुज
(D) समान्तर चतुर्भुज
हल :
विकल्प (B) सही है।

प्रश्न 7.
यदि किसी चतुर्भुज के विकर्ण असमान हैं तथा एक-दूसरे को समकोण पर समद्विभाजित करते हों तो वह होगा :
(A) आयत
(B) वर्ग
(C) समचतुर्भुज
(D) समान्तर चतुर्भुज
हल :
विकल्प (C) सही है।

प्रश्न 8.
समान्तर चतुर्भुज ABCD में ∠A = 75° हो, तो ∠B का मान है :

(A) 105°
(B) 110°
(C) 90°
(D) 75°.
हल :
∠A + ∠B = 180° (अन्तः कोण)
⇒ 75° + ∠B = 180°
∴ ∠B = 180° – 75° = 105°.
अतः विकल्प ‘A’ सही है।

प्रश्न 9.
वर्ग की भुजा एवं उसके विकर्ण की लम्बाइयों का अनुपात है:

(A) 1 : \(\sqrt{2}\)
(B) 3 : \(\sqrt{2}\)
(C) \(\sqrt{2}\) : 1
(D) \(\sqrt{2}\) : 3
हल :
AC² = AB² + BC²
= x² + x² = 2x²
∴ AC = \(\sqrt{2}\)x
∴ AB : AC = x : \(\sqrt{2}\)x
= 1 : \(\sqrt{2}\)
अतः विकल्प ‘A’ सही है।

प्रश्न 10.
चित्र में, ABCD समान्तर चतुर्भुज है, तो x का मान होगा:
(A) 25°
(B) 60°
(C) 75°
(D) 45°.
हल :

हम जानते हैं कि
∠A = ∠C
3x – 20° = x + 70°
या 2x = 90°
∴ x = 45°
(3x-20)
अतः विकल्प ‘D’ सही है।

प्रश्न 11.
रिक्त स्थानों की पूर्ति करो :
(i) किसी ||^gm के विकर्ण एक दूसरे को ……………………. करते हैं।
(ii) समान्तर चतुर्भुज के संलग्न कोण होते हैं।
(iii) किसी ||^gm के सम्मुख कोण ………………. होते हैं।
(iv) किसी ||^gm की सम्मुख भुजाएँ …………………… होती हैं।
(v) किसी चतुर्भुज की भुजाओं के मध्य बिन्दुओं को एक क्रम से मिलाने वाले रेखाखण्डों द्वारा बना चतुर्भुज ………………. होता है।
(vi) किसी समान्तर चतुर्भुज का एक कोण समकोण हो तो वह ………………….. कहलाता है।
(vii) किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के …………………. होती है।
(viii) पतंग एक ……………….. चतुर्भुज नहीं है।
संलग्न चित्र को ध्यान से देखिए

(ix) …………. समान्तर रेखाएँ हैं।
(x) …………. समान रेखाएँ हैं।
(xi) समान कोणों के नाम हैं ………………।
(xii) सम्पूरक कोणों के नाम है ………………।
हल :
(i) समद्विभाजित,
(ii) सम्पूरक,
(iii) बराबर,
(iv) समान,
(v) समान्तर चतुर्भुज,
(vi) आयत,
(vii) समान्तर तथा आधी,
(viii) समान्तर
(ix) AB || DC तथा AD || BC,
(x) AB = DC तथा AD = BC,
(xi) ∠A = ∠C तथा ∠B = ∠D
(xii) ∠A व ∠B, ∠B व ∠C, ∠C व ∠D, तथा ∠D व ∠A.

प्रश्न 12.
ΔABC में, D, E, F क्रमश: भुजाओं AB, BC और CA के मध्य बिन्दु हैं। सिद्ध कीजिए कि बिन्दुओं D, E,F को मिलाने पर ABC चार सर्वांगसम त्रिभुजों में विभाजित हो जाता है।

हल :
ΔABC में, बिन्दु D, E तथा F क्रमश: भुजाओं AB, AC तथा BC के मध्य बिन्दु ।
रचना: DE, EF तथा DF को मिलाया।
सिद्ध करना है ΔADE ≅ ΔDBF ≅ ΔEFC ≅ ΔDEF
∵ D और E क्रमश: भुजा AB व BC के मध्य बिन्दु है।
∴ DE || BC
इसी प्रकार DF || AC
और EF || AB है।
∴ ADEF, BDFE और DFCE समान्तर चतुर्भुज
∵ समान्तर चतुर्भुज BDFE में DF विकर्ण है।
∴ ΔBDF ≅ ΔFED
(∵ समान्तर चतुर्भुज को विकर्ण दो बराबर सर्वांगसम त्रिभुजों में बाँटता है)
इसी प्रकार ΔDAE ≅ ΔFED
और ΔEFC ≅ ΔFED
ΔADE ≅ ΔDBF ≅ ΔEFC ≅ ΔDEF इति सिद्धम् ।

प्रश्न 13.
D, E व F एक ΔABC की भुजा BC, AC AB के मध्य बिन्दु है। सिद्ध कीजिए कि AD, भुजा EF का समद्विभाजक है।
हल :

दिया है ΔABC
में, D, E व F क्रमश: BC, AC व AB के मध्य बिन्दु हैं।
सिद्ध करना है AD, EF को समद्विभाजित करता है।
रचना: DE, EF तथा DF को मिलाया ।
उपपत्ति: D व E क्रमश: BC व AC के मध्य बिन्दु (दिया है)
∴ DE || AB अथवा DE || AF ……..(i)
इसी प्रकार D व F क्रमश: BC व AB के मध्य बिन्दु (दिया है)
∴ DF || AC अथवा DF || AE ……….(ii)
(i) व (ii) से,
AEDF एक समान्तर चतुर्भुज है।
∵ समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं और AD व EF समान्तर चतुर्भुज AEDF के विकर्ण हैं।
∴ AD, EF को समद्विभाजित करता है। इति सिद्धम् ।

प्रश्न 14.
ABCD एक समचतुर्भुज है और P, Q, R, S क्रमश: AB, BC, CD तथा DA के मध्य बिन्दु हैं। सिद्ध कीजिए कि PQRS एक आयत है।
हल :
दिया है : समचतुर्भुज ABCD में P, Q, R, व S क्रमश: AB, BC, CD व DA के मध्य बिन्दु हैं।

सिद्ध करना है : PQRS एक आयत हैं।
रचना : विकर्ण AC तथा BD खींचे।
उपपत्ति: ΔABC में P एवं Q क्रमश: AB तथा BC के मध्य बिन्दु हैं। (दिया है)
∴ PQ || AC ……..(i)
तथा PQ = \(\frac {1}{2}\)AC ……..(ii)
इसी प्रकार ΔADC में,
SR || AC ……..(iii)
तथा SR = \(\frac {1}{2}\)AC ……..(iv)
∴ समीकरण (i) एवं (iii) से.
PQ || SR ……..(v)
पुन: समीकरण (ii) तथा (iv) सं.
PQ = SR ……..(vi)
∴ समीकरण (v) व (vi) से,
PQRS एक समान्तर चतुर्भुज हैं। ………(vii)
पुनः SR || AC ….(iii) से
∴ SG = MN …..(viii)
इसी प्रकार ΔABP में,
∴ SP || DB
SN || GM ……..(ix)
समीकरण (viii) तथा (ix) से,
SNMG एक समान्तर चतुर्भुज है
∴ ∠GMN = ∠GSN
(||^gm के सम्मुख कोण) … (x)
किन्तु समचतुर्भुज के विकर्ण समकोण पर काटते हैं
∴ ∠GMN = 90° ……….. (xi)
समीकरण (x) व (xi) से,
∠GSN = ∠RSP = 90° ………. (xii)
∴ समीकरण (vii) व (xii) से,
PQRS एक आयत है। इति सिद्धम् ।

प्रश्न 15.
चित्र में ABCD एक समान्तर चतुर्भुज है। P और Q क्रमशः सम्मुख भुजाओं AB और CD के मध्य- बिन्दु हैं। सिद्ध कीजिए कि PRQS एक समान्तर चतुर्भुज है।
हल :

दिया है : समान्तर चतुर्भुज ABCD में AB और CD के मध्य बिन्दु क्रमश: P और Q हैं।
सिद्ध करना है :
PQRS एक समान्तर चतुर्भुज है।
उपपत्ति: चूँकि P और Q क्रमश: AB और CD के मध्य- बिन्दु हैं।
∴ AP = \(\frac {1}{2}\)AB
और CQ = \(\frac {1}{2}\)CD ……….(i)
लेकिन AB = CD
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
⇒ \(\frac {1}{2}\)AB = \(\frac {1}{2}\)CD
⇒ AP = CQ ……….(ii)
और AB || DC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
⇒ AP || CQ ……….(iii)
इस प्रकार चतुर्भुज APCQ में,
AP || CQ और APCQ [समीकरण (ii) और (iii) से]
⇒ APCQ एक समान्तर चतुर्भुज है। ………..(iv)
इसी प्रकार BPDQ एक समान्तर चतुर्भुज है। ……..(v)
अब समीकरण (iv) से,
AQ || PC ⇒ SQ || RP ……. (vi)
समीकरण (v) से,
BQ || PD ⇒ RQ || PS … (vii)
समी. (vi) व (vii) से,
SPRQ एक समान्तर चतुर्भुज है। इति सिद्धम् ।

प्रश्न 16.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC । AD, बहिष्कोण PAC को समद्विभाजित करता है और CD || BA दर्शाइए कि :

(i) ∠DAC = ∠BCA
(ii) ABCD एक समान्तर चतुर्भुज है।
हल :
दिया है : समद्विबाहु ΔABC में AB = AC, तथा बहिष्कोण PAC का समद्विभाजक AD.
रचना : AD = BC काटी DC को मिलाया
सिद्ध करना है : (i) ∠DAC = ∠BCA
(ii) ABCD एक समान्तर चतुर्भुज है।
उपपत्ति:
(i) ABC समद्विबाहु त्रिभुज है, जिसमें
AB = AC (दिया है)
∴ ∠ABC = ∠ACB ……..(1)
(समान भुजाओं के सम्मुख कोण)
बहिष्कोण ∠PAC = ∠ABC + ∠ACB ……….(2)
समीकरण (1) और (2) से,
∠PAC = 2∠ACB ………..(3)
∵ AD, कोण ∠PAC को समद्विभाजित करती है।
∴ ∠PAC = 2∠DAC …….(4)
समीकरण (3) व (4) से,
2∠DAC = 2∠ACB
∠DAC = ∠ACB. इति सिद्धम् ।

(ii) ∠DAC = ∠ACB (एकान्तर कोण)
रेखाखण्ड BC और AD को तिर्यक रेखा AC काटती है।
∴ BC || AD
और BA || CD (दिया है)
अत: ABCD समान्तर चतुर्भुज है। इति सिद्धम् ।

प्रश्न 17.
एक चतुर्भुज ABCD के विकर्ण परस्पर लम्ब हैं। सिद्ध कीजिए कि इनकी भुजाओं के मध्य बिन्दुओं को मिलाने वाले रेखाखण्डों से एक आयत बनता है।
हल :

दिया है चतुर्भुज ABCD के विकर्ण AC व BD इस प्रकार है कि AC ⊥ BD तथा E, F, G H क्रमश: AB, BC, CD व AD के मध्य बिन्दु हैं। P तथा Q क्रमश: भुजाओं GH व GF के मध्य बिन्दु हैं।
सिद्ध करना है : EFGH एक आयत है।
उपपत्ति: ΔADC में, G व H क्रमश: CD तथा AD के मध्य बिन्दु है। (दिया है)
∴ GH || AC व GH = \(\frac {1}{2}\)AC ……(i)
पुन: ΔABC में,
E व F क्रमश: AB तथा BC के मध्य बिन्दु हैं। (दिया है)
∴ EF || AC एवं EF = \(\frac {1}{2}\)AC ……(ii)
समीकरण (i) व (ii) से,
GH || EF तथा GH = EF … (iii)
चतुर्भुज EFGH की सम्मुख भुजाएँ बराबर व परस्पर समान्तर हैं।
∴ EFGH एक समान्तर चतुर्भुज है।
इसी प्रकार GF || DB
तथा GH || AC
∴ ORGP एक समान्तर चतुर्भुज है, जिसका ∠POR = 90°
∴ ∠PGR = ∠POR = 90° (||^gm के सम्मुख कोण)
∴ GHEF एक आयत है। इति सिद्धम् ।

प्रश्न 18.
समान्तर चतुर्भुज ABCD में विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ । सिद्ध कीजिए कि APCQ एक समान्तर चतुर्भुज है।
हल :

दिया है समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार हैं कि
DP = BQ
सिद्ध करना है: APCQ एक समान्तर चतुर्भुज है।
उपपत्ति: ΔAPD और ΔCQB में,
AD = BC
(समान्तर चतुर्भुज की सम्मुख भुजाएँ)
∠ADP = ∠CBQ (एकान्तर कोण)
DP = BQ. (दिया है)
ΔAPD ≅ ΔCQB
अर्थात् (SAS नियम)
AP = CQ ……….(1)
इसी प्रकार ΔCPD और ΔAQB में, हम सिद्ध कर सकते हैं कि
CP = AQ ……….(2)
समीकरण (1) और (2) से,
APCQ एक समान्तर चतुर्भुज है। इति सिद्धम् ।

प्रश्न 19.
सिद्ध कीजिए कि त्रिभुज की एक भुजा के मध्य- बिन्दु से, एक अन्य भुजा के समान्तर खींची गई रेखा, तीसरी भुजा को उसके मध्य बिन्दु पर प्रतिच्छेदित करती है।
हल :

दिया है त्रिभुज ABC में, AB का मध्य बिन्दु D है। D से BC के समान्तर खींची गई रेखा त्रिभुज की भुजा AC
को बिन्दु E पर प्रतिच्छेदित करती है।
सिद्ध करना है E, AC का मध्य- बिन्दु है। रचना AE पर कोई बिन्दु E किया तथा D और E को मिलाया ।
उपपत्ति : मान लीजिए E, भुजा AC का मध्य-बिन्दु नहीं है, और मान लीजिए कि E, भुजा AC का मध्य- बिन्दु है।
अब त्रिभुज ABC में, D, AB का मध्यबिन्दु है, और E’, AC का मध्य-बिन्दु है।
∴ DE’ || BC ……..(1)
परन्तु DE || BC (दिया है) …….. (2)
समीकरण (1) और (2) से स्पष्ट है कि दो प्रतिच्छेदी रेखाएँ DE और DE’ दोनों रेखा BC के समान्तर हैं।
परन्तु यह तो अंतर्विरोध है।
इस प्रकार हमारी कल्पना गलत है।
अतः AE = EC
अर्थात् E, AC का मध्य बिन्दु है। इति सिद्धम् ।

प्रश्न 20.
समान्तर चतुर्भुज ABCD के विकर्ण BD पर A और C से डाले गये लम्ब क्रमश: AP तथा CQ हैं।
सिद्ध कीजिए कि AP = CQ.
हल :
सिद्ध करना है:
AP = CQ

उपपत्ति: विकर्ण समान्तर चतुर्भुज को दो समान क्षेत्रफल वाले त्रिभुजों में बाँटता है।
∴ ΔABD का क्षेत्रफल = ΔBDC का क्षेत्रफल
त्रिभुज का क्षे. = \(\frac {1}{2}\) × आधार × ऊँचाई
∴ \(\frac {1}{2}\)BD × AP = \(\frac {1}{2}\)BD × CQ
∴ AP = CQ.

प्रश्न 21.
दी गई आकृति में, D, E और F क्रमशः भुजाओं BC, CA तथा AB के मध्य बिन्दु हैं। यदि, AB = 4.3 सेमी, BC = 5.6 सेमी, और AC = 3.9 सेमी हैं तो निम्नलिखित का परिमाप ज्ञात कीजिए: (i) ΔDEF और (ii) चतुर्भुज BDEF

हल :
(i) त्रिभुज की किन्ही दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड सम्मुख भुजा का आधा होता है।
अतः ΔDEF में,
DE = \(\frac {1}{2}\)AB
EF = \(\frac {1}{2}\)BC
DF = \(\frac {1}{2}\)AC
∴ ΔDEF का परिमाप = DE + EF + DF
= \(\frac {1}{2}\)AB + \(\frac {1}{2}\)BC + \(\frac {1}{2}\)AC
= \(\frac {1}{2}\)(AB + BC + AC)
= \(\frac {1}{2}\)(4.3 + 5.6 + 3.9)
= \(\frac {1}{2}\)(13.8)
= 6.9 सेमी।

(ii) चतुर्भुज BDEF का परिमाप
= BD + DE + EF + BF
= \(\frac {1}{2}\)BC + \(\frac {1}{2}\)AB + \(\frac {1}{2}\)BC + \(\frac {1}{2}\)AB
= AB + BC
= 4.3 + 5.6
= 9.9 सेमी।

प्रश्न 22.
ΔABC का ∠B समकोण है और P, भुजा AC का मध्य बिन्दु है। सिद्ध कीजिए कि PB = PA = \(\frac {1}{2}\)AC
हल :
दिया है ΔABC में, ∠B = 90° व P, AC का मध्य बिन्दु है।

सिद्ध करना है PB = PA = \(\frac {1}{2}\)AC
रचना: PC पर एक ΔPDC बनाया जिसमें PB = PD
उपपत्ति : ΔAPB व ΔCPD में,
PA = PC (दिया है)
∠1 = ∠2 (शीर्षभिमुख कोण)
PB = PD (रचना से)
∴ ΔAPB ≅ ΔCPD (SAS नियम)
∴ AB = CD ……(i)
तथा ∠BAP = ∠DCP
किन्तु ये एकान्तर कोण हैं
∴ AB || CD ………..(i)
पुन: ∠ABC + ∠DCB = 180°
किन्तु ∠ABC = 90°
∴ ∠DCB = 90° ………..(ii)
पुन: ΔMBC व ΔDCB में,
BC = BC (उभयनिष्ठ)
∠ABC = ∠DCB (प्रत्येक 90°)
AB = CD ((i) से)
∴ ΔABC ≅ ΔDCB (SAS नियम)
तब AC = BD
⇒ \(\frac {1}{2}\)AC = \(\frac {1}{2}\)BD
किन्तु \(\frac {1}{2}\)AC = AP
तथा \(\frac {1}{2}\)BD = BP
∴ PB = PA = \(\frac {1}{2}\)AC.
इति सिद्धम् ।

प्रश्न 23.
त्रिभुज ABC में, भुजा AB को M और N तीन बराबर भागों में बाँटते हैं। दोनों रेखाखण्ड MP और NQ भुजा BC के समान्तर हैं और AC को क्रमश: P और Q पर मिलते हैं। सिद्ध कीजिए कि P और Q भुजा AC को भी तीन बराबर भागों में बाँटते हैं।
हल :

दिया है ΔABC में,
AM = MN = NB
उपपत्ति: क्योंकि MP || BC व NQ || BC
∴ MP || NQ || BC …(i)
AB व AC, MP, NO एवं BC को क्रमश: M, N
तथा P व O पर इस प्रकार काटती है कि
MN = NB (दिया है)
PQ = QC …(ii)
पुन: M, AN का मध्य बिन्दु है,
तथा MP || NQ [(i) से]
∴ AP = NQ ….(iii)
अब (ii) तथा (iii) से
AP = PQ = QC इति सिद्धम् ।

प्रश्न 24.
सिद्ध कीजिए कि त्रिभुज की माध्यिका उसको समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
हल :
दिया है त्रिभुज ABC में AD भुजा BC की माध्यिका है।
सिद्ध करना है:
ΔABD का क्षेत्रफल = ΔACD का क्षेत्रफल

रचना: शीर्ष A से सम्मुख भुजा BC पर AM लम्ब को डाला।
उपपत्ति: ΔABC में AD माध्यिका है।
∵ BD = CD ……(i)
∴ त्रिभुज ABD तथा त्रिभुज ADC के आधार एक ही रेखा BC (CD) पर होने और दोनों त्रिभुजों के एक ही शीर्ष A होने से AM दोनों त्रिभुजों की ऊँचाई है।
∴ ΔABD का क्षेत्रफल | क्षेत्रफल = \(\frac {1}{2}\)BD × AM
ΔACD का क्षेत्रफल = \(\frac {1}{2}\)CD × AM
परन्तु, BD = CD [समीकरण (i) से]
∴ ΔABD का क्षेत्रफल = ΔACD का क्षेत्रफल
इति सिद्धम्

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 1 संख्या पद्धति Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 1 संख्या पद्धति

वस्तुनिष्ठ प्रश्न :

प्रश्न 1.
\(2^{\frac{2}{3}} \cdot 2^{\frac{1}{2}}\) का मान होगा :
(A) 26
(B) 4
(C) 6
(D) – 2
हल :

अतः सही विकल्प ‘A’ है।

प्रश्न 2.
(\(\sqrt{m}\) – \(\sqrt{m}\))(\(\sqrt{11}\) + \(\sqrt{7}\)) का मान होगा :
(A) 172
(B) 18
(C) 4
(D) 77
हल:
(\(\sqrt{m}\) – \(\sqrt{m}\))(\(\sqrt{11}\) + \(\sqrt{7}\))
= (\(\sqrt{11}\))² – (\(\sqrt{7}\))²
= 11 – 7 = 4
अतः सही विकल्प ‘C’ है।

प्रश्न 3.
अपरिमेय संख्या होगी :
(A) \(\frac {2}{4}\)
(B) \(\sqrt{3}\)
(C) \(\sqrt{9}\)
(D) \(\frac {3}{4}\)
हल :
अपरिमेय संख्या \(\sqrt{3}\) है।
अतः सही विकल्प ‘B’ है।

प्रश्न 4.
अनवसानी आवर्ती संख्या होगी :
(A) \(\frac {1}{3}\)
(B) \(\frac {1}{2}\)
(C) \(\frac {7}{8}\)
(D) \(\frac {3}{2}\)
हल :
अनवसानी आवर्ती में अंश में हर का भाग देने पर शेषफल आता है अर्थात् शेषफल 0 (शून्य) नहीं आता है तथा भागफल की पुनरावृत्ति होती रहती है। \(\frac {1}{3}\) = 0.333…
अत: सही विकल्प ‘A’ है।

प्रश्न 5.
समस्त परिमेय और अपरिमेय संख्याओं का संग्रह कहलाता है:
(A) पूर्णांक संख्याएँ
(B) वास्तविक संख्याएँ
(C) प्राकृत संख्याएँ
(D) सांत परिमेय संख्याएँ
हल :
परिमेय और अपरिमेय संख्याओं के संग्रह को वास्तविक संख्याएँ कहते हैं।
अतः सही विकल्प ‘B’ है।

प्रश्न 6.
\(\frac{1}{\sqrt{3}}\) किस प्रकार की संख्या है ?
(A) परिमेय
(B) अपरिमेय
(C) प्राकृत संख्या
(D) पूर्णांक संख्या
हल:
\(\frac{1}{\sqrt{3}}\) में अंश (1) परिमेय संख्या है और हर (\(\sqrt{3}\)) अपरिमेय संख्या है।
परिमेय संख्या / अपरिमेय संख्या = अपरिमेय संख्या
अतः सही विकल्प ‘B’ है।

प्रश्न 7.
यदि किसी संख्या के अंश में हर का भाग देने पर शेषफल शून्य प्राप्त होता है, तो वह होगा :
(A) असांत दशमलव
(B) असांत अनावर्ती
(C) सांत एवं असांत दोनों
(D) सांत दशमलव ।
हल :
जब किसी भिन्न के अंश में हर का भाग देने पर शेषफल शून्य प्राप्त होता है, वह भिन्न परिमेय सांत दशमलव भिन्न कहलाती है।
अतः सही विकल्प ‘D’ है।

प्रश्न 8.
0.333…. को \(\frac {p}{q}\) के रूप में लिखा जा सकता है:
(A) \(\frac {1}{0.3}\)
(B) \(\frac {3}{10}\)
(C) \(\frac {1}{3}\)
(D) इनमें से कोई नहीं।
हल:
0.333… = \(0 . \overline{3}\)
माना x = \(0 . 3\overline{3}\)
10x = \(3 . \overline{3}\)
9x = 3 (घटाने पर)
x = \(\frac{3}{9}=\frac{1}{3}\)
सही विकल्प ‘C’ है।

प्रश्न 9.
किसी परिमेय और अपरिमेय संख्या का अन्तर होगा :
(A) परिमेय
(B) अपरिमेय
(C) सांत दशमलव
(D) इनमें से कोई नहीं
हल :
परिमेय तथा अपरिमेय संख्याओं का अन्तर सदैव अपरिमेय होता है।
अतः विकल्प ‘B’ सही है।

प्रश्न 10.
(\(\sqrt{3}\))⁶ का मान होगा :
(A) 3\(\sqrt{3}\)
(B) 3
(C) 9
(D) 27.
हल :
(\(\sqrt{3}\))⁶ = \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\) × \(\sqrt{3}\)
= 3 × 3 × 3
= 27
अत: सही विकल्प ‘D’ है।

लघु उत्तरीय प्रश्न :

प्रश्न 11.
– 2 और 5 के बीच तीन परिमेय संख्याएँ ज्ञात कीजिए।
हल :

प्रश्न 12.
निम्नलिखित संख्याओं को दशमलव संख्या में व्यक्त कीजिए तथा दशमलव प्रसार का प्रकार बताइए :
(i) \(\frac {3}{11}\)
(ii) \(\frac {1}{7}\)
(iii) \(\frac {1}{16}\)
हल :

प्रश्न 13.
\(0 . \overline{361}\) को परिमेय संख्या में बदलिए ।
हल :
माना कि x = \(0 . \overline{361}\)
x = 0.361361361 …….(1)
समी. (1) में 1000 से गुणा करने पर,
1000x = 361.361361 …….(2)
समी (2) में से समी (1) घटाने पर
999x = 361
∴ x = \(\frac {361}{999}\)
⇒ अतः \(0 . \overline{361}\) = \(\frac {361}{999}\)

प्रश्न 14.
निम्नलिखित को सरल कीजिए:
(i) x² × x^-2 × x^-3
(ii) 2x³ ÷ 2x^-3
(iii) \(\frac{x}{\sqrt{5}+1}\) = \(\frac{\sqrt{5}-1}{x}\)
(iv) (2\(\sqrt{5}\) + 1) + (1 – 2\(\sqrt{5}\)) – 2.
हल :
(i) x² × x^-2 × x^-3 = x^2-2-3
= x^2-5
= x^-3 = \(\frac{1}{x^3}\)

(ii) 2x³ ÷ 2x^-3 = \(\frac {2}{2}\) x^3-(-3)
= x³⁺³ = x⁶

(iii) \(\frac{x}{\sqrt{5}+1}\) = \(\frac{\sqrt{5}-1}{x}\)
x × x = (\(\sqrt{5}\) – 1)(\(\sqrt{5}\) + 1)
x² = (\(\sqrt{5}\))² – (1)² = 5 – 1
x² = 4
x = ±2.

(iv) (2\(\sqrt{5}\) + 1)+(1 – 2\(\sqrt{5}\)) – 2
= (2\(\sqrt{5}\) – 2\(\sqrt{5}\)) + (1 + 1) – 2
= 0 + 2 – 2 = 0

प्रश्न 15.
वास्तविक संख्या रेखा पर \(\sqrt{3}\) का स्थान निर्धारित कीजिए।
हल :
सबसे पहले XY रेखा खींची। रेखा पर बिन्दु O पर 0 (शून्य) से इकाई लम्बाई (1 इकाई) पर बिन्दु 4 लिया। बिन्दु 4 पर लम्ब AB = 1 इकाई खींचा। O और B को मिलाया है।

अब OB के B बिन्दु पर एकांक लम्बाई का लम्ब BD खींचा तथा O और D को मिलाया। OD = \(\sqrt{(\sqrt{2})^2+(1)^2}\) = \(\sqrt{3}\) प्राप्त होता है। O को केन्द्र मानकर OD त्रिज्या का चाप खींचा, जो संख्या रेखा को बिन्दु पर काटता है। अत: बिन्दु Q अपरिमेय संख्या \(\sqrt{3}\) को निरूपित करता है।

प्रश्न 16.
सिद्ध कीजिए कि \(\sqrt{3}\) अपरिमेय संख्या है।
हल :
भाग विधि से वर्गमूल :

∴ \(\sqrt{3}\) = 1.732050807…………
अतः असांत अनावर्ती अपरिमेय संख्या है। इति सिद्धम्

प्रश्न 17.
\(\frac{\sqrt{3}-1}{\sqrt{3}+1}\) = a + b\(\sqrt{3}\)
तब a तथा b के मान ज्ञात कीजिए।
हल :
दी हुई संख्या में (\(\sqrt{3}\) – 1) का अंश और हर में गुणा करने पर,

प्रश्न 18.
[(1)³ + (2)³ + (3)³]\(\frac {-5}{2}\) का मान ज्ञात कीजिए ।
हल :
[(1)³ + (2)³ + (3)³]\(\frac {-5}{2}\)
⇒ [1 + 8 + 27]\(\frac {-5}{2}\)
⇒ (36)\(\frac {-5}{2}\)
⇒ [(6)²]^-5/2
⇒ (6)^{2×\(\frac {-5}{2}\)}
⇒ \(\frac{1}{(6)^5}\)
⇒ \(\frac {1}{7776}\)

प्रश्न 19.
यदि धनात्मक संख्याएँ हैं, तो का मान ज्ञात कीजिए।
\(\sqrt{x^{-1} y} \cdot \sqrt{y^{-1} z} \cdot \sqrt{z^{-1} x}\)
हल :

प्रश्न 20.
6\(\sqrt{5}\) को 3\(\sqrt{5}\) से गुणा कीजिए।
हल :
6\(\sqrt{5}\) × 3\(\sqrt{5}\) = 6 × 3 × \(\sqrt{5}\) × \(\sqrt{5}\)
= 18 × 5 = 90.

प्रश्न 21.
\(\frac{3}{\sqrt{8}}\) का परिमेयकरण कीजिए।
हल :
\(\sqrt{8}\) का अंश और हर में गुणा करने पर,

प्रश्न 22.
यदि b = \(\sqrt[5]{243}\) हो, तो b का मान ज्ञात कीजिए।
हल :
b = \(\sqrt[5]{243}\)
⇒ b = (243)^1/5
= (3 × 3 × 3 × 3 × 3)^1/5
= [(3)⁵]^1/5
= 3^5×1/5
∴ b = 3

प्रश्न 23.
\(\frac{3}{\sqrt{48}-\sqrt{75}}\) का मान क्या होगा ?
हल :

प्रश्न 24.
\(\frac{1}{3+\sqrt{2}}\) के हर का परिमेयकरण कीजिए।
हल :
अंश और हर में (3 – \(\sqrt{2}\)) का गुणा करने पर,
\(\frac{3-\sqrt{2}}{(3+\sqrt{2}) \times(3-\sqrt{2})}\) ⇒ \(\frac{3-\sqrt{2}}{(9-2)}\)
{∵ a² – b² = (a+b) (a – b)}
⇒ \(\frac{3-\sqrt{2}}{7}\)

प्रश्न 25.
यदि (x)^y = 128, तो x तथा y का मान ज्ञात कीजिए ।
हल :
(x)^y = 128 = (2)⁷
x^y = 2⁷
आधार तथा घातकी तुलना करने पर,
x = 2
y = 7.

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.6

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
एक बेलनाकार बर्तन के आधार की परिधि 132 सेमी और उसकी ऊँचाई 25 सेमी है। इस बेर्तन में कितने लीटर पानी आ सकता है ? (1000 सेमी³ = 1 लीटर)
हल:
माना आधार की त्रिज्या r सेमी और बेलनाकार बर्तन की ऊँचाई h सेमी है।
आधार की परिधि = 132 सेमी
⇒ 2πr = 132
⇒ 2 × \(\frac{22}{7}\) × r = 132
r = \(\left(\frac{132 \times 7}{2 \times 22}\right)\) सेमी = 21 सेमी
बेलनाकार बर्तन का आयतन = πr²h
= (\(\frac{22}{7}\) × 21 × 21 × 25 ) सेमी³
= 34650 सेमी³
∴ पात्र में जल आ सकता है = \(\left(\frac{34650}{1000}\right)\) लीटर
= 34.65 लीटर जल।

प्रश्न 2.
लकड़ी के एक बेलनाकार पाइप का आन्तरिक व्यास 24 सेमी है और बाहरी व्यास 28 सेमी है। इस पाइप की लम्बाई 35 सेमी है। इस पाइप का द्रव्यमान ज्ञात कीजिए, यदि 1 सेमी³ लकड़ी का द्रव्यमान 0.6 ग्राम है।
हल:
पाइप का आन्तरिक व्यास = 24 सेमी
∴ आन्तरिक त्रिज्या (r₁) = \(\frac{24}{2}\) सेमी = 12 सेमी
पाइप का बाहरी व्यास = 28 सेमी
∴ बाहरी त्रिज्या (r₂) = \(\frac{28}{2}\) सेमी = 14 सेमी
तथा पाइप की ऊँचाई (h) = 35 सेमी
प्रयुक्त लकड़ी का आतयन = पाईप का बाहरी आयतन – पाईप का भीतरी आवतन
= πr₂²h – πr₁²h
= πh (r₂² – r₁²)
= πh (r₂ – r₁)(r₂ + r₁)
= \(\frac{22}{7}\) × 35(14 – 12)(14 + 12)
= 22 × 5 × 2 × 26 = 5720 सेमी³
∴ लकड़ी की आयतन = (21560 – 15840) सेमी³
= 5720 सेमी³
∵ 1 सेमी³ लकड़ी की द्रव्यमान = 0.6 ग्राम
∴ 5720 सेमी लकड़ी का द्रव्यमान = 0.6 × 5720 g
= 3432 ग्राम
= \(\frac{3432}{1000}\) किग्रा = 3.432 किग्रा।
(∵ 1000 ग्राम = 1 किग्रा)

प्रश्न 3.
एक सोफ्ट ड्रिंक (soft drink) दो प्रकार के पैकों में उपलब्ध है: (i) लम्बाई 5 सेमी और चौड़ाई 4 सेमी वाले एक आयताकार आधार का टिन का डिब्बा जिसकी ऊंचाई 15 सेमी है और (ii) व्यास 7 सेमी वाले वृत्तीय आधार और 10 सेमी ऊंचाई वाला एक प्लास्टिक का बेलनाकार डिब्बा। किस डिब्बे की धारिता अधिक है और कितनी अधिक है?
हल:
(i) टीन के डिब्बे की लम्बाई (l) = 5 सेमी
चौड़ाई (b) = 4 सेमी और ऊँचाई (h) = 15 सेमी
∴ टीन के डिब्बे का आयतन = lbh
= 5 × 4 × 15 घन सेमी
= 300 घन सेमी
∴ टीन के डिब्बे की धारिता = 300 घन सेमी

(ii) वृत्तीय आधार वाले डिब्बे का व्यास = 7 सेमी
∴ वृत्तीय आधार वाले डिब्बे की त्रिज्या (r) = \(\frac{7}{2}\)सेमी
डिब्बे की ऊँचाई (h’) = 10 सेमी
∴ बेलनाकार डिब्बे का आयतन = πr²h’
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 10\) घन सेमी
= 385 घन सेमी
∴ बेलनाकार डिब्बे की धारिता = 385 घन सेमी।
अतः स्पष्ट है कि बेलनाकार डिब्बे की धारिता = 385 – 300 = 85 घन सेमी अधिक है।

प्रश्न 4.
यदि एक बेलन का पाश्र्व पृष्ठीय क्षेत्रफल 94.2 सेमी² है और उसकी ऊंचाई 5 सेमी है, तो ज्ञात कीजिए:
(i) आधार की त्रिज्या
(ii) बेलन का आयतन (π = 3.14 लीजिए)
हल:
बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 94.2 सेमी²
(i) 2πrh = 94.2 सेमी²
⇒ 2 × 3.14 × r × 5 = 94.2
⇒ r = \(\frac{94.2}{2 \times 3.14 \times 5}\) सेमी
∴ आधार की त्रिज्या = 3 सेमी।

(ii) बेलन का आयतन = πr²h
= 3.14 × 3 × 3 × 5 सेमी³
= 141.3 सेमी³।

प्रश्न 5.
10 मीटर गहरे एक बेलनाकार बर्तन के आंतरिक वक्र पृष्ठ को पेंट कराने का व्यय ₹ 2,200 है। यदि पेंट कराने की दर ₹20 प्रति मीटर है, तो निम्न ज्ञात कीजिए:
(i) बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) आधार की त्रिज्या
(iii) बर्तन की धारिता।
हल:
(i) बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल

(ii) माना वर्तन के आधार की त्रिज्या = r मीटर
और ऊँचाई = h मीटर
∴ 2πrh = 110
⇒ 2 × \(\frac{22}{7}\) × r × 10 = 110
r = \(\frac{110 \times 7}{2 \times 22 \times 10}=\frac{7}{4}\) = 1.75
अतः बर्तन के आधार की त्रिज्या = 1.75 मीटर

(iii) बर्तन की धारिता = πr²h
= \(\left(\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times 10\right)\) मीटर³
= 96.25 मीटर³।

प्रश्न 6.
ऊँचाई 1 मी वाले एक बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसको बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी ?
हल:
बेलनाकार बर्तन की धारिता = 15.4 लीटर
= \(\left(15.4 \times \frac{1}{1000}\right)\) मीटर³
= 0.0154 मीटर³
माना आधार की त्रिज्या मीटर और बर्तन की ऊँचाई h मीटर है, तब
आयतन = πr²h = πr² × 1 = πr²
[∵ h = 1 मीटर]
⇒ πr² = 0.0154
⇒ \(\frac{22}{7}\) × r² = 0.0154
⇒ r² = \(\frac{0.0154 \times 7}{22}\)
= 0.0049
∴ r = \(\sqrt{0.0049}\) = 0.07 मीटर
इस प्रकार, बर्तन के आधार की त्रिज्या = 0.07 मीटर
वर्तन के निर्माण के लिए आवश्यक धातु की शीट = बर्तन का कुल पृष्ठीय क्षेत्रफल
= 2πrh + πr2 = 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 0.07 (1 + 0.07) मीटर2
= 44 × 0.01 × 1.07 मीटर2
= 0.4708 मीटर2

प्रश्न 7.
सीसे की एक पेंसिल लकड़ी के एक बेलन के अभ्यंतर में ग्रेफाइट से बने ठोस बेलन को डालकर बनाई गई है। पेंसिल का व्यास 7 मिमी है और ग्रेफाइट का व्यास 1 मिमी है। यदि पेंसिल की लम्बाई 14 सेमी है, तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए।
हल:
ग्रेफाइट का व्यास = 1 मिमी
ग्रेफाइट की त्रिज्या (r) = \(\frac{1}{2}\) मिमी
= \(\frac{1}{2 \times 10}\) सेमी = \(\frac{1}{20}\) सेमी
और ग्रेफाइट की ऊँचाई (h) = 14 सेमी
∴ ग्रेफाइट का आयतन = πr²h
= \(\frac{22}{7} \times \frac{1}{20} \times \frac{1}{20} \times 14\) सेमी³
= \(\frac{11}{110}\) सेमी³ = 0.11 सेमी³
पेंसिल का व्यास = 7 मिमी
∴ पेंसिल की त्रिज्या (R) = \(\frac{7}{2}\) = \(\frac{7}{20}\) सेमी
तथा पेंसिल की ऊँचाई (h) = 14 सेमी
∴ पेंसिल का आयतन = πR²h
= \(\frac{22}{7} \times \frac{7}{20} \times \frac{7}{20} \times 14\) सेमी³
= \(\frac{539}{100}\) सेमी³ = 5.39 सेमी²
लकड़ी का आयतन = पेंसिल का आयतन – ग्रेफाइट का आयतन
= (5.39 – 0.11) सेमी³ = 5.28 सेमी³।

प्रश्न 8.
एक अस्पताल के एक रोगी को प्रतिदिन 7 सेमी व्यास वाले एक बेलनाकार कटोरे में सूप (soup) दिया जाता है। यदि कटोरा सूप से 4 सेमी ऊंचाई तक भरा जाता है, तो इस अस्पताल में 250 रोगियों के लिए प्रतिदिन कितना सूप तैयार किया जाता है?
हल:
बर्तन का व्यास = 7 सेमी
बर्तन की त्रिज्या (r) = \(\frac{7}{2}\) सेमी
बर्तन में सूप की ऊँचाई (h) = 4 सेमी
बर्तन में सूप का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 4\) सेमी³
= 22 × 7 सेमी³ = 154 सेमी³
अस्पताल में दिए जाने वाले सूप की मात्रा = एक रोगी को प्राप्त सूप × रोगियों की संख्या
= 154 × 250 = 38500 घन सेमी.
(∵ 1000 घन सेमी = 1 लीटर)
= \(\frac{38500}{1000}\) ली. = 38.5 ली.।