Month: October 2024

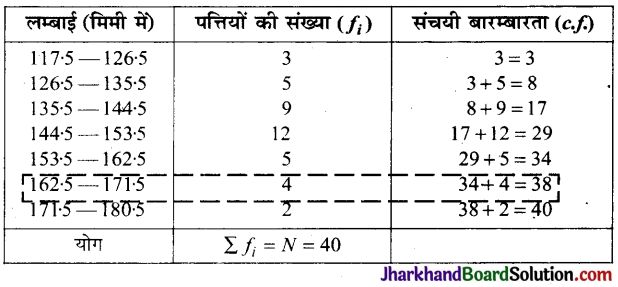
Jharkhand Board JAC Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Exercise 12.3

(जब तक अन्यथा न कहा जाय, का प्रयोग कीजिए)

प्रश्न 1.
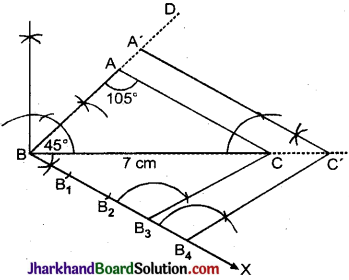
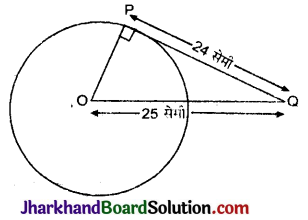
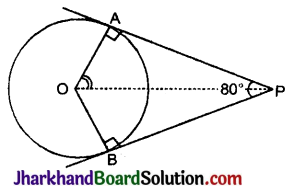
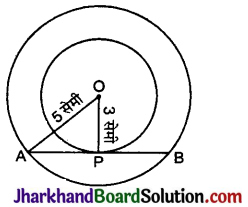
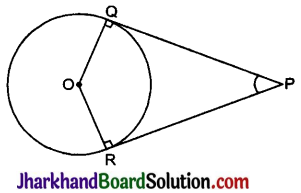
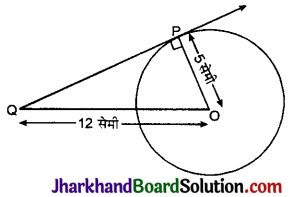
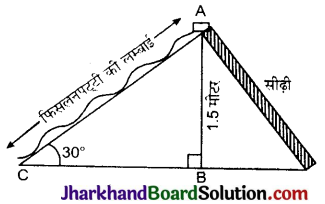
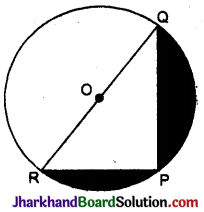
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 सेमी, PR = 7 सेमी तथा O वृत्तं का केन्द्र है।

हल :
दिया है, PQ = 24 सेमी
PR = 7 सेमी
RQ वृत्त का व्यास है।
∴ ∠RPQ = 90° (अर्द्धवृत्त में बना कोण)
समकोण ΔRPQ में, पाइथागोरस प्रमेय से,
QR² = RP² + PQ²
QR = \(\sqrt{R P^2+P Q^2}\)
⇒ QR = \(\sqrt{(7)^2+(24)^2}\)
= \(\sqrt{49+576}\) = \(\sqrt{625}\)
∴ QR = 25 सेमी
वृत्त का व्यास (QR) = 25 सेमी
वृत्त की त्रिज्या (r) = \(\frac {25}{2}\)
छायांकित भाग का क्षेत्रफल = अर्द्धवृत्त का क्षेत्रफल – ΔRPQ का क्षेत्रफल

अतः छायांकित भाग का क्षेत्रफल 161.53 सेमी²

प्रश्न 2.
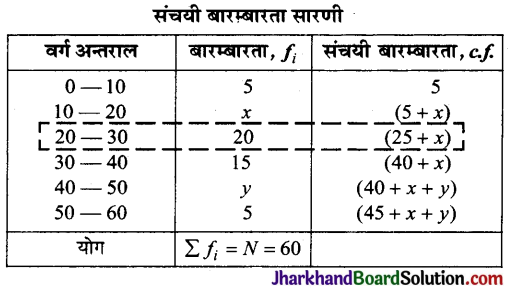
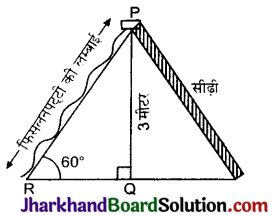
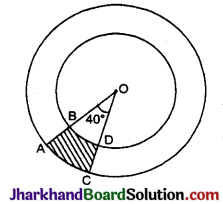
दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केन्द्र O वाले दोनों संकेन्द्रीय वृत्तों की त्रिज्याएँ क्रमशः 7 सेमी और 14 सेमी हैं तथा ∠AOC = 40° है।

हल :
दिया है, छोटे वृत्त की त्रिज्या (r) = 7 सेमी
बड़े वृत्त की त्रिज्या (R) = 14 सेमी
केन्द्र पर बना कोण (θ) = 40°
छायांकित भाग का क्षेत्रफल = बड़े त्रिज्यखण्ड OAC का क्षेत्रफल – छोटे त्रिज्यखण्ड OBD का क्षेत्रफल

अतः छायांकित भाग का क्षेत्रफल = \(\frac {154}{3}\)सेमी²

प्रश्न 3.
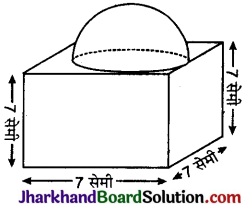
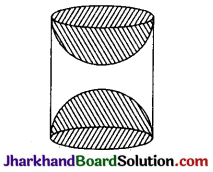
दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं।

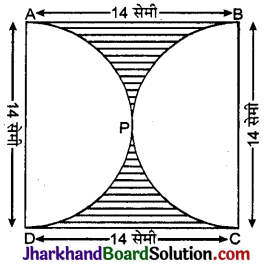
हल :
दिया है, वर्ग की भुजा = 14 सेमी
अर्धवृत्त का व्यास (AD = BC) = 14 सेमी
अर्धवृत्त की त्रिज्या (R) = \(\frac {14}{2}\) = 7 सेमी
∴ वर्ग ABCD का क्षेत्रफल = (भुजा)²
= 14 × 14 = 196 सेमी²
अर्धवृत्त का क्षेत्रफल = \(\frac {1}{2}\)πr²
= \(\frac{1}{2}=\frac{22}{7}\) × 7 × 7
= 77 सेमी²
दो अर्धवृत्तों का क्षेत्रफल = 2 × 77 = 154 सेमी²
∴ छायांकित भाग का क्षेत्रफल = वर्ग ABCD का क्षेत्रफल – दो अर्धवृत्तों का क्षेत्रफल
= 196 – 154 = 42 सेमी²
अतः छायांकित भाग का क्षेत्रफल = 42 वर्ग सेमी

प्रश्न 4.
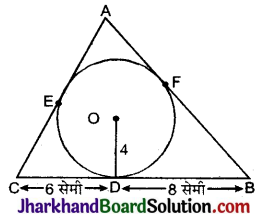
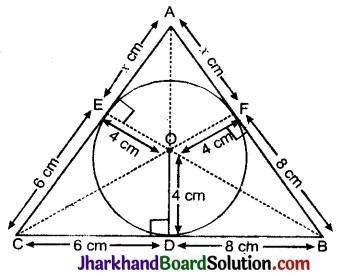
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 सेमी वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केन्द्र मानकर 6 सेमी त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।

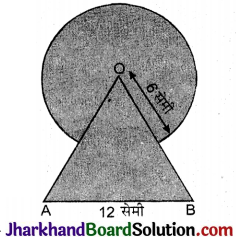
हल :
दिया है, चाप की त्रिज्या (R) = 6 सेमी
समबाहु त्रिभुज OAB की भुजा = 12 सेमी
OA = OB = AB = 12 सेमी
त्रिज्यखण्ड का केन्द्रीय कोण θ = 60°
[∵ समबाहु त्रिभुज का प्रत्येक कोण 60° का होता है]
वृत्त के दीर्घ त्रिज्यखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – वृत्त के लघु त्रिज्यखण्ड का क्षेत्रफल

∴ छायांकित भाग का क्षेत्रफल = समबाहु ΔOAB का क्षेत्रफल + वृत्त के दीर्घ त्रिज्यखण्ड का क्षेत्रफल
= (600 + 36\(\sqrt{3}\))

प्रश्न 5.
भुजा 4 सेमी वाले एक वर्ग के प्रत्येक कोने से 1 सेमी त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है। तथा बीच में 2 सेमी व्यास का एक वृत्त भी काटा गया है, जैसा कि आकृति में दर्शाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए ।

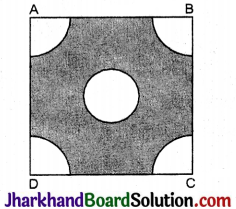
हल :
माना ABCD एक वर्ग है
जिसकी प्रत्येक भुजा = 4 सेमी
∴ वर्ग का क्षेत्रफल = (भुजा)²
= (4)² = 16 सेमी²
∴ वृत्तों के चतुर्थांश की त्रिज्या (r) = 1 सेमी
∴ चारों चतुर्थांश का क्षेत्रफल = 4 × \(\frac {1}{4}\)πr²
= πr² = \(\frac {22}{7}\) × (1)²
= \(\frac {22}{7}\)भुजा²
∵ बीच में काटे गये वृत्त का व्यास = 2 सेमी
त्रिज्या (R) = \(\frac {2}{2}\) = 1 सेमी
∴ वृत्त का क्षेत्रफल = πR²
= \(\frac {22}{7}\) × (1)²
= \(\frac {22}{7}\)सेमी²
∴ छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल – 4 चतुर्थांशों का क्षेत्रफल – वृत्त का क्षेत्रफल
= (16 – \(\frac {22}{7}\) – \(\frac {22}{7}\)) = (\(\frac{112-22-22}{7}\))
= \(\frac {68}{7}\) वर्ग सेमी

प्रश्न 6.
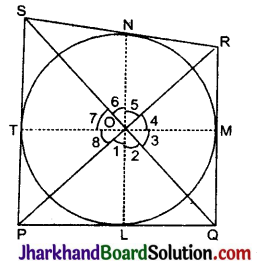
एक वृत्ताकार मेजपोश जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु त्रिभुज ABC छोड़ते हुए एक डिजाइन बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए।
हल :

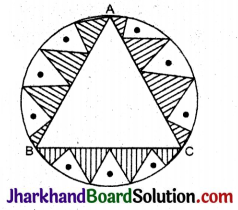
दिया है, ΔABC एक समबाहु त्रिभुज है।
∴ ∠A = ∠B = ∠C = 60°
∠BOC = 2 ∠BAC
= 2 × 60 = 120°
OB तथा OC वृत्ताकार मेजपोश की त्रिज्याएँ हैं।
∴ OB = 32 सेमी
केन्द्र O से OM ⊥ BC खींचा।
∴ BM = \(\frac {1}{2}\)BC
ΔOMB ≅ ΔOMC (RHS सर्वांगसमता नियम से)
∠BOM = ∠COM = \(\frac {120}{2}\)
= 60° (CPCT)
∴ ∠OBM = 180°- (90° + 60°) = 30°
इसी प्रकार,
समकोण ΔOBM में,

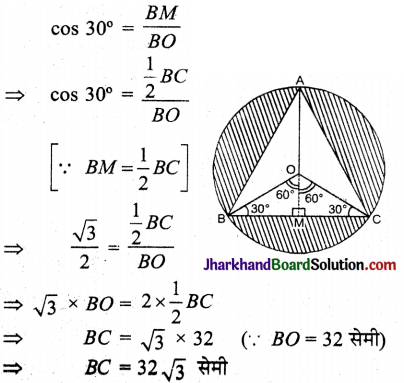
∴ समबाहु ΔABC की भुजा = 32\(\sqrt{3}\)
∴ समबाहु ΔABC का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\) × (सेमी)²
= \(\frac{\sqrt{3}}{4}\) × (32\(\sqrt{3}\))²
= \(\frac{\sqrt{3}}{4}\) × 1024 × 3 = 768\(\sqrt{3}\) वर्ग सेमी
∴ मेजपोश की त्रिज्या = 32 सेमी
∴ सम्पूर्ण मेजपोश का क्षेत्रफल = πr² = \(\frac {22}{7}\) × 32 × 32
= \(\frac {22528}{7}\) वर्ग सेमी
अतः छायांकित भाग का क्षेत्रफल = मेजपोश का क्षेत्रफल – समबाहु त्रिभुज का क्षेत्रफल
= (\(\frac {22528}{7}\) – 768\(\sqrt{3}\)) वर्ग सेमी

प्रश्न 7.
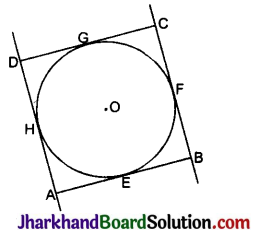
दी गई आकृति में, ABCD भुजा 14 सेमी वाला एक वर्ग है। A, B, C और D को केन्द्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

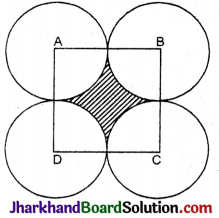
हल :
दिया है, वर्ग ABCD की भुजा = 14 सेमी
∴ वर्ग ABCD का क्षेत्रफल = (भुजा)²
= (14 × 14)
= 196 वर्ग सेमी
त्रिज्यखण्ड का कोण (θ) = 90°
[क्योंकि वर्ग का प्रत्येक कोण 90° होता है]
वृत्त की त्रिज्या (r) = \(\frac {14}{2}\) = 7 सेमी
∴ चारों चतुर्थाश का क्षेत्रफल = 4 × \(\frac {1}{4}\)πr² = πr²
= \(\frac {22}{7}\) × 7 × 7
= 154 वर्ग सेमी
∴ अभीष्ट छायांकित भाग का क्षेत्रफल
= वर्ग का क्षेत्रफल – चारों चतुर्थांश का क्षेत्रफल
= 196 – 154 = 42 सेमी²

प्रश्न 8.
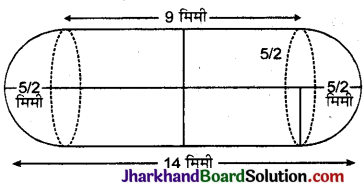
दी गई आकृति एक दौड़ने का पथ (racing track) दर्शाती है, जिसके बाएँ और दाएँ सिरे अर्धवृत्ताकार हैं।

दोनों आन्तरिक समान्तर रेखाखण्डों के बीच की दूरी 60 मीटर है तथा इनमें से प्रत्येक रेखाखण्ड 106 मीटर लम्बा है। यदि यह पथ 10 मीटर चौड़ा है तो ज्ञात कीजिए :
(i) पथ के आन्तरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी ।
(ii) पथ का क्षेत्रफल ।
हल :
दिया है, अर्धवृत्ताकार पथों की आन्तरिक त्रिज्या (r) = \(\frac {60}{2}\)मीटर = 30 मीटर
∴ दोनों अर्धवृत्तों की आन्तरिक परिधि
= 2 × (\(\frac {1}{2}\) × 2πr) = 2πr
= 2 × × 30 मीटर
= \(\frac {1320}{7}\)मीटर

दोनों आन्तरिक समान्तर रेखाखण्डों की लम्बाई = 106 मीटर + 106 मीटर
= 212 मीटर
∴ पथ के किनारों के अनुदिश 1 चक्कर लगाने में चली गई दूरी = दोनों अर्द्धवृत्तों की आन्तरिक परिधि + दोनों समान्तर रेखाखण्डों की लम्बाई
= (\(\frac {1320}{7}\) + 212) मीटर
= \(\frac{1320+1484}{7}\)
= \(\frac {2804}{7}\)मीटर = 400.57 मीटर
अतः पथ के आन्तरिक किनारों के अनुदिश 1 पूरा चक्कर लगाने में चली गई दूरी = 400.57 मीटर

(ii) ∵ वृत्ताकार पथ भागों की आन्तरिक त्रिज्या (r) = 30 मीटर
तथा पथ की चौड़ाई = 10 मीटर
∴ वृत्ताकार पथ के भागों की बाह्य त्रिज्या (R) = (30 + 10) मीटर
= 40 मीटर
दोनों वृत्ताकार भागों का क्षेत्रफल = πR² – πr²
= π[R² – r²]
= \(\frac {22}{7}\)[(40)² – (30)²]
= \(\frac {22}{7}\)[1600 – 900]
= \(\frac {22}{7}\) × 700 = 2200 वर्ग मीटर
वृत्ताकार भागों के अतिरिक्त पथ का क्षेत्रफल = 2 × ( लम्बाई × चौड़ाई)
= 2 × (106 × 10)
= 2 × 1060
= 2120 वर्ग मीटर
∴ पथ का कुल क्षेत्रफल = (2200 + 2120) मीटर²
= 4320 मीटर²
अतः पथ का क्षेत्रफल = 4320 वर्ग मीटर

प्रश्न 9.
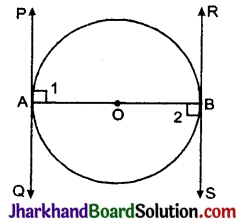
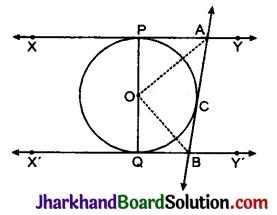
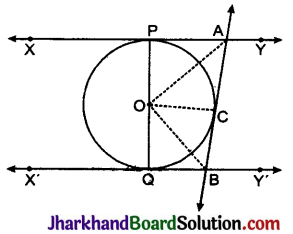
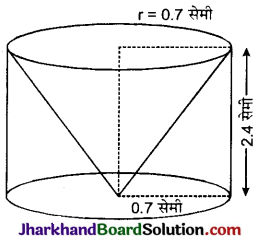
आकृति में, AB और CD केन्द्र O वाले एक वृत्त के दो परस्पर लम्ब व्यास हैं तथा OD छोटे वृत्त का व्यास है । यदि OA = 7 सेमी है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल :
दिया है, AB और CD एक वृत्त के दो परस्पर लम्ब व्यास है।
∴ AB ⊥ CD
आधे वृत्त ABC का क्षेत्रफल = \(\frac {1}{2}\)πR²
= \(\frac{1}{2}=\frac{22}{7}\) × 7 × 7
= 77 सेमी²
छोटे वृत्त का क्षेत्रफल = πr² = \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)
= 38.50 सेमी²
ΔABC का क्षेत्रफल = \(\frac {1}{2}\) × आधार × ऊँचाई
= \(\frac {1}{2}\)AB × OC
= \(\frac {1}{2}\) × 14 × 7 = 49 सेमी²
∴ छायांकित भाग का क्षेत्रफल = आधे वृत्त ABC का क्षेत्रफल + छोटे वृत्त का क्षेत्रफल – ΔABC का क्षेत्रफल
= (77 + 38.5 – 49) सेमी²
= 66.5 सेमी²
अतः छायांकित भाग का क्षेत्रफल = 66.5 वर्ग सेमी

प्रश्न 10.
एक समबाहु त्रिभुज ABC का क्षेत्रफल 17320-5 सेमी 2 है। इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है (देखिए आकृति) । छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
(π = 3.14 और \(\sqrt{3}\) = 1.73205 लीजिए ।)

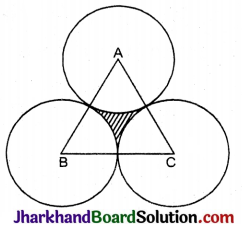
हल :
दिया है, समबाहु त्रिभुज ABC का क्षेत्रफल
= 17320.5 सेमी²
समबाहु त्रिभुज ABC का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\) (भुजा)²
⇒ 17320.5 = \(\frac{\sqrt{3}}{4}\)(भुजा)²
⇒ \(\frac{\sqrt{3}}{4}\)(भुजा)² = 17320.5
⇒ (भुजा)² = \(\frac{17320.5 \times 4}{1.73205}\)
⇒ (भुजा)² = \(\frac{173205}{10} \times \frac{100000 \times 4}{173205}\) = 40000
⇒ (भुजा) = \(\sqrt{4 \times 100 \times 100}\)
⇒ भुजा = 2 × 100 = 200 सेमी
∴ AB = BC = AC = 200 सेमी
वृत्त की त्रिज्या (R) = \(\frac{AB}{2}=\frac{200}{2}\) = 100 सेमी
त्रिज्यखण्ड का कोण (θ) = 60°

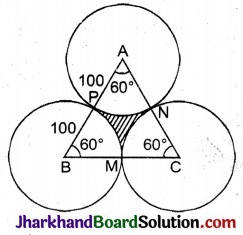
त्रिज्यखण्ड PAN का क्षेत्रफल =

∴ तीनों त्रिज्यखण्डों का क्षेत्रफल = 3 × 5233.33
= 15699.99 सेमी²
≅ 15700 सेमी²
∴ अभीष्ट छायांकित भाग का क्षेत्रफल = त्रिभुज का क्षेत्रफल – तीनों त्रिज्यखण्डों का क्षेत्रफल
= 17320.5 – 15700
= 1620.5 सेमी²
अतः छायांकित भाग का क्षेत्रफल = 1620.5 सेमी²

प्रश्न 11.
एक वर्गाकार रूमाल पर, नौ वृत्ताकार डिजाइन बने हैं, जिनमें से प्रत्येक की त्रिज्या 7 सेमी है (देखिए आकृति) । रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए ।

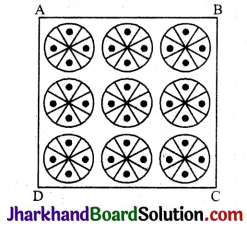
हल :
दिया है, प्रत्येक वृत्त की त्रिज्या (r) = 7 सेमी
∴ प्रत्येक वृत्त का क्षेत्रफल = πr² = \(\frac {22}{7}\) × 7 × 7
= 154 वर्ग सेमी
∴ नौ वृत्ताकार डिजाइनों का क्षेत्रफल = 9 × 154 = 1386 वर्ग सेमी
प्रत्येक वृत्त का व्यास = 2 × 7 = 14 सेमी
∵ प्रत्येक पंक्ति में 3 वृत्त हैं।
∴ वर्गाकार रूमाल की भुजा = 3 × वृत्त का व्यास = 3 × 14 = 42 सेमी
∴ रूमाल का कुल क्षेत्रफल = 42 × 42 वर्ग सेमी
= 1764 वर्ग सेमी
∴ रूमाल का शेष भाग = रूमाल का कुल क्षेत्रफल – डिजाइन का क्षेत्रफल
= 1764 – 1386
= 378 वर्ग सेमी
अतः रूमाल के शेष भाग का क्षेत्रफल = 378 वर्ग सेमी

प्रश्न 12.
आकृति में, OACB केन्द्र O और त्रिज्या 3.5 सेमी वाले एक वृत्त का चतुर्थाश है। यदि OD = 2 सेमी है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :
(i) चतुर्थांश OACB
(ii) छायांकित भाग ।

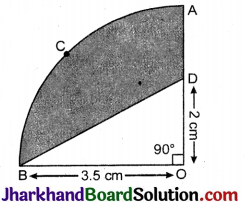
हल :
दिया है, वृत्त की त्रिज्या (r) = 3.5 सेमी
तथा OD = 2 सेमी
(i) चतुर्थांश OACB का क्षेत्रफल
= \(\frac {1}{4}\) × πr² = \(\frac{1}{4}=\frac{22}{7}\) × (3.5)²
= \(\frac{1}{4}=\frac{22}{7}\) × 3.5 × 3.5 = \(\frac {38.5}{4}\) वर्म सेमी
= \(\frac {77}{8}\)वर्ग सेमी = 9.625 वर्ग सेमी

(ii) छायांकित भाग का क्षेत्रफल = चतुर्थांश OACB का क्षेत्रफल – समकोण त्रिभुज OBD का क्षेत्रफल
= \(\frac{77}{8}-\frac{1}{2}\) × OB × OD
= \(\frac{77}{8}-\frac{1}{2}\) × त्रिभुज × 2
= \(\frac{77}{8}-\frac{1}{2}\) × 3.5 × 2
= \(\frac{77}{8}-\frac{7}{2}\)
= \(\frac{77-28}{8}\) = \(\frac {49}{8}\)वर्ग सेमी
= 6.125 वर्ग सेमी।
अतः छायांकित भाग का क्षेत्रफल
= 6.125 वर्ग सेमी

प्रश्न 13.
दी गई आकृति में, एक चतुर्थांश OPBQ के अन्तर्गत एक वर्ग OABC बना हुआ है। यदि OA = 20 सेमी है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

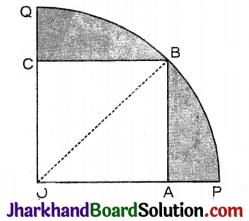
(π = 3.14 लीजिए)
हल :
दिया है, वर्ग OABC की भुजा OA = 20 सेमी
AB = OA
∴ समकोण ΔOAB में,
OB² = OA² + AB²
= (20)² + (20)²
= 400 + 400 = 800
⇒ OB = \(\sqrt{800}\)
∴ OB = 20\(\sqrt{2}\) सेमी
वर्ग OABC का क्षेत्रफल = (भुजा)²
= (20)² = 400 वर्ग सेमी
चतुर्थांश की त्रिज्या (r) = 20\(\sqrt{2}\) सेमी
चतुर्थांश का कोण θ = 90°

अभीष्ट छायांकित भाग का क्षेत्रफल
= त्रिज्यखण्ड का क्षेत्रफल – वर्ग का क्षेत्रफल
= 628 – 400
= 228 सेमी²
अतः छायांकित भाग का क्षेत्रफल = 228 सेमी²

प्रश्न 14.
AB और CD केन्द्र O तथा त्रिज्याओं 21 सेमी और 7 सेमी वाले दो संकेन्द्रीय वृत्तों के क्रमशः दो चाप हैं। (देखिए दी गई आकृति) यदि ∠AOB = 30° है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।

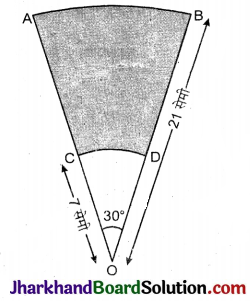
हल :
दिया है, AOB त्रिज्यखण्ड की त्रिज्या OB = 21 सेमी
तथा COD त्रिज्यखण्ड की त्रिज्या OC = 7 सेमी
और केन्द्र पर बना कोण = 30°

अतः छायांकित क्षेत्र का क्षेत्रफल = त्रिज्यखण्ड AOB का क्षेत्रफल – त्रिज्यखण्ड COD का क्षेत्रफल
= \(\frac{231}{2}=\frac{77}{6}\) = (\(\frac{693-77}{6}\))
= \(\frac{616}{6}=\frac{308}{3}\)सेमी²

प्रश्न 15.
दी गई आकृति में, ABC त्रिज्या 14 सेमी वाले एक वृत्त का चतुर्थांश है तथा BC को व्यास मानकर एक अर्धवृत्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

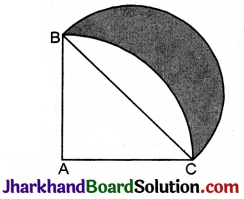
हल :
दिया है, चतुर्थांश ABC की त्रिज्या (r) = 14 सेमी
∴ चतुर्थांश ABC का क्षेत्रफल = \(\frac {1}{4}\) × πr²
= \(\frac{1}{4}=\frac{22}{7}\) × 14 × 14
= 154 वर्ग सेमी
समकोण ΔABC का क्षेत्रफल = \(\frac {1}{2}\) × AC × AB
[∵ AB = AC = r = 14]
= \(\frac {1}{2}\) × 14 × 14
= 98 वर्ग सेमी
समकोण ΔABC में,
⇒ BC² = AC² + AB²
⇒ BC² = 14² + 14²
⇒ BC² = 196 + 196
⇒ BC² = 392.
⇒ BC = \(\sqrt{392}\)
⇒ BC = 14\(\sqrt{2}\) सेमी
∴ अर्धवृत्त का व्यास BC = 14\(\sqrt{2}\) सेमी
अर्धवृत्त की त्रिज्या R = \(\frac{14 \sqrt{2}}{2}\) = 7\(\sqrt{2}\) सेमी
∴ अर्धवृत्त का क्षेत्रफल = \(\frac {1}{2}\)πR²
= \(\frac{1}{2}=\frac{22}{7}\) × 7\(\sqrt{2}\) × 7\(\sqrt{2}\)
= \(\frac{22 \times 14}{2}\)
= 154 वर्ग सेमी
∴ छायांकित भाग का क्षेत्रफल = अर्द्धवृत्त का क्षेत्रफल – [चतुर्थांश ABC का क्षेत्रफल – समकोण त्रिभुज का क्षेत्रफल ]
= [154 – (154 – 98)]
= [154 – 154 + 98] = 98 वर्ग सेमी
अतः छायांकित भाग का क्षेत्रफल = 98 वर्ग सेमी

प्रश्न 16.
दी गई आकृति में, छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 सेमी त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है।

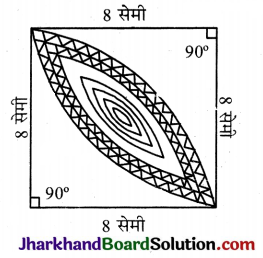
हल :
वर्ग की भुजा = 8 सेमी
वर्ग का क्षेत्रफल = (8)² = 64 वर्ग सेमी
विकर्ण BD वर्ग ABCD को दो बराबर भागों में बाँटती है

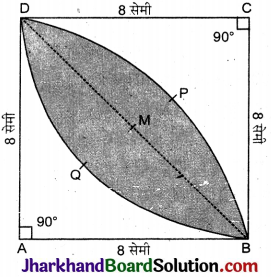
∴ ΔABD का क्षेत्रफल = ΔBDC का क्षेत्रफल त्रिज्यखण्ड का कोण (θ) = 90°
त्रिज्यखण्ड ABPD का क्षेत्रफल = πr² × \(\frac {θ}{360°}\)
= \(\frac {22}{7}\) × 8 × 8 × \(\frac {90°}{360°}\)
= \(\frac {22}{7}\) × 64 × \(\frac {1}{4}\) = \(\frac{22 \times 16}{7}\)
= \(\frac {352}{7}\)वर्ग सेमी
अब ΔABD का क्षेत्रफल = \(\frac {1}{2}\) × AB × AD
= \(\frac {1}{2}\) × 8 × 8
= 32 वर्ग सेमी
∴ वृत्तखण्ड का अर्द्ध छायांकित भाग (DMBPD) का क्षेत्रफल = त्रिज्यखण्ड ABPD का क्षेत्रफल – ΔABD का क्षेत्रफल
= \(\frac {352}{7}\) – 32 = \(\frac {128}{7}\)वर्ग सेमी
∴ छायांकित भाग का क्षेत्रफल
= 2 × वृत्तखण्ड DMBPD का क्षेत्रफल
= 2 × \(\frac{128}{7}=\frac{256}{7}\)वर्ग सेमी
अतः छायांकित भाग का क्षेत्रफल = \(\frac {256}{7}\) वर्ग सेमी।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 11 रचनाएँ Exercise 11.1

निम्नलिखित में से प्रत्येक के लिए रचना का औचित्य भी दीजिए :

प्रश्न 1.
7.6 सेमी लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए ।
हल :
दिया है : रेखाखण्ड AB = 7.6 सेमी ।
रचना के चरण :
1. एक रेखाखण्ड AB = 7.6 सेमी खींचा।
2. रेखाखण्ड AB के बिन्दु A से न्यूनकोण बनाती हुई किरण AX खींची।
3. किरण AX के परकार की सहायता से (5 + 8) = 13 समान भाग किये।

4. BA₁₃ को मिलाया।
5. बिन्दु A₅ से A₁₃B के समान्तर रेखा A₅P खींची जो AB को बिन्दु P पर प्रतिच्छेद करती है अर्थात् ∠BA₁₃A = ∠PA₅A बनाया।
तब AP : PB = 5 : 8
अत: रेखा AB के AP व PB अभीष्ट भाग हैं।
औचित्य (उपपत्ति) : ΔAA₅P तथा AA₁₃B में,
A₁₃B || A₅P
∴ आधारभूत समानुपातिकता प्रमेय से,

अत: बिन्दु P, AB को 5 : 8 के अनुपात में विभाजित करता है।
दोनों भागों को मापने पर,
AP = 2.9 सेमी
तथा PB = 4.7 सेमी।
वैकल्पिक विधि :
रचना 1. एक रेखाखण्ड AB = 7.6 सेमी खींचा।
2. AB के बिन्दु A से AB रेखाखण्ड के ऊपर की ओर न्यूनकोण बनाती हुई किरण AX खींची।
3. AB के बिन्दु B से AB रेखाखण्ड के नीचे की ओर उतना ही कोण (∠BAX) बनाती हुई BY किरण खींची।
4. किरण AX के बिन्दु 4 से समान लम्बाई के आठ बराबर भाग किए अर्थात् AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈ हों।

5. किरण BY के बिन्दु B से समान लम्बाई के आठ बराबर भाग किए अर्थात् BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈ हो।
6. A₅B₈ को मिलाया, जो AB को बिन्दु C पर काटता है, तब
AC : CB = 5 : 8.
औचित्य (उपपत्ति) : ΔACA₅ और Δ BCB₈ में,
∠ACA₅ = ∠BCB₈ [शीर्षाभिमुख कोण]
∠CAA₅ = ∠CBB₈ [रचना से]
∴ ΔACA₅ ~ ΔBCB₈ [AA समरूपता कसौटी]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

प्रश्न 2.
4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{2}{3}\) गुनी हों।
हल :
माना ΔABC है जिसमें AB = 5 सेमी, AC = 4 सेमी और BC = 6 सेमी ।

रचना के चरण :

1. एक रेखाखण्ड BC = 6 सेमी खींचा।
2. B को केन्द्र मानकर 5 सेमी की त्रिज्या से एक चाप लगाया।
3. C को केन्द्र मानकर 4 सेमी के बराबर त्रिज्या से चाप लगाइए जो पहले चाप को 4 बिन्दु पर काटता है।
4. AB और AC को मिलाइए। अतः ΔABC वांछित त्रिभुज है।
5. आधार BC के नीचे की ओर कोई न्यूनकोण बनाती BX किरण खींची।
6. BX किरण पर तीन बिन्दु इस प्रकार अंकित किए कि BB₁ = B₁B₂ = B₂B₃ हो ।
7. B₃C को मिलाया।
8. B₃C के समान्तर B₂C’ रेखा खींची जो BC को C’ पर काटती है।
9. बिन्दु C’ से CA के समान्तर C’A’ रेखा खींची अर्थात् ∠ACB = ∠A’C’B बनाया।

इस प्रकार ΔA’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{2}{3}\) गुनी हैं।
औचित्य (उपपत्ति) : अब ΔB₂BC’ और ΔB₃BC में,
∠B = ∠B [उभयनिष्ठ]
∠BB₂C’ = ∠BB₃C [रचना से]
∴ ΔB₂BC’ ~ ΔB₃BC [A-A समरूप कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एकसमान अनुपात में होंगी।

इसी प्रकार ΔA’BC’ और ΔABC में,
∠B = ∠B (उभयनिष्ठ)
∠A’C’B = ∠ACB (रचना से)
∴ ΔA’BC’ ~ ΔABC (A-A समरूपता कसौटी से)
∴ आधारभूत समानुपातिक प्रमेय से,
\(\frac{A’B}{AB}\) = \(\frac{BC’}{BC}\) = \(\frac{C’A’}{CA}\) = \(\frac{2}{3}\)
⇒ A’B = \(\frac{2}{3}\)AB
और BC’ = \(\frac{2}{3}\)BC
C’A’ = \(\frac{2}{3}\)CA.

प्रश्न 3.
5 सेमी, 6 सेमी और 7 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{7}{5}\) गुनी हों।
हल :
माना कि त्रिभुज ABC है जिसमें AB = 7 सेमी, BC = 6 सेमी और AC = 5 सेमी है।

रचना के चरण :

1. सर्वप्रथम AB रेखाखण्ड 7 सेमी खींचा।
2. रेखाखण्ड AB के बिन्दु से परकार में 5 सेमी का चाप लेकर एक चाप लगाया तथा बिन्दु B से 6 सेमी त्रिज्या का दूसरा चाप लगाया जो पहले वाले चाप को C बिन्दु पर काटता है।
3. AC व BC को मिलाया। इस प्रकार ΔABC प्राप्त हुआ।
4. आधार AB के नीचे की ओर कोई न्यूनकोण बनाती हुई AX किरण खींची।
5. किरण AX पर सात बिन्दु A₁, A₂, A₃, A₄, A₅, A₆, A₇ इस प्रकार अंकित किए कि
   AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇
6. BA₅ को मिलाया।
7. बिन्दु A₇ से A₅B के समान्तर एक रेखा A₇B’ खींची। माना कि यह AB को बढ़ाने पर B’ पर इस प्रकार मिलती है कि AB’ = \(\frac{7}{5}\)AB
8. बिन्दु B’ से BC के समान्तर एक रेखा B’C खींची जो AC को बढ़ाने पर C’ पर मिलती है।

ΔAB’C’ अभीष्ट त्रिभुज है।
औचित्य (उपपत्ति) : अब ΔAA₅B और ΔAA₇B’ में,
∠A = ∠A (उभयनिष्ठ)
∠AA₅B = ∠AA₇B’ (संगत कोण)
∴ ΔAA₅B ~ ΔAA₇B’ (A-A समरूपता कसौटी से)
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होती हैं।

पुन: ΔABC और ΔAB’C’ में,
∠A = ∠A (उभयनिष्ठ)
∠ABC = ∠AB’C’ (रचना से)
∴ ΔABC ~ ΔAB ‘C’ [A-A समरूपता कसौटी से]
समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं।

अत: ΔAB’C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{7}{5}\) गुनी हैं।

प्रश्न 4.
आधार 8 सेमी तथा ऊँचाई 4 सेमी के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 1\(\frac{1}{2}\) गुनी हों।
हल :
माना कि आधार AB = 8 सेमी और ऊँचाई 4 सेमी वाला एक समद्विबाहु ΔABC है।
रचना के चरण :
1. रेखाखण्ड AB = 8 सेमी खींचा।
2. रेखाखण्ड AB का लम्ब समद्विभाजक किया जो AB रेखाखण्ड को M बिन्दु पर काटता है।
3. बिन्दु M को केन्द्र मानकर लम्ब समद्विभाजक में से 4 सेमी काटा, जिस पर C बिन्दु अंकित किया।
4. AC, BC को मिलाकर त्रिभुज ABC प्राप्त किया।
5. बिन्दु A पर AB के नीचे की ओर न्यूनकोण बनाती हुई किरण AX खींची।

6. AX किरण पर तीन बिन्दु A₁, A₂, A₃ इस प्रकार अंकित किए कि AA₁ = AA₂ = AA₃ हो ।
7. बिन्दु A₂ और B को मिलाया।
8. बिन्दु A₃ से A₂B के समान्तर एक रेखा A₃B’ खींचते हैं जो कि AB को आगे बढ़ाने पर B’ पर काटती है।
9. B’ से BC के समान्तर एक रेखा B’C’ खींचते हैं जो AC को बढ़ ने पर C’ पर मिलती है।
अत: ΔAB’C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ मूल त्रिभुज की 1\(\frac{1}{2}\) गुनी हैं।
औचित्य (उपपत्ति) : ΔA₃AB’ और ΔA₂AB में,
∠A = ∠A (उभयनिष्ठ)
∠B’A₃A = ∠BA₂A (रचना से)
∴ ΔA₃AB’ ~ ΔA₂AB [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होती हैं।

प्रश्न 5.
एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60° हो । फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हों।
हल :

रचना के चरण :

1. रेखाखण्ड BC = 6 सेमी खींचा।
2. रेखाखण्ड BC के बिन्दु B पर 60° का कोण (∠CBX= 60°) बनाया।
3. बिन्दु B को केन्द्र मानकर और 5 सेमी त्रिज्या लेकर एक चाप खींचा जो BX को A पर प्रतिच्छेद करता है।
4. बिन्दु A और C को मिलाया रेखाखण्ड BC के बिन्दु B के नीचे की ओर न्यूनकोण बनाती हुई किरण BY खींची।
5. किरण BY पर चार बिन्दु B₁, B₂, B₃, B₄ इस प्रकार अंकित किए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हो। बिन्दु B₄ और C को मिलाया।
6. बिन्दु B₃ से B₄C के समान्तर एक रेखा B₃C’ खींची जो BC को C’ पर प्रतिच्छेद करती है।
7. बिन्दु C’ से CA के समान्तर एक रेखा C’A’ खींची जो BA को A’ पर प्रतिच्छेद करती है।

अतः ΔA’BC’ अभीष्ट त्रिभुज है जिसकी संगत भुजाएँ ΔABC की संगत भुजाओं के \(\frac{3}{4}\) गुनी हैं।
औचित्य (उपपत्ति) :
∵ ΔB₃BC’ और ΔB₄BC में,
∠B = ∠B [उभयनिष्ठ]
∠C’B₃B = ∠CB₄B [ संगत कोण]
ΔB₃BC’ ~ ΔB₄BC [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

इसी प्रकार ΔBC’A’ और ΔBCA समरूप होते हैं।
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।

अर्थात् ΔA’BC’ की भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हैं।

प्रश्न 6.
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी हैं।
हल :
दिया है : ΔABC जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हैं।
रचना के चरण :
1. सर्वप्रथम BC = 7 सेमी का रेखाखण्ड खींचा।
2. BC रेखाखण्ड के बिन्दु B पर 45° का कोण बनाती किरण BD खींची
3. ∵ ∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∴ ∠C = 180° – 150° = 30°

BC रेखाखण्ड के बिन्दु C पर 30° का कोण बनता है। तथा बिन्दु C से एक किरण खींची जो BD को A पर प्रतिच्छेद करती है। इस प्रकार ΔABC प्राप्त हुआ।
4. आधार BC के नीचे बिन्दु B पर कोई न्यूनकोण बनाती हुई किरण BX खींची।
5. BX रेखा पर चार बिन्दु B₁, B₂, B₃, B₄ इस प्रकार अंकित किए कि BB₁ = B₁B₁ = B₂B₃ = B₃B₄ हो ।
6. बिन्दु B₃ को C से मिलाया।
7. बिन्दु B₄ से B₃C के समान्तर एक रेखा B₄C’ खींची जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करती है।
8. बिन्दु C’ से CA के समान्तर एक रेखा C’A’ खींची जो BA को बढ़ाने पर A’ पर प्रतिच्छेद करती है।
अत: ΔA’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी हैं।
औचित्य (उपपत्ति) : ΔB₄BC’ तथा B₃BC में,
∠B = ∠B (उभयनिष्ठ)
∠C’B₄B = ∠CB₃B (रचना से)
∴ ΔB₄BC’ ~ ΔB₃BC [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होती हैं।

प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 सेमी तथा 3 सेमी लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{5}{3}\) गुनी हों।
हल :
दिया है : समकोण त्रिभुज जिसकी समकोण बनाने वाली भुजाएँ 3 सेमी व 4 सेमी हैं।
रचना के चरण :
1. सर्वप्रथम रेखाखण्ड BC = 4 सेमी खींचा।
2. BC के बिन्दु B से BC पर 90° का कोण बनाती हुई BY रेखा खींची और उसमें से BA = 3 सेमी काटी।
3. AC की मिलाया ।
इस प्रकार ΔABC प्राप्त होता है।
4. BC के बिन्दु B पर BC के नीचे की ओर न्यूनकोण बनाती हुई BX किरण खींची।
5. किरण BX पर पाँच बिन्दु B₁, B₂, B₃, B₄, B₅ इस प्रकार अंकित किए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हो।

6. बिन्दु B₃ और ‘C’ को मिलाया।
7. B₅ से B₃C के समान्तर एक रेखा B₅C’ खींची जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करे।
8. पुन: C’ से CA के समान्तर एक रेखा C’A’ खींची जो BY पर A’ पर मिलती है। ΔA’BC’ अभीष्ट त्रिभुज है। जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{5}{3}\) गुनी हैं।
औचित्य (उपपत्ति): ΔB₅C’B तथा ΔB₃CB में,
∠B = ∠B (उभयनिष्ठ)
∠C’B₅B = ∠CB₃B ( रचना से)
∴ ΔB₅C’B ~ ΔB₃CB, [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 10 वृत्त Ex 10.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 10 वृत्त Exercise 10.2

प्रश्न सं. 1, 2, 3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।

प्रश्न 1.
एक बिन्दु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 सेमी तथा 2 की केन्द्र से दूरी 25 सेमी है। वृत्त की त्रिज्या है :
(A) 7 सेमी
(B) 12 सेमी
(C) 15 सेमी
(D) 24.5 सेमी
हल:
एक वृत्त जिसका केन्द्र O है। बाह्य बिन्दु Q से स्पर्श रेखा PQ की लम्बाई 24 सेमी तथा Q की केन्द्र O से दूरी 25 सेमी है।
∴ ∠QPO = 90° [प्रमेय 10.1 से]

समकोण ΔQPO में,
OQ² = PQ² + OP²
⇒ (25)² = (24)² + OP²
⇒ OP² = (25)² – (24)²
⇒ OP² = 625 – 576
⇒ OP² = 49
⇒ OP = \(\sqrt{49}\)
∴ OP = 7 सेमी
अतः सही विकल्प (A) है।

प्रश्न 2.
चित्र में, यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110, तो ∠PTQ बराबर है:

(A) 60°
(B) 70°
(C) 80°
(D) 90°
हल:
हम जानते हैं कि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्बवत् होती है।
∴ ∠OPT = 90°
तथा ∠OQT = 90°
अब चतुर्भुज POQT में,
∠POQ + ∠OQT + ∠PTQ + ∠TPO = 360°
⇒ 110° + 90° + ZPTO + 90° = 360°
⇒ ∠PTQ = 360° – 290°
∴ ∠PTQ = 70°
अतः सही विकल्प (B) है।

प्रश्न 3.
यदि एक बिन्दु से 0 केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ∠POA है:
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हल:
वृत्त का केन्द्र O है और बिन्दु P से PA व PB वृत्त पर स्पर्श रेखाएँ हैं जिनके बीच ∠APB = 80° है।

OA तथा OB वृत्त की त्रिज्याएँ हैं।
चूँकि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∠A = 90° और ∠B = 90°
∴ ∠AOB व ∠APB सम्पूरक हैं।
∠AOB + ∠APB = 180°
⇒ ∠AOB = 180° – ∠APB
⇒ ∠AOB = 180° – 80°
∴ ∠AOB = 100°
हम जानते हैं कि OP रेखा, ∠AOB को समद्विभाजित करती है।
∠POA = \(\frac{1}{2}\)∠AOB
= \(\frac{1}{2}\) × 100° = 50°
∠POA = 50°
अतः सही विकल्प (A) है।

प्रश्न 4.
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
हल:
दिया है एक वृत्त जिसका केन्द्र O तथा व्यास AB हैं। PQ और RS बिन्दु A व B पर स्पर्श रेखाएँ हैं।

सिद्ध करना है: PQ || RS
उपपत्ति: ∵ OA त्रिज्या है और PQ स्पर्श रेखा, OA त्रिज्या पर लम्ब है।
[प्रमेय 10.1 से ]
∴ ∠1 = 90°
इसी प्रकार,
RS ⊥ OB
∴ ∠2 = 90°
अब ∴ ∠1 = ∠2
परन्तु यह दो समान्तर रेखाओं के एकान्तर कोण हैं, जब एक तिर्यक रेखा उन्हें काटती है।
∴ PQ || RS
अतः किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर समान्तर होती हैं।

प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
हल:
दिया है: एक वृत्त जिसका केन्द्र O है। AB इसकी स्पर्श रेखा है जो वृत्त को P पर स्पर्श करती है।
सिद्ध करना है: लम्ब PQ वृत्त के केन्द्र O से जाता है।
उपपत्ति: यदि सम्भव हो, तो माना PQ, AB के लम्बवत् है, जो O से नहीं गुजरती है।
OP को मिलाया।

∵ वृत्त के बिन्दु पर स्पर्श रेखा, स्पर्श बिन्दु पर त्रिज्या के लम्बवत् होती है, इसलिए
AB ⊥ OP अर्थात् ∠OPB = 90°
तथा ∠QPB = 90° (रचना से)
∴ ∠QPB = ∠OPB, जो सम्भव नहीं है क्योंकि रेखाखण्ड OP रेखा PQ के बराबर नहीं हो सकता है।
यह हमारी कल्पना के विपरीत है।
अतः स्पर्श रेखा AB के स्पर्श बिन्दु P पर खींचा गया लम्ब PQ, वृत्त के केन्द्र से होकर जाता है।

प्रश्न 6.
एक बिन्दु A से, जो एक वृत्त के केन्द्र से 5 सेमी दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई 4 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
एक वृत्त जिसका केन्द्र ‘O’ है। वृत्त के बाहर इसके केन्द्र से 5 सेमी की दूरी पर कोई बिन्दु A है।
स्पर्श रेखा की लम्बाई = PA = 4 सेमी
∵ हम जानते हैं कि वृत्त पर स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∴ ∠OPA = 90°

समकोण ΔOPA में, पाइथागोरस प्रमेय से,
OA² = OP² + PA²
(5)² = OP² + (4)²
⇒ OP² = 25 – 16
⇒ OP² = 9
⇒ OP = \(\sqrt{9}\) ⇒ OP = 3 सेमी
अतः वृत्त की त्रिज्या 3 सेमी है।

प्रश्न 7.
दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 सेमी तथा 3 सेमी हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल:
माना O केन्द्र वाले दो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ OA तथा OP क्रमश: 5 सेमी व 3 सेमी हैं।
बड़े वृत्त की एक जीवा AB है जो छोटे वृत्त को बिन्दु P पर स्पर्श करती है।
∠OP ⊥ AB (प्रमेय 10.1 से)
∠OPA = 90°

∴ समकोण ΔOPA में, पाइथागोरस प्रमेय से,
AP² + OP² = OA²
⇒ AP² + (3)² = (5)²
⇒ AP² = (5)² – (3)²
= 25 – 9 = 16
∴ AP = 4 सेमी
परन्तु बड़े वृत्त में, जीवा AB पर केन्द्र O से OP लम्ब है।
∴ बिन्दु P, जीवा AB को समद्विभाजित करता है।
AP = BP = 4 सेमी
जीवा AB की लम्बाई = AP + BP
= 4 + 4
= 8 सेमी
अतः बड़े वृत्त की जीवा की लम्बाई 8 सेमी।

प्रश्न 8.
एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है। सिद्ध कीजिए:
AB + CD = AD + BC
हल:
दिया है: O केन्द्र वाले वृत्त के परिगत एक चतुर्भुज ABCD जिसकी भुजाएँ AB, BC, CD तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R और S पर स्पर्श करती हैं।

सिद्ध करना है: AB + CD = AD + BC
उपपत्ति: हम जानते हैं कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई बराबर होती है।
अब B, वृत्त के बाहर स्थित कोई बिन्दु है और BP, BQ वृत्त पर स्पर्श रेखाएँ हैं।
∴ BP = BQ …..(1)
इसी प्रकार, AP = AS …..(2)
और DR = DS …..(3)
और CR = CQ …..(4)
समीकरण (1), (2), (3) व (4) को जोड़ने पर,
BP + AP + DR+ CR = BQ + AS + DS + CQ
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC

प्रश्न 9.
आकृति में, XY तथा XY’ 0 केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A पर तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB = 90° है।

हल:
दिया है: XY तथा X’Y’, O केन्द्र वाले वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर एक अन्य स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है। OA तथा OB को मिलाया।

सिद्ध करना है: ∠AOB = 90°
रचना: OC मिलाया।
उपपत्ति: XY और X’Y’ वृत्त की दो स्पर्श रेखाएँ हैं, जो वृत्त को P और Q पर स्पर्श करती हैं। बिन्दु C से वृत्त की स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर काटती है।
∴ बिन्दु A से वृत्त पर AP व AC स्पर्श रेखाएँ हैं।
∴ AP = AC
ΔOPA तथा ΔOCA में,
OP = OC (वृत्त की त्रिज्याएँ)
AP = AC (बाह्य बिन्दु से वृत्त की स्पर्श रेखाएँ)
OA = OA (उभयनिष्ठ भुजा)
∴ ΔOPA ≅ ΔOCA (SSS सर्वांगसमता गुणधर्म से )
सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं।
∠POA = ∠AOC …..(1)
इसी प्रकार बिन्दु B से वृत्त पर BQ और BC स्पर्श रेखाएँ हैं।
अतः BQ = BC
ΔOQB तथा ΔOBC में,
OQ = OC (वृत्त की त्रिज्याएँ)
BQ = BC (बिन्दु B से वृत्त पर स्पर्श रेखाएँ)
OB = OB (उभयनिष्ठ भुजा)
∴ ΔOQB ≅ ΔOCB
⇒ ∠BOQ = ∠COB …..(2)
∵ ∠POA + ∠AOC + ∠COB + ∠BOQ = 180°
समीकरण (1) व (2) से,
⇒ ∠AOC + ∠AOC + ∠COB + ∠COB = 180°
⇒ 2(∠AOC + ∠COB) = 180°
⇒ ∠AOC + ∠COB = \(\frac{180^{\circ}}{2}\) = 90°
∴ ∠AOB = 90°

प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है।
हल:
दिया है: एक वृत्त जिसका केन्द्र O है। वृत्त के बाहर स्थित किसी बिन्दु P से PQ और PR दिए गए वृत्त पर स्पर्श रेखाएँ हैं।

सिद्ध करना है: ∠ROQ + ∠QPR = 180°
उपपत्ति : OQ त्रिज्या है तथा बिन्दु P से PQ स्पर्श रेखा है जो वृत्त को बिन्दु Q पर स्पर्श करती है।
∠OQP = 90°
[∵ स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है]
इसी प्रकार, ∠ORP = 90°
अब चतुर्भुज ROQP में,
∠ROQ + ∠PRO + ∠OQP + ∠QPR = 360°
⇒ ∠ROQ + 90° + 90° + ∠QPR = 360°
⇒ ∠ROQ + ∠QPR = 360° – 180°
⇒ ∠ROQ + ∠QPR = 180°
अत: ∠QPR, ∠ROQ का सम्पूरक है।

प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है।
हल:
दिया है: केन्द्र O वाले वृत्त के परिगत एक समान्तर चतुर्भुज ABCD खींचा जिसकी भुजाएँ वृत्त को क्रमश: E, F, G, H बिन्दुओं पर स्पर्श करती हैं।

सिद्ध करना है: ABCD एक समचतुर्भुज है।
उपपत्ति: ∵ बाहरी बिन्दु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लम्बाई समान होती है।
अब वृत्त के बाहर स्थित बिन्दु B से BE और BF वृत्त पर दो स्पर्श रेखाएँ हैं।
∴ BE = BF …..(1)
इसी प्रकार, AE = AH …..(2)
CG = CF …..(3)
तथा DG = DH …..(4)
समीकरण (1), (2), (3) व (4) को जोड़ने पर,
(BE + AE) + (CG + DG) = (BF + CF) + (AH+DH)
⇒ AB + CD = BC + AD …..(5)
∵ दिया है, ABCD एक समान्तर चतुर्भुज है।
∴ AB = CD
और BC = AD …..(6)
समान्तर चतुर्भुज की सम्मुख भुजाएँ
समीकरण (5) व (6) से,
AB + AB = BC + BC
⇒ 2AB = 2BC
⇒ AB = BC
∴ AB = BC = CD = AD
अत: ABCD एक समचतुर्भुज है।

प्रश्न 12.
4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाइयाँ क्रमशः 8 सेमी और 6 सेमी हैं। भुजाएँ AB और AC ज्ञात कीजिए।

हल:
4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक ΔABC खींचा गया है। त्रिभुज की भुजाएँ BC, CA, AB वृत्त को क्रमश: D, E F बिन्दुओं पर स्पर्श करती हैं।
∵ किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई समान होती है।
∴ AE = AF = x सेमी (माना)
CE = CD = 6 सेमी
और BF = BD = 8 सेमी
OF, OE, OA, OB तथा OC को मिलाया।

हम जानते हैं कि वृत्त की स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∴ OD ⊥ BC, OE ⊥ AC और OF ⊥ AB
ΔABC में, b = AC = (x + 6) सेमी
a = CB
= (6 + 8) सेमी = 14 सेमी
c = BA(8 + x) सेमी

ΔOBC का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × 14 × 4
= 28 सेमी² …..(2)
ΔBOA का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × (8 + x) × 4
= ( 16 + 2x ) सेमी² …..(3)
ΔAOC का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × (6 + x) × 4
= (12 + 2x) सोमी² …(4)
ΔABC का क्षेत्रफल = ΔOBC का क्षेत्रफल + ΔBOA का क्षेत्रफल + ΔAOC का क्षेत्रफल
\(\sqrt{48 x^2+672 x}\) = 28 + 16 + 2x + 12 + 2x
⇒ \(\sqrt{48 x^2+672 x}\) = 4x + 56
⇒ \(\sqrt{48 x^2+672 x}\) = 4(x + 14)
दोनों पक्षों का वर्ग करने पर
48x² + 672x = 16(x + 14)²
⇒ 48x(x + 14 ) = 16(x + 14)²
⇒ 3x = x + 14
⇒ 2x = 14
⇒ x = \(\frac{14}{2}\) = 7
∴ AC = (x + 6) सेमी
= (7 + 6) = 13 सेमी
और AB = (x + 8 ) सेमी
= (7 + 8) = 15 सेमी
अतः AB = 15 सेमी
और AC = 13 सेमी।

प्रश्न 13.
सिद्ध कीजिए कि वृत्त के परिगत बने चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
हल:
दिया है: केन्द्र O वाले वृत्त के परिगत बना चतुर्भुज PQRS जिसकी भुजाएँ PQ, QR, RS और SP वृत्त को क्रमश: L, M, N, T बिन्दुओं पर स्पर्श करती हैं।

सिद्ध करना है: ∠POQ + ∠SOR = 180°
और ∠SOP + ∠ROQ = 180°
रचना: वृत्त के केन्द्र O से P, Q, R, S, L, M, N तथा T को मिलाया।
उपपत्ति: OL, OM, ON तथा OT वृत्त की त्रिज्याएँ हैं तथा QL, MQ, RN तथा ST वृत्त पर स्पर्श रेखाएँ हैं।
QL ⊥ OL, QM ⊥ OM, RN ⊥ ON तथा ST ⊥ OT (प्रमेय 10.1 से)।
अब समकोण ΔOMQ तथा समकोण ΔOLQ में
∠OMQ = ∠OLQ (प्रत्येक 90° है)
कर्ण OQ = कर्ण OQ (उभयनिष्ठ भुजा)
तथा OM = OL (वृत्त की समान त्रिज्याएँ)
∴ ΔΟΜQ ≅ ΔΟLQ (RHS सर्वागसमता गुणधर्म से)
⇒ ∠3 = ∠2 (CPCT)
इसी प्रकार, ∠4 = ∠5
∠6 = ∠7 तथा ∠8 = ∠1
∵ वृत्त के केन्द्र बिन्दु पर बने सभी कोणों का योग 360° होता है।
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
⇒ ∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
⇒ 2(∠1 + ∠2 + ∠5 + ∠6) = 360°
⇒ (∠1 + ∠2) + (∠5 + ∠6) = 180°
∠POQ + ∠SOR = 180°
[∵ ∠1 + ∠2 = ∠POQ तथा ∠5 + ∠6 = ∠SOR]
इसी प्रकार ∠SOP + ∠ROQ = 180°
अतः वृत्त के परिगत बने चतुर्भुज के आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.1

प्रश्न 1.
दो घनों, जिनमें से प्रत्येक का आयतन 64 सेमी³ है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :

माना कि घन की प्रत्येक भुजा = x सेमी
घन का आयतन = 64 सेमी³ (दिया है)
हम जानते हैं,
घन का आयतन = (भुजा)³
⇒ 64 = (x)³
⇒ x = \(\sqrt[3]{64}\)
∴ x = 4 सेमी
∴ घन की भुजा = 4 सेमी
∵ जब दोनों घनों को साथ-साथ जोड़ा जाता है, तो घनाभ बन जाता है।
जिसकी लम्बाई (l) = 2x = 2 × 4 = 8 सेमी
चौड़ाई (b) = x = 4 सेमी
ऊँचाई (h) = x = 4 सेमी

∴ घनाभ का पृष्ठीय क्षेत्रफल = 2 × (lb + bh + hl)
= 2 × (8 × 4 + 4 × 4 + 4 × 8)
= 2 × (32 + 16 + 32)
= 2 × 80
= 160 वर्ग सेमी
अतः नये घनाभ का पृष्ठीय क्षेत्रफल
= 160 वर्ग सेमी

प्रश्न 2.
कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन ध्यारोपित है। अर्द्धगोले का व्यास 14 सेमी है और इस बर्तन (पात्र) की कुल चाई 13 सेमी है। इस बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल :
दिया है,
अर्द्धगोले तथा बेलन की उभयनिष्ठ त्रिज्या (r) = \(\frac {14}{2}\) = 7 सेमी
∴ अर्द्धगोले की त्रिज्या (r) = 7 सेमी
बेलन की त्रिज्या (r) = 7 सेमी
∵ बर्तन की कुल ऊँचाई = 13 सेमी
∴ बेलन की ऊँचाई (h) = (13 – 7) = 6 सेमी
बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल
= बेलन का आन्तरिक पृष्ठीय क्षेत्रफल + अर्द्धगोले का आन्तरिक पृष्ठीय क्षेत्रफल
= 2πrh + 2πr² = 2πr (h + r)
= 2 × \(\frac {22}{7}\) × 7× (6 + 7)
= 44 × 13 = 572 वर्ग सेमी
अतः बर्तन (पात्र) का कुल आन्तरिक पृष्ठीय क्षेत्रफल = 572 वर्ग सेमी।

प्रश्न 3.
एक खिलौना त्रिज्या 3.5 सेमी वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊंचाई 15.5 सेमी है। इस खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल :
दिया है,
शंकु की त्रिज्या (r) = अर्द्धगोले की त्रिज्या (r)
= 3.5 सेमी
तथा खिलौने की ऊँचाई = 15.5 सेमी
∴ शंकु की ऊँचाई (h) = (15.5 – 3.5) सेमी = 12 सेमी
शंकु की तिर्यक ऊँचाई (l) = \(\sqrt{(3 \cdot 5)^2+(12)^2}\)
= \(\sqrt{(3 \cdot 5)^2+(12)^2}\)
= \(\sqrt{(3 \cdot 5)^2+(12)^2}\)
= \(\sqrt{12 \cdot 25+144}\)
= \(\sqrt{156.25}\)
∴ l = 12.5 सेमी
बर्तन का कुल पृष्ठीय क्षेत्रफल = शंकु का पृष्ठीय क्षेत्रफल + अर्द्धगोले का पृष्ठीय क्षेत्रफल
= πrl + 2πr²
= πr (l + 2r)
= \(\frac {22}{7}\) × 3.5 × (12.5 + 2 × 3.5)
= 22 × 0.5 × (12.5 + 7)
= 11 × 19.5
= 214.5 सेमी²
अतः बर्तन का कुल पृष्ठीय क्षेत्रफल
= 214.5 वर्ग सेमी

प्रश्न 4.
भुजा 7 सेमी वाले एक घनाकार ब्लॉक के ऊपर एक अर्द्धगोला रखा हुआ है। अर्द्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल
दिया है,
∵ अर्द्धगोले का आधार घन के ऊपरी फलक पर टिका है ।

∴ अर्द्धगोले का अधिकतम व्यास = घन की भुजा 7 सेमी (दिया है)
∴ अर्द्धगोले की त्रिज्या (r) = \(\frac {7}{2}\)सेमी
ठोस का पृष्ठीय क्षेत्रफल
= घन का सम्पूर्ण पृष्ठीय क्षेत्रफल + अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल – वृत्तीय आधार का क्षेत्रफल
= 6 × (भुजा)² + 2πr² – πr²
= 6 × (भुजा)² + πr²
= 6 × (7)² + \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)
= 6 × 49 + \(\frac {77}{2}\)
= 294 + 38.5 = 332.5 वर्ग सेमी
अतः अर्द्धगोले का अधिकतम व्यास = 7 सेमी
तथा ठोस का पृष्ठीय क्षेत्रफल = 332.5 वर्ग सेमी।

प्रश्न 5.
एक घनाकार ब्लॉक के एक फलक को अन्दर की ओर से काटकर एक अर्द्धगोलाकार गड्डा इस प्रकार बनाया गया है कि अर्द्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
माना कि घन की भुजा = a

∴ अर्द्धगोले का व्यास = घन की भुजा
⇒ 2r = a
⇒ r = \(\frac {a}{2}\)
अर्द्धगोले की त्रिज्या (r) = \(\frac {a}{2}\)
शेष बचे ठोस का पृष्ठीय क्षेत्रफल = घन का कुल पृष्ठीय क्षेत्रफल – घन के तल का क्षेत्रफल + अर्द्धगोले का आन्तरिक वक्र पृष्ठीय क्षेत्रफल
= 6a² – πr² + 2πr²
= 6a² + πr²
= 6a² + π(\(\frac {a}{2}\))²
= 6a² + π\(\frac{a^2}{4}\)
= a²[6 + \(\frac {π}{4}\)]सेमी²
= \(\frac{a^2}{4}\)(24 + π)सेमी²
अतः शेष बचे ठोस का पृष्ठीय क्षेत्रफल
= \(\frac{a^2}{4}\)(24 + π) वर्ग सेमी

प्रश्न 6.
दवा का एक कैप्सूल (capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्द्धगोला लगा हुआ है (देखिए आकृति)। पूरे कैप्सूल की लम्बाई 14 मिमी है और उसका व्यास 5 मिमी है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल :
दिया है,
कैप्सूल का व्यास = 5 मिमी
∴ बेलनाकार भाग तथा अर्ध गोले की उभयनिष्ठ त्रिज्या(r) = \(\frac {5}{2}\) मिमी

कैप्सूल की आन्तरिक लम्बाई (h) = 14 मिमी
बेलनाकार भाग की लम्बाई = [14 – \(\frac {5}{2}\) – \(\frac {5}{2}\)] मिमी
= (14 – 5) मिमी = 9 मिमी
कैप्सूल का पृष्ठीय क्षेत्रफल = बेलन का पृष्ठीय क्षेत्रफल + 2 अर्द्धगोलों का पृष्ठीय क्षेत्रफल
= 2πrh + 2 × (2πr²)
= 2πrh + 4πr² = 2πr (h + 2r)
= 2 × \(\frac{22}{7} \times \frac{5}{2}\) × (9 + 2 × \(\frac {5}{2}\))
= \(\frac {110}{7}\) × (9 + 5) = \(\frac{110 \times 14}{7}\) = 220 मिमी²
अतः कैप्सूल का पृष्ठीय क्षेत्रफल = 220 वर्ग मिमी

प्रश्न 7.
कोई तम्बू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमशः 2.1 मीटर और 4 मीटर हैं तथा शंकु की तिर्यक ऊँचाई 2.8 मीटर है तो इस तम्बू को बनाने में प्रयुक्त कैनवास (canvas) का क्षेत्रफल ज्ञात कीजिए। साथ ही, ₹500 प्रति वर्ग मीटर की दर से इसमें प्रयुक्त कैनवास की लागत ज्ञात कीजिए। (ध्यान दीजिए कि तम्बू के आधार को कैनवास से नहीं ढका जाता है।)

हल :
दिया है,
बेलन का व्यास = शंकु का व्यास = 4 मी.
∴ बेलन और शंकु की उभयनिष्ठ त्रिज्या (r) = \(\frac {4}{2}\)
= 2 मीटर
शंकु की त्रिज्या = बेलन की त्रिज्या = r = 2सेमी
बेलन की ऊँचाई (h) = 2.1 मीटर
तथा शंकु की तिर्यक ऊँचाई (l) = 2.8 मीटर
तम्बू का वक्र पृष्ठीय क्षेत्रफल = बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल + शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
= 2πrh + πrl = πr (2h + l)
= \(\frac {22}{7}\) × 2 × (2 × 2.1 + 2.8)
= \(\frac {22}{7}\) × (4.2 + 2.8)
= \(\frac {22}{7}\) × 7 = 44 मीटर²
∴ तम्बू का वक्र पृष्ठीय क्षेत्रफल = 44 मीटर²
∵ 1 मीटर² कैनवास की लागत = ₹ 500
∴ 44 मीटर² कैनवास की लागत = 44 × 500 = ₹ 22000
अतः कैनवास की कुल लागत = ₹ 22000

प्रश्न 8.
ऊँचाई 2.4 सेमी और व्यास 1.4 सेमी वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेण्टीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
दिया है,
बेलन का व्यास = 1.4 सेमी
∴ बेलन तथा शंकु की उभयनिष्ठ त्रिज्या (r) = \(\frac {1.4}{2}\) = 0.7 सेमी

बेलन की ऊँचाई (h) = 2.4 सेमी
शंक्वाकार खोल की तिर्यक ऊँचाई (l) = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(0 \cdot 7)^2+(2 \cdot 4)^2}\)
= \(\sqrt{0.49+5 \cdot 76}\)
= \(\sqrt{6.25}\)
l = 2.5 सेमी
शेष बचे ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + बेलन के आधार का क्षेत्रफल + शंक्वाकार का वक्र पृष्ठीय क्षेत्रफल
= 2πrh + πr² + πrl = πr(2h + r + l)
= \(\frac {22}{7}\) × 0.7 × [2 × 2.4 + 0.7 + 2.5]
= 2.2 × [4.8 + 0.7 + 2.5]
= 2.2 × 8 = 17.6 ≈ 8 वर्ग सेमी
अतः शेष बचे ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = 18 वर्ग सेमी

प्रश्न 9.
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्द्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा कि आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 सेमी है और आधार की त्रिज्या 3.5 सेमी है, तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल :
दिया है,
बेलन की त्रिज्या (r) = 3.5 सेमी
अर्द्धगोले की त्रिज्या (r) = 3.5 सेमी
तथा बेलन की ऊँचाई (h) = 10 सेमी
वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + दोनों अर्द्धगोलों का पृष्ठीय क्षेत्रफल
= 2πrh + 2 × 2πr²
= 2πrh + 4πr² = 2πr (h + 2r)
= 2 × \(\frac {22}{7}\) × 3.5 × (10 + 2 × 3.5)
= 2 × 22 × 0.5 × (10 + 7)
= 22 × 17 = 374 वर्ग सेमी
अतः वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल = 374 वर्ग सेमी

Jharkhand Board JAC Class 10 Maths Solutions Chapter 14 सांख्यिकी Ex 14.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 14 सांख्यिकी Exercise 14.4

प्रश्न 1.
निम्नलिखित बंटन किसी फैक्टरी के 50 श्रमिकों की दैनिक आय दर्शाता है

उपरोक्त बंटन को एक ‘से कम प्रकार’ के संचयी बारम्बारता बंटन में बदलिए और उसका तोरण खींचिए ।
हल :
‘से कम’ प्रकार का संचयी बारम्बारता बंटन

(i) अब बिन्दुओं A(120, 12), B (140, 26), C (160, 34 ) D ( 180, 40) और E(200, 50) को ग्राफ पेपर पर अंकित करते हैं।
(ii) अंकित बिन्दुओं को वक्र के रूप में हाथ से जोड़कर तोरण प्राप्त करते हैं।

अत: ABCDE अभीष्ट तोरण है।

प्रश्न 2.
किसी कक्षा के 35 विद्यार्थियों की मेडिकल जाँच के समय, उनके भार निम्नलिखित रूप में रिकॉर्ड किए गए –

भार (किग्रा में)	विद्यार्थियों की संख्या
38 से कम 40 से कम 42 से कम 44 से कम 46 से कम 48 से कम 50 से कम 52 से कम	0 3 5 9 14 28 32 35

उपरोक्त आँकड़ों के लिए ‘से कम’ प्रकार का तोरण खींचिए। इसके बाद माध्यक भार ज्ञात कीजिए।
हल :
‘से कम’ प्रकार का बंटन

भार (किग्रा में)	संचयी बारम्बारता	तोरण पर स्थित बिन्दु
38 से कम 40 से कम 42 से कम 44 से कम 46 से कम 48 से कम 50 से कम 52 से कम	0 3 5 9 14 28 32 35	A(38, 0) B(40, 3) C(42, 5) D(44, 9) E(46, 14) F(48, 28) G(50, 32) H (52, 35)

अब बिन्दुओं A(38, 0), B(40, 3), C(42, 5), D(44, 9), E (46, 14), F(48, 28), G(50, 32) तथा H (52, 35) को ग्राफ पेपर अंकित करते हैं। इन बिन्दुओं को वक्र के रूप में हाथ से जोड़कर तोरण प्राप्त करते हैं।

अत: ABCDEFGH अभीष्ट तोरण है।

माध्यक ज्ञात करना. :

∵ \(\frac{\Sigma f}{2}=\frac{N}{2}=\frac{35}{2}\) = 17.5
(i) Y-अक्ष पर 17.5 पर एक बिन्दु अंकित किया।
(ii) इस बिन्दु से X- अक्ष के समान्तर रेखा खींची जो वक्र को बिन्दु P पर काटती है।
(iii) बिन्दु P का भुज ज्ञात किया जो कि 46.8 है।
अतः अभीष्ट माध्यक 46.8 किग्रा है।

प्रश्न 3.
निम्नलिखित सारणी किसी गाँव के 100 फार्मों में किग्रा प्रति हेक्टेअर गेहूँ का उत्पादन दर्शाती है :

इस बंटन को ‘से अधिक प्रकार के बंटन में बदलिए और फिर उसका तोरण खींचिए ।
हल :
दिए गए बंटन को ‘से अधिक’ प्रकार के बंटन में बदलना

(i) अब बिन्दुओं A(50, 100); B(55, 98); C (60, 90); D(65, 78); E (70, 54) और F(75, 16) को ग्राफ पेपर पर अंकित करते हैं।
(ii) इन बिन्दुओं को वक्र के रूप में हाथ से जोड़कर तोरण प्राप्त करते हैं।

अत: ABCDEF अभीष्ट तोरण है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Exercise 8.3

प्रश्न 1.
निम्नलिखित के मान निकालिए :
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\)
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59°
हल:
(i) sin 18° = sin (90° – 72°)
= cos 72°
[∵ sin (90° – θ) = cos θ]
∴ \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}=\frac{\cos 72^{\circ}}{\cos 72^{\circ}}=1\)

(ii) tan 26° = tan (90° – 64°)
= cot 64°
[∵ tan (90° – θ) = cot θ]
∴ \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}=\frac{\cot 64^{\circ}}{\cot 64^{\circ}}=1\)

(iii) cos 48° – sin 42°
= cos (90° – 42°) – sin 42°
= sin 42°- sin 42°
[∵ cos (90° – θ) = sin θ]
= 0

(iv) cosec 31° – sec 59°
= cosec (90° – 59°) – sec 59°
= sec 59° – sec 59°
= 0
[∵ cosec (90° – θ) = sec θ]

प्रश्न 2.
दिखाइए कि:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
हल:
(i) L.H.S. = tan 48° tan 23° tan 42° tan 67°
= tan 48° tan 23° tan (90° – 48°) tan (90° – 23°)
= tan 48° tan 23° cot 48° cot 23° [∵ tan (90° – θ) = cot θ)
= tan 48° tan 23° × \(\frac{1}{\tan 48^{\circ}} \times \frac{1}{\tan 23^{\circ}}\)
= 1 = R.H.S.
L.H.S. = R.H.S.

(ii) L.H.S.= cos 38° cos 52° – sin 38° sin 52°
= cos (90° – 52°) cos (90° – 38°) – sin 38° sin 52°
= sin 52°.sin 38° – sin 38°.sin 52°
= 0 = R.H.S.
L.H.S. = R.H.S.

प्रश्न 3.
यदि tan 2A = cot (A – 18°), जहाँ 2A एक न्यूनकोण है, तो A का मान ज्ञात कीजिए।
हल:
दिया है : tan 2A = cot (A – 18°)
A का मान ज्ञात करने के लिए हमें दोनों ओर या तो cot θ या tan θ चाहिए।
[∵ cot (90° – θ) = tan θ]
cot (90° – 2A) = cot (A – 18°)
90° – 2A = A – 18°
3A = 108°
∴ A = 36°

प्रश्न 4.
यदि tan A = cot B, तो सिद्ध कीजिए कि A + B = 90°
हल:
∵ tan A = cot B
⇒ tan A = tan (90° – B)
[∵ cot θ = tan (90° – θ)]
⇒ A = 90° – B
∴ A + B = 90°
अत: tan A = cot B होने पर A + B = 90° होगा।

प्रश्न 5.
यदि sec 4A = cosec (A – 20°), जहाँ 4A एक न्यूनकोण है, तो A का मान ज्ञात कीजिए।
हल:
दिया है, sec 4A = cosec (A – 20°)
A का मान ज्ञात करने के लिए हमें दोनों ओर sec θ या cosec θ चाहिए।
⇒ cosec (90° – 4A) = cosec (A – 20°)
[∵ cosec (90° – θ) = sec θ]
90° – 4A = A – 20°
5A = 110°
A = 22°

प्रश्न 6.
यदि A, B और C त्रिभुज ABC के अन्तःकोण हों, तो दिखाइए कि
\(\sin \frac{(B+C)}{2}=\cos \frac{A}{2}\)
हल:
यदि A, B और C त्रिभुज ABC के अन्त:कोण हो तो त्रिभुज के तीनों अन्तः कोणों का योग
A + B + C = 180°
या B + C = 180° – A

[∵ sin (90° – θ) = cos θ]

प्रश्न 7.
sin 67° + cos 75° को 0° और 45° के बीच के कोणों के त्रिकोणमितीय अनुपातों के पदों में व्यक्त कीजिए।
हल:
sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°
{∵ sin (90° – θ) = cos θ
और cos (90° – θ) = sin θ}

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 14 सांख्यिकी Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 14 सांख्यिकी

लघूत्तरात्मक/निबन्धात्मक प्रश्न :

प्रश्न 1.
निम्न बंटन का बहुलक ज्ञात कीजिए :

हल:
बहुलक के लिए, दिये गये आँकड़ों में अधिकतम बारम्बारता 61 है।
इसका संगत वर्ग-अंतराल 60 – 80 है।
बहुलक वर्ग = 60 – 80
l = 60, f₁ = 61, f₀ = 52, f₂ = 38, h = 20

प्रश्न 2.
यदि नीचे दिए हुए बंटन का माध्यम 28.5 हो तो x और y के मान ज्ञात कीजिए।

हल:

परन्तु बारम्बारता का योग Σf_i = N = 80 है। अंतिम संचयी बारम्बारताओं के योग के बराबर होता है।
∴ 45 + x + y = 80
⇒ x + y = 80 – 45
⇒ x + y = 35 ……(1)
अब \(\frac{N}{2}=\frac{80}{2}=40\)
तथा बंटन का माध्यक = 28.5 है।
जोकि वर्ग अंतराल 20 – 30 में स्थिति है।
माध्यम वर्ग = 20 – 30
l = 20, f = 20, c = 5 + x और h = 10

57 = 75 – x
x = 18
x का मान समी. (1) में रखने पर 18 + y = 35
अतः y = 17

प्रश्न 3.
नीचे दिए गए बंटन का माध्य 50 हो तो x व y के मान ज्ञात कीजिए :

वर्ग अन्तराल	बारंबारता
0 – 20	17
20 – 40	x
40 – 60	32
60 – 80	y
80 – 100	19
योग	120

हल:
संचयी बारम्बारता सारणी

वर्ग अन्तराल	बारंबारता	संचयी बारंबारता c.f.
0 – 20	17	17
20 – 40	X	17 + x
40 – 60	32	(49 + x)
60 – 80	Y	(49 + x + y)
80 – 100	19	(68 + x + y)
योग	Σfi = N = 120

परन्तु बारम्बारताओं का योग Σf_i = N = 120 है अंतिम संचयी बारम्बारता वर्ग बारम्बारताओं के योग के बराबर होता है।
68 + x + y = 120
x + y = 120 – 68
x + y = 52 …..(1)
अब \(\frac{N}{2}=\frac{120}{2}=60\)
तथा बंटन का माध्यक = 50 है।
जोकि वर्ग अन्तराल 40 – 60 में स्थिति है।
माध्यक वर्ग = 40 – 60
l = 40, f = 32, c = 17 + x और h = 20

⇒ 50 = 320 + 215 – 5x
⇒ 400 – 535 = -5x ⇒ 5x = 135 ⇒ x = 27
x का मान समीकरण (1) में रखने पर
27 + y = 52
y = 25

प्रश्न 4.
निम्नलिखित आँकड़ों का माध्यक 525 है। यदि बारम्बारताओं का योग 100 है तो x और y के मान ज्ञात कीजिए।

वर्ग-अन्तराल	बारम्बारता
0 – 100	2
100 – 200	5
200 – 300	x
300 – 400	12
400 – 500	17
500 – 600	20
600 – 700	y
700 – 800	9
800 – 900	7
900 – 1000	4

हल:

दिया है : Σ(f) = N = 100
अतः 76 + x + y = 100 ⇒ x + y = 100 – 76 = 24 …..(1)
माध्यक 525 है जो वर्ग 500 – 600 में स्थित है।
∴ l = 500; ƒ = 20, C = 36 + x, h = 100

x = 14 – 5
∴ x = 9
समीकरण (1) से, 9 + y = 24
⇒ y = 24 – 9
∴ y = 15
अतः x = 9 और y = 15

प्रश्न 5.
गणित की एक परीक्षा में 30 विद्यार्थियों द्वारा प्राप्त किए गए अंकों का बंटन निम्नलिखित है :

इन आँकड़ों से कल्पित माध्य विधि से माध्य ज्ञात कीजिए एवम् बहुलक भी ज्ञात कीजिए।
हल:
माना कि कंल्पित माध्य (A) = 47.5

समान्तर माध्य (x) = A + \(\frac{\Sigma f_i d_i}{\Sigma f_i}\) = 47.5 + \(\frac{435}{30}\)
= 47.5 + 14.5 = 62
दी गयी सारणी से स्पष्ट है कि सबसे अधिक बारम्बारता 7 है।
अतः 7 के संगत वर्ग अन्तराल 40 – 55 है। अतः बहुलक वर्ग 40 – 55 होगा।
l = 40, f₀ = 3, f₁ = 7, ƒ₂ = 6 तथा h = 15

अतः माध्य = 62 तथा बहुलक = 52

प्रश्न 6.
निम्न बंटन का कल्पित माध्य मानकर माध्यx ज्ञात कीजिए :

हल:

समान्तर माध्य (x) = A + \(\frac{\Sigma f_i d_i}{\Sigma f_i}\)
= 47.5 + \(\frac{465}{30}\)
= 47.5 + 15.5 = 63
दी गयी सारणी से स्पष्ट है कि सबसे अधिक बारम्बारता 7 है।

प्रश्न 7.
एक मेडिकल की प्रवेश परीक्षा में 400 विद्यार्थियों के प्राप्तांक निम्न सारणी में दर्शाये गए हैं :

उपर्युक्त बंटन को एक ‘से कम’ प्रकार के संचयी बारम्बारता बंटन में बदलिए और उसका तोरण खींचिए।
हल:
‘से कम’ प्रकार का संचयी बारम्बारता बंटन

(i) बिन्दुओं A(450, 30); B(500, 75); C(550, 135); D(600, 187); E(650, 241); F(700, 308); G(750, 353) और H(800, 400) को ग्राफ पेपर पर उचित पैमाना मानकर अंकित किया।
(ii) इन सभी बिन्दुओं को हाथ से जोड़कर ‘से कम प्रकार’ का तोरण खींचा।

अत: ABCDEFG ही अभीष्ट तोरण है।

प्रश्न 8.
कक्षा X के 60 विद्यार्थियों के अंक निम्नवत् हैं :

इस बंटन को ‘कम प्रकार’ के बंटन में बदलिए। तोरण वक्र खींचकर माध्यक ज्ञात कीजिए।
हल:
‘कम प्रकार’ का संचयी बारम्बारता बंटन

अब बिन्दुओं A(10, 4), B(15, 12), C(20, 22), D(25, 42), E(30, 60) को ग्राफ पेपर पर अंकित किया। अब सभी बिन्दुओं को हाथ से जोड़ते हुए तोरण खींचा।

माध्यक के लिए :
(i) Y-अक्ष पर 30 विद्यार्थियों पर एक बिन्दु अंकित किया।
(ii) इस बिन्दु से X-अक्ष के समान्तर रेखा खींची जो वक्र को P बिन्दु पर काटती है।
(iii) बिन्दु P का भुज ज्ञात किया जो कि 22 है।
अतः माध्यक = 22 अंक।

प्रश्न 9.
किसी मोहल्ले के एक शॉपिंग कॉम्प्लेक्स (shopping complex) की 30 दुकानों द्वारा अर्जित किए गए वार्षिक लाभों से निम्नलिखित बारम्बारता बंटन प्राप्त होता है।

लाभ (लाख रु. में)	दुकानों की संख्या
5 से अधिक या बराबर	30
10 से अधिक या बराबर	28
15 से अधिक या बराबर	16
20 से अधिक या बराबर	14
25 से अधिक या बराबर	10
30 से अधिक या बराबर	7
35 से अधिक या बराबर	3

उपर्युक्त आँकड़ों से (i) ‘अधिक प्रकार’ का तोरण वक्र खींचिए।
(ii) एक ही अक्षों पर दोनों तोरण खींचिए। इसके बाद माध्यक लाभ ज्ञात कीजिए।
हल:
(i) बिन्दुओं A(5, 30); B(10, 28); C(15, 16); D(20, 14); E(25, 10); F(30, 7) और G(35, 3) को उचित पैमाना मानकर ग्राफ पेपर पर अंकित करते हैं। सभी बिन्दुओं को एक मुक्त हस्त से जोड़ते हुए तोरण खीचते है।
अत: A B C D E F G ही अभीष्ट तोरण है।

(ii) दिये गये बारम्बारता बंटन से, वर्ग-अन्तराल, संगत बारम्बारताएँ और संचयी बारम्बारता सारणी बनाते हैं।

अब बिन्दुओं (10, 2); (15, 14); (20, 16); (25, 20); (30, 23); (35, 27); (40, 30) को ग्राफ पेपर पर अंकित करते हैं। इन सभी बिन्दुओं को मुक्त हस्त से जोड़कर ‘कम प्रकार’ का तोरण खींचते हैं।
इस वक्र को ‘अधिक प्रकार’ के वक्र के साथ आलेखित करने से दोनों प्रकार के वक्र एक ही अक्ष पर प्राप्त हो जाते हैं।

दोनों तोरण के प्रतिच्छेद बिन्दु से क्षैतिज अक्ष पर लम्ब डालने पर प्राप्त लाभ माध्यक होगा।
अतः माध्यक = ₹ 17.5 लाख

प्रश्न 10.
निम्न बारंबारता का बहुलक 36 है। लुप्त बारंबारता (f) का मान ज्ञात कीजिए :

हल:
दिए गए बारंबारता बंटन का बहुलक 36 है, इसलिए बहुलक वर्ग 30-40 है।
∴ l = 30, f₀ = f, f₁ = 16, f₂ = 12 तथा h = 10

⇒ 6 × (20 – f) = (16 – f) × 10
⇒ 120 – 6f = 160 – 10f
⇒ 10f – 6f = 160 – 120
⇒ 4f = 40
⇒ f = 10
अतः लुप्त बारंबारता, f = 10.

प्रश्न 11.
निम्न आँकड़ों का बहुलक ज्ञात कीजिए :

हल:

वर्ग	बारम्बारता
0 – 20	6
20 – 40	8
40 – 60	10 = f0
60 – 80	12 = f1
80 – 100	6 = f2
100 – 120	5
120 – 140	3

∵ अधिकतम बारंबारता = 12
∴ बहुलक वर्ग = 60 – 80
∴ l = 60, f₀ = 10, f₁ = 12, f₂ = 6, h = 20
अब बहुलक = \(60+\left(\frac{12-10}{2 \times 2-10-6}\right) \times 20\)
= \(60+\frac{2}{8} \times 20\)
= 60 + 5 = 65

प्रश्न 12.
निम्न तालिका एक गाँव की 100 फार्मों में गेहूँ की प्रति हैक्टेयर (क्विंटलों में) उपज के आँकड़ें दर्शाता है :

उपरोक्त बंटन को ‘से अधिक’ प्रकार के बंटन में बदलकर उसका तोरण खींचिए।
हल:

अब तोरण बिन्दुओं को ग्राफ पर अंकित करके मुक्त हस्त से वक्र खींचते हैं जैसे कि निम्न आकृति में दर्शाया गया है।
इस प्रकार प्राप्त वक्र को “से अधिक प्रकार” का तोरण कहते हैं।

प्रश्न 13.
निम्न बारंबारता बंटन का बहुलक ज्ञात कीजिए।

हल:

यहाँ अधिकतम वर्ग बारंबारता 16 है तथा इस बारंबारता का संगत वर्ग 30 – 40 है।
अतः बहुलक वर्ग 30 – 40 है।
अब बहुलक़ वर्ग = 30 – 40
बहुलक वर्ग की निम्न सीमा (l) = 30 तथा वर्ग माप (h) = 10
f₁ = 16, f₀ = 10 तथा f₂ = 12

प्रश्न 14.
नीचे दी गई सारणी में 280 लोगों का वेतन मान दर्शाया गया है :

वेतन (हजार ₹ में)	लोगों की संख्या
5 – 10	49
10 – 15	133
15 – 20	63
20 – 25	15
25 – 30	6
30 – 35	7
35 – 40	4
40 – 45	2
45 – 50	1

उपर्युक्त आँकड़ों से माध्यक वेतन मान ज्ञात कीजिए।
हल:

वेतन	बारंबारता	संचयी बारंबारता
5 – 10	49	49
10 – 15	133	182
15 – 20	63	245
20 – 25	15	260
25 – 30	6	266
30 – 35	7	273
35 – 40	4	277
40 – 45	2	279
45 – 50	1	280
	N = 280

\(\frac{N}{2}=\frac{280}{2}\) = 140
माध्यम वर्ग = 10 – 15
f = 133
c.f. = 49
h = 5

अतः लोगों का माध्यक वेतन ₹ 13.42 है।

प्रश्न 15.
निम्नलिखित बंटन को ‘से कम प्रकार’ के बंटन में बदलिए और फिर उसका तोरण खींचिए :

वर्ग अन्तराल	बारंबारता
30 – 40	7
40 – 45	5
50 – 60	8
60 – 70	10
70 – 80	6
80 – 90	6
90 – 100	8

हल:

वर्ग अन्तराल	बारंबारता	तोरण बिन्दु
40 से कम	7	(40, 7)
50 से कम	12	(50, 12)
60 से कम	20	(60, 20)
70 से कम	30	(70, 30)
80 से कम	36	(80, 36)
90 से कम	42	(90, 42)
100 से कम	50	(100, 50)

अब तोरण बिन्दुओं को ग्राफ पर अंकित करके मुक्त-हस्त से वक्र खींचते हैं। जैसे कि निम्न आकृति में दर्शाया गया है। इस प्राकर प्राप्त वक्र को “से कम प्रकार” का तोरण कहते हैं।

वस्तुनिष्ठ प्रश्न :

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क).

1. ऐसे आँकड़े जिनका व्यवस्थितिकरण वर्गों के रूप में होता है, ……………… आँकड़े कहलाते हैं।
2. यदि कोई प्रेक्षण वर्ग की उच्च सीमा में आता है, तो उसे अगले ……………… में लेते हैं।
3. जिस प्रेक्षण की बारंबारता अधिकतम होती है वह उन प्रेक्षणों का ……………… कहलाता है।
4. 100 प्रेक्षणों वाले एक बंटन के ‘से कम प्रकार’ का तोरण तथा ‘से अधिक प्रकार’ का तोरण बिन्दु (58, 50) पर प्रतिच्छेद करते हैं। इस बंटन का माध्यक ……………… है।
5. माध्यक वर्ग वह वर्ग है जिसकी संचयी बारंबारता ……………… से अधिक तथा समीपतय होती है।

उत्तर:

1. वर्गीकृत,
2. अन्तराल,
3. बहुलक,
4. 58,
5. \(\frac{n}{2}\)

निम्न में सत्य / असत्य बताइए :

प्रश्न (ख).

1. अधिकतम बारंबारता वाले वर्ग को माध्यिका वर्ग कहते हैं।
2. f₀ बहुलक वर्ग से ठीक अगले वर्ग की बारंबारता होती है।
3. संचयी बारंबारता दो प्रकार की होती है-‘से कम प्रकार’ तथा ‘से अधिक प्रकार’ की।
4. सभी प्रेक्षणों के योगफल को, प्रेक्षणों की कुल संख्या से भाग देने पर माध्यक प्राप्त होता है।
5. माध्यकं = 3 × बहुलक – 2 × बहुलक

उत्तर:

1. असत्य,
2. असत्य,
3. सत्य,
4. असत्य,
5. असत्य

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
एक बंटन का माध्य तथा माध्यक क्रमशः 14 तथा 15 है। अतः बहुलक का मान होगा :
(A) 16
(B) 17
(C) 17
(D) 13
हल:
बहुलक 3 × माध्यक – 2 × माध्य
= 3 × 15 – 2 × 14
= 45 – 28
= 17
अत: सही विकल्प (B) है।

प्रश्न 2.
बारम्बारता बंटन के माध्य, मध्यिका तथा बहुलक के बीच निम्न सम्बन्ध है :
(A) बहुलक = 3 माध्य – 2 माध्यिका
(B) बहुलक = 3 मध्यिका – 2 माध्य
(C) बहुलक = 2 माध्यिका – 3 माध्य
(D) बहुलक = माध्यिका + 2 माध्य।
हल:
बारम्बारता बंटन के लिए माध्य, माध्यिका और बहुलक के बीच निम्नलिखित सम्बन्ध होता है-
बहुलक = 3 मध्यका – 2 माध्य
अत: सही विकल्प (B) है।

प्रश्न 3.
यदि x_i वर्गीकृत आँकड़ों के वर्गअन्तरालों के मध्य बिन्दु हैं, f_i इनकी संगत बारम्बारताएँ हैं तथा माध्य \(\bar{x}\) है, तो Σ(f_ix_i – \(\bar{x}\)) बराबर है :
(A) 0
(B) -1
(C) 1
(D) 2
हल:
सही विकल्प (A) है।

प्रश्न 4.
वर्गीकृत आँकड़ों की ‘से कम प्रकार’ और ‘से अधिक प्रकार’ की संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के भुज से आँकड़ों का प्राप्त होना है :
(A) माध्य
(B) माध्यक
(C) बहुलक
(D) उपरोक्त सभी
हल:
सही विकल्प (B) है।

प्रश्न 5.
संचयी बारम्बारता सारणी का उपयोग होता है, ज्ञात करने में :
(A) माध्य
(B) बहुलक
(C) माध्यक
(D) सभी में।
हल:
संचयी बारम्बारता सारणी माध्यक ज्ञात करने के लिए सहायक होती है। अतः सही विकल्प (C) है।

प्रश्न 6.
दिए गए सूत्र \(\bar{X}\) = a + h\(\bar{x}\) में, u_i का मान होगा :
(A) h(x_i – a)
(B) \(\frac{x_i-a}{h}\)
(C) \(\frac{a-x_i}{h}\)
(D) \(\frac{x_i+a}{h}\)
हल:
u_i = \(\frac{x_i-a}{h}\) होता है।
अत: सही विकल्प (B) होगा।

प्रश्न 7.
निम्न बंटन पर विचार कीजिए-

माध्यक वर्ग और बहुलक वर्ग की निम्न सीमाओं का योग है :
(A) 15
(B) 25
(C) 30
(D) 35
हल:
दिए गए आँकड़ों में अधिकतम बारम्बारता 20 है। इसके संगत वर्ग अन्तराल 15 – 20 है । अत: बहुलक वर्ग = 15 – 20 होगा।
माध्यक के लिए,

यहाँ N = 66 ⇒ \(\frac{N}{2}=\frac{66}{2}\) = 33
33 से ठीक बड़ी संचयी बारम्बारता 37 के संगत वर्ग अन्तराल 10 – 55 है।
अतः माध्यक वर्ग = 10 – 15
अतः माध्यक वर्ग और बहुलक वर्ग की निम्न सीमाओं का योग 10 + 15 = 25
अत: सही विकल्प (B) है।

प्रश्न 8.
निम्नलिखित बारम्बारता बंटन में 25 वर्ष से कम आयु के विद्यार्थियों की संख्या है :

(A) 8
(B) 6
(C) 17
(D) 25
हल:

आयु (वर्षो में)	विद्यार्थियों की संख्या
10 से कम	3
15 से कम	9
20 से कम	17
25 से कम	25
30 से कम	27

अतः उपर्युक्त सारणी में 25 वर्ष से कम आयु के विद्यार्थियों की संख्या 25 होगी।
अत: सही विकल्प (D) है।

प्रश्न 9.
बंटन :

प्राप्तांक	विद्यार्थियों की संख्या
0 से अधिक या उसके बराबर	63
10 से अधिक या उसके बराबर	58
20 से अधिक या उसके बराबर	55
30 से अधिक या उसके बराबर	51
40 से अधिक या उसके बराबर	48
50 से अधिक या उसके बराबर	42

के लिए वर्ग 30 – 40 की बारम्बारता है :
(A) 3
(B) 4
(C) 48
(D) 51
हल:
दी गयी संचयी बारम्बारता सारणी को सामान्य बारम्बारता सारणी में परिवर्तित करेंगे।

प्राप्तांक	विद्यार्थियों की संख्या
0 – 10	63 – 58 = 5
10 – 20	58 – 55 = 3
20 – 30	55 – 51 = 4
30 – 40	51 – 48 = 3
40 – 50	48 – 42 = 6

अतः वर्ग 30 – 40 की बारम्बारता 3 है।
अत: सही विकल्प (A) है।

प्रश्न 10.
यदि 5, 7, 9, x का समान्तर माध्य 9 हो, तो x का मान है :
(A) 11
(B) 15
(C) 18
(D) 16
हल:

⇒ 9 × 4 = 21 + x
⇒ 36 = 21 + x
∴ x = 36 – 21 = 15
अत: सही विकल्प (B) है।

प्रश्न 11.
बंटन :

के लिए, माध्यक वर्ग की उपरि सीमा और बहुलक वर्ग की निम्न सीमा का अन्तर है :
(A) 0
(B) 19
(C) 20
(D) 38
हल:
दिए आँकड़ों में अधिकतम बारम्बारता 20 है। इसके संगत वर्ग अन्तराल 125 – 145 है। अत: बहुलक वर्ग = 125 – 145 होगा।
माध्यक के लिए संचयी बारम्बारता सारणी

वर्ग	बारम्बारता (fi)	संचयी बारम्बारता (cf)
65 – 85	4	4
85 – 105	5	9
105 – 125	13	22
125 – 145	20	42
145 – 165	14	56
165 – 185	7	63
185 – 205	4	67
योग	Σfi = 67

यहाँ N = 67 ⇒ \(\frac{N}{2}=\frac{67}{2}\) = 33.5
33.5 से ठीक बड़ी संचयी बारम्बारता 42 के संगत वर्ग अन्तराल 125 – 145 है। अतः माध्यक वर्ग = 125 – 145.
∴ माध्यक वर्ग की उपरि सीमा और बहुलक वर्ग की निम्न सीमा का अन्तर 145 – 125 = 20
अतः सही विकल्प (C) है।

प्रश्न 12.
चार छात्रों के सांख्यिकी में प्राप्तांक 53, 75, 42, 70 हैं। उनके प्राप्तांकों का समान्तर माध्य है :
(A) 42
(B) 64
(C) 60
(D) 56
हल:

= \(\frac{240}{4}\)
= 60
अतः सही विकल्प (C) है।

प्रश्न 13.
बंटन 3, 5, 7, 4, 2, 1, 4, 3, 4 का बहुलक है :
(A) 7
(B) 4
(C) 3
(D) 1
हल:
ऊपर दी गई सारणी को देखने से स्पष्ट होता है कि 4 की बारम्बारता सबसे अधिक (3 बार है)। अतः इसका बहुलक 4 होगा।
अत: सही विकल्प (B) है।

प्रश्न 14.
किसी स्कूल के छात्रों की संख्या उनकी आयु के अनुसार निम्न प्रकार है :

इसका बहुलक है :
(A) 41
(B) 12
(C) 3
(D) 17
हल:
ऊपर की सारणी से स्पष्ट होता है कि बारम्बारता 41 सबसे अधिक है तथा इसका संगत आयु वर्ग 12 है। अतः इसका बहुलक 12 होगा।
अत: सही विकल्प (B) है।

प्रश्न 15.
बंटन 2, 3, 4, 7, 5, 1 का माध्यक होगा :
(A) 4
(B) 7
(C) 11
(D) 3.5
हल:
पदों को आरोही क्रम में रखने पर 1, 2, 3, 4, 5, 7
यहाँ पदों की संख्या N = 6 जो कि सम है, अतः


अत: सही विकल्प (D) है।

प्रश्न 16.
बंटन 1, 3, 2, 5, 9 का माध्यक होगा :
(A) 3
(B) 4
(C) 2
(D) 20
हल:
पदों को आरोही क्रम में रखने पर, 1, 2, 3, 5, 9
यहाँ पदों की संख्या (N) = 5 है जो कि विषम है।
माध्यक = \(\frac{1}{2}\) वें पद का मान = \(\frac{1}{2}\) वें पद का मान
= \(\frac{1}{2}\) वें पद का मान
= 3 वें पद का मान = 3
अत: सही विकल्प (A) है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 10 वृत्त Ex 10.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 10 वृत्त Exercise 10.1

प्रश्न 1.
एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं ?
हल:
किसी वृत्त की परिधि पर स्थित प्रत्येक बिन्दु से एक स्पर्श रेखा खींची जा सकती है। परन्तु वृत्त की परिधि पर असंख्य बिन्दु होते हैं। इसलिए वृत्त पर असंख्य (अनन्त) स्पर्श रेखाएं खींच सकते हैं।

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए :
(i) किसी वृत्त की स्पर्श रेखा उसे ……………… बिंदु पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को ……………… कहते हैं।
(iii) एक वृत्त की ……………… समांतर स्पर्श रेखाएँ हो सकती हैं।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को ………………. कहते हैं।
हल:
(i) केवल एक,
(ii) छेदक,
(iii) अधिकतम दो,
(iv) स्पर्श बिंदु

प्रश्न 3.
5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी, PQ की लम्ब है।
(A) 12 सेमी
(B) 13 सेमी
(C) 8.5 सेमी
(D) \(\sqrt{119}\) सेमी।
हल:
OQ = 12 सेमी
OP = 5 सेमी

∵ PQ एक स्पर्श रेखा है जो त्रिज्या OP पर लम्ब है।
समकोण ΔPOQ में, पाइथागोरस प्रमेय से,
OQ² = PQ² + OP²
(12)² = PQ² + (5)²
⇒ PQ² = (12)² – (5)²
⇒ PQ² = 144 – 25
⇒ PQ² = 119
∴ PQ = \(\sqrt{119}\) सेमी
अत: सही विकल्प (D) है।

प्रश्न 4.
एक वृत्त खींचिए और एक दी गई रेखा के समान्तर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
हल:
माना O केन्द्र का एक वृत्त है और PQ एक दी गई रेखा है। हमें PQ के समान्तर दो रेखाएँ (माना CD व AB) खींचनी हैं जिनमें CD स्पर्श रेखा और AB छेदक रेखा हो।

रचना विधि : (i) रेखा PQ पर केन्द्र बिन्दु से लम्ब ON खींचा जो वृत्त को C पर काटे।
(ii) त्रिज्या OC के बिन्दु C पर लम्ब CD खींचा। CD स्पर्श रेखा है।
(iii) OC पर एक बिन्दु M से लम्ब AB खींचा। AB छेदक रेखा है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 14 सांख्यिकी Ex 14.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 14 सांख्यिकी Exercise 14.3

प्रश्न 1.
निम्नलिखित बारम्बारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली की मासिक खपत दर्शाता है। इन आँकड़ों से माध्यक, माध्य और बहुलक ज्ञात कीजिए। इनकी तुलना भी कीजिए ।

मासिक खपत (इकाइयों में)	उपभोक्ताओं की संख्या
65-85 85-105 105-125 125-145 145-165 165-185 185-205	4 5 13 20 14 8 4

हल :
माध्य के लिए :

यहाँ N = 68
∴ \(\frac{N}{2}=\frac{68}{2}\) = 34 से ठीक बड़ी संचयी बारम्बारता 42 के संगत वर्ग अन्तराल 125 – 145 है।
∴ माध्यक वर्ग = 125 – 145
अतः l = 125; N = 68; f = 20, C = 22 और h = 20

माध्य के लिए :

माना कल्पित माध्य (4) = 135, वर्ग अन्तराल (h) = 20

बहुलक के लिए :

दिए गए आँकड़ों में अधिकतम बारम्बारता 20 है। इसके संगत वर्ग अन्तराल 125-145 है।
∴ बहुलक वर्ग 125-145
∴ l = 125; f₁ = 20; f₀ = 13; f₂ = 14 और h = 20
अतः दिए गए आँकड़ों का माध्यक = 137, माध्य = 137.05 तथा बहुलक = 135.77 (लगभग) मात्रक है।

प्रश्न 2.
यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो, तो x और y के मान ज्ञात कीजिए :

हल :

परन्तु बारम्बारताओं का योग Σf_i = N = 60 है। अन्तिम संचयी बारम्बारता वर्ग बारम्बारताओं के योग के बराबर होता है।
∴ 45 + x + y = 60
⇒ x + y = 60 – 45
⇒ x + y = 15 …(i)
अब \(\frac{N}{2}=\frac{60}{2}\) = 30 तथा बंटन का माध्यक = 28.5 है,
जो कि वर्ग-अन्तराल 20 – 30 में स्थित है।
∴ माध्यक वर्ग = 20 – 30
∴ l = 20; f = 20; C = 5 + x और h = 10

x का मान समीकरण (i) में प्रतिस्थापित करने पर,
8 + y = 15 ⇒ y = 15 – 8 = 7
अत: x = 8 और y = 7

प्रश्न 3.
एक जीवन बीमा एजेण्ट 100 पॉलिसी धारकों की आयु के बंटन के निम्नलिखित आँकड़े ज्ञात करता है। माध्यक आयु परिकलित कीजिए, यदि पॉलिसी केवल उन्हीं व्याक्यिों को दी जाती है, जिनकी आयु 18 वर्ष या उससे अधिक हो, परन्तु 60 वर्ष से कम हो।

आयु (वर्षो में)	पॉलिसी धारकों की संख्या
20 से कम 25 से कम 30 से कम 35 से कम 40 से कम 45 से कम 50 से कम 55 से कम 60 से कम	2 6 24 45 78 89 92 98 100

हल :

यहाँ N = 100
∴ \(\frac{N}{2}=\frac{100}{2}\) = 50 से ठीक बड़ी संचयी बारम्बारता 78 के संगत वर्ग अन्तराल 35 – 40 है।
∴ माध्यक वर्ग 35 – 40
∴ l = 35, \(\frac{N}{2}\) = 50, C = 45, f = 33 और h = 5

अतं : दिएा गएा आँकड़ों से माध्यक आयु 35.76 वर्ष है।

प्रश्न 4.
एक पौधे की 40 पत्तियों की लम्बाइयाँ निकटतम मिलीमीटरों में मापी जाती हैं तथा प्राप्त आंकड़ों को अग्रलिखित सारणी के रूप में निरूपित किया जाता है:

लम्बाई (मिमी)	पत्तियों की संख्या
118-126 127-135 136-144 145-153 154-162 163-171 172-180	3 5 9 12 5 4 2

पत्तियों की माध्यक लम्बाई ज्ञात कीजिए।
हल :
दिए गए वर्ग लगातार नहीं हैं। इसलिए पहले इसे लगातार (सतत) वर्ग में बदलेंगे।

यहाँ N = 40
∴ \(\frac{N}{2}=\frac{40}{2}\) = 20 से ठीक बड़ी संचयी बारम्बारता 29 के संगत वर्ग अन्तराल 144.5 – 153.5 है।
∴ माध्यक वर्ग = 144.5 – 153.5
l = 144.5, f = 12, C = 17 और h = 9

अतः पत्तियों की माध्यक लम्बाई 146.75 मिमी है।

प्रश्न 5.
निम्नलिखित सारणी 400 नीऑन लैम्पों के जीवनकालों (Life time) को प्रदर्शित करती है :

जीवनकाल (घण्टों में)	लैम्पों की संख्या
1500 -2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000	14 56 60 86 74 62 48

एक लैम्प का माध्यक जीवनकाल ज्ञात कीजिए।
हल :

जीवन काल (घण्टों में)	लैम्पों की संख्या	संचयी बारम्बारता (c.f.)
1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000	14 56 60 86 74 62 48	14=14 (14+56) = 70 (70+60) = 130 (130+86)=216 (216+74) = 290 (290+62) = 352 (352+48) = 400
योग	Σf<sub>i</sub> = N = 400

योग N = 400
∴ \(\frac{N}{2}=\frac{400}{2}\) = 200 से ठीक बड़ी संचयी बारम्बारता 216 के संगत वर्ग अन्तराल 3000 – 3500 है:
∴ माध्यक वर्ग = 3000 – 3500
∴ l = 3000; \(\frac{N}{2}\) = 200; f = 86, C = 130 और h = 500
माध्यक = l + (\(\frac{\frac{N}{2}-C}{f}\)) × h = 3000 + (\(\frac{200-130}{86}\)) × 500
= 3000 + \(\frac{70 \times 500}{86}\)
= 3000 + 406.98 (लगभग) = 3406.98
अतः एक लैम्प का माध्यक जीवनकाल = 3406.98 घण्टे हैं।

प्रश्न 6.
एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (surnames) लिए गए और उनमें प्रयुक्त अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारम्बारता बंटन प्राप्त हुआ:

कुलनामों में माध्यक अक्षरों की संख्या ज्ञात कीजिए। कुलनामों में माध्य अक्षरों की संख्या ज्ञात कीजिए। साथ ही कुलनामों का बहुलक ज्ञात कीजिए।
हल :

माध्यक के लिए :
यहाँ N = 100
\(\frac{N}{2}=\frac{100}{2}\) = 50 से ठीक बड़ी संचयी बारम्बारता 76 के संगत वर्ग अन्तराल 7-10 है।
∴ माध्यक वर्ग 7 – 10
∴ l = 7, \(\frac{N}{2}\) = 50 , f = 40, C = 36 और h = 3
माध्यक = l + (\(\frac{\frac{N}{2}-C}{f}\)) × h = 7 + (\(\frac{50-36}{40}\)) × 3 = 7 + \(\frac{14 \times 3}{40}\)
= 7 + \(\frac {21}{20}\)
= 7 + 1.05 = 8.05
अत: माध्यक = 8.05

माध्य के लिए :

Σf_ix_i = 832, Σf_i = 100
माध्य (\(\bar{x}\)) = \(\frac{\sum f_i x_i}{\sum f_i}\) = \(\frac {832}{100}\) = 8.32
अतः माध्य अक्षरों की संख्या = 8.32 है।

बहुलक के लिए :

दिए गए आँकड़ों में अधिकतम बारम्बारता 40 है। इसके संगत वर्ग अन्तराल 7 – 10 है।
∴ बहुलक वर्ग = 7 – 10
∴ l = 7, f₁ = 40, f₀ = 30, f₂ = 16 और h = 3

अतः कुलनामों में माध्यक अक्षरों की संख्या = 8.05, माध्य अक्षरों की संख्या 8.32 तथा बहुलक 7.88.

प्रश्न 7.
नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यक भार ज्ञात कीजिए।

हल :
माध्यक के लिए संचयी बारम्बारता सारणी

यहाँ N = 30
\(\frac{N}{2}=\frac{30}{2}\) = 15 से ठीक बड़ी संचयी बारम्बारता 19 के संगत वर्ग अन्तराल 55-60 है।
∴ माध्यक वर्ग = 55 – 60
∴ l = 55, \(\frac{N}{2}\) = 15, C = 13, f = 6 और h = 5
माध्यक = l + (\(\frac{\frac{N}{2}-C}{f}\)) × h = 55 + (\(\frac{15-13}{6}\)) × 5
= 55 + \(\frac{2}{6}\) × 5 = 55 + \(\frac{5}{3}\) × 5 = 55 + \(\frac{5}{3}\) = 55 + \(\frac{5}{3}\) = 55 + 1.67 = 56.67 किग्रा (लगभग)
अतः विद्यार्थियों का माध्यक भार = 56.67 किग्रा (लगभग) है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Ex 9.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Exercise 9.1

प्रश्न 1.
सर्कस का एक कलाकार एक 20 m लम्बी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खम्भे के शिखर से बंधा हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो, तो खम्भे की ऊँचाई ज्ञात कीजिए।

हल:
माना कि खम्भे की ऊँचाई AB = h मीटर
तथा डोरी की लम्बाई AC = 20 मीटर
भूमि स्तर के साथ डोरी द्वारा बनाया गया कोण 30° है,
अर्थात् ∠ACB = 30°
समकोण ΔABC में,
sin 30° = लम्ब / कर्ण = \(\frac{A B}{A C}\)
[∵ लम्ब व कर्ण में त्रिकोणमितीय अनुपात sin θ का होता है ]
\(\frac{1}{2}=\frac{h}{20}\)
⇒ 2h = 20
∴ h = \(\frac{20}{2}\) = 10 मीटर
अतः खम्भे की ऊँचाई 10 मीटर है।

प्रश्न 2.
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिन्दु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 मीटर है। पेड़ की ऊँचाई ज्ञात कीजिए ।
हल:
माना आँधी से पहले पेड़ की लम्बाई BD है।
आँधी के पश्चात् पेड़ A स्थान से टूटकर पेड़ का शिखर जमीन पर C बिन्दु पर पड़ता है।

अर्थात् AD = AC = h₂ मीटर (माना)
और AB = h₁ मीटर (माना)
BC = 8 मीटर
टूटा हुआ भाग जमीन से 30° का कोण बनाता है।
अत : ∠ACB = 30°
समकोण ΔABC में,
tan 30° = \(\frac{A B}{B C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h_1}{8}\)
⇒ \(\sqrt{3}\)h1 = 8
∴ h1 = \(\frac{8}{\sqrt{3}}\) मीटर
पुन: समकोण ΔABC में,
cos 30° = \(\frac{B C}{A C}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{8}{h_2}\)
⇒ h2\(\sqrt{3}\) = 16
⇒ h2 = \(\frac{16}{\sqrt{3}}\) मीटर
पेड़ की कुल लम्बाई (BD) = AB + AD

= 8\(\sqrt{3}\) = 8 × 1.732
= 13.86 मीटर
अतः पेड़ की ऊँचाई 13.86 मीटर या 8\(\sqrt{3}\) मीटर है।

प्रश्न 3.
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5 मीटर की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 मीटर की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लम्बाई क्या होनी चाहिए?
हल:
स्थिति I. जब ठेकेदार 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी लगाता है तो उसकी ऊँचाई AB = 1.5 मीटर तथा फिसलनपट्टी का भूमि के साथ कोण ACB = 30° है।
माना फिसलनपट्टी की लम्बाई AC मीटर है।

समकोण ΔABC में,
sin 30° = \(\frac{A B}{A C}\)
⇒ \(\frac{1}{2}=\frac{1.5}{x}\)
⇒ x = 1.5 × 2
∴ AC = 3 मीटर
स्थिति II. जब ठेकेदार 5 वर्ष से अधिक उम्र के बच्चों के लिए फिसलनपट्टी लगाता है, तो उसकी ऊँचाई PQ = 3 मीटर होती है और फिसलनपट्टी का भूमि के साथ कोण 60° है अर्थात् ∠PRQ = 60°

माना फिसलनपट्टी की लम्बाई (PR) y मीटर है।
समकोण ΔPQR में,

अत: 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी की लम्बाई = 3 मीटर तथा इससे अधिक उम्र के बच्चों के लिए फिसलनपट्टी की लम्बाई = 2\(\sqrt{2}\) मीटर

प्रश्न 4.
भूमि के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 30 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
हल:
माना मीनार की ऊँचाई BC h मीटर है। मीनार के आधार B से 30 मीटर दूर भूमि पर स्थित बिन्दु A है अर्थात् AB = 30 मीटर मीनार के शिखर का उन्नयन कोण 30° है। अर्थात् ∠BAC = 30°

समकोण ΔABC में,

= 10 × 1.732
∴ h = 17.32 m (लगभग)
अतः मीनार की ऊँचाई 10\(\sqrt{3}\) मीटर या 17.32 मीटर

प्रश्न 5.
भूमि से 60 मीटर की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिन्दु से बाँध दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लम्बाई ज्ञात कीजिए।
हल:
माना AX एक क्षैतिज रेखा है। रेखा पर स्थित बिन्दु C से 60 मीटर की ऊँचाई पर एक पतंग B उड़ रही है यह पतंग B भूमि पर स्थित एक बिन्दु A से तनी हुई डोरी AB द्वारा बँधी हुई है। डोरी AB का भूमि के साथ कोण CAB = 60° है।

समकोण ΔACB में,
sin 60° = \(\frac{B C}{A B}\)
= \(\frac{\sqrt{3}}{2}=\frac{60}{A B}\)
\(\sqrt{3}\)AB = 60 × 2
AB = \(\frac{120}{\sqrt{3}}\)
AB = \(\frac{120}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{120}{3} \sqrt{3}\)
= 40\(\sqrt{3}\) मीटर
= 40 × 1.732 मीटर
= 69.28 मीटर
अतः डोरी की लम्बाई = 40\(\sqrt{3}\) मीटर या 69.28 मीटर।

प्रश्न 6.
1.5 मीटर लम्बा एक लड़का 30 मीटर ऊँचे एक भवन से कुछ दूरी पर खड़ा है जब वह ऊंचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है?
हल:
माना PQ एक भवन है जिसकी ऊँचाई 30 मीटर हैं। भवन के आधार Q से x मीटर की दूरी पर बिन्दु R पर एक लड़का OR खड़ा है जिसकी ऊँचाई OR 1.5 मीटर है।
तब OS || RQ तथा OR || SQ
∴ SQ = OR = 1.5 मीटर
∴ PS = PQ – SQ
= 30 – 1.5 = 28.5 मीटर

लड़के की आँख से भवन के शिखर का उन्नयन कोण 30° है तथा लड़का भवन की ओर कुछ दूरी चलता है, तो भवन के शिखर का उन्नयन कोण 60° हो जाता है, तब
∠POS = 30° तथा ∠PTS = 60°
तब समकोण ΔPSO से,
tan 30° = \(\frac{P S}{O S}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{28.5}{O S}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{28.5}{x}\) (∵ OS = RQ = x मीटर)
⇒ x = 28.5\(\sqrt{3}\)
अतः OS = 28.5\(\sqrt{3}\)
माना लड़का कुछ दूरी चलकर बिन्दु 7 पर पहुँचता है जहाँ से उसकी आँख का कोण PTS, 60° हो जाता है। तब समकोण ΔPTS में,

अतः लड़के द्वारा भवन की ओर तय की गई दूरी 19\(\sqrt{3}\) मीटर है।

प्रश्न 7.
भूमि के एक बिन्दु से एक 20 मीटर ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमश: 45° और 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हल:
माना कि BC एक भवन है, जिसकी ऊँचाई 20 मीटर है।

भवन के शिखर बिन्दु C पर एक संचार मीनार CD है।
संचार मीनार के तल C और शिखर D से उन्नयन कोण क्रमश: 45° और 60° हैं।
अर्थात् ∠CAB = 45° और ∠DAB = 60°
समकोण ΔABC में,
tan 45° = \(\frac{B C}{A B}\)
⇒ 1 = \(\frac{20}{A B}\)
∴ AB = 20 मीटर
पुन: समकोण ΔABD में,
tan 60° = \(\frac{B D}{A B}\)
\(\sqrt{3}\) = \(\frac{B D}{20}\)
∴ BD = 20\(\sqrt{3}\) मीटर
संचार मीनार की ऊँचाई CD = BD – BC
= 20\(\sqrt{3}\) – 20 = 20 (\(\sqrt{3}\) – 1)
= 20 (1.732 – 1)
= 20 × 0.732 = 14.64 मीटर
अतः संचार मीनार की ऊँचाई = 20 (\(\sqrt{3}\) – 1) मीटर या 14.64 मीटर है।

प्रश्न 8.
एक पेडस्टल के शिखर पर एक 1.6 मीटर ऊँची मूर्ति लगी है। भूमि के एक बिन्दु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिन्दु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊंचाई ज्ञात कीजिए।
हल:
माना पेडस्टल की ऊँचाई BC = h मीटर
दिया है: मूर्ति की ऊँचाई CD = 1.6 मीटर है।
क्षैतिज भूमि पर स्थित बिन्दु A से मूर्ति के शिखर D का उन्नयन कोण BAD = 60° तथा पेडस्टल के शिखर C का उन्नयन कोण BAC = 45° है।

समकोण ΔABC में,
tan 45° = \(\frac{B C}{A B}\)
⇒ 1 = \(\frac{h}{A B}\)
∴ AB = h मीटर
पुनः समकोण ΔABD में,
tan 60° = \(\frac{B D}{A B}\)
⇒ \(\sqrt{3}=\frac{B C+C D}{A B}\)
⇒ \(\sqrt{3}=\frac{h+1.6}{h}\)
⇒ \(\sqrt{3}\)h = h + 1.6
⇒ \(\sqrt{3}\)h – h = 1.6
⇒ h (\(\sqrt{3}\) – 1) = 1.6
∴ h = \(\frac{1.6}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\)
\(\frac{1.6(\sqrt{3}+1)}{3-1}\)
∴ h = \(\frac{1.6}{2}(\sqrt{3}+1)\)
= 0.8 (\(\sqrt{3}\) + 1) मीटर
अतः पेडस्टल की ऊँचाई = 0.8 (\(\sqrt{3}\) + 1) मीटर।

प्रश्न 9.
एक मीनार के पाद-बिन्दु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद-बिन्दु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 मीटर ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
हल:
माना कि AB कोई मीनार है जिसकी ऊँचाई 50 मीटर है।
मीनार के पाद बिन्दु B से भवन की चोटी D का उन्नयन कोण 30° है जबकि भवन के आधार बिन्दु C से मीनार की चोटी 4 का उन्नयन कोण 60° है।
अर्थात् ∠CBD = 30° और ∠ACB = 60°

माना भवन की ऊँचाई CD = h मीटर
समकोण ΔABC में,
tan 60° = \(\frac{A B}{B C}\)
⇒ \(\sqrt{3}=\frac{50}{B C}\)
∴ BC = \(\frac{50}{\sqrt{3}}\)
पुन: समकोण ΔBCD में,
tan 30° = \(\frac{C D}{B C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{\frac{50}{\sqrt{3}}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{\sqrt{3} h}{50}\)
⇒ \(\sqrt{3}\) × \(\sqrt{3}\)h = 50
⇒ 3h = 50
h = \(\frac{50}{3}=16 \frac{2}{3}\) मीटर
अतः भवन की ऊँचाई 16\(\frac{2}{3}\) मीटर है।

प्रश्न 10.
एक 80 मीटर चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खम्भे लगे हुए हैं। इन दोनों खम्भों के बीच सड़क के एक बिन्दु से खम्भों के शिखर के उन्नयन कोण क्रमशः 60° और 30° हैं। खम्भों की ऊँचाई और खम्भों से बिन्दु की दूरी ज्ञात कीजिए।
हल:
माना BC और DE दो बराबर ऊँचाई के खम्भे हैं जिनकी ऊँचाई / मीटर है। इन दोनों खम्भों के बीच सड़क BD पर एक बिन्दु से खम्भों के शिखर के उन्नयन कोण क्रमश: 60° और 30° है।

अर्थात् ∠CAB = 60° और ∠DAE = 30°
BC = DE = h मीटर (माना)
BD = 80 मीटर
DA = x मीटर (माना)
∴ AB = BD – DA
AB = (80 – x) मीटर
समकोण ΔADE में,
tan 30° = \(\frac{E D}{D A}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{x}\)
h = \(\frac{x}{\sqrt{3}}\) मीटर ….(i)
पुन: समकोण ΔABC में,
tan 60° = \(\frac{1}{2}\)
⇒ \(\frac{\sqrt{3}}{1}=\frac{h}{80-x}\)
h = (80 – x)\(\sqrt{3}\) …(ii)
समीकरण (i) व (ii) से
\(\frac{x}{\sqrt{3}}=\sqrt{3}(80-x)\)
⇒ x = \(\sqrt{3}\) × \(\sqrt{3}\) (80 – x)
⇒ x = 3(80 – x)
⇒ x = 240 – 3x
⇒ x + 3x = 240
⇒ 4x = 240
∴ x = \(\frac{240}{4}\) = 60 मीटर
AD = 60 मीटर
और AB = 80 – 60 = 20 मीटर
समीकरण (i) से,
h = \(\frac{60}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{60}{3} \sqrt{3}\)
= 20\(\sqrt{3}\)
अर्थात् h = 20 × 1.732
= 34.64 मीटर।
अतः खम्भे की ऊँचाई 34.64 मीटर है बिन्दु की खम्भों से दूरी क्रमश: 20 मीटर और 60 मीटर है।

प्रश्न 11.
एक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधरत: खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिन्दु से 20 मी दूर और इस बिन्दु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30° है (देखिए आकृति)। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

हल:
माना नहर की चौड़ाई BC = x मीटर है।
तथा टीवी टॉवर की ऊँचाई AB = h मीटर है।
भिन्न-भिन्न स्थितियों में टॉवर के शिखर के उन्नयन कोण क्रमश: 30° और 60° हैं।
समकोण ΔABC में,
tan 60° = \(\frac{A B}{B C}\)
⇒ \(\sqrt{3}=\frac{h}{x}\)
∴ h = x\(\sqrt{3}\) मीटर …(i)
पुनः समकोण ΔABD में,
⇒ tan 30° = \(\frac{A B}{B D}=\frac{A B}{D C+B C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{20+x}\)
⇒ \(\sqrt{3}\)h = 20 + x
⇒ \(\sqrt{3}\) × x\(\sqrt{3}\) = 20 + x [समीकरण (i) से]
⇒ 3x = 20 + x
⇒ 3x – x = 20
⇒ 2x = 20
∴ x = \(\frac{20}{2}\)
अत: BC = 10 मीटर
समी. (i) में x का मान प्रतिस्थापन करने पर,
h = 10\(\sqrt{3}\)
h = 10 × 1.732 = 17.32 मीटर
AB = 17.32 मीटर
अतः टावर की ऊँचाई = 17.32 मीटर
तथा नहर की चौड़ाई = 10 मीटर

प्रश्न 12.
7 मीटर ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
हल:
माना AB एक केबल टॉवर है। उसी धरातल में एक भवन CD है जिसकी ऊँचाई 7 मीटर है।
केबल टॉवर के शिखर को उन्नयन कोण और पाद का अवनमन कोण क्रमश: 60° और 45° हैं।

अर्थात ∠ACE = 60°
और ∠ECB = 45°
BD || CE, CD || BE
∴ CD = BE = 7 मीटर
अब समकोण त्रिभुज CBD में,
tan 45° = \(\frac{C D}{D B}\)
⇒ 1 = \(\frac{7}{D B}\)
∴ DB = 7 मीटर
CE = DB = 7 मीटर
पुन: समकोण त्रिभुज AEC में,
tan 60° = \(\frac{A E}{C E}\)
⇒ \(\sqrt{3}=\frac{A E}{7}\)
∴ AE = 7\(\sqrt{3}\) मीटर
तब टॉवर AB की ऊँचाई = AE + EB
= 7\(\sqrt{3}\) + 7
= 7\(\sqrt{3}\) + 1) मीटर
अतः केबल टॉवर की ऊँचाई = 7(\(\sqrt{3}\) + 1) मीटर ।

प्रश्न 13.
समुद्र तल से 75 मीटर ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो, तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
हल:
माना 75 मीटर ऊँचे एक प्रकाश स्तम्भ PQ के शिखर P से, A और B जहाजों के अवनमन कोण क्रमश: 30° और 45° हैं।
∴ ∠SPA = 30° = ∠PAQ (एकान्तर कोण)
तथा ∠SPB = 45° = ∠PBQ (एकान्तर कोण)

माना जहाजों के बीच की दूरी AB = x मीटर
समकोण ΔPQB में,
tan 45° = \(\frac{P Q}{B Q}\)
⇒ 1 = \(\frac{75}{B Q}\)
∴ BQ = 75 मीटर
पुन: समकोण ΔPQA में,
tan 30° = \(\frac{P Q}{A Q}=\frac{P Q}{A B+B Q}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{75}{x+75}\)
⇒ x + 75 = 75\(\sqrt{3}\)
x = 75\(\sqrt{3}\) – 75
= 75 (\(\sqrt{3}\) – 1) मीटर
= 75 × 0.732 = 54.90 मीटर
अतः दो जहाजों के बीच की दूरी 75 (\(\sqrt{3}\) – 1) या 54.90 मीटर है।

प्रश्न 14.
1.2 मीटर लम्बी एक लड़की भूमि से 88.2 मीटर की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है (देखिए आकृति)। इस अन्तराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए ।

हल:
माना 1.2 मीटर लम्बी लड़की की आँख ‘A’ है। भूमि से 88.2 मीटर की ऊँचाई पर उड़ रहे गुब्बारे की विभिन्न दूरियों पर उन्नयन कोण क्रमश: 60° और 30° हैं।

∠BAE = 60° और ∠DAC = 30°
BE = CD = 88.2 – 1.2 = 87 मीटर
समकोण ΔABE में,
tan 60° = \(\frac{B E}{A B}\)
⇒ \(\sqrt{3}=\frac{87}{x}\)
⇒ x = \(\frac{87}{\sqrt{3}}\) ….(1)
पुन: समकोण ΔACD में,
tan 30° = \(\frac{C D}{A C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{87}{x+y}\)
⇒ x + y = 87\(\sqrt{3}\)
⇒ x = 87\(\sqrt{3}\) – y ….(2)
समीकरण (1) व (2) से
\(\frac{87}{\sqrt{3}}\) = 87\(\sqrt{3}\) – y
87 = 87 × 3 – \(\sqrt{3}\)y
\(\sqrt{3}\)y = 87 × 3 – 87
\(\sqrt{3}\)y = 261 – 87
\(\sqrt{3}\)y = 174
y = \(\frac{174}{\sqrt{3}}\)
y = \(\frac{174}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
y = \(\frac{174 \sqrt{3}}{3}\)
y = 58\(\sqrt{3}\) मीटर
अतः गुब्बारे द्वारा तय की गई दूरी = 58\(\sqrt{3}\) मीटर

प्रश्न 15.
एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एकसमान चाल से जाती है। छः सेकण्ड बाद कार का अवनमन कोण 60° हो गया। इस बिन्दु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
हल:
माना BCD एक सीधा राजमार्ग है जिसके बिन्दु D पर, AD मीनार खड़ी है जिसकी ऊँचाई h मीटर है। मीनार के शिखर 4 से एक कार B का अवनमन कोण 30° है। 6 सेकण्ड बाद कार का अवनमन कोण 60° हो जाता है।
∵ 6 सेकण्ड में कार द्वारा तय की गई दूरी = BC समकोण ΔABD से,
tan 30° = \(\frac{A D}{B D}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{B D}\)
BD = \(\sqrt{3}\)h …..(i)

पुन: समकोण ΔACD में,
tan 60° = \(\frac{A D}{C D}\)
⇒ \(\sqrt{3}=\frac{h}{C D}\)
∴ h = \(\sqrt{3}\)CD …(ii)
समी (i) मैं h का मान रखने पर
BD = \(\sqrt{3}\) · \(\sqrt{3}\)CD
⇒ BD = 3CD (∵ BD = BC + CD)
⇒ BC + CD = 3CD
⇒ BC = 3CD – CD
⇒ BC = 2CD
⇒ CD = \(\frac{1}{2}\)BC
चूँकि कार एक समान चाल से चल रही है तथा CD दूरी BC की आधी है।
अत: CD दूरी चलने में लगा समय = \(\frac{1}{2}\) × BC दूरी चलने में लगा समय
= \(\frac{1}{2}\) × 6 = 3 सेकण्ड
अतः कार को मीनार के पाद तक पहुँचने में लगा समय = 3 सेकण्ड ।

प्रश्न 16.
मीनार के आधार से और एक सरल रेखा में 4 मीटर और 9 मीटर की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई 6 मीटर है।
हल:
माना CD एक मीनार है जिसकी ऊँचाई h मीटर है।

मीनार के आधार से 4 मीटर दूरी पर बिन्दु B है तथा 9 मीटर दूरी पर बिन्दु A है।
माना ∠DBC = 6 है तो
इसका पूरक ∠DAB = 90° – 6 होगा।
समकोण ΔDCB में,
tan θ = \(\frac{D C}{B C}\)
⇒ tan θ = \(\frac{h}{4}\) …(i)
पुन: समकोण ΔDCA में,
tan (90° – θ) = \(\frac{D C}{A C}\)
⇒ cot θ = \(\frac{h}{9}\)
\(\frac{1}{\tan \theta}=\frac{h}{9}\) …(ii)
समी (i) व (ii) का गुणा करने पर
tan θ × \(\frac{1}{\tan \theta}=\frac{h}{4} \times \frac{h}{9}\)
⇒ \(1=\frac{h^2}{36}\)
⇒ h₂ = 36
⇒ h = \(\sqrt{36}\)
∴ h = 6 मीटर
अतः मीनार की ऊँचाई = 6 मीटर।

Jharkhand Board JAC Class 10 Science Solutions Chapter 15 हमारा पर्यावरण Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 15 हमारा पर्यावरण

Jharkhand Board Class 10 Science हमारा पर्यावरण Textbook Questions and Answers

अभ्यास प्रश्न (पृष्ठ संख्या-297)

प्रश्न 1.
निम्न में से कौन-से समूहों में केवल जैव निम्नीकरणीय पदार्थ हैं-
(a) घास, पुष्प तथा चमड़ा
(b) घास, लकड़ी तथा प्लास्टिक
(c) फलों के छिलके, कंक एवं नींखू का रस
(d) केक, लकड़ी एवं घास
उत्तर:
(a) घास, पुष्प तथा चमड़ा।

प्रश्न 2.
निम्न में से कौन आहार श्रंखला का निर्माण करते हैं-
(a) घास, गेहूँ तथा आम
(b) घास, बकरी तथा मानव
(c) बकरी, गाय तथा हाथी
(d) घास, मछली तथा बकरी
उत्तर:
(b) घास, बकरी तथा मानव।

प्रश्न 3.
निम्न में से कौन पर्यावरण-मित्र व्यवहार कहलाते हैं-
(a) बाजार जाते समय सामान के लिए कपछे का थैला ले जाना
(b) कार्य समाप्त हो जाने पर लाइट (बलंज) तथा पंखे का स्विच बन्द करना
(c) माँ द्वारा स्कूटर से वियालय छोड़े के बजाय तुम्तारे विद्यालय तक पैदल जाना
(d) उपरोक्त सभी
उत्तर:
(d) उपरोक्त सभी।

प्रश्न 4.
क्या होगा यदि हम एक पोषी स्तर के सभी जीवों को समाप्त कर दें (मार डालें)?
उत्तर:
खाद्य श्रृंखला के सभी पोषी स्तरों के जीव भोजन के लिए एक-दूसरे पर निर्भर करते हैं। यदि किसी एक पोषी स्तर के सभी जीव मार दिए जाएँ तो पूरी खाद्य श्रृंखला नष्ट हो जायगी। ऐसा इसलिए होता है क्योंकि इससे खाद्य शृंखला में ऊर्जा का प्रवाह रुक जाता है।

प्रश्न 5.
क्या किसी पोषी स्तर के सभी सदस्यों को हटाने का प्रभाव भिन्न-भिन्न पोषी स्तरों के लिए अलग-अलग होगा? क्या किसी पोषी स्तर के जीवों को पारितंत्र को प्रभावित किए बिना हटाना संभव है?
उत्तर:
अलग-अलग नहीं होते। यह सभी पर समान प्रभाव डालता होता नहीं सभी पोषी स्तरों के लिए प्रभाव है। किसी पोषी स्तर के जीवों को पारितंत्र को प्रभावित किए बिना हटाना संभव नहीं है। इनका हटाना पारितः पारितंत्र में विभिन्न प्रकार के प्रभाव डालता है तथा असंतुलन करता है।

प्रश्न 6.
जैविक आवर्धन (Biological magnification) क्या है? क्या पारितंत्र के विभिन्न स्तरों पर जैविक आवर्धन का प्रभाव भी भिन्न-भिन्न होगा?
उत्तर:
जब कोई हानिकारक रसायन जैसे डी.डी.टी. किसी खाद्य श्रृंखला में प्रवेश करता है तो इसका सान्द्रण धीरे-धीरे प्रत्येक पोषी स्तर में बढ़ता जाता है। इस परिघटना को जैविक आवर्धन कहते हैं। इस आवर्धन का स्तर अलग-अलग पोषी स्तरों पर भिन्न-भिन्न होगा।

प्रश्न 7.
हमारे द्वारा उत्पादित अजैव निम्नीकरणीय कचरे से कौन-सी समस्याएँ उत्पन्न होती हैं?
उत्तर:
अजैव निम्नीकरणीय कचरे के ढेर पर्यावरण में बहुत लम्बे समय तक रहते हैं और नष्ट नहीं होते। अतः वे बहुत-सी समस्याएँ उत्पन्न करते हैं। जैसे-

• ये जल प्रदूषण करते हैं जिससे जल पीने योग्य नहीं रहता।
• ये भूमि प्रदूषण करते हैं जिससे भूमि की सुन्दरता नष्ट होती है।
• ये नालियों में पानी के प्रवाह को रोकते हैं।
• ये वायुमण्डल को भी विषैला बनाते

प्रश्न 8.
यदि हमारे द्वारा उत्पादित सारा कचरा जैव निम्नीकरणीय हो तो क्या इनका हमारे पर्यावरण पर कोई प्रभाव नहीं पड़ेगा?
उत्तर:
जैव निम्नीकरणीय अपशिष्ट लम्बे समय तक नहीं रहते हैं। अतः उनका हानिकारक प्रभाव वातावरण पर पड़ता तो है पर केवल कुछ समय लिए ही रहता है। ये पदार्थ लाभदायक पदार्थों में बदले जा सकते हैं तथा सरल पदार्थों में तोड़े जा सकते हैं। अतः हमारे वातावरण पर इनका भी प्रभाव पड़ता है लेकिन केवल कुछ समय तक ही रहता है।

प्रश्न 9.
ओजोन परत की क्षति हमारे लिए चिंता का विषय क्यों है? इस क्षति को सीमित करने के लिए क्या कदम उठाए गए हैं?
उत्तर:
ओजोन परत की क्षति हमारे लिए अत्यंत चिंता विषय है क्योंकि यदि क्षति अधिक होती है तो अधिक -से-अधिक पराबैंगनी विकिरणें पृथ्वी पर आएँगी जो हमारे लिए निम्न प्रकार हानिकारक प्रभाव डालती हैं।

• इनका प्रभाव त्वचा पर पड़ता है जिससे त्वचा के कैंसर की संभावना बढ़ जाती है।
• पौधों में वृद्धि दर कम हो जाती है।
• ये सूक्ष्म जीवों तथा अपघटकों को मारती हैं इससे पारितंत्र में असंतुलन उत्पन्न हो जाता है।
• ये पौधों में पिगमेंटों को नष्ट करती हैं।

ओजोन परत की क्षति कम करने के उपाय :

• एरोसोल तथा क्लोरोफ्लोरो कार्बन यौगिक का कम से कम उपयोग करना।
• सुपरसोनिक विमानों का कम से कम उपयोग करना।
• संसार में नाभिकीय विस्फोटों पर नियंत्रण करना।

Jharkhand Board Class 10 Science हमारा पर्यावरण InText Questions and Answers

पाठगत प्रश्न (पृष्ठ संख्या – 292)

प्रश्न 1.
पोषी स्तर क्या हैं? एक आहार श्रृंखला का उदाहरण दीजिए तथा इसमें विभिन्न पोषी स्तर बताइए।
उत्तर:
आहार श्रृंखला का प्रत्येक चरण अथवा कड़ी एक पोषी स्तर बनाते हैं।
उदाहरण – दी गई आहार श्रृंखला में चार पोषी स्तर हैं-

प्रश्न 2.
पारितंत्र में अपमार्जकों की क्या भूमिका है?
उत्तर:
पारितंत्र में अपमार्जक का कार्य है कि वह जंतु मृत शरीरों को विघटित करके सरल पदार्थ में न दें। यह मृत कार्बनिक पदार्थों का अपघटन कर निम्न भूमिका निभाते हैं-

• यह पृथ्वी की सतह को साफ करते हैं तथा नई पीढ़ी के लिए स्थान उपलब्ध कराते हैं।
• यह जटिल कार्बनिक पदार्थों को सरल अकार्बनिक पदार्थों में बदल देते हैं जो भू-रासायनिक चक्र में शामिल हो जाते हैं तथा पौधों द्वारा पुनः उपयोग में लाए जाते हैं।

पाठगत प्रश्न (पृष्ठ संख्या-295)

प्रश्न 1.
क्या कारण है कि कुछ पदार्थ जैव निम्नीकरणीय होते हैं और कुछ अजैव निम्नीकरणीय?
उत्तर:
कुछ पदार्थों का जीवाणु अथवा दूसरे मृतजीवियों (saprophytes) द्वारा अपघटन हो जाता है परंतु कुछ पदार्थों का जैविक प्रक्रम द्वारा अपघटन नहीं हो पाता है। अतः सब्जियों के अपशिष्ट, जंतुओं के अपशिष्ट, पत्ते आदि जैव निम्नीकरणीय हैं क्योंकि जीवाणु और कवक जैसे सूक्ष्मजीव इन्हें जटिल से सरल कार्बनिक पदार्थों में बदल देते हैं जबकि प्लास्टिक, पॉलीथीन आदि अजैव निम्नीकरणीय हैं क्योंकि इनका अपघटन नहीं हो पाता है।

प्रश्न 2.
ऐसे दो तरीके सुझाइए जिनमें जैव निम्नीकरणीय पदार्थ पर्यावरण को प्रभावित करते हैं।
उत्तर:
जैव निम्नीकरणीय पदार्थ पर्यावरण को निम्न दो तरीकों से प्रभावित करते हैं-

• पौधों तथा जंतुओं के अवशेष के अपघटन (decomposition) से वातावरण दूषित होता है तथा दुर्गंध (foul smell) फैलती है, जिससे आस-पास रहने वाले लोगों को परेशानी होती है।
• कूड़े-कचरे के ढेर पर अनेक प्रकार की मक्खियाँ, मच्छर आदि पैदा होते हैं, जो कई प्रकार के रोगों के वाहक होते हैं।
  मीथेन गैस, हाइड्रोजन सल्फाइड गैस, CO₂ गैस अपघटन प्रक्रम में निकलते हैं, जिससे प्रदूषण बढ़ता है।

प्रश्न 3.
ऐसे दो तरीके बताइए जिनमें अजैव निम्नीकरण पदार्थ पर्यावरण को प्रभावित करते हैं।
उत्तर:

• अजैव निम्नीकरणीय पदार्थों, जैसे- प्लास्टिक, पॉलीथीन, पीड़कनाशक (DDT) एवं रसायन आदि का अपघटन नहीं होता। ये पदार्थ लम्बे समय तक पर्यावरण में बने रहते हैं तथा जल एवं मृदा प्रदूषण फैलाते हैं।
• अजैव निम्नीकरणीय रासायनिक उर्वरक के अत्यधिक प्रयोग से मिट्टी या तो अम्लीय या क्षारीय हो जाती है, जिससे उर्वरा शक्ति घट जाती है।
• DDT जैसे पीड़कनाशक खाद्यान्न, सब्जियों, फलों आदि के माध्यम हमारे शरीर में पहुँच जाते हैं तथा हमारे स्वास्थ्य को हानि पहुँचाते हैं।

पाठगत प्रश्न (पृष्ठ संख्या – 296)

प्रश्न 1.
ओजोन क्या है तथा यह किसी पारितंत्र को किस प्रकार प्रभावित करती है?
उत्तर:
ओजोन ऑक्सीजन का एक अपर रूप है। इसका एक अणु ऑक्सीजन के तीन परमाणुओं से मिलकर बना होता है। इसका अणुसूत्र O₃ है।

यह ऑक्सीजन के तीन अणुओं की सूर्य के प्रकाश (sun rays) की उपस्थिति में अभिक्रिया द्वारा बनती है।

ओजोन पृथ्वी की सतह पर एक आवरण बनाती है जो पराबैंगनी विकिरणों से बचाती है। यह पराबैंगनी विकिरण हमारे लिए बहुत हानिकारक है। इस प्रकार यह पारितंत्र को नष्ट होने से बचाती है।

प्रश्न 2.
आप कचरा निपटान की समस्या कम करने में क्या योगदान कर सकते हैं? किन्हीं दो तरीकों का वर्णन कीजिए।
उत्तर:

• पदार्थ दो प्रकार के होते हैं- जैव निम्नीकरणीय तथा अजैव निम्नीकरणीय। इनमें से हमें जैव निम्नीकरणीय पदार्थों का अधिक उपयोग करना चाहिए।
• जैव निम्नीकरणीय पदार्थों को खाद में बदल देना चाहिए तथा अजैव निम्नीकरणीय अपशिष्टों को चक्रण के लिए फैक्ट्री में भेज देना चाहिए।

क्रिया-कलाप – 15.1

• संभवत: आपने एक जल जीवशाला (aquarium) देखी होगी। आइए इसे बनाने का प्रयास करते हैं।
• जल जीवशाला बनाते समय हमें किन बातों का ध्यान रखना होगा ? मछलियों को तैरने के लिए पर्याप्त स्थान (एक बड़ा जार भी ले सकते हैं) जल, ऑक्सीजन एवं भोजन।
• हम एक वायु पंप (वातित्र) द्वारा ऑक्सीजन पम्प कर सकते हैं तथा मछली का भोजन बाजार में उपलब्ध होता है।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
यदि हम इसमें कुछ पौधे लगा दें तो यह एक स्वनिर्वाह तंत्र बन जाएगा। क्या आप सोच सकते हैं कि यह कैसे होता है? एक जल जीवशाला मानव निर्मित पारितंत्र का उदाहरण है।
उत्तर:
पौधे प्रकाश संश्लेषण की क्रिया में O₂  गैस छोड़ते हैं। यह O₂ पौधों तथा जन्तुओं की श्वसन क्रिया में उपयोग की जाती है इस क्रिया में CO₂ गैस निकलती CO₂ प्रकाश संश्लेषण में काम आती है। इस प्रकार की जल जीवशाला आत्मनिर्भर बन जाती है।

प्रश्न 2.
क्या हम जल जीवशाला बनाने के उपरांत इसे ऐसे ही छोड़ सकते हैं? यदा-कदा इसकी सफाई की क्या आवश्यकता है? क्या हमें इसी प्रकार तालाबों एवं झीलों की सफाई भी करनी चाहिए? क्यों और क्यों नहीं?
उत्तर:
हम जल जीवशाला को ऐसे ही नहीं छोड़ सकते। इसे कभी-कभी साफ करने की आवश्यकता है क्योंकि यह पौधों तथा जन्तुओं की जैव प्रक्रियाओं द्वारा प्रदूषित हो जाती है। इसी प्रकार हमें तालाबों की सफाई की भी आवश्यकता है क्योंकि ये प्राकृतिक जल जीवशाला हैं। ये भी जीवों की प्रक्रियाओं द्वारा प्रदूषित होते रहते हैं।

क्रिया-कलाप के प्रश्नोत्तर

क्रिया-कलाप – 15.2

प्रश्न 1.
जल जीवशाला बनाते समय क्या आपने इस बात का ध्यान रखा कि ऐसे जलीय जीवों को साथ न रखें जो दूसरों को खा जाएँ। अन्यथा क्या हुआ होता? समूह बनाइए और चर्चा कीजिए कि उपर्युक्त समूहों में जीव एक-दूसरे पर किस प्रकार निर्भर करते हैं?
उत्तर:
यदि हम जल जीवशाला में ऐसे जीव या जन्तु रखें जो एक-दूसरे को खा जाते हैं वो जल जीवशाला नष्ट हैं क्योंकि वे एक-दूसरे को खा जाते हैं अतः विशेष ध्यान रखना चाहिए।

समूहों की एक-दूसरे पर निर्भरता – पादप, सूक्ष्म जीव तथा हरे शैवाल हरे पौधे उत्पादकों का समूह होता है। जो कि उपभोक्ता समूह (जन्तु सूक्ष्मजीव, जन्तु मछली आदि को O₂ तथा भोजन प्रदान करते हैं। जन्तु का समूह CO₂ अपमार्जक जन्तुओं के अपशिष्ट पदार्थों तथा मृतक शरीर को सरल पदार्थों में बदल देते हैं जोकि पौधे करते हैं।

प्रश्न 2.
जलीय जीवों के नाम उसी क्रम में लिखिए जिसमें एक जीव दूसरे जीव को खाता है तथा एक ऐसी श्रृंखला की स्थापना कीजिए जिसमें कम-से-कम तीन चरण हों।
उत्तर:
शैवाल → डाएटम → मछली

प्रश्न 3.
क्या आप किसी एक समूह को सबसे अधिक महत्त्व का मानते हैं? क्यों अथवा क्यों नहीं?
उत्तर:
प्रथम पोषी स्तर में पौधे आते हैं ये स्वपोषी होते हैं। बिना पौधों के खाद्य श्रृंखला नहीं चल सकती अतः पौधों को विशेष महत्त्व दिया जाता है।

क्रिया-कलाप के प्रश्नोत्तर

क्रिया-कलाप – 15.3

प्रश्न 1.
समाचार-पत्रों में तैयार खाद्य सामग्री या भोज्य पदार्थों में पीड़क एवं रसायनों की मात्रा के विषय में प्राय: ही समाचार छपते रहते हैं। कुछ राज्यों ने इन पदार्थों पर रोक भी लगा दी है। इस प्रकार की रोक के औचित्य पर चर्चा कीजिए।
उत्तर:
हाँ, पीड़क तथा रसायनों पर रोक लगाना जरूरी है।

प्रश्न 2.
आपके विचार में इन खाद्य पदार्थों में पीड़कनाशियों का स्रोत क्या है? क्या यह पीड़कनाशी अन्य खाद्य स्रोतों के माध्यम से हमारे शरीर में पहुँच सकते हैं?
उत्तर:
विभिन्न फसलों को रोग एवं पीड़कों से बचाने के लिए पीड़कनाशक (Pesticides) एवं रसायन का प्रयोग किया जाता है, जो हमारे खाद्यान्न गेहूँ, चावल, सब्जियाँ, फल, माँस में पहुँच जाते हैं तथा मनुष्य में सर्वाधिक मात्रा में संचित हो जाते हैं। हाँ, ये अन्य खाद्य स्रोतों के माध्यम से भी हमारे शरीर में पहुँच सकते हैं।

प्रश्न 3.
किन उपायों द्वारा शरीर में इन पीड़कनाशियों की मात्रा कम की जा सकती है। चर्चा कीजिए।
उत्तर:

• पीड़कनाशियों का उपयोग कम-से-कम करें।
• पीड़कनाशियों जैसे D.D.T. के स्थान पर नीम जैसे प्राकृतिक पीड़कनाशी का प्रयोग करें।

क्रिया-कलाप के प्रश्नोत्तर

क्रिया-कलाप – 15.4

प्रश्न 1.
पुस्तकालय, इंटरनेट अथवा समाचार-पत्रों से पता लगाइए कि कौन-से रसायन ओजोन परत के अपक्षय के लिए उत्तरदायी हैं?
उत्तर:
मुख्यत: क्लोरोफ्लोओरो कार्बन (CFCs) द्वारा ओजोन परत में अपक्षय होता है।

प्रश्न 2.
पता लगाइए कि इन पदार्थों के उत्पादन एवं उत्सर्जन के नियमन सम्बन्धी कानून ओजोन क्षरण कम करने में कितने सफल रहे हैं। क्या पिछले कुछ वर्षों में ओजोन छिद्र के आकार में कुछ परिवर्तन आया है।
उत्तर:
हाँ, 1987 में संयुक्त राष्ट्र पर्यावरण कार्यक्रम (UNEP) में सर्वानुमति बनी कि CFCs के उत्पादन को 1986 के स्तर पर ही सीमित रखा जाए, जिससे ओजोन-छिद्र के आकार में हाल के वर्षों में कमी हुई।

क्रिया-कलाप – 15.5

• अपने घर से कचरा एकत्र कीजिए। इसमें पूरे दिन में उत्पन्न कूड़ा-कचरा, जैसे कि रसोई का कूड़ा (संदूषित भोजन, सब्जियों के छिलके, चाय की उपयोग की गई पत्तियाँ, दूध की खाली थैली तथा खाली डिब्बे), रद्दी कागज, दवा की खाली बोतल / स्ट्रिप्स, बबल पैक, पुराने फटे कपड़े तथा टूटे जूते आदि सकते हैं।
• इसे विद्यालय के बगीचे में एक गड्ढे में दबा दीजिए। यदि ऐसा स्थान उपलब्ध न हो तो इस कचरे को किसी पुरानी बाल्टी अथवा गमले में एकत्र करके उसे 15 em मोटी मिट्टी की गर्त से ढक दीजिए।
• इसे नम रखिए तथा 15 दिनों के अंतराल पर इसका अवलोकन करते रहिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
वह कौन-से पदार्थ हैं जो लम्बे समय बाद भी अपरिवर्तित रहते हैं?
उत्तर:
दूध के पैकेट खाली डिब्बे, खाली दवा की बोतलें, स्ट्रिप्स तथा टूटे जूते।

प्रश्न 2.
वे कौन-से पदार्थ हैं जिनके स्वरूप एवं संरचना में परिवर्तन आता है?
उत्तर:
रसोई का कूड़ा, खराब भोजन, सब्जियों के छिलके, चाय की उपयोग की गयी पत्तियाँ, रद्दी कागज, पुराने फटे कपड़े।

प्रश्न 3.
जिन पदार्थों के स्वरूप में समय के साथ परिवर्तन आया है, उनमें कौन-से पदार्थ अतिशीघ्र परिवर्तित हुए हैं?
उत्तर:
संदूषित भोजन तथा सब्जियों के छिलके।

क्रिया-कलाप – 15.6
पुस्तकालय अथवा इंटरनेट द्वारा ‘जैव निम्नीकरणीय’ एवं ‘अजैव निम्नीकरणीय’ पदार्थों के विषय में अधिक जानकारी प्राप्त कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
अजैव निम्नीकरणीय पदार्थ कितने समय तक पर्यावरण में इसी रूप में बने रह सकते हैं?
उत्तर:
ये पदार्थ निष्क्रिय होते हैं तथा पर्यावरण में लम्बे समय तक रहते हैं। ये पदार्थ दशक से शताब्दी तक में नष्ट होते हैं।

प्रश्न 2.
आजकल ‘जैव निम्नीकरणीय प्लास्टिक’ उपलब्ध हैं। इन पदार्थों के विषय में और अधिक जानकारी प्राप्त कीजिए तथा पता लगाइए कि क्या उनसे पर्यावरण को हानि हो सकती है अथवा नहीं।
उत्तर:
आजकल बहुत-सी जैव प्लास्टिक समाचारों में कुछ हैं- फैब्रिक बहुलक जैव निम्नीकरणीय प्लास्टिक अपेक्षाकृत जैव अनिम्नीकरणीय प्लास्टिक से कम हानि पहुँचाते हैं। फिर भी इनका अधिक उत्पादन व उपयोग लम्बे समय तक पदार्थों के चक्रण को प्रभावित करेगा और हैं इनमें से इनके अपघटक उत्पाद भूमि तथा जल प्रदूषण कर सकते हैं।

क्रिया-कलाप के प्रश्नोत्तर

क्रिया-कलाप – 15.7

प्रश्न 1.
पता लगाइए कि घरों में उत्पादित कचरे का क्या होता है? क्या किसी स्थान से इसे एकत्र करने का कोई प्रबंध है?
उत्तर:
हाँ, कचरे एक विशेष स्थान पर एकत्र करने का प्रबन्ध है।

प्रश्न 2.
पता लगाइए कि स्थानीय निकायों (पंचायत, नगरपालिका, आवास कल्याण समिति) द्वारा इसका निपटान किस प्रकार किया जाता है? क्या वहाँ जैव अपघटित तथा अजैव अपघटित कचरे को अलग-अलग करने की व्यवस्था है?
उत्तर:
जैव अपघटित तथा अजैव अपघटित कचरे की अलग व्यवस्था है तथा इनका निपटान अलग-अलग तरीकों से किया जाता है।

जैव अपघटित कचरे को खाद में बदल दिया जाता है। अजैव अपघटित कचरे तथा पदार्थों को पुनः चक्रण के लिए भेज दिया जाता है जिसमें बहुत अधिक समय (वर्षों) लगता है। यह गड्ढों, नीचे धँसी भूमि (Low land area) आदि को भरने में काम आता है।

प्रश्न 3.
गणना कीजिए कि एक दिन में घर से कितना कचरा उत्पादित होता है?
उत्तर:
लगभग 2 kg से 4kg रोजाना।

प्रश्न 4.
इसमें से कितना कचरा जैव निम्नीकरणीय है?
उत्तर:
लगभग 2 kg से 3 kg रोजाना।

प्रश्न 5.
गणना कीजिए कि कक्षा में प्रतिदिन कितना कचरा उत्पादित होता है?
उत्तर:
1\(\frac { 1 }{ 2 }\) kg से 2kg रोजाना।

प्रश्न 6.
इसमें कितना कचरा जैव निम्नीकरणीय है?
उत्तर:
1 kg से 1\(\frac { 1 }{ 2 }\) kg रोजाना।

प्रश्न 7.
इस कचरे के निपटान के कुछ उपाय सुझाइये।
उत्तर:
कक्षा के कचरे में अधिकतर कागज, फलों के छिलके, बनी हुई सब्जी तथा ब्रेड के टुकड़े होते हैं। ये अधिकतर जैव अपघटित पदार्थ हैं और इनका कम्पोस्ट बनाकर स्कूल बगीचे में उपयोग किया जा सकता है।

क्रिया-कलाप के प्रश्नोत्तर

क्रिया-कलाप – 15.8

प्रश्न 1.
पता लगाइए कि आपके क्षेत्र में मल व्ययन की क्या व्यवस्था है? क्या वहाँ इस बात का प्रबंध है कि स्थानीय जलाशय एवं जल के अन्य स्रोत अनउपचारित वाहित मल से प्रभावित न हों ?
उत्तर:
शहर के विभिन्न भागों से प्रदूषित जल को इकट्ठा किया जाता है तथा इसे जल चक्रण केन्द्रों पर भेज दिया जाता है। यह सीवेज को एक बड़े टैंक में एकत्र किया जाता है तथा आधुनिक तकनीकी से इसका उपचार किया जाता है जैसे ग्राइडिंग, सैटलिंग, उदासीनीकरण, जैविक उपचार तथा क्लोरीनीकरण आदि उचित उपचार के बाद जल को नदी अथवा दूसरे स्रोतों में छोड़ दिया जाता है जहाँ इसका पुनः चक्रण किया जाता है।

प्रश्न 2.
अपने क्षेत्र में पता लगाइए कि स्थानीय उद्योग अपने अपशिष्ट (कूड़े-कचरे एवं तरल अपशिष्ट) के निपटान का क्या प्रबंध करते हैं? क्या वहाँ इस बात का प्रबंधन है जिससे सुनिश्चित हो सके कि इन पदार्थों से भूमि तथा जल का प्रदूषण नहीं होगा ?
उत्तर:
विभिन्न औद्योगिक इकाइयाँ अपने अपशिष्ट जल का उपचार विभिन्न तरीकों से करते हैं। इसके बाद इसे नदी आदि में छोड़ दिया जाता है। उपचार की विधियाँ अपशिष्ट जल में उपस्थित रसायनों पर निर्भर करती हैं।

क्रिया-कलाप के प्रश्नोत्तर

क्रिया-कलाप – 15.10

प्रश्न 1.
इंटरनेट अथवा पुस्तकालय की सहायता से. पता लगाएँ कि इलेक्ट्रॉनिक वस्तुओं के निपटान के समय किन खतरनाक वस्तुओं से आपको सुरक्षापूर्वक छुटकारा पाना है? ये पदार्थ पर्यावरण को किस प्रकार प्रभावित करते हैं?
उत्तर:
हानिकारक व खतरनाक पदार्थ – इलेक्ट्रॉनिक आइटम तार, काँच के टुकड़े, प्लास्टिक आदि के साथ लैंड, सिलिकॉन तथा कैडमियम भी होते हैं। ये बहुत विषैले होते हैं। ये मानव व दूसरे जन्तुओं की जनसंख्या को प्रभावित करते हैं। ये जल व भूमि प्रदूषण के कारण होता है। इनके कारण फेफड़े, परिसंचरण एवं वृक्क की गम्भीर बीमारी उत्पन्न होती हैं।

पर्यावरण में इन रसायनों का जैविक आवर्धन होता है तथा यह अधिक मात्रा में मानव शरीर में एकत्र हो जाते हैं। परिणामस्वरूप शरीर की मेटाबोलिज्म प्रभावित होती है जिससे गम्भीर बीमारियाँ हो जाती हैं।

प्रश्न 2.
पता लगाइए कि प्लास्टिक का पुनः चक्रण किस प्रकार होता है? क्या प्लास्टिक के पुनः चक्रण का पर्यावरण पर कोई समाघात होता है?
उत्तर:
प्लास्टिक के चक्रण में प्लास्टिक को पिघलाकर कुछ रसायनों जैसे सल्फर तथा एस्फाल्ट में मिलाकर सड़क बनाने के काम आता है। इस प्रक्रिया में हानिकारक गैसें वायु में मिल जाती हैं तथा वायु प्रदूषण होता है। कभी-कभी प्लास्टिक को विलायकों में घोल दिया जाता है तब यह रंगहीन हो जाता है या विभिन्न रंगों में मिला देते हैं। अन्त में प्लास्टिक अलग कर लिया जाता है तथा पुनः चक्रण को भेज देते हैं। इस प्रकार विलायक वाष्पित हो जाता है और वायु प्रदूषण फैलता है।