Month: November 2024

Jharkhand Board JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.1 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.1

Question 1.
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 4x² – 3x + 7
(ii) y² + \( \sqrt{2} \)
(iii) 3\( \sqrt{t} \) + t\( \sqrt{2} \)
(iv) y + \(\frac{2}{y}\)
(v) x¹⁰ + y³ + t⁵⁰
Answer:
(i) 4x² – 3x + 7
There is only one variable x with whole number powers so this is a polynomial in one variable.

(ii) y² + \( \sqrt{2} \)
There is only one variable y with whole number powers so this is a polynomial in one variable.

(iii) 3\( \sqrt{t} \) + t\( \sqrt{2} \)
There is only one variable t but in 3\( \sqrt{t} \) power of t is \(\frac{1}{2}\) which is not a whole number. So, 3\( \sqrt{t} \) + t\( \sqrt{2} \) is not a polynomial.

(iv) y + \(\frac{2}{y}\)
There is only one variable y but \(\frac{2}{y}\) = 2y^-1 So, the power of y is not a whole number in the second term. Hence, y + \(\frac{2}{y}\) is not a polynomial.

(v) x¹⁰ + y³ + t⁵⁰
There are three variables x, y and t. So, this is not a polynomial in one variable.

Question 2.
Write the coefficients of x² in each of the following:
(i) 2 + x² + x
(ii) 2 – x² + x³
(iii) \(\frac{π}{2}\)x² + x
(iv) \( \sqrt{2} \) – 1
Answer:
(i) Coefficient of x² = 1
(ii) Coefficient of x² = -1
(iii) Coefficient of x² = \(\frac{π}{2}\)
(iv) Coefficient of x² = 0

Question 3.
Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Answer:
3x³⁵ + 7 and 4x¹⁰⁰ are binomials of degree 35 and monomial of degree 100 respectively.

Question 4.
Write the degree of each of the following polynomials:
(i) 5x³ + 4x² + 7x
(ii) 4 – y²
(iii) 5t – \( \sqrt{7} \)
(iv) 3
Answer:
(i) 5x³ has highest power in the given polynomial, which is 3. Therefore, degree of polynomial is 3.
(ii) -y² has highest power in the given polynomial, which is 2. Therefore, degree of polynomial is 2.
(iii) 5t has highest power in the given polynomial, which is 1. Therefore, degree of polynomial is 1.
(iv) There is no variable in the given polynomial. Therefore, degree of polynomial is 0.

Question 5.
Classify the following as linear, quadratic and cubic polynomials:
(i) x² + x
(ii) x – x³
(iii) y + y² + 4
(iv) 1 + x
(v) 3t
(vi) r²
(vii) 7x³
Answer:
(i) x² + x Quadratic Polynomial
(ii) x – x³ Cubic Polynomial
(iii) y + y² + 4 Quadratic Polynomial
(iv) 1 + x Linear Polynomial
(v) 3t Linear Polynomial
(vi) r² Quadratic Polynomial
(vii) 7x³ Cubic Polynomial

Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 Triangles Ex 7.2 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.2

Page-123

Question 1.
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A

Answer:
Given: AB = AC, the bisectors of ∠B and ∠C intersect each other at O.
Proof:
(i) Since ABC is an isosceles with AB = AC,
∴ ∠B = ∠C (Angles opposite to equal sides are equal)
⇒ \(\frac{1}{2}\)∠B = \(\frac{1}{2}\)∠C (As OB and OC bisects ∠B and ∠C)
⇒ ∠OBC = ∠OCB (Angle bisectors)
⇒ OB = OC (Sides opposite to the equal angles are equal)

(ii) In ΔABO and ΔAOC,
AB = AC (Given)
AO = AO (Common)
OB = OC (Proved above)
Therefore, ΔABO ≅ ΔACO by SSS congruence criterion.
∠BAO = ∠CAO (by CPCT)
Thus, AO bisects ∠A.

Question 2.
In ΔABC, AD is the perpendicular bisector of BC (see Fig). Show that ΔABC is an isosceles triangle in which AB = AC.

Answer:
Given: AD is the perpendicular bisector of BC
To prove: AB = AC
Proof: In ΔADB and ΔADC,
AD = AD (Common)
∠ADB = ∠ADC = 90° (AD ⊥ BC)
BD = CD (AD bisects BC)
Therefore, ΔADB ≅ ΔADC by SAS congruence criterion.
AB = AC (by CPCT)
∴ AABC is an isosceles triangle.

Page-124

Question 3.
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig). Show that these altitudes are equal.

Answer:
Given BE and CF are altitudes.
To prove: BE = CF
Proof: In ΔAEB and ΔAFC,
∠A = ∠A (Common)
∠AEB = ∠AFC (Right angles)
AB = AC (Given)
Therefore, ΔAEB ≅ ΔAFC by AAS congruence criterion.
Thus, BE = CF (CPCT)

Question 4.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig). Show that

(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
Answer:
Given: BE = CF
Proof: (i) In ΔABE and ΔACF,
∠A = ∠A (Common)
∠AEB = ∠AFC (Right angles)
BE = CF (Given)
Therefore, ΔABE ≅ ΔACF by AAS congruence criterion.

(ii) Thus, AB = AC by CPCT and therefore, ABC is an isosceles triangle.

Question 5.
ABC and DBC are two isosceles triangles on the same base BC (see Fig). Show that ∠ABD = ∠ACD.

Answer:
Given: ABC and DBC are two isosceles triangles.
To prove: ∠ABD = ∠ACD
Proof: In ΔABD and ΔACD,
AD = AD (Common)
AB = AC (ABC is an isosceles triangle)
BD = CD (BCD is an isosceles triangle)
Therefore, ΔABD ≅ ΔACD by SSS congruence criterion.
Thus, ∠ABD = ∠ACD (CPCT)

Question 6.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig). Show that ∠BCD is a right angle.

Answer:
Given: AB = AC and AD = AB
To prove: ∠BCD is a right angle.
Proof: In ΔABC,
AB = AC (Given)
AB = AD (Given)
∴ AC = AD …(i)
AB = AC (Given)
⇒ ∠ACB = ∠ABC (Angles opposite to the equal sides are equal.)

In ΔACD,
AD = AC (From (i))
⇒ ∠ADC = ∠ACD (Angles opposite to the equal sides are equal.)
In ΔBCD, ∠B + ∠C + ∠D = 180°
⇒ ∠B + (∠BCA + ∠DCA) + ∠D = 180°
⇒ 2 ∠BCA + 2 ∠ACD = 180°
(∵∠ACB = ∠ABC and ∠ADC = ∠ACD)
⇒ ∠BCA + ∠ACD = 90°
⇒ ∠BCD = 90°.

Question 7.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

Answer:
Given: ∠A = 90° and AB = AC
Proof: AB = AC
⇒ ∠C = ∠B (Angles opposite to the equal sides are equal)
Now, ∠A + ∠B + ∠C = 180° (Sum of the interior angles of the triangle)
⇒ 90° + 2∠B = 180° (∵∠B = ∠C)
⇒ 2∠B = 90°
⇒ ∠B = 45°
Thus, ∠B = ∠C = 45°

Question 8.
Show that the angles of an equilateral triangle are 60° each.

Answer:
Let ABC be an equilateral triangle.
BC = AC = AB (Length of all sides in an equilateral triangle is same)
⇒ ∠A = ∠B = ∠C (Sides opposite to the equal angles are equal)
Also, ∠A + ∠B + ∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
Therefore, ∠A = ∠B = ∠C = 60°
Thus, the angles of an equilateral triangle are 60° each.

Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 Triangles Ex 7.1 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.1

Page-118

Question 1.
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see Fig). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

Answer:
Given: AC = AD and AB bisects ∠A
To prove: ΔABC ≅ ΔABD
Proof: In AABC and AABD,
AB = AB (Common)
AC = AD (Given)
∠CAB = ∠DAB (AB is bisector)
Therefore, ΔABC ≅ ΔABD by SAS congruence criterion.
BC = BD (By CPCT).

Page-119

Question 2.
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig). Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

Answer:
Given: AD = BC and ∠DAB = ∠CBA
Proof:
(i) In ΔABD and ΔBAC,
AB = BA (Common)
∠DAB = ∠CBA (Given)
AD = BC (Given)
Therefore, ΔABD ≅ ΔBAC by SAS
congruence criterion.

(ii) Since, ΔABD ≅ ΔBAC Therefore, BD = AC (by CPCT)

(iii) Since, ΔABD ≅ ΔBAC Therefore, ∠ABD = ∠BAC (by CPCT)

Question 3.
AD and BC are equal perpendiculars to a line segment AB (see Fig). Show that CD bisects AB.

Answer:
Given: AD and BC are perpendiculars to AB.
To prove: CD bisects AB i.e. OA = OB
Proof: In ΔAOD and ΔBOC,
∠A = ∠B = 90° (Perpendicular)
∠AOD = ∠BOC (Vertically opposite angles)
AD = BC (Given)
Therefore, ΔAOD ≅ ΔBOC by AAS congruence criterion.
Now, AO = OB (CPCT) i.e. CD bisects AB.

Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig). Show that ΔABC ≅ ΔCDA.

Answer:
Given: l || m and p || q
To prove: ΔABC ≅ ΔCDA
Proof: In ΔABC and ΔCDA,
As l || m
∴ ∠BCA = ∠DAC
(Alternate interior angles) AC = CA (Common)
As p 11q
∴ ∠BAC = ∠DCA (Alternate interior angles)
Therefore, ΔABC ≅ ΔCDA by ASA congruence criterion.

Question 5.
Line l is the bisector of an angle ∠A and B is any point on P. BP and BQ are perpendiculars from B to the arms of ∠A (See Fig.) Show that

(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Answer:
Given: l is the bisector of an angle ∠A.
BP and BQ are perpendiculars.
Proof:
(i) In AAPB and AAQB,
∠P = ∠Q (Right angles)
∠BAP = ∠BAQ (l is bisector)
AB = AB (Common)
Therefore, ΔAPB ≅ ΔAQB by AAS congruence criterion.

(ii) BP = BQ by CPCT.
(∵ ΔAPB ≅ ΔAQB)
Therefore, B is equidistant from the arms of ∠A.

Page-120

Question 6.
In Fig, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Answer:
Given: AC = AE, AB = AD and ∠BAD = ∠EAC
To prove: BC = DE
Proof: ∠BAD = ∠EAC
∠BAD + ∠DAC = ∠EAC + ∠DAC (Adding ∠DAC both sides)
⇒ ∠BAC = ∠EAD
In AABC and AADE,
AC = AE (Given)
∠BAC = ∠EAD AB = AD (Given)
Therefore, ΔABC ≅ ΔADE by SAS congruence criterion.
BC = DE (by CPCT).

Question 7.
AB is a line segment and P is its mid¬point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig). Show that

(i) ΔDAP ≅ ΔEBP
(ii) AD = BE
Answer:
Given: P is mid-point of AB.
∠BAD = ∠ABE and ∠EPA = ∠DPB
Proof:
(i) ∠EPA = ∠DPB
∠EPA + ∠DPE = ∠DPB + ∠DPE (Adding ∠DPE both sides)
⇒ ∠DPA = ∠EPB
In ΔDAP and ΔEBP,
∠DPA = ∠EPB
AP = BP (P is mid-point of AB)
∠BAD = ∠ABE (Given)
Therefore, ΔDAP ≅ ΔEBP by ASA congruence criterion.

(ii) AD = BE (by CPCT)

Question 8.
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig). Show that:

(i) ΔAMC ≅ ΔBMD
(ii) ∠DRC is a right angle.
(iii) ΔDBC ≅ ΔACB
(iv) CM = \(\frac{1}{2}\)AB
Answer:
Given: ∠C = 90°, M is the mid-point of AB and DM = CM
Proof:
(i) In ΔAMC and ΔBMD,
AM = BM (M is the mid-point of AB)
∠CMA = ∠DMB (Vertically opposite angles)
CM = DM (Given)
Therefore, ΔAMC ≅ ΔBMD by SAS congruence criterion.

(ii) ∠ACM = ∠BDM (by CPCT)
Therefore, AC || BD as alternate interior angles are equal.
Now, ∠ACB + ∠DBC = 180° (co-interior angles)
⇒ 90° + ∠DBC = 180°
⇒ ∠DBC – 90°

(iii) In ΔDBC and ΔACB,
BC = CB (Common)
∠ACB = ∠DBC (Right angles)
DB = AC (by CPCT)
Therefore, ΔDBC ≅ ΔACB by SAS congruence criterion.

(iv) DC = AB (CPCT)
DM + CM = AB
⇒ CM + CM = AB (∵ DM = CM)
⇒ CM = AB
⇒ CM = \(\frac{1}{2}\) AB

Jharkhand Board JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.4

Question 1.
Determine which of the following polynomials has (x + 1) a factor:
(i) x³ + x² + x + 1
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² – (2 + \( \sqrt{2} \))x + \( \sqrt{2} \)
Answer:
(i) If (x + 1) is a factor of p(x)
=x³ + x² + x + 1, p(-1) must be zero.
p(-1) = (-1)³ + (-1)² + (-1) + 1
= – 1 + 1 – 1 + 1 = 0
Therefore, x + 1 is a factor of this polynomial.

(ii) If (x+ 1) is a factor of p(x)
= x⁴ + x³ + x² + x + 1, p(-1) must be zero.
∴ p(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1) + 1
= 1 – 1 + 1 – 1 + 1 = 1 ≠ 0
Therefore, x + 1 is not a factor of this polynomial.

(iii) If (x + 1) is a factor of polynomial
x⁴ + 3x³ + 3x² + x + 1, p(-1) must be 0.
P(-1) = (-1)⁴ + 3(-1)³ + 3(-1)² + (-1) + 1
= 1 – 3 + 3 – 1 + 1 = 1 ≠ 0
Therefore, x + 1 is not a factor of this polynomial.

(iv) If (x + 1) is a factor of polynomial
p(x) = x³ – x² – (2 + \( \sqrt{2} \))x + \( \sqrt{2} \) , p(-1) must be 0.
p(-1) = (-1)³ – (-1)² – (2 + \( \sqrt{2} \))(-1) + \( \sqrt{2} \)
= -1 – 1 + 2 + \( \sqrt{2} \) + \( \sqrt{2} \)
= 2\( \sqrt{2} \) ≠ 0
Therefore, x + 1 is not a factor of this polynomial.

Question 2.
Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x³ + x² – 2x – 1, g(x) = x + 1
(ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2
(iii) p(x) = x³ – 4x² + x + 6, g(x) = x – 3
Answer:
(i) If g(x) = x + 1 is a factor of given polynomial p(x), then p(- 1) must be zero.
P(-1) = 2(-1)³ + (-1)² – 2(-1) – 1
= 2(-1) + 1 + 2 – 1 = 0
Hence, g(x) = x + 1 is a factor of p(x).

(ii) If g(x) = x + 2 is a factor of given polynomial p(x),then p(-2) must be 0.
p(-2) = (-2)³ + 3(-2)² + 3(-2) + 1
= – 8 + 12 – 6 + 1 = -1 ≠ 0
Hence g(x) = x + 2 is not a factor of p(x).

(iii) If g(x) = x – 3 is a factor of given polynomial p(x), then p(3) must be 0.
p(3) = (3)³ – 4(3)² + 3 + 6 = 27 – 36 + 9 = 0

Therefore, g(x) = x – 3 is a factor of p(x).

Page – 44

Question 3.
Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
(i) p(x) = x² + x + k
(ii) p(x) = 2x² + kx + \( \sqrt{2} \)
(iii) p(x) = kx² – \( \sqrt{2} \) x + 1
(iv) p(x) = kx² – 3x + k
Answer:
(i) If x – 1 is a factor of polynomial p(x)
= x² + x + k, then p(1) = 0
⇒ (1)²+ 1 + k = 0
⇒ 2 + k = 0
⇒ k = – 2
Therefore, value of k is – 2.

(ii) If x – 1 is a factor of polynomial p(x) = 2x² + kx + \( \sqrt{2} \) , then p(1) = 0
⇒ 2(1)² + k(1) + = 0
⇒ 2 + k + \( \sqrt{2} \) = 0
⇒ k = – 2 – \( \sqrt{2} \) = – (2 + \( \sqrt{2} \))
Therefore, value of k is – (2 + \( \sqrt{2} \) ).

(iii) If x – 1 is a factor of polynomial p(x) = kx² – \( \sqrt{2} \) x + 1, then p(1) = 0
⇒ k(1)² – \( \sqrt{2} \) (1) + 1 = 0
⇒ k – \( \sqrt{2} \) +1 = 0
⇒ k = \( \sqrt{2} \) – 1
Therefore, value of k is \( \sqrt{2} \) – 1.

(iv) If x – 1 is a factor of polynomial p(x) = kx² – 3x + k, then p(1) = 0
⇒ k(1)² – 3(1) + k = 0
⇒ k – 3 + k= 0
⇒ 2k – 3 = 0
Therefore, value of k is \(\frac{3}{2}\)

Question 4.
Factorise:
(i) 12x² – 7x + 1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6
(iv) 3x² – x – 4
Answer:
(i) 12x² – 7x + 1
= 12x² – 4x – 3x+ 1
= 4x (3x – 1) – 1 (3x – 1)
= (3x – 1) (4x – 1)

(ii) 2x² + 7x + 3
= 2x² + 6x + x + 3
= 2x (x + 3) + 1 (x + 3)
= (x + 3) (2x + 1)

(iii) 6x² + 5x – 6
= 6x² + 9x – 4x – 6
= 3x (2x + 3) – 2 (2x + 3)
= (2x + 3) (3x – 2)

(iv) 3x² – x – 4
= 3x² – 4x + 3x – 4
= x (3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)

Question 5.
Factorise:
(i) x³ – 2x² – x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20
(iv) 2y³ + y² – 2y – 1
Answer:
(i) Let p(x) = x³ – 2x² – x + 2
Factors of 2 are ±1 and ± 2
By trial method, we find that p(-1) = 0
So, (x + 1) is factor of p(x)

Now, Dividend = Divisor × Quotient + Remainder
= (x + 1) (x² – 3x + 2)
= (x + 1) (x² – x – 2x + 2)
= (x+ 1) {x(x – 1) – 2(x – 1)}
= (x + 1) (x – 1) (x – 2)

(ii) Let p(x) = x³ – 3x² – 9x – 5
Factors of 5 are ±1 and ±5
By trial method, we find that
p(5) = 0
So, (x – 5) is factor of p(x)

Now, Dividend = Divisor × Quotient + Remainder
= (x – 5) (x² + 2x + 1)
= (x – 5) (x² + x + x + 1)
= (x – 5) {x(x + 1) +l(x + 1)}
= (x – 5) (x + 1) (x + 1)

(iii) Let p(x) = x³ + 13x² + 32x + 20
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
P(-1) = 0
So, (x+1) is factor ofp(x)

Now, Dividend = Divisor × Quotient + Remainder
= (x + 1) (x² + 12x + 20)
= (x + 1) (x² + 2x + 10x + 20)
= (x + 1) {x(x+2) +10(x+2)}
= (x + 1) (x+2) (x+10)

(iv) Let p(y) = 2y³ + y² – 2y – 1
Factors of ab = 2 × (-1) = – 2 are ±1 and ±2
By trial method, we find that p(1) = 0
So, (y – 1) is factor of p(y)

Now, Dividend = Divisor × Quotient + Remainder
= (y – 1) (2y² + 3y + 1)
= (y – 1) (2y² + 2y + y + 1)
= (y – 1) {2y(y + 1) + 1(y + 1)}
= (y – 1 )(2y + 1) (y + 1)

Jharkhand Board JAC Class 10 Maths Solutions Chapter 12 Areas Related to Circles Ex 12.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 12 Areas Related to Circles Exercise 12.3

Unless stated otherwise, use π = \(\frac{22}{7}\)

Question 1.
Find the area of the shaded region in the figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.

Solution:
Given, PQ = 24 cm, PR = 7 cm.
We know any triangle drawn from diameter RQ to the circle is 90°.
Here, ∠RPQ = 90°
In right ΔRPQ, RQ² = PR² + PQ² (By Pythagoras theorem)
RQ² = 7² + 24²
RQ² = 49 + 576
RQ² = 625
RQ = 25 cm
∴ Area of ΔRPQ = \(\frac{1}{2}\) × RP × PQ
= \(\frac{1}{2}\) × 7 × 24 = 84 cm²
∴ Area of semi-circle = \(\frac{\pi r^2}{2}=\frac{22}{7 \times 2}\left(\frac{25}{2}\right)^2\) (∵ r = \(\frac{\mathrm{PQ}}{2}=\frac{25}{2}\) cm)
= \(\frac{11 \times 625}{28}=\frac{6875}{28} \mathrm{~cm}^2\)
∴ Area of the shaded region = Area of the semi-circle – Area of right ΔRPQ
= \(\frac{6875}{28}-84\)
= \(\frac{6875-2352}{28}=\frac{4523}{28}\) cm².

Question 2.
Find the area of the shaded region in the figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.

Solution:
R – radius of the bigger circle, r – radius of the smaller circle.
Area of the shaded portion = Area of sector OAC – Area of sector OBD

Question 3.
Find the area of the shaded region in the figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.

Solution:
Area of the shaded portion = Area of the square – 2 × Area of one semicircle
= (14 × 14) – 2 × \(\frac{\pi r^2}{2}\) [∵ r = 7]
= 14 × 14 – 2 × \(\frac{22}{7} \times \frac{7 \times 7}{2}\)
= 196 – 154 = 42 cm².

Question 4.
Find the area of the shaded region in the figure, where a circular are of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.

Solution:
Area of the shaded portion = Area of the circle of radius 6 cm + Area of equilateral ΔABC – Area of the sector

Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.

Solution:
Area of the shaded portion = Area of the square – Area of the 4 quadrants – Area of the circle
= (4 × 4) – 4 × area of one quadrant – area of the circle

Question 6.
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the figure. Find the area of the design.

Solution:
Area of the design (shaded region) = Area of the circle – Area of ΔABC
Area of equilateral triangle ABC = \(\frac{\sqrt{3} a^2}{4}\)
In ΔABC, AL ⊥ BC.

Alternative Method:

Area of shaded region
= 3[Area of segments]
= 3[Area of sector – Area of ΔOBC]
= 3[\(\pi r^2 \frac{\theta}{360^{\circ}}-\frac{1}{2}\) × BC × OL]

Question 7.
In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region.

Solution:
Area of the shaded region = Area of the square – Area of the 4 quadrants
= Area of the square – 4 × area of one quadrant
= (14)² – 4 × \(\frac{1}{4}\)πr²
= (14)² – 4 × \(\frac{1}{4} \times \frac{22}{7}\) × 7 × 7
= 196 – 154
= 42 cm².

Question 8.
The figure depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m. long. If the track is 10 m wide, find:
(i) the distance around the track along its inner edge.
(ii) the area of the track.

Solution:
i) Distance around the inner track

ii) Area of the track:

Area of the track = l × b + l × b + 2\(\left[\frac{\pi \mathrm{R}^2}{2}-\frac{\pi \mathrm{r}^2}{2}\right]\) r = 30 mts, R = (30 + 10) = 40 mts.
= 106 × 10 + 106 × 10 + 2 × \(\frac{\pi}{2}\)(R² – r²)
= 1060 + 1060 + \(\frac{22}{7}\)[40² – 30²]
= 2120 + \(\frac{22}{7}\)[1600 – 900]
= 2120 + \(\frac{22}{7}\)[700]
= 2120 + 2200
= 4320 m².

Question 9.
In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Solution:
Given,
OA = 7 cm
∴ OD = 7 cm
Now, area of smaller circle whose diameter (OD) = 7 cm is

Now,
Area of ΔABC = \(\frac{1}{2}\) × AB × OC
= \(\frac{1}{2}\) × 2 × OA × OC
= \(\frac{1}{2}\) × 14 × 7 (∵ OA = OC)
= 49 cm².
Area of semi-circle ABCA = \(\frac{\pi r^2}{2}=\frac{22}{7 \times 2}(7)^2\)
= 77 cm²
∴ Area of segments BC and AC = Area of semi-circle – Area of AABC
= 77 – 49 = 28 cm²
∴ Area of total shaded region = Area of small circle + Area of segments BC and AC
= \(\frac{77}{2}\) + 28
= 38.5 + 28
= 66.5 cm².

Question 10.
The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle. Find the area of the shaded region. (Use π = 3.14 and \(\sqrt{3}\) = 1.73205).

Solution:
Area of the shaded portion = Area of equilateral ΔABC – Area of sector Axy – Area of sector Bxz – Area of sector Cyz.
π = 3.14, θ = 60°, r = ?, r = \(\frac{a}{2}\)
Area of the shaded portion = Area of the equilateral Δ – 3 × Area of one sector

Area of the shaded region = Area of ΔABC – \(\frac{3 \times \pi r^2 \theta}{360}\)
= 17320.5 – \(\frac{3 \times 3.14 \times 100 \times 100 \times 60}{360}\)
= 17320.5 – 1.57 × 10000
= 17320.5 – 15700.0
= 1620.5 sq.cm.

Question 11.
On a square handkerchief, nine circular designs each of radius 7 cm are made. Find the area of the remaining portion of the handkerchief.

Solution:
Number of circular designs = 9
Radius of the circular design = 7 cm
There are three circles in one side of the square handkerchief.
∴ Side of the square = 3 × diameter of circle = 3 × 14 = 42 cm
Area of the square = 42 × 42 cm² = 1764 cm²
Area of the circle = πr² = \(\frac{22}{7}\) × 7 × 7 = 154 cm²
Total area of the design = 9 × 154 = 1386 cm²
Area of the remaining portion of the handkerchief = Area of the square – Total area of the design
= 1764 – 1386
= 378 cm².

Question 12.
In the figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm find the area of the (i) quadrant OACB, (ii) shaded region.

Solution:

Question 13.
In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)

Solution:
Radius of the quadrant = Diagonal of the square (OB)
OB² = OA² + AB²
= 20² + 20²
= 400 + 400
= 800
OB2 = 400 × 2
OB = \(\sqrt{400 \times 2}\) = 20\(\sqrt{2}\)
Area of the shaded region = Area of the quadrant OPBQ – Area of the square OABC
= \(\frac{1}{4}\) πr² – (OA)²
= \(\frac{1}{4}\) × 3.14 × 20\(\sqrt{2}\) × 20\(\sqrt{2}\) – (20)²
= \(\frac{1}{4}\) × 3.14 × 400 × \(\sqrt{4}\) – 400
= \(\frac{1}{4}\) × 3.14 × 400 × 2 – 400
= 100 × 2 × 3.14 – 400
= 100 × 2(3.14 – 2)
= 200 × 1.14
= 228 sq.cm.

Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O. If ∠AOB = 30°, find the area of the shaded region.

Solution:
R = 21, r = 7, θ = 30°, π = \(\frac{22}{7}\)
Area of the shaded region = Area of sector OAB – Area of sector OCD

Question 15.
In the figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Solution:
BC² = 14² + 14²
BC² = 196 + 196 = 392
BC = \(\sqrt{392}\) = \(\sqrt{196 \times 2}\) = 14\(\sqrt{2}\) = d
r = \(\frac{14 \sqrt{2}}{2}=7 \sqrt{2}\)
Radius of the sector = 14.
Area of the shaded region Area of the semicircle BEC – Area of the segment BDCB

Question 16.
Calculate the area of the designed region in the figure common between the two quadrants of circles of radius 8 cm each.

Solution:
Area of the design = Area of sector DXB + Area of ΔDCB
Area of the segment DXB = Area of the sector DXBC – Area of ΔDCB

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.5 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.5

Question 1.
Classify the following numbers as rational or irrational:
(i) 2 – \(\sqrt{5}\)
(ii) (3 + \( \sqrt{23}\)) – \(\sqrt{23}\)
(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
(iv) \(\frac{1}{\sqrt{2}}\)
(v) 2π
Answer:
(i) 2 – \(\sqrt{5}\) = 2 – 2.2360679…
= -0.2360679…
Since the number is non-terminating non-recurring therefore, it is an irrational number.

(ii) (3 + \(\sqrt{23}\)) – \(\sqrt{23}\)
3 + \( \sqrt{23}\) – \(\sqrt{23}\)
= 3 = \(\frac{3}{1}\)
The number is rational number as it can represented in \(\frac{p}{q}\) form, where p, q ∈ Z, q ≠ 0

(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
The number is rational number as it can represented in \(\frac{p}{q}\) form, where p, q ∈ Z, q ≠ 0

(iv) \(\frac{1}{\sqrt{2}}\)
= 0.7071067811…
Since the number is non-terminating non-recurring therefore, it is an irrational number.

(v) 2π = 2 × 3.1415… = 6.2830…
Since the number is non-terminating non-recurring therefore, it is an irrational number.

Question 2.
Simplify each of the following expressions:
(i) (3 + \(\sqrt{3}\)) (2 + \(\sqrt{2}\))
(ii) (3 + \(\sqrt{3}\)) (3 – \(\sqrt{3}\))
(iii) (\(\sqrt{5}\) + \(\sqrt{2}\))²
(iv) (\(\sqrt{5}\) – \(\sqrt{2}\))(\(\sqrt{5}\) + \(\sqrt{2}\))
Answer:
(i) (3 + \(\sqrt{3}\)) (2 + \(\sqrt{2}\))
= 3 × 2 + 2\(\sqrt{3}\) + 3\(\sqrt{2}\) + \(\sqrt{3}\) ×\(\sqrt{2}\)
= 6 + 2\(\sqrt{3}\) + 3\(\sqrt{2}\) + \(\sqrt{6}\)

(ii) (3 + \(\sqrt{3}\)) (3 – \(\sqrt{3}\))
= 3²– (\(\sqrt{3}\))² = 9 – 3 = 6
[∵ (a + b) (a – b) = a² – b²]

(iii) (\(\sqrt{5}\) + \(\sqrt{2}\))²
= (\(\sqrt{5}\))² + (\(\sqrt{2}\))² + 2 × \(\sqrt{5}\) × \(\sqrt{2}\)
[∵ (a + b)² = a² + b² + 2ab]
= 5 + 2 + 2 × \(\sqrt{5}\) ×\(\sqrt{2}\)
= 7 + 2\(\sqrt{10}\)

(iv) (\(\sqrt{5}\) – \(\sqrt{2}\))(\(\sqrt{5}\) + \(\sqrt{2}\))
= (\(\sqrt{5}\))² – (\(\sqrt{2}\))²
= 5 – 2 = 3
[∵ (a + b) (a – b) = a² – b²]

Question 3.
Recall, 7t is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, n = c/d. This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
Answer:
There is no contradiction. When we measure a value with a scale, we only obtain an approximate value. We never obtain an exact value. Therefore, we may not realise that either c or d is irrational. The value of n is almost equal to 22/7 or 3.14159…

Question 4.
Represent \(\sqrt{9.3}\) on the number line.
Answer:
Step 1: Draw a line segment AB of 9.3 units. Extend it to C so that BC is of 1 unit.
Step 2: Now, AC = 10.3 units. Find the midpoint of AC and name it as O.
Step 3: Draw a semicircle with radius OC and centre O.
Step 4: Draw a perpendicular line segment BD to AC at point B which intersects the semicircle at D. Also, Join OD.
Step 5: Now, OBD is a right angled triangle.

Here, OD = 10.3/2 (radius of semicircle),
OC = \(\frac{10.3}{2}\), BC = 1
OB = OC – BC = (\(\frac{10.3}{2}\)) – 1 = \(\frac{8.3}{2}\)
Using Pythagoras theorem
OD² = BD² + OB²

Thus, the length of BD is \(\sqrt{9.3}\) units.

Step 6: Taking BD as radius and B as centre draw an arc which touches the line segment AC extended at the point E. The point E is at a distance of \(\sqrt{9.3}\) from B as shown in the figure.

Question 5.
Rationalise the denominators of the following:
(i) \(\frac{1}{\sqrt{7}}\)
(ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
(iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)
(iv) \(\frac{1}{\sqrt{7}-2}\)
Answer:
(i) \(\frac{1}{\sqrt{7}}\) = \(\frac{1 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}}\) = \(\frac{\sqrt{7}}{7}\)

(ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)

(iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)

(iv) \(\frac{1}{\sqrt{7}-2}\)

Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 Triangles Ex 7.5 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.5

Page-133

Question 1.
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.

Answer:
In ΔABC, we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC and CA of this triangle. 0 is the point where these bisectors meet. Therefore, O is the point which is equidistant from all the vertices of ΔABC.

Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Answer:
The point which is equidistant from all the sides of a triangle is called the incentre of the triangle. Incentre of a triangle is the intersection point of the angle bisectors of the interior angles of that triangle.

In ΔABC, we can the find the incentre of this triangle by drawing the angle bisectors of the interior angles ∠A, ∠B and ∠C of this triangle. O is the point where these angle bisectors meet. Therefore, O is the point equidistant from all the sides of ΔABC.

Question 3.
In a huge park people are concentrated at three points (see the given figure)
A: where there are different slides and swings for children,
B: near which a man-made lake is situated.
C: which is near to a large parking and exit.

Answer:
Maximum number of persons can approach the ice-cream parlour if it is equidistant from A, B and C. Now, A, B and C form a triangle. In a triangle, at the circumcentre is the only point that it equidistant from its vertices. So, the ice-cream parlour should be set up at the circumcentre of ΔABC.

Question 4.
Complete the hexagonal and star shaped rangolies (see the given figure) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

Answer:
It can be observed that hexagonal-shaped rangoli has 6 equilateral triangles in it.

Area of ∆OAB = \(\frac{\sqrt{3}}{4}\) (side)² = \(\frac{\sqrt{3}}{4}\) (5)²
= \(\frac{\sqrt{3}}{4}\) (25) = \(\frac{25 \sqrt{3}}{4}\) cm²

Area of hexagonal-shaped rangoli
= \(6 \times \frac{25 \sqrt{3}}{4}=\frac{75 \sqrt{3}}{2}\) cm²

Area of equilateral triangle having its side as 1 cm = \(\frac{\sqrt{3}}{4}\) (1)² = \(\frac{\sqrt{3}}{4}\) cm²

Number of equilateral triangles of 1 cm side that can be filled in this hexagonal-shaped rangoli
= \(\frac{\frac{75 \sqrt{3}}{2}}{\frac{\sqrt{3}}{4}}\) = 150
Star-shaped rangoli has 12 equilateral triangles of side 5 cm in it.

Area of star-shaped rangoli
= \(12 \times \frac{\sqrt{3}}{4} \times(5)^2=75 \sqrt{3}\) cm²

Number of equilateral triangles of 1 cm side that can be filled in this star-shaped rangoli
= \(\frac{75 \sqrt{3}}{\frac{\sqrt{3}}{4}}\) = 300
Therefore, star-shaped rangoli has more equilateral triangles in it.

JAC Jharkhand Board Class 8th Solutions in Hindi & English Medium

• JAC Class 8 Maths Solutions
• JAC Class 8 Science Solutions
• JAC Class 8 Social Science Solutions
• JAC Class 8 English Solutions
• JAC Class 8 Hindi Solutions
• JAC Class 8 Sanskrit Solutions
• JAC Class 8 Social Science Notes

Jharkhand Board JAC Class 9 Maths Solutions Chapter 8 Quadrilaterals Ex 8.2 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 8 Quadrilaterals Ex 8.2

Page-150

Question 1.
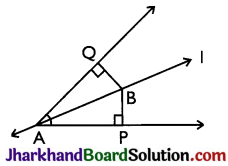
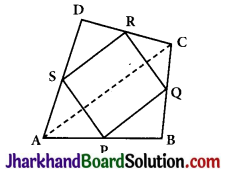
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig). AC is a diagonal. Show that:
(i) SR || AC and SR = \(\frac {1}{2}\)AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

Answer:
(i) In ΔDAC,
R is the mid-point of DC and S is the mid-point of DA.
Thus by mid-point theorem, SR || AC and SR = \(\frac {1}{2}\)AC

(ii) In ΔBAC,
P is the mid-point of AB and Q is the mid-point of BC.
Thus by mid-point theorem, PQ || AC
and PQ = \(\frac {1}{2}\) AC
Also, SR = \(\frac {1}{2}\) AC
Thus, PQ = SR

(iii) SR || AC (Proved)
and, PQ || AC (Proved)
⇒ SR || PQ (Lines parallel to same line are parallel to each other)
Also, PQ = SR(Proved)
Thus, PQRS is a parallelogram.
(A quadrilateral in which a pair of sides is equal and parallel is a parallelogram).

Question 2.
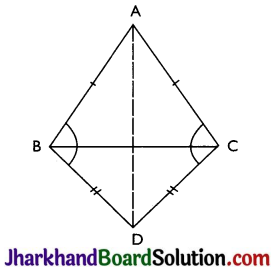
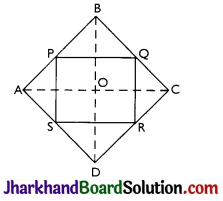
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

Answer:
Given: ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.

To Prove: PQRS is a rectangle.

Construction: AC and BD are joined.

Proof: P and Q are mid-points of AB and BC respectively
⇒ PQ || AC and PQ = \(\frac{1}{2}\) AC …(i)
(By mid-point theorem)
Also, S are R are mid-points of AD and CD respectively, so, by mid-point theorem,
SR || AC and SR = \(\frac{1}{2}\)AC …(ii)
From (i) and (ii)
∴ PQ || SR and PQ = SR
⇒ PQRS is a parallelogram
As ABCD is a rhombus
AB = BC (sides of rhombus)
⇒ \(\frac{1}{2}\) AB = \(\frac{1}{2}\) BC
⇒ BP = BQ (As P and Q are mid-points of AB and BC respectively)
So, in ΔBPQ
∠BPQ = ∠BQP …(i)
(Angles opposite to equal sides are equal)
Also, BC = CD (Sides of rhombus)
⇒ \(\frac{1}{2}\) BC = \(\frac{1}{2}\) CD
⇒ CQ = CR (As Q and R are midpoint of BC and CD respectively)
So, in ACQR
∠CQR = ∠CRQ …(ii) (Angle opposites to equal sides are equal)
AB || CD (Opposite sides of a parallelogram)
⇒ ∠B + ∠C =180 …(iii)
(sum of angles on same sides of transversal is 180°)

In ΔBPQ, ∠BPQ + ∠BQP + ∠B = 180° (Angles sum property)
In ΔCQR, ∠CQR + ∠CRQ + ∠C = 180° (Angle sum property)

On adding both the equations, we get
∠BPQ + ∠BQP + ∠B + ∠CQR + ∠CRQ + ∠C = 360°
⇒ 180° + ∠BPQ + ∠BQP + ∠CQR + ∠CRQ = 360° [From (ii)]
⇒ 180° + 2 ∠BQP + 2 ∠CQR = 360° [From (i) and (ii)]
⇒ 2 (∠BQP + ∠CQR) = 360° – 180° = 180°
⇒ ∠BQP + ∠CQR = \(\frac{180°}{2}\) = 90° …(iv)

Now, ∠BQP + ∠CQR + ∠PQR = 180° (sum of angles on a straight line is 180°)
90° + ∠PQR = 180° [From (iv)]
⇒ ∠PQR = 180° – 90° = 90°
So, PQRS is a parallelogram in which one angle is 90°
⇒ PQRS is a rectangle.

Question 3.
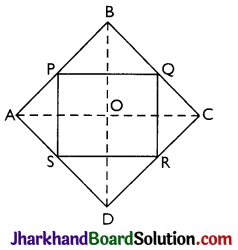
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Answer:
Given: ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively.
To Prove PQRS is a rhombus.
Construction: AC and BD are joined.
Proof: In ∆ABC
P and Q are the mid-points of AB and BC respectively
Thus, PQ || AC and PQ = \(\frac{1}{2}\) AC (Mid-point theorem) …(i)
In ∆ADC, SR AC and SR = \(\frac{1}{2}\) AC (Mid-point theorem) …(ii)
From (i) and (ii)
∴ PQ = SR and PQ || SR
⇒ PQRS is a parallelogram.
(As in quadrilateral PQRS one pair of opposite sides is equal and parallel to each other, so, it is a parallelogram.)
AB = CD (opposite sides of rectangle)
⇒ AB = CD
⇒ BP = CR(As P and R are midpoints of AB and CD respectively)

Consider ∆PBQ and ∆RCQ
BP = CR (Proved)
BQ = CQ [As Q is a mid-point of BC]
∠B = ∠C = 90° (As each angle of a rectangle ABCD is of 90°)
⇒ ΔPBQ ≅ ΔRCQ by SAS congruence criterion.
⇒ PQ = QR (CPCT)
Also, PQ = RS and PS = QR (As opposite sides of parallelogram are equal)
∴ PQ = QR = RS = PS
So, PQRS is a parallelogram in which all sides are equal.
⇒ PQRS is a rhombus.

Question 4.
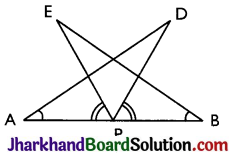
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig). Show that F is the mid-point of BC.

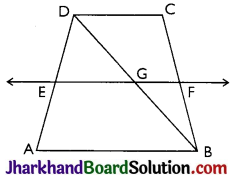
Answer:
Given: ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD.
To prove: F is the mid-point of BC.
Proof: BD intersects EF at G.
In ∆BAD,
E is the mid-point ofAD andalsoEG || AB.
Thus, G is the mid-point of BD (Converse of mid-point theorem)
Now, EG || AB
⇒ EF || AB
⇒ GF || AB
Also, AB || CD
∴ CD || GF (Lines parallel to same line are parallel to each other)

In ABCD, G is a mid-point of BD and CD || GF
⇒ F is a mid-point of BC (By converse of mid-point theorem)
Now, in ∆BDC,
G is the mid-point of BD and also GF || AB || DC.
Thus, F is the mid-point of BC (Converse of mid-point theorem)

Page-151

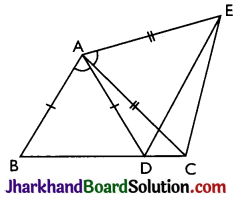
Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig). Show that the line segments AF and EC trisect the diagonal BD.

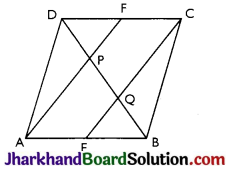
Answer:
Given: ABCD is a parallelogram. E and F are the mid-points of sides AB and CD respectively.
To prove: AF and EC trisect the diagonal BD.
Proof: ABCD is a parallelogram.
Therefore, AB || CD, also, AE || FC
Now, AB = CD (Opposite sides of parallelogram ABCD)
⇒ \(\frac{1}{2}\) AB = \(\frac{1}{2}\) CD
⇒ AE = FC (E and F are midpoints of sides AB and CD)
AECF is a parallelogram
(AE and CF are parallel and equal to each other)
AF || EC (Opposite sides of a parallelogram)

Now, in ADQC,
⇒ F is mid-point of side DC and FP || CQ (as AF || EC).
P is the mid-point of DQ (Converse of mid-point theorem)
⇒ DP = PQ …………(i)
Similarly, in AAPB,
E is mid point of side AB and EQ || AP (as AF || EC).
Q is the mid-point of PB (Converse of mid-point theorem)
⇒ PQ = QB ………….. (ii)

From equations (i) and (i),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.

Question 6.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.

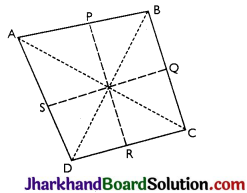
Answer:
Let ABCD be a quadrilateral and p, Q, R and S are the mid-points of AB, BC, CD and DA respectively.

Now, In ∆ACD, R and S are the mid-points of CD and DA respectively.
Thus SR || AC and SR = \(\frac{1}{2}\) AC (by mid-point theorem)
Also, in DABC, P and Q are mid-point of AB and BC respectively
⇒ PQ || AC and PQ = \(\frac{1}{2}\) AC (by mid-point theorem)
So, PQ = SR and PQ || SR.
Thus, PQRS is parallelogram, [since one pair of opposite sides is equal and parallel]
PR and QS are the diagonals of the parallelogram PQRS.
So, they will bisect each other. (As diagonals of a parallelogram bisect each other.)

Question 7.
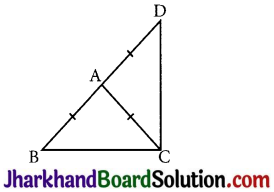
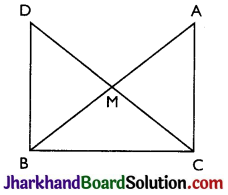
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac {1}{2}\)AB

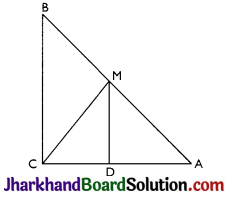
Answer:
(i) In ∆ACB
M is the mid-point of AB and MD|| BC
Thus, D is the mid-point of AC (Converse of mid-point theorem)

(ii) ∠ACB = ∠ADM (Corresponding angles)
As ∠ACB = 90°
Thus, ∠ADM = 90° i.e. MD ⊥ AC

(iii) In ∆AMD and ∆CMD,
AD = CD (D is the mid-point of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (common)
Thus, ΔADM ≅ ΔCDM by SAS congruence criterion.
AM = CM by CPCT
also, AM = \(\frac{1}{2}\) AB (M is mid point of AB)
Hence, CM = MA = \(\frac{1}{2}\) AB

JAC Board Class 9th Social Science Solutions Geography Chapter 2 Physical Features of India

JAC Class 9th Geography Physical Features of India InText Questions and Answers 

Find Out (Page No. 8)

Question 1.
The names of the glaciers and passes that lie in the Great Himalayas?
Answer:
Glaciers in the Great Himalayas: Siachin, Milam, Gangotri, Bhagirathi, Baltoro, Pindari.
Passes in the Great Himalayas: Burgil, Zoji La, Shipki La, Bara Lacha La, Nathu La, Bomdi La, Thaga La, Lipulekh La.

Question 2.
The name of the states where highest peaks are located.
Answer:

Highest Peaks	States
Kanchenjunga	Sikkim
Nanga Parbat	Jammu & Kashmir (Union Territory)
Nanda Devi	Uttarakhand
Kamet	Uttarakhand
Namcha Barwa	Arunachal Pradesh

Question 3.
Find the location of Mussoorie, Nainital, Ranikhet from your atlas and also name the state where they are located.
Answer:

Place	States
Mussoorie	Uttarakhand
Nainital	Uttarakhand
Ranikhet	Uttarakhand

JAC Class 9th Geography Physical Features of India Textbook Questions and Answers 

Question 1.
Choose the right answer from the four alternatives given below:
1. A landmass bounded by sea on three sides is referred to as:
(a) Coast
(b) Island
(c) Peninsula
(d) None of the above.
Answer:
(c) Peninsula

2. Mountain ranges in the eastern part of India forming its boundary with Myanmar are collectively called as:
(a) Himachal
(b) Uttarakhand
(c) Purvachal
(d) None of the above.
Answer:
(c) Purvachal

3. The Western Coastal Strip, south of Goa is referred to as:
(a) Coromandel
(b) Konkan
(c) Kannad
(d) Northern Circar
Answer:
(c) Kannad

4. The highest peak in the Eastern Ghats is:
(a) Anai Mudi
(b) Kanchenjunga
(c) Mahendragiri
(d) Khasi
Answer:
(c) Mahendragiri

Question 2.
Answer the following questions briefly:
1. What is the ‘bhabar’?
Answer:
Bhabar is a narrow belt of plain which is about 8 to 16 km wide. It is covered with pebbles deposited by rivers lying parallel to the slopes of the Shiwaliks.

2. Name the three major divisions of the Himalayas from North to South
Answer:
(a) The Great or Inner Himalayas or the ‘Himadri’.
(b) The Middle or Lesser Himalayas or the ‘Himachal’.
(c) The Outer Himalayas or the ‘Shiwaliks’.

3. Which plateau lies between the Aravalli and the Vindhya ranges?
Answer:
The Malwa Plateau.

4. Name the island group of India having a coral origin.
Answer:
The Lakshadweep Islands.

Question 3.
Distinguish between:
1. Bhangar and Khadar
2. Western Ghats and Eastern Ghats.
Answer:
1. Difference between Bhangar and Khadar:

Bhangar	Khadar
1. It is the older alluvial soil.	1. It is the newer alluvial soil.
2. It often contains kankar or nodules with calcium carbonates in sub-soil.	2. It is finer, more sandy and free from kankar nodules.
3. Bangar is not renewed frequently. Hence, it is less fertile.	3. Khadar is renewed frequently and is more fertile.
4. It is found away from the river at a higher ground level.	4. It is found near river channels, in deltas and in floodplains.

2. Difference between Western Ghats and Eastern Ghats:

Western Ghats	Eastern Ghats
1. The Western Ghats form the western side or edge of the Deccan Plateau.	1. The Eastern Ghats form the eastern side or edge of the Deccan Plateau.
2. These Ghats are regular and comparatively higher in elevation.	2. These ghats have a relatively lower elevation.
3. These lie parallel to the western coast.	3. These lie parallel to the eastern coast.
4. Their average elevation is 900-1600 metres.	4. Their average elevation is 600 metres.
5. They are continuous and can be crossed through passes only.	5. They are discontinuous and irregular and dissected by rivers draining into the Bay of Bengal.
6. The highest peak is Anai Mudi.	6. The highest peak is Mahendragiri.
7. Soil is highly fertile. Rice, spices, rubber, coconuts, cashew nuts, etc. are grown.	7. Soil is relatively less fertile. Groundnuts, rice, cotton, tobacco, coconuts, etc. are grown

Question 4.
Which are the major physiographic divisions of India? Contrast the relief of the Himalayan region with that of the Peninsular Plateau.
Answer:
The major physiographic divisions of India are:

1. The Himalayan Mountains
2. The Northern Plains
3. The Peninsular Plateau
4. The Indian Desert
5. The Coastal Plains
6. The Islands

The contrast between the relief of the Himalayan region with that of the Peninsular Plateau is as follows:

The Himalayan Region	The Peninsular Plateau
1. These are young fold mountains.	1. These are a part of the oldest structure of the earth’s crust.
2. These are formed of sedimentary rocks.	2. These are formed of igneous and metamorphic rocks.
3. These consists of three parallel ranges: Himadri, Himachal, Shiwa- liks.	3. It consists of two sections: The Central Highlands, The Deccan Plateau
4. Mostly glaciers and passes are found in this region.	4. Glaciers and passes are not found in this region.
5. These contain the highest mountains.	5. These are formed of low hills.
6. It is the origin of snow-fed, perennial rivers.	6. It has rainfed, seasonal rivers.

Question 5.
Give an account of the Northern Plains of India.
Answer:
A description of the Northern Plains of India is given hereunder:

1. The Northern plains lie to the south of the Himalayas.
2. The Northern plains have been formed by the interplay of the three major river systems, namely, the Indus, the Ganga and the Brahmaputra along with then tributaries.
3. It spreads over an area of 7 lakhs sq. km. It is about 2400 km long and 240 to 320 km broad.
4. It is formed of alluvial soil.
5. With a rich soil cover combined with adequate water supply and favourable climate, it is agriculturally a very productive part of India.
6. On the basis of the difference in the relief, the plain is divided into four sections
   • Bhabar,
   • Tarai,
   • Bhangar,
   •  Khadar.

Question 6.
Write short notes on the following:
1. The Indian Desert
2. The Central Highlands
3. The Island Groups of India.
Answer:
1. The Indian Desert:
(a) The Indian desert lies towards the western margins of the Aravalli Hills.

(b) It is an undulating sandy plain covered with sand dunes called Barchans.

(c) This region receives very low rainfall: below 150 mm per year.

(d) It has an arid climate with low vegetation cover.

(e) Luni is the only large river in this region.

2. The Central Highlands :
(a) The part of the Peninsular plateau lying to the North of the Narmada river, covering a major area of the Malwa plateau, is known as the Central Highlands.

(b) The Vindhyan range is bounded by the Satpura range on the south and the Aravallis on the North-West. The further westward extension gradually merges with the sandy and rocky desert of Rajasthan.

(c) The flow of the rivers draining this region, namely, the Chambal, the Kalisindh, the Betwa and the Ken is from South-West to North-East, thus, indicating the slope.

(d) The Central Highlands are wider in the west but narrower in the east. The eastward extensions of this plateau are locally known as the Bundelkhand and Baghelkhand.

(e) The Chotanagpur plateau marks the further eastward extension, drained by the Damodar river.

3. The Island Groups of India:
(a) The Lakshadweep and the Andaman and Nicobar islands are the two main island groups of India.

(b) The Lakshadweep Islands group lies close to the Malabar coast of Kerala. This group of islands is composed of small coral islands. It covers a small area of 32 sq.km. Kavaratti island is the capital of Lakshadweep.

(c) The Andaman and Nicobar islands located in the Bay of Bengal extend from North to South. They are bigger in size and are more numerous and scattered. Port Blair is the capital of this island group.

On an outline map of India, show the following:
1. Mountain and hill ranges: the Karakoram, the Zaskar, The Patkai Bum, the Jaintia, le Vindhya range, the Aravalli, and the Cardamom hills.
2. Peaks: K2, Kanchenjunga, Nanga Parbat and the Anai Mudi.
3. Plateaus: Chhota Nagpur and Malwa.
4. The Indian Desert, Western Ghats, Lakshadweep Islands.
Answer:

Locate the peaks, passes, ranges, plateaus, hills and dunes hidden in the puzzle. Try t find where these features are located. You may start your search horizontally, vertically diagonally.

Answer:
Peaks: Kanchenjunga, Everest, Anai Mudi, Aravali

Passes: Nathu La, Shipki La, Bomdi La.

Ranges: Maikal, Sahyadri, Vindhyan.

Plateau: Chotanagpur, Malwa.

Hills: Jaintia, Kaimur, Garo, Nilgiri, Cardamom

Students can locate the above features on a map under the guidance of their teacher

JAC Class 9 Social Science Solutions

JAC Board Class 9th Social Science Solutions History Chapter 4 Forest Society and Colonialism

JAC Class 9th History Forest Society and Colonialism InText Questions and Answers 

Activity (Page No. 81)

Question 1.
Each mile of railway track required between 1,760 and 2,000 sleepers. If one average sized tree yields 3 to 5 sleepers for a 3 metre wide broad gauge track, calculate approximately how many trees would have to be cut to lay one mile of track.
Answer:
Average number of sleepers required to lay one mile railway track = \(\frac{1760+2000}{2}=1880 \)
Average number of sleepers made by 1 tree = \(\frac{3+5}{2}=4\)
Thus, number of trees would have to be cut to lay one mile of track = \(\frac{1880}{4}=470 \)
Approximately, 470 trees would have to be cut to lay one mile of track.

Activity (Page No. 83)

Question 1.
If you were the Government of India in 1862 and responsible for supplying the railways with sleepers and fuel on such a large scale, what were the steps you would have taken?
Answer:
if I were the Government of India in 1862 and responsible for supplying the railways with sleepers and fuel on such a large scale, I would have taken the following steps:

1. I would have planned a systematic utilisation of the forest wealth; rules about the use of forest resources would have been framed.
2. Instead of using wood, iron or stone would have been used for making sleepers. Coal is used as fuel for running the railways engines.
3. Along with cutting down the forests, a plan for afforestation on a large-scale would have been initiated simultaneously.

Activity (Page No. 86)

Question 1.
Children living around forest areas can often identify hundreds of species of trees and plants. How many species of trees can you name?
Answer:
Fruiting Trees: Mango, Guava, Lemon, Banana etc.
Medicinal Plants: Tulsi, Neem, Babool, Sarpagandha etc.

Activity (Page No. 96)

Question 1.
Have there been changes in forest areas where you live ? Find out what these changes are and why they have happened.
Answer:
Yes, there have been many changes in forest areas where I live. These changes are as follows :

1. There have been strict restrictions on the hunting of wild animals.
2. A tremendous increase in the number of wild animals could be seen in these areas.
3. There have been many check posts of forests protection offices established.
4. Smuggling of elephant’s teeth and skin of tiger has been strictly prohibited.
5. There have been cleaning of rivers flowing through the forest areas. These changes have been made to protect the environment.

Question 2.
Write a dialogue between a colonial forester and an adivasi discussing the issue of hunting in the forest.
Answer:
A Sample dialouge is given below:
Colonial Forester: Who are you? What are you doing in this forest?

Adivasi: Sir, I am an adivasi. I live in nearby village. I came here to collect fruits and for hunting rabbits.

Colonial Forester: Don’t you know about the prohibition of hunting in forests?

Adivasi: But Sir, my children are hungry since five days. I came here to fulfill their food requirements.

Colonial Forester: I don’t care about it. I just know that hunting in forest is illegal. It is a crime and you will deserve a punishment for this.

Adivasi: But sir, this is our forest. Means if we, advasis, are restricted from hunting, then what other work we people will do? How will we care our family and our daily needs? Our family will die of starvation.

Colonial Forester: Look, you are arguing with me

Adivasi: Sir, we are dependent on these forests. Please let us do hunting. We will give you a share of our hunt.

Colonial Forester: Shut up! No, not at all. I have to report about you to our Forest Officer. Come with me.
Colonial forester arrests the adivasi and takes him away to his officer.

JAC Class 9th History Forest Society and Colonialism Textbook Questions and Answers 

Question 1.
Discuss how the changes in forest management in the colonial period affected the*) following groups of people:
1. Shifting cultivators
2. Nomadic and pastoralist communities
3. Firms trading in timber/forest produce.
4. Plantation owners
5. Kings/British officials engaged in shikar (hunting).
Answer:
1. Shifting cultivators:
Restriction on shifting cultivation resulted in displacement of many communities from their homes in the forests. Many were reduced to the level of starvation. Many changed their occupation and some became labourers.

2. Nomadic and Pastoralist Communities:
The forest laws deprived people of their customary rights and that meant severe hardship for the Nomadic and Pastoralist communities. They could not cut wood for their houses could not graze their cattle or collect fruits and roots, and hunting and fishing were declared illegal. Some of the nomadic communities began to be called ‘Criminal Tribes’ and were instead forced to work in factories, mines and plantations under government supervision. They were also recruited for work in plantations. Their wages were low and conditions of work were very bad.

3. Firms trading in timber/forest produce:
Under the new forest laws, lucrative opportunities opened up in the trade of forest products, specially timber. However, the trade was completely regulated under colonial government. The British governments gave many large European trading firms the sole right to trade in the forest products of particular areas.

4. Plantation owners:
Changes in forest management favoured the plantation owners who were mostly Europeans. They were given free land to destroy natural forests to make way for tea, coffee and rubber plantation, to meet the Europeans’ growing need for these commodities. But the workers on these plantations were paid very low wages. They had to live in very bad conditions;

5. Kings/British officials engaged in shikar (hunting):
Hunting of tiger and other animals had been a part of the culture of the court and nobility for centuries. The British saw large animals as a sign of a wild, primitive and savage society. Therefore, they provided strong incentives to encourage people to take guns and kill these dangerous animals. This hunting as a game for pleasure flourished under the new forest laws.

Question 2.
What are the similarities between colonial management of the forests in Bastar and in Java ?
Answer:
Bastar is located in the southernmost part of Chhattisgarh in India, while Java is located in Indonesia. The colonial power in India was the British, while in Java it was the Dutch. The similarities between colonial management of the forests in Bastar and Java are as follows :

1. A large number of trees were cut down for shipbuilding and railways.
2. There was restriction on hunting at the both places.
3. Nomads and pastoralists were restricted to enter the forests.
4. In both of the places defaulters of forests laws were punished, harassed and
5. Both Bastar and Java witnessed rebellion against rulers.
6. Both the governments displaced the local communities from their traditional livelihood in order to make full use of the forest produce.
7. Both restricted the villagers from practising shifting cultivation.

Question 3.
Between 1880 and 1920, forest cover in the Indian subcontinent declined by 9.7 million hectares, from 108.6 million hectares to 98.9 million hectares. Discuss the role of the following factors in this decline :
1. Railways
2. Shipbuilding
3. Agricultural expansion .
4. Commercial farming
5. Tea/Coffee plantations
6. Adivasis and other peasant users.

1. Railways:
Colonial rulers needed sleepers to lay railway lines which were made of hard wood. Each mile of railway track required more than 1800 sleepers. By 1890, about 25,500 km of track had been laid. As the railway tracks spread through India, a larger and larger number of trees were felled. Forests around the railway tracks started disappearing fast. Wood was used as a fuel to run the locomotives.

2. Shipbuilding:
By the early nineteenth century, there was shortage of oak
trees in England which were the basic input for ship industry. This created a problem of timber supply for the Royal Navy. By the 1820s, search parties were sent to explore the forest resources of India. Within a decade, trees were being felled on a massive scale and vast quantities of timber were being exported from India. ‘

3. Agricultural expansion: In 1600, approximately one sixth of the total of India’s land area was under cultivation but now it is 42% because of the increasing population. In the early nineteenth century, the colonial state thought that forests were unproductive. They were considered to be wilderness that had to be brought under cultivation, so that the land could yield agricultural products and revenue, and enhance the income of the state. So, between 1880 and 1920, cultivated area rose by 6.7 million hectares.

4. Commercial farming:
Commercial farming was also responsible for deforestation. The Britishers directly encouraged the production of commercial crops like jute, sugar, cotton, tea, wheat etc. They encouraged their production because these crops were required as raw material and cereals were required to feed the growing urban population of Europe. Thus, forests were cleared for growing commercial crops.

5. Tea/Coffee plantations:
Large areas of forests were also cleared to make way for plantation crops like tea, coffee and rubber. These crops were grown to meet the Europeans’ growing demand. Plantation owners made big profits, making the workers work for long hours and at low wages.

6. Adivasis and other peasant users:
Adivasis and peasants cleared forests for shifting cultivation and commercial farming. Apart from this, they cut down the trees for fuel.

Question 4.
Why are forests affected by wars?
Answer:
Forests are affected by wars due to various reasons which are as follow :

1. In the modern times, the defending armies hid themselves and their war material under the cover of the thick forests to avoid detection. As such the enemy forces target forest areas to capture the opposing soldiers and their war materials.
2. Because of pre-occupation of the participant countries in the war, many proposals for promoting the forests culture have to be abandoned half-way and many such forests became prey of neglect.
3. To meet war needs, sometimes forests are cut indiscriminately and as a result forests vanished with no times one after the other.
4. Fearing the capture of forest areas by the enemy, sometimes the existing governments themselves cut down the trees recklessly, destroy the saw mills and bum huge piles of logs.
5. Finding the forest staff in difficulty and engaged during the war times, some people expand their agricultural land at the cost of the forest land.

JAC Class 9 Social Science Solutions