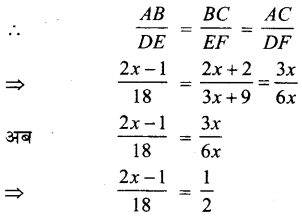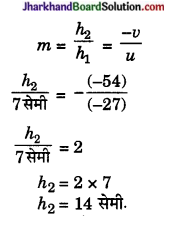Class 10

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.3

Question 1.
Find the area of the triangle whose vertices are :
1. (2, 3), (-1, 0), (2, -4)
2. (5, 1), (3, 5), (5, 2)
Answer:
1. Let A (2, 3), B(-1, 0) and C(2, – 4) be the vertices of ΔABC. Then, using the formula, the area of ΔABC is given by \(\frac{1}{2}\)[2 (0 + 4) + (-1) (- 4 – 3) + 2(3 – 0)]
= \(\frac{1}{2}\)(8 + 7 + 6)
= \(\frac{21}{2}\) sq units
Thus, the area of the triangle with given vertices is \(\frac{21}{2}\) sq units.

2. The vertices of the triangle are given to be (-5, -1), (3, – 5) and (5, 2).
Then, using the formula, the area of the triangle is given by
= \(\frac{1}{2}\)[-5(-5 – 2) + 3(2 + 1) + 5 (-1 + 5)]
= \(\frac{1}{2}\)(35 + 9 + 20)
= \(\frac{1}{2}\)(64)
= 32 sq units
Thus, the area of the triangle with given vertices is 32 sq units.

Question 2.
In each of the following find the value of ‘k’, for which the points are collinear:
1. (7, -2), (5, 1), (3, k)
2. (8, 1), (k, – 4), (2, – 5)
Answer:
1. If the points (7, -2), (5, 1) and (3, k) are collinear, then the area of imaginary triangle formed by those points as vertices must be zero.
∴ \(\frac{1}{2}\)[7 (1 – k) + 5 (k + 2) + 3(- 2 – 1)] = 0
∴ \(\frac{1}{2}\)[7 – 7k + 5k + 10 – 9] = 0
∴ – 2k + 8 = 0
∴ 2k = 8
∴ k = 4

2. If the points (8, 1), (k, – 4) and (2, – 5) are collinear, then the area of imaginary triangle formed by those points as vertices must be zero.
∴ \(\frac{1}{2}\)[8 (- 4 + 5) + k(-5 – 1) + 2(1 + 4)] = 0
∴ 8 – 6k + 10 = 0
∴ 18 = 6k
∴ k = 3

Question 3.
Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are (0, – 1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Answer:
Let A (0, – 1), B (2, 1) and C(0, 3) be the vertices of ΔABC and let D, E and F be the midpoints of the sides BC, CA and AB respectively.
Then, coordinates of D = (\(\frac{2+0}{2}, \frac{1+3}{2}\)) = (1, 2)
Coordinates of E = (\(\frac{0+0}{2}, \frac{3-1}{2}\)) = (0, 1)
Coordinates of F = (\(\frac{0+2}{2}, \frac{-1+1}{2}\)) = (1, 0)
Area of ΔDEF
= \(\frac{1}{2}\)[1(1 – 0) + 0(0 – 2) + 1 (2 – 1)]
= \(\frac{1}{2}\)(1 + 0 + 1)
= 1 sq unit
Area of ΔABC
= \(\frac{1}{2}\)[0(1 – 3) + 2(3 + 1) + 0 (- 1 – 1)]
= \(\frac{1}{2}\)(0 + 8 + 0)
= 4 sq units
Then, area of ΔDEF : area of ΔABC = 1 : 4.
Thus, the area of triangle formed by joining the midpoints of the sides of the triangle with given vertices is 1 sq unit and the required ratio of areas is 1 : 4.

Question 4.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, – 2), (- 3, – 5), (3, – 2) and (2, 3).

Answer:
Let A(- 4, – 2), B(- 3, – 5), C(3, – 2) and D (2, 3) be the vertices of quadrilateral ABCD.
Drawing diagonal AC, we get two triangles ABC and ADC.
The vertices of ΔABC are A (-4, – 2), B(-3, 5) and C(3, -2).
Area of ΔABC
= \(\frac{1}{2}\)[-4(-5 + 2) + (-3) (-2 + 2) + 3(-2 + 5)]
= \(\frac{1}{2}\)[12 + 0 + 9]
= \(\frac{21}{2}\) sq units
The vertices of ΔADC are A(-4, -2), D(2, 3) and C(3, -2).
∴ Area of ΔADC
= \(\frac{1}{2}\)[- 4(3 + 2) + 2(- 2 + 2) + 3(- 2 – 3)]
= \(\frac{1}{2}\)(-20 + 0 – 15)
= \(\frac{1}{2}\)(- 35)
But area of a triangle cannot be negative.
Hence, we take the numerical value.
∴ Area of ΔADC = \(\frac{35}{2}\)sq units.
Now, area of quadrilateral ABCD
= area of ΔABC + area of ΔADC
= (\(\frac{21}{2}=\frac{35}{2}\)) sq units
= 28 sq units
Thus, the area of the given quadrilateral is 28 sq units.

Question 5.
You have studied in Class IX, that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A(4, 6), B (3, – 2) and C (5, 2).
Answer:

A (4, – 6) , B (3, – 2) and C (5, 2) are the vertices of ΔABC.
Let AD be a median of ΔABC.
Then, D is the midpoint of BC.
∴ Coordinates of D are (\(\frac{3+5}{2}, \frac{-2+2}{2}\)), ie., (4, 0)
Area of ΔABC
= \(\frac{1}{2}\)[4(- 2 – 2) + 3(2 + 6) + 5(- 6 + 2)]
= \(\frac{1}{2}\)[-16 + 24 – 20]
= \(\frac{1}{2}\) (-12)
= 6 sq units (∵ Area cannot be negative.) ………(1)
Vertices of ΔADB are A (4, – 6), D (4, 0) and B (3, -2)
Area of ΔADB
= \(\frac{1}{2}\)[4(0 + 2) + 4(- 2 + 6) + 3(- 6 – 0)]
= \(\frac{1}{2}\)[18 + 16 – 18]
= 3 sq units ……(2)

Vertices of ΔADC are A (4, – 6), D (4, 0) and C (5, 2).
Area of ΔADC
= \(\frac{1}{2}\)[4 (0 – 2) + 4 (2 + 6) + 5 (- 6 – 0)]
= \(\frac{1}{2}\)[- 8 +32 – 30]
= \(\frac{1}{2}\)[-6]
= 3 sq units (∵ Area cannot be negative.) ……(3)
From (1), (2) and (3), we get
Area of ΔADB = Area of ΔADC = \(\frac{1}{2}\) Area of ΔABC
Thus, median AD divides ΔABC into two triangles ADB and ADC of equal areas.
The same result can be proved for other two medians BE and CF.
Hence, the statement that “A median of a triangle divides it into two triangles of equal areas.” is verified.

Students should go through these JAC Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल

भूमिका :
पिछली कक्षाओं में हमने समान्तर चतुर्भुअत : समचतुर्भुज तथा वर्ग के परिमाप तथा क्षेत्रफल के बारे में पढ़ा था। इस अध्याय में हम प्रारम्भ में वृत्त के परिमाप तथा क्षेत्रफल का पुनरावलोकन करेंगे तथा त्रिज्यखण्ड, वृत्तखण्ड का क्षेत्रफल ज्ञात करने के बारे में सीखेंगे। हम वृत्तों के भागों तथा वृत्तों से सम्बद्ध समतल आकृतियों के कुछ संयाजनों के क्षेत्रफलों के बारे में भी अध्ययन करेंगे।
→ वृत्त (Circle) : वृत्त एक ऐसे बिन्दु का बिन्दु पथ है जो एक समतल में एक नियत बिन्दु से सदैव समान (अचर) दूरी पर गति करता है।
→ केन्द्र (Centre) : निश्चित बिन्दु को वृत्त का केन्द्र (O) कहते हैं।
→ त्रिज्या (Radius) : एक रेखाखण्ड जो वृत्त पर एक बिन्दु तथा इसके केन्द्र को जोड़ती है. त्रिज्या कहलाती है।
→ व्यास (Diameter) : केन्द्र से होकर गुजरने वाली जीवा जिसके अन्तः बिन्दु वृत्त पर होते हैं, वृत्त का व्यास कहलाता है।
व्यास = 2 × त्रिज्या
→ जीवा (Chord) : वृत्त पर दो बिन्दुओं को जोड़ने वाले रेखाखण्ड को वृत्त की जीवा कहते हैं।
→ चाप (Arc) : वृत्त पर दो बिन्दुओं के बीच की दूरी को वृत्त का चाप कहते हैं।
→ वृत्तीय क्षेत्र (Circular region) : वह क्षेत्र जिसमें सभी बिन्दु या तो वृत्त पर या वृत्त के अन्दर स्थित होते हैं वृत्तीय क्षेत्र कहलाता है।
→ अर्द्धवृत्तीय क्षेत्र (Semi circular region) : जब दो चाप बराबर होते हैं तब प्रत्येक एक अर्द्धवृत्त होता है तथा दोनों वृत्तखण्ड व त्रिज्यखण्ड बराबर होते हैं और प्रत्येक को अर्द्धवृत्तीय क्षेत्र से जाना जाता है।
→ संकेन्द्रीय वृत्त (Concentric Circles) : ऐसे दो या दो से ज्यादा वृत्त जिनका केन्द्र समान हो तथा त्रिज्याएँ विभिन्न हों, संकेन्द्रीय वृत्त कहलाते हैं।

वृत्त का परिमाप और क्षेत्रफल – एक समीक्षा
वृत्त की परिधि (Circumference of Circle) :
वृत्त का एक चक्कर लगाने पर तय की गई दूरी को वृत्त का परिमाप या परिधि कहते हैं। किसी भी वृत्त की परिधि और व्यास का अनुपात एक निश्चित अचर राशि होती है। इस अनुपात की अचर राशि को ग्रीक अक्षर π द्वारा प्रदिर्शित करते हैं।

अतः π = परिधि / व्यास
परिधि = π × व्यास
= π × 2 = 2πr
वृत्त की परिधि = 2πr
व्यवहार में π का मान प्रायः \(\frac{22}{7}\) अथवा 3.14 लिया जाता है परन्तु π एक अपरिमेय संख्या है जिससे इसका दशमलव अनावर्ती और असान्त है। आर्यभट्ट ने इसका मान 3.1416 ज्ञात किया था जो दशमलव के 4 स्थानों तक शुद्ध है।

वृत्त का क्षेत्रफल (Area of Circle) :

वृत्त का क्षेत्रफल = \(\frac{1}{2}\) × r × (वृत्त की परिधि)
= \(\frac{1}{2}\) × r × (2πr) = πr²
अतः वृत्त का क्षेत्रफल = π(त्रिज्या)²
वृत्त का व्यास वृत्त को दो समान भागों में विभाजित करता है। अतः
अर्द्धवृत्त का परिमाप = πr + 2r
अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr²

वलयिका का क्षेत्रफल (Area of an Annullus) :

चित्र में, एक वलयिका का केन्द्र O है और जिसकी बाह्य और अन्तः त्रिज्याएँ क्रमशः r₁ और r₂ (r₁ > r₂) हैं।
वलयिका का क्षेत्रफल = दोनों वृत्तों के बीच का क्षेत्रफल
= बड़े वृत्त का क्षेत्रफल – छोटे वृत्त का क्षेत्रफल
= πr₁² – πr₂²
= π(r₁² – r₂²)
= π × (त्रिज्याओं के वर्गों का अन्तर)
अतः वलयिका का क्षेत्रफल = π(r₁² – r₂²)

त्रिज्यरखण्ड और वृत्तरखण्ड के क्षेत्रफल :
वृत्त के त्रिज्यखण्ड का क्षेत्रफल (Area of a Sector of a Circle) :
किसी भी वृत्त की दो त्रिज्याओं और एक चाप से घिरे हुए क्षेत्र को वृत्त का त्रिज्यखण्ड (Sector) कहते हैं।
चित्र में, वृत्त का एक त्रिज्यखण्ड AOB है। माना कि ∠AOB = θ है और θ < 180° जब कोण 6 का मान बढ़ता है तो चाप AB की लम्बाई भी उसी अनुपात में बढ़ती है। जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो

चाप की लम्बाई = अर्द्धवृत्त के चाप की लम्बाई
= πr
∵ केन्द्र पर 180° कोण अन्तरित करने वाले चाप की लम्बाई = πr
∴ केन्द्र पर θ कोण अन्तरित करने वाले चाप की लम्बाई = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
इसी प्रकार, जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो उसके संगत त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi r^2}{2}\)
∴ वृत्त के केन्द्र पर θ कोण अन्तरित करने पर बने त्रिज्यखण्ड का क्षेत्रफल
= \(\frac{\pi r^2 \theta}{2 \times 180^{\circ}}\)
= \(\frac{\pi r^2 \theta}{360^{\circ}}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
यदि r त्रिज्या के वृत्त में कोण θ के त्रिज्यखण्ड के चाप की लम्बाई L और क्षेत्रफल A है, तो
L = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
और A = \(\frac{\pi r^2 \theta}{360}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
चाप की लम्बाई (L) और त्रिज्यखण्ड के क्षेत्रफल (A) में सम्बन्ध :
A = \(\frac{1}{2}\)Lr
यहाँ कोण θ को डिग्री में लेते हैं।

वृत्तखण्ड का क्षेत्रफल (Area of Segment of a Circle) :
वृत्त की प्रत्येक जीवा वृत्त को दो भागों में विभाजित करती है। इससे बने प्रत्येक भाग को वृत्तखण्ड कहते हैं। छोटे भाग को लघु वृत्तखण्ड तथा बड़े भाग को दीर्घ वृत्तखण्ड कहते हैं।
चित्र में, वृत्त का केन्द्र O हैं और इसकी त्रिज्या r है। जीवा PQ वृत्त को दो भागों में विभाजित करती है। हमें लघु वृत खण्ड PRQ का क्षेत्रफल ज्ञात करना है।

माना ∠POQ = θ
ΔΡΟΜ ≅ ΔQΟΜ (RHS सर्वांगसमता नियम से)
∠POM = ∠QOM = \(\frac{\theta}{2}\)
त्रिज्यखण्ड OPRQ का क्षेत्रफल = लघु वृत्तखण्ड PRQ का क्षेत्रफल + ΔPOQ का क्षेत्रफल
∴ लघु वृत्तखण्ड PRQ का क्षेत्रफल = त्रिज्यखण्ड OPRQ का क्षेत्रफल – ΔPOQ का क्षेत्रफल

यदि हम दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात करना चाहें, तो वृत्त के क्षेत्रफल में से लघु वृत्तखण्ड का क्षेत्रफल घटाकर ज्ञात कर सकते हैं।
अतः दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड PRQ का क्षेत्रफल
= πr² – \(\left[\frac{\pi r^2 \theta}{360^{\circ}}-\frac{r^2}{2} \sin \theta\right]\)
∴ दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = πr² – \(\frac{r^2}{2}\left[\frac{\pi \theta}{180^{\circ}}-\sin \theta\right]\)

समतल आकृतियों के संयोजन के क्षेत्रफल (Areas of Combinations of Plane Figures) :
समतल आकृतियों के छायांकित भाग का क्षेत्रफल ज्ञात करने के लिए निम्न सूत्रों की आवश्यकता होगी :

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Exercise 8.1

प्रश्न 1.
ΔABC में, जिसका कोण B समकोण है, AB = 24 सेमी और BC = 7 सेमी है। निम्नलिखित का मान ज्ञात कीजिए :
(i) sin A, cos A,
(ii) sin C, cos C
हल:
समकोण ΔABC में,
∠B = 90°
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (24)² + (7)²
= 576 + 49 = 625
AC = 25 सेमी

(i) समकोण ΔABC में,
sin A = \(\frac{A B}{A C}=\frac{7}{25}\)
और cos A = \(\frac{B C}{A C}=\frac{24}{25}\)

(ii) समकोण ΔABC में,
sin C = \(\frac{A B}{A C}=\frac{24}{25}\)
और cos C = \(\frac{B C}{A C}=\frac{7}{25}\)

प्रश्न 2.
चित्र में, tan P – cot R का मान ज्ञात कीजिए।

हल:
समकोण ΔPQR में, पाइथागोरस प्रमेय से,
PR² = QR² + PQ²
⇒ (13)² = QR² + (12)²
⇒ 169 = QR² + 144
⇒ QR² = 169 – 144
⇒ QR² = 25
⇒ QR = 5
tan P = \(\frac{Q R}{P Q}=\frac{5}{12}\)
और cot R = \(\frac{Q R}{P Q}=\frac{5}{12}\)
तब tan P – cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0

प्रश्न 3.
sin A = \(\frac{3}{4}\) तो cos A और tan A के मान परिकलित कीजिए।
हल:
माना कि ABC एक समकोण Δ है जिसमें
∠B = 90°

∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC

माना कि BC = 3k तथा AC = 4k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ (4k)² = AB² + (3k)²
⇒ 16k² = AB² + 9k²
⇒ AB² = 16k² – 9k²
⇒ AB² = 7k²
AB² = 7k²
AB = k\(\sqrt{7}\)


अतः cos A = \(\frac{\sqrt{7}}{4}\) तथा tan A = \(\frac{3}{\sqrt{7}}\)

प्रश्न 4.
यदि 15 cot A = 8 हो, तो sin A और sec A के मान ज्ञात कीजिए।
हल:
माना कि ABC एक समकोण Δ है, जिसमें ∠B = 90°.

∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC
15 cot A = 8 (दिया है)
⇒ cot A = \(\frac{8}{15}\)

माना कि AB = 8k
तथा BC = 15k
समकोण ΔABC में,
AC² = AB² + BC²
= (8k)² + (15k)²
= 64k² + 225k²
= 289k²
AC = \(\sqrt{289 k^2}\)
∴ AC = 17k

प्रश्न 5.
यदि sec θ = \(\frac{13}{12}\) हो, तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
हल:
माना कि ABC एक समकोण Δ है, जिसमें ∠B = 90° और ∠A = θ है।
∠θ के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC

माना कि AC = 13k और AB = 12k
समकोण ΔABC में,
AC² = AB² + BC²
(13k)² = (12k)² + BC²
BC² = (13k)² – (12k)²
= 169k² – 144k² = 25k²
∴ BC = 5k

प्रश्न 6.
यदि ∠A और ∠B न्यूनकोण हैं, जहाँ cos A = cos B, तो दिखाइए कि ∠A = ∠B.
हल:
माना कि ABC एक समकोण Δ है, जिसमें कोण C = 90°, तब ∠A तथा ∠B न्यूनकोण होंगे।

दिया है : cos A = cos B
⇒ \(\frac{A C}{A B}=\frac{B C}{A B}\)
⇒ AC = BC
ABC में, AC = BC
∵ ΔABC एक समद्विबाहु Δ है और बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
∴ ∠A = ∠B

प्रश्न 7.
यदि cot θ = \(\frac{7}{8}\), तो
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ का मान निकालिए।
हल:
माना कि ABC एक समकोण त्रिभुज है, जिसमें ∠B = 90° और ∠A = θ है।
आधार = AB, लम्ब = BC तथा कर्ण = AC

माना कि AB = 7k तथा BC = 8k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (7k)² + (8k)²
= 49k² + 64k² = 113k²
AC = ±\(\sqrt{113 k^2}\)
∴ AC = k\(\sqrt{113}\)
(∵ AC ≠ k\(\sqrt{113}\), क्योंकि भुजा ऋणात्मक नहीं हो सकती है)

[सूत्रः (a + b) (a – b) = a² – b² से]

प्रश्न 8.
यदि 3 cot = A, तो जाँच कीजिए कि \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A है या नहीं।
हल:
माना कि ABC एक समकोण Δ है, जिसमें कोण B समकोण है।
∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC
दिया है, 3 cot A = 4
cot A = \(\frac{4}{3}\)

माना कि AB = 4k, BC = 3k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (4k)² + (3k)²
= 16k² + 9k² = 25k²
⇒ AC = ±\(\sqrt{25 k^2}\)
∴ AC = 5k
[∵ AC ≠ -5k, क्योंकि भुजा ऋणात्मक नहीं हो सकती है]

R.H.S. = cos² A – sin² A
= \(\left(\frac{4}{5}\right)^2-\left(\frac{3}{5}\right)^2\)
= \(\frac{16}{25}-\frac{9}{25}\)
= \(\frac{16-9}{25}=\frac{7}{25}\) …(2)
L.H.S. = R.H.S.
अर्थात् \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A

प्रश्न 9.
त्रिभुज ABC में, जिसका कोण B समकोण है, यदि tan A = \(\frac{1}{\sqrt{3}}\) तो निम्नलिखित के मान ज्ञात कीजिए:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
हल:
दिया है, एक ΔABC, जिसका कोण B समकोण

माना कि AB = \(\sqrt{3}\)k तथा BC = k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (\(\sqrt{3}\)k)² + (k)²
= 3k² + k² = 4k²
⇒ AC = ±2k
∴ AC = 2k
(AC ≠ -2k, क्योंकि दूरी ऋणात्मक नहीं हो सकती)
∠A के लिए,
आधार = AB, लम्ब = BC, कर्ण = AC

प्रश्न 10.
ΔPQR में, जिसका कोण Q समकोण है, PR + QR = 25 सेमी और PQ = 5 सेमी है। sin P, cos P और tan P के मान ज्ञात कीजिए।
हल:
दिया है, ΔPQR में कोण Q समकोण है।

तथा PR + QR = 25 सेमी
PQ = 5 सेमी
माना कि QR = x सेमी
∴ PR = (25 – x) सेमी
अब समकोण ΔPQR में, पाइथागोरस प्रमेय से,
PR² = QR² + PQ²
(25 – x)² = (x)² + (5)²
625 – 50x + x² = x² + 25
– 50x = -600
x = \(\frac{-600}{-50}\) = 12 सेमी
∴ QR = 12 सेमी
PR = 25 – 12 = 13 सेमी

प्रश्न 11.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए:
(i) tan A का मान सदैव 1 से कम होता है।
(ii) कोण A के किसी मान के लिए sec A = \(\frac{12}{5}\)
(iii) cos A, कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) cot A, cot और A का गुणनफल होता है।
(v) किसी भी कोण θ के लिए sin θ = \(\frac{4}{3}\)
हल:
(I) ∵ tan A = लम्ब / आधार
tan A का मान 1 से कम तभी हो सकता है, जब लम्ब, आधार से छोटा हो।
परन्तु ऐसा सदैव होना आवश्यक नहीं है।
अतः कथन असत्य है।

(ii) sec A = कर्ण / आधार = \(\frac{12}{5}\)
चूँकि sec A का मान सदैव 1 के बराबर या 1 से बड़ा होता है।
अतः कथन सत्य है।

(iii) ∵ cos A कोण A की cosine का संक्षिप्त रूप होता है, जबकि cosecant का अर्थ cosec A है।
अतः दिया हुआ कथन असत्य है।

(iv) cot A का अर्थ ∠A के cotangent से है।
स्वतन्त्र रूप में cot का कोई अस्तित्व ही नहीं है। अतः cot और A का गुणनफल कभी भी cot A नहीं हो सकता है।
अतः दिया हुआ कथन असत्य है।

(v) किसी समकोण त्रिभुज में कोण θ के लिए, यदि sin θ = \(\frac{4}{3}\), तो इसका अर्थ है कि θ की सम्मुख भुजा
और कर्ण का अनुपात 4 : 3 है।
परन्तु कर्ण, समकोण त्रिभुज की सबसे बड़ी भुजा होती है।
अतः दिया गया कथन असत्य है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 1 Real Numbers Ex 1.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 1 Real Numbers Exercise 1.2

Question 1.
Express each number as a product of its prime factors:
1. 140
2. 156
3. 3825
4. 5005
5. 7429
Solution:
1. Using factor tree method, we have

Thus, 140 = 2 × 2 × 5 × 7
= 2² × 5 × 7

2. Using factor tree method, we have

Thus, 156 = 2 × 2 × 3 × 13
= 2² × 3 × 13

3. Using factor tree method, we have

Thus, 3825 = 3 × 3 × 5 × 5 × 17
= 3² × 5² × 17

4. Using factor tree method, we have

Thus, 5005 = 5 × 7 × 11 × 13

5. Using factor tree method, we have

Thus, 7429 = 17 × 19 × 23

Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers:
1. 26 and 91
2. 510 and 92
3. 336 and 54
Solution:
1. Using factor tree method, we have

∴ 26 = 2 × 13 and 91 = 7 × 13
Then, LCM (26, 91) = 2 × 7 × 13 = 182 and HCF (26, 91) = 13
Now, LCM × HCF = 182 × 13 = 2366 and 26 × 91 = 2366.
Hence, LCM × HCF = product of the two numbers.

2. Using factor tree method, we have

∴ 510 = 2 × 3 × 5 × 17 and
92 = 2 × 2 × 23 = 2² × 23
Then,
LCM (510, 92) = 2² × 3 × 5 × 17 × 23
= 23,460
and HCF (510, 92) = 2
Now, LCM × HCF = 23,460 × 2 = 46,920
and 510 × 92 = 46,920
Hence, LCM × HCF = product of the two numbers.

3. Using factor tree method, we have

∴ 336 = 2 × 2 × 2 × 2 × 3 × 7
= 2⁴ × 3 × 7 and
54 = 2 × 3 × 3 × 3 = 2 × 3³
Then, LCM (336, 54) = 2⁴ × 3³ × 7 = 3024
and HCF (336, 54) = 2 × 3 = 6
Now, LCM × HCF = 3024 × 6 = 18,144 and
336 × 54 = 18,144.
Hence, LCM × HCF = product of the two numbers.

Question 3.
Find the LCM and HCF of the following integers by applying the prime factorisation method:
1. 12, 15 and 21
2. 17, 23 and 29
3. 8, 9 and 25
Solution:
1. Using factor tree method, we have

∴ 12 = 2 × 2 × 3 = 2² × 3, 15 = 3 × 5 and 21 = 3 × 7
Then,
LCM (12, 15, 21) = 2² × 3 × 5 × 7 = 420 and HCF (12, 15, 21) = 3.

2. 17 = 17 × 1, 23 = 23 × 1 and 29 = 29 × 1 as each of the given numbers is a prime.
Then, LCM (17, 23, 29) = 17 × 23 × 29
= 11,339
and HCF (17, 23, 29) = 1.

3. Using factor tree method, we have

∴ 8 = 2 × 2 × 2 = 2³, 9 = 3 × 3 = 3²
and 25 = 5 × 5 = 5²
Then, LCM (8, 9, 25) = 2³ × 3² × 5²
= 1800
and HCF (8, 9, 25) = 1.

Question 4.
Given that HCF (306, 657) = 9 find LCM (306, 657).
Solution:
We know, LCM (a, b) =

Taking a = 306 and b = 657, we get
LCM (306, 657) = \(\frac{306 \times 657}{\mathrm{HCF}(306,657)}\)
= \(\frac{306 \times 657}{9}\)
= 34 × 657
= 22,338
Thus, LCM (306, 657) = 22,338.

Question 5.
Check whether 6ⁿ can end with the digit 0 for any natural number n.
Solution:
If a number ends with digit 0, it would be divisible by 5 as well as 2. Hence, any number ending with digit 0, must have 2 and 5 both in its prime factorisation.
Now, 6ⁿ = (2 × 3)ⁿ = 2ⁿ × 3ⁿ for any natural number n. Thus, 6n has only two prime factors 2 and 3. So, the prime factorisation of 6ⁿ does not include 5 and hence 6ⁿ cannot end with digit 0 for any natural number n.

Question 6.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
7 × 11 × 13 + 13 = 13 (7 × 11 + 1)
= 13 (77 + 1)
= 13 (78)
= 13 × 2 × 3 × 13
(∵ 78 = 2 × 3 × 13)
= 2 × 3 × 13²
Thus, 7 × 11 × 13 + 13 can be expressed as a product of primes. Hence, 7 × 11 × 13 + 13 is a composite number.
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5(7 × 6 × 4 × 3 × 2 × 1 + 1)
= 5 (1008 + 1)
= 5 × 1009
Thus, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 can be expressed as a product of primes. Hence, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 is a composite number.

Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
Here, the LCM of the timings (in minutes) taken by Sonia and Ravi will answer the question satisfying all the conditions as mentioned in the question.
Now, 12 = 2 × 2 × 3 = 2² × 3 and
18 = 2 × 3 × 3 = 2 × 3².
Then, LCM (12, 18) = 2² × 3² = 36
Hence, after 36 minutes, Sonia and Ravi meet again at the starting point if they both start at the same point and at the same time and go in the same direction.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.1

Question 1.
Find the distance between the following pairs of points :
1. (2, 3), (4, 1)
2. (- 5, 7), (1, 3)
3. (a, b), (- a, – b)
Answer:
1. Let A (2, 3) and B (4, 1) be the given points. Then,
AB = \(\sqrt{(2-4)^2+(3-1)^2}\)
= \(\sqrt{4+4}\) = \(\sqrt{8}\) = 2\(\sqrt{2}\)
Thus, the distance between the given points is 2\(\sqrt{2}\).

2. Let A (- 5, 7) and B (- 1, 3) be the given points. Then,
AB = \(\sqrt{(-5+1)^2+(7-3)^2}\)
= \(\sqrt{16+16}\) = \(\sqrt{32}\) = 4\(\sqrt{2}\)
Thus, the distance between the given points is 4\(\sqrt{2}\).

3. Let P (a, b) and Q(- a, – b) be the given points. Then,
PQ = \(\sqrt{(a+a)^2+(b+b)^2}\)
= \(\sqrt{4 a^2+4 b^2}\)
= 2\(\sqrt{a^2+b^2}\)
Thus, the distance between the given points is 2\(\sqrt{a^2+b^2}\).

Question 2.
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in section 7.2.
Answer:
Let A (0, 0) and B (36, 15) be the given points.
Then,
AB = \(\sqrt{(0-36)^2+(0-15)^2}\)
= \(\sqrt{1296+225}\) = \(\sqrt{1521}\) = 39
Thus, the distance between the given points is 39.
Yes, now we can find the distance between the two towns A and B discussed in section 7.2 in the textbook.

Town B is located 36 km east and 15 km north of the town B. So, if we take town A to be situated at the origin with coordinates (0, 0) then the coordinates of town B become (36, 15). Now, as calculated above, the distance between A(0, 0) and B (36, 15) is 39. Hence, the distance between town A and town B is 39 km.

Question 3.
Determine if the points (1, 5), (2, 3) and (- 2, – 11) are collinear.
Answer:
Let A(1, 5), B(2, 3) and C (- 2, – 11) be the given points. Then,

Now, 14.56 + 2.24 = 16.80 ≠ 16.28
Thus, AB + BC ≠ AC
Moreover, BC + AC ≠ AB and AC + AB ≠ BC are obvious.
Hence, the given points are not collinear.

Question 4.
Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
Answer:
Let the given points A (5, – 2), B (6, 4) and C(7, – 2) be the vertices of ΔABC. Then,

Here, in ΔABC, AB = BC ≠ AC.
Hence, ABC is an isosceles triangle.
Thus, the given points (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Question 5.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the given figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

Answer:
Here A(3, 4), B(6, 7), C (9, 4) and D(6, 1) give the position of points where those four friends are seated. Then,

Thus, in quadrilateral ABCD,
AB = BC = CD = DA and AC = BD.
In other words, all the sides of quadrilateral ABCD are equal and its diagonals are also equal.
Hence, ABCD is a square.
So. Champa is correct stating that ABCD is a square.

Question 6.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
1. (- 1, – 2), (1, 0), (1, 2), (- 3, 0)
2. (- 3, 5), (3, 1), (0, 3), (- 1, – 4)
3. (4, 5), (7, 6), (4, 3), (1, 2)
Answer:
1. If possible, let A (- 1, – 2), B(1, 0), C(- 1, 2) and D(- 3, 0) be the vertices of quadrilateral ABCD. Then,

Thus, in quadrilateral ABCD,
AB = BC = CD = DA and AC = BD.
Hence, ABCD is a square.

2. If possible, let A (- 3, 5), B(3, 1), C(0, 3) and D(- 1, – 4) be the vertices of quadrilateral ABCD. Then,

Hence, A, B and C are collinear points in which C lies between A and B.
Hence, A, B, C and D do not form a quadrilateral.

3. If possible, let A (4, 5), B(7, 6), C(4, 3) and D (1, 2) be the vertices of quadrilateral ABCD. Then,


Thus, in quadrilateral ABCD, AB = CD, BC = DA, i.e., both the pairs of opposite sides are equal, but AC ≠ BD. i.e.. diagonals are not equal.
Hence, ABCD is a parallelogram.

Question 7.
Find the point on the x-axis which is equidistant from (2,-5) and (-2, 9).
Answer:
Here, A (2, – 5) and B(- 2, 9) are two given points.
Coordinates of any point of the x-axis are of the form (x, 0).
Let P(x, 0) be the required point on the x-axis which is equidistant from A and B.
So, PA = PB
∴ PA² = PB²
∴ (x – 2)² + (0 + 5)² = (x + 2)² +(0 – 9)²
∴ x² – 4x + 4 + 25 = x² + 4x + 4 + 81
∴ -8x=56
∴ x = – 7
Thus, the required point on the x-axis which is equidistant from (2, – 5) and (- 2, 9) is (- 7, 0).

Question 8.
Find the values of y for which the distance between the points P (2, – 3) and Q(10, y) is 10 units.
Answer:
The distance between P(2, – 3) and 9(10, y) is given to be 10.
∴ PQ = 10
∴ PQ² = 100
∴ (2 – 10)² + (- 3 – y)² = 100
∴ 64 + 9 + 6y + y² = 100
∴ y² + 6y – 27 = 0
∴ (y + 9) (y – 3) = 0
∴ y + 9 = 0 or y – 3 = 0
∴ y = – 9 or y = 3
Thus, the required values of y are – 9 and 3.

Question 9.
If Q(0, 1) is equidistant from P (5, – 3) and R(x, 6), find the values of x. Also find the distances QR and PR.
Answer:
Q(0, 1) is equidistant from P(5, -3) and R (x, 6).
∴ PQ = RQ
∴ PQ² = RQ²
∴ (5 – 0)² + (- 3 – 1)² = (x – 0)² + (6 – 1)²
∴ 25 + 16 = x² + 25
∴ x² = 16
∴ x = ± 4
∴ x = 4 or x = – 4

Thus, x = ± 4, QR = \(\sqrt{41}\) and PR = \(\sqrt{82}\) or 9\(\sqrt{2}\).

Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (- 3, 4).
Answer:
Here, point P(x, y) is given to be equidistant from points A (3, 6) and B (- 3, 4).
∴ PA = PB
∴ PA² = PB²
∴ (x – 3)² + (y – 6)² = (x + 3)² + (y – 4)²
∴ x² – 6x + 9 + y² – 12y + 36 = x² + 6x + 9 + y² – 8y + 16
∴ – 12x – 4y + 20 = 0
∴ 3x + y – 5 = 0 (Dividing by – 4)
Thus, 3x + y – 5 = 0 is the required relation between x and y.

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 6 त्रिभुज Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 6 त्रिभुज

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
दी गई आकृति में रेखाखण्ड XY, त्रिभुज ABC की भुजा AC के समान्तर है तथा त्रिभुज को दो समान भागों में बाँटती है। अनुपात \(\frac{AX}{AB}\) ज्ञात कीजिए।

हल :
दिया है
XY || AC
ΔBXY और ΔBAC में
∠BXY = ∠BAC (संगत कोण)
∠BYX = ∠BCA (संगत कोण)
∴ ΔBXY ~ ΔBAC (AA समरूपता गुणधर्म से )

⇒ \(\frac{AX}{AB}\) = \(\frac{2-\sqrt{2}}{2}\)
अतः \(\frac{AX}{AB}\) = \(\frac{2-\sqrt{2}}{2}\)
∴ AY : AB = (2 – \(\sqrt{2}\)) : 2

प्रश्न 2.
BE और CF एक समकोण ΔABC की माध्यिकाएँ है तथा इस Δ का कोण A समकोण है। सिद्ध कीजिए : 4 (BE² + CF²) = 5BC².
हल :
दिया है : BE तथा CF समकोण ΔABC की माध्यिकाएँ है तथा ∠A = 90° हैं।

सिद्ध करना है: 4(BE² + CF²) = 5BC²
उपपत्ति: समकोण ΔABC में,
BC² = AB² + AC² ……….(1)
समकोण ΔABE में,
BE² = AE² + AB²
BE² = (\(\frac{AC}{2}\))² + AB²
[∵ BE, ΔABC की माध्यिका है
∴ AE = CE = \(\frac{1}{2}\)AC]
BE² = \(\frac{A C^2}{4}\) + 4AB² ……………(2)
अब समकोण ΔCAF में,
CF² = CA² + AF²
CF² = AC² + (\(\frac{AB}{2}\))²
[∵ BF, ΔABC की माध्यिका है
∴ AF = BF = \(\frac{1}{2}\)AB]
CF² = AC² + \(\frac{A B^2}{4}\)
4CF² = 4AC² + AB² …………(3)
समी. (2) और (3) को जोड़ने पर
4 (BE² + CF²) = AC² + 4AB² + 4AC² + AB²
4 (BE² + CF²) = 5 (AC² + AB²)
4 (BE² + CF²) = 5BC²
[समी. (1) के प्रयोग से] इति सिद्धम् ।

प्रश्न 3.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के परिमापों का अनुपात किन्हीं दो संगत भुजाओं के अनुपात के समान होता है।
हल :
दिया है: ΔABC ~ ΔDEF

सिद्ध करना है :

प्रश्न 4.
दी गई आकृति में DE || BC तथा AD : DB = 7 : 5 है, तो क्षेत्रफल (ΔDEF) / क्षेत्रफल (ΔCFB) का मान ज्ञात कीजिए।

हल :
दिया है
DE || BC तथा AD : DB = 7 : 5
ΔADE तथा ΔABC में,
∠ADE = ∠ABC (संगत कोण)
∠AED = ∠ACB (संगत कोण)
∴ ΔADE ~ ΔABC (AA समरूपता गुणधर्म से)
\(\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}\) ……………(1)
[समरूप त्रिभुज की संगत भुजाएँ समानुपाती होती हैं।]
परन्तु AD : DB = 7 : 5

ΔDFE तथा ΔCFB में
∠DEF = ∠CBF (एकान्तर कोण)
∠DFE = ∠CFB(शीर्षाभिमुख कोण)
∴ ΔDFE ~ ΔCFB
(AA समरूपता गुणधर्म से)

प्रश्न 5.
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गये समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
हल :
दिया है : समकोण त्रिभुज ABC की भुजाओं AB, BC तथा AC पर समबाहु त्रिभुज खींचे गए हैं।
सिद्ध करना है : ar (ΔABN) + ar (ΔBCL) = ar(ΔACM)

उपपत्ति : ∵ ΔABN तथा ΔACM के प्रत्येक कोण 60° का होगा ।
अतः ΔABN ~ ΔACM (AA समरूपता गुणधर्म से)

प्रश्न 6.
दिया है कि ΔABC ~ ΔPQR, यदि \(\frac{AB}{PQ}=\frac{1}{3 }\) है, तो ar(ΔABC) / ar(ΔPQR) का मान ज्ञात कीजिए।
हल :
दिया है, ΔABC ~ ΔPQR

प्रश्न 7.
निम्न आकृति में, ∠D = ∠E तथा \(\frac{AB}{DB}=\frac{AE}{EC}\) है, तो सिद्ध कीजिए कि ΔBAC एक समद्विबाहु त्रिभुज है।

हल :
ΔADE
∠D = ∠E (दिया है)
⇒ AD = AE
(∵ बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।)
दिया है, \(\frac{AD}{DB}=\frac{AE}{EC}\)
⇒ \(\frac{AD}{DB}=\frac{AD}{EC}\) [समी. (i) से]
⇒ DB = EC …………….(ii)
समीकरण (i) व (ii) को जोड़ने पर,
AD + DB = AE + EC
⇒ AB = AC
अत: ΔABC एक समद्विबाहु त्रिभुज हैं।

प्रश्न 8.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है कि D, BC का मध्य बिन्दु है । त्रिभुजों ABC और BDE के क्षेत्रफलों में अनुपात ज्ञात कीजिए।
हल :
हम जानते हैं कि समबाहु त्रिभुज समरूप होते हैं,
अर्थात् ΔABC ~ ΔBDE
∵ D, BC का मध्य बिन्दु है,
∴ BC = 2BD ……….(i)

अत: ΔABC का क्षे. ΔBDE का क्षे. = 4 : 1

प्रश्न 9.
निम्न चित्र में, MN || BC और AM : MB = 1 : 2, तो ΔAMN का क्षेत्रफल / ΔABC का क्षेत्रफल का मान ज्ञात कीजिए।

हल :
दिया है, AM = 1K और MB = 2K
∴ AB = AM + MB = 1K + 2K = 3K
ΔAMN और ΔABC में,
∠A = ∠A (उभयनिष्ठ)
∠AMN = ∠ABC (संगत कोण)
∴ ∠AMN ~ ∠ABC (AA समरूपता से)
समरूप त्रिभुजों के क्षेत्रफल के प्रमेय से,

प्रश्न 10.
निम्न चित्र में, यदि AD ⊥ BC, तो सिद्ध कीजिए कि AB² + CD² = BD² + AC²

हल :
समकोण ΔADC मे, पाइथागोरस प्रमेय से,
AC² = AD² + CD²
⇒ AD² = AC² – CD² ……….(i)
पुन: समकोण ΔADB में, पाइथागोरस प्रमेय से
AB² = AD² + BD²
⇒ AD² = AB² – BD² ……….(ii)
समीकरण (i) और (ii) से,
AB² – BD² = AC² – CD²
⇒ AB² + CD² = AC² + BD² इति सिद्धम्

प्रश्न 11.
निम्न चित्र में, यदि ΔABC ~ ΔDEF तथा उनकी भुजाओं की लम्बाइयाँ (सेमी में) उन पर अंकित है, तो प्रत्येक त्रिभुज की भुजाओं की लम्बाई ज्ञात कीजिए।

हल :
दिया है, ΔABC ~ ΔDEF

⇒ 4x – 2 = 18
⇒ x = \(\frac{20}{4}\) = 5
ΔABC में,
AB = 2x – 1 = 2 × 5 – 1 = 9 इकाई
BC = 2x + 2 = 2 × 5 + 2 = 12 इकाई
CD = 3x = 3 × 5 = 15 इकाई
ΔDEF में,
DE = 18 इकाई
EF = 3x + 9 = 3 × 5 + 9 = 24 इकाई
DF = 6x = 6 × 5 = 30 इकाई

प्रश्न 12.
चित्र में, यदि PQ || BC तथा PR || CD है, तो सिद्ध कीजिए कि \(\frac{QB}{AQ}=\frac{DR}{AR}\)

हल :
ΔABC में, PQ || BC
∴ आधारभूत आनुपातिकता प्रमेय से,
\(\frac{AQ}{QB}=\frac{AP}{PC}\) ………….(i)
पुन: ΔADC में,
PR || CD
∴ आधारभूत आनुपातिकता प्रमेय से,
\(\frac{AR}{RD}=\frac{AP}{PC}\) ………….(ii)
समीकरण (i) व (ii) से,
\(\frac{AQ}{QB}=\frac{AR}{RD}\)
अतः \(\frac{QB}{AQ}=\frac{DR}{AR}\) (इति सिद्धम्)

प्रश्न 13.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 16 : 81 है तो इनकी भुजाओं का अनुपात ज्ञात कीजिए।
हल :
समरूप त्रिभुजों के क्षेत्रफल के प्रमेय से,
समरूप त्रिभुज के क्षेत्रफलों का अनुपात = संगत भुजाओं के वर्गों का अनुपात
⇒ 16 : 81 = संगत भुजाओं के वर्गों का अनुपात
⇒ संगत भुजाओं का अनुपात = \(\sqrt{\frac{16}{81}}\) = \(\frac{4}{4}\) = 4 : 9

प्रश्न 14.
निम्न आकृति में, ABC एक त्रिभुज है। यदि \(\frac{AD}{AB}=\frac{AE}{AC}\), तो सिद्ध कीजिए DE || BC है ।

हल :

आधारभूत आनुपातिकता प्रमेय के विलोम से DE || BC (इति सिद्धम)

प्रश्न 15.
यदि दो समरूप त्रिभुजों की संगत माध्यिकाओं का अनुपात 9 : 16 है, तो इनके क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
∵ दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के वर्ग के अनुपात के बराबर होता है ।
∴ क्षेत्रफलों का अनुपात = (9)² : (16)² = 81 : 256

प्रश्न 16.
दो समरूप त्रिभुजों के परिमाप क्रमश: 25 सेमी तथा 15 सेमी है। यदि पहले त्रिभुज की एक भुजा की लंबाई 9 सेमी है, तो दूसरे त्रिभुज की संगत भुजा की लंबाई ज्ञात कीजिए।
हल :
माना दूसरे त्रिभुज की संगत भुजा की लंबाई x सेमी है।
∵ समरूप त्रिभुज की संगत भुजा की लंबाई का अनुपात उनके परिमाप के अनुपात के बराबर होता है।
∴ \(\frac{25}{15}=\frac{9}{x}\)
⇒ x = \(\frac{15 \times 9}{25}\) = 5.4 सेमी
अत: दूसरे त्रिभुज की संगत भुजा = 5.4 सेमी

प्रश्न 17.
चित्र में ΔABC में, DE || BC है तथा AD = 2.4 सेमी, AB = 3 सेमी और AC = 8 सेमी है, तो AE की लम्बाई क्या है?

हल :
चित्र में,
DE || BC
तथा
AD = 2.4 सेमी
AB = 3.2 सेमी
AC = 8 सेमी

प्रश्न 18.
निम्न आकृति में, ΔABC तथा ΔXYZ दर्शाए गए हैं। यदि ABC = 3.8 सेमी, AC = 3\(\sqrt{3}\) सेमी, BC = 6 सेमी, XY = 6\(\sqrt{3}\) सेमी, XY = 7.6 सेमी, YZ = 12 सेमी तथा ∠A = 65°, ∠B = 70° हों, तो ∠Y का मान ज्ञात कीजिए।
हल :
ΔABC में,
∠A + ∠B + ∠D = 180°
65° + 70° + ∠C = 180°
∠C = 180° – 135° = 45°
अब ΔABC और ΔXYZ में

अर्थात् ΔABC ~ ΔXYZ
∴ ∠A = ∠X = 65°, ∠B = ∠Z = 70°
तथा ∠C = ∠Y = 45°

प्रश्न 19.
निम्न चित्र में, समबाहु त्रिभुज ABC में, AD ⊥ BC, BE ⊥ AC तथा CF ⊥ AB है। सिद्ध कीजिए:
4(AD² + BE² + CF²) = 9AB²

हल :
ΔADB और ΔADC में,
और AB = AC (दिया है)
∠B = ∠C (प्रत्येक कोण 60° है।)
और ∠ADB = ∠ADC (प्रत्येक कोण 90° है।)
∴ ΔADB ≅ ΔADC
⇒ BD = DC
⇒ BD = DC = \(\frac{1}{2}\)BC
∵ ΔADB एक समकोण त्रिभुज है,
∴ AB² = AD² + BD²
⇒ AB² = AD² + (\(\frac{BC}{2}\))²
⇒ AB² = AD² + \(\frac{B C^2}{4}\)
⇒ 4AB² = 4AD² + AB²
⇒ 3AB² = 4AD² …………(i)
इसी प्रकार से, ABEC एक समकोण त्रिभुज है,
∴ BC² = BE² + EC²
⇒ AB² = BE² + (\(\frac{AC}{2}\))²
[∵ BC = AB और EC = AE = \(\frac{AC}{2}\)]
⇒ AB² = BE² + (\(\frac{AC}{2}\))²
⇒ 4AB² = 4BE² + AC²
⇒ 4AB² = 4BE² + AB² [∵ AB = AC]
⇒ 3AB² = 4BE² …………..(ii)
अब समकोण ΔBFC में,
BC² = BF² + CF²
⇒ AB² = (\(\frac{AB}{2}\))² + CF²
⇒ AB² = \(\frac{A B^2}{4}\) + CF²
⇒ 4AB² = AB² + 4CF²
⇒ 3AB² = 4CF² ……..(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर
9AB = 4(AD² + BE² + CF²) इति सिद्धम

प्रश्न 20.
दी गई आकृति में, ABC एक समद्विबाहु त्रिभुज है, जिसका कोण C है तथा AC = 4 सेमी है। AB की लम्बाई ज्ञात कीजिए।

हल :
दिया है, ΔABC एक समद्विबाहु त्रिभुज है,
∠C = 90° तथा AC = 4 सेमी
∴ ΔABC एक समद्विबाहु त्रिभुज है। अतः
BC = AC
ΔABC में, पाइथागोरस प्रमेय से,
AB² = AC² + BC²
AB² = AC² + AC² (∵BC = AC)
= 2 × AC²
= 2 × 4²
= 32
⇒ AB = \(\sqrt{32}\)
AB = 4\(\sqrt{2}\) सेमी

प्रश्न 21.
कर्ण BC पर एक ही तरफ दो समकोण त्रिभुज ABC, DBC बनाए गए है। यदि AC तथा BD एक- दूसरे बिन्दु पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि :
AP × PC = BP × DP
हल :
दिया है, ΔABC तथा ΔDBC समकोण त्रिभुज हैं।
ΔABC व ΔDBC में,
∠BAC = ∠BDC = 90°
∠BPA = ∠CPD (शीर्षाभिमुख होगा )

अत: AA समरूपता में,
ΔABC ~ ΔDBC
\(\frac{AP}{BP}=\frac{DP}{PC}\)
[∵ समरूप त्रिभुजों की संगत भुजाओं का अनुपात समान होता है।]
⇒ AP × PC = DP × BP इति सिद्धम्

प्रश्न 22.
दी गई आकृति में, DE || BC, AD = 1 सेमी तथा BD = 2 सेमी है। ΔABC तथा ΔADE के क्षेत्रफलों में क्या अनुपात है?

हल :
दिया है, DE || BC, AD = 1 सेमी तथा BD = 2 सेमी
चूँकि, DE || BC
इसीलिए, ∠ADE = ∠DBC ( संगत कोण)

अतः ar(ΔABC) : ar(ΔADE) = 9 : 1

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. दो आकृतियाँ, जिनके आकार समान हों, परन्तु उनकी आमाप समान न हो, ……………… कहलाती हैं।
2. दो आकृतियाँ जिनके आकार तथा आमाप दोनों समान हों, …………. आकृतियाँ कहलाती है।
3. दो त्रिभुज समरूप होते हैं यदि उनके संगत कोण ……………….. हों ।
4. त्रिभुजों की समरूपता को प्रकट करने के लिए उनक शीर्षों की संगतताओं को सही …………….. में लिखना आवश्यक है।
5. यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करें, तो वह तीसरी भुजा के होती है।

हल :

1. समरूप,
2. सर्वांगसम
3. समान,
4. क्रम,
5. समांतर ।

निम्न में सत्य / असत्य ज्ञात कीजिए :

प्रश्न (ख)

1. दो समरूप त्रिभुजों के क्षेत्रफल त्रिभुजों की संगत भुजाओं के वर्गों के अनुपात में होते हैं।
2. एक समद्विबाहु त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
3. यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो पहली भुजा का सम्मुख कोण अधिक कोण होता है।
4. पाइथागोरस प्रमेय के बौधायन प्रमेय के नाम से भी जाना जाता है।
5. सभी वृत्त सर्वागसम होते हैं।

हल :

1. सत्य,
2. असत्य,
3. असत्य,
4. सत्य,
5. असत्य ।

(ग) बहुविकल्पात्मक प्रश्न :

प्रश्न 1.
यदि ΔABC ~ ΔDEF इस प्रकार है कि AB = 1.2 सेमी तथा DE = 1.4 सेमी है, तो त्रिभुजों ABC तथा DEF के क्षेत्रफलों में अनुपात है:
(A) 49 : 36
(B) 6 : 7
(C) 7 : 6
(D) 36 : 49
हल :
ΔABC ~ ΔDEF

अत: सही विकल्प (D) है।

प्रश्न 2.
चित्र में, ABC एक समद्विबाहु समकोण त्रिभुज है जिसका समकोण C है। अतः
(A) AB² = 2AC²
(B) BC² = 2AB²
(C) AC² = 2AB²
(D) AB² = 4AC²

हल :
समकोण समद्विबाहु ΔABC में,
AB² = AC² + BC²
AB² = AC² + (AC) ² [∵ BC = AC]
AB² = AC² + AC²
AB² = 2AC²
अत: सही विकल्प (A) हैं।

प्रश्न 3.
चित्र में, DE || BC है। यदि \(\frac{AB}{DB}\) = \(\frac{3}{2}\) तथा AE = 2.7 सेमी है, तो EC बराबर है :

(A) 2.0 सेमी
(B) 1.8 सेमी
(C) 4.0 सेमी
(D) 2.7 सेमी
हल :
ΔABC में DE || BC
∴ आधारभूत समानुपातिक प्रमेय से,

अत: सही विकल्प (B) है।

प्रश्न 3.
यदि ΔABC ~ ΔDEF हो एवं AB = 10 सेमी, DE = 8 सेमी हो, तो ΔABC का क्षेत्रफल : ΔDEF का क्षेत्रफल होगा :
(A) 25 : 16
(B) 16 : 25
(C) 4 : 5
(D) 5 : 4
हल :
ΔABC ~ ΔDEF

अत: सही विकल्प (A) है।

प्रश्न 4.
ΔABC में यदि D, BC का मध्य- बिन्दु इस प्रकार है कि \(\frac{AB}{AC}=\frac{BD}{DC}\) हो एवं ∠B = 70°, ∠C = 70° हो, तो ∠BAD की माप होगी :
(A) 60°
(B) 30°
(C) 20°
(D) 50°
हल :
ΔABC में,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 70° + 70° = 180°

⇒ ∠A = 180° – 140°
∴ ∠A = 40°
अतः \(\frac{AB}{AC}=\frac{BD}{DC}\) और ∠B = ∠C
⇒ ΔABD ~ ΔACD
(SAS समरूपता कसौटी से )
∴ ∠BAD और ∠DAC आपस में बराबर होंगे।
∠BAD + ∠DAC = 40°
⇒ 2∠BAD = 40°
∴ ∠BAD = \(\frac{40°}{2}\) = 20°
अत: सही विकल्प (C) है।

प्रश्न 5.
दी गई आकृति में, XY || QR, \(\frac{PQ}{XQ}=\frac{7}{3}\) तथा PR = 6.3 सेमी है, तो YR बराबर है :
(A) 2.7 सेमी
(B) 18.9 सेमी
(C) 2.1 सेमी
(D) 0.9 सेमी

हल :
दिया है
त्रिभुज PQR में XY || QR, \(\frac{PQ}{XQ}\) = \(\frac{7}{3}\) तथा PR = 6.3 सेमी।
आधारभूत आनुपातिक प्रमेय से,

अत: विकल्प (A) सही है।

प्रश्न 6.
एक 12 मीटर लम्बी ऊर्ध्वाधर छड़ की जमीन पर छाया की लम्बाई 8 मीटर लम्बी है। यदि इसी समय एक मीनार की छाया की लम्बाई 40 मीटर हो, तो मीनार की ऊँचाई होगी :
(A) 60 मीटर
(B) 60 सेमी
(C) 40 सेमी
(D) 80 सेमी
हल :
माना ऊर्ध्वाधर AB छड़ है और BC उसकी छाया है। PQ मीनार है और CQ उसकी छाया है।

ΔABC और ΔPQC में,
∠ACB = ∠PCQ (उभयनिष्ठ)
∠ABC = ∠PQC (प्रत्येक 90°)
कोण-कोण समरूपता गुणधर्म से,
ΔABC ~ ΔPOC
∴ \(\frac{AB}{PQ}=\frac{BC}{QC}\) (∵ समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं)
⇒ \(\frac{12}{PQ}=\frac{8}{40}\)
∴ PQ = \(\frac{40 \times 12}{8}\)
= 5 × 12 = 60 मीटर
अतः सही विकल्प (A) है।

प्रश्न 7.
आकृति में, DE || BC है यदि AD = x, DB = x – 2, AE = x + 2 तथा EC = x – 1 हो, तो x का मान होगा :

(A) 3
(B) 2
(C) 4
(D) 1
हल :
ΔABC में,
DE || BC
\(\frac{AD}{BD}=\frac{AE}{EC}\)
⇒ \(\frac{x}{x-2}=\frac{x+2}{x-1}\)
⇒ x(x – 1) = (x – 2) (x + 2)
⇒ x² – x = x² – 4
∴ x = 4
अत: सही विकल्प (C) है।

प्रश्न 8.
आकृति में ΔACB ~ ΔAPQ है यदि BC = 8 सेमी, BA = 6.5 सेमी, PQ = 4 सेमी और AP = 2.8 सेमी हो, तो 40 का मान होगा :

(A) 5.6 सेमी
(B) 6.8 सेमी
(C) 10.5 सेमी
(D) 3.25 सेमी
हल :
ΔACB ~ ΔAPQ

अत: सही विकल्प (D) है।

प्रश्न 9.
यदि ΔABC में AB = 5 सेमी, BC = 12 सेमी और AC = 13 सेमी है, तो ∠B का मान होगा:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
हल :
ΔABC में,
(AB)² + (BC)² = (5)² + (12)²
= 25 + 144 = 169
= (AC)²
∴ AB² + BC² = AC²
पाइथागोरस प्रमेय के विलोम से,
ΔABC समकोण त्रिभुज है जिसमें
∠B = 90°
अत: सही विकल्प (C) है।

प्रश्न 10.
दो समरूप ΔABC और ΔPQR हैं जिनके क्षेत्रफल क्रमशः 100 सेमी² तथा 144 सेमी² है और ΔABC की ऊँचाई 6 सेमी है तो ΔPQR की ऊँचाई होगी :
(A) 12 सेमी
(B) 6.3 सेमी
(C) 7.2 सेमी
(D) 4.8 सेमी
हल :
हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत ऊँचाइयों के वर्गों के अनुपात के समान होता है। माना ΔPQR की संगत ऊँचाई x सेमी है।

अत: सही विकल्प (C) है।

प्रश्न 11.
यदि ΔABC और ΔDEF में \(\frac{AB}{DE}=\frac{BC}{FD}\) हो, तो वे समरूप होंगे, यदि :
(A) ∠B = ∠E
(B) ∠A = ∠D
(C) ∠B = ∠D
(D) ∠A = ∠F
हल :
सही विकल्प (C) है।

प्रश्न 12.
यदि ΔDEF और ΔPQR में ∠D = ∠Q और ∠R = ∠E हो, तो निम्नलिखित में से कौन-सा सही नहीं है?
(A) \(\frac{EF}{PR}=\frac{DF}{PQ}\)
(B) \(\frac{DE}{PQ}=\frac{EF}{RP}\)
(C) \(\frac{DE}{QR}=\frac{DF}{PQ}\)
(D) \(\frac{EF}{RP}=\frac{DE}{QR}\)
हल :
सही विकल्प (B) है।

प्रश्न 13.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 16 : 81 है, तो त्रिभुजों की भुजाओं का अनुपात होगा :
(A) 4 : 9
(B) 16 : 81
(C) 9 : 4
(D) 2 : 3
हल :
हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के समान होता है ।
अतः दोनों भुजाओं का अनुपात = 4 : 9
अत: सही विकल्प (A) है।

Students should go through these JAC Class 10 Maths Notes Chapter 11 रचनाएँ will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 11 रचनाएँ

भूमिका :
कक्षा IX में, हमने कुछ रचनाओं के बारे में सीखा था जैसे कि किसी रेखाखण्ड का लम्ब समभाजक खींचना, किसी कोण का समद्विभाजक खींचना, त्रिभुजों की रचनाएँ करना इत्यादि और उनका औचित्य भी दिया था। इस अध्याय में पिछली रचनाओं के ज्ञान का उपयोग करते हुए कुछ और रचनाओं के बारे में अध्ययन करेंगे। जैसे एक रेखाखण्ड का विभाजन, किसी त्रिभुज के समरूप दूसरे त्रिभुज की रचना, वृत्त पर स्पर्श रेखा की रचना इत्यादि।

→ रचना (Construction) : कल्पना करने और बनाने की कला।

→ समरूप आकृतियाँ (Similar figures) : ऐसी ज्यामितीय आकृतियाँ जिनका रूप (shape) समान है, परन्तु जरूरी नहीं कि आकार भी समान हो, समरूप आकृतियाँ कहलाती हैं।

→ चाप (Arc) : वक्र रेखा पर दो बिन्दुओं के बीच की दूरी चाप कहलाता है।

→ स्पर्श रेखा (Tangent) : एक सीधी रेखा जो वृत्त को सिर्फ एक बिन्दु पर स्पर्श करती है, स्पर्श रेखा कहलाती है।

→ स्पर्श बिन्दु (Point of Contact) : वह बिन्दु जिस पर स्पर्श रेखा वृत्त को स्पर्श करती है, स्पर्श बिन्दु कहलाता है।

→ संकेन्द्रीय वृत्त (Concentric circles) : यदि दो वृत्तों का केन्द्र एक हो तथा विभिन्न त्रिज्याएँ हो, संकेन्द्रीय वृत्त कहलाते हैं।

Jharkhand Board JAC Class 10 Science Solutions Chapter 8 How do Organisms Reproduce? Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 8 How do Organisms Reproduce?

Jharkhand Board Class 10 Science How do Organisms Reproduce? Textbook Questions and Answers

Question 1.
Asexual reproduction takes place through budding in…
A. amoeba
B. yeast
C. plasmodium
D. leishmania
Answer:
yeast

Question 2.
Which of the following is not a part of the female reproductive system in human beings?
A. Ovary
B. Uterus
C. Vas deferens
D. Fallopian tube
Answer:
Vas deferens

Question 3.
The anther contains
A. sepals
B. ovules
C. pistil
D. pollen grains
Answer:
pollen grains

Question 4.
What are the advantages of sexual reproduction over asexual reproduction?
Answer:
The advantages of sexual reproduction over asexual reproduction are as follows:

• Sexual reproduction involves fusion of male and female gametes from male and female parents to form zygote. Thus, new generation shows variation as DNA copies from two different individuals are received.
• Sexual reproduction involves gamete formation. During male and female gamete formation, meiosis takes place. New combination of genes occur during meiosis. This also leads to variation. Combining variation from two individuals would create new combination of variants.
• Sexual reproduction create variation generation after generation, which is useful for survival of species over time.
• The inbuilt tendency for variation during sexual reproduction is the basis for evolution.

Question 5.
What are the functions performed by the testis in human beings?
Answer:
The functions performed by the testis in human beings :

• to produce sperms
• to secrete testosterone.

Question 6.
Why does menstruation occur?
Answer:
When egg is not fertilised, the thick-spongy and highly vascular inner lining of uterus breaks causing menstruation in woman.

Question 7.
Draw a labelled diagram of the longitudinal section of a flower.
Answer:
Flower is the reproductive organ in flowering plants (angiosperms).

Parts of a flower: Sepals, petals, stamens and pistils. Among these stamens and pistils are reproductive parts.

Stamens : It is a male reproductive part. It consists filament and an anther.
Anther produces pollen grains that are yellowish in colour.

Pistil : It is present in the centre of a flower and is the female reproductive part. It is made up of three parts :

• Ovary : bottom swollen part
• Style : middle elongated part
• Stigma : terminal sticky part.

The ovary contains ovules and each ovule has an egg cell.

Types of flowers on the basis of reproductive parts are as follows :

• Unisexual flowers : When flower contains either stamens or pistil, it is called unisexual flower, e.g., Papaya, watermelon.
• Bisexual flowers : When flower contains both stamens and pistil, it is called bisexual flowers, e.g., Hibiscus, mustard, datura.

Question 8.
What are the different methods of contraception?
Answer:

Question 9.
How are the modes for reproduction different in unicellular and multi-cellular organisms?
Answer:
Unicellular organisms multiply by simple cell division, i.e., by fission, budding, multi-cellular organisms have complex body organisation. They need to use more complex ways of reproduction mainly by sexual reproduction.

Question 10.
How does reproduction help in providing stability to populations of species?
Answer:
Reproduction gives rise to new offsprings of a species. No organism is immortal. High death-rate reduce the size of population. The rates of birth and death in a given population will determine its size.

So, reproduction is the process by which organisms increase their population and help in providing stability to population of species.

Question 11.
What could be the reasons for adopting contraceptive methods?
Answer:
The reasons for adopting contraceptive methods :

• To prevent unwanted pragnancies.
• To control human population.
• To prevent the transmission of sexually transmitted diseases especially by using condoms or vaginal covering.

Jharkhand Board Class 10 Science How do Organisms Reproduce? InText Questions and Answers

Question 1.
What is the importance of DNA copying in reproduction?
Answer:
Importance of DNA copying in reproduction :

• Transmission of hereditary information of parents to offsprings.
• Formation of variations by changes in DNA leads to evolution of species over a period of time.

Question 2.
Why is variation beneficial to the species but not necessarily for the individual?
Answer:
When reproduction takes place, new DNA copies are generated. They may show some amount of variations. The variations may not be beneficial for an individual. But when such variations go on accumulating over a longer time span, they may change the species. This change leads to evolution.

Question 3.
How does binary fission differ from multiple fission?
Answer:

• Binary fission is a type of fission, in which parent cell splits into two cells, example Amoeba, bacteria.
• Multiple fission is a type of fission in which single celled organisms divide into many daughter cells at one time, example Plasmodium.

Question 4.
How will an organism be benefitted if it reproduces through spores?
Answer:
Spores remain coated with protective envelope under unfavourable condition. This helps to survive in adverse conditions. They germinate only after favourable conditions return. Thus organism is benefitted by spore formation.

Question 5.
Can you think of reasons why more complex organisms cannot give rise to new individuals through regeneration?
Answer:
More complex organisms cannot give rise to new individuals due to following reasons :

• Different cell types perform different specialised functions.
• Complex organisms have tissues and organs.
• In complex organisms the regenerative ability is lost due to specialisation of tissues and organs.
• Reproduction in more complex organisms is the function of a specific cell type.
• Specialized cells to carry out regeneration are not present in complex animals.

Question 6.
Why is vegetative propagation practised for growing some types of plants?
Answer:
Vegetative propagation is practised for growing some types of plants because:

• Plants produced by vegetative propagation can bear flowers and fruits earlier than those produced from seeds.
• Plants that have lost their capability to produce seeds can be propagated by this method.
• It helps in retaining useful characters from generation to generation.

Question 7.
Why is DNA copying an essential part of the process of reproduction?
Answer:
DNA copying is an essential part of the process of reproduction because entire genetic information of parents is passed on to next generation through DNA. The DNA in the nucleus of the cell is the information source for making proteins which in turn form the body designs.

Question 8.
How is the process of pollination different from fertilisation?
Answer:
Pollination is the process of transfer of pollen grains from the anther of a stamen to the stigma of a carpel. Fertilisation is the process of fusion of male gamete with a female gamete to form a zygote.

Question 9.
What is the role of the seminal vesicles and the prostate gland?
Answer:
The secretion of the seminal vesicles and the prostate gland makes transport of sperms easier and provides nutrition to the sperms.

Question 10.
What are the changes seen in girls at the time of puberty?
Answer:
In girls, breast size begins to increase, with darkening of the skin of the nipples and menstruation begins at the time of puberty.

Question 11.
How does the embryo get nourishment inside the mother’s body?
Answer:
The embryo gets nourishment from the mother’s blood with the help of special tissue called placenta. Placenta contains villi on the embryo’s side of the tissue through which glucose and oxygen pass from the mother to embryo.

Question 12.
If a woman is using a copper-T will it help in protecting her from sexually transmitted diseases?
Answer:
No, a copper-T will not help in protecting woman from sexually transmitted diseases because during sexual intercourse fluid of male and female body directly come in contact.

Activity 8.1 [T. B. Pg. 129]

To observe the asexual reproduction method -Budding in yeast.

Apparatus : Test tube, conical flask, cotton plug, cover slip, glass slide, microscope, dropper.

Materials: Water, sugar, dry yeast granules.

Procedure:

• Take 100mL of water in conical flask. Add 10g sugar and dissolve it to prepare sugar solution.
• Take 20 mL of sugar solution in glass test tube. Add little amount of dry yeast granules. Shake the mixture and close the test tube tightly with cotton plug.
• Keep the test tube in warm place for 1 to 2 hours.
• Take one or two drops of yeast solution on the glass slide with the help of dropper.
• Now put a cover slip over it and observe under the microscope.
  

Questions :

Questions 1.
What is seen under the microscope?
Answer:
Yeast cells are seen under the microscope.

Questions 2.
Explain meaning of Bud.
Answer:
Bud is an outgrowth on yeast cell surface due to cell division.

Questions 3.
Can yeast live in the dormant condition?
Answer:
Yes.

Activity 8.2 [T. B. Pg. 129]

To observe the growth of fungus-Rhizopus on the piece of bread.

Apparatus : Petridish, Magnifying glass.

Material: Wet slice of bread.

Procedure :

• Wet a slice of bread in water. Now put the wet piece of bread in petridish. Keep the petridish in dark, moist and cool environment for a week.
• Now observe the bread slice with help of magnifying glass.
  

Questions :

Question 1.
What is seen on the slice of bread?
Answer:
Network of white cotton fibres-like structure is seen on the slice of bread.

Question 2.
From where did the fungi arrive on bread?
Answer:
The fungal spores arrived on bread from air.

Question 3.
Which fungi grow on the bread?
Answer:
Rhizopus fungi grow on the bread.

Question 4.
Why do spores of fungi germinate on the bread?
Answer:
Spores of fungi germinate on the bread because on bread moist environment and nutrients are available.

Question 5.
Reproduction through spore formation is which type of reproduction method ?
Answer:
Asexual reproduction.

Question 6.
Compare the growth of yeast and mould.
Answer:
Yeast is a type of fungus that grows as a single cell. Mould is a type of fungus that grows multicellular filamentous structures called hyphae.

These tubular branches from a single organism have multiple, genetically identical nuclei. The reproduction in yeast occurs by budding. Mould reproduces by formation of sexual or asexual spores.

Activity 8.3 [T. B. Pg. 129]

To observe binary fission in Amoeba. Apparatus: Microscope, permanent slide of Amoeba.

Procedure:

• Observe a permanent slide of Amoeba under a microscope.
• Observe another permanent slide of Amoeba showing binary fission.
• Compare your observations in both the slides.
  

Questions :

Question 1.
Is Amoeba prokaryotic or eukaryotic organism ?
Answer:
Eukaryotic.

Question 2.
Can you give the sequence of binary fission in Amoeba?
Answer:
The sequence of binary fission in Amoeba : Nuclear division → Cytoplasmic division → Cell divides into two daughter cells.

Question 3.
Which unicellular, eukaryotic organisms reproduce through binary fission?
Answer:
Amoeba, Paramoecium, Leishmania. Euglena, etc.

Activity 8.4 [T. B. Pg. 130]

To observe filamentous algae under a microscope.

Apparatus : Microscope, slide, coverslip. Materials : Glycerine, pond water, blotting paper.

Procedure:

• Collect water from a lake or pond that appears dark green and contains filamentous structure.
• Put one or two filaments on a slide.
• Put a drop of glycerine on the filaments and cover it with a coverslip.
• Observe the slide under a microscope.
  

Questions :

Question 1.
State the example of filamentous organism.
Answer:
Filamentous algae : Spirogyra.

Question 2.
Can you identify different tissues in the filaments?
Answer:
No, filament of spirogyra is devoid of tissues.

Question 3.
Why is filament of spirogyra green in colour?
Answer:
A green colour of the filament of spirogyra is due to presence of chlorophyll.

Question 4.
Is spirogyra a prokaryotic or eukaryotic organism?
Answer:
Eukaryotic organism.

Question 5.
How do spirogyra reproduce asexually?
Answer:
Spirogyra reproduces asexually by fragmentation.

Activity 8.5 [T. B. Pg. 132]

To study the vegetative propagation in potato.

Apparatus : Tray, cotton

Material: Potato

Procedure:

• Take potato tuber and observe its surface.
• Observe the pits on its surface and bud present in the pit.
• Make circle around them with the help of marker.
• Cut the potato into small pieces in such a way that, some of them possess bud.
• Now put wet cotton in the tray and put the potato pieces on it.
• Water for some days in tray, so that cotton remains wet.
• Observe the changes that occur in the potato piece.
  

Questions:

Question 1.
Is potato tuber root or stem?
Answer:
Potato tuber is stem.

Question 2.
Which other plants except potato produce buds for vegetative propagation?
Answer:
Bulbs of Ginger, amorphophalus, etc. produce buds for vegetative propagation.

Question 3.
Which are the potato pieces, that give rise to fresh green shoots and roots ?
Answer:
Only those potato pieces having bud, give rise to fresh green shoots and roots.

Activity 8.6 [T. B. Pg. 132]

To show vegetative propagation by stem cuttings.

Materials : Money-plant (pothos)

Procedure:

• Select a money-plant. Cut some pieces which contain at least one node of leaf.
• Cut out some other portions between two leaves.
• Dip one end of all the pieces in water.
• Observe over the next few days.

Questions :

Question 1.
Which pieces grow and give rise to fresh leaves?
Answer:
Those pieces with at least one node of leaf can grow and give rise to fresh leaves.

Question 2.
State your conclusion.
Answer:
Node is essential in a stem cutting for vegetative propagation of money-plant.

Question 3.
Can you give some other example to show vegetative propagation by stem cuttings?
Answer:
Rose, hibiscus, lemon, sugarcane, tamarind, etc.

Activity 8.7 [T. B. Pg. 135]

To observe the different parts of seed.

Materials : Seeds of Bengal gram [chana], water, wet cloth.

Procedure:

• Soak a few seeds of Bengal gram (chana) and keep them overnight.
• Drain the excess water and cover the seeds with a wet cloth and leave them for a day.
• Make sure that the seeds do not become dry.
• Cut open the seeds carefully and observe the different parts.
  

Questions :

Question 1.
What is an embryo of plant?
Answer:
An embryo is a future plant which develops into seedling.

Question 2.
Which are the structures seen in an embryo?
Answer:
A radicle, plumule and cotyledons occur in an embryo.

Question 3.
What is the role of cotyledon in chana?
Answer:
Cotyledons store food nutrients in chana and provide these nutrients during seed germination.

Question 4.
Which parts in seed are known as future root and as future shoot?
Answer:
Radicle is known as future root and plumule as future shoot.

Question 5.
How is an embryo formed from zygote?
Answer:
The zygote divides several times to form an embryo.

Jharkhand Board JAC Class 10 Science Solutions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन

Jharkhand Board Class 10 Science प्रकाश-परावर्तन तथा अपवर्तन Textbook Questions and Answers

अभ्यास प्रश्न (पृष्ठ संख्या-204-206)

1. निम्न में से कौन-सा पदार्थ लेंस बनाने के लिए प्रयुक्त नहीं किया जा सकता?
(a) जल
(b) काँच
(c) प्लास्टिक
(d) मिट्टी
उत्तर:
(d) मिट्टी।

2. किसी बिंब का अवतल दर्पण द्वारा बना प्रतिबिंब आभासी, सीधा तथा बिंब से बड़ा पाया गया। वस्तु की स्थिति कहाँ होनी चाहिए?
(a) मुख्य फोकस तथा वक्रता केन्द्र के बीच
(b) वक्रता केन्द्र पर
(c) वक्रता केन्द्र से परे
(d) दर्पण के ध्रुव तथा मुख्य फोकस के बीच
उत्तर:
(d) दर्पण के ध्रुव तथा मुख्य फोकस के बीच।

3. किसी बिंब का वास्तविक तथा समान साइज का प्रतिबिंब प्राप्त करने के लिए बिंब को उत्तल लेंस के सामने कहाँ रखें?
(a) लेंस के मुख्य फोकस पर
(b) फोकस दूरी की दोगुनी दूरी पर
(c) अनंत पर
(d) लेंस के प्रकाशिक केन्द्र तथा मुख्य फोकस के बीच
उत्तर:
(b) फोकस दूरी की दोगुनी दूरी पर।

4. किसी गोलीय दर्पण तथा किसी पतले गोलीय लेंस दोनों की फोकस दूरियाँ 15 cm हैं। दर्पण तथा लेंस संभवत: हैं-
(a) दोनों अवतल
(b) दोनों उत्तल
(c) दर्पण अवतल तथा लेंस उत्तल
(d) दर्पण उत्तल तथा लेंस अवतल
उत्तर:
(a) दोनों अवतल।

5. किसी दर्पण से आप चाहे कितनी ही दूरी पर खड़े हों, आपका प्रतिबिंब सदैव सीधा प्रतीत होता है। संभवतः दर्पण है-
(a) केवल समतल
(b) केवल अवतल
(c) केवल उत्तल
(d) या तो समतल अथवा उत्तल
उत्तर:
(d) या तो समतल अथवा उत्तल

6. किसी शब्दकोश (Dictionary) में पाए गए छोटे अक्षरों को पढ़ते समय आप निम्न में से कौन-सा लेंस पसंद करेंगे?
(a) 50 cm फोकस दूरी का एक उत्तल लेंस
(b) 50 cm फोकस दूरी का एक अवतल लेंस
(c) 5 cm फोकस दूरी का एक उत्तल लेंस
(d) 5 cm फोकस दूरी का एक अवतल लेंस
उत्तर:
(c) 5 cm फोकस दूरी का एक उत्तल लेंस।

प्रश्न 7.
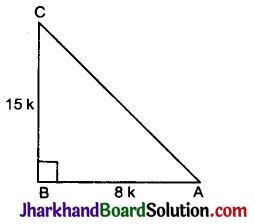
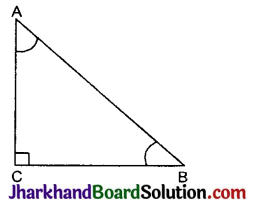
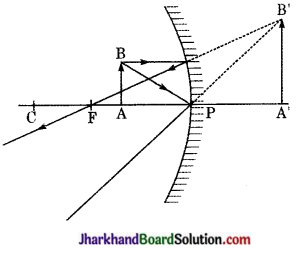
15 cm फोकस दूरी के एक अवतल दर्पण का उपयोग करके हम किसी बिंब का सीधा प्रतिबिंब बनाना चाहते हैं। बिंब ‘दर्पण से दूरी का परिसर (Range) क्या होना चाहिए? प्रतिबिंब की प्रकृति कैसी है? प्रतिबिंब बिंब से बड़ा है अथवा छोटा? इस स्थिति में प्रतिबिंब बनने का एक किरण आरेख बनाइए।
उत्तर:
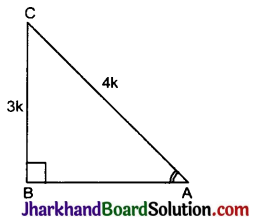
बिंब का दर्पण से दूरी दर्पण के ध्रुव से 0 से 15 सेमी के बीच है (अर्थात्, 15 सेमी से कम है)।

• प्रतिबिंब की प्रकृति आभासी तथा सीधा
• प्रतिबिंब, बिंब से बड़ा है।
  

प्रश्न 8.
निम्न स्थितियों में प्रयुक्त दर्पण का प्रकार बताइए-
(a) किसी कार का अग्रदीप (हैडलाइट)
(b) किसी वाहन का पार्श्व / पश्च दृष्टि दर्पण
(c) सौर मट्टी
अपने उत्तर की कारण सहित पृष्टि कीजिए।
उत्तर:
(a) किसी कार के हैड लाइट में अवतल दर्पण का प्रयोग किया जाता है क्योंकि वह प्रकाश को परावर्तित कर सकता है।

(b) किसी वाहन के पार्श्व तथा पश्च दृश्य के लिए उत्तल दर्पण का प्रयोग किया जाता है क्योंकि यह वस्तु का सीधा प्रतिबिंब बनाता है और पीछे के ट्रैफिक के विस्तृत क्षेत्र को देख सकता है।

(c) सौर भट्टी में अवतल दर्पण का प्रयोग किया जाता है, क्योंकि दर्पण सूर्य की किरणों को वस्तु पर फोकस करके उसे ताप प्रदान करता है।

प्रश्न 9.
किसी उत्तल लेंस का आधा भाग काले कागज से ढक दिया गया है। क्या यह लेंस किसी बिंब का पूरा प्रतिबिंब बना पाएगा? अपने उत्तर की प्रयोग द्वारा जाँच कीजिए। अपने प्रेक्षणों की व्याख्या कीजिए।
उत्तर:
हाँ, उत्तल लेंस आधा भाग काले कागज से ढकने के बावजूद भी वस्तु का पूरा प्रतिबिंब बनाता है। चूँकि प्रकाश किरणें लेंस के आधा भाग वस्तु पर से गुजरती हैं और वस्तु का पूरा प्रतिबिंब बनाती हैं।

प्रश्न 10.
5 cm लंबा कोई बिंब 10 cm फोकस दूरी के किसी अभिसारी लेंस से 25. cm दूरी पर रखा जाता है। प्रकाश किरण आरेख खींचकर बनने वाले प्रतिबिंब की स्थिति, साइज तथा प्रकृति ज्ञात कीजिए। उत्तर:
वस्तु की लंबाई (h) = 5 cm
वस्तु की दूरी (u) = – 25 cm
फोकस दूरी (f) = + 10 cm
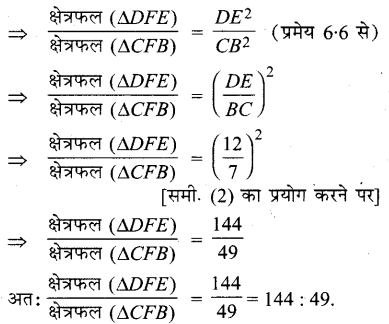
चूँकि \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac{1}{v}=\frac{1}{u}+\frac{1}{f}\)
⇒ \(\frac{1}{v}=\frac{1}{-25}+\frac{1}{10}\)
⇒ \(\frac{1}{v}=\frac{-2+5}{50}=\frac{+3}{50}\)
⇒ v = + \(\frac { 50 }{ 3 }\)
= + 16.56 cm
v का धनात्मक चिन्ह यह दर्शाता है कि प्रतिबिंब लेंस के प्रकाशीय केन्द्र के दाई तरफ 16.67 cm की दूरी पर बनेगा। इसलिए प्रतिबिंब वास्तविक तथा उलटा बनेगा।
आवर्धन m = \(\frac{h_1}{h}=\frac{v}{u}\)
या h₁ = h x \(\frac { v }{ u }\)
प्रतिबिंब का आकार

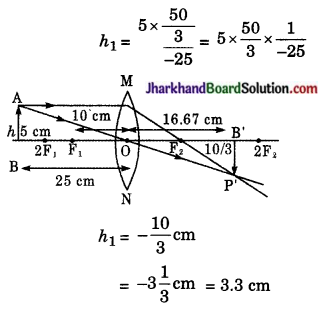
h₁ का ऋणात्मक चिन्ह दर्शाता है कि प्रतिबिंब उलटा बनेगा। यह मुख्य अक्ष के नीचे बनेगा।
इस प्रकार, एक वास्तविक, उलटा प्रतिबिंब लेंस की दाईं तरफ 16.67 की दूरी पर 3\(\frac { 1 }{ 3 }\)cm लंबा बनेगा।

प्रश्न 11.
15 cm फोकस दूरी का कोई अवतल लेंस किसी बिंब का प्रतिबिंब लेंस से 10 cm दूरी पर बनाता है। बिंब लेंस से कितनी दूरी पर स्थित है? किरण आरेख खींचिए।
उत्तर:
फोकस दूरी f = 15 सेमी, प्रतिबिंब की दूरी v = – 10 सेमी, बिंब दूरी u = ?

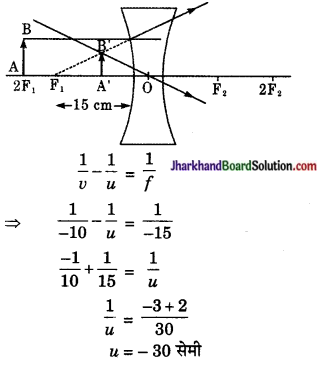
अर्थात्, बिंब अवतल लेंस से 30 सेमी की दूरी पर है।

प्रश्न 12.
15 cm फोकस दूरी के किसी उत्तल दर्पण से कोई बिंब 10 cm दूरी पर रखा है। प्रतिबिंब की स्थिति तथा प्रकृति ज्ञात कीजिए।
उत्तर:
फोकस दूरी f = 15 सेमी, बिंब की दूरी = – 10 सेमी, प्रतिबिंब दूरी v = ?
हम जानते हैं कि \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
⇒ \(\frac{1}{-10}+\frac{1}{v}=\frac{1}{15}\)
\(\frac{1}{v}=\frac{1}{15}+\frac{1}{10}\)
\(\frac{1}{v}=\frac{2+3}{30}\)
\(\frac{1}{v}=\frac{5}{30}\)
v = 6 सेमी
अर्थात्, प्रतिबिंब दर्पण के पीछे 6 सेमी की दूरी पर बनता है। प्रतिबिंब वास्तविक तथा उलटा है।

प्रश्न 13.
एक समतल दर्पण द्वारा उत्पन्न आवर्धन + 1 है। इसका क्या अर्थ है?
उत्तर:
धनात्मक चिन्ह यह दर्शाता है कि प्रतिबिंब आभासी, सीधा तथा समान आकार का बना है।

प्रश्न 14.
5.0 सेमी लंबाई का कोई बिंब 30 सेमी वक्रता त्रिज्या के किसी उत्तल दर्पण के सामने 20 सेमी. दूरी पर रखा गया है। प्रतिबिंब की स्थिति, प्रकृति तथा साइज ज्ञात कीजिए।
उत्तर:
यहाँ, बिंब की ऊँचाई h₁ = 5 सेमी,
वक्रता त्रिज्या R = 30 सेमी
\(\frac { R }{ 2 }\) = f
या फोकस दूरी f = \(\frac { 30 }{ 2 }\) = + 15 सेमी
बिंब दूरी u = – 20 सेमी
प्रतिबिंब की दूरी = ?
प्रतिबिंब की ऊँचाई h₂ = ?
तो प्रतिबिंब की दूरी v = ?
प्रतिबिंब की ऊँचाई h₂ = ?
हम जानते हैं कि \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ v }\) + \(\frac { 1 }{ -20 }\) = \(\frac { 1 }{ +15 }\)
\(\frac { 1 }{ v }\) = \(\frac { 1 }{ 15 }\) + \(\frac { 1 }{ 20 }\) = \(\frac { 4+3 }{ 60 }\)
v = \(\frac { 60 }{ 7 }\) सेमी = 8.57 सेमी
प्रतिबिंब दर्पण के पीछे 8.6 सेमी की दूरी पर बना है।

अर्थात्, प्रतिबिंब का आकार 2.175 (या 2.2 सेमी) है। प्रतिबिंब आभासी सीधा तथा छोटी है।

प्रश्न 15.
7.0 cm साइज का कोई बिंब 18 सेमी फोकस दूरी के अवतल दर्पण के सामने 27 सेमी दूरी पर रखा गया है। दर्पण से कितनी दूरी पर किसी परदे को रखें कि उस पर वस्तु का स्पष्ट फोकसित प्रतिबिंब प्राप्त किया जा सके। प्रतिबिंब का साइज तथा प्रकृति ज्ञात कीजिए।
उत्तर:
यहाँ, बिंब की ऊँचाई h₁ = 5 सेमी,
बिंब दूरी u = – 27 सेमी,
फोकस दूरी f = – 18 सेमी,
तो प्रतिबिंब की दूरी v = ?
प्रतिबिंब की ऊँचाई h₂ = ?
हम जानते हैं कि
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ -27 }\) + \(\frac { 1 }{ v }\) = \(\frac { 1 }{ -18 }\)
\(\frac { 1 }{ v }\) = \(\frac { -1 }{ 18 }\) + \(\frac { 1 }{ 27 }\)
= \(\frac { -3+2 }{ 5 }\)
v = – 54 सेमी.
अर्थात्, परदे को दर्पण से 54 सेमी की दूरी पर रखी जानी चाहिए।

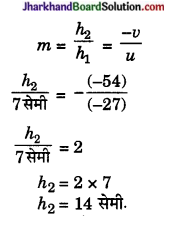
h₂ = 14 सेमी.
अर्थात्, प्रतिबिंब की ऊँचाई 14 सेमी है तथा यह वास्तविक और उलटा है।

प्रश्न 16.
उस लेंस की फोकस दूरी ज्ञात कीजिए जिसकी क्षमता – 2.0D है। यह किस प्रकार का लेंस है?
उत्तर:
P = \(\frac { 1 }{ f }\)
– 20 = \(\frac { 1 }{ f }\)
f = \(\frac { -1 }{ 2 }\) मी
f = – \(\frac { 1 }{ 2 }\) x 100 मी
f = 50 मी = – 0.50 सेमी
अर्थात्, लेंस की फोकस दूरी 0.40 मी है तथा यह अवतल लेंस है।

प्रश्न 17.
कोई डॉक्टर + 1.5D क्षमता का संशोधक लेंस निर्धारित करता है। लेंस की फोकस दूरी ज्ञात कीजिए। क्या निर्धारित लेंस अभिसारी है अथवा अपसारी?
उत्तर:
P = \(\frac { 1 }{ f }\)
1.5 = \(\frac { 1 }{ f }\)
f = \(\frac { 1 }{ 1.5 }\) मी = \(\frac { 10 }{ 15 }\) मी
= \(\frac { 2 }{ 3 }\) मी = + 0.67 मी
अर्थात्, लेंस की फोकस दूरी + 0.67 मी है निर्धारित लेंस अभिसारी है।

Jharkhand Board Class 10 Science प्रकाश-परावर्तन तथा अपवर्तन InText Questions and Answers

पाठगत प्रश्न (पृष्ठ संख्या – 185 )

प्रश्न 1.
अवतल दर्पण के मुख्य फोकस की परिभाषा लिखिए।
उत्तर:
अवतल दर्पण पर मुख्य अक्ष के समांतर आपतित किरणें परावर्तित होकर दर्पण की मुख्य फोकस के जिस बिन्दु पर मिलती है प्रतिच्छेदी है, वह बिन्दु अवतल दर्पण का मुख्य फोकस कहलाता है।

प्रश्न 2.
एक गोलीय दर्पण की वक्रता त्रिज्या 20 सेमी है। इसकी फोकस दूरी क्या होगी?
उत्तर:
हम जानते हैं कि,
R = 2f
जहाँ, R = 20 सेमी
∴ f = \(\frac { 20 }{ 2 }\) = 10 सेमी
गोलीय दर्पण की फोकस दूरी = 10 सेमी

प्रश्न 3.
उस दर्पण का नाम बताइए जो बिंब का सीधा तथा आवर्धित प्रतिबिंब बना सके।
उत्तर:
अवतल दर्पण।

प्रश्न 4.
हम वाहनों में उत्तल दर्पण को पश्च-दृश्य दर्पण के रूप में वरीयता क्यों देते हैं?
उत्तर:
वाहनों में उत्तल दर्पण को पश्च- दृश्य दर्पण के रूप में वरीयता निम्न कारणों से देते हैं-

• यह सदैव सीधा एवं छोटा प्रतिबिंब बनाते हैं।
• इनका दृष्टि- क्षेत्र बहुत अधिक होता है क्योंकि ये बाहर की ओर वक्रित होते हैं।

अतः समतल दर्पण की तुलना में उत्तल दर्पण ड्राइवर को अपने पीछे के बहुत बड़े क्षेत्र को देखने में सक्षम बनाते हैं।

पाठगत प्रश्न (पृष्ठ संख्या-188)

प्रश्न 1.
उस उत्तल दर्पण की फोकस दूरी ज्ञात कीजिए जिसकी वक्रता त्रिज्या 32 cm है।
उत्तर:
उत्तल दर्पण की वक्रता त्रिज्या
R = 32 cm
अतः f = \(\frac { R }{ 2 }\) = \(\frac { 32 }{ 2 }\)
= 16 cm
अतः उत्तल दर्पण की फोकस दूरी 16 cm होगी।

प्रश्न 2.
कोई अवतल दर्पण अपने सामने 10 em दूरी पर रखे किसी बिंब का तीन गुणा आवर्धित (बड़ा) वास्तविक प्रतिबिंब बनाता है। प्रतिबिंब दर्पण से कितनी दूरी पर है?
उत्तर:
बिंब- दूरी u = – 10 cm
आवर्धन m = – 3 चूँकि प्रतिबिंब वास्तविक है।
m = – \(\frac { v }{ u }\)
⇒ – 3 = \(\frac { v }{ -10 }\)
∴ v = – 30 cm
अतः प्रतिबिंब दर्पण के सामने 30 cm की दूरी पर बनता है।

पाठगत प्रश्न (पृष्ठ संख्या – 194)

प्रश्न 1.
वायु में गमन करती प्रकाश की एक किरण जल में तिरछी प्रवेश करती है। क्या प्रकाश किरण अभिलंब की ओर झुकेगी अथवा अभिलंब से दूर हटेगी? बताइए क्यों?
उत्तर:
प्रकाश की किरण जब वायु से जल में गमन करती है तो यह अभिलंब की ओर झुकती है, क्योंकि जल, वायु की तुलना में सघन माध्यम है अर्थात् प्रकाश की किरणें विरल से सघन माध्यम में प्रवेश करने पर अभिलंब की ओर झुकेंगी।

प्रश्न 2.
प्रकाश वायु से 1.50 अपवर्तनांक की काँच की प्लेट में प्रवेश करता है। काँच में प्रकाश की चाल कितनी है? निर्वात में प्रकाश की चाल 3 x 10⁸ m/s है।
उत्तर:
दिया है-
निर्वात में प्रकाश की चाल
(c) = 3 x 10⁸ m/s
काँच की प्लेट का अपवर्तनांक
(n_m) = 1.50
n_m = \(\frac { c }{ u }\);
v = काँच में प्रकाश की चाल
⇒ 1.50 = \(\frac{3 \times 10^8}{v}\)
⇒ v = \(\frac{3 \times 10^8}{1.5}=\frac{30 \times 10^8}{15}\)
= 2 x 10⁸ m/s
अतः काँच में प्रकाश की चाल = 2 x 10⁸ m/s

प्रश्न 3.
पाठ्य पुस्तक की सारणी 10.3 से अधिकतम प्रकाशित घनत्व के माध्यम को ज्ञात कीजिए। न्यूनतम प्रकाशित घनत्व के माध्यम को भी ज्ञात कीजिए।
उत्तर:
दिए गए सारणी 10.3 के अवलोकन से पता चलता है कि अधिकतम प्रकाशित घनत्व का माध्यम हीरा है जिसका अपवर्तनांक (n) = 2.42 है तथा न्यूनतम प्रकाशिक घनत्व का माध्यम वायु है, जिसका अपवर्तनांक (n) = 1.0003 है।

प्रश्न 4.
आपको किरोसिन, तारपीन का तेल तथा जल दिए गए हैं। इसमें से किसमें प्रकाश सबसे अधिक तीव्र गति से चलता है? पाठ्य पुस्तक की सारणी 10.3 में दिए गए आँकड़ों का उपयोग कीजिए।
उत्तर:
किरोसिन, तारपीन का तेल और जल में, प्रकाश सबसे अधिक तीव्र गति से जल में चलता है।

प्रश्न 5.
हीरे का अपवर्तनांक 2.42 है। इस कथन का क्या अभिप्राय है?
उत्तर:
हीरे का अपवर्तनांक 2.42 है। इस कथन का तात्पर्य है कि वायु अथवा निर्वात में प्रकाश की चाल का अनुपात और हीरे में प्रकाश की चाल का अनुपात 2.42 के बराबर है। दूसरे शब्दों में हीरे में प्रकाश की चाल उसकी निर्वात में चाल की 2.42 गुना कम हो जाती है।

पाठगत प्रश्न (पृष्ठ संख्या – 203)

प्रश्न 1.
किसी लेंस की 1 डाइऑप्टर क्षमता को परिभाषित कीजिए।
उत्तर:
जब एक लेंस की फोकस दूरी 1 मीटर हो तो लेंस की क्षमता 1 डाइऑप्टर कहलाती है।

प्रश्न 2.
कोई उत्तल लेंस किसी सुई का वास्तविक तथा उलटा प्रतिबिंब उस लेंस से 50 सेमी दूर बनाता है। यह सुई, उत्तल लेंस के सामने कहाँ रखी है, यदि इसका प्रतिबिंब उसी साइज का बन रहा है जिस साइज का बिंब है। लेंस की क्षमता भी ज्ञात कीजिए।
उत्तर:
यहाँ, प्रतिबिंब दूरी = + 50 सेमी
v = 50 सेमी
m = 1
P = \(\frac { 1 }{ f }\) = ?
लेंस द्वारा वास्तविक प्रतिबिंब के लिए,
m = \(\frac { v }{ u }\)
1 = \(\frac { u }{ v }\)
v = u
∴ u = – 50 सेमी
∴ बिंब दूरी = 50 सेमी
अब, \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ 50 }\) – \(\frac { 1 }{ -50 }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1+1 }{ 50 }\) = \(\frac { 1 }{ f }\)
∴ f = 25 सेमी
P = \(\frac{\frac{2}{25}}{100}\) मी =\(\frac{\frac{1}{1}}{4}\)
P = 4 डाइऑप्टर

प्रश्न 3.
2 मी फोकस दूरी वाले किसी अवतल लेंस की क्षमता ज्ञात कीजिए।
उत्तर:
अवतल लेंस के लिए
f = – 2 मी
∴ P = \(\frac { 1 }{ f }\)
∴ P = – \(\frac { 1 }{ 2 }\)
P = – 0.5 डाइऑप्टर

क्रिया-कलाप – 10.1

• एक बड़ी चमकदार चम्मच लीजिए। इसके वक्रित पृष्ठ में अपना चेहरा देखने का प्रयत्न कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
क्या आप प्रतिबिंब देख पाते हैं? यह छोटा है या बड़ा?
उत्तर:
हाँ। प्रतिबिंब छोटा है।

प्रश्न 2.
चम्मच को धीरे-धीरे अपने चेहरे से दूर ले जाइए। प्रतिबिंब को देखते रहिए। यह कैसे परिवर्तित होता है?
उत्तर:
इसका आकार छोटा होता जा रहा है।

प्रश्न 3.
चम्मच को उलटा कीजिए (पलटिए) तथा दूसरे पृष्ठ से क्रियाकलाप को दोहराइए। अब प्रतिबिंब कैसा दिखाई देगा?
उत्तर:
पहले, प्रतिबिंब उलटा था परन्तु अब प्रतिबिंब सीधा है।

प्रश्न 4.
दोनों पृष्ठों पर प्रतिबिंब के अभिलक्षणों की तुलना कीजिए।
उत्तर:

आंतरिक पृष्ठ	बाहरी पृष्ठ
(i) कभी-कभी प्रतिबिंब उलटा तथा कभी सीधा दिखाई देता है।	(i) प्रतिबिंब हमेशा सीधा होता है।
(ii) प्रतिबिंब का आकार कभी छोटा तो कभी बड़ा दिखाई देता है।	(ii) प्रतिबिंब हमेशा छोटा होता है।

क्रियाकलाप – 10.2

चेतावनी-सूर्य की ओर या दर्पण द्वारा परावर्तित सूर्य के प्रकाश की ओर सीधा मत देखिए। यह आपकी आँखों को क्षतिग्रस्त कर सकता है।

• एक अवतल दर्पण को अपने हाथ में पकड़िए तथा इसके परावर्तक पृष्ठ को सूर्य की ओर कीजिए।
• दर्पण द्वारा परावर्तित प्रकाश को दर्पण के पास रखी एक कागज की शीट पर डालिए।
• कागज की शीट को धीरे-धीरे आगे पीछे कीजिए जब तक कि आपको कागज की शीट पर प्रकाश का एक चमकदार, तीक्ष्ण बिन्दु प्राप्त न हो जाए।
• दर्पण तथा कागज को कुछ मिनट के लिए उसी स्तिथि में पकड़े रखिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
आप क्या देखते हैं? ऐसा क्यों होता है?
उत्तर:
कागज जलना शुरू हो जाता है। सूर्य से आने वाला प्रकाश दर्पण के द्वारा एक तीक्ष्ण, चमकदार बिन्दु के रूप में अभिकेन्द्रित होता है जिससे ऊष्मा उत्पन्न होती है और कागज जलने लगता है।

क्रिया-कलाप – 10.3
(i) आप अवतल दर्पण की फोकस दूरी ज्ञात करने की विधि पहले ही सीख चुके हैं। क्रियाकलाप 10.2 में आपने देखा है कि आपको कागज पर मिला प्रकाश का तीक्ष्ण चमकदार बिन्दु वास्तव में सूर्य का प्रतिबिंब है। यह अत्यंत छोटा, वास्तविक तथा उलटा ॰ै। दर्पण से इस प्रतिबिंब की दूरी मापकर आपने अवतल दर्पण की लगभग फोकस दूरी ज्ञात की थी।

(ii) एक अवतल दर्पण लीजिए। ऊपर वर्णित विधि से इसकी सन्निकट फोकस दूरी ज्ञात कीजिए। फोकस दूरी का मान नोट कीजिए। (आप किसी दूरस्थ वस्तु का प्रतिबिंब एक कागज की शीट पर प्राप्त करके भी फोकस दूरी ज्ञात कर सकते हैं)।

(iii) मेज पर चॉक से एक लाइन बनाइए। अवतल दर्पण को एक स्टैंड पर रखिए। स्टैंड को लाइन पर इस प्रकार रखिए कि दर्पण का ध्रुव इस लाइन पर स्थित हो।

(iv) चॉंक से पहली लाइन के समांतर और इसके आगे, दो लाइनें इस प्रकार खींचिए की किन्हीं दो उत्तरोत्तर लाइनों के बीच की दूरी दर्पण की फोकस दूरी के बराबर हो। ये लाइनें अब क्रमशः बिन्दुओं P, rmF तथा C की स्थितियों के तद्नुरूपी होंगी। याद रखिए-छोटे द्वारक के गोलीय दर्पण के लिए मुख्य फोकस F, ध्रुव P तथा वक्रता केन्द्र C को मिलाने वाली रेखा के मध्य बिन्दु पर स्थित होता है।

(v) एक चमकीला बिंब, जैसे एक जलती हुई मोमबत्ती C से बहुत दूर किसी स्थिति पर रखिए। एक कागज का परदा रखिए तथा इसको दर्पण के सामने आगे-पीछे तब तक खिसकाइए जब तक कि आपको इस पर मोमबत्ती की लौ का तीक्ष्ण तथा चमकीला प्रतिबिंब प्राप्त न हो जाए।

(vi) प्रतिबिंब को ध्यानपूर्वक देखिए। इसकी प्रकृति, स्थिति तथा बिंब के साइज के सापेक्ष इसका आपेक्षिक साइज नोट कीजिए।

(vii) इस क्रियाकलाप को मोमबत्ती की निम्न स्थितियों के लिए दोहराइए-

• C से थोड़ा दूर
• C पर
• F तथा C के बीच
• F पर तथा
• P और F के बीच।

(viii) इनमें से एक स्थिति में आप परदे पर प्रतिबिंब प्राप्त नहीं कर पाएँगे। इस अवस्था में बिंब की स्थिति को अभिनिर्धारित कीजिए। तब, इसके आभासी प्रतिबिंब को सीधे दर्पण में देखिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
अपने प्रेक्षणों को नोट कीजिए तथा सारणीबद्ध कीजिए।
उत्तर:
किसी अवतल दर्पण से बिंब की विभिन्न स्थितियों के लिए बने प्रतिबिंब-

बिंब की स्थिति	प्रतिबिंब की स्थिति	प्रतिबिंब का साइज	प्रतिबिंब की प्रकृति
(a) अनंत पर	फोकस F पर	अत्यधिक छोटा, बिंदु साइज	वास्तविक एवं उल्टा
(b) C से परे	F तथा C के बीच	छोटा	वास्तविक तथा उल्टा
(c) C पर	C पर	समान साइज	वास्तविक तथा उल्टा
(d) C तथा F के बीच	C से परे	विवर्धित (बड़ा)	वास्तविक तथा उल्टा
(e) F पर	अनंत पर	अत्यधिक विवर्धित	वास्तविक तथा उल्टा
(f) P तथा F के बीच	दर्पण के पीछे	विवर्धित (बड़ा)	आभासी तथा सीधा

अवतल दर्पण द्वारा बिंब की विभिन्न स्थितियों के लिए बने प्रतिबिंब का किरण आरेख-

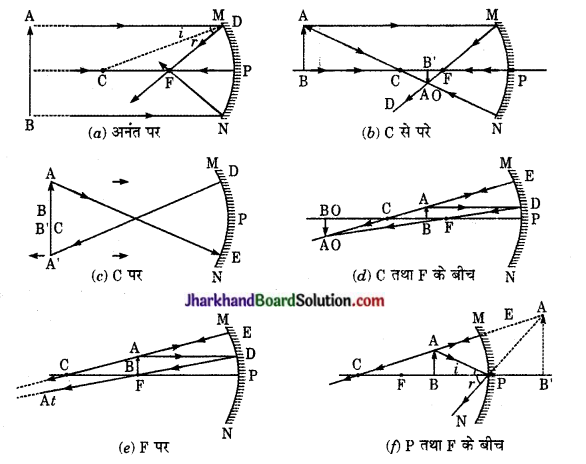
क्रिया-कलाप – 10.4

• (i) सारणी 10.1 में दर्शायी गई बिंब की प्रत्येक स्थिति के लिए स्वच्छ किरण आरेख खींचिए।
• (ii) प्रतिबिंब का स्थान निर्धारित करने के लिए आप पूर्व अनुच्छेद में वर्णित कोई दो किरणें ले सकते हैं।
• (iii) अपने चित्रों की तुलना ऊपर दिये गये चित्रों से कीजिए।
• (iv) प्रत्येक दशा में बनने वाले प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज का वर्णन कीजिए।
• (v) अपने परिणामों को सुविधाजनक प्रारूप में सारणीबद्ध कीजिए।

संकेत-अवतल दर्पण द्वारा प्रतिबिंब का बनना दर्शाने के लिए किरण आरेख तथा प्रत्येक दशा में बनने वाले प्रतिबिम्ब की प्रकृति, स्थिति एवं आपेक्षिक साइज का वर्णन क्रियाकलाप -10.3 में दिया गया है।

क्रिया-कलाप- 10.5

• कोई उत्तल दर्पण लीजिए। इसे हाथ में पकड़िए।
• दूसरे हाथ में एक सीधी बड़ी पेंसिल पकड़िए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
दर्पण में पेंसिल का प्रतिबिंब देखिए प्रतिबिंब सीधा है या उलटा? क्या यह छोटा है अथवा विवर्धित (बड़ा) है?
उत्तर:
सीधा तथा छोटा।

प्रश्न 2.
पेंसिल को धीरे-धीरे दर्पण से दूर ले जाइए। क्या प्रतिबिंब छोटा होता जाता है या बड़ा होता जाता है?
उत्तर:
छ्छेटा प्रतिबिम्ब बनता है।

प्रश्न 3.
क्रियाकलाप को सावधानीपूर्वक दोहराइए। बताइए कि जब बिंब को दर्पण से दूर ले जाते हैं तो प्रतिबिंब फोकस के निकट आता है अथवा उससे और दूर चला जाता है?
उत्तर:
प्रतिबिंब फोकस के निकट आता है। प्रतिबिंब फोकस के निकट बनता है।

क्रियाकलाप – 10.6

• समतल दर्पण में किसी दूरस्थ बिम्ब जैसे कोई दूरस्थ पेड़ का प्रतिबिम्ब देखिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
क्या आप पूर्ण लम्बाई (Full length) का प्रतिबिंब देख पाते हैं?
उत्तर:
पूर्ण लम्बाई का प्रतिबिम्ब नहीं देख पाते हैं।

प्रश्न 2.
विभिन्न साइज के समतल दर्पण लेकर प्रयोग दोहराइए। क्या आप दर्पण में बिंब का संपूर्ण प्रतिबिंब देख पाते हैं?
उत्तर:
नहीं।

प्रश्न 3.
इस क्रियाकलाप को अवतल दर्पण लेकर दोहराइए। क्या यह दर्पण बिंब की पूरी लंबाई का प्रतिबिंब बना पाता है?
उत्तर:
नहीं।

प्रश्न 4.
अब एक उत्तल दर्पण लेकर इस प्रयोग को दोहराइए। क्या आपको सफलता मिली? अपने प्रेक्षणों की कारण सहित व्याख्या कीजिए।
उत्तर:
हाँ, अब हमें बिंब का संपूर्ण प्रतिबिंब देख पाने में सफलता मिली। उत्तल दर्पण हमेशा छोटा, सीधा तथा आभासी प्रतिबिंब बनाता है। इसलिए दूर का बिंब उत्तल दर्पण में साफ देखा जा सकता है।

क्रियाकलाप- 10.7

• पानी से भरी एक बाल्टी की तली पर एक सिक्का रखिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
अपनी आँख को पानी के ऊपर किसी पार्श्व (Side) में रखकर सिक्के को एक बार में उठाने का प्रयत्न कीजिए। क्या आप सिक्का उठने में सफल हो पाते हैं?
उत्तर:
नहीं।

प्रश्न 2.
इस क्रियाकलाप को दोहराइए। आप इसे एक बार में करने में क्यों सफल नहीं हो पाए थे?
उत्तर:
क्योंकि अपवर्तन के कारण सिक्का अपने वास्तविक स्थान से ऊपर की ओर उठा हुआ प्रतीत होता है।

प्रश्न 3.
अपने मित्रों से इसे करने के लिए कहिए। उनके साथ अपने अनुभव की तुलना कीजिए।
उत्तर:
छात्र स्वयं करें।

क्रिया-कलाप – 10.8

• किसी मेज पर एक बड़ा उथला कटोरा रखकर उसकी तली में एक सिक्का रखिए।
• कटोरे से धीरे-धीरे दूर हटिए। जब सिक्का ठीक दिखाई देना बन्द हो जाए तो रूक जाइए।
• अपने मित्र से सिक्के को विक्षुब्ध किए बगैर कटोरे में पानी डालने को कहिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
अपनी स्थिति से सिक्के को देखते रहिए। क्या सिक्का उसी स्थिति से पुनः दिखाई देने लगता है? यह कैसे संभव हो पाता है?
उत्तर:
कटोरे में पानी डालने पर सिक्का पुन: उसी स्थिति में दिखाई देने लगता है क्योंकि अपवर्तन के कारण सिक्के की स्थिति उसकी वास्तविक स्थिति से उठी हुई प्रतीत होती है, इसलिए सिक्का दिखाई देने लगता है।

क्रिया-कलाप-10.9

• मेज पर रखे एक सफेद कागज की शीट पर एक मोटी सीधी रेखा खींचिए।
• इस रेखा के ऊपर एक काँच का स्लैब इस प्रकार रखिए कि इसकी एक कोर इस रेखा से कोई कोण बनाएँ।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
स्लैब के नीचे आए रेखा के भाग को पार्श्व (side) से देखिए आप क्या देखते हैं? क्या काँच के स्लैब के नीचे की रेखा कोरों (edges) के पास मुड़ी हुई प्रतीत होती है?
उत्तर:
हाँ, ऐसा रोशनी के अपवर्तन के कारण हो रहा है।

प्रश्न 2.
अब काँच के स्लैब को इस प्रकार रखिए कि यह रेखा के अभिलंबवत हो। अब आप क्या देखते हैं? क्या काँच के स्लैब के नीचे रेखा का भाग मुड़ा हुआ प्रतीत होता है?
उत्तर:
अब, रेखा सीधी है और मुड़ी हुई प्रतीत नहीं हो रही क्योंकि रोशनी की सीधी किरण में अपवर्तन नहीं होता है।

प्रश्न 3.
रेखा को काँच के स्लैब के ऊपर से देखिए। क्या स्लैब के नीचे रेखा का भाग उठा हुआ प्रतीत होता है? ऐसा क्यों होता है?
उत्तर:
हाँ, ऐसा अपवर्तन के कारण होता है। इसकी वजह से बिंब की स्थिति वास्तविक स्थिति से उठी हुई दिखाई देती है।

क्रिया-कलाप – 10.10

• एक ड्राइंग बोर्ड पर सफेद कागज की एक शीट, ड्राइंग पिनों की सहायता से लगाइए।
• शीट के ऊपर बीच में काँच का एक आयताकार स्लैब रखिए।
• पेंसिल से स्लैब की रूपरेखा खींचिए। इस रूपरेखा का नाम ABCD रखते हैं।
• चार एकसमान ऑलपिन लीजिए।
• दो पिर्ने, मान लीजिए E तथा F ऊर्ध्वाधरत: इस प्रकार लगाइए कि पिनों को मिलाने वाली रेखा कोर AB से कोई कोण बनाती हुई हो।
• पिन E तथा F के प्रतिबिंबों को विपरीत फलक से देखिए। दूसरी दो पिनों, माना G तथा H, को इस प्रकार लगाइए कि ये पिर्ने एवं E तथा F के प्रतिबिंब एक सीधी रेखा पर स्थित हों।
• पिनों तथा स्लैब को हटाइए।
  
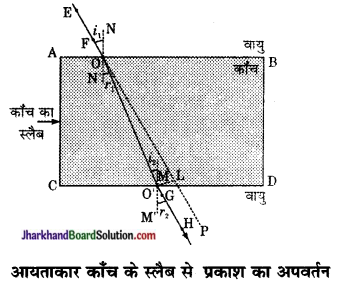
• पिनों E तथा F की नोकों (tip) की स्थितियों को मिलाइए तथा इस रेखा को AB तब बढ़ाइए। मान लीजिए EF, AB से बिंदु पर मिलती है। इसी प्रकार पिनों G तथा H की नोकों की स्थितियों को मिलाइए तथा इस रेखा को कोर CD तक बढ़ाइए। मान लीजिए HG, CD से O’ पर मिलती है।
• O तथा O’ को मिलाइए EF को भी P तक बढ़ाइए, जैसा कि चित्र में बिंदुकित रेखा द्वारा दर्शाया गया है।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
क्या होता है जब प्रकाश की किरणें काँच के स्लैब में प्रवेश करती हैं?
उत्तर:
प्रकाश का अपवर्तन होता है और यह अभिलंब की तरफ मुड़ जाती है। ऐसा प्रकाश की चाल काँच के स्लैब में अपेक्षाकृत कम होने के कारण होता है।

प्रश्न 2.
क्या होता है जब प्रकाश की किरणें स्लैब से बाहर निकलती हैं?
उत्तर:
वायु में प्रकाश की चाल अधिक होती है अतः प्रकाश अभिलंब से दूर मुड़ जाता है।

प्रश्न 3.
निर्गत किरण तथा आपतित किरण के बीच की लंबवत दूरी को क्या कहते हैं?
उत्तर:
पाश्विक विस्थापन।

प्रश्न 4.
आपतित कोण तथा निर्गत कोण के बीच क्या संबंध होता है अगर आपतित किरण तथा निर्गत किरण दोनों का माध्यम समान हो ?
उत्तर:
आपतित कोण = निर्गत कोण।

क्रिया-कलाप – 10.11

चेतावनी- इस क्रियाकलाप को करते समय अथवा अन्यथा भी सूर्य की ओर सीधे या लेंस से न देखें। यदि आप रेसा करेंगे तो आपकी आँखों को क्षति हो सकती है

• एक उत्तल लेंस को अपने हाथ में पकड़िए। इसे की ओर निर्दिष्ट कीजिए।
• सूर्य के प्रकाश को एक कागज की शीट पर फोकसित कीजिए। सूर्य का एक तीक्ष्ण चमकदार प्रतिबिंब प्राप्त कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
कागज तथा लेंस को कुछ समय के लिए उसी स्थिति में पकड़े रखिए। कागज को देखते रहिए। क्या होता है? ऐसा क्यों होता है?
उत्तर:
कागज पूरी तरह जल गया। लेंस की मदद से सूर्य के प्रकाश को एक बिंदु पर फोकसित किया गया। सूर्य की किरणों में ऊर्जा होती है जिससे कि ऊष्मा उत्पन्न हुई और कागज जल गया।

क्रिया-कलाप – 10.12

• एक उत्तल लेंस लीजिए। क्रियाकलाप 10.11 में वर्णित विधि द्वारा इसकी सन्निकट फोकस दूरी ज्ञात कीजिए।
• एक लंबी मेज पर चॉक का प्रयोग करके पाँच समांतर सीधी रेखाएँ इस प्रकार खींचिए कि किन्हीं दो उत्तरोतर रेखाओं के बीच की दूरी लेंस की फोकस दूरी के बराबर हो।
• लेंस को एक लेंस स्टैंड पर लगाइए। इसे मध्य रेखा पर इस प्रकार रखिए कि लेंस का प्रकाशिक केन्द्र इस रेखा पर स्थिति हो।
• लेंस के दोनों ओर दो रेखाएँ क्रमशः लेंस के स तथा 2F के तदनुरूपी होंगी। इन्हें उचित अक्षरों द्वारा अंति कीजिए, जैसे क्रमश: 2F₁, F₁, F₂ तथा 2F₂।
• एक जलती हुई मोमबत्ती को बाईं ओर, 2 F₁ से काफी दूर रखिए। लेंस के विपरीत दिशा में रखे एक परदे पर इसका स्पष्ट एवं तीक्ष्ण प्रतिबिंब बनाइए।
• प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज नोट कीजिए।
• इस क्रियाकलाप में बिंब को 2F₁ से थोड़ा दूर, F₁ तथा 2F₁ के बीच, F₁ पर तथा F₁ और 0 के बीच रखकर दोहराइए। अपने प्रेक्षणों को नोट कीजिए तथा सारणीबद्ध कीजिए।

सारणी में बिंब की विभिन्न स्थितियों के लिए उत्तल लेंस द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज सारणी में दर्शाई गयी है।

बिंब की स्थिति	प्रतिबिंब की स्थिति	प्रतिबिंब का आपेक्षिक साइज	प्रतिबिंब की प्रकृति
अनंत पर	फोकस F2 पर	अत्यधिक छोटा,	वास्तविक तथा उलटा
2F1 से परे	F2तथा 2F2 के बीच	बिन्दु आकार	वास्तविक तथा उलटा
2F1 पर	2F2 पर	छोटा	वास्तविक तथा उलटा
F1 तथा 2F1 के बीच	2F2 से परे	रापान साइज	वास्तविक तथा उलटा
फोकस F1 पर	अनंत पर	नक़ (लिर्धर्धित	वास्तविक तथा उलटा
फोकस F1 तथा प्रकाशिक केन्द्र O के बीच	जिस ओर बिंब है	असीमित चप थे बड़ा	आभासी तथा सीधा

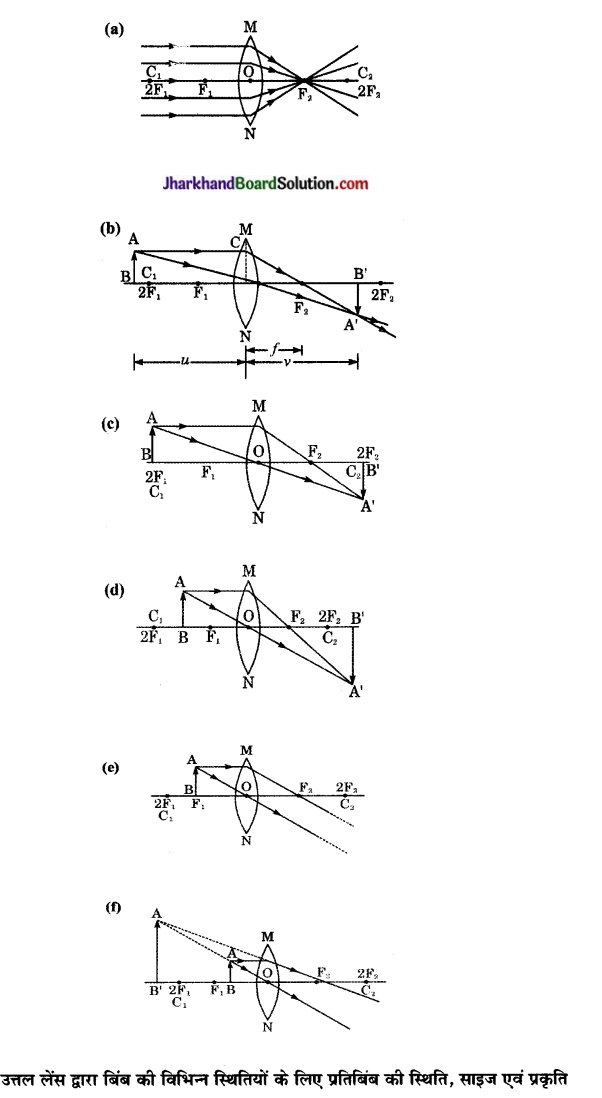
क्रिया-कलाप – 10.13

• एक अवतल लेंस लीजिए। इसे एक लेंस स्टैंड पर रखिए।
• लेंस के एक ओर एक जलती हुई, मोमबत्ती को रखिए।
• लेंस के दूसरी ओर से प्रतिबिम्ब का प्रेक्षण कीजिए। प्रतिबिंब को यदि संभव हो तो परदे पर प्राप्त करने का प्रयत्न कीजिए। यदि ऐसा संभव न हो तो प्रतिबिंब को लेंस में से सीधे ही देखिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
प्रतिबिंब की प्रकृति, आपेक्षिक आकार तथा सन्निकट स्थिति नोट कीजिए।
उत्तर:
प्रतिबिंब फोकस F₁ तथा प्रकाशीय केन्द्र O के मध्य बना है। इसका आपेक्षिक साइज छोटा, आभासी तथा सीधा है।

प्रश्न 2.
मोमबत्ती को लेंस से दूर ले जाइए। प्रतिबिंब के साइज में परिवर्तन नोट कीजिए। जब मोमबत्ती को लेंस से बहुत दूर रखा जाता है तो प्रतिबिंब के साइज पर क्या प्रभाव पड़ता है?
उत्तर:
प्रतिबिंब छोटा हो जाता है।

Students must go through these JAC Class 10 Science Notes Chapter 2 Acids, Bases and Salts to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 2 Acids, Bases and Salts

→ Acid: Acids are sour in taste. Acid turns wet blue litmus paper to red. It releases H⁺ ions in an aqueous solution. Acid has a pH value lower than 7. H⁺(aq) ions in the solution are responsible for acidic character.

→ Base: Bases are bitter in taste. Base turns wet red litmus paper to blue. It releases OH^– ions in an aqueous solution. Base has a pH value higher than 7. OH^–(aq) ions in the solution are responsible for basic character.

→ Indicator: Indicator changes colour in presence of acid or base or it changes odour (smell) in presence of acid or base.

• Synthetic indicators : Methyl orange and Phenolphthalein.
• Natural indicators : Extract of red cabbage leaves, turmeric, vanilla extract, onion, starch.

→ On reaction with metal, acid liberates dihydrogen (H₂) gas and forms corresponding salt, while, base reacts with active metal to form dihydrogen gas and a salt is formed which has a negative ion (anion) consisting of metal and oxygen.

→ Acid reacts with metal carbonate, or metal hydrogen carbonate and forms the corresponding salt, carbon dioxide gas and water.

→ Aqueous solutions (solutions prepared in water) of acids and bases conduct electricity because they produce hydrogen ions (H⁺(aq)) and hydroxide ions (OH^–(aq)) responsible for conducting electricity.

→ pH scale: pH scale is useful to determine the nature of the solution whether acidic or basic.

• For acidic solution : pH < 7, pOH > 7
• For basic solution : pH > 7, pOH < 7
• For neutral solution : pH = 7, pOH = 7

→ Most of the metabolic reactions taking place in living bodies are within a narrow pH range of 7.0 to 7.8.

→ Mixing of a concentrated acid or a base with water is a highly exothermic reaction.

→ Neutralisation reaction: The chemical reaction in which acid and base neutralise each otiier to form corresponding salt and water is called neutralisation reaction. Salts have various uses in daily life and in industries.

→ Substance (Compound) and its uses:

• Vanilla, onion, clove : As olfactory indicator
• Milk of magnesia : As an antacid
• Sodium chloride (NaCl) : In the preparation of sodium hydroxide, baking soda, washing soda, bleaching powder and in various substances used in daily life.
• Sodium hydroxide (NaOH) : For making soaps, detergent, in purification of petroleum, in laboratory.
• Bleaching powder (CaOCl₂) : Used as bleaching agent, as disinfectant and as an oxidising agent.
• Baking soda (NaHCO₃): Used as an antacid, as disinfectant, in laboratory, making food soft and spongy and used in soda-acid fire-extinguishers.
• Washing soda (Na₂CO₃) : Used in making glass, soaps, as cleansing agents for domestic purposes, in paper and textile industries and in laboratory.
• Plaster of paris (CaSO₄.\(\frac { 1 }{ 2 }\)H₂O) : Used in construction industry, as plaster for supporting fractured bones, chalk for blackboard, making toys, in decoration material, making moulds and in laboratory.

Jharkhand Board JAC Class 10 Science Solutions Chapter 7 Control and Coordination Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 7 Control and Coordination

Jharkhand Board Class 10 Science Control and Coordination Textbook Questions and Answers

Question 1.
Which of the following is a plant hormone?
A. Insulin
B. Thyroxin
C. Estrogen
D. Cytokinin
Answer:
Cytokinin

Question 2.
The gap between two neurons is called a ………………..
A. dendrite
B. synapse
C. axon
D. impulse
Answer:
synapse

Question 3.
The brain is responsible for ……………….
A. thinking
B. regulating the heartbeat
C. balancing the body
D. all of the above
Answer:
all of the above

Question 4.
What is the function of receptors in our body? Think of situations where receptors do not work properly. What problems are likely to arise?
Answer:
The function of receptors : To receive collect information about changes in the environment around us in form of stimuli. This information pass to central nervous system through sensory nerves in form of impulse.

If receptors do not work properly, external stimuli cannot be received and body will not respond towards it.

Question 5.
Draw the structure of a neuron and explain its function.
Answer:
Structure of neuron:

Function of neuron:
The information is acquired at the end of the dendritic tip of a nerve cell and sets off a chemical reaction that creates an electrical impulse. This impulse travels from the dendrite to the cell body and then along the axon to its end. At the end of the axon, the electrical impulse sets off the release of some chemicals (Neurotransmitters) which cross the synapse and start a similar electrical impulse in a dendrite of the next neuron.

Thus, neuron is specialised for conducting information via electrical impulses from one part of the body to another.

Question 6.
How does phototropism occur in plant?
Answer:
To observe the response of plant parts to light OR To study phototropism in plants.
Materials: Conical flask, wire mesh, cardboard box open from one side, water, two-three freshly germinated bean seeds.

Procedure:

• Fill a conical flask with water.
• Cover the neck of the flask with a wire mesh.
• Keep two-three freshly germinated bean seeds on the wire mesh.
• Take a cardboard box which is open from one side.
• Keep the flask in the box in such a manner that the open side of the box faces light coming from a window.
• Observe after two or three days and note down your observation.
• Now turn the flask and leave it undisturbed in this condition for a few days and then observe.
  

Observation: In the initial position of flask, the shoot bends towards light and roots turn away from light.
After turning the flask, position of shoot and roots change, i.e., shoot goes away from light and roots turn towards light but after a few days shoot again shows bending towards light and roots move away from light.

Questions:

Question 1.
Have the old parts of the shoot and root changed direction?
Answer:
Yes, shoot always grows towards light as it positively phototropic and root goes in opposite direction of light.

Question 2.
Are there differences in the direction of the new growth?
Answer:
No, growth pattern or direction follows environmental stimulus.

Question 3.
What can we conclude from this activity?
Answer:
We can conclude from this activity that shoot shows positive phototropism and roots show negative phototropism.

Question 7.
Which signals will get disrupted in case of a spinal cord injury?
Answer:
In case of a spinal cord injury following signals will get disrupted :

• Reflex action
• Sensory impulses from different organs of body to brain through spinal cord will not be conducted
• Motor impulses from brain to different organs of body through spinal cord will not be transmitted.

Question 8.
How does chemical coordination occur in plants?
Answer:
The chemical coordination occurs in plants by means of plant hormones. They help to coordinate growth, development and. responses to the environment. They are synthesised at places away from where they act and reach to the areas of action by simple diffusion.

Question 9.
What is the need for a system of control and coordination in an organism?
Answer:
In multicellular organisms, body organisation is complex. Different organs s and tissues perform different specialised functions. Therefore, it is necessary that all the organs work together in a proper coordinating way, it needs a system of control and coordination.

In human beings, well-developed nervous and endocrine system were evolved for control and coordination.

Question 10.
How are involuntary actions and reflex actions different from each other?
Answer:

Involuntary actions	Reflex actions
These are controlled by medulla a part of hind-brain.	These are controlled by spinal cord in general.
Functioning of internal body parts are involuntary actions.	It is involuntary response to external stimuli without the knowledge of cerebrum.
Such actions go on continued under normal condition also, e.g., heartbeats, breathing, peristalsis, etc.	It is shown under a condition of emergency. Such as to pull hand away on touching to hot object.
It occurs in controlled rhythmic way.	It is a quick action.

Question 11.
Compare and contrast nervous and hormonal mechanisms for control and coordination in animals.
Answer:

Nervous mechanism	Hormonal mechanism
Neuron is the main functional unit in nervous mechanism.	Hormone acts as chemical messenger in hormonal mechanism.
Impulse is generated at dendrite and it passes along the axon through cell body.	Hormone is secreted from endocrine gland and is transported through blood circulation.
The neural responses are quick.	The hormonal actions are slow.
Its effect is short lasting.	Its effect is long lasting.
Impulse is delivered to other neuron, gland or muscle cells.	Information is received by target cells who have specific molecules on their surfaces.

Question 12.
What is the difference between the manner in which movement take place in a sensitive plant and the movement in our legs?
Answer:

Movement in a sensitive plant	Movement in our legs
It occurs in response to touch.	It is voluntary action as per our need.
Neural signals are not involved in such movement.	Neural signals from cerebellum are involved in such movements.
No specific protein is present in plant cells for it.	A specific protein is present in our muscle cells for it.
Plant cells change their shape by changing the amount of water in it.	A special proteins change both their shape and their arrangement in response to nervous impulses due to which the muscle cells shorten.

Jharkhand Board Class 10 Science Control and Coordination InText Questions and Answers

Question 1.
What is the difference between a reflex action and walking?
Answer:
Reflex action is an involuntary action controlled by spinal cord. Thinking is not involved in such action.

Walking is a voluntary action and is controlled by a cerebellum, a part of hind-brain. This action is shown as per wish of an individual.

Question 2.
What happens at the synapse between two neurons?
Answer:
Synapse is the gap between nerve endings of axon of one neuron and dendrites of another neuron. At the end of axon, the electrical impulse sets off the release of some chemicals. These chemicals cross the synapse and start a similar electrical impulse in a dendrite of the next neuron.

Question 3.
Which part of the brain maintains posture and equilibrium of the body?
Answer:
Cerebellum is the part of the brain that maintains posture and equilibrium of the body.

Question 4.
How do we detect the smell of an agarbatti (incense stick)?
Answer:
Olfactory receptors in our nose are stimulated by the smell of agarbatti. This causes generation of impulse which is received at dendrite of sensory neuron. Such impulse is transmited to brain. In cerebrum message is interpreted and we detect the smell.

Question 5.
What is the role of the brain in reflex action?
Answer:
Generally reflex action is shown by spinal cord and there is no active role of brain in it. However the information input also goes to the brain.

In some reflex actions such as mouth watering on seeing delicious food, heartbeats, breathing, movement of diaphragm, yawning, blinking of eyes, sneezing, etc. brain is involved.

Question 6.
What are plant hormones?
Answer:
Plant hormones are chemical compounds produced by plant itself and help to coordinate growth, development and responses to the environment.

Question 7.
How is the movement of leaves of the sensitive plant different from the movement of a shoot towards light?
Answer:

Question 8.
Give an example of a plant hormone that promotes growth.
Answer:
An example of a plant hormone that promotes growth : Auxin.

Question 9.
How do auxins promote the growth of a tendril around a support?
Answer:
Auxins are growth promoting plant hormones that induce cell elongation. When tendril comes in contact with a support, auxin stimulates faster growth on to a part of tendril away from the support. This causes the tendril to coil around the support.

Question 10.
Design an experiment to demonstrate hydrotropism.
Answer:
The type of movement of the growing plant organ, which is induced by stimulus of water is called hydrotropism.

To demonstrate hydrotropism.

Apparatus-Materials: clay, two plants, two glass

Procedure: Take two glass troughs each filled to about 1/3 with clay. Label the trough as (A) and (B). Plant two, almost equal sized cuttings, S one in each of the troughs. Add water in trough (A) and keep the clay of trough (B) dry. However in trough (B) place a small clay pot (or a cup of clay) filled with water quite close to the cutting. (See the figure) Add daily a small quantity of? water in trough (A) but not in trough (B). Dig out the clay carefully in both the troughs after about a week or more.

Observation : It will be seen that the cutting in trough (A) shows a simple and straight growth of the root, while that in trough (B) shows the root curved in the direction of clay pot filled with water.

Conclusion: It can be concluded that the root grows and elongates in the direction of source of water. It means that the root shows positive hydrotropism.

Question 11.
How does chemical coordination take place in animals?
Answer:
In animals, endocrine glands secretes S chemical substances (Hormones) in precise quantities. They are directly released in blood and through blood circulation they reach to their target (Functional) site. Specific cells of body have specific molecules with which hormone molecules bind and transmit information.

Thus, chemical coordination take place in animals.

Question 12.
Why is the use of iodised salt advisable?
Answer:
The use of iodised salt is advisable because iodine is essential for the synthesis of thyroxin hormone in thyroid gland. Deficiency of iodine causes goitre. Iodised salt fulfills the requirement of iodine of body and protects agains goitre disease.

Question 13.
How does our body respond when adrenaline is secreted into the blood?
Answer:
Adrenaline prepares our body in an emergency situation. When adrenaline is secreted into the blood body shows following responses:
The heart beats faster, breathing rate increases, blood pressure increases, skeletal muscles become more active, etc. This is known as fight or flight response.

Question 14.
Why are some patients of diabetes treated by giving injections of insulin?
Answer:
Insulin is a pancreatic hormone which helps in regulating blood sugar level. In the patients of diabetes, the blood sugar level rises due to deficiency of insulin. So, some patients of diabetes are treated by giving injections of insulin to maintain blood sugar level.

Activity 7.1 [T. B. Pg. 115]

To detect the taste bud (gustatory receptor) and its function.

• Put some sugar on your tongue In the mouth.
• Block your nose by pressing it between your thumb and index finger.
• Now eat sugar again.
• While eating lunch, block your nose in the same way and notice If you can fully appreciate the taste of food you are eating.

Questions:

Question 1.
How does the sugar taste?
Answer:
The taste of sugar is sweet.

Question 2.
Is there any difference in the taste of sugar while you block your nose?
Answer:
When we eat sugar after blocking our nose, we find no difference in the taste of sugar.

Question 3.
Is there a difference in how sugar and food taste If your nose Is blocked? If so, why might be happening?
Answer:
If we block our nose, we feel the taste but cannot fully appreciate because the olfactory receptors are not stimulated. We cannot feel the smell.

Question 4.
Do you come across a similar situation when you have a cold?
Answer:
Yes, when we have a cold, olfactory receptors are covered with excessive secreted mucus.

Activity 7.2 [T. B. Pg. 121]

To observe the response of plant parts to light OR To study phototropism in plants.

Materials: Conical flask, wire mesh, cardboard box open from one side, water, two-three freshly germinated bean seeds.

Procedure:

• Fill a conical flask with water.
• Cover the neck of the flask with a wire mesh.
• Keep two-three freshly germinated bean seeds on the wire mesh.
• Take a cardboard box which is open from one side.
• Keep the flask in the box in such a manner that the open side of the box faces light coming from a window.
• Observe after two or three days and note down your observation.
• Now turn the flask and leave it undisturbed in this condition for a few days and then observe.
  

Observation: In the initial position of flask, the shoot bends towards light and roots turn away from light.

After turning the flask, position of shoot and roots change, i.e., shoot goes away from light and roots turn towards light but after a few days shoot again shows bending towards light and roots move away from light.

Questions:

Question 1.
Have the old parts of the shoot and root changed direction?
Answer:
Yes, shoot always grows towards light as it positively phototropic and root goes in opposite direction of light.

Question 2.
Are there differences in the direction of the new growth?
Answer:
No, growth pattern or direction follows environmental stimulus.

Question 3.
What can we conclude from this activity?
Answer:
We can conclude from this activity that shoot shows positive phototropism and roots show negative phototropism.

Activity 7.3 [T. B. Pg. 123]

Identify the endocrine glands mentioned in the diagram.

Activity 7.4 [T. B. Pg. 125]

To know some important hormones and their functions.
Complete the following given table:

No.	Hormone	Endocrine Gland	Function
1.	Growth hormone	Pituitary gland	Stimulates growth in all organs.
2.	Thyroxin	Thyroid gland	Regulates metabolism for body growth.
3.	Insulin	Pancreas	Regulate blood sugar level
4.	Testosterone	Testes	Development of secondary sexual characters in male
5.	Estrogen	Ovaries	Development of female sex organs, regulates menstrual cycle, etc.
6.	Adrenaline	Adrenal gland	Prepares body for an emergency condition, i.e., either fight or flight.
7.	Releasing hormones	Hypo-thalamus	Stimulates pituitary gland to release hormones