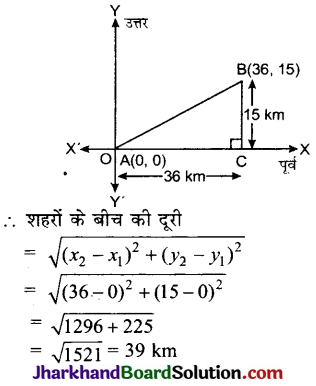
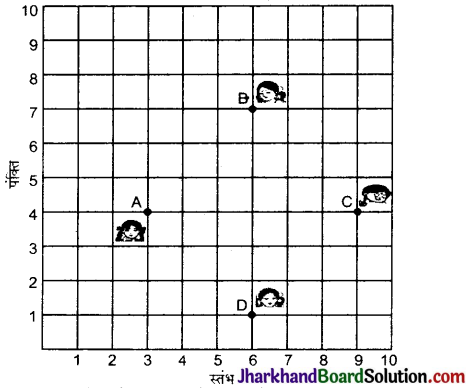
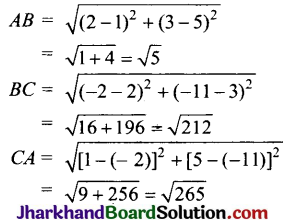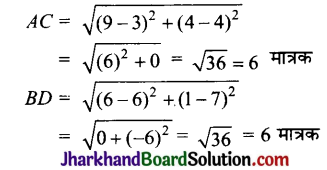Jharkhand Board JAC Class 10 Science Important Questions Chapter 5 तत्वों का आवर्त वर्गीकरण Important Questions and Answers.
JAC Board Class 10 Science Important Questions Chapter 5 तत्वों का आवर्त वर्गीकरण
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
एक तत्त्व (M) आवर्त सारणी के वर्ग IIIA में है। इसके क्लोराइड तथा ऑक्साइड के सूत्र लिखिए|
उत्तर:
वर्ग IIIA में तत्त्व M की संयोजकता 3 है। क्लोरीन की संयोजकता 1 तथा ऑक्सीजन की संयोजकता 2 होती है। अत: क्लोराइड का सूत्र MCl3 तथा ऑक्साइड का सूत्र M2O3 है।
प्रश्न 2.
एक तत्त्व (M) के सल्फाइड का सूत्र M2S5 है। यह तत्त्व आवर्त सारणी के किस उप वर्ग में होगा?
उत्तर:
सूत्र M2S5 के अनुसार M की संयोजकता 5 है – अतः यह उपवर्ग VA में होगा।
प्रश्न 3.
तत्त्वों के गुण उनके परमाणु क्रमांकों के आवर्ती फलन होते हैं।” इस कथन का अर्थ सरल भाषा में समझाइए।
उत्तर:
इसका अर्थ है कि यदि तत्त्वों को उनके बढ़ते हुए परमाणु क्रमांकों के क्रम में व्यवस्थित किया जाय तो एक निश्चित अन्तराल पर स्थित तत्त्वों के गुणों में समानता होती है।
प्रश्न 4.
हाइड्रोजन के तीन समस्थानिक 1H1, 1H2 तथा 1H3 हैं। इन्हें आवर्त सारणी के किन आवर्ती/ उपवर्गों में रखा जाता है?
उत्तर:
तीनों समस्थानिकों का परमाणु क्रमांक 1 है – अतः तीनों को प्रथम आवर्त के प्रथम उपवर्ग IA में रखा जाता है। जाता है।
प्रश्न 5.
अधिकतम कितने तत्त्व हो सकते हैं- (i) आवर्त संख्या n में, (ii) किसी आवर्त के p-ब्लॉक तथा d-ब्लॉक में, (iii) किसी आवर्त के f-ब्लॉक में।
उत्तर:
(i) n = 1 में 2 तत्त्व
n = 2 तथा 3 में से प्रत्येक में 8 तत्त्व
n = 4 तथा 5 में से प्रत्येक में 18 तत्त्व
n = 6 तथा 7 में से प्रत्येक में 32 तत्त्व
(ii) p-ब्लॉक में 6 तत्त्व; d-ब्लॉक में 10 तत्त्व,
(iii) f-ब्लॉक में 14 तत्त्व।

प्रश्न 6.
सबसे हल्के तथा सबसे भारी प्राकृतिक तत्त्वों के नाम, प्रतीक तथा परमाणु क्रमांक लिखिए।
उत्तर:
- सबसे हल्का तत्त्व- हाइड्रोजन (H) 1
- सबसे भारी तत्त्व – यूरेनियम (U) 92
प्रश्न 7.
कुछ तत्त्वों के इलेक्ट्रॉनिक विन्यास निम्नवत् हैं। इनके नाम लिखिए तथा आवर्त सारणी में उपवर्ग बताइए-
A – 2. 4
B – 2, 8, 5
C – 2, 8,
D – 2,5
उत्तर:
A – 2, 4 → कार्बन, IV – A
B – 2, 8, 5 → फॉस्फोरस, V – A
C – 2, 8, 6 → सल्फर, VI – A
D – 2, 5 → नाइट्रोजन, V – A
प्रश्न 9.
निम्नलिखित परमाणुओं से बनने वाले आयनों के प्रतीक आवेश सहित लिखिए-
(i) Cl
(ii) S
(iii) Na
उत्तर:
(i) Cl → Cl1, (ii) S → S2- (iii) Na →
प्रश्न 10.
आवर्त क्या है?
उत्तर:
आवर्त सारणी में क्षैतिज पंक्तियों को आवर्त कहते हैं।
प्रश्न 11.
मेण्डलीफ ने कितने तत्त्वों का वर्गीकरण किया था?
उत्तर:
63 तत्त्व।
प्रश्न 12.
उन तत्त्वों नाम लिखिए (किन्हीं दो) जिनकी खोज की भविष्यवाणी मेण्डलीफ ने की थी?
उत्तर:
टाइटेनियम (Ti) व गैलियम (Ga)।
प्रश्न 13.
आवर्त सारणी में समूह क्या होते हैं?
उत्तर:
आवर्त सारणी में ऊर्ध्वाधर कॉलम को समूह कहते हैं।
प्रश्न 14.
आधुनिक आवर्त सारणी में कितने समूह व आवर्त हैं?
उत्तर:
7 आवर्त व 18 समूह
प्रश्न 15.
आधुनिक आवर्त नियम लिखो।
उत्तर:
तत्त्वों के भौतिक एवं रासायनिक गुण उनकी परमाणु संख्या के आवर्ती फलन होते हैं।
प्रश्न 16.
आवर्त सारणी में शून्य समूह की स्थिति बताओ।
उत्तर:
आवर्त सारणी में शून्य समूह दाहिनी तरफ अंत में है।
प्रश्न 17.
शून्य समूह के तत्त्वों के नाम लिखो।
उत्तर:
हीलियम (He), निऑन (Ne), आर्गन (Ar), क्रिप्टॉन (Kr), जीनॉन (Xe), रेडॉन (Rn)।
प्रश्न 18.
आवर्त सारणी में उस तत्त्व की स्थिति बताओ जिसकी परमाणु संख्या 13 है।
उत्तर:
यह तत्त्व आवर्त सारणी के समूह 13 और तीसरे आवर्त में स्थित है।
प्रश्न 19.
न्यूलैंड्स का अष्टक सिद्धांत क्या है?
उत्तर:
न्यूलैंड्स ने तत्त्वों को परमाणु द्रव्यमान के आरोही क्रम में इस प्रकार व्यवस्थित किया कि प्रत्येक आठवें तत्त्व का गुणधर्म पहले तत्त्व के गुणधर्म के समान है।
प्रश्न 20.
मेण्डलीफ के द्वारा अनुमानित एका- ऐलुमिनियम तथा एका- सिलिकॉन तत्त्वों की किस नाम से खोज हुई?
उत्तर:
- एका ऐलुमिनियम → गैलियम (Ga)
- एका सिलिकॉन → जर्मेनियम (Ge)

प्रश्न 21.
मेण्डलीफ के आवर्त सारणी का क्या सिद्धांत है?
उत्तर:
तत्त्वों के गुणधर्म उनके परमाणु द्रव्यमान का आवर्त फलन होते हैं।
प्रश्न 22.
किसी वर्ग (समूह) में उपस्थित तत्त्वों में क्या समानता होती है?
उत्तर:
किसी समूह में तत्त्वों की संयोजकता समान रहती है। उदाहरण के लिए पहले समूह में प्रत्येक तत्त्व की संयोजकता 1 है।
प्रश्न 23.
मेण्डलीफ ने अपने आवर्त सारणी में तत्त्वों को किस आधार पर व्यवस्थित किया?
उत्तर:
मेण्डलीफ ने बढ़ते हुए परमाणु द्रव्यमान, मूल गुणधर्म तथा रासायनिक गुणधमों में समानता को आधार मानकर तत्त्वों को आवर्त सारणी में व्यवस्थित किया।
प्रश्न 24.
किसी तत्त्व के ऑक्साइड का सूत्र E2O3 है तथा E एक क्रियाशील धातु है। E आवर्त सारणी के किस समूह में स्थित है?
उत्तर:
यह सारणी के 13वें समूह में स्थित है क्योंकि E की संयोजकता 3 है।
प्रश्न 25.
निम्नलिखित तत्त्वों को उनके धात्विक गुणों के बढ़ते हुए क्रम में व्यवस्थित कीजिए- Mg, Ca, K, Ge, Ga
उत्तर:
Ge < Ga < Mg < Ca < K
प्रश्न 26.
क्लोरीन के दो समस्थानिक Cl-35 तथा Cl-37 हैं। क्या आधुनिक आवर्त सारणी में इन्हें दो स्थानों पर रखना चाहिए? उत्तर की पुष्टि कीजिए।
उत्तर:
नहीं क्योंकि Cl की परमाणु संख्या 17 है और आधुनिक आवर्त सारणी का आधार परमाणु संख्या ही है।
प्रश्न 27.
आधुनिक आवर्त सारणी में कितने आवर्त (पीरियड) हैं?
उत्तर:
सात (7)।
प्रश्न 28.
मेण्डलीफ ने जिस समय आवर्त सारणी बनायी, उस समय तक कितने तत्वों की खोज हो चुकी थी?
उत्तर:
63 ।
प्रश्न 29.
मेण्डलीफ ने अपनी आवर्त सारणी में कितने तत्त्वों को रखा है?
उत्तर:
56 तत्त्व।
प्रश्न 30.
आवर्त सारणी के आवर्त तीन के उन तत्त्वों के नाम लिखो जिनका आकार
- सबसे बड़ा और
- सबसे छोटा हो।
उत्तर:
प्रश्न 31.
निम्नलिखित जोड़ों में से कौन-सा तत्त्व आकार में दूसरों से छोटा है?
उत्तर:
प्रश्न 32.
आवर्त के दो गुणधर्म लिखो।
उत्तर:
- आवर्त के सभी तत्त्वों में भरे हुए कोशों की संख्या समान होती है।
- आवर्त में आगे बढ़ने पर तत्त्वों के गुणों में क्रमिक परिवर्तन होते हैं।
प्रश्न 33.
समूह की दो विशेषताएँ लिखो।
उत्तर:
- वर्ग के सभी तत्त्वों में संयोजी कोश में इलेक्ट्रॉनों की संख्या समान होती है।
- वर्ग में ऊपर से नीचे जाने पर तत्त्वों के गुणों में क्रमिक परिवर्तन होते हैं।
प्रश्न 34.
संयोजी इलेक्ट्रॉन क्या हैं?
उत्तर:
किसी तत्त्व के बाह्यतम कोश में इलेक्ट्रॉनों की संख्या को संयोजी इलेक्ट्रॉन कहते हैं।
प्रश्न 35.
किसी आवर्त और समूह में तत्त्वों के धात्विक 5 गुण किस प्रकार बदलते हैं?
उत्तर:
आवर्त में बाएँ से दाएँ जाने पर धात्विक गुण घटता है तथा वर्ग में ऊपर से नीचे जाने पर धात्विक गुण बढ़ता है।
प्रश्न 36.
उन दो तत्त्वों के नाम लिखिए जिनका सम्बन्ध निम्नलिखित से है-
- कार्बन समूह
- बोरॉन समूह
- ऑक्सीजन समूह
उत्तर:
- सिलिकॉन (Si) व जर्मेनियम (Ge)
- ऐलुमिनियम (Al) व गैलियम (Ga)
- सल्फर (S) व सिलीनियम (Se).
प्रश्न 37.
निम्नलिखित यौगिकों में बताइए कि हाइड्रोजन विद्युत धनी है अथवा विद्युत ऋणी-
उत्तर:
- NH3 में विद्युत – धनी
- HCl में विद्युत धनी में विद्युत-
- H2S धनी
- PH3 में विद्युत ऋणी

प्रश्न 38.
ऐसे यौगिक का उदाहरण दीजिए जिससे नाइट्रोजन ऋणायन के रूप में हो। इस आयन का आवेश भी लिखिए।
उत्तर:
ऐलुमिनियम नाइट्राइड (AIN) में आयन N आवेश 3e.
प्रश्न 39.
आधुनिक आवर्त नियम क्या है? स्पष्टीकरण दीजिए।
उत्तर:
आधुनिक आवर्त नियम के अनुसार तत्त्वों के भौतिक तथा रासायनिक गुण उनके परमाणु क्रमांक के आवर्ती फलन होते हैं।
प्रश्न 40.
परमाणु क्रमांक 17 वाले तत्त्व की आवर्त सारणी में स्थिति बताइए तथा कारण देकर स्पष्ट करें।
उत्तर:
परमाणु क्रमांक 17 अर्थात् (Cl17)
इलेक्ट्रॉनिक विन्यास = 2, 8, 7
या 1s² 28² 2p6, 3s² 3p5
अत: आवर्त → = 3 है।
तथा वर्ग → = 2 + 5 = 7 है।
लघु उत्तरीय प्रश्न
प्रश्न 1.
निम्नलिखित का संक्षिप्त विवरण दीजिए – (i) डॉबेराइनर का त्रिक नियम; (ii) न्यूलैण्ड का अष्टक – नियम; (iii) संक्रमण तत्त्व; (iv) विकर्ण सम्बन्ध।
उत्तर:
(i) डॉबेराइनर का त्रिक नियम (1817) – इस नियम के अनुसार, “यदि समान गुण वाले तीन तत्त्वों को परमाणु भारों की वृद्धि के क्रम में रखा जाय तो बीच वाले भार, अन्य दो तत्त्वों के परमाणु भारों के माध्य (औसत) के लगभग बराबर होता है।” उदाहरणार्थ-
(i) \(\frac { Li }{ 7 }\), \(\frac { Na }{ 23 }\), \(\frac { K }{ 39 }\)
∴ Na = \(\frac { 7+39 }{ 2 }\) = 23
(ii) \(\frac { Cl }{ 35.5 }\), \(\frac { Br }{ 80 }\), \(\frac { I }{ 127 }\)
∴ Br = \(\frac { 35.5+127 }{ 2 }\) = 81
परन्तु सभी तत्त्वों के त्रिक न बनाये जा सकने के कारण यह नियम असफल रहा।
(ii) न्यूलैण्ड का अष्टक नियम (1864-66) – इस नियम के अनुसार, “जब तत्त्वों को उनके परमाणु भारों के बढ़ते हुए क्रम के अनुसार व्यवस्थित किया जाता है तो किसी भी तत्त्व के भौतिक व रासायनिक गुण इसके बाद आने वाले आठवें तत्त्व के गुणों से मिलते-जुलते हैं।
| क्र. सं. | तत्त्व |
| 1. | हाइड्रोजन (H) |
| 2. | लीथियम (Li) |
| 3. | बेरीलियम (Be) |
| 4. | बोरॉन (B) |
| 5. | कार्बन (C) |
| 6. | नाइट्रोजन (N) |
| 7. | ऑक्सीजन (O) |
| 8. | फ्लोरीन (F) |
| 9. | सोडियम (Na) |
| 10. | मैग्नीशियम (Mg) |
| 11. | ऐलुमीनियम (Al) |
| 12. | सिलिकॉन (Si) |
| 13. | फॉस्फोरस (P) |
| 14. | सल्फर (S) |
| 15. | क्लोरीन (Cl) |
| 16. | पोटैसियम (K) |
| 17. | कैल्शियम (Ca) |
| 18. | क्रोमियम (Cr) |
| 19. | टाइटेनियम (Ti) |
| 20. | मैंगनीज (Mn) |
| 21. | आयरन (Fe) |
जैसा कि उपर्युक्त सारणी से व्यक्त होता है, यह नियम क्रम संख्या 18 के बाद समुचित रूप से लागू नहीं होता अर्थात् इसकी वैधता केवल कम परमाणु भारों के तत्त्वों तक ही सीमित थी।
(iii) संक्रमण तत्त्व-जिन तत्त्वों के d-कक्षक आंशिक रूप से भारी होते हैं, संक्रमण तत्त्व कहलाते हैं। Fe (26) = 1s², 2s² 2p6, 3s² 3p6 3d6, 4s²। दीघांकार आवर्त सारणी में इनका स्थान s-तथा p-ब्लॉक तत्त्वों के माध्यम है।
(iv) विकर्ण सम्बन्ध- आवर्त सारणी के दूसरे लघु आवर्त में आठ तत्त्व हैं तथा तीसरे लघु आवर्त में भी आठ तत्त्व हैं। इन तत्त्वों को प्रारूपिक तत्त्व कहते हैं तथा इन आवर्ती के तत्वों को विकर्ण सम्बन्ध कहते हैं अर्थात् विकर्ण से सिरों पर स्थित दोनों तत्त्वों के गुणों में समानता है।
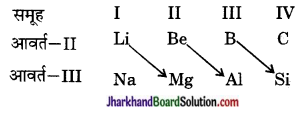
प्रश्न 2.
(i) मेण्डलीफ का आवर्त नियम लिखिए। इसमें क्या संशोधन करके आधुनिक आवर्त नियम प्राप्त किया गया? मेण्डलीफ के आवर्त सारणी तथा आधुनिक आवर्त सारणी बनाने के आधार में क्या मौलिक अंतर है?
अथवा
(ii) आधुनिक आवर्त नियम क्या है? आधुनिक आवर्त नियम पर टिप्पणी लिखिए।
उत्तर:
(i) मेण्डलीफ का आवर्त नियम-यदि तत्त्वों को परमाणु भार के बढ़ते हुए क्रम में व्यवस्थित किया जाय तो तत्वों के भौतिक तथा रासायनिक गुण उनके परमाणु भारों के आवर्ती फलन (periodic function of their atomic weights) होते हैं। उपर्युक्त नियम में ‘परमाणु भार’ के स्थान पर ‘परमाणु क्रमांक’ का उपयोग करके आधुनिक आवर्त नियम प्राप्त किया गया, जिसके अनुसार तत्त्वों के भौतिक तथा रासायनिक गुण उनके परमाणु क्रमांक (Atomic Number) के आवर्ती फलन होते हैं।
मेण्डलीफ का आवर्त नियम तत्त्वों के परमाणु भारों पर आधारित है जबकि आधुनिक आवर्त नियम तत्त्वों के परमाणु क्रमांकों पर आधारित है।
(ii) आधुनिक आवर्त नियम – यदि तत्त्वों को परमाणु क्रमांक के बढ़ते हुए क्रम में रखा जाय तो तत्त्वों के भौतिक तथा रासायनिक गुण उनके परमाणु क्रमांक के आवर्ती फलन होते हैं।
प्रश्न 3.
किसी तत्त्व के विभिन्न समस्थानिकों को मेण्डलीफ की मूल आवर्त सारणी में रखने में क्या कठिनाई थी? आधुनिक आवर्त सारणी में यह कठिनाई कैसे दूर हो गयी?
उत्तर:
समस्थानिकों का स्थान – अनेक तत्त्वों के ऐसे एक से अधिक समस्थानिक पाये जाते हैं जिनके परमाणु भार तो भिन्न होते हैं परन्तु रासायनिक गुण समान, जैसे हाइड्रोजन के तीन समस्थानिक H-1, H-2, H-3, क्लोरीन के दो समस्थानिक Cl-35, Cl-37, कार्बन के दो समस्थानिक C-12, C-14 आदि हैं।
परमाणु भार के आधार पर क्रमायोजित करने से इन समस्थानिकों को भी सारणी में पृथक स्थान मिलना चाहिए परन्तु मेण्डलीफ की आवर्त सारणी में ऐसा संभव नहीं था। आधुनिक आवर्त सारणी में तत्त्व का स्थान उसके परमाणु क्रमांक से निर्धारित होता है। अतः किसी तत्त्व के विभिन्न समस्थानिकों का परमाणु क्रमांक समान होने के कारण उन्हें सारणी में एक ही स्थान पर रखा जाता है।
प्रश्न 4.
दीर्घाकार आवर्त सारणी के मुख्य लक्षण क्या हैं? अंतिम चार आवर्ती के तत्त्वों की संख्या लिखिए।
अथवा
दीर्घाकार आवर्त सारणी की चार मुख्य विशेषताओं पर टिप्पणी लिखिए। दीर्घाकार आवर्त सारणी की विशेषताएँ लिखिए।
अथवा
उत्तर:
दीघांकार आवर्त सारणी के लक्षण – इसके मुख्य लक्षण निम्नवत् हैं-
(1) इस सारणी में 7 क्षैतिज पंक्तियाँ (Horizontal rows) हैं, जिन्हें आवर्त (Period) कहते हैं तथा 18 ऊर्ध्वाधर स्तम्भ (Vertical columns) हैं, जिन्हें वर्ग (Group) या समूह कहते हैं।
(2) प्रत्येक आवर्त को चाहे वह लघु हो अथवा दीर्घ, एक ही रेखा में रखा गया है अर्थात् मेण्डलीफ की सारणी की भाँति उसे प्रथम तथा द्वितीय उपश्रेणियों में नहीं बाँटा गया।
(3) प्रत्येक आवर्त में, उपकोशों में अंतिम इलेक्ट्रॉन के प्रवेश के अनुसार तत्त्वों को उपवर्गों में निम्नलिखित क्रम में रखा गया है-
s – उपकोश – IA, IIA [ अधिकतम 2 इलेक्ट्रॉन]
p – उपकोश – III-A, IV-A, V-A, VI-A, VII-A तथा 0 [अधिकतम 6 इलेक्ट्रॉन]
d – उपकोश – III-B, IV-B, V-B, VI-B, VII-B, VIII, VIII, VIII, I-B, II-B [ अधिकतम 10 इलेक्ट्रॉन]
इस प्रकार इस सारणी में किसी तत्त्व की स्थिति से ज्ञात हो जाता है कि उसमें अंतिम इलेक्ट्रॉन की आपूर्ति किस कोश तथा किस उपकोश में हुई है। यह स्थिति इसका भी ज्ञान कराती है कि परमाणु में कौन-से कोश तथा उपकोश पूर्णतः भरे जा चुके हैं।
(4) दीर्घाकार आवर्त सारणी में तत्त्वों को चार खण्डों अथवा ब्लॉकों (blocks) में स्पष्टत: विभाजित किया गया है। इन्हें क्रमश: 3, p, d तथा f ब्लॉक के तत्त्व कहते हैं। किसी एक ब्लॉक के तत्त्वों के लक्षणों में अनेक समानताएँ तथा अन्य ब्लॉक के तत्त्वों से भिन्नताएँ होती हैं।
(5) लैन्थेनाइड तथा एक्टिनाइड श्रेणियों को अलग लिखा गया है तथा इनके स्थानों का मुख्य सारणी में स्थान तारांकित (* तथा **) किया गया है अर्थात् इन श्रेणियों को मुख्य सारणी में इन तारांकित स्थानों पर लिखा जाना चाहिए। परन्तु ऐसा करने से, सारणी में कुल 32 स्तम्भ हो जाते हैं, तथा सारणी की लम्बाई (मुद्रण में) असुविधाजनक हो जाती है। अतः इन श्रेणियों को अलग लिखा जाता है। ये f – ब्लॉक के तत्त्व होते हैं।
(6) इस सारणी में धात्वीय एवं अधात्वीय तत्त्वों को, संक्रमण तत्त्वों को तथा अक्रिय तत्त्वों को स्पष्टतः अलग देखा जा सकता है।

प्रश्न 5.
आवर्त सारणी के ‘लघु’ तथा ‘दीर्घ आवर्त’ से क्या तात्पर्य है? आवर्त 1 से 6 तक प्रत्येक में तत्त्वों की संख्याएँ लिखिए।
अथवा
आवर्त सारणी में आवत के चार मुख्य लक्षण लिखिए।
उत्तर:
आवर्त सारणी के प्रथम तीन आवर्त ‘लघु-आवर्त’ कहलाते हैं। इनमें तत्त्वों की संख्या कम होती है। इसके आगे के आवर्त 4, 5, 6 तथा 7 दीर्घ आवर्त’ कहलाते हैं। इनमें तत्त्वों की संख्या अधिक होती है। तत्त्वों की संख्याएँ निम्नवत हैं-
| आवर्त | तत्त्वों की संख्या |
| 1 | 2 |
| 2 | 8 |
| 3 | 8 |
| 4 | 18 |
| 5 | 18 |
| 6 | 32 |
प्रश्न 6.
स्पष्ट कीजिए कि-
(i) लघु आवर्त में परमाणुओं के बाह्यतम कोश में इलेक्ट्रॉनों का वितरण किस प्रकार बदलता है?
(ii) किसी A उपवर्ग में परमाणुओं के बाह्यतम कोश में इलेक्ट्रॉन वितरण में क्या भिन्नता या समानता होती है।
(iii) तत्त्वों का विकर्ण सम्बन्ध एवं सम्बन्धित दो तत्त्व।
अथवा
विकर्णी सम्बन्ध पर संक्षिप्त टिप्पणी लिखिए।
उत्तर:
(i) लघु आवर्त में पहले 8-उपकोश 1 तथा 2 इलेक्ट्रॉन तथा उपकोश के पूर्ण (2 इलेक्ट्रॉन) हो जाने के बाद p-उपकोश में क्रमश: 1, 2, 3, 4, 5 तथा 6 इलेक्ट्रॉनों की पूर्ति होती है।
(ii) किसी उपवर्ग में परमाणु के बाह्यतम कोश में इलेक्ट्रॉनों की संख्या समान होती हैं, परन्तु उपवर्ग में परमाणु क्रमांक के बढ़ने के साथ बाह्यतम कोश की मुख्य क्वाण्टम संख्या, आवर्त संख्या के साथ 1 से 7 तक बढ़ती जाती हैं।
उदाहरणतः उपवर्ग II-A के परमाणुओं में बाह्यतम कोश में 2 इलेक्ट्रॉन 8- उपकोश में होते हैं, परन्तु बाह्यतम कोश क्रमश: 1, 2, 3, 4, 5, 6 तथा 7 क्वाण्टम संख्या का होगा।
(iii) तत्त्वों का विकर्ण सम्बन्ध – द्वितीय आवर्त के पहले तीन तत्त्व (Li, Be B) तीसरे आवर्त के तत्त्वों तथा अगले वर्ग के दूसरे तत्त्व के साथ गुणों में समानता प्रदर्शित करते हैं। इसे विकर्ण सम्बन्ध कहते हैं।
उदाहरणत:
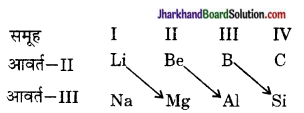
प्रश्न 7.
निम्न ऑक्साइडों को उनके क्षारकीय गुण के घटते हुए क्रम में लिखिए-
Al2O3, Na2O, MgO, P2O5
उत्तर:
P2O5, Al2O3, MgO, Na2O.
प्रश्न 8.
मेण्डलीफ की आवर्त सारणी के वर्ग तथा आवर्त की दो-दो विशेषताएँ लिखिए।
उत्तर:
मेण्डलीफ की आवर्त सारणी के वर्गों की विशेषताएँ –
- 0 से VIII तक कुल 9 वर्ग होते हैं।
- धात्विक लक्षण या धनविद्युती लक्षण – परमाणु क्रमांक में वृद्धि क्रम के साथ बढ़ता है।
- विद्युत ऋणीयता- किसी परमाणु की अपनी और इलेक्ट्रॉन आकर्षित करने की प्रवृत्ति परमाणु क्रमांक के वृद्धि के साथ घटती है।
आवर्ती की विशेषताएँ-
- आवर्त सारणी में आवर्ती की क्रम संख्या एक से सात तक होती है।
- आवर्त में धात्वीय गुण परमाणु क्रमांक की वृद्धि के साथ-साथ घटता है। क्रमांक के बढ़ने के साथ घटता है।
- आवर्त में ऑक्साइडों का क्षारीय गुण परमाणु
प्रश्न 9.
आवर्त सारणी के किसी आवर्त में बाएँ से दाएँ चलने पर निम्नलिखित गुणों में क्या परिवर्तन होता है-
- विद्युत धनात्मक गुण
- धात्विक गुण
- ऑक्साइडों का क्षारीय गुण?
उत्तर:
- विद्युत धनात्मक गुण – परमाणु क्रमांक वृद्धि अर्थात् बायें से दायें जाने पर घटता है।
- धात्विक गुण धात्विक गुण भी परमाणु क्रमांक वृद्धि के साथ घटता है।
- ऑक्साइडों का क्षारीय गुण आवर्त में क्षारीय गुण परमाणु क्रमांक वृद्धि के साथ-साथ घटता है।
प्रश्न 10.
आवर्त सारणी के द्वितीय आवर्त में निम्नलिखित गुणों में किस प्रकार का परिवर्तन होता है? समझाइए (i) धात्विक गुण (ii) हाइड्रोजन से सम्बन्धित संयोजकता।
उत्तर:
आवर्त सारणी के द्वितीय आवर्त में परिवर्तन-
- धात्विक गुण – परमाणु क्रमांक वृद्धि के साथ तत्त्वों के धात्विक गुण घटते हैं।
- हाइड्रोजन से सम्बन्धित संयोजकता – हाइडोजन के अनुसार तत्त्वों की संयोजकता बढ़ती है।
प्रश्न 11.
आवर्त सारणी के द्वितीय आवर्त में निम्नलिखित गुणों में किस प्रकार परिवर्तन होता है?
- धन विद्युती गुण
- ऑक्साइडों की प्रकृति
- आयनन विभव।
उत्तर:
- धनविद्युती गुण- परमाणु क्रमांक के वृद्धि क्रम के साथ बढ़ता है।
- ऑक्साइडों की प्रकृति- आवर्त में ऑक्साइडों का क्षारीय गुण परमाणु क्रमांक के बढ़ने के साथ-साथ घटता है।
- आयनन विभव- किसी परमाणु से इलेक्ट्रॉन विस्थापित करने के लिए आवश्यक ऊर्जा परमाणु क्रमांक में वृद्धि क्रम के साथ बढ़ती है।
प्रश्न 12.
परमाणु क्रमांक 17 वाले तत्त्व की आवर्त सारणी में वर्ग तथा आवर्त लिखिए।
अथवा
परमाणु क्रमांक 17 वाले तत्त्व की आवर्त सारणी में स्थिति बताइए।
उत्तर:
परमाणु क्रमांक = 17
इलेक्ट्रॉनिक विन्यास 2, 8, 7
आवर्त – 3
वर्ग-VIIA ।
प्रश्न 13.
परमाणु क्रमांक 11 वाले तत्त्व के समूह एवं आवर्त लिखिए।
उत्तर:
परमाणु क्रमांक = 11
इलेक्ट्रॉनिक विन्यास = 2, 8, 1
आवर्त – 3
वर्ग – I A ।
प्रश्न 14.
तत्त्व Mg आवर्त सारणी के द्वितीय समूह में है। यदि Mg का तुल्यांकी भार 12 है तो तत्त्व का परमाणु भार ज्ञात करें।
उत्तर:
Mg द्वितीय समूह में है।
इसलिए Mg की संयोजकता 2 होगी।
अत: परमाणु भार = तुल्यांकी भार x संयोजकता
= 12 x 2 = 24
प्रश्न 15.
निम्न में से किस तत्त्व का ऑक्साइड प्रबल क्षारीय है और क्यों?
Na, Mg, Al एवं Si
उत्तर:
Na का ऑक्साइड Na2 प्रबल क्षारीय है क्योंकि किसी आवर्त में बायें से दायें जाने पर तत्त्वों के ऑक्साइडों की क्षारीयता घटती जाती है।
प्रश्न 16.
आवर्त सारणी के किसी आवर्त में बायें से दायें जाने पर निम्नलिखित गुणों में क्या परिवर्तन होता है?
(i) परमाणु त्रिज्या
(ii) विद्युत ऋणात्मकता
(iii) आयनन विभव।
उत्तर:
आवर्त सारणी में आवर्त में बाएँ से दाएँ जाने पर निम्नलिखित परिवर्तन होते हैं-
- परमाणु त्रिज्या – परमाणु त्रिज्या घटेगी।
- विद्युत ऋणात्मकता प्रत्येक आवर्त में बाएँ से दाएँ चलने पर तत्त्व की ऋणविद्युत प्रकृति में क्रमिक वृद्धि होती है; जैसे P से S अधिक ऋणविद्युत है।
- आयनन विभव – प्रत्येक आवर्त में बाएँ से दाएँ चलने पर तत्त्व की आयनन विभव में कमी आयेगी।
प्रश्न 17.
इलेक्ट्रॉनिक विन्यास के आधार पर आप कैसे छाँटोगे –
(i) समान रासायनिक गुणों वाले तत्त्व
(ii) आवर्त का पहला तत्त्व
(iii) आवर्त का अंतिम तत्त्व
उत्तर:
(i) समान रासायनिक गुणों वाले तत्त्वों का इलेक्ट्रॉनिक विन्यास समान होता है।
(ii) आवर्त के पहले तत्त्व के बाह्यतम कोश केवल एक इलेक्ट्रॉन होता है।
(iii) आवर्त के अंतिम तत्त्व के बाह्यतम कोश में 8 इलेक्ट्रॉन होते हैं।
प्रश्न 18.
मेण्डलीफ की आवर्त सारणी में हाइड्रोजन के स्थान पर टिप्पणी कीजिए।
उत्तर:
आवर्त सारणी में हाइड्रोजन का स्थान विवादास्पद है। एक संयोजी इलेक्ट्रॉन होने के कारण इसे IA समूह में क्षार धातुओं के ऊपर रखा गया है, लेकिन इसके कुछ गुण हैलोजन के समान होने के कारण इसे
इनके साथ स्थान मिलना चाहिए। इस कारण इसकी स्थिति अनिश्चित रही।
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
मेण्डलीफ के आवर्त नियम का उल्लेख करते हुए, मेण्डलीफ की संशोधित आवर्त सारणी के लक्षण लिखिए।
उत्तर:
मेण्डलीफ का आवर्त नियम (Mendeleeff’s Periodic Law) – इसके अनुसार तत्त्वों के भौतिक रासायनिक गुण उनके परमाणु- भारों के आवर्ती फलन (periodic function of their atomic weights) हैं अर्थात् यदि तत्त्वों को बढ़ते हुए परमाणु- भारों के क्रम में व्यवस्थित किया जाय तो निश्चित एवं समान क्रम- अन्तरालों के बाद लगभग समान गुण वाले तत्त्व पाये जाते हैं।
मेण्डलीफ की संशोधित आवर्त सारणी के लक्षण (Characteristics of Mendeleeff’s Modified Periodic Table ) – मेण्डलीफ की (Columns) संशोधित आवर्त सारणी को सात श्रेणियों (Series) जिनको आवर्त (Period) कहते हैं तथा नौ स्तम्भों में, जिन्हें वर्ग अथवा समूह (Groups ) कहते हैं, में विभाजित किया गया है।
सारणी में श्रेणियों को बाएँ से दाहिने तथा वर्गों को ऊपर से नीचे लिखा जाता है। श्रेणियों का नामांकन 1 से 7 तक तथा वर्गों का नामांकन I, II, III, IV, V, VI, VII VIII तथा 0 किया गया है। आवर्त 4, 5, 6 तथा में वर्ग I से VII तक प्रत्येक वर्ग को उपवर्गों A तथा B में विभाजित किया गया है तथा प्रत्येक वर्ग या समूह में आवर्त 1, 2 तथा 3 के तत्त्व उपवर्ग A के अन्तर्गत रखे गये हैं।
आवर्त सारणी के प्रथम आवर्त में केवल दो तत्त्व, H वर्ग 1 में तथा He वर्ग 0 में रखे गये हैं। द्वितीय तथा तृतीय आवर्त में से प्रत्येक में आठ तत्त्व हैं जो I से VII तक तथा वर्ग में आते हैं। इन्हें लघु आवर्त (Short periods) कहते हैं।
आवर्त 4 एवं 5 में से प्रत्येक में 18 तत्त्व हैं, जिनमें से 8 तत्त्व उपवर्ग A (I से VII तथा 0) में 7 तत्त्व उपवर्ग B (I से VII) में तथा 3 तत्त्व वर्ग 8 में रखे गये हैं।
आवर्त 6 में 32 तत्त्व तथा आवर्त 7 में अब तक ज्ञात 28 तत्त्व रखे गये हैं।
सारणी के वर्गों तथा आवतों के सामान्य लक्षण निम्नवत् हैं-
(i) प्रत्येक आवर्त में तत्त्वों का क्रम बढ़ते हुए परमाणु क्रमांकों के अनुसार है।
(ii) प्रत्येक आवर्त में बाएँ से दाहिने जाने पर तत्त्वों के (बढ़ता हुआ या घटता हुआ) परिवर्तन गुणों में क्रमिक होता जाता है।
उदाहरणत:
प्रत्येक आवर्त में बढ़ते हुए परमाणु क्रमांक के अनुसार तत्त्वों की धन- वैद्युत संयोजकता बढ़ती तथा ऋण वैद्युत संयोजकता घटती जाती है।
(iii) एक ही वर्ग या समूह स्थित तत्त्वों के गुण (जैसे- संयोजकता, विद्युत धनात्मकता अथवा ऋणात्मकता तथा अन्य) में समानता पायी जाती हैं।
(iv) तत्त्व का परमाणु क्रमांक उसका मौलिक लक्षण हैं जो तत्त्व की विशेषताओं को व्यक्त करता है।
(v) सारणी में किसी तत्त्व के स्थान (आवर्त तथा वर्ग या समूह) के अनुसार उसके गुणों को बताया सकता है।
प्रश्न 2.
मेण्डलीफ की प्रारंभिक आवर्त सारणी के दोष बताइए। इनका निवारण मेण्डलीफ की संशोधित आवर्त सारणी में किस प्रकार किया गया है?
उत्तर:
मेण्डलीफ की प्रारंभिक आवर्त सारणी के प्रमुख दोष निम्नवत् हैं-
1. तत्त्वों का क्रम बढ़ते परमाणु भार के अनुसार न होना- मेण्डलीफ की आवर्त सारणी में तत्त्वों के ऐसे चार युग्म (pairs) हैं जिनमें अधिक परमाणु भार का तत्त्व, कम परमाणु भार के तत्त्व से पहले रखा गया है। ये युग्म हैं-
- आर्गन (Ar ) – 39.4 तथा पोटैशियम (K) 39.1
- कोबाल्ट (Co) – 58.94 तथा निकिल (Ni)-58.96
- टेलुरियम (Te) – 127.61 तथा आयोडीन (I)-126.91
- थोरियम (Th) – 232.12 तथा प्रोटोएक्टीनियम (Pa) – 231
2. समस्थानिकों का स्थान- अनेक तत्त्वों के ऐसे एक से अधिक समस्थानिक पाये जाते हैं जिनके परमाणु भार तो भिन्न होते हैं परन्तु रासायनिक गुण समान, जैसे हाइड्रोजन के तीन समस्थानिक H-1, H-2, H-3, क्लोरीन के दो समस्थानिक C1-35, C1-37, कार्बन के दो समस्थानिक C-12, C-14 आदि परमाणु भार के आधार पर क्रमायोजित करने से इन समस्थानिक को भी सारणी में पृथक स्थान मिलना चाहिए, परन्तु मेण्डलीफ की आवर्त सारणी में ऐसा संभव नहीं था।
3. हाइड्रोजन का द्वैध व्यवहार हाइड्रोजन; जो कि प्रथम वर्ग A की धातुओं (Li, Na, K…….) और सप्तम वर्ग A के तत्त्वों (F, Cl, Br, I) के गुणों से समानता रखता है, को निश्चित स्थान नहीं दिया जा सकता है।
4. असमान तत्त्वों को एक ही वर्ग में रखना- प्रथम समूह A के क्षारीय धातु और B के मुद्रा-धातु व सप्तम् वर्ग A के हैलोजन और B के Mn धातु में काफी असमानता होते हुए भी वे एक साथ रखे गये हैं।
| IA | VII |
| (H) | (H) |
| Li | F |
| Rb | Cl |
| Cs | Br |
| Fr | I |
5. अक्रिय गैसों (जैसे हीलियम, निऑन, आर्गन आदि को सारणी में कोई स्थान नहीं दिया गया।
मेण्डलीफ की आवर्त सारणी में संशोधन वैज्ञानिक मोज्ले (Mosley) ने X- विकिरणों के स्पेक्ट्रमों के अध्ययन के द्वारा एक तत्त्वों के एक नवीन लक्षण, परमाणु क्रमांक (Atomic Number) का प्रतिपादन किया।
किसी तत्त्व के परमाणु के नाभिक में प्रोटॉनों की संख्या अथवा नाभिक के धनावेश (मूल आवेश पदों में) को तत्त्व का परमाणु क्रमांक कहते हैं। वैज्ञानिकों ने यह पाया कि यदि तत्त्वों को उनके परमाणु क्रमांकों के बढ़ते क्रम में व्यवस्थित किया जाय तो मेण्डलीफ की प्रारंभिक आवर्त सारणी के अनेक दोष दूर हो जाते हैं। इस आधार पर मेण्डलीफ द्वारा प्रतिपादित आवर्त नियम में संशोधन करके आधुनिक आवर्त नियम निम्नवत् प्रस्तुत किया गया-
“तत्त्वों के भौतिक एवं रासायनिक गुण उनके परमाणु क्रमांकों के आवर्ती फलन होते हैं।”
इस नियम आधार पर मेण्डलीफ की आवर्त सारणी में संशोधन किया गया। इसके अतिरिक्त सारणी में अक्रिय गैसों का एक नया वर्ग (शून्य वर्ग) जोड़ा गया तथा दुर्लभ मृदा तत्त्वों (Rare Earth Elements) एवं एक्टिनाइड तत्त्वों के स्थान निर्धारित किये गये।
किसी तत्त्व के सभी समस्थानिकों का परमाणु क्रमांक समान होने के कारण उनके स्थान निर्धारण की त्रुटि स्वतः ही दूर हो गयी।

प्रश्न 3.
मेण्डलीफ की संशोधित आवर्त सारणी के आवर्ती तथा वर्गों / उपवर्गों की विशेषताएँ या लक्षणों को लिखिए।
उत्तर:
(i) आवर्त सारणी की विशेषताएँ (Char- acteristics of Periodic Table)
1. आवर्त सारणी में आवर्ती की क्रम संख्या एक से सात तक होती है।
2. पहले आवर्त में केवल दो तत्त्व हैं इसलिए इसे अतिलघु आवर्त कहते हैं तथा इसमें सिर्फ हाइड्रोजन तथा हीलियम हैं।
3. आवर्त दो व तीन में आठ-आठ तत्त्व होते हैं तथा इनको लघु आवर्त कहते हैं। तीसरे आवर्त के तत्त्वों (Na, Mg, Al, Si, P, S, CI) को प्रारूपी तत्त्व (Typical Elements) कहते हैं।
4. चौथे और पाँचवें आवर्त में 18-18 तत्त्व होते हैं इसलिए इनको दीर्घ आवर्त (Long period) कहते हैं।
5. छठे तथा सातवें आवर्त में 32-32 तत्त्व आते हैं इसलिए इनको अतिदीर्घ आवर्त कहते हैं सातवें आवर्त में उस समय सिर्फ 13 तत्त्व ही ज्ञात थे।
6. प्रत्येक दीर्घ आवर्त में आठ तत्त्वों को सामान्य तत्त्व (Normal element) तथा शेष दस तत्त्वों को संक्रमण तत्त्व (Transition elements) कहते हैं।
7. अतिदीर्घ छठे और सातवें आवर्त में आठ सामान्य तत्त्व 10 संक्रमण तत्त्व तथा 14 अन्त: संक्रमण तत्त्व हैं। छठी श्रेणी के अन्त संक्रमण तत्त्व लैन्थेनाइड तथा सातवीं श्रेणी के अन्तः संक्रमण तत्त्व एक्टिनाइड कहलाते हैं। इन्हें मुख्य सारणी के नीचे अलग दिखाया जाता है।
8. प्रत्येक आवर्त किसी क्षार धातु (Li, Na, K) से आरम्भ होकर किसी अक्रिय गैस, जैसे- हीलियम, निऑन, आर्गन आदि पर समाप्त हो जाता है।
9. प्रत्येक आवर्त में तत्त्वों के भौतिक तथा रासायनिक गुणधर्मों, जैसे- धात्वीय प्रकृति, घनत्व, क्वथनांक, गलनांक और ऑक्साइड की प्रकृति में नियमित परिवर्तन ( Grada- tion) होता है।
10. द्वितीय आवर्त के पहले तीन तत्त्व ( लीथियम, बेरीलियम तथा बोरॉन) तीसरे आवर्त के तत्त्वों तथा अगले वर्ग के दूसरे तत्त्व के साथ विकर्ण समानता प्रदर्शित करते हैं। इस कारण इनके गुण समान होते हैं। जैसे- लीथियम, मैग्नीशियम के साथ, बेरीलियम, ऐलुमिनियम के साथ तथा बोरॉन, सिलिकॉन के साथ विकर्ण समानता प्रदर्शित कराता है।
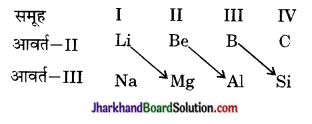
11. तत्त्वों का आवर्त में विद्युत धनात्मक गुण परमाणु क्रमांक की वृद्धि के साथ-साथ घटता है।

12. धात्वीय गुण – आवर्त में धात्वीय गुण परमाणु क्रमांक की वृद्धि के साथ-साथ घटता है।

13. संयोजकता (हाइड्रोजन के अनुसार) हाइड्रोजन के अनुसार तत्त्वों की संयोजकता पहले वर्ग 1 से 4 तक बढ़ती है और उसके उपरान्त 4 से 1 तक घटती है।
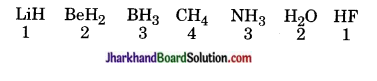
संयोजकता – (ऑक्सीजन के अनुसार) ऑक्सीजन के अनुसार संयोजकता वर्ग एक से आठ तक लगातार बढ़ती है।

14. ऑक्साइडों का क्षारीय गुण आवर्त में ऑक्साइडों का क्षारीय गुण परमाणु क्रमांक के बढ़ने के साथ-साथ घटता है।

क्वथनांक, गलनांक, विशिष्ट ताप में इसी प्रकार से क्रम पाया जाता है।
15. परमाणु त्रिज्या – प्रत्येक आवर्त में पहले वर्ग से सातवें वर्ग की ओर जाने पर तत्त्वों की परमाणु त्रिज्या का मान क्रमानुसार घटता है तथा किसी वर्ग में ऊपर से नीचे जाने पर परमाणु त्रिज्या का मान बढ़ता जाता है।
(ii) वर्गों तथा उपवर्गों की विशेषताएँ-
(i) ‘0’ से ‘VIII’ तक कुल 9 वर्ग होते हैं।
(ii) प्रत्येक वर्ग की वर्ग संख्या अपनी विशिष्ट संयोजकता (Valency) को प्रकट करती है जैसे ‘0’ वर्ग के तत्त्वों की संयोजकता शून्य है, ‘I’ वर्ग के तत्त्वों की संयोजकता 1 है तथा III वर्ग के तत्त्वों की संयोजकता 3 है।
(iii) कुछ अपवादों को छोड़कर एक वर्ग के तत्त्वों के गुण समान होते हैं।
(iv) एक वर्ग में नीचे के तत्त्वों का परमाणु भार ऊपर के तत्त्वों के परमाणु भार से अधिक होता है।
(v) शून्य तथा आठवें वर्ग को छोड़कर अन्य वर्गों को उपवर्गों (Sub-groups ) में विभाजित किया गया है। इनको उपवर्ग ‘A’ (अ) तथा उपवर्ग ‘B’ (ब) कहते हैं। सारणी में उपवर्ग ‘A’ को बायीं ओर तथा उपवर्ग ‘B’ को दायाँ लिखते हैं। एक उपवर्ग में उपस्थित तत्त्वों में अधिक समानता पायी जाती है तथा ये तत्त्व दूसरे उपवर्ग में उपस्थित तत्त्वों से भिन्न होते हैं, जैसे प्रथम वर्ग के उप-समूह ‘A’ में 6 तत्त्व Li, Na, K, Rb, Cs व Fr हैं तथा उपवर्ग ‘B’ में Cu, Ag तथा Au उपस्थित हैं। उपवर्ग A तथा B में उपस्थित तत्त्वों में अन्तर पाया जाता है।
(vi) एक ही वर्ग में परमाणु क्रमांक के वृद्धि- के साथ तत्त्वों के गुणों में क्रमबद्ध परिवर्तन होता है।
(क) धात्विक लक्षण या धन विद्युती लक्षण-परमाणु क्रमांक के वृद्धि क्रम के साथ बढ़ता है।
(ख) आयनन विभव (Ionisation Poten-tial) – अर्थात् किसी परमाणु से इलेक्ट्रॉन विस्थापित करने के लिए आवश्यक ऊर्जा परमाणु क्रमांक में वृद्धि क्रम के साथ घटती है।
(ग) विद्युत ऋणीयता (Electronega-tivity) – अर्थात् किसी परमाणु की अपनी ओर इलेक्ट्रॉन आकर्षित करने की प्रवृत्ति परमाणु क्रमांक के वृद्धि क्रम के साथ घटती है।
(vii) विभिन्न समूहों में उपस्थित तत्त्व सामान्य (Nor-mal), संक्रमण (Transitional), दुर्लभ मृदा (Rare earth) तथा एक्टिनाइड (Actinied ) हो सकते हैं। आधुनिक प्रणाली में ‘B’ उपवर्ग (भारी धातुएँ) के तत्त्व संक्रमण तत्त्व कहलाते हैं और उपवर्ग ‘A’ के तत्त्व (हल्की धातु तथा अधातु) सामान्य तत्त्व (Normal elements) कहलाते हैं।
प्रश्न 4.
मेण्डलीफ की आवर्त सारणी की उपयोगिता का विवरण दीजिए।
उत्तर:
मेण्डलीफ की आवर्त सारणी की उपयोगिता (Utility of Mendeleeff’s Periodic Table)
1. तत्त्वों का वर्गीकरण – मेण्डलीफ की आवर्त सारणी का मुख्य उपयोग यह है कि 109 तत्त्वों के भौतिक केवल तथा रासायनिक गुणों का अध्ययन अलग-अलग न रहकर 9 समूहों तक सीमित रह गया है।
2. परमाणु भार का आकलन – चूँकि किसी वर्ग विशेष में उपस्थित तत्त्व की संयोजकता उसकी वर्ग संख्या के बराबर होती है, यदि तत्त्व का तुल्यांकी भार ज्ञात है तो उसका परमाणु भार निम्नलिखित सूत्र से ज्ञात कर सकते हैं-
परमाणु भार = तुल्यांकी भार x संयोजकता
3. संदेहास्पद परमाणु भारों का सही निर्धारण- मेण्डलीफ आवर्त सारणी की सहायता से बहुत से तत्त्वों के परमाणु भारों का सही निर्धारण करने में सहायता मिली। जैसे, Be का परमाणु भार इसकी संयोजकता तीन मानकर 4.5 x 3 = 13.5 माना जाता था। 4.5 इसका तुल्यांकी भार है, परन्तु मेण्डलीफ ने इसे द्विसंयोजी मानकर द्वितीय वर्ग में रखा। बाद में इसका परमाणु भार 4.5 x 2 9 निकाला गया जो इसके रासायनिक व्यवहार से पूर्णतः मेल खाता है।
4. नये तत्त्वों की खोज में- मेण्डलीफ की आवर्त सारणी में दो क्रमागत तत्त्वों के परमाणु भार में लगभग दो से तीन इकाइयों का अन्तर है। जहाँ अन्तर छह या छह से अधिक इकाई का हुआ, वहीं मेण्डलीफ ने दोनों तत्त्वों के मध्य एक रिक्त स्थान छोड़ दिया। उसने इन तत्त्वों के गुणों का वर्णन भी इस वर्ग के गुणों के आधार पर कर दिया। उदाहरणार्थ, मेण्डलीफ की मूल आवर्त सारणी में बाद में खोजे गये तत्त्व स्कैण्डियम (Se), गैलियम (Ga) तथा जर्मेनियम (Ge) के स्थान रिक्त थे जिनको उसने क्रमशः एका बोरॉन, एका ऐलुमिनियम तथा एका सिलिकॉन नाम दिया था।
प्रश्न 5.
(i) मेण्डलीफ की आवर्त सारणी में कुछ रिक्त स्थान क्यों थे?
(ii) मेण्डलीफ के वर्गीकरण की कोई तीन सीमाएँ लिखिए।
(iii) किसी आवर्त में परमाणु क्रमांक बढ़ने पर परमाणुओं के इलेक्ट्रॉनिक विन्यास में किस प्रकार परिवर्तन होता है?
उत्तर:
(i) मेण्डलीफ का अनुमान था कि रिक्त स्थानों की पूर्ति नए तत्त्वों की खोज से होगी। मेण्डलीफ ने आवर्त सारणी की सहायता से रिक्त स्थानों के अज्ञात तत्त्वों के गुण का पूर्वानुमान किया। अब उन सभी तत्त्वों की खोज हो चुकी है, जिनके लिए मेण्डलीफ ने सारणी में रिक्त स्थान छोड़े थे। इन तत्त्वों के गुण लगभग वही पाए गए हैं जो मेण्डलीफ ने इनकी खोज से पहले बता दिए थे।
उदाहरण-स्कैंडियम, गैलियम, जर्मेनियम।
(ii) मेण्डलीफ के वर्गीकरण की तीन सीमाएँ-
- आवर्त सारणी में हाइड्रोजन का कोई एक निश्चित स्थान होना।
- समस्थानिकों और समभारिकों को आवर्त सारणी में स्थान देने में कठिनाई।
- अधिक परमाणु भार के तत्त्व को कम परमाणु भार के तत्त्व से पहले रखना।
उदाहरण – कोबाल्ट (परमाणु द्रव्यमान (भार) 58.9] को आवर्त सारणी में निकिल [परमाणु द्रव्यमान (भार) 58.7] से पहले रखा गया।
(iii) किसी आवर्त में परमाणु क्रमांक बढ़ने पर संयोजकता इलेक्ट्रॉन में बाएँ से दाएँ जाने पर इकाई की वृद्धि होती है क्योंकि शेलों की संख्या अपरिवर्तित रहती है।
जै-Na : 2, 8, 1; Mg: 2, 8, 2; Al: 2, 8, 3.
प्रश्न 6.
क्या कारण है कि समान गुणों वाले तत्त्व एक नियमित अंतराल के बाद उपस्थित होते हैं यदि तत्त्वों को उनके बढ़ते हुए परमाणु संख्या के क्रम में रखा गया हो?
अथवा
आप कैसे कह सकते हैं कि आधुनिक आवर्त सारणी का आधार तत्त्वों का इलेक्ट्रॉन विन्यास है?
उत्तर:
आवर्त सारणी के पहले आवर्त में 2, दूसरे और तीसरे आवर्त में 8-8 तथा चौथे और पाँचवें आवर्त में 18-18 तत्त्वों की उपस्थिति परमाणु की प्रथम, द्वितीय, तृतीय कोश (ऊर्जा स्तरों) की इलेक्ट्रॉन क्षमता से सम्बन्धित है। इस प्रकार हम इस निष्कर्ष पर पहुँचते हैं, कि आवर्त वर्गीकरण का आधार परमाणु संख्या अर्थात् इलेक्ट्रॉन की संख्या तथा अंततः इलेक्ट्रॉन विन्यास है।
यदि हम प्रथम तीन आवर्त के तत्त्वों के इलेक्ट्रॉन विन्यास पर दृष्टिपात करें तो हम पाते हैं विन्यास कि तत्त्वों के बाह्यतम कोश में उपस्थित इलेक्ट्रॉन की संख्या एक नियमित अंतराल के बाद समान होती है अर्थात् दोहराई जाती है जैसे- लीथियम, सोडियम तथा पोटैशियम के इलेक्ट्रॉन विन्यास से विदित है Li का इलेक्ट्रॉन = 2, 1, Na का 2, 8, 1 तथा K का 2, 8, 8, 1.
जैसा कि हम जानते हैं कि तत्त्वों के गुण उनके बाह्यतम कोश में उपस्थित इलेक्ट्रॉन (संयोजकता इलेक्ट्रॉन) की संख्या पर निर्भर करते हैं। संयोजकता इलेक्ट्रॉनों की संख्या समान होने पर उनके गुण भी समान होते हैं। यही कारण है कि नियमित अंतराल के बाद समान गुणों वाले तत्त्वों की पुनरावृत्ति होती है।
प्रश्न 7.
Na (परमाणु क्रमांक 11) और Al (परमाणु क्रमांक l3) आवर्त सारणी में एक तत्त्व की दूरी पर हैं। इनकी संयोजकता क्रमश: 1 तथा 3 है। C1 (परमाणु क्रमांक 17) और K (परमाणु क्रमांक 19) भी आवर्त सारणी में एक तत्त्व की दूरी पर हैं। किन्तु फिर भी दोनों की संयोजकता एक है। दोनों में अन्तर बताइए। प्रकार हैं-
उत्तर:
Na11 और Al13 के इलेक्ट्रॉन विन्यास निम्न
Na11 = 2, 8, 1 Al13 = 2, 8, 3.
Na11 के इलेक्ट्रॉन विन्यास में केवल 1 इलेक्ट्रॉन ही बाह्य कक्षा में है। अतः इसकी संयोजकता 1 है। Al के पास 3 संयोजी इलेक्ट्रॉन हैं अतः इसकी संयोजकता 3 है।
अब, CI और K के इलेक्ट्रॉन विन्यास क्रमश: हैं-
Cl17 = 2, 8, 7 और K19 = 2, 8, 8, 1
Cl के पास 7 संयोजी इलेक्ट्रॉन होने के कारण इसे अपनी बाह्य कक्षा में एक इलेक्ट्रॉन ग्रहण करने की आवश्यकता होती है। अतः इसकी संयोजकता 1 है। जबकि K एक इलेक्ट्रॉन त्यागकर पूर्ण इलेक्ट्रॉन विन्यास प्राप्त कर लेता है। अतः इसकी संयोजकता भी 1 है।
प्रश्न 5.
आधुनिक आवर्त नियम क्या है? आधुनिक आवर्त सारणी में तत्त्वों का वर्गीकरण समझाइए।
उत्तर:
मेण्डलीफ द्वारा प्रतिपादित आवर्त नियम में संशोधन करके आधुनिक आवर्त नियम निम्नवत् प्रस्तुत किया गया –
“तत्त्वों के भौतिक एवं रासायनिक गुण उनके परमाणु क्रमांकों के आवर्ती फलन होते हैं।” आधुनिक आवर्त सारणी में तत्त्वों का वर्गीकरण (Classification of Elements in Modern Periodic Table) – आधुनिक आवर्त सारणी का आधार परमाणुओं का इलेक्ट्रॉनिक विन्यास है। इसके अनुसार ” तत्त्वों के भौतिक तथा रासायनिक गुण उनके इलेक्ट्रॉनिक विन्यास के आवर्ती फलन होते हैं।”
आवर्त सारणी में उपस्थित सभी तत्त्वों को उनके इलेक्ट्रॉनिक विन्यास के आधार पर निम्नलिखित चार प्रकार के तत्त्वों में विभक्त किया जा सकता है-
1. अक्रिय तत्त्व (Inert Elements) – इस वर्ग ऐसे तत्त्व रखे गये हैं जिनके सभी कोश पूर्ण होते हैं, उदाहरणत: शून्य समूह के तत्त्व- हीलियम, निऑन, आर्गन इनके बाह्यतम कोश (Outermost shell) का इलेक्ट्रॉनिक विन्यास ns².np6 होता है। (हीलियम को इत्यादि। छोड़कर 292)
2. सामान्य तत्त्व (Normal Elements) – ये ऐसे तत्त्व हैं जिनके परमाणुओं के बाहरी कोश ही अपूर्ण होते हैं तथा बाकी सब पूर्ण होते हैं। ऐसे तत्त्वों के बाहरी कोश का सामान्य सूत्र ns1 से ns², np5 तक होता है। इस वर्ग में धातु, अधातु, उपधातु सभी आते हैं और यह सभी क्रियाशील तत्त्व होते हैं इनको दो भागों में बाँटा जा सकता है-
(क) 8 ब्लॉक के तत्त्व (Elements of s block) – s ब्लॉक के तत्त्वों के रासायनिक गुणधर्म उनके परमाणुओं के बाहरी कक्ष के उपकोश पर निर्भर करते हैं। इनमें I-A तथा II-A वर्ग आते हैं। ये सभी क्रियाशील धातु होते हैं।
(ख) p-ब्लॉक के तत्त्व (Elements of p- block) – p-ब्लॉक के तत्त्वों के रासायनिक गुणधर्म उनके परमाणुओं निर्भर के बाहरी कक्ष के p उपकोश के इलेक्ट्रॉनों पर करते हैं। इसमें IIIA, IVA, VA, VIA, VIIA के तत्त्व आते हैं और इनके बाहरी कक्ष के p उपकोश में 1 से 5 तक इलेक्ट्रॉन हो सकते हैं। मुख्य रूप से इनमें अधातु आते हैं। जैसे- फ्लोरीन, क्लोरीन, ऑक्सीजन इत्यादि।
3. संक्रमण तत्त्व (Transition Elements) – इस वर्ग में ऐसे तत्त्व उपस्थित होते हैं जिनके दो बाहरी कोश अपूर्ण होते हैं और उनका सामान्य सूत्र (n-1)dxns² होता है जबकि x = 1, 2 …………. 10 तक। इनके बाहरी कक्ष से लगी हुई d उपकोश अपूर्ण होती है इसलिए इन्हें d – ब्लॉक के तत्त्व कहते हैं। इन तत्त्वों की चार श्रेणियाँ होती हैं जिनमें क्रमश: 3d (Sc – Zn), 4d (Y – Cd), 5d (LaHg) तथा 6d श्रेणी (अपूर्ण) है।
संक्रमण तत्त्व निम्नलिखित गुणों को प्रदर्शित करते हैं-
- ये रंगीन आयन बनाते हैं, Fe2+ (हरा), Fe3+ (नारंगी)।
- ये अनुचुम्बकीय (paramagnetic) होते हैं।
- ये उत्प्रेरक का कार्य करते हैं।
- ये परिवर्ती संयोजकता दिखाते हैं
- ये संकीर्ण आयन (Complex-ion) बनाते हैं।
4. आन्तरिक संक्रमण तत्त्व (Inner Transition Elements)-इस वर्ग में ऐसे तत्त्व रखे गये हैं जिनके परमाणुओं की अंतिम तीन कक्ष अपूर्ण होती हैं। यह तत्त्व f उपकोश को भरने के कारण बनते हैं। अत: इन्हें f-ब्लॉक के तत्त्व कहते हैं। इनका सामान्य सूत्र (n – 2 )fx, (n – 1)s²p6d1.ns² होता है जबकि x = 1, 2 ….. 14 तक 14f लैन्थेनाइड श्रेणी (Ce – 58 से Lu – 71 तक) तथा 5f एक्टिनाइड श्रेणी (Ac – 89 से Lw 103 तक), प्रत्येक में 14 तत्त्व होते हैं जो f-कक्षक में क्रमश: 1 से 14 इलेक्ट्रॉनों की आपूर्ति से बनते हैं। इन तत्त्वों के बाहरी दो कोशों का विन्यास समान होने के कारण इनके गुणों में बहुत समानता होती है।
5. प्रारूपिक तत्त्व (Typical Elements) – आवर्त सारणी के तृतीय आवर्त के (Na से C1 तक) तत्त्वों को प्रारूपिक तत्त्व कहते हैं क्योंकि ये तत्त्व अपने वर्गों तथा A – उपवर्गों के तत्त्वों की संयोजकता तथा अन्य रासायनिक लक्षणों का प्रतिनिधित्व करते हैं।
बहुविकल्पीय प्रश्न-
निर्देश: प्रत्येक प्रश्न में दिये गये वैकल्पिक उत्तरों में से सही विकल्प चुनिए-
1. प्रारूपिक तत्त्व है-
(a) Na
(b) K
(c) Se
(d) He
उत्तर:
(a) Na
2. किसी आवर्त में बायें से दायें बढ़ने पर तत्त्वों की-
(a) धन विद्युती प्रकृति बढ़ती है
(b) धात्विकता बढ़ती जाती है।
(c) आयनिक त्रिज्या बढ़ती जाती है।
(d) तत्त्वों के ऑक्साइडों की क्षारीय प्रकृति घटती जाती है
उत्तर:
(d) तत्त्वों के ऑक्साइडों की क्षारीय प्रकृति घटती जाती है
3. किसी समूह में ऊपर से नीचे की ओर बढ़ने पर –
(a) आयनिक त्रिज्या घटती जाती है।
(b) सुचालकता घटती जाती है
(c) घनत्व घटता जाता है
(d) धात्विकता बढ़ती जाती है।
उत्तर:
(d) धात्विकता बढ़ती जाती है।
4. मेण्डलीफ आवर्त सारणी में एक दोष यह है कि-
(a) हैलोजन परिवार के सदस्यों को एक समूह में रखा गया है
(b) इसके आधार पर अज्ञात तत्त्वों के गुणों के बारे में कोई भविष्यवाणी नहीं की जा सकती है
(c) सर्वथा भिन्न गण वाले तत्त्व एक ही समूह में स्थान पा गये हैं
(d) सारणी को बनाने में कोई आधारभूत सिद्धान्त नहीं रखा गया है
उत्तर:
(c) सर्वथा भिन्न गण वाले तत्त्व एक ही समूह में स्थान पा गये हैं
5. Li विकर्ण सम्बन्ध प्रकट करता है-
(a) Na के साथ
(b) K के साथ
(c) Al के साथ
(d) Mg के साथ
उत्तर:
(d) Mg के साथ
6. परमाणु क्रमांक 17 वाले तत्त्व का आवर्त सारणी में स्थान है-
(a) VII आवर्त, VII वर्ग
(b) III आवर्त, VII वर्ग
(c) IV आवर्त, VII वर्ग
(d) II आवर्त, VI वर्ग
उत्तर:
(b) III आवर्त, VII वर्ग
7. आधुनिक आवर्त नियम प्रतिपादित करने वाले वैज्ञानिक हैं-
(a) प्राउट
(b) न्यूलैंड
(c) मेण्डलीफ
(d) मोज्ले
उत्तर:
(d) मोज्ले
8. आधुनिक आवर्ती वर्गीकरण का आधार है-
(a) परमाणु भार
(b) परमाणु क्रमांक
(c) संयोजकता
(d) रासायनिक क्रियाशीलता
उत्तर:
(b) परमाणु क्रमांक

9. आवर्त सारणी के किसी समूह में परमाणु क्रमांक की वृद्धि के साथ बढ़ता है-
(a) धन विद्युती लक्षण
(b) आयनन विभव
(c) विद्युत ऋणीयता
(d) अधात्विक लक्षण
उत्तर:
(a) धन विद्युती लक्षण
10. Be का विकर्ण सम्बन्ध है-
(a) Mg
(b) Al
(c) B
(d) Na
उत्तर:
(b) Al
11. द्वितीय आवर्त में तत्त्वों की संख्या होती है-
(a) 2
(b) 8
(c) 10
(d) 18
उत्तर:
(b) 8
12. ये तत्त्व परिवर्ती संयोजकता प्रकट करते हैं-
(a) नॉर्मल
(b) प्रारूपिक
(c) संक्रमण
(d) ये सभी
उत्तर:
(c) संक्रमण
13. क्षार धातुएँ हैं-
(a) Be, Mg, Ca
(b) Li, Na, K
(c) B, Al, Ga
(d) Cu, Ag, Au
उत्तर:
(b) Li, Na, K
14. किस तत्त्व की विद्युत-धनात्मकता सबसे अधिक है-
(a) F
(b) Mg
(c) Na
(d) K
उत्तर:
(d) K
15. सर्वाधिक हाइड्रोजन संयोजकता होती है समूह ……… के तत्त्वों की।
(a) I
(b) VII
(c) IV
(d) 0
उत्तर:
(c) IV
16. तत्त्व A, B, C, D तथा E के परमाणु क्रमांक क्रमश: 9, 11, 17, 12 तथा 13 हैं। तत्त्वों का कौन सा युग्म समान समूह से सम्बन्धित है?
(a) A तथा B
(b) B तथा D
(c) A तथा C
(d) D तथा E
उत्तर:
(c) A तथा C
17. कोई तत्त्व जो क्षारकीय ऑक्साइड बनाते हैं, उसका परमाणु संख्या है—
(a) 18
(b) 14
(c) 17
(d) 19
उत्तर:
(d) 19
18. निम्नलिखित में से कौन-सा तत्त्व अम्लीय ऑक्साइड बनता है?
(a) परमाणु क्रमांक 7 युक्त तत्त्व
(b) परमाणु क्रमांक 3 वाला तत्त्व
(c) परमाणु क्रमांक 12 वाला तत्त्व
(d) परमाणु क्रमांक 19 वाला
उत्तर:
(a) परमाणु क्रमांक 7 युक्त तत्त्व
19. परमाणु क्रमांक 14 वाला तत्त्व कठोर है तथा अम्लीय ऑक्साइड एवं एक सहसंयोजक हैलाइड बनाता है। यह तत्त्व निम्नलिखित में से किस वर्ग से सम्बन्धित है?
(a) धातु
(b) उपधातु
(c) अधातु
(d) बायीं ओर वाले तत्त्व
उत्तर:
(b) उपधातु
20. आवर्त सारणी में एक समूह में ऊपर से नीचे जाने पर निम्नलिखित में से क्या नहीं बढ़ता है?
(a) परमाणु की त्रिज्या
(b) धात्विक अभिलक्षण
(c) संयोजकता
(d) एक तत्त्व में कोशों की संख्या
उत्तर:
(c) संयोजकता
21. निम्नलिखित में से किस तत्त्व में अधिकतम संयोजी इलेक्ट्रॉन (Valence electron) हैं-
(a) Na
(b) Mg
(c) C
(d) P
उत्तर:
(d) P
22. सर्वाधिक ऑक्सीजन-संयोजकता होती है समूह के तत्त्वों की।
(a) I
(b) VII
(c) IV
(d) 0
उत्तर:
(b) VII
23. तत्त्वों के गुण निर्भर करते हैं, उनके परमाणुओं-
(a) में प्रोटॉनों की संख्या पर
(b) में न्यूट्रॉनों की संख्या पर
(c) के द्रव्यमान पर
(d) उपर्युक्त किसी पर नहीं
उत्तर:
(a) में प्रोटॉनों की संख्या पर
24. यूरेनियम है-
(a) क्षार धातु
(b) अधातु
(c) स्थायी तत्त्व
(d) अन्त: संक्रमण धातु
उत्तर:
(d) अन्त: संक्रमण धातु
25. परमाणु क्रमांक 18 का तत्त्व होगा-
(a) वर्ग ‘शून्य में
(b) वर्ग VIII में
(c) आवर्त सं. 4 में
(d) संक्रमण धातुओं में
उत्तर:
(a) वर्ग ‘शून्य में
26. एक तत्त्व M के ऑक्साइड का सूत्र MO है। इसके नाइट्रेट का सूत्र होगा-
(a) MNO3
(b) M(NO3)2
(c) M2NO3
(d) M2(NO2)2
उत्तर:
(b) M(NO3)2
27. उभयधर्मी ऑक्साइड है-
(a) Na2 O
(b) P2O5
(c) Al2O3
(d) MgO5
उत्तर:
(c) Al2O3

28. निम्न में ऊष्मीय ऑक्साइड है-
(a) Al2O3
(b) K2O
(c) MgO
(d) P2O5
उत्तर:
(d) P2O5
29. निम्नलिखित में क्षारीय धातु है-
(a) Na
(b) Be
(c) Al
(d) Zn
उत्तर:
(b) Be
30. एक तत्त्व N के कार्बोनेट का सूत्र NCO3 है। इसके क्लोराइड का सूत्र होगा-
(a) MCl2
(b) MCl3
(c) MCl
(d) M2Cl
उत्तर:
(a) MCl2
रिक्त स्थानों की पूर्ति कीजिए
- किसी कोश में इलेक्ट्रॉनों की अधिकतम संख्या ……………….. सकती है।
- एक ही ……………….. को सभी तत्त्वों के संयोजकता इलेक्ट्रॉनों की संख्या समान होती है।
- डॉबेराइनर ने तत्त्वों को ……………….. में वर्गीकृत किया जबकि ……………….. ने अष्टक का सिद्धान्त दिया।
- मेण्डलीफ ने तत्त्वों को उनके ……………….. को आरोही क्रम तथा रासायनिक गुणधर्मों के आधार पर व्यवस्थित किया।
- ………………. ने आवर्त सारणी में खाली स्थानों के आधार पर नए तत्त्वों की भविष्यवाणी की।
- तत्त्वों को परमाणु ………………. के आरोही क्रम में व्यवस्थित करने से होने वाली विसंगतियाँ, परमाणु के आरोही क्रम में व्यवस्थित करने से दूर हो गई तत्त्व के इस आधारभूत गुणधर्म अर्थात् परमाणु संख्या की खोज मोज्ले ने की।
उत्तर:
- 2n²
- समूह
- त्रिक, न्यूलैंड्स
- परमाणु द्रव्यमान
- मेण्डलीफ
- द्रव्यमान संख्या

![]()
![]()
![]()



![]()


![]()


































 है।
है।