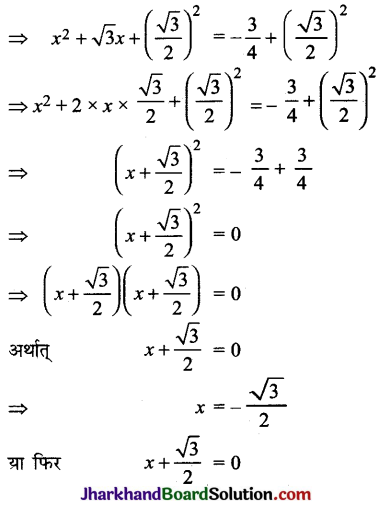Class 10

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.3

प्रश्न 1.
निम्नलिखित समान्तर श्रेढियों का योग ज्ञात कीजिए:
(i) 2, 7, 12, …, 10 पदों तक।
(ii) -37, -33, -29, …, 12 पदों तक।
(iii) 0.6, 1.7, 2.8, …. 100 पदों तक।
(iv) \(\frac{1}{15}, \frac{1}{12}, \frac{1}{10}, \ldots 11\) पदों तक।
हल:
(i) दी गई समान्तर श्रेढी = 2, 7, 12, ….. 10 पदों तक
प्रथम पद a = 2 तथा सार्वअन्तर d = 7 – 2 = 5
पदों की संख्या n = 10
n पदों का योग S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₁₀ = \(\frac{10}{5}\)[2 × 2 + (10 – 1) × 5]
= 5[4 + 9 × 5]
= 5[4 + 45] = 5 × 49 = 245
अतः 10 पदों तक योग = 245

(ii) दी गई समान्तर श्रेढी = -37, -33, -29, …, 12 पदों तक
प्रथम पद a = -37
तथा सार्वअन्तर d = – 33 – (-37) = 4
और पदों की संख्या n = 12
∵ n पदों तक योग S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
∴ S₁₂ = \(\frac{12}{2}\)[2 × (-37) + (12 – 1) × 4)
= 6[- 74 + 11 × 4]
= 6[-74 + 44]
= 6 × (-30) = -180
अतः 12 पदों तक योग = -180

(iii) दी गई समान्तर श्रेढी = 0.6, 1.7, 2.8, …. 100
पदों तक
प्रथम पद a = 0.6
सार्वअन्तर d = 1.7 – 0.6 = 1.1
और पदों की संख्या n = 100
n पदों का योगफल S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
∴ S₁₀₀ = \(\frac{100}{2}\)[2 × 0.6 + (100 – 1) × 1.1]
= 50[1.2 + 99 × 1.1]
= 50[1.2 + 108.9]
= 50 × 110.1 = 5505
अतः 100 पदों तक योग = 5505

(iv) दी गई समान्तर श्रेढी = \(\frac{1}{15}, \frac{1}{12}, \frac{1}{10}, \ldots, 11\) पदों तक

प्रश्न 2.
नीचे दिए हुए योगफलों को ज्ञात कीजिए :
(i) 7 + 10\(\frac{1}{2}\) + 14 +…+ 84.
(ii) 34 + 32 + 30 +…+ 10
(iii) -5 + (8) + (11) +…+ (-230)
हल:
(1) दिया गया है,
7 + 10\(\frac{1}{2}\) + 14 +…+ 84.
स्पष्ट है कि यह एक समान्तर श्रेढी है।
यहाँ प्रथम पद a = 7
सार्वअन्तर d = 10\(\frac{1}{2}\) – 7
= \(\frac{21}{2}-7=\frac{21-14}{2}=\frac{7}{2}\)
दिया है, nवाँ पद a_n = 84
a + (n – 1)d = 84

∴ अनुक्रम में 23 पद हैं।
सूत्र : S_n = \(\frac{n}{2}\)(a + l) से
∴ 23 पदों का योगफल
⇒ S₂₃ = \(\frac{23}{2}\)(7 + 84)
= \(\frac{23}{2}\) × 91 = \(\frac{2093}{2}\)
= 1046\(\frac{1}{2}\)
अतः 7 + 10\(\frac{1}{2}\) + 14 +…+ 84 = 1046\(\frac{1}{2}\)

(ii) दिया गया है: 34 + 32 + 30 + … + 10
स्पष्ट है कि यह एक समान्तर श्रेढी है।
यहाँ प्रथम पद = 34
और सार्वअन्तर d = 32 – 34 = -2
यदि अनुक्रम में पदों की संख्या n हो, तो
nवाँ पद a_n = 10
⇒ a + (n – 1)d = 10
⇒ 34 + (n – 1) × (-2) = 10
⇒ (n – 1) × (-2) = 10 – 34 = -24
⇒ (n – 1) = \(\frac{-24}{-2}\) = 12
⇒ n = 13
∴ अनुक्रम में कुल 13 पद हैं।
सूत्र : S_n = \(\frac{n}{2}\)(a + l)
13 पदों का योग S₁₃ = \(\frac{13}{2}\) = (34 + 10)
= \(\frac{13}{2}\) × 44 = 286
अत: 34 + 32 + 30 + … + 10 = 286

(iii) दिया गया है:
– 5 + (-8) + (-11) + … + (-230) स्पष्ट है कि यह एक समान्तर श्रेढी है।
प्रथम पद a = -5
तथा सार्वअन्तर d = (-8) – (-5)
= – 8 + 5 = -3
यदि अनुक्रम में पदों की संख्या n हो, तो
अनुक्रम का nवाँ पद a_n = -230
⇒ a + (n – 1)d = -230
⇒ -5 + (n – 1) × – 3 = -230
⇒ 5 + (n – 1)3 = 230
⇒ (n – 1)3 = 230 – 5 = 225
(n – 1) = \(\frac{225}{3}\) =75
∴ n = 75 + 1 = 76
तब n पदों तक योगफल
S_n = \(\frac{n}{2}\)(a + l)
∴ 76 पदों तक योगफल
S₇₆ = \(\frac{76}{2}\)[-5 + (-230)]
= \(\frac{76}{2}\) × (-235)
= 38 × (-235) = -8930
अत: -5 + (-8) + (-11) + … + (-230)
= -8930

प्रश्न 3.
एक A. P. में,
(i) a = 5, d = 3 और a_n = 50 दिया है। n और S_n ज्ञात कीजिए।
(ii) a = 7 और a₁₃ = 35 दिया है। d और S₁₃ ज्ञात कीजिए।
(iii) a₁₂ = 37 और d = 3 दिया है। a और S₁₂ कीजिए।
(iv) a₃ = 15 और S₁₀ = 125 दिया है। d और a₁₀ ज्ञात कीजिए।
(v) d = 5 और S₉ = 75 दिया है। a और a₉ ज्ञात कीजिए।
(vi) a = 2, d = 8 और S_n = 90 दिया है। n और a_n ज्ञात कीजिए।
(vii) a = 8, a_n = 62 और S_n = 210 दिया है। n और d ज्ञात कीजिए।
(viii) a_n = 4, d = 2 और S_n = -14 दिया है। n और a ज्ञात कीजिए।
(ix) a = 3, n = 8 और S_n = 192 दिया है। d ज्ञात कीजिए।
(x) l = 28, S_n = 144 और कुल 9 पद हैं। a ज्ञात कीजिए।
हल:
(i) दिया गया है,
a = 5, d = 3 और अन्तिम पद (a_n) = 50
∵ अनुक्रम A. P. है और a_n = 50
⇒ a + (n – 1)d = 50
⇒ 5 + (n – 1)3 = 50
⇒ 5 + 3n – 3 = 50 ⇒ 3n = 50 + 3 – 5
⇒ 3n = 48
∴ n = \(\frac{48}{3}\) = 16
अब S_n = \(\frac{n}{2}\)(a + l)
= \(\frac{16}{2}\)(5 + 50) = 8 × 55 = 440
अत: n = 16 तथा S_n = 440

(ii) दिया है: a = 7, a₁₃ = 35
a + (n – 1)d = 35
⇒ 7 + (13 – 1)d = 35
⇒ 12d = 35 – 7 = 28
⇒ d = \(\frac{28}{12}=\frac{7}{3}\)
सूत्र : S_n = \(\frac{n}{2}\)[a + l] से
अब S₁₃ = \(\frac{13}{2}\)[7 + 35]
⇒ S₁₃ = \(\frac{13}{2}\) × 42 = 13 × 21 = 273
अतः d = \(\frac{7}{3}\) तथा S₁₃ = 273

(iii) दिया है: a₁₂ = 37, d = 3
∵ a₁₂ = 37
a + (n – 1)d = 37
⇒ a + (12 – 1)3 = 37
⇒ a = 37 – 33 = 4
अब S₁₂ = \(\frac{12}{2}\)[4 + 37] [∵ S_n = \(\frac{n}{2}\)[a + l]से]
S₁₂ = 6 × 41 = 246
अतः a = 4 तथा S₁₂ = 246

(iv) दिया है: a₃ = 15, S₁₀ = 125
∵ a₃ = 15
⇒ a + (3 – 1)d = 15
⇒ a + 2d = 15 ….(1)
∵ दिया है S₁₀ = 125
\(\frac{10}{2}\)[2a + (10 – 1)d] = 125
⇒ 5[2a + 9d] = 125
⇒ 2a + 9d = \(\frac{125}{5}\)
⇒ 2a + 9d = 25 …(2)
समीकरण (1) से, a = 15 – 2d ….(3)
a का मान समीकरण (2) में प्रतिस्थापित करने पर,
2(15 – 2d) + 9d = 25
⇒ 30 – 4d + 9d = 25
⇒ 5d = 25 – 30
d = \(\frac{-5}{5}\) = -1
d का मान समीकरण (3) में प्रतिस्थापित करने पर,
a = 15 – 2(-1)
⇒ a = 15 + 2 = 17
अब a₁₀ = 17 + (10 – 1) (-1)
[∵ a_n = a + (n – 1)d]
= 17 – 9 = 8
अत: d = -1 और a₁₀ = 8

(v) दिया है: d = 5 और S₉ = 75
∵ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
∵ S₉ = \(\frac{9}{2}\)[2a + (9 – 1)5]
⇒ 75 = \(\frac{9}{2}\)[2a + 8 × 5] [∵ S₉ = 75]
⇒ \(\frac{75 \times 2}{9}\) = 2a + 40

(vi) दिया है: a = 2, d = 8 और S_n = 90
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
90 = \(\frac{n}{2}\)[2 × 2 + (n – 1)8]
90 = \(\frac{n}{2}\)[4 + 8n – 8]
90 = \(\frac{n}{2}\)[8n – 4]
90 = \(\frac{n}{2}\) × 4(2n – 1)
90 = 2n(2n – 1)
\(\frac{90}{2}\) = n(2n – 1)
45 = 2n² – n
2n² – n – 45 = 0
2n² – (10 – 9) – 45 = 0
2n² – 10n + 9n – 45 = 0
2n(n – 5) + 9(n – 5) = 0
(2n + 9) (n – 5) = 0
n = 5 या –\(\frac{9}{2}\)
∵ n का मान सदैव धन पूर्णांक होता है।
∴ n = 5
तब a₅ = a + (5 – 1)d
= 2 + 4 × 8
= 2 + 32 = 34
अतः n = 5 तथा a_n = 34

(vii) दिया है: a = 8, a_n = 62
और S_n = 210
∵ S_n = \(\frac{n}{2}\)(a + a_n)
⇒ 210 = \(\frac{n}{2}\)(8 + 62)
⇒ 210 = \(\frac{n}{2}\) × 70
⇒ \(\frac{210 \times 2}{70}\) = 6
∵ a_n = 62
⇒ a + (n – 1)d = 62
⇒ 8 + (6 – 1)d = 62
⇒ 8 + 5d = 62
⇒ 5d = 62 – 8 = 54
d = \(\frac{54}{2}\)
अत: n = 6 तथा d = \(\frac{54}{2}\)

(viii) दिया है: a_n = -4, d = 2 और S_n = -14
∵ a_n = 4
a + (n – 1)d = 4
a + (n – 1)2 = 4
a + 2n – 2 = 4
a + 2n = 6 …..(1)
∵ S_n = -14
\(\frac{n}{2}\)[2a + (n – 1)2] = -14
n[a + n – 1] = – 14 ….(2)
समीकरण (1) से a = 6 – 2n समीकरण (2) में a के
स्थान पर (6 – 2n) रखने पर,
n[6 – 2n + n – 1] = -14
∴ n[5 – n] = – 14
⇒ 5n – n² = -14
⇒ n² – 5n + 2n – 14 = 0
⇒ n(n – 7) + 2(n – 7) = 0
⇒ (n – 7) (n + 2) = 0
⇒ n = 7 या n = – 2
n का मान सदैव धनपूर्णांक होता है। इसलिए n = 7
तब a = 6 – 2n
= 6 – (2 × 7)
= 6 – 14 = -8
अतः a = -8 तथा n = 7

(ix) a = 3, n = 8 और S_n = 192
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
परन्तु S_n = 192
⇒ \(\frac{n}{2}\)[2a + (n – 1)d] = 192
⇒ \(\frac{8}{2}\)[2 × 3 + (8 – 1)d] = 192
⇒ 4[6 + 7d] = 192
⇒ 24 + 28d = 192
⇒ 28d = 192 – 24 = 168
∴ d = \(\frac{168}{28}\) = 6
अतः d = 6

(x) दिया है: l = 28, S_n = 144 और कुल पदं n = 9
हम जानते हैं कि S_n = \(\frac{n}{2}\)[a + l]
144 = \(\frac{9}{2}\)[a + 28]
288 = 9[a + 28]
288 = 9a + 252
9a = 288 – 252
9a = 36
∴ a = 4
अतः a = 4

प्रश्न 4.
636 योग प्राप्त करने के लिए A. P. : 9, 17, 25, … के कितने पद लेने चाहिए ?
हल:
दी गई A. P.: 9, 17, 25, …
प्रथम पद a = 9 सार्वअन्तर d = 17 – 9 = 8
माना पदों की संख्या n है।
S_n = 636
⇒ \(\frac{n}{2}\)[2a + (n – 1)d] = 636
⇒ \(\frac{n}{2}\)[2 × 9 + (n – 1)8] = 636
⇒ \(\frac{n}{2}\)[18 + 8n – 8] = 636
⇒ \(\frac{n}{2}\)[8n + 10] = 636
⇒ n(4n + 5) = 636
⇒ 4n² + 5n = 636
⇒ 4n² + 5n – 636 = 0
⇒ 4n² + 53n – 48n – 636 = 0
⇒ n(4n + 53 ) -12(4n + 53 ) = 0
⇒ (4n + 53 ) (n – 12) = 0
⇒ n – 12 = 0 या 4n + 53 = 0
⇒ n = 12 या –\(\frac{53}{4}\)
∵ n ऋणात्मक नहीं हो सकता।
अतः n = –\(\frac{53}{4}\) को छोड़ देते हैं।
∴ n = 12
अतः दी गई A.P के 12 पदों का योग 636 है।

प्रश्न 5.
किसी A. P का प्रथम पद 5, अन्तिम पद 45 और योग 400 है। पदों की संख्या और सार्वअन्तर ज्ञात कीजिए।
हल:
दिया है, प्रथम पद a = 5,
अन्तिम पद l = a_n = 45
और S_n = 400
∵ a_n = 45
a + (n – 1)d = 45
⇒ 5 + (n – 1)d = 45
⇒ (n – 1)d = 45 – 5
⇒ (n – 1)d = 40 ….(1)
और S_n = 400
\(\frac{n}{2}\)[a + l] = 400
⇒ \(\frac{n}{2}\)[5 + 45] = 400
⇒ 25n = 400
∴ n = \(\frac{400}{25}\) = 16
n का मान समीकरण (1) में प्रतिस्थापित करने पर,
(16 – 1)d = 40
⇒ 15d = 40
∴ d = \(\frac{40}{15}=\frac{8}{3}\)
अत: n = 16 और d = \(\frac{8}{3}\)

प्रश्न 6.
किसी A. P. के प्रथम और अन्तिम पद क्रमशः 17 और 350 हैं। यदि सार्वअन्तर 9 है, तो इसमें कितने पद हैं और इनका योग क्या है ?
हल:
दिया है,
प्रथम पद a = 17
अन्तिम पद l = a_n = 350
और सार्वअन्तर d = 9
∵ a_n = 350
a + (n – 1)d = 350
⇒ 17 + (n – 1)9 = 350
⇒ 9(n – 1) = 350 – 17 = 333
⇒ n – 1 = \(\frac{333}{9}\) = 37
n = 37 + 1 = 38
अब S_n = \(\frac{n}{2}\)(a + l)
= \(\frac{38}{2}\)(17 + 350)
= 19 × 367 = 6973
अतः n = 38 और पदों का योग (S_n) = 6973

प्रश्न 7.
उस A. P. के प्रथम 22 पदों का योग ज्ञात कीजिए, जिसमें d = 7 है और 22वाँ पद 149 है।
हल:
d = 7, n = 22
∵ 22वाँ पद a₂₂ = 149
⇒ a + (22 – 1)d = 149
⇒ a + 21 × 7 = 149
⇒ a + 147 = 149
∴ a = 149 – 147 = 2
तब प्रथम 22 पदों का योग
S₂₂ = \(\frac{n}{2}\)(a + l) = \(\frac{22}{2}\)(2 + 149)
= 11 × 151 = 1661
अतः दी गई A.P के प्रथम 22 पदों का योग = 1661

प्रश्न 8.
उस A. P. के प्रथम 51 पदों का योग ज्ञात कीजिए, जिसके दूसरे और तीसरे पद क्रमशः 14 और 18 हैं।
हल:
A.P का दूसरा पद a₂ = 14
तथा तीसरा पद a₃ = 18
∴ सार्वअन्तर d = a₃ – a₂ = 18 – 14 = 4
∵ दूसरा पद = 14
∴ a + d = 14
⇒ a + 4 = 14
⇒ a = 14 – 4
⇒ a = 10
∵ a = 10, d = 4
तब n पदों का योग S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₅₁ = \(\frac{51}{2}\) [2 × 10 + (51 – 1)4]
= \(\frac{51}{2}\)[20 + 50 × 4]
= \(\frac{51}{2}\)[20 +200]
= \(\frac{51}{2}\) × 220 = 51 × 110 = 5610
अतः दी गई A.P के प्रथम 51 पदों का योग = 5610

प्रश्न 9.
यदि किसी A.P. के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है, तो इसके प्रथम n पदों का योग ज्ञात कीजिए।
हल:
माना A.P का पहला पद a तथा सार्वअन्तर d है।.
∵ प्रथम 7 पदों का योग
S₇ = 49
⇒ \(\frac{7}{2}\)[2a + (7 – 1)d] = 49
[∵ सूत्र S_n = \(\frac{n}{2}\)[2a + (n – 1)d] से]
⇒ \(\frac{7}{2}\)[2a + 6d] = 49
⇒ 7(a + 3d ) = 49
⇒ a + 3d = \(\frac{49}{7}\)
⇒ a + 3d = 7
⇒ a = 7 – 3d …(1)
दूसरी शर्त के अनुसार,
S₁₇ = 289
⇒ \(\frac{n}{2}\)[2a + (n – 1)d] = 289
⇒ \(\frac{17}{2}\)[2a + (17 – 1)d] = 289
⇒ \(\frac{1}{2}\)[2a + 16d] = \(\frac{289}{17}\)
⇒ a + 8d = 17
a का मान समीकरण (1) से प्रतिस्थापित करने पर,
7 – 3d + 8d = 17
5d = 17 – 7 = 10
d = \(\frac{10}{5}\) = 2
d का मान समीकरण (1) में प्रतिस्थापित करने पर,
a = 7 – 3 × 2
= 7 – 6 = 1
अब S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{n}{2}\)[2 × 1 + (n – 1) × 2]
= \(\frac{n}{2}\)[2 + 2n – 2]
= \(\frac{n}{2}\) × [2n] = n × n = n²
अतः दी गई A.P. के प्रथम n पदों का योग n² है।

प्रश्न 10.
दर्शाइए किa₁, a₂, …, a_n, … से एक A. P. बनती है, यदि a_n नीचे दिए अनुसार परिभाषित है :
(i) a_n = 3 + 4n,
(ii) a_n = 9 – 5n
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
हल:
(i) दिया है, a_n = 3 + 4n …(1)
n के विभिन्न मान समीकरण (1) में प्रतिस्थापित करने पर,
a₁ = 3 + 4 (1) = 7
a₂ = 3 + 4(2) = 11
a₃ = 3 + 4(3) = 15, …
सार्वअन्तर (d) = a₂ – a₁ = 11 – 7 = 4
a₃ – a₂ = 15 – 11 = 4
∵ a₂ – a₁ = a₃ – a₂ = 4
अतः अनुक्रम 7, 11, 15, …. है।
और दिया गया अनुक्रम A.P. है।
यहाँ a = 7, d = 4 और n = 15
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
∴ S₁₅ = \(\frac{15}{2}\)[2(7) + (15 – 1)4]
= \(\frac{15}{2}\)[14 + 56]
= \(\frac{15}{2}\) × 70 = 15 × 35 = 525
∴ S₁₅ = 525

(ii) दिया है कि a_n = 9 – 5n …. (1)
n के विभिन्न मान समीकरण (1) में प्रतिस्थापित करने पर,
a₁ = 9 – 5(1) = 4
a₂ = 9 – 5(2) = -1
a₃ = 9 – 5(3) = -6
सार्वअन्तर (d) = a₂ – a₁ = – 1 – 4 = -5
और a₃ – a₂ = – 6 + 1 = -5
∵ a₂ – a₁ = a₃ – a₂ = -5
अतः अनुक्रम 4, -1, -6 … है।
और दिया गया अनुक्रम A.P. है।
यहाँ a = 4, d = – 5 और n = 15
तब प्रथम 15 पदों का योगफल ज्ञात करना है।
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₅ = \(\frac{15}{2}\) [2 × 4 + (15 – 1) × (-5)]
= \(\frac{15}{2}\)[8 + 14 × (-5)]
= \(\frac{15}{2}\)[8 – 70]
\(\frac{15}{2}\) × (-62) = 15 × (-31) = -465
अत: S₁₅ = -465

प्रश्न 11.
यदि किसी A.P के प्रथम n पदों का योग 4n – n² है, तो इसका प्रथम पद (अर्थात् S₁) क्या है ? प्रथम दो पदों का योग क्या है? दूसरा पद क्या है ? इसी प्रकार, तीसरे 10वें और nवें पद ज्ञात कीजिए।
हल:
∵ A.P के प्रथम n पदों का योगफल
S_n = 4n – n²
n = 1 रखने पर,
S₁ = 4 × 1 – 1²= 3
∴ प्रथम पद a₁ = S₁ = 3
n = 2 रखने पर,
S₂ = 4 × 2 – 2² = 8 – 4 = 4
द्वितीय पद a₂ = S₂ – S₁ = 4 – 3 = 1
n = 3 रखने पर,
S₃ = 4 × 3 – 3² = 12 – 9 = 3
∴ तीसरा पद a₃ = S₃ – S₂
[∵ a_n = S_n – S_n-1]
= 3 – 4 = -1
n = 9 रखने पर,
S₉ = 4 × 9 – 9² = 36 – 81 = -45
∴ 10 रखने पर
S₁₀ = 4 × 10 – 10²
= 40 – 100 = -60
n = 10वीं पद a₁₀ = S₁₀ – S₉
= -60 – (-45)
= -60 + 45 = -15
∵ S_n = 4n – n²
और S_n-1 = 4 (n – 1) – (n – 1)²
= (n – 1) {4 – n + 1}
= (n – 1) (5 – n)
= 5n – n² – 5 + n
= 6n – n² – 5
अब a_n = S_n – S_n-1
= (4n – n²) – (6 – n² – 5)
= 4n – n² – 6n + n² + 5
= 5 – 2n
अतः S₁ =3
प्रथम दो पदों का योग S₂ = 4
दूसरा पद a₂ = 1
तीसरा पद a₃ = -1
10वीं पद a₁₀ = -15
तथा n वाँ पद a_n = 5 – 2n

प्रश्न 12.
ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य हैं।
हल:
6 से विभाज्य धन पूर्णांकों की सूची :
6, 12, 18, 24, 30, …. 40 पदों तक
प्रथम पद a = 6 तथा सार्वअन्तर d = 12 – 6 = 6, n = 40
∵ प्रथम n पदों का योगफल S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
∴ प्रथम 40 पदों का योगफल
S₄₀ = \(\frac{40}{2}\)[2 × 6 + (40 – 1)6]
= 20[12 + 39 × 6]
= 20[12 + 234]
= 20 × 246 = 4920
अत: 6 से विभाज्य प्रथम 40 धन पूर्णांकों का योग = 4920

प्रश्न 13.
8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
हल:
8 के प्रथम 15 गुणजों की सूची :
8, 16, 24, 32… 15 पदों तक
∴ S = 8 + 16 + 24 + 32 + … + 120
= 8[1 + 2 + 3 + 4 +…+ 15]
= 8 [\(\frac{15}{2}\)(1 + 15)] [सूत्र: S_n = [\(\frac{n}{2}\)(a + l)से]
= 8[\(\frac{15}{2}\) × 16]
= 8 × 120 = 960
अतः 8 के प्रथम 15 गुणजों का योगफल = 960

प्रश्न 14.
0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
हल:
0 और 50 के बीच की विषम संख्याओं की सूची:
1, 3, 5, 7, …., 49
प्रथम पद a = 1, सार्वअन्तर d = 3 – 1 = 2, a_n = 49
∵ a_n = 49
∴ a(n – 1)d = 49
⇒ 1 + (n – 1)2 = 49
⇒ (n – 1)2 = 48
⇒ (n – 1) = 24
∴ n = 25
A.P. 1, 3, 5, 7, …. का 25 पदों तक योगफल
∵ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₂₅ = \(\frac{25}{2}\)[2 × 1 + (25 – 1) × 2]
= \(\frac{25}{2}\)[2 + 24 × 2]
= \(\frac{25}{2}\) [2 + 48]
= \(\frac{25}{2}\) × 50 = 625
अतः 0 और 50 के बीच विषम संख्याओं का योगफल = 625

प्रश्न 15.
निर्माण कार्य से सम्बन्धित किसी ठेके में, एक निश्चित तिथि के बाद कार्य को विलम्ब से पूरा करने के लिए जुर्माना लगाने का प्रावधान इस प्रकार है: पहले दिन के लिए ₹ 200, दूसरे दिन के लिए ₹ 250, तीसरे दिन के लिए ₹ 300, इत्यादि, अर्थात् प्रत्येक उत्तरोत्तर दिन का जुर्माना अपने से ठीक पहले दिन के जुर्माने से ₹ 50 अधिक है। एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करनी पड़ेगी, यदि वह इस कार्य में 30 दिन का विलम्ब कर देता है ?
हल:
दिया है, पहले, दूसरे और तीसरे दिन के विलम्ब के लिए जुर्माना है- ₹ 200, ₹ 250, ₹ 300
अब, जुर्माना अगले दिन ₹ 50 के अन्तर से बढ़ता जाता है :
∴ ₹ 200 ₹ 250, ₹ 300, ₹ 350… यह एक समान्तर श्रेढी है।
प्रथम पद a = 200; d = 50 और n = 30
30 दिन के पश्चात् दी जाने वाली जुमनि की राशि = S30
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₃₀ = \(\frac{30}{2}\)[2(200) + (30 – 1)50]
= 15[400 + 1450] = 15(1850) = 27750
अतः यदि ठेकेदार कार्य में 30 दिन विलम्ब करता है, तो उसे जुर्माने के रूप में ₹ 27,750 देने होंगे।

प्रश्न 16.
किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन के लिए 7 नकद पुरस्कार देने के लिए ₹ 700 की राशि रखी गई है। यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से ₹ 20 कम है, तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए।
हल:
माना पहला पुरस्कार ₹ a है।
∴ दूसरा पुरस्कार a₂ = ₹ (a – 20)
तीसरा पुरस्कार a₃ = ₹ a – 20 – 20
= ₹ (a – 40)
∴ समान्तर श्रेढी a, (a – 20) (a – 40), … है।
यहाँ प्रथम पद = a, सार्वअन्तर d = (a – 20) – a = – 20
पदों की संख्या n = 7 तथा 7 पदों का योगफल S₇ = 700
तब, S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₇ = \(\frac{7}{2}\)[2a + (7 – 1) (-20)]
700 = \(\frac{7}{2}\)[2a + 6(-20)]
700 = \(\frac{7}{2}\)[2a – 120]
700 = \(\frac{7}{2}\)2(a – 60)
\(\frac{700}{7}\) = a – 60
a = 100 + 60
a = 160
पहला पुरस्कार = ₹ 160 शेष पुरस्कार क्रम से ₹20-20 कम हैं।
अतः पुरस्कार ₹ 160, ₹ 140 ₹ 120, ₹ 100, ₹ 80, ₹ 60, ₹ 40 है।

प्रश्न 17.
एक स्कूल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अन्दर और बाहर पेड़ लगाने के बारे में सोचा। यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा। उदाहरणार्थ, कक्षा 1 का एक अनुभाग 1 पेड़ लगाएगा, कक्षा II का एक अनुभाग 2 पेड़ लगाएगा, कक्षा III का एक अनुभाग 3 पेड़ लगाएगा, इत्यादि और ऐसा कक्षा XII तक के लिए चलता रहेगा। प्रत्येक कक्षा के तीन अनुभाग हैं। इस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी ?
हल:
प्रत्येक कक्षा में तीन अनुभाग हैं।
कक्षा I द्वारा लगाए गए कुल पेड़ = 3 × 1 =3
कक्षा II द्वारा लगाए गए कुल पेड़ = 3 × 2 = 6
कक्षा III द्वारा लगाए गए कुल पेड़ = 3 × 3 = 9
कक्षा IV द्वारा लगाए गए कुल पेड़ = 3 × 4 = 12
……………………………………………….
……………………………………………….
तब 3, 6, 9, 12, ……….. एक समान्तर श्रेढी बनती है।
यहाँ a = 3, सार्वअन्तर d = 6 – 3 = 3
तब कक्षा XII तक के कुल विद्यार्थियों द्वारा लगाए गए पेड़ों का योगफल = S₁₂
∵ S_n= \(\frac{n}{2}\)[2a – (n – 1)d]
∴ S₁₂ = \(\frac{12}{2}\)[2 × 3 + (12 – 1) × 3]
= 6[6 + 33] = 6 × 39 = 234
अतः वायु प्रदूषण को रोकने के लिए विद्यार्थियों द्वारा लगाए गए पेड़ों की संख्या 234 होगी,

प्रश्न 18.
केन्द्र A से प्रारम्भ करते हुए, बारी-बारी से केन्द्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm… वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसा कि आकृति में दर्शाया गया है। 13 क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लम्बाई क्या है ? (लीजिए π = \(\frac{22}{7}\))
हल:

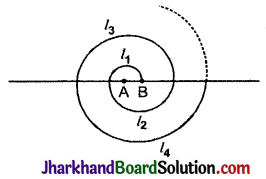
पहले अर्धवृत्त की त्रिज्या r₁ = 0.5 सेमी
दूसरे अर्धवृत्त की त्रिज्या r₂ = 1.0 सेमी
तीसरे अर्धवृत्त की त्रिज्या r₃ = 1.5 सेमी
चौथे अर्धवृत्त की त्रिज्या r₄ = 2.0 सेमी
………………………………………
………………………………………
13 वें अर्धवृत्त की त्रिज्या r₁₃ = ?
प्रथम पद (r₁) = r = 0.5 सेमी
सार्वअन्तर d = 1.0 – 0.5
= 0.5 सेमी
पदों की संख्या n = 13
∴ r₁₃ = r + (n – 1)d
= 0.5 + (13 – 1) × 0.5
⇒ r₁₃ = 0.5 + 12 × 0.5
= 0.5 + 6.0 = 6.5
∴ r₁₃ = 6.5 सेमी
इन अर्धवृत्तों की वृत्तीय परिधियाँ:
πr₁, πr₂, πr₃, …… πr₁₃
∴ 13 क्रमागत अर्धवृत्तों से बने सर्पिल की लम्बाई
= πr₁ + πr₂ + πr₃ + πr₄ +…. + πr₁₃
= π[r₁ + r₂ + r₃ + r₄ +…+ r₁₃]
= π[0.5 + 1.0 + 1.5 + 2.0 +…+ 6.5]
= π[\(\frac{13}{2}\)(0.5 + 6.5)] [सूत्र S_n = \(\frac{n}{2}\)[a + l] से]
= π[\(\frac{13}{2}\) × 7.0] = \(\frac{22}{7} \times \frac{13}{2} \times 7\) [π = \(\frac{22}{7}\)]
= 143
अतः सर्पिल की लम्बाई = 143 सेमी

प्रश्न 19.
200 लट्ठों (logs) को णेरी के रूप में इस प्रकार रखा जाता है सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लट्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं ?

हल:
यहाँ S_n = 200, a₁ = 20, a₂ = 19, a₃ = 18
d = 19 – 20 = 18 – 19 = -1
माना पंक्तियों की संख्या = n
S_n = \(\frac{n}{2}\)[2a + (n – 1) × d]
200 = \(\frac{n}{2}\)[2 × 20 + (n – 1) × – 1]
⇒ 400 = n (40 – n + 1)
⇒ 400 = n(41 – n)
⇒ 400 = 41n – n²
⇒ n² – 41n + 400 = 0
⇒ n² – 25n – 16n + 400 = 0
⇒ n(n – 25) – 16(n – 25) = 0
⇒ (n – 25)(n – 16) = 0
∴ n = 25 या n = 16
अतः पंक्तियों की संख्या 25 या 16 होगी।
Q₂₅ = a + (n – 1)d
= 20 + (24) × (-1) = -4, जो कि सम्भव नहीं है।
Q₁₆ = a + (n – 1)d
= 20 + 15 × (-1) = 20 – 15 = 5
अतः 16 पंक्तियाँ है तथा सबसे ऊपरी पंक्ति में 5 लट्ठे रखे गये हैं।

प्रश्न 20.
एक आलू दौड़ (potato race) में, प्रारम्भिक स्थान पर एक बाल्टी रखी हुई है, जो पहले आलू से 5 मीटर की दूरी पर है तथा अन्य आलुओं को एक सीधी रेखा में परस्पर 3 मीटर की दूरियों पर रखा गया है। इस रेखा पर 10 आलू रखे गए हैं, जैसा कि चित्र में दिखाया गया है।

प्रत्येक प्रतियोगी बाल्टी से चलना प्रारम्भ करती है, निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है, और वह ऐसा तब तक करती रहती है, जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी ?
हल:
पहले आलू की बाल्टी से दूरी = 5 मीटर
दूसरे आलू की बाल्टी से दूरी = (5 + 3) = 8 मीटर
तीसरे आलू की बाल्टी से दूरी = (8 + 3) = 11 मीटर
चौथे आलू की बाल्टी से दूरी = (11 + 3) = 14 मीटर
∵ एक बार बाल्टी से चलकर आलू को उठाना पड़ता है और उसे फिर बाल्टी में वापस डालना पड़ता है।
∴ पहला आलू उठाने के लिए तय की गई दूरी = 2 × 5 = 10 मीटर
उत्तरोत्तर आलुओं के बीच की दूरी = 3 मीटर
∴ दूसरा आलू उठाने के लिए तय की गई दूरी = 2 × 8 = 16 मीटर
तीसरा आलू उठाने के लिए तय की गई दूरी = 2 × 11 = 22 मीटर
चौथा आलू उठाने के लिए तय की गई दूरी = 2 × 14 = 28 मीटर
और यह प्रक्रिया चलती रहती है। इससे स्पष्ट है कि यह स्थिति एक A. P. बन जाती है।
10 मी., 16 मी., 22 मी., 28 मी., …… 10 पदों तक
∴ a = 10
d = 16 – 10 = 6
n = 10
प्रतियोगी को कुल दूरी दौड़नी पड़ेगी = S₁₀
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₀ = \(\frac{10}{2}\)[2 × 10 + (10 – 1) × 6]
= 5[20 + 9 × 6] = 5[20 + 54]
= 5 × 74 = 370 मीटर
अतः प्रतियोगी द्वारा चली दूरी = 370 मीटर।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Exercise 4.3

प्रश्न 1.
यदि निम्नलिखित द्विघात समीकरणों के मूलों का अस्तित्व हो, तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए :
(i) 2x² – 7x + 3 = 0
(ii) 2x² + x – 4 = 0
(iii) 4x² + 4\(\sqrt{3}\)x + 3 = 0
(iv) 2x² + x + 4 = 0
हल:
(i) दिया गया द्विघात समीकरण है :
2x² – 7x + 3 = 0
x² – \(\frac{7}{2}\)x + \(\frac{3}{2}\) = 0
[प्रत्येक पद में x² के गुणांक से भाग देने पर]
\(\left[x^2-\frac{7}{2} x\right]+\frac{3}{2}=0\)
[वह भाग जिसे पूर्ण वर्ग बनाना है, अलग करने पर]
\(x^2-\frac{7}{2} x=-\frac{3}{2}\)
x के गुणांक के आधे का वर्ग दोनों पक्षों में जोड़ने पर :

दोनों पक्षों का वर्गमूल लेने पर,

अत: अभीष्ट मूल 3 और \(\frac{1}{2}\) होंगे।

(ii) दी गई द्विघात समीकरण है :
2x² + x – 4 = 0
2x² + x = 4
x² + \(\frac{1}{2}\)x = \(\frac{4}{2}\)
x के गुणांक \(\frac{1}{2}\) के आधे का वर्ग दोनों पक्षों में जोड़ने पर

(iii) दी गई द्विघात समीकरण है:
4x² + 4\(\sqrt{3}\)x + 3 = 0
⇒ 4x² + 4\(\sqrt{3}\)x = -3
⇒ x² + \(\frac{4 \sqrt{3}}{4} x\) = \(-\frac{3}{4}\)
x² + \(\sqrt{3}\)x = \(-\frac{3}{4}\)
x के गुणांक के आधे का वर्ग दोनों पक्षों में जोड़ने पर

x = \(-\frac{\sqrt{3}}{2}\)
अतः दी गई समीकरण के मूल \(-\frac{\sqrt{3}}{2}\) और \(-\frac{\sqrt{3}}{2}\) हैं।

(iv) दिया गया द्विघात समीकरण है:
2x² + x + 4 = 0
x² + \(\frac{1}{2}\)x + 2 = 0
[प्रत्येक पद को 2 से भाग देने पर]

जो कि एक काल्पनिक संख्या है,
अतः दिए गए समीकरण के मूल वास्तविक नहीं हैं।

प्रश्न 2.
उपर्युक्त प्रश्न (1) में दिए गए द्विघात समीकरणों के मूल, द्विघाती सूत्र का उपयोग करके ज्ञात कीजिए।
हल:
(i) दिया गया द्विघात समीकरण है :
2x² – 7x + 3 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = 7 तथा c = 3
श्रीधराचार्य सूत्र से,

अतः समीकरण के मूल 3, \(\frac{1}{2}\)

(ii) दिया गया द्विघात समीकरण है।
2x² + x – 4 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = 1 तथा c = – 4
श्रीधराचार्य सूत्र से,

अतः द्विघात समीकरण के मूल \(\frac{-1-\sqrt{33}}{4}\) और \(\frac{-1+\sqrt{33}}{4}\) होंगे।

(iii) दिया गया द्विघात समीकरण है:
4x² + 4\(\sqrt{3}\)x + 3 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 4, b = 4\(\sqrt{3}\), c = 3
श्रीधराचार्य सूत्र से,

\(\frac{-4 \sqrt{3} \pm \sqrt{0}}{8}\)
x = \(\frac{-4 \sqrt{3}}{8}=\frac{-\sqrt{3}}{2}\)
अत: दिये गये द्विघात समीकरण के मूल \(-\frac{\sqrt{3}}{2}\) और \(-\frac{\sqrt{3}}{2}\) है।

(iv) दिया गया द्विघात समीकरण है:
2x² + x + 4 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = 1, c = 4
श्रीधराचार्य सूत्र से,

∵ \(\sqrt{-31}\) एक काल्पनिक संख्या है।
अतः दिए गये समीकरण के मूलों का अस्तित्व नहीं है।

प्रश्न 3.
निम्न समीकरणों के मूल ज्ञात कीजिए :
(i) \(x-\frac{1}{x}\) = 3, x ≠ 0
(ii) \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\), x ≠ -4, 7
हल:
(i) दिया गया समीकरण है:
\(x-\frac{1}{x}\) = 3, x ≠ 0
⇒ \(\frac{x^2-1}{x}\) = 3
⇒ x² – 1 = 3x [वज्रगुणन से]
⇒ x² – 3x – 1 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 1, b = -3 तथा c = -1
द्विघात सूत्र से,

(ii) दिया गया समीकरण है:

[दोनों पक्षों को 11 से भाग देने पर]
⇒ x² – 3x – 28 = -30
⇒ x² – 3x – 28 + 30 = 0
⇒ x² – 3x + 2 = 0
⇒ x² – (2 + 1)x + 2 = 0
⇒ x² – 2x – x + 2 = 0
⇒ x (x – 2) – 1 (x – 2)
⇒ (x – 2) (x – 1) = 0
या तो x – 2 = 0 या फिर x – 1 = 0
जब x – 2 = 0 तो x = 2
जब x – 1 = 0 तो x = 1
अतः दी गई द्विघात समीकरण के मूल 1 और 2 है ।

प्रश्न 4.
3 वर्ष पूर्व रहमान की आयु (वर्षों में) का व्युत्क्रम और अब से 5 वर्ष पश्चात् आयु के व्युत्क्रम का योग \(\frac{1}{3}\) है। उसकी वर्तमान आयु ज्ञात कीजिए।
हल:
माना रहमान की वर्तमान आयु = x वर्ष
3 वर्ष पूर्व रहमान की आयु = (x – 3) वर्ष
अब से 5 वर्ष पश्चात् रहमान की आयु = (x + 5) वर्ष
प्रश्नानुसार,
\(\frac{1}{x-3}+\frac{1}{x+5}=\frac{1}{3}\)
\(\frac{x+5+x-3}{(x-3)(x+5)}=\frac{1}{3}\)

⇒ 6x + 6 = x² + 2x – 15
⇒ x² + 2x – 15 – 6x – 6 = 0
⇒ x² – 4x – 21 = 0, जो कि x में द्विघात है।
इसकी तुलना ax² + bx + c = 0 से करने पर,
a = 1, b = – 4, c = – 21
द्विघात सूत्र से

∵ आयु ऋणात्मक नहीं हो सकती।
इसलिए हम x = -3 को छोड़ देते हैं।
∴ x = 7
अतः रहमान की वर्तमान आयु = 7 वर्ष।

प्रश्न 5.
एक क्लास टेस्ट में शेफाली के गणित और अंग्रेजी में प्राप्त किए गए अंकों का योग 30 है। यदि उसको गणित में 2 अंक अधिक और अंग्रेजी में 3 अंक कम मिले होते, तो उनके अंकों का गुणनफल 210 होता। उसके द्वारा दोनों विषयों में प्राप्त किए गए अंक ज्ञात कीजिए।
हल:
माना शेफाली ने गणित में x अंक प्राप्त किए।
अंग्रेजी और गणित दोनों के प्राप्तांकों का योग 30 है।
तब अंग्रेजी में प्राप्तांक = (30 – x) अंक
यदि उसको गणित में 2 अंक अधिक मिलते अर्थात् गणित में (x + 2) अंक मिलते और अंग्रेजी में 3 अंक कम मिलते अर्थात् अंग्रेजी में (30 – x – 3) या (27 – x) अंक मिलते तो अंकों का गुणनफल = (x + 2) (27 – x)
= 27x – x² + 54 – 2x
= 25x – x² + 54
परन्तु प्रश्नानुसार, अंकों का गुणनफल = 210
∴ 210 = 25x – x² + 54
⇒ x² – 25x – 54 + 210 = 0
⇒ x² – 25x + 156 = 0
उक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 1, b = -25 तथा c = 156
द्विघात सूत्र से,

तब शेफाली ने गणित में या तो 13 अंक प्राप्त किए या फिर 12 अंक प्राप्त किए।
यदि उसने गणित में 12 अंक प्राप्त किए तो अंग्रेजी में (30 – 12) = 18 अंक प्राप्त किए और यदि उसने गणित में 13 अंक प्राप्त किए तो अंग्रेजी में (30 – 13) = 17 प्राप्त किए।
अतः शेफाली ने गणित व अंग्रेजी में क्रमशः 12 व 18 अंक अथवा 13 व 17 अंक प्राप्त किए।

प्रश्न 6.
एक आयताकार खेत का विकणं उसकी छोटी भुजा से 60 मी अधिक लंबा है। यदि बड़ी भुजा छोटी भुजा से 30 मी अधिक हो, तो खेत की भुजाएँ ज्ञात कीजिए।
हल:
माना कि एक आयताकार खेत की छोटी भुजा = AD = x मीटर

आयताकार खेत की लम्बी भुजा = AB = (x + 30) मीटर
और आयताकार खेत का विकर्ण = DB = (x + 60) मीटर
एक आयत में लम्बाई और चौड़ाई के बीच का कोण समकोण होता है।
∴ ∠DAB = 90°
समकोण त्रिभुज DAB में, पाइथागोरथ प्रमेय से,
(DB)² = (AD)² + (AB)²
(x + 60)² = (x)² + (x + 30)²
⇒ x² + 3600 + 120x = x² + x² + 900 + 60x
⇒ x² + 3600 + 120x – x² – x² – 900 – 60x = 0
⇒ -x² + 60x + 2700 = 0
या, x² – 60x – 2700 = 0
इसकी तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर
a = 1, b = -60, c = -2700
द्विघात सूत्र से,

स्थिति (I)-धनात्मक चिह्न लेने पर
x = \(\frac{60+120}{2}=\frac{180}{2}\)
⇒ x = 90
स्थिति (II) ऋणात्मक चिह्न लेने पर
x = \(\frac{60-120}{2}=\frac{-60}{2}\)
⇒ x = -30
∴ x = 90 और -30
∵ किसी भुजा की लम्बाई ऋणात्मक नहीं हो सकती।
इसलिए x = -30 को छोड़ देते हैं।
अत: x = 90 मीटर
आयताकार खेत की छोटी भुजा = 90 मीटर
आयताकार खेत की लम्बी भुजा = (90 + 30) मीटर = 120 मीटर।

प्रश्न 7.
दो संख्याओं के वर्गों का अन्तर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का आठ गुना है। दोनों संख्याएँ ज्ञात कीजिए।
हल:
माना बड़ी संख्या = x
छोटी संख्या = y
प्रश्न की प्रथम शर्त के अनुसार,
x² – y² = 180 …..(i)
प्रश्न की द्वितीय शर्त के अनुसार,
y² = 8x …..(ii)
समीकरण (ii) से y² का मान समीकरण (i) में रखने पर
x² – 8x = 180
= x² – 8x – 180 = 0
इसकी तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 1, b = – 8, c = -180
द्विघात सूत्र से,

स्थिति (I)-धनात्मक चिह्न लेने पर,
x = \(\frac{8+28}{2}=\frac{36}{2}\) = 18
स्थिति (II)-ऋणात्मक चिह्न लेने पर,
\(\frac{8-28}{2}=\frac{-20}{2}\) = -10
अतः x = 18 और -10
जब x = 18 हो, तो समीकरण (ii) से,
y² = 8 × 18 = 144
⇒ y = ±\(\sqrt{144}\)
⇒ y = ± 12
जब x = -10 हो, तो समीकरण (ii) से,
y2 = 8 × (-10)
⇒ y2 = -80
⇒ y = ±\(\sqrt{-80}\) (एक काल्पनिक संख्या)
इसे छोड़ देते हैं।
∴ y = +12
अर्थात् y = +12 और -12
अतः अभीष्ट संख्याएँ 18 और 12 या 18, -12 होंगी।

प्रश्न 8.
एक रेलगाड़ी एकसमान चाल से 360 किमी की दूरी तय करती है। यदि यह चाल 5 किमी / घण्टा अधिक होती, तो वह उसी यात्रा में 1 घण्टा कम समय लेती। रेलगाड़ी की चाल ज्ञात कीजिए।
हल:
माना रेलगाड़ी की चाल x किमी/ घण्टा है।
360 किमी दूरी तय करने में लगा समय

यदि रेलगाड़ी की चाल 5 किमी / घण्टा अधिक होती अर्थात् चाल = (x + 5) किमी/घण्टा
∴ समय = \(\frac{360}{x+5}\) घण्टा
यह समय पहले समय से 1 घण्टा कम है (दिया है)

इस समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 1, b = 5 तथा c = – 1800
तब द्विघात सूत्र से,

∵ रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती।
अतः रेलगाड़ी की चाल = 40 किमी / घण्टा।

प्रश्न 9.
दो पानी के नल एक साथ एक हौज को 9\(\frac{3}{8}\) घंटों में भर सकते हैं। बड़े व्यास वाला नल हौज को भरने में, कम व्यास वाले नल से 10 घण्टे कम समय लेता है। प्रत्येक नल द्वारा अलग-अलग हौज को भरने के समय ज्ञात कीजिए।
हल:
माना कि बड़े व्यास वाले नल द्वारा हौज को भरने में लिया गया समय = x घण्टे
कम व्यास वाले नल द्वारा हौज को भरने में लिया गया समय = (x + 10) घण्टे
बड़े व्यास वाले नल द्वारा हौज का 1 घण्टे में भरा गया भाग = \(\frac{1}{x}\) भाग
छोटे व्यास वाले नल द्वारा हौज का 1 घण्टे में भरा गया भाग = \(\frac{1}{x+10}\) भाग
प्रश्नानुसार यदि दोनों नल एक साथ खुले हों तो 1 घण्टे में हौज भरेगा = \(\left(\frac{1}{x}+\frac{1}{x+10}\right)\) भाग
दिया है, दोनों नल एक साथ हौज को भरने में 9\(\frac{3}{8}\) अर्थात् \(\frac{75}{8}\) घण्टे लेते हैं।

⇒ 150x + 750 = 8x² + 80x
⇒ 8x² + 80x – 150x – 750 = 0
⇒ 8x² – 70x – 750 = 0
⇒ 2(4x² – 35x – 375) = 0
⇒ 4x² – 35x – 375 = 0
इसकी तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 4, b = – 35, c = -375
द्विघात सूत्र से,

स्थिति (II)-ऋण चिह्न लेने पर,
x = \(\frac{35-85}{8}\)
= \(\frac{-50}{8}=\frac{-25}{4}\) घण्टे
∵ समय ऋणात्मक नहीं हो सकता है।
∴ x = \(\frac{-25}{4}\) को छोड़ देते हैं।
∴ x = 15 घण्टे
अतः बड़े व्यास वाले नल द्वारा हौज को भरने में लगा समय = 15 घण्टे
और छोटे व्यास वाले नल द्वारा हौज को भरने में लगा समय = (15 + 10) घण्टे
= 25 घण्टे

प्रश्न 10.
मैसूर और बंगलौर के बीच की 132 किमी यात्रा करने में एक एक्सप्रेस रेलगाड़ी, सवारीगाड़ी से 1 घण्टा समय कम लेती है (मध्य के स्टेशनों पर ठहरने का समय ध्यान में न लिया जाए)। यदि एक्सप्रेस रेलगाड़ी की औसत चाल, सवारीगाड़ी की औसत चाल से 11 किमी/ घण्टा अधिक हो, तो दोनों रेलगाड़ियों की औसत चाल ज्ञात कीजिए।
हल:
माना सवारी गाड़ी की औसत चाल x किमी / घण्टा है।
∵ एक्सप्रेस रेलगाड़ी की औसत चाल सवारीगाड़ी की औसत चाल की अपेक्षा 11 किमी/ घण्टा अधिक है।
∴ एक्सप्रेस गाड़ी की औसत चाल = (x + 11) किमी / घण्टा
तब 132 किमी यात्रा में सवारीगाड़ी द्वारा लिया गया

⇒ x² + 11x = 1452
⇒ x² + 11x – 1452 = 0
इस समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर
a = 1, b = 11, c = -1452
श्रीधराचार्य से,

∵ रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती है।
इस कारण x = -44 अस्वीकार्य है।
अतः सवारीगाड़ी की औसत चाल = 33 किमी / घण्टा है।
तथा एक्सप्रेस गाड़ी की औसत चाल (33 + 11) = 44 किमी / घण्टा है।

प्रश्न 11.
दो वर्गों के क्षेत्रफलों का योग 468 वर्ग मीटर है। यदि उनके परिमापों का अन्तर 24 मीटर हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
हल:
माना एक वर्ग की भुजा x मीटर है।
उस वर्ग का परिमाप = 4x मीटर
∵ दोनों परिमापों का अन्तर 24 मीटर है।
∴ दूसरे वर्ग का परिमाप = 4x + 24 मीटर
तब दूसरे वर्ग की भुजा = \(\frac{4 x+24}{4}\)
= \(\frac{4(x+6)}{4}\)
= (x + 6) मीटर
पहले वर्ग का क्षेत्रफल = x² वर्ग मीटर
दूसरे वर्ग का क्षेत्रफल = (x + 6)² वर्ग मीटर
= x² + 12x + 36 वर्ग मीटर
∵ दोनों वर्गों के क्षेत्रफलों का योग = 468 वर्ग मीटर
∴ x² + (x² + 12x + 36) = 468
⇒ 2x² + 12x + 36 – 468 = 0
⇒ 2x² + 12x – 432 = 0
⇒ 2(x² + 6x – 216) = 0
⇒ x² + 6x – 216 = 0
⇒ x² + 18x – 12x – 216 = 0
⇒ x(x + 18) – 12(x + 18) = 0
⇒ (x + 18 ) (x – 12) = 0
जब x + 18 = 0 हो, तो x = -18
या फिर x – 12 = 0 हो, तो x = 12
वर्ग की भुजा ऋणात्मक नहीं हो सकती है।
इस कारण x = -18 को छोड़ने पर
∴ x = 12
छोटे वर्ग की भुजा = 12 मीटर
तथा बड़े वर्ग की भुजा = x + 6 = 12 + 6 = 18 मीटर
अतः वर्गों की भुजाएँ क्रमश: 12 मीटर व 18 मीटर हैं।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 14 सांख्यिकी Ex 14.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 14 सांख्यिकी Exercise 14.1

प्रश्न 1.
विद्यार्थियों के एक समूह द्वारा पर्यावरण संचेतना अभियान के अंतर्गत एक सर्वेक्षण किया गया, जिसमें उन्होंने एक मोहल्ले के 20 घरों में लगे हुए पौधों से सम्बन्धित निम्नलिखित आँकड़े एकत्रित किए। प्रति घर माध्य पौधों की संख्या ज्ञात कीजिए ।

माध्य ज्ञात करने के लिए आपने किस विधि का प्रयोग किया और क्यों ?
हल :
उपर्युक्त सारणी में पौधों की संख्या और घरों की संख्या के मान अत्यधिक कम होने के कारण प्रत्यक्ष विधि का प्रयोग करेंगे :

∴ माध्य (\(\bar{x}\)) = \(\frac{\sum f_i x_i}{\sum f_i}\)
= \(\frac {162}{20}\) = 8.1
अतः प्रति घर में पौधों की माध्य संख्या = 8.1 पौधे ।

प्रश्न 2.
किसी फैक्टरी के 50 श्रमिकों की दैनिक मजदूरी के निम्नलिखित बंटन पर विचार कीजिए:

एक उपयुक्त विधि का प्रयोग करते हुए, इस फैक्टरी के श्रमिकों की माध्य दैनिक मजदूरी ज्ञात कीजिए।
हल :

∴ माध्य (\(\bar{x}\)) = \(\frac{\sum f_i x_i}{\sum f_i}\)
= \(\frac {27260}{50}\)
= ₹ 545.20
अतः श्रमिकों की माध्य दैनिक मजदूरी = ₹ 545.20

प्रश्न 3.
निम्नलिखित बंटन एक मोहल्ले के बच्चों के दैनिक जेब खर्च को दर्शाता है। माध्य जेब खर्च ₹18 है। लुप्त बारम्बारता f ज्ञात कीजिए :

हल :


अतः लुप्त बारम्बारता f = 20 है।

प्रश्न 4.
किसी अस्पताल में, एक डॉक्टर द्वारा 30 महिलाओं की जाँच की गई और उनके हृदय स्पंदन (beat) की प्रति मिनट संख्या नोट करके नीचे दर्शाए अनुसार संक्षिप्त रूप में लिखी गई। एक उपयुक्त विधि चुनते हुए, इन महिलाओं के हृदय स्पंदन की प्रति मिनट माध्य संख्या ज्ञात कीजिए ।

हल :

∴ माध्य (\(\bar{x}\)) = A + \(\frac{\sum f_i d_i}{\sum f_i}\)
= 75.5 + \(\frac {12}{30}\) = 75.5 + 0.4 = 75.9
अतः महिलाओं के हृदय स्पंदन की प्रति मिनट माध्य संख्या = 75.9

प्रश्न 5.
किसी फुटकर बाजार में, फल विक्रेता पेटियों में रखे आम बेच रहे थे। इन पेटियों में आमों की संख्याएँ भिन्न-भिन्न थी । पेटियों की संख्या के अनुसार, आमों का बंटन निम्नलिखित था :

एक पेटी में रखे आमों की माध्य संख्या ज्ञात कीजिए। आपने माध्य ज्ञात करने की किस विधि का प्रयोग किया है?
हल :
माना कल्पित माध्य (A) = 57, वर्ग माप (h) = 3
पद – विचलन विधि द्वारा :

माध्य (\(\bar{x}\)) = A + \(\frac{\sum f_i u_i}{\sum f_i}\) × h
⇒ \(\bar{x}\) = 57 + \(\frac {25}{400}\) × 3 = 57 + (0.0625) × 3
= 57 + 0.1875 = 57.1875 = 57.19 (लगभग)
अतः पेटी में रखे आमों की माध्य संख्या = 57.19 है। हमने पद विचलन विधि का प्रयोग किया है।

प्रश्न 6.
निम्नलिखित सारणी किसी मोहल्ले के 25 परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है :

एक उपयुक्त विधि द्वारा भोजन पर हुआ माध्य व्यय ज्ञात कीजिए ।
हल :
माना कल्पित माध्य (A) = 225, वर्ग माप (h) = 50
पद- विचलन विधि से :

माध्य (\(\bar{x}\)) = A + \(\frac{\sum f_i u_i}{\sum f_i}\) × h
= 225 + \(\frac {-7}{25}\) × 50
= 225 + (-14) = 211
अतः प्रति परिवार भोजन पर होने वाला दैनिक व्यय का माध्य = ₹ 211

प्रश्न 7.
वायु में सल्फर डाइ आक्साइड (SO₂) की सान्द्रता (भाग प्रति मिलियन में) को ज्ञात करने के लिए, एक नगर के 30 मोहल्लों से आँकड़े एकत्रित किए गए, जिन्हें नीचे प्रस्तुत किया गया है :

वायु में SO₂ की सान्द्रता का माध्य ज्ञात कीजिए ।
हल :

अतः वायु में SO₂ की सान्द्रता का माध्य = 0.099 भाग प्रति मिलियन

प्रश्न 8.
किसी कक्षा अध्यापिका ने पूरे सत्र के लिए अपनी कक्षा के 40 विद्यार्थियों की अनुपस्थिति निम्नलिखित रूप में रिकॉर्ड (record) की। एक विद्यार्थी जितने दिन अनुपस्थित रहा उनका माध्य ज्ञात कीजिए :

हल :

अतः एक विद्यार्थी जितने दिन अनुपस्थित रहा उनका माध्य= 12.48 दिन है।

प्रश्न 9.
निम्नलिखित सारणी 35 नगरों की साक्षरता दर (प्रतिशत में) दर्शाती है। माध्य साक्षरता दर ज्ञात कीजिए :

हल :
माना कल्पित माध्य (A) = 70
वर्ग माप (h) = 10
पद – विचलन विधि से :

माध्य (\(\bar{x}\)) = A + \(\frac{\sum f_i u_i}{\sum f_i}\) × h
\(\bar{x}\) = 70 + \(\frac {-2}{35}\) × 10 = 70 + \(\frac {-20}{35}\)
= 70 + (-0.57) = 70 – 0.57 = 69.43
अतः माध्य साक्षरता दर = 69.43% है।

Jharkhand Board JAC Class 10 Science Solutions Chapter 7 नियंत्रण एवं समन्वय Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 7 नियंत्रण एवं समन्वय

Jharkhand Board Class 10 Science नियंत्रण एवं समन्वय Textbook Questions and Answers

प्रश्न 1.
निम्नलिखित में से कौन-सा पादप हॉर्मोन है-
(a) इंसुलिन
(b) थायरॉक्सिन
(c) एस्ट्रोजन
(d) साइटोकाइनिन
उत्तर:
(d) साइटोकाइनिन।

प्रश्न 2.
दो तंत्रिका कोशिका के मध्य खाली स्थान को कहते हैं-
(a) दुमिका
(b) सिनेप्स
(c) एक्सॉन
(d) आवेग
उत्तर:
(b) सिनेप्स।

प्रश्न 3.
मस्तिष्क उत्तरदायी है-
(a) सोचने के लिए
(b) हृदय स्पंदन के लिए
(c) शरीर का संतुलन बनाने के लिए
(d) उपर्युक्त सभी
उत्तर:
(d) उपर्युक्त सभी।

प्रश्न 4.
हमारे शरीर में ग्राही का क्या कार्य है? ऐसी स्थिति पर विचार कीजिए जहाँ ग्राही उचित प्रकार से कार्य नहीं कर रहा हो। क्या समस्याएँ उत्पन्न हो सकती हैं?
उत्तर:
ग्राही, हमारी ज्ञानेन्द्रियों में स्थित एक खास कोशिकाएँ होती हैं, जो वातावरण से सभी सूचनाएँ ढूँढ़ सकती हैं और उन्हें केंद्रीय तंत्रिका तंत्र (मेरुरण्जु तथा मस्तिष्क) में पहुँचाती हैं। मस्तिष्क के भाग अग्रमस्तिष्क में विभिन्न ग्राही से संवेदी आवेग (सूचनाएँ) प्राप्त करने के लिए क्षेत्र होते हैं। इसके अलग-अलग क्षेत्र सुनने, सूँघने, देखने आदि के लिए विशिष्टीकृत होते हैं। यदि कोई ग्राही उचित प्रकार कार्य नहीं करेगी तो उस ग्राही द्वारा एकत्र की गई सूचना मस्तिष्क तक नहीं पहुँचेगी। जैसे-

• यदि रेटिना की कोशिका अच्छी तरह कार्य नहीं करेंगी, तो हम देख नहीं पाएँगे जिससे हम अंधे भी हो सकते हैं।
• जिढ्वा द्वार मीठा, नमकीन आदि स्वाद का पता लगाना संभव नहीं हो पाएगा।

प्रश्न 5.
एक तंत्रिका कोशिका (न्यूरॉन) की संरचना बनाइये तथा इसके कार्यों का वर्णन कीजिए।
उत्तर:

तंत्रिका कोशिका के कार्य-न्यूरॉन या तंत्रिका कोशिका तंत्रिका तंत्र की संरचनात्मक व क्रियात्मक इकाई है। इसके निम्न तीन भाग होते हैं-

• दुमिका
• कोशिकाकाय
• एक्सॉन।

सूचनाओं का आवेग द्रुमिका से कोशिकाकाय की ओर चलता है तथा फिर एक्सॉन में से होता हुआ सिनेप्स तक पहुँचता है। फिर इसे पार करता हुआ एक न्यूरॉन से दूसरे में गुजरता हुआ मेरुरज्जु तक पहुँचता है। इसी प्रकार सूचनाएँ मस्तिष्क से कार्यकारी अंग (पेशी, ग्रंथि) तक पहुँचती हैं।

प्रश्न 6.
पादप में प्रकाशानुवर्तन किस प्रकार होता है?
उत्तर:
दिशिक या अनुवर्तन गति जो प्रकाश उद्दीपन के प्रभाव में, प्रकाश की ओर अथवा उसके विपरीत होती है उसे प्रकाशानुवर्तन कहते हैं। तने प्रकाश की ओर मुड़ते हैं जबकि जड़ें प्रकाश के विपरीत मुड़कर अनुक्रिया करती हैं।

प्रश्न 7.
मेरुरज्जु आघात में किन संकेतों के आवागमन में व्यवधान होगा ?
उत्तर:

• सभी संकेत जो मस्तिष्क से दूर या मस्तिष्क की ओर मेरुरज्जु से होकर चलते हैं, उनके आवागमन में व्यवधान उत्पन्न होगा।
• प्रतिवर्ती क्रिया नहीं संपादित होगी।

प्रश्न 8.
पादप में रासायनिक समन्वय किस प्रकार होता है?
उत्तर:
पौधों की विशेष कोशिकाओं द्वारा कुछ रासायनिक पदार्थ स्रावित होते हैं जिन्हें पादप हॉर्मोन कहते हैं। विभिन्न प्रकार के पादप हॉर्मोन वृद्धि व विकास तथा वातावरण के साथ समन्वय स्थापित करते हैं। ये पादप हॉर्मोन क्रिया स्थान से दूर कहीं स्रावित होकर विसरण द्वारा उस स्थान तक पहुँचकर कार्य करते हैं।

प्रश्न 9.
एक जीव में नियंत्रण एवं समन्वय के तंत्र की क्या आवश्यकता है?
उत्तर:
एक जीव में नियंत्रण एवं समन्वय के तंत्र की आवश्यकता दो प्रकायों को करने के लिए होती है-
(1) इससे शरीर के विभिन्न अंगों का निर्माण होता है एवं अंगतंत्र एक व्यवस्थित तरीके से कार्य करते हैं और उनमें समन्वय बना रहता है। उदाहरण के लिए जब हम भोजन करने की सोचते हैं तो हम भोजन लेकर मुँह की तरफ ले जाते हैं, दाँत और जबड़े की पेशियाँ भोजन को तोड़ती हैं, लार ग्रंथियाँ लार का स्रावण करती हैं।

(2) बस से कूदना, आग की लौ से अपना हाथ पीछे खींच लेना, भूख के कारण मुँह में पानी आना। इन सभी उदाहरणों में एक सामान्य विचार आता है कि जो कुछ हम करते हैं उसके बारे में विचार नहीं करते, या अपनी क्रियाओं को नियंत्रण में महसूस नहीं करते हैं। फिर भी ये वे स्थितियाँ हैं जहाँ हम अपने पर्यावरण में होने वाले परिवर्तनों के प्रति अनुक्रिया कर रहे हैं। इन परिस्थितियों के लिए हमें नियंत्रण व समन्वय तंत्र की आवश्यकता होती है।

प्रश्न 10.
अनैच्छिक क्रियाएँ तथा प्रतिवर्ती क्रियाएँ एक-दूसरे से किस प्रकार भिन्न हैं?
उत्तर:
अनैच्छिक क्रियाएँ तथा प्रतिवर्ती क्रियाएँ निम्न प्रकार से एक-दूसरे से भिन्न हैं-

अनैच्छिक क्रियाएँ	प्रतिवर्ती क्रियाएँ
1. वे क्रियाएँ जिनका नियंत्रण हमारे सोचने से नहीं होत है या ऐसी क्रियाएँ जो शरीर में निरन्तर चलती रहती हैं।	1. वह क्रियाएँ जिनमें किसी बाह्य उद्दीपन के प्रति अनुक्रियाएँ होती हैं प्रतिवर्ती क्रियाएँ कहलाती हैं।
2. इसका नियंत्रण पश्चमस्तिष्क स्थित मेडुला द्वारा होता है।	2. इनका नियंत्रण मुख्यतः मेरुज्जु द्वारा होता है तथा प्रत्यावर्ती चाप के रूप में क्रियान्वित होता है।
3. उदाहरण के लिए- हृदय का स्पन्दन, साँस लेना, श्वसन क्रिया द्वारा ऊर्जा का उत्पादन, भोजन देखकर लार का निकलना, वर्ज्य पदार्थों का उत्सर्जन आदि।	3. उदाहरण के लिए-किसी गर्म वस्तु को स्पर्श करने पर हाथ शीघ्रता से हटाना।

प्रश्न 11.
जंतुओं में नियंत्रण एवं समन्वय के लिए तंत्रिका तथा हॉर्मोन क्रियाविधि की तुलना तथा व्यतिरेक (Contrast) कीजिए।
उत्तर:
जंतुओं में नियंत्रण एवं समन्वय के लिए तंत्रिका तथा हॉर्मोन क्रियाविधि की तुलना तथा व्यतिरेक

जंतुओं में तंत्रिका द्वारा नियंत्रण एवं समन्वय	जंतुओं में हॉर्मोन द्वारा नियंत्रण एवं समन्वय
1. यह नियंत्रण एवं समन्वय से सम्बन्धित क्रियाविधि होती है।	1. यह क्रियाविधि भी नियंत्रण एवं समन्वय से सम्बन्धित है।
2. तंत्रिका क्रियाविधि में रासायनिक परिवर्तन मांसपेशियों की कोशिकाओं में होता है।	2. शरीर के एक अंग में उत्पन्न हॉर्मोन शरीर के अन्य भागों को भेजे जाते हैं।
3. यह मस्तिष्क एवं मेरुरज्जु द्वारा नियंत्रित होती है।	3. यह अन्तः स्रावी ग्रन्थियों द्वारा स्रावित होते हैं।

प्रश्न 12.
छुई-मुई पादप में गति तथा हमारी टाँग में होने वाली गति के तरीके में क्या अंतर है?
उत्तर:
छुई-मुई पौधे में गति-छुई-मुई में स्पर्श उद्दीपन के प्रति अनुक्रिया के फलस्वरूप गति होती है। यदि पत्ती को छूते हैं तब उद्दीपन पत्ती के आधार तक संचरित हो जाता है और पत्तियाँ नीचे झुक जाती हैं। यह आधार कोशिकाओं में परासरणीय दाब कम होने के कारण होता है। जब उद्दीपन समय समाप्त हो जाता है तब परासरणीय दाब पुनः स्थापित हो जाता है तथा पत्तियाँ सामान्य अवस्था में आ जाती हैं। यह वृद्धि अनाश्रित गति है।

छुई-मुई में स्पर्श बिंदु (उद्दीपन) से अलग भाग में गति होती है। इसमें सूचना विशिष्ट ऊतकों से होकर नहीं बल्कि विद्युत रासायनिक संकेतों के रूप में एक कोशिका से दूसरी कोशिका तक संचरित होती है। पादप कोशिकाओं की रचना उनमें पानी की मात्रा के परिवर्तन से परिवर्तित होती है जिसके परिणामस्वरूप गति होती है।

हमारे पैर की गति-हमारे पैर की पेशियाँ तंत्रिकाओं से सम्बद्ध होती हैं जिनमें गति करने हेतु आवश्यक सूचनाएँ मस्तिष्क द्वारा भेजी जाती हैं।

सूचनाएँ विद्युत रासायनिक संकेतों के रूप में संचरित होती हैं। यह पेशियों तक पहुँचकर रासायनिक संकेतों में बदल जाती हैं जिसके परिणामस्वरूप पैर में गति होती है। अतः पैर में गति पेशियों के सिकुड़ने एवं फैलने से होती है जो मस्तिष्क द्वारा नियंत्रित होती रहती है।

Jharkhand Board Class 10 Science नियंत्रण एवं समन्वय InText Questions and Answers

पाठगत प्रश्न (पृष्ठ संख्या-132)

प्रश्न 1.
प्रतिवर्ती क्रिया तथा टहलने के बीच क्या अन्तर है?
उत्तर:
प्रतिवर्ती क्रिया तथा टहलने के बीच अन्तर निम्न प्रकार हैं-

प्रतिवर्ती क्रिया	टहलना
1. प्रतिवर्ती क्रिया मेरुण्जु द्वारा नियंत्रित होती है।	1. टहलना मस्तिष्क के भाग अनुमस्तिष्क द्वारा नियंत्रित होती है।
2. यह अनैच्छिक (Involuntary) क्रियाएँ हैं।	2. यह ऐच्छिक (voluntary) क्रियाएँ हैं।
3. यह क्रिया अत्यंत तेज अर्थात् एक सेकण्ड के सूक्ष्म अंश में ही पूर्ण हो जाती है।	3. इस क्रिया में अधिक समय लगता है क्योंकि पहले मस्तिष्क विचार करता है तथा सूचना को तंत्रिका के माध्यम से पेशियों तक पहुँचाता है।

प्रश्न 2.
दो तंत्रिका कोशिकाओं (न्यूरॉन) के मध्य अंतर्ग्रथन (सिनेप्स) में क्या होता है?
उत्तर:
अंतर्ग्रथन पर विद्युत तरंगों के रूप में आने वाला तंत्रिका आवेग कुछ रसायन के स्रावण को प्रेरित करता है। ये रसायन अंतर्ग्रथन को पार करके अगली तंत्रिका कोशिका में समान प्रकार का तंत्रिका आवेग उत्पन्न करते हैं।

प्रश्न 3.
मस्तिष्क का कौन-सा भाग शरीर की स्थिति तथा संतुलन का अनुरक्षण करता है?
उत्तर:
अनुमस्तिष्क।

प्रश्न 4.
हम एक अगरबत्ती की गंध का पता कैसे लगाते हैं?
उत्तर:
अगरबत्ती की गंध का पता अग्रमस्पिक द्वारा लगाया जाता है। यहाँ गंध की संवेदना के लिए अलग संवेदी केंद्र होता है जहाँ सूचना प्राप्त होती है।

प्रश्न 5.
प्रतिवर्ती क्रिया में मस्तिष्क की क्या भूमिका है?
उत्तर:
प्रतिवर्ती क्रिया मेरुरज्जु द्वारा सम्पन्न होती है। प्रतिवर्ती चाप इसी मेरुरज्जु में बनते हैं यद्यपि आगत सूचनाएँ मस्तिष्क तक दी जाती हैं। सामान्य प्रतिवर्ती क्रिया जैसे पुतली के आकार में परिवर्तन तथा कोई सोची क्रिया जैसे कुर्सी खिसकाना। उसको मध्य एक और पेशी गति का सेट है जिस पर हमारे सोचने का कोई नियंत्रण नहीं है। इन अनैच्छिक क्रियाओं में से कई मध्यमस्तिष्क तथा पश्चमस्तिष्क से नियंत्रित होती हैं। ये सभी अनैच्छिक क्रियाएँ जैसे रक्तदाब, लार आना तथा वमन (उल्टी आना) पश्चमस्तिष्क स्थित मेडुला द्वारा नियंत्रित होती हैं।

पाठगत प्रश्न (पृष्ठ संख्या-136)

प्रश्न 1.
पादप हॉर्मोन क्या हैं?
उत्तर:
विविध पादप हॉर्मोन वृद्धि, विकास तथा पर्यावरण के प्रति अनुक्रिया के समन्वय में सहायता करते हैं। इनके संश्लेषण का स्थान इनके क्रिया क्षेत्र से दूर होता है और साधारण विसरण द्वारा वे क्रिया क्षेत्र तक पहुँच जाते हैं।

प्रश्न 2.
छुई-मुई पादप की पत्तियों की गति, प्रकाश की ओर प्ररोह की गति से किस प्रकार भिन्न है?
उत्तर:

छुई-मुई पादप की पत्तियों की गति	प्रकाश की ओर प्ररोह की गति
1. इसमें पत्तियों की गति किसी खास दिशा में नहीं होती है अर्थात् उद्दीपक (स्पर्श) की दिशा पर निर्भर नहीं करती है।	1. इसमें प्ररोह की गति उद्दीपक (प्रकाश) की दिशा में होती है।
2. इसमें वृद्धि नहीं होती है।	2. इसमें वृद्धि होती है।
3. अनुक्रिया की गति बहुत तीव्र होती है।	3. अनुक्रिया की गति धीमी होती है।
4. यह गति हॉर्मोन के द्वारा नहीं होती है।	4. यह गति ऑक्सिन हॉर्मोन के द्वारा होती है।
5. यह जल की मात्रा में परिवर्तन के कारण होता है।	5. यह प्ररोह के दोनों ओर असमान वृद्धि के कारण होता है।

प्रश्न 3.
एक पादप हॉर्मोन का उदाहरण दीजिए जो वृद्धि को बढ़ाता है।
उत्तर:

• ऑक्सिन पौधे के तने की लम्बाई को बढ़ाता है।
• जिब्बेरेलिन पौधे के तने की वृद्धि करता है।

प्रश्न 4.
किसी सहारे के चारों ओर एक प्रतान की वृद्धि में ऑक्सिन किस प्रकार सहायक है?
उत्तर:
प्रतान स्पर्श के प्रति संवेदनशील होता है। प्रतान जैसे ही किसी स्पर्श के सम्पर्क में आते हैं ऑक्सिन दूसरी ओर विसरित हो जाता है जिससे उस ओर की कोशिकाएँ अधिक लम्बी होने लगती हैं और प्रतान विपरीत दिशा में मुड़ता है। इस प्रकार वह सहारे के चारों ओर लिपटकर पौधे को सहारा देता है।

प्रश्न 5.
जलानुवर्तन दर्शाने के लिए एक प्रयोग की अभिकल्पना कीजिए।
उत्तर:
जलानुवर्तन प्रदर्शित करने के लिए बीजों का अंकुरण एक ऐसी जमीन के ऊपर करवाते हैं जो एक तरफ नम है तथा दूसरी तरफ सूखी।

मूलांकुर पहले तो धनात्मक गुरुत्वानुवर्तन दर्शांते हुए नीचे की ओर गति करते हैं। परन्तु जल्दी ही गीली जमीन की ओर मुड़ने लगते हैं। यह धनात्मक जलानुवर्तन गति को प्रदर्शित करता है।

पाठगत प्रश्न (पृष्ठ संख्या-138)

प्रश्न 1.
जंतुओं में रासायनिक समन्वय कैसे होता है?
उत्तर:
जंतुओं में रासायनिक समन्वय कुछ रासायनिक पदार्थ जिसे हॉर्मोन कहते हैं के द्वारा होता है। ये अंत:स्रावी ग्रंथियों द्वारा स्नावित होते हैं। स्रावित होने वाले हॉर्मोन का समय और मात्रा का नियंत्रण पुनर्भरण क्रिया विधि से किया जाता है।

प्रश्न 2.
आयोडीन युक्त नमक के उपयोग की सलाह क्यों दी जाती है?
उत्तर:
आयोडीन युक्त नमक के उपयोग की सलाह इसलिए दी जाती है क्योंकि आयोडीन, थाइराइड ग्रंथि जो कार्बोहाइड्रेट, वसा और प्रोटीन के उपापचय हेतु थायरॉक्सिन हॉर्मोन स्वावित करती है, के लिए आवश्यक है। यह हॉर्मोन संतुलित वृद्धि व विकास के लिए उत्तरदायी है। आयोडीन की कमी से घेंधा रोग हो जाता है।

प्रश्न 3.
जब एड़ीनलीन रुधिर में स्वावित होती है तो हमारे शरीर में क्या अनुक्रिया होती है?
उत्तर:
एड्रीनलीन सीधे रक्त में स्रावित होता है तथा शरीर के विभिन्न भागों में रुधिर प्रवाह के साथ फैलता है। यह मुख्य रूप से हुदय पर प्रभाव डालता है, जिससे हदय तेजी से धड़कने लगता है और पेशियों में ऑक्सीजन अधिक मात्रा में पहुँचाना शुरू करता है जिससे पेशियाँ अधिक सक्रिय हो जाती हैं। ये पेशियाँ शरीर की विभिन्न क्रियाविधियों को नियंत्रित करती हैं।

प्रश्न 4.
मधुमेह के कुछ रोगियों की चिकित्सा इंसुलिन का इंजेक्शन देकर क्यों की जाती है?
उत्तर:
इंसुलिन हॉर्मोन रक्त शर्करा को नियंत्रित करता है। मधुमेह के रोगी में अग्याशय ग्रंथि के अल्प सक्रियता के कारण यह हॉर्मोन कम मात्रा में स्रावित होता है जिससे रक्त शर्करा बढ़ जाती है। इसके शरीर पर घातक परिणाम होते हैं। इसलिए इंसुलिन का इंजेक्शन देकर रोगी की रक्त शर्करा को नियमित किया जाता है।

क्रिया-कलाप-7.1

प्रश्न 1.
कुछ चीनी अपने मुँह में रखिए। इसका स्वाद कैसा है?
उत्तर:
चीनी मीठी लगती है।

प्रश्न 2.
अपनी नाक को अँगूठा तथा तर्जनी अँगुली से दबाकर बंद कर लीजिए। अब फिर से चीनी खाइए। इसके स्वाद में क्या कोई अंतर है?
उत्तर:
हाँ, चीनी के स्वाद में अंतर महसूस होता है।

प्रश्न 3.
खाना खाते समय उसी तरह से अपनी नाक बंद कर लीजिए तथा ध्यान दीजिए कि जिस भोजन को आप खा रहे हैं, क्या आप उस खाने का पूरा स्वाद ले रहे हैं।
उत्तर:
छात्र अपने आप महसूस करें।

प्रश्न 4.
जब नाक बन्द होती है, तो क्या आप चीनी तथा भोजन के स्वाद में कोई अंतर महसूस करते हैं? यदि हाँ, तो आप सोचते होंगे कि यह क्यों होता है? इस तरह के अंतर जानने के लिए और उनके संभावित हल खोजने के लिए पढ़िए तथा चर्चा करिए। जब आपको जुकाम हो जाता है तब भी क्या आप इसी तरह की स्थिति का सामना करते हैं?
उत्तर:
हाँ।

क्रिया-कलाप-7.2

• एक शंकु फ्लास्क को जल से भर लीजिए।
• फ्लास्क की ग्रीवा को तार के जाल से ढक दीजिए।
• एक ताजा छोटा सेम का पौधा तार की जाली पर इस प्रकार रख दीजिए कि उसकी जड़ें जल में भीगी रहें।
  
• एक ओर से खुला हुआ गत्ते का एक बॉक्स लीजिए।
  
• फ्लास्क को बॉक्स में इस प्रकार रखिए कि बॉक्स की खुली साइड खिड़की की ओर हो जहाँ से प्रकाश आ रहा है।
• दो या तीन दिन बाद आप देखेंगे कि प्ररोह प्रकाश की ओर झुक जाता है तथा जड़ें प्रकाश से दूर चली जाती हैं।
• अब फ्लास्क को इस प्रकार घुमाइए कि प्ररहह प्रकाश से दूर तथा जड़ प्रकाश की ओर हो जाएँ। इसे इस अवस्था में कुछ दिन के लिए विक्षोभरहित छोड़ दीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
क्या प्ररोह और जड़ के पुराने भागों ने दिशा बदल दी है?
उत्तर:
पौधों के पुराने भाग जड़ और तने बहुत कम दिशा बदलते हैं जबकि नए भाग अधिक दिशा बदले हैं।

प्रश्न 2.
क्या ये अंतर नयी वृद्धि की दिशा मं हैं?
उत्तर:
हाँ, नयी वृद्धि की दिशा में अधिक परिवर्तन होता है।

प्रश्न 3.
इस क्रिया-कलाप से हम क्या निष्कर्ष निकालते हैं?
उत्तर:
उपर्युक्त क्रिया-कलाप में तने द्वारा ऋणात्मक गुरुत्वानुवर्तन और जड़ों द्वारा धनात्मक गुरुत्वानुवर्तन प्रदर्शित होता है।

क्रिया-कलाप-7.3

• चित्र देखिए।
• चित्र में दर्शाई गई अंतःस्रावी ग्रंथियों की पहचान कीजिए।
• इनमें से कुछ ग्रंथियों को पुस्तक में वर्णित किया गया है। पुस्तकालय में पुस्तकों की सहायता से एवं अध्यापकों के साथ चर्चा करके कुछ अन्य ग्रंथियों के कार्यों के बारे में जानकारी प्राप्त करें।

उत्तर:
अन्य ग्रंधियों के कार्यों के बारे में जानकारी प्राप्त कर निम्न तालिका में प्रदर्शित किया गया है-

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 बहुपद Exercise 2.4

प्रश्न 1.
सत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याएँ उसकी शून्यक हैं। प्रत्येक स्थिति में शून्यकों और गुणांकों के बीच के सम्बन्ध को भी सत्यापित कीजिए :
(i) 2x³ + x² – 5x + 2; \(\frac{1}{2}\), 1, -2
(ii) x³ – 4x² + 5x – 2; 2, 1, 1
हल:
(i) माना त्रिघात बहुपद p(x) = 2x³ + x² – 5x + 2
दी गई संख्याएँ = \(\frac{1}{2}\), 1, -2

\(\frac{1}{2}\), बहुपद p(x) का एक शून्यक है।
अब p(1) = 2 (1)³ + (1)² – 5(1) + 2
= 2 + 1 – 5 + 2
= 0
∴ 1 बहुपद p(x) का शून्यक है।
अब p(-2) = 2(-2)³ + (-2)² – 5(-2) + 2
= 2 × -8 + 4 + 10 + 2
= -16 + 16 = 0
∴ -2 बहुपद p(x) का शून्यक है।
अतः \(\frac{1}{2}\), 1 व -2 बहुपद 2x³ + x² – 5x + 2 के शून्यक हैं।
शून्यकों का योग = \(\frac{1}{2}\) + 1 + (-2) = –\(\frac{1}{2}\)
दो शून्यकों को साथ लेकर उनके गुणनफलों का योग
= \(\frac{1}{2}\) × 1 + 1 × (-2) + (-2) × \(\frac{1}{2}\)
= \(\frac{1}{2}\) – 2 – 1 = \(\frac{1}{2}\) – 3 = –\(\frac{5}{2}\)
शून्यकों का गुणनफल = \(\frac{1}{2}\) × 1 × -2 = -1
बहुपद 2x³ + x² – 5x + 2 के पदों की तुलना त्रिघात बहुपद ax³ + bx² + cx + d से करने पर,
a = 2, b = 1, c = -5 और d = 2 यदि बहुपद के शून्यक α, β और γ हों तो,
शून्यकों का योग (α + β + γ) = –\(\frac{b}{a}\) = –\(\frac{1}{2}\)
तथा αβ + βγ + γα = \(\frac{c}{a}=-\frac{5}{2}\)
और शून्यकों का गुणनफल = αβγ = \(\frac{-d}{a}\)
= \(\frac{-2}{2}\) = -1
∴ बहुपद के शून्यकों और गुणांकों के बीच सम्बन्ध सही है।

(ii) त्रिघात बहुपद p(x) = x³ – 4x² + 5x – 2 दी गई संख्याएँ = 2, 1, 1
अब p(2) = (2)³ – 4(2)² + 5(2) – 2
= 8 – 4 × 4 + 10 – 2
= 8 – 16 + 10 – 2 = 0
अत: 2 बहुपद p(x) का शून्यक है।
पुनः p(1) = (1)³ – 4(1)² + 5(1) – 2
= 1 – 4 + 5 – 2 = 0
अतः 1 बहुपद p(x) का शून्यक है।
अतः स्पष्ट है कि बहुपद x³ – 4x² + 5x – 2 के शून्यक 2, 1 और 1 है।
इन शून्यकों का योगफल = 2 + 1 + 1 = 4
शून्यकों का गुणनफल = 2 × 1 × 1 = 2
दो शून्यकों को साथ लेकर उनके गुणनफलों का योग
= ( 2 × 1) + (1 × 1) + (1 × 2) = 5
अब बहुपद x³ – 4x² + 5x – 2 के पदों की तुलना ax³ + bx² + cx + d से करने पर a = 1, b = – 4, c = 5 तथा d = -2
यदि शून्यक α, β व γ हों, तो
शून्यकों का योग = (α + β + γ)
= \(-\frac{b}{a}=-\frac{-4}{1}\) = 4
दो शून्यकों को साथ लेकर उनके गुणनफलों का योग = (αβ + βγ + γα)
= \(\frac{c}{a}=\frac{5}{1}\) = 5
तथा शून्यकों का गुणनफल = αβγ = \(\frac{-d}{a}\)
= \(-\left(\frac{-2}{1}\right)\) = 2
अत: बहुपद के शून्यकों का उनके गुणांकों से उक्त सम्बन्ध सत्य है।

प्रश्न 2.
एक त्रिघात बहुपद प्राप्त कीजिए जिसके शून्यकों का योग, दो शून्यकों को एक साथ लेकर उनके गुणनफलों का योग तथा तीनों शून्यकों के गुणनफल क्रमशः 2, -7, -14 हों।
हल:
माना बहुपद के शून्यक α, β और γ हों, तो
शून्यक का योग (α + β + γ) = 2
दो शून्यकों को साथ लेकर उनके गुणनफलों का योग (αβ + βγ + γα) = -7
शून्यकों का गुणनफल αβγ = -14
∴ वांछित त्रिघात बहुपद
= x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ
= x³ – 2x² + (-7)x – (-14)
= x³ – 2x² – 7x + 14
अतः अभीष्ट बहुपद x³ – 2x² – 7x + 14 है।

प्रश्न 3.
यदि बहुपद x³ – 3x² + x + 1 के शून्यक a – b, a, a + b हों, तो a और b ज्ञात कीजिए।
हल:
दिया गया बहुपद x³ – 3x² + x + 1
दिए गए बहुपद की तुलना Ax³ + Bx² + Cx + D से करने पर A = 1, B = -3, C = 1 तथा D = 1.
शून्यकों का योग = \(-\frac{B}{A}=-\left(\frac{-3}{1}\right)\) = 3
परन्तु शून्यक a – b, a तथा a + b हैं।
∴ a – b + a + a + b = 3
⇒ 3a = 3 ⇒ a = \(\frac{3}{3}\) = 1
शून्यकों का गुणनफल = \(-\frac{D}{A}=-\left(\frac{1}{1}\right)\) = -1
परन्तु शून्यकों का गुणनफल = (a – b) (a) (a + b)
= a(a² – b²)
तब a(a² – b²) = -1
∴ 1(1² – b²) = -1
⇒ 1 – b² = – 1
⇒ b² = 2 ⇒ b ± \(\sqrt{2}\)
अतः a = 1 और b ± \(\sqrt{2}\).

प्रश्न 4.
यदि बहुपद x⁴ – 6x³ – 26x² + 138x – 35 के दो शून्यक 2 ± \(\sqrt{3}\) हों, तो अन्य शून्यक ज्ञात कीजिए।
हल:
दिया है कि दो शून्यक (2 + \(\sqrt{3}\)) और (2 – \(\sqrt{3}\)) है।
∴ [x – (2 + \(\sqrt{3}\))] [x – (2 – \(\sqrt{3}\))]
= [(x – 2) – \(\sqrt{3}\)] [(x – 2) + \(\sqrt{3}\)]
= (x – 2)² – (\(\sqrt{3}\))2 = x² – 4x + 1
दिए गए बहुपद का एक गुणनखण्ड है।
पुन: x⁴ – 6x³ – 26x² + 138x – 35 को x² – 4x + 1 से विभाजित करने पर

विभाजन एल्गोरिथ्म का प्रयोग करने पर
∴ x⁴ – 6x³ – 26x² + 138x – 35
= (x² – 4x + 1) (x² – 2x – 35)
= (x² – 4x + 1 ) [x² – (7 – 5)x – 35]
= (x² – 4x + 1 ) [x² – 7x + 5x – 35]
= (x² – 4x + 1) [x(x – 7) + 5(x – 7)]
= (x² – 4x + 1)(x – 7)(x + 5)
अब बहुपद के अन्य शून्यकः
यदि x + 5 = 0 हो, तो x = -5
या फिर x – 7 = 0 हो, तो x = 7
अतः दिए गए चार घात वाले बहुपद के अन्य शून्यक -5 और 7 हैं।

प्रश्न 5.
यदि बहुपद x⁴ – 6x³ + 16x² – 25x + 10 को एक अन्य बहुपद x² – 2x + k से भाग दिया जाए और शेषफल x + a आता हो, तो k और a ज्ञात कीजिए।
हल:
दिया है कि बहुपद x⁴ – 6x³ + 16x² – 25x + 10 को x² – 2x + k से भाग देने पर शेषफल x + a आता है।

बहुपद x⁴ – 6x³ + 16x² – 25x + 10 के लिए विभाजन एल्गोरिथ्म का प्रयोग करने पर,
x⁴ – 6x³ + 16x² – 25x + 10 = (x – 2x + k) [x² – 4x + (8 – k)] + [(-9 + 2k)x + (10 – 8k + k²)
∴ भागफल = x² – 4x + (8 – k)
और शेषफल = (-9 + 2k)x + (10 – 8k + k²)
परन्तु शेषफल = x + a
∴ (-9 + 2k)x + (10 – 8k + k²) = x + a
समान गुणांकों की तुलना करने पर,
-9 + 2k = 1 तथा 10 – 8k + k² = a
या 2k = 1 + 9
या 2k = 10
या k = \(\frac{10}{2}\) = 5
अब k का मान 10 – 8k + k² = a में रखने पर,
10 – 8(5) + (5)² = a
या 10 – 40 + 25 = a
या -40 + 35 = a
या -5 = a
अर्थात् a = -5
अतः k = 5 और a = -5

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Exercise 4.2

प्रश्न 1.
गुणनखण्ड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए :
(i) x² – 3x – 10 = 0
(ii) 2x² + x – 6 = 0
(iii) \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
(iv) 2x² – x + \(\frac{1}{8}\) = 0
(v) 100x² – 20x + 1 = 0
हल:
(i) दिया गया द्विघात समीकरण है :
x² – 3x – 10 = 0
⇒ x² – (5 – 2)x – 10 = 0
⇒ x² – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0
⇒ (x – 5) (x + 2) = 0
यहाँ या तो (x – 5) = 0 या फिर (x + 2) = 0
यदि x – 5 = 0 हो तो x = 5 और
यदि x + 2 = 0 हो तो x = – 2
अतः द्विघात समीकरण के मूल 5 या -2 है।

(ii) दिया गया द्विघात समीकरण है :
2x² + x – 6 = 0
⇒ 2x² + (4 – 3)x – 6 = 0
⇒ 2x² + 4x – 3x – 6 = 0
⇒ 2x(x + 2) – 3(x + 2) = 0
⇒ (x + 2) (2x – 3) = 0
यहाँ या तो (x + 2) = 0 या फिर (2x – 3) = 0
यदि x + 2 = 0 हो, तो x = -2
यदि 2x – 3 = 0 हो, तो
⇒ 2x = 3 या x = \(\frac{3}{2}\)
अतः द्विघात समीकरण के मूल – 2 या \(\frac{3}{2}\) है।

(iii) दिया गया द्विघात समीकरण है:
\(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) =0
\(\sqrt{2}\)x² + (5 + 2)x + 5\(\sqrt{2}\) = 0
\(\sqrt{2}\)x² + 5x + 2x + 5\(\sqrt{2}\) = 0
x(\(\sqrt{2}\)x + 5) + \(\sqrt{2}\)(\(\sqrt{2}\)x + 5) = 0
(\(\sqrt{2}\)x + 5) (x + \(\sqrt{2}\)) = 0
यहाँ या तो (\(\sqrt{2}\)x + 5) = 0 या फिर (x + \(\sqrt{2}\)) = 0
यदि \(\sqrt{2}\)x + 5 = 0 हो, तो
\(\sqrt{2}\)x – 5 ⇒ x = \(-\frac{5}{\sqrt{2}}\)
यदि x + \(\sqrt{2}\) = 0 हो, तो x = –\(\sqrt{2}\)
अतः द्विघात समीकरण के मूल \(-\frac{5}{\sqrt{2}}\) या –\(\sqrt{2}\) होंगे।

(iv) दिया गया द्विघात समीकरण है:
2x² – x – \(\frac{1}{8}\) = 0
⇒ \(\frac{16 x^2-8 x+1}{8}\) = 0
⇒ 16x² – 8x + 1 = 0
⇒ 16x² – 4x – 4x + 1 = 0
⇒ 4x(4x – 1) -1 (4x – 1) = 0
⇒ (4x – 1) (4x – 1) = 0
अर्थात् 4x – 1 = 0 या 4x – 1 = 0
x = \(\frac{1}{4}\) या x = \(\frac{1}{4}\)
अतः द्विघात समीकरण के मूल \(\frac{1}{4}\) या \(\frac{1}{4}\) अर्थात् दोनों मूल समान होंगे।

(v) दिया गया द्विघात समीकरण है:
100x² – 20x + 1 = 0
100x² – 10x – 10x + 1 = 0
⇒ 10x(10x – 1) – 1(10x – 1) = 0
⇒ (10x – 1) (10x – 1) = 0
अर्थात् 10x – 1 = 0 या फिर 10x – 1 = 0
या 10x = 1 या 10x = 1
या x = \(\frac{1}{10}\) या x = \(\frac{1}{10}\)
अतः द्विघात समीकरण के दोनों मूल समान होंगे।
∴ x = \(\frac{1}{10}\) और \(\frac{1}{10}\)

प्रश्न 2.
उदाहरण 1 में दी गई समस्याओं को हल कीजिए:
(i) जॉन और जीवंती दोनों के पास कुल मिलाकर 45 कंचे हैं। दोनों पाँच-पाँच कंचे खो देते हैं। अब उनके पास कंचों की संख्या का गुणनफल 124 है। हम जानना चाहेंगे कि प्रारम्भ में उनके पास कितने-कितने कंचे थे ?
(ii) एक कुटीर उद्योग एक दिन में कुछ खिलौने निर्मित करता है। प्रत्येक खिलौने का मूल्य (₹ में), 55 में से एक दिन में निर्मित खिलौनों की संख्या को घटाने से प्राप्त संख्या के बराबर है। किसी दिन कुल निर्माण लागत ₹ 750 थी। हम उस दिन निर्माण किए गए खिलौनों की संख्या ज्ञात करना चाहेंगे।
हल:
(i) माना प्रारम्भ में जॉन के पास x कंचे थे।
दोनों के पास कुल मिलाकर 45 कंचे थे।
∴ जीवंती के पास प्रारम्भ में कंचों की संख्या = (45 – x)
जब जॉन 5 कंचे खो देता है, तो उसके पास कंचों की संख्या = (x – 5)
इसी प्रकार,
जब जीवंती 5 कंचे खो देती है, तो उसके पास शेष कंचों की संख्या
= (45 – x – 5) = (40 – x)
अब कंचों की संख्या का गुणनफल = (x – 5) (40 – x)
= 40x – x² – 200 + 5x
= – x² + 45x – 200
परन्तु प्रश्नानुसार,
-x² + 45x – 200 = 124
⇒ -x² + 45x – 200 – 124 = 0
⇒ -x² + 45x – 324 = 0
⇒ -(x² – 45x + 324) = 0
⇒ x² – 45x + 324 = 0
⇒ x² – (36 + 9)x + 324 = 0
⇒ x² – 36x – 9x + 324=0
⇒ x(x – 36 ) – 9(x – 36) = 0
(x – 36) (x – 9) = 0
या तो x – 36 = 0 या फिर x – 9 = 0
यदि x – 36 = 0 तो x = 36
और यदि x – 9 = 0 तो x = 9
अत: जॉन के पास कंचों की संख्या = 36 अथवा 9 तब स्पष्ट है कि
यदि जॉन के पास 36 कंचे हैं, तो जीवन्ती के पास 9 कंचे होंगे।
और यदि जॉन के पास 9 कंचे हैं, तो जीवंती के पास 36 कंचे होंगे।
अतः उनके पास कंचों की संख्या (9, 36) अथवा (36, 9)।

(ii) माना उस विशेष दिन x खिलौने निर्मित किए गए।
∴ प्रत्येक खिलौने का मूल्य = ₹ (55 – x)
∴ उस दिन निर्मित सभी खिलौनों की लागत
= ₹ x(55 – x)
= ₹ (55x – x²)
परन्तु प्रश्नानुसार उस दिन की निर्माण लागत ₹ 750 थी।
⇒ 55x – x² = 750
⇒ 55x – x² – 750 = 0
⇒ x² – 55x + 750 = 0
⇒ x² – (30 + 25)x + 750 = 0
⇒ x² – 30x – 25x + 750 = 0
⇒ x(x – 30 ) – 25 (x – 30 ) = 0
⇒ (x – 30) (x – 25) = 0
अर्थात् x – 30 = 0 या फिर x – 25 = 0
∴ x = 30 या x = 25
x = 30 और 25
अतः उस दिन निर्मित खिलौनों की संख्या 30 या 25 है।

प्रश्न 3.
ऐसी दो संख्याएँ ज्ञात कीजिए, जिनका योग 27 हो और गुणनफल 182 हो।
हल:
माना कि पहली संख्या x है।
दिया है, दोनों संख्याओं का योग 27 है।
∴ दूसरी संख्या = 27 – x
दिया है, संख्याओं का गुणनफल = x(27 – x)
= 27x – x²
प्रश्नानुसार, 27x – x² = 182
⇒ -x² – 27x – 182 = 0
⇒ x² – 27x + 182 = 0
⇒ x² – 13x – 14x + 182 = 0
⇒ (x – 13) – 14(x – 13) = 0
⇒ (x – 13 ) (x – 14) = 0
अर्थात् या तो
x – 13 = 0 या फिर x – 14 = 0
∴ x = 13 या x = 14
∴ x = 13, 14
अतः दो संख्याएँ 13 और 14 हैं।

प्रश्न 4.
दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 हो।
हल:
माना कि पहला धनात्मक पूर्णांक x है
तथा दूसरा क्रमागत धनात्मक पूर्णांक (x + 1) होगा।
प्रश्नानुसार, (x²) + (x + 1 )² = 365
⇒ x² + x² + 1 + 2x = 365
⇒ 2x² + 2x + 1 – 365 = 0
⇒ 2x² + 2x – 364 = 0
⇒ x² + x – 182 = 0
⇒ x² + 14x – 13x – 182 = 0
⇒ x(x + 14) – 13 (x + 14) = 0
⇒ (x + 14) (x – 13) = 0
या तो x + 14 = 0 या x – 13 = 0
⇒ x = -14 या x = 13
∵ हमें धनात्मक पूर्णांक चाहिए।
इसलिए x = -14 सम्भव नहीं है।
∴ x = 13
∴ दूसरा धनात्मक पूर्णांक = 13 + 1 = 14
अतः दो अभीष्ट क्रमागत धनात्मक पूर्णांक 13 और 14 है।

प्रश्न 5.
एक समकोण त्रिभुज की ऊँचाई इसके आधार से 7 सेमी कम है। यदि कर्णे 13 सेमी हो, तो अन्य दो भुजाएँ ज्ञात कीजिए।
हल:
माना कि समकोण त्रिभुज का आधार = x सेमी
इसलिए, समकोण त्रिभुज की ऊँचाई (लम्ब) = (x – 7 ) सेमी
दिया है, समकोण त्रिभुज का कर्ण = 13 सेमी
पाइथागोरस प्रमेय के अनुसार,
(आधार)² + (लम्ब)² = (कर्ण)²
(x)² + (x – 7)² = (13)²
⇒ x² + x² + 49 – 14x = 169
⇒ 2x² – 14x + 49 – 169 = 0
⇒ 2x² – 14x – 120 = 0
⇒ 2[x² – 7x – 60] = 0
⇒ x² – 7x – 60= 0
⇒ x² – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5 (x – 12) = 0
⇒ (x – 12) (x + 5) = 0
या तो x – 12 = 0 या x + 5 = 0
⇒ x = 12 या x = -5
∵ त्रिभुज की लम्बाई कभी ऋणात्मक नहीं हो सकती।
इसलिए हम x = -5 को छोड़ देते हैं।
∴ x = 12
अतः समकोण त्रिभुज का आधार = 12 सेमी
समकोण त्रिभुज की ऊँचाई (लम्ब) = (12 – 7) सेमी 5 सेमी।
अतः त्रिभुज की अन्य दो भुजाएँ 5 सेमी और 12 सेमी हैं।

प्रश्न 6.
एक कुटीर उद्योग एक दिन में कुछ बर्तनों का निर्माण करता है। एक विशेष दिन यह देखा गया कि प्रत्येक नग की निर्माण लागत (₹ में) उस दिन के निर्माण किए बर्तनों की संख्या के दुगने से 3 अधिक थी। यदि उस दिन की कुल निर्माण लागत ₹ 90 थी, तो निर्मित बर्तनों की संख्या और प्रत्येक नग की लागत ज्ञात कीजिए।
हल:
माना कि एक विशेष दिन में निर्मित बर्तनों की संख्या x थी।
∵ प्रत्येक नग की लागत निर्मित बर्तनों की संख्या के दुगने से 3 अधिक थी।
∴ प्रत्येक नग की लागत = ₹ (2x + 3)
तब उस दिन निर्मित सभी बर्तनों की लागत = ₹ x × (2x + 3)
= ₹ (2x² + 3x)
प्रश्नानुसार,
उस दिन की कुल निर्माण लागत = ₹ 90
∴ 2x² + 3x = 90
⇒ 2x² + 3x – 90 = 0
⇒ 2x² + (15 – 12)x – 90 = 0
⇒ 2x² + 15x – 12x – 90 = 0
⇒ x(2x + 15) – 6(2x + 15) = 0
⇒ (2x + 15) (x – 6) = 0
यदि 2x + 15 = 0 हो, तो 2x = -15 ⇒ x = –\(\frac{15}{2}\)
और यदि x – 6 = 0 हो, तो x = 6
∵ बर्तनों की संख्या ऋणात्मक नहीं हो सकती है।
अतः x = –\(\frac{15}{2}\) को छोड़ देते हैं।
∴ x = 6 अर्थात् निर्मित बर्तनों की संख्या = 6
तब प्रत्येक नग की लागत = ₹ (2x + 3)
= ₹ (2 × 6 + 3)
= ₹ (12 + 3) = 15
अतः निर्मित बर्तनों की संख्या 6 तथा प्रत्येक नग की लागत ₹ 15 है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 15 प्रायिकता Ex 15.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 15 प्रायिकता Exercise 15.2

प्रश्न 1.
दो ग्राहक श्याम और एकता एक विशेष दुकान पर एक ही सप्ताह में जा रहे हैं (मंगलवार से शनिवार तक) । प्रत्येक द्वारा दुकान पर किसी दिन या किसी अन्य दिन जाने के परिणाम समप्रायिक हैं। इसकी क्या प्रायिकता है कि दोनों उस दुकान पर
(i) एक ही दिन जाएँगे ?
(ii) क्रमागत दिनों में जाएँगे?
(iii) भिन्न-भिन्न दिनों में जाएँगे ?
हल :
दो ग्राहक श्याम और एकता एक विशेष दुकान पर एक ही सप्ताह में (मंगलवार से शनिवार तक) जा रहे हैं। प्रत्येक ग्राहक द्वारा दुकान पर किसी दिन या किसी अन्य दिन जाने के परिणाम समप्रायिक हैं। सम्भव परिणाम निम्न होंगे-

(i) यदि दोनों ग्राहकों को एक ही दिन जाने के अनुकूल परिणाम (T, T); (W, W), (Th, Th), (F, F); (S, S)
दोनों ग्राहकों के एक ही दिन जाने के अनुकूल परिणामों की संख्या = 5
अतः दोनों ग्राहकों को दुकान पर एक ही दिन जाने की प्रायिकता = \(\frac{5}{25}=\frac{1}{5}\)
P(A) = \(\frac {1}{5}\)

(ii) ग्राहकों के क्रमागत दिनों में
अनुकूल परिणाम
(श्याम, एकता) = (T, W), (W, Th), (Th, F), (F, S)
या (एकता, श्याम) = (W, T), (Th, W), (F, Th), (S, F)
अतः कुल अनुकूल परिणामों की संख्या = 8
अतः दोनों ग्राहकों के क्रमागत दिनों में जाने की प्रायिकता = \(\frac {8}{25}\)

(iii) दोनों ग्राहकों को दुकान पर एक ही दिन न जाने की प्रायिकता P(A) = 1 – P(A) = 1 – \(\frac{1}{5}=\frac{4}{5}\)

प्रश्न 2.
एक पासे के फलकों पर संख्याएँ 1, 2, 2, 3, 3 और 6 लिखी हुई हैं। इसे दो बार फेंका जाता है तथा दोनों बार प्राप्त हुई संख्याओं के योग लिख लिए जाते हैं। दोनों बार फेंकने के बाद, प्राप्त योग के कुछ सम्भावित मान निम्नलिखित सारणी में दिए हैं। इस सारणी को पूरा कीजिए।

इसकी क्या प्रायिकता है कि कुल योग (i) एक सम संख्या होगा ?, (ii) 6 है ?, (iii) कम से कम 6 है ? सारणी की पूर्ति
हल:

(i) कुल योग सम संख्या होने के अनुकूल परिणाम = (2, 4, 4, 4, 4, 4, 4, 4, 4, 6, 6, 6, 6, 8, 8, 8, 8, 12)
कुल योग सम संख्या होने के अनुकूल परिणामों की संख्या = 18
अतः योग सम हीने की प्रायिकता = \(\frac{18}{36}=\frac{1}{2}\)

(ii) कुल योग 6 होने के अनुकूल परिणामों की संख्या = 4
अतः योग 6 होने की प्रायिकता = \(\frac{4}{36}=\frac{1}{9}\)

(iii) कुल योग कम से कम 6 होने के अनुकूल परिणाम = 7, 8, 8, 6, 6, 9, 6, 6, 9, 7, 8, 8, 9, 9, और 12 कुल योग कम से कम 6 होने के अनुकूल परिणामों की संख्या = 15
योग कम से कम 6 होने की प्रायिकंता = \(\frac{15}{36}=\frac{5}{12}\)

प्रश्न 3.
एक थैले में 5 लाल गेंद और कुछ नीली गेंदें हैं। यदि इस थैले में से नीली गेंद निकालने की प्रायिकता लाल गेंद निकालने की प्रायिकता की दुगनी है, तो थैले में नीली गेंदों की संख्या ज्ञात कीजिए।
हल :
माना थैले में नीली गेंदों की संख्या x है।
∴ कुल गेंदों की संख्या = 5 लाल + x नीली
= (5 + x)
थैले में से यादृच्छया 1 गेंद निकालने पर,
कुल सम्भव परिणामों की संख्या = (5 + x)
लाल गेंद निकलने के अनुकूल परिणामों की संख्या = 5
∴ लाल गेंद निकलने की प्रायिकता = \(\frac{5}{5+x}\)
नीली गेंद निकलने की प्रायिकता = \(\frac{x}{5+x}\)
नीली गेंद निकलने की प्रायिकता, लाल गेंद निकलने की प्रायिकता की दुगुनी है।
∴ \(\frac{x}{5+x}\) = 2 × \(\frac{5}{5+x}\)
⇒ \(\frac{x}{5+x}\) = \(\frac{10}{5+x}\)
∴ x = 10
अतः थैले में नीली गेंदों की संख्या = 10

प्रश्न 4.
एक पेटी में 12 गेंदें हैं, जिनमें सेx गेंदें काली हैं। यदि इनमें से एक गेंद यादृच्छया निकाली जाती है, तो इसकी प्रायिकता ज्ञात कीजिए कि यह गेंद काली है।
यदि इस पेटी में 6 काली गेंदें और डाल दी जाएँ, तो काली गेंद निकालने की प्रायिकता पहली प्रायिकता की दुगनी हो जाती है। x का मान ज्ञात कीजिए।
हल :
पेटी में गेंदों की कुल संख्या = 12
काली गेंदों की संख्या = x
यदि पेटी में से एक गेंद यादृच्छया निकाली जाती है तो गेंद निकालने के कुल सम्भव परिणामों की संख्या = 12
निकाली गई गेंद काली होने के अनुकूल परिणामों की संख्या = x
अतः निकाली गई गेंद काली होने की प्रायिकता = \(\frac {x}{12}\)
यदि पेटी में 6 काली गेंदें और मिला दी जाएँ तो काली गेंद निकलने के अनुकूल परिणामों की संख्या = x + 6
कुल सम्भव परिणामों की संख्या 12 + 6 = 18
अतः अब काली गेंद निकलने की प्रायिकता = \(\frac{x+6}{18}\)
वर्तमान प्रायिकता = 2 × पहले की प्रायिकता

प्रश्न 5.
एक जार में 24 कंचे हैं जिनमें कुछ हरे हैं और शेष नीले हैं। यदि इस जार में से यादृच्छया एक कंचा निकाला जाता है तो इस कंचे के हरा होने की प्रायिकता \(\frac {2}{3}\) है। जार में नीले कंचों की संख्या ज्ञात कीजिए।
हल :
जार में कुल कंचों की संख्या 24 है।
कुल सम्भव परिणामों की संख्या = 24
माना जार में हरे कंचों की संख्या x है।
∴ घटना के अनुकूल परिणामों की संख्या = x
जब जार में से 1 कचा यादृच्छया निकाला जाता है तो
कंचे के हरे होने की प्रायिकता = \(\frac {x}{24}\)
दिया है, कंचे के हरे होने की प्रायिकता = \(\frac {2}{3}\)
∴ \(\frac{x}{24}=\frac{2}{3}\)
⇒ 3x = 2 × 24
⇒ x = \(\frac {48}{3}\)
∴ x = 16
जार में हरे कंचों की संख्या = 16
तथा जार में नीले कंचों की संख्या = 24 – 16 = 8
अतः जार में नीले कंचों की संख्या = 8

Jharkhand Board JAC Class 10 Science Solutions Chapter 3 धातु एवं अधातु Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 3 धातु एवं अधातु

Jharkhand Board Class 10 Science धातु एवं अधातु Textbook Questions and Answers

प्रश्न 1.
निम्न में कौन-सा युगल विस्थापन अभिक्रिया प्रदर्शित करता है-
(a) NaCl विलयन एवं कॉपर धातु
(b) MgCl₂ विलयन एवं ऐलुमिनियम धातु
(c) FeSO₄ विलयन एवं सिल्वर धातु
(d) AgNO₃ विलयन एवं कॉपर धातु
उत्तर:
(d) AgNO₃ विलयन एवं कॉपर धातु।

प्रश्न 2.
लोहे के फ्राइंग पैन (frying pan) को जंग से बचाने के लिए निम्न में से कौन-सी विधि उपयुक्त है?
(a) ग्रीज लगाकर
(b) पेंट लगाकर
(c) जिंक की परत चढ़ाकर
(d) ये सभी
उत्तर:
(c) जिंक की परत चढ़ाकर।

प्रश्न 3.
कोई धातु ऑक्सीजन के साथ अभिक्रिया कर उच्च गलनांक वाला यौगिक निर्मित करती है यह यौगिक जल में विलेय है। यह तत्त्व क्या हो सकता है?
(a) कैल्सियम
(b) कार्बन
(c) सिलिकन
(d) लोहा
उत्तर:
(a) कैल्सियम

प्रश्न 4.
खाद्य पदार्थ के डिब्बों पर जिंक की बजाय टिन की परत होती है क्योंकि-
(a) टिन की अपेक्षा जिंक मँहगा है।
(b) टिन की अपेक्षा जिंक का गलनांक अधिक है
(c) टिन की अपेक्षा जिंक अधिक अभिक्रियाशील है
(d) टिन की अपेक्षा जिंक कम अभिक्रियाशील है
उत्तर:
(c) टिन की अपेक्षा जिंक अधिक अभि-क्रियाशील है।

प्रश्न 5.
आपको एक हथौड़ा, बैटरी, बल्ब, तार एवं स्विच दिया गया है-
(a) इनका उपयोग कर धातुओं एवं अधातुओं के नमूनों को कैसे अलग कर सकते हैं?
(b) धातुओं एवं अधातुओं में विभेदन के लिए इन परीक्षणों की उपयोगिताओं का आकलन कीजिए।
उत्तर:
(a) नीचे दिए गए चित्र के अनुरूप हम एक परिपथ बनाएँगे।

यदि नमूने को विद्युत परिपथ में लगाने पर स्विच ऑन करने पर बल्ब जलता है, तो दिया गया नमूना एक धातु है।

(b) यह विधि धातु एवं अधातु की जाँच के लिए बहुत ही उपयोगी है, किन्तु ग्रेफाइट एक अपवाद है क्योंकि यह अधातु होते हुए भी विद्युत का चालक है।

प्रश्न 6.
उभयधर्मी ऑक्साइड क्या होते हैं? दो उभयधर्मी ऑक्साइडों का उदाहरण दीजिए।
उत्तर:
वे ऑक्साइड जो अम्ल तथा क्षार दोनों से अभिक्रिया कर लवण प्रदान करते हैं, उभयधर्मी ऑक्साइड कहलाते हैं। उदाहरण के लिए ऐलुमिनियम ऑक्साइड निम्नलिखित तरीके से अम्लों तथा क्षारों के साथ अभिक्रिया करता है

जिंक ऑक्साइड एक अन्य उभयधर्मी ऑक्साइड है।

प्रश्न 7.
दो धातुओं के नाम बताइए जो तनु अम्ल से हाइड्रोजन को विस्थापित कर देंगे तथा दो धातुएँ जो ऐसा नहीं कर सकती हैं।
उत्तर:
हाइड्रोजन को विस्थापित करने वाली धातुएँ – मैग्नीशियम, जिंक हाइड्रोजन को विस्थापित नहीं कर सकने वाली धातुएँ – कॉपर, सोना।

प्रश्न 8.
किसी धातु M के विद्युत अपघटनी परिष्करण में आप ऐनोड, कैथोड एवं विद्युत अपघट्य किसे बनाएँगे?
उत्तर:
इस प्रक्रिया में अशुद्ध धातु को ऐनोड बनाया जाता है तथा शुद्ध धातु की एक पतली पट्टी को कैथोड बनाया जाता है। धात्विक लवण का उपयोग विद्युत अपघट्य के रूप में किया जाता है। उपकरणों को दिए गए चित्र के अनुसार व्यवस्थित किया जाता है। विद्युत अपघट्य से विद्युत प्रवाहित करने पर ऐनोड पर स्थित शुद्ध

ताँबे का विद्युत अपघटनी परिष्करण अम्लीकृत कॉपर सल्फेट का विलयन विद्युत अपघट्य है। अशुद्ध ताँबा ऐनोड है जबकि शुद्ध ताँबे की पट्टी कैथोड का कार्य करती है। विद्युत धारा प्रवाहित करने पर शुद्ध ताँबा कैथोड पर निक्षेपित हो जाता है।

धातु विद्युत अपघट्य में घुल जाता है। शुद्ध धातु की इतनी ही मात्रा कैथोड पर जमा हो जाती है। विलयशील अशुद्धियाँ विलयन में पहुँच जाती हैं जबकि अविलयशील अशुद्धियाँ ऐनोड के नीचे जम जाती हैं, जिन्हें ऐनोड पंक कहा जाता है।

प्रश्न 9.
प्रत्यूष ने सल्फर चूर्ण को स्पैचुला में लेकर उसे गर्म किया। चित्र के अनुसार एक परखनली को उल्टा करके उसने उत्सर्जित गैस को एकत्र किया।

(a) गैस की क्रिया क्या होगी
(i) सूखे लिटमस पत्र पर?
(ii) आर्द्र लिटमस पत्र पर?

(b) ऊपर की अभिक्रियाओं के लिए संतुलित रासायनिक अभिक्रिया लिखिए।
उत्तर:
(a) (i) सूखे लिटमस पत्र पर कोई क्रिया नहीं होती।
(ii) यह गैस आर्द्र नीले लिटमस पत्र को लाल कर देती है।

(b) S + O₂ → SO₂

प्रश्न 10.
लोहे को जंग से बचाने के लिए दो तरीके बताइए।
उत्तर:

1. यशदलेपन – इस प्रक्रिया में लोहे की वस्तुओं के ऊपर जिंक की एक परत चढ़ाई जाती है।
2. पेंटिंग – इस प्रक्रिया में लोहे की वस्तुओं पर पेंट किया जाता है।

प्रश्न 11.
ऑक्सीजन के साथ संयुक्त होकर अधातुएँ कैसा ऑक्साइड बनाती हैं?
उत्तर:
क्षारीय तथा उभयधर्मी ऑक्साइड।

प्रश्न 12.
कारण बताइए-
(a) प्लैटिनम, सोना एवं चाँदी का उपयोग आभूषण बनाने के लिए किया जाता है।
(b) सोडियम, पोटैशियम एवं लीथियम को तेल के अंदर संगृहीत किया जाता है।
(c) ऐलुमिनियम अत्यधिक अभिक्रियाशील धातु है। फिर भी इसका उपयोग खाना बनाने वाले बर्तन बनाने के लिए किया जाता है।
(d) निष्कर्षण प्रक्रम में कार्बोनेट एवं सल्फाइड अयस्क को ऑक्साइड में परिवर्तित किया जाता है।
उत्तर:
(a) प्लैटिनम, सोना एवं चाँदी बहुत कम अभिक्रियाशील हैं तथा संक्षारित भी नहीं होते। उनकी चमक भी तेज होती है। इन्हीं कारणों से इनका उपयोग आभूषण बनाने के लिए किया जाता है।

(b) सोडियम एवं पोटैशियम जैसी धातुएँ इतनी अभिक्रियाशील हैं कि खुले में रखने पर तत्काल आग पकड़ लेती हैं। अर्थात् उन्हें बचाने तथा आग लगने से रोकने के लिए उन्हें किरोसीन तेल के अंदर संगृहीत किया जाता है।

(c) ऐलुमिनियम संक्षारित नहीं होता, साथ ही यह ऊष्मा का सुचालक है।

(d) किसी धातु को उसके सल्फाइड और कार्बोनेट की अपेक्षा उसके ऑक्साइड से प्राप्त करना अधिक आसान है। इसलिए अपचयन से पहले धातु सल्फाइड एवं कार्बोनेट को धातु ऑक्साइड में बदल लेना चाहिए।

प्रश्न 13.
आपने ताँबे के मलीन बर्तन को नींबू या इमली के रस से साफ करते अवश्य देखा होगा। यह खट्टे पदार्थ बर्तन को साफ करने में क्यों प्रभावी हैं?
उत्तर:
ताँबे के ऊपर आर्द्र वायु तथा CO₂ के कारण कॉपर कार्बोनेट की एक हरी-सी परत बन जाती है, जो क्षारकीय प्रकृति की होती है। इसलिए जब इसे नींबू या इमली के रस से साफ करते हैं, तो इसमें मौजूद अम्ल क्षारक को उदासीन कर देता है और बर्तन साफ हो जाता है।
कॉपर कार्बोनेट + साइट्रिक अम्ल → कॉपर साइट्रेट + CO₂ + H₂O

प्रश्न 14.
रासायनिक गुणधर्मों के आधार पर धातुओं एवं अधातुओं में विभेद कीजिए।
उत्तर:
धातुओं एवं अधातुओं में निम्न प्रकार से विभेद किया जा सकता है-

धातु	अधातु
1. धातुएँ क्षारकीय ऑक्साइड बनाती हैं।	1. अधातुएँ अम्लीय या उदासीन ऑक्साइड बनाती हैं।
2. धातुएँ तनु HCl या तनु H2SO4 से अभिक्रिया कर H2 गैस मुक्त करती हैं, क्योंकि हाइड्रोजन को विस्थापित कर देती हैं।	2. अधातुएँ तनु HCl या तनु H2SO4 से अभिक्रिया नहीं करती हैं क्योंक हाइड्रोजन को विस्थापित नहीं करती हैं।
3. धातुएँ अपचायक होती हैं।	3. अधातुएँ उपचायक होती हैं।
4. धातुएँ इलेक्ट्रॉन त्यागकर धनात्मक आयन बनाती हैं।	4. अधातुएँ इलेक्ट्रॉन ग्रहण कर ऋणात्मक आयन बनाती है।
5. धातुएँ जल (या भाप) से हाइड्रोजन को विस्थापित कर देती हैं।	5. अधातुएँ जल से या भाप से अभिक्रिया नहीं करती हैं। अतः हाइड्रोजन को जल से विस्थापित नहीं करती हैं।
6. सभी धातुएँ H2 से संयोग कर हाइड्राइड नहीं बनाती हैं (केवल Na, K, Ca जैसे क्रियाशील तत्त्व बनाती हैं)।	6. सभी अधातुएँ H2 से संयोग कर हाइड्राइड बनाती हैं।

प्रश्न 15.
एक व्यक्ति प्रत्येक घर में सुनार बनकर जाता है। उसने पुराने एवं मलीन सोने के आभूषणों में पहले जैसी चमक पैदा करने का ढोंग रचाया। कोई संदेह किये बिना ही एक महिला अपने सोने के कंगन उसे देती है जिसे वह एक विशेष विलयन में डाल देता है। कंगन नए की तरह चमकने लगते हैं लेकिन उनका वजन अत्यन्त कम हो जाता है। वह महिला बहुत दुखी होती है तथा तर्क-वितर्क के पश्चात् उस व्यक्ति को झुकना पड़ता है। एक जासूस की तरह क्या आप उस विलयन की प्रकृति के बारे में बता सकते हैं?
उत्तर:
उस सुनार द्वारा ऐक्वारेजिया विलयन का उपयोग किया गया।

प्रश्न 16.
गर्म जल का टैंक बनाने में ताँबे का उपयोग होता है परंतु इस्पात (लोहे की मिश्रधातु) का नहीं। इसका कारण बताइए।
उत्तर:
गर्म लोहा उबलते पानी से उत्पन्न भाप के साथ अभिक्रिया करता है, किंतु ताँबा जल के साथ अभिक्रिया नहीं करता है।

Jharkhand Board Class 10 Science धातु एवं अधातु InText Questions and Answers

पाठगत प्रश्न (पृष्ठ संख्या-45)

प्रश्न 1.
ऐसी धातु का उदाहरण दीजिए जो-
(i) कमरे के ताप पर द्रव होती है।
(ii) चाकू से आसानी से काटा जा सकता है।
(iii) ऊष्मा की सबसे अच्छी चालक होती है।
(iv) ऊष्मा की कुचालक होती है।
उत्तर:
(i) मर्करी (Hg)।
(ii) सोडियम (Na) लीथियम (Li) और पोटैशियम (K)।
(iii) सिल्वर (Ag) तथा कॉपर (Cu)।
(iv) लेड (Pb) तथा मर्करी (Hg )।

प्रश्न 2.
आघातवर्ध्य तथा तन्य का अर्थ बताइए।
उत्तर:
कुछ धातुओं को पीटकर पतली चादर बनाया जा सकता है। इस गुणधर्म को आघातवर्ध्यता कहते हैं। सोना तथा चाँदी सबसे अधिक आघातवर्ध्य धातुएँ हैं। धातु के पतले तार के रूप में खींचने की क्षमता को तन्यता कहा जाता है। सोना सबसे अधिक तन्य धातु है।

पाठगत प्रश्न (पृष्ठ संख्या – 51)

प्रश्न 1.
सोडियम को किरोसीन तेल में डुबो कर क्यों रखा जाता है?
उत्तर:
सोडियम सामान्य ताप पर भी नमी तथा ऑक्सीजन के साथ तेजी से अभिक्रिया करती है। किन्तु यह किरोसीन के साथ न तो कोई अभिक्रिया करती है और न ही इसमें घुलती है। अतः सोडियम को किरोसीन तेल में डुबो कर रखा जाता है।

प्रश्न 2.
इन अभिक्रियाओं के लिए समीकरण लिखिए:
(i) भाप के साथ आयरन।
(ii) जल के साथ कैल्सियम तथा पोटैशियम।
उत्तर:
(i) 2Fe + 3H₂O → Fe₂O₃ + 3H₂

(ii) Ca + 2H₂O → Ca(OH)₂ + H₂
2K + 2H₂O → 2KOH + H₂ + ऊष्मा

प्रश्न 3.
A, B, C एवं D चार धातुओं के नमूनों को लेकर एक-एक करके निम्न विलयन में डाला गया। इससे प्राप्त परिणाम को निम्न प्रकार से सारणीबद्ध किया गया है:

धातु	आयरन (II) सल्फेट	कॉपर (II) सल्फेट	जिंक सल्फेट	सिल्वर नाइट्रेट
A	कोई अभिक्रिया नहीं	विस्थापन
B	विस्थापन		कोई अभिक्रिया नहीं
C	कोई अभिक्रिया नहीं	कोई अभिक्रिया नहीं	कोई अभिक्रिया नहीं	विस्थापन
D	कोई अभिक्रिया नहीं	कोई अभिक्रिया नहीं	कोई अभिक्रिया नहीं	कोई अभिक्रिया नहीं

इस सारणी का उपयोग कर धातु A, B, C एवं D के सम्बन्ध में निम्न प्रश्नों के उत्तर दीजिए:
(i) सबसे अधिक अभिक्रियाशील धातु कौन-सी है?
(ii) धातु B को कॉपर (II) सल्फेट के विलयन में डाला जाए तो क्या होगा?
(iii) धातु A, B, C एवं D को अभिक्रियाशीलता के घटते हुए क्रम में व्यवस्थित कीजिए।
उत्तर:
(i) धातु B सर्वाधिक अभिक्रियाशील धातु है।
(ii) विस्थापन अभिक्रिया घटित होगी।
(iii) धातु B > धातु A धातु C धातु D

प्रश्न 4.
अभिक्रियाशील धातु को तनु हाइड्रोक्लोरिक अम्ल में डाला जाता है तो कौन-सी गैस निकलती है? आयरन के साथ तनु H₂SO₄ की रासायनिक अभिक्रिया लिखिए।
उत्तर:
धातु के लवण के साथ हाइड्रोजन गैस निकलती है।
Fe + H₂SO₄ → FeSO₄ + H₂

प्रश्न 5.
जिंक को आयरन (II) सल्फेट के विलयन में डालने से क्या होता है? इसकी रासायनिक अभिक्रिया लिखिए।
उत्तर:
जिंक आयरन (II) सल्फेट विलयन से आयरन को विस्थापित कर देता है।
Zn + FeSO₄ → ZnSO₄ + Fe

पाठगत प्रश्न (पृष्ठ संख्या – 54)

प्रश्न 1.
(i) सोडियम, ऑक्सीजन एवं मैग्नीशियम के लिए इलेक्ट्रॉन-बिंदु संरचना लिखिए।
(ii) इलेक्ट्रॉन के स्थानांतरण के द्वारा Na₂0 एवं MgO का निर्माण दर्शाइए।
(iii) इन यौगिकों में कौन-से आयन उपस्थित हैं?
उत्तर:

(iii) Na₂O यौगिक में उपस्थित आयन-धन आयन (Na⁺) तथा ऋण आयन (O^2-)।
MgO में उपस्थित आयन-धन आयन (Mg²⁺) तथा ऋण आयन (O^2-)।

प्रश्न 2.
आयनिक यौगिकों का गलनांक उच्च क्यों होता है?
उत्तर:
आयनिक यौगिक ठोस एवं कठोर होते हैं। ऐसा आयनों के बीच मजबूत अन्तर- आयनिक आकर्षण बल के कारण होता है। इस आकर्षण बल को कम करने के लिए अत्यधिक मात्रा में ऊर्जा की आवश्यकता होती है। यही कारण है कि आयनिक यौगिकों का गलनांक उच्च होता है।

पाठगत प्रश्न (पृष्ठ संख्या – 59)

प्रश्न 1.
निम्न पदों की परिभाषा दीजिए- (1) खनिज, (2) अयस्क, (3) गैंग.
उत्तर:

1. खनिज – वे तत्त्व या यौगिक जो भू-पर्पटी में प्राकृतिक रूप से पाए जाते हैं, उन्हें खनिज कहते हैं।
2. अयस्क-कुछ स्थानों पर खनिजों में कई विशेष धातुएँ अत्यधिक मात्रा में होती हैं जिन्हें आसानी से निकाला जा सकता है। इन खनिजों को अयस्क कहते हैं।
3. गैंग – पृथ्वी से प्राप्त खनिज अयस्कों में मिट्टी, रेत, आदि जैसी कई अशुद्धियाँ होती हैं जिन्हें गैंग कहा जाता है।

प्रश्न 2.
दो धातुओं के नाम बताइए जो प्रकृति में मुक्त अवस्था में पाई जाती हैं।
उत्तर:
सोना एवं प्लैटिनम।

प्रश्न 3.
धातु को उसके ऑक्साइड से प्राप्त करने के लिए किस रासायनिक प्रक्रिया का उपयोग किया जाता है?
उत्तर:
कार्बन द्वारा अपचयन की प्रक्रिया।

पाठगत प्रश्न (पृष्ठ संख्या – 61)

प्रश्न 1.
जिंक, मैग्नीशियम एवं कॉपर के धात्विक ऑक्साइडों को निम्न धातुओं के साथ गर्म किया गया-

धातु	जिंक	मैग्नीशियम	कॉपर
जिंक ऑक्साइड
मैग्नीशियम ऑक्साइड
कॉपर ऑक्साइड

किस स्थिति में विस्थापन अभिक्रिया घटित होगी?
उत्तर:
(i) जब जिंक ऑक्साइड को मैग्नीशियम के साथ गर्म किया जाता है तो जिंक ऑक्साइड मैग्नीशियम के साथ द्विविस्थापन अभिक्रिया करके निम्न प्रकार से उत्पाद बनाएगा-

(ii) और (iii) जब मैग्नीशियम ऑक्साइड और कॉपर ऑक्साइड को जिंक के साथ गर्म किया जाता है तो कोई भी अभिक्रिया उत्पन्न नहीं होती है।

प्रश्न 2.
कौन सी धातु आसानी से संक्षारित नहीं होती है?
उत्तर:
सोना, चाँदी और कॉपर आदि धातुएँ आसानी से संक्षारित नहीं होतीं।

प्रश्न 3.
मिश्रधातु क्या होते हैं?
उत्तर:
दो या दो से अधिक धातुओं के समांगी मिश्रण को मिश्रधातु कहते हैं। इसे तैयार करने के लिए पहले मूल धातु को गलित किया है और फिर दूसरे तत्त्वों को एक निश्चित अनुपात में इसमें विलीन किया जाता है। फिर इसे कमरे के तापमान पर ठंडा किया जाता है।

क्रिया-कलाप – 3.1

प्रश्न 1.
आयरन, कॉपर, ऐलुमिनियम और मैग्नीशियम के नमूने लीजिए। प्रत्येक नमूना कैसा दिखाई देता है उस पर ध्यान दीजिए।
उत्तर:
आयरन, कॉपर, ऐलुमिनियम और मैग्नीशियम के नमूने हल्के चमकदार दिखाई देते हैं।

प्रश्न 2.
रेगमाल से रगड़कर प्रत्येक नमूने की सतह को साफ करके उसके स्वरूप पर फिर से ध्यान दीजिए।
उत्तर:
रेगमाल से रगड़ने पर प्रत्येक नमूने की सतह को साफ करने पर इन नमूनों की चमक बढ़ जाती है। धातु के इस गुणधर्म को धात्विक चमक कहते हैं।

क्रिया-कलाप – 3.2

प्रश्न 1.
आयरन, कॉपर, ऐलुमिनियम तथा मैग्नीशियम धातुओं को तेज धार वाले चाकू से काटने का प्रयास करें तथा अपने प्रेक्षणों को दर्ज करें।
उत्तर:
ये धातुएँ काटने में बहुत कठोर हैं।

प्रश्न 2.
सोडियम को चाकू से काटिए। आपने क्या देखा?
उत्तर:
सोडियम को चाकू की सहायता से आसानी से काटा जा सकता है।

क्रिया-कलाप – 3.3

• आयरन, जिंक, लेड तथा कॉपर के टुकड़े लीजिए।
• किसी एक धातु को लोहे के ब्लॉक (खंड) पर रखकर चार-पाँच बार हथौड़े से प्रहार कीजिए। आपने क्या देखा?
• अन्य धातुओं के साथ भी यही क्रिया कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
इन धातुओं के आकार में हुए परिवर्तन को लिखिए।
उत्तर:
ये धातुएँ पीटने पर पतली चादर में बदल जाती हैं।

क्रिया-कलाप – 3.4
(i) अधातुओं की सूची बनाइए जिसके तार आप अपने दैनिक जीवन में देखते हैं।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
इनमें कौन-सी धातुएँ तार के रूप में भी उपलब्ध हैं?
उत्तर:
आयरन, कॉपर, ऐलुमिनियम तार के रूप में भी उपलब्ध हैं।

क्रिया-कलाप – 3.5

• ऐलुमिनियम या कॉपर का तार लीजिए। क्लैंप की मदद से इस तार को स्टैंड से कंस दीजिए जैसा चित्र में दिखाया गया है।
  
• तार के खुले सिर पर मोम का उपयोग कर एक पिन चिपका दीजिए।
• स्पिरिट लैंप, मोमबत्ती या बर्नर से क्लैंप के निकट तार को गर्म कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
थोड़ी देर बाद आप क्या देखते हैं?
उत्तर:
मोम पिघल जाता है तथा सारे पिन नीचे गिर जाती हैं।

प्रश्न 2.
क्या धातु का तार द्रवित होता है?
उत्तर:
धातु का तार द्रवित नहीं होता है।

क्रिया-कलाप – 3.6

• चित्र की तरह एक विद्युत सर्किट (परिपथ) तैयार कीजिए।
  
• जिस धातु की जाँच करनी है उसे परिपथ में टर्मिनल (A) तथा टर्मिनल (B) के बीच उसी प्रकार रखिए जैसा चित्र में दिखाया गया है।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
क्या बल्ब जलता है? इससे क्या पता चलता है?
उत्तर:
हाँ, बल्ब जलता है। इससे यह पता चलता है कि धातुएँ विद्युत की सुचालक होती हैं।

क्रिया-कलाप – 3.7

• कार्बन (कोल या ग्रेफाइट), सल्फर तथा आयोडीन के नमूने एकत्र कीजिए।
• इन अधातुओं से 3.1 से 3.6 तक के क्रिया-कलापों को दोहराइए तथा अपने प्रेक्षणों को लिखिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
धातुओं एवं अधातुओं से सम्बन्धित अपने प्रेक्षणों को सारणी 3.1 में संकलित कीजिए।
उत्तर:

क्रिया-कलाप – 3.8

• मैग्नीशियम की एक पट्टी तथा थोड़ा सल्फर चूर्ण लीजिए।
• मैग्नीशियम की पट्टी का दहन कीजिए। उसकी राख को इकट्ठा करके उसे पानी में घोल दीजिए।
• लाल तथा नीले लिटमस पेपर से प्राप्त विलयन की जाँच कीजिए।
• अब सल्फर के चूर्ण का दहन कीजिए। दहन से उत्पन्न धुएँ को एकत्र करने के लिए उसके ऊपर एक परखनली रख दीजिए।
• इस परखनली में जल डालकर उसे अच्छी तरह मिला दीजिए।
• नीले तथा लाल लिटमस पेपर से इस विलयन की जाँच कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
मैग्नीशियम के दहन से जो उत्पाद मिला है वह अम्लीय है या क्षारकीय?
उत्तर:
क्षारकीय।

प्रश्न 2.
सल्फर के दहन से उत्पन्न पदार्थ अम्लीय है या क्षारकीय।
उत्तर:
सल्फर के दहन से उत्पन्न पदार्थ अम्लीय है।

प्रश्न 3.
क्या आप इन अभिक्रियाओं के समीकरण लिख सकते हैं?
उत्तर:

1. 2Mg + O₂ → 2MgO
2. S + O₂ → SO₂
3. MgO + H₂O → 1 Mg (OH) ₂
4. SO₂ + H₂O → H₂SO₃ सल्फ्यूरस अम्ल (एक अम्ल)

क्रिया-कलाप – 3.9

• एकत्र की गई किसी धातु को चिमटे से पकड़कर ज्वाला पर उसका दहन कीजिए।
• अन्य धातुओं के साथ भी यही क्रिया दोहराइए।
• इससे उत्पन्न पदार्थ को एकत्र कीजिए।
• उत्पाद तथा धातु की सतह को ठंडा होने दीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
किस धातु का दहन आसानी से होता है?
उत्तर:
सोडियम (Na) तथा मैग्नीशियम (Mg) का।

प्रश्न 2.
जब धातु का दहन हो रहा था, तो ज्वाला का रंग क्या था?
उत्तर:
Mg के दहन पर चमकदार श्वेत (सफेद) ज्वाला तथा Na के दहन पर पीले रंग की ज्वाला निकल रही थी।

प्रश्न 3.
दहन के पश्चात् धातु की सतह कैसी प्रतीत होती है?
उत्तर:
चाँदी की तरह श्वेत।

प्रश्न 4.
धातुओं को ऑक्सीजन के साथ अभि-क्रियाशीलता के आधार पर घटते क्रम में व्यवस्थित कीजिए।
उत्तर:
Na > Mg > Al > Zn > Fe > Pb > Cu.

प्रश्न 5.
क्या इनके उत्पाद जल में घुलनशील हैं?
उत्तर:
Mg, Al, Cu Fe Pb और Zn के उत्पाद घुलनशील नहीं हैं जबकि सोडियम के उत्पाद घुलनशील हैं।

क्रिया-कलाप – 3.10

• क्रिया-कलाप 3.9 की तरह समान धातुओं के नमूने एकत्र दीजिए।
• ठंडे जल से आधे भरे बीकर में नमूने के छोटे टुकड़ों को अलग-अलग डालिए।
• जो धातुएँ ठंडे जल के साथ अभिक्रिया नहीं करती हैं उन्हें ऐसे बीकरों में डालिए जो गर्म जल से आधे भरे हुए हों।
• जो धातुएँ गर्म जल के साथ अभिक्रिया नहीं करती उसके लिए चित्र की तरह उपकरण व्यवस्थित कीजिए तथा भाप के साथ उसकी अभिक्रिया को प्रेक्षित कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
कौन-सी धातु ठंडे जल से अभिक्रिया करती है? ठंडे पानी के साथ अभिक्रियाशीलता के आधार पर उन्हें आरोही क्रम में व्यवस्थित कीजिए।
उत्तर:
सोडियम, पोटैशियम तथा कैल्सियम जल के साथ अभिक्रिया करते हैं। उनकी अभिक्रियाशीलता का आरोही क्रम निम्न है-
कैल्सियम < पोटैशियम < सोडियम

प्रश्न 2.
क्या कोई धातु जल में आग उत्पन्न करती है?
उत्तर:
हाँ, सोडियम एवं पोटैशियम।

प्रश्न 3.
क्या कोई धातु थोड़ी देर बाद जल में तैरने लगती है?
उत्तर:
हाँ, कैल्सियम तथा मैग्नीशियम।

प्रश्न 4.
कौन-सी धातुएँ भाप के साथ भी अभिक्रिया नहीं करती हैं?
उत्तर:
सीसा, कॉपर, चाँदी तथा सोना।

प्रश्न 5.
जल के साथ अभिक्रियाशीलता के आधार पर धातुओं को अवरोही क्रम में व्यवस्थित कीजिए।
उत्तर:
सोडियम > पोटैशियम > कैल्सियम > मैग्नीशियम > ऐलुमिनियम लोहा सीसा > कॉपर > चाँदी > पारा।

क्रिया-कलाप – 3.11

• सोडियम तथा पोटैशियम के अतिरिक्त बाकी सभी धातुओं के नमूने एकत्र कीजिए। यदि नमूने मलीन हैं तो रेगमाल से रगड़कर उन्हें साफ कर लीजिए।
• सावधानी – सोडियम तथा पोटैशियम को नहीं लीजिए क्योंकि वे ठंडे जल के साथ भी तेजी से अभिक्रिया करते हैं।
• नमूनों को अलग-अलग तनु हाइड्रोक्लोरिक अम्ल युक्त परखनलियों में डालिए।
• थर्मामीटर को परखनलियों में इस प्रकार लटका दें कि उसका बल्ब अम्ल में डूब जाए।
• बुलबुले बनने की दर का सावधानीपूर्वक प्रेक्षण कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
कौन-सी धातुएँ तनु हाइड्रोक्लोरिक अम्ल के साथ तेजी से अभिक्रिया करती हैं?
उत्तर:
मैग्नीशियम।

प्रश्न 2.
आपने किस धातु के साथ सबसे अधिक ताप रिकॉर्ड किया?
उत्तर:
मैग्नीशियम।

प्रश्न 3.
तनु अम्ल के साथ अभिक्रियाशीलता के आधार पर धातुओं को अवरोही क्रम में व्यवस्थित कीजिए।
उत्तर:
Mg > Al > Zn > Fe.

क्रिया-कलाप – 3.12

• कॉपर का एक स्वच्छ तार एवं आयरन की एक कील लीजिए।
• कॉपर के तार को परखनली में रखे आयरन सल्फेट के विलयन तथा आयरन की कील को दूसरी परखनली में रखे कॉपर सल्फेट के विलयन में डाल दीजिए।
• 20 मिनट के बाद अपने प्रेक्षणों को रिकॉर्ड कीजिए।
• आपको किस परखनली में कोई अभिक्रिया हुई है, इसका पता चलता है?
  

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
किस परखनली में कोई अभिक्रिया हुई है?
उत्तर:
उस परखनली में जिसमें लोहे की कील को CuSO₄ विलयन में डुबोया गया है।

प्रश्न 2.
किस आधार पर आप कह सकते हैं कि वास्तव में कोई अभिक्रिया हुई है?
उत्तर:
विलयन के रंग में परिवर्तन तथा कॉपर के जमा होने के आधारों पर हम कह सकते हैं कि कोई अभिक्रिया हुई है।

प्रश्न 3.
क्या आप अपने प्रेक्षणों को क्रिया-कलाप 3.9, 3.10 तथा 8.11 से कोई सम्बन्ध स्थापित कर सकते हैं?
उत्तर:
हाँ, लोहा, कॉपर से अधिक अभिक्रियाशील है।

प्रश्न 4.
इस अभिक्रिया के लिए संतुलित रासायनिक समीकरण लिखिए।
उत्तर:
Fe + CuSO₄ → FeSO₄ + Cu.

प्रश्न 5.
यह किस प्रकार की अभिक्रिया है?
उत्तर:
यह विस्थापन अभिक्रिया है।

क्रिया-कलाप – 3.13

• विज्ञान की प्रयोगशाला से सोडियम क्लोराइड, पोटैशियम आयोडाइड, बेरियम क्लोराइड या किसी अन्य लवण का नमूना लीजिए।
• धातु के स्पैचुला पर छोटी मात्रा में नमूने को लीजिए तथा इसे ज्वाला पर गर्म कीजिए। अन्य नमूनों के साथ भी यही क्रिया दोहराइए।
• आप क्या देखते हैं? क्या ये नमूने ज्वाला को रंग प्रदान करते हैं? क्या यौगिक पिघलते हैं?
  
• नमूने को जल, पेट्रोल एवं किरोसिन में घोलने का प्रयास कीजिए। क्या ये घुलनशील हैं?

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
इन लवणों की भौतिक अवस्था क्या है?
उत्तर:
इन लवणों की भौतिक अवस्था ठोस है।

प्रश्न 2.
चित्र की तरह एक परिपथ बनाइए और किसी एक लवण के विलयन में इलैक्ट्रोड डाल दीजिए। आप क्या देखते हैं? इसी प्रकार अन्य लवण नमूनों की भी जाँच कीजिए।
उत्तर:
बल्ब जलने लगता है। इससे यह प्रदर्शित होता है कि लवण का विलयन विद्युत का सुचालक है।

प्रश्न 3.
इन यौगिकों की प्रकृति के सम्बन्ध में आप क्या निष्कर्ष निकालते हैं?
उत्तर:

1. आयनिक यौगिक ठोस एवं कठोर होते हैं।
2. आयनिक यौगिकों के द्रवणांक एवं क्वथनांक उच्च होते हैं।
3. ये जल में विलयशील हैं किन्तु किरोसीन एवं पेट्रोल जैसे कार्बनिक विलायकों में अविलयशील हैं।
4. ठोस अवस्था में आयनिक यौगिक विद्युत के सुचालक नहीं होते क्योंकि दृढ़ संरचना के कारण आयन गति नहीं कर पाते किंतु पिघली अवस्था में आयनिक यौगिक विद्युत के सुचालक होते हैं।

क्रिया-कलाप – 3.14
(i) तीन परखनली लीजिए एवं प्रत्येक में स्वच्छ लोहे की कीलें डाल दीजिए।

(ii) इन परखनलियों को A, B तथा C नाम दीजिए। परखनली A में थोड़ा जल डालकर एवं कॉर्क से बंद कर दीजिए।

परखनली A में वायु एवं जल दोनों उपस्थित हैं। परखनली B में जल में विलीन वायु नहीं है। परखनली C में शुष्क वायु है।

(iii) परखनली B में उबलता हुआ आसवित जल डालकर उसमें 1 mL तेल मिलाइए एवं कॉर्क से बंद कर दीजिए। तेल जल पर तैरने लगेगा एवं वायु को जल में विलीन होने से रोक देगा।

(iv) परखनली C में थोड़ा निर्जल कैल्सियम क्लोराइड डालकर उसे कॉर्क से बंद कर दीजिए। निर्जल कैल्सियम क्लोराइड वायु की नमी को सोख लेगा। इन परखनलियों को कुछ दिन छोड़ने के बाद उनका प्रेक्षण कीजिए।
उत्तर:
छात्र स्वयं करें।

Jharkhand Board JAC Class 10 Science Solutions Chapter 4 कार्बन एवं इसके यौगिक Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 4 कार्बन एवं इसके यौगिक

Jharkhand Board Class 10 Science कार्बन एवं इसके यौगिक Textbook Questions and Answers

प्रश्न 1.
एथेन का आण्विक सूत्र – C₂H₆ है। इसमें – (a) 6 सहसंयोजक आबंध हैं, (b) 7 सहसंयोजक आबंध हैं, (c) 8 सहसंयोजक आबंध हैं, (d) 9 सहसंयोजक आबंध हैं।
उत्तर:
(b) 7 सहसंयोजक आबंध हैं।

प्रश्न 2.
ब्यूटेनॉन चर्तु कार्बन यौगिक है जिसका प्रकार्यात्मक समूह – (a) कार्बोक्सिलिक अम्ल, (b) ऐल्डिहाइड, (c) कीटोन, (d) ऐल्कोहॉल
उत्तर:
(c) कीटोन।

प्रश्न 3.
खाना बनाते समय यदि बर्तन की तली बाहर से काली हो रही है तो इसका मतलब है कि-
(a) भोजन पूरी तरह नहीं पका है।
(b) ईंधन पूरी तरह से नहीं जल रहा है।
(c) ईंधन आर्द्र है।
(d) ईंधन पूरी तरह से जल रहा है।
उत्तर:
(b) ईंधन पूरी तरह से नहीं जल रहा है।

प्रश्न 4.
CH₃Cl में आबंध निर्माण का उपयोग कर सहसंयोजक आबंध की प्रकृति समझाइए।
उत्तर:
CH₃Cl में तीन एकल बंध कार्बन व हाइड्रोजन परमाणुओं के बीच जुड़े होते हैं और एक एकल बंध कार्बन व क्लोरीन के बीच होता है।

अत: कार्बन का अष्टक पूर्ण हो जाता है तथा प्रत्येक हाइड्रोजन के बाहरी कक्ष में भी 2 इलेक्ट्रॉन हो जाते हैं और Cl का भी अष्टक पूर्ण हो जाता है इसलिए इलेक्ट्रॉनों की साझेदारी द्वारा सहसंयोजक आबंध बनता है।

प्रश्न 5.
इलेक्ट्रॉन बिन्दु संरचना बनाइए-
(a) एथेनॉइक अम्ल
(b) H₂S
(c) प्रोपेनोन
(d) F₂
उत्तर:

प्रश्न 6.
समजातीय श्रेणी क्या है? उदाहरण के साथ समझाइए।
उत्तर:
कार्बनिक यौगिकों का वह समूह जिनका सामान्य सूत्र एवं क्रियात्मक समूह एक जैसा होता है उसे समजात श्रेणी कहते हैं तथा उसके सदस्यों को समजात गण कहते हैं।
जैसे-

• मेथेनाल – CH₃OH
• एथनॉल – CH₃CH₂OH
• प्रोपेनाल – CH₃CH₂CH₂OH

समजातीय श्रेणी के सदस्यों के निम्नलिखित लक्षण हैं-

• सभी सदस्यों को एक सामान्य सूत्र द्वारा प्रदर्शित कर सकते हैं।
• सभी सदस्यों का एक ही क्रियात्मक समूह होता है।
• प्रत्येक क्रमागत सदस्य के अणुसूत्र में – CH₂ का अंतर होता है।
• प्रत्येक क्रमागत सदस्य के अणुभार में 14 U का अंतर होता है।
• किसी एक सदस्य का गुणधर्म के आधार पर सभी सदस्यों का सामान्य गुणधर्म ज्ञात कर सकते हैं।

प्रश्न 7.
भौतिक एवं रासायनिक गुणधर्मों के आधार पर एथनॉल एवं एथेनॉइक अम्ल में कैसे अन्तर करेंगे?
उत्तर:
(i) भौतिक गुण के आधार पर अन्तर-

एथनॉल	एथेनॉइक अम्ल
1. इसकी विशिष्ट अभिलाक्षंतिक गंध होती है।	1. इसकी सिरके जैसी गंध होती है।
2. इसका क्वथनांक 351 K होता है।	2. इसका क्वथनांक 391 K होता है।
3. इसका गलनांक 156 K होता है।	3. इसका गलनांक 290 K होता है।

(ii) रास।यनिक गुण के आधार पर अन्तर-

एथनॉल	एथेनॉइक अम्ल
1. यह उद, गसीन पदार्थ है।	1. यह अम्लीय पदार्थ है।
2. एथनॉरन Na2CO3 से अभित्रक्रिया नहीं करता है।	2. यह Na2CO3 से क्रिया करके सोडियम लवण एवं CO2 गैस बनाता है।
3. क्षारीय KMnO4 की उपस्थिथि में एथेनॉइक अम्ल बनाता है। इस क्रक्रिया में KMnO4 का बैंगनी रंग उड़ जाता है।	3. यह क्षारीय KMnO2 से अभिक्रिया नहीं करता है। अतः KMnO4 का रंग भी नहीं उड़ता है।

प्रश्न 8.
जब साबुन को जल में डाला जाता है तो मिसेल का निर्माण क्यों होता है? क्या एथनॉल जैसे दूसरे विनायकों में भी मिसेल का निर्माण होगा?
उत्तर:
साबुन के अणु के दो मुख्य भाग होते हैं- एक जल रागी और दूसरा जलविरागी भाग । कार्बन श्रृंखला वाला भाग जलविरागी होता है और आयनिक भाग जिसमें सोडियम या पोटैशियम परमाणु होता है वह जलरागी होता है। यह जब पानी जैसे ध्रुवीय विलायक में डाले जाते हैं तब अपने आवेशित भाग के कारण जलरागी भाग बाहर (जल की ओर) होता है। इस प्रकार मिसेल बनते हैं। एथनॉल एक अध्रुवीय विलायक है। अतः इसमें जलरागी भाग के लिए आकर्षण भी नहीं होता है। अतः एथनॉल में साबुन घोलने पर मिसेल नहीं बनेंगे।

प्रश्न 9.
कार्बन एवं उसके यौगिकों का उपयोग अधिकतर अनुप्रयोगों में ईंधन के रूप में क्यों किया जाता है?
उत्तर:
कार्बन और इसके यौगिक दहन के परिणामस्वरूप अधिक मात्रा में ऊष्मा देते हैं। कार्बन और हाइड्रोजन की प्रतिशत मात्रा अधिक होने के कारण इनका सामान्य ज्वलन ताप होता है। इनका रखरखाव आसान होता है तथा दहन नियन्त्रित किया जा सकता है। इसलिए कार्बन और उसके यौगिकों का उपयोग ईंधन के रूप में होता है।

प्रश्न 10.
कठोर जल को साबुन से उपचारित करने पर झाग के निर्माण को समझाइए।
उत्तर:
कठोर जल कैल्सियम और मैग्नीशियम के घुलनशील लवण होते हैं जब साबुन से ये लवण क्रिया करते हैं तब अघुलनशील लवण बनाते हैं जिसे स्कम या झाग कहते हैं।

प्रश्न 11.
यदि आप लिटमस पत्र (नाल एवं नीला) से साबुन की जाँच करें तो आपका प्रेक्षण क्या होगा?
उत्तर:
साबुन की प्रकृति क्षारीय होती है। अतः यह लाल लिटमस को नीला कर देता है।

प्रश्न 12.
हाइड्रोजनीकरण क्या है? इसका औद्योगिक उपयोग क्या है?
उत्तर:
असंतृप्त हाइड्रोकार्बन श्रृंखला में हाइड्रोजन के योग को हाइड्रोजनीकरण कहते हैं। यह क्रिया उत्प्रेरक की उपस्थिति में कराई जाती है।

प्रश्न 13.
दिए गए हाइड्रोकार्बन C₂H₆, C₃H₆, C₂H₂ एवं CH₄ में किसमें संकलन अभिक्रिया होती है?
उत्तर:
C₂H₂ और C₃H₆ में योग अभिक्रिया होगी क्योंकि उपर्युक्त दोनों यौगिक असंतृप्त हाइड्रोकार्बन हैं। इनमें द्वि या त्रि-बन्ध उपस्थित हैं।

प्रश्न 14.
मक्खन एवं खाना बनाने वाले तेल के बीच रासायनिक अन्तर समझने के लिए एक परीक्षण बताइए।
उत्तर:
मक्खन संतृप्त हाइड्रोकार्बन है जबकि खाद्य तेल असंतृप्त हाइड्रोकार्बन है। इस अंतर को निम्न प्रकार से प्रदर्शित किया जा सकता है-

• थोड़े से मक्खन को गर्म करके उसमें कुछ बूँदें ब्रोमीन जल डालते हैं। ब्रोमीन जल का रंग नहीं उड़ता। इससे यह पता चलता है कि मक्खन संतृप्त कार्बनिक यौगिक है।
• खाद्य तेल में कुछ बूँदें ब्रोमीन जल की डालकर हिलाते हैं। कुछ समय बाद ब्रोमीन जल का रंग उड़ जाता है। इससे यह पता चलता है कि खाद्य तेल असंतृप्त कार्बनिक यौगिक हैं।

प्रश्न 15.
साबुन की सफाई प्रक्रिया की क्रियाविधि समझाइए।
उत्तर:
बहुत से मैल तैलीय होते हैं और तेल पानी में अघुनशील है। साबुन के सोडियम तथा पोटैशियम लवण के होते हैं जो लंबी श्रृंखला वाले कार्बोक्सिलिक अम्ल से बनते हैं साबुन का आयनिक भाग जल में घुल है जबकि कार्बन श्रृंखला तेल में घुल जाती है। इस प्रकार साबुन के अणु मिसेली संरचना तैयार करते हैं जहाँ पर अणु का एक सिरा तेल कण की जाता ओर तथा आयनिक सिरा बाहर की ओर होता है। इससे पानी में इमल्शन बनता है। इस प्रकार साबुन का मिसेल मैल को पानी में घुलाने में मदद करता है और हमारे कपड़े साफ हो जाते हैं।

Jharkhand Board Class 10 Science कार्बन एवं इसके यौगिक InText Questions and Answers

पाठगत प्रश्न (पृष्ठ संख्या-68)

प्रश्न 1.
CO₂ सूत्र वाले कार्बन डाइऑक्साइड की इलेक्ट्रॉन बिन्दु संरचना क्या होगी?
उत्तर:

प्रश्न 2.
सल्फर के आठ परमाणुओं से बने सल्फर के अणु की इलेक्ट्रॉन बिन्दु संरचना क्या होगी?
संकेत:
सल्फर के आठ परमाणु एक अँगूठी के रूप में आपस में जुड़े होते हैं।

पाठगत प्रश्न (पृष्ठ संख्या – 76)

प्रश्न 1.
पेन्टेन के लिए आप कितने संरचनात्मक समावयवी का चित्रण कर सकते हैं।
उत्तर:
पेन्टेन के लिए तीन संरचनात्मक समावयवी का चित्रण किया जा सकता है-

प्रश्न 2.
कार्बन के दो गुणधर्म कौन-से हैं जिनके कारण हमारे चारों ओर कार्बन यौगिकों की विशाल संख्या दिखाई देती है?
उत्तर:
कार्बन यौगिकों की बहुतायत के निम्नलिखित दो कारण हैं-

• कार्बन परमाणु शृंखलन (Catenation).
• कार्बन परमाणु की चतुः संयोजकता।

शृंखलन कार्बन परमाणुओं का विशेष गुण होता है जिसके कारण कार्बन परमाणु सीधी, शाखित या चक्रीय श्रृंखलाएँ बना लेते हैं। चतु: संयोजकता परमाणुओं के कारण कार्बन अपने ही के साथ एकल, द्वि या त्रिक सहसंयोजक आबंध बनाते हैं।

उपर्युक्त कारणों से कार्बन बहुत अधिक संख्या में बनाता है। अतः हमारे चारों ओर कार्बनिक यौगिकों की विशाल संख्या दिखाई देती है।

प्रश्न 3.
साइक्लोपेन्टेन का सूत्र तथा इलेक्ट्रॉन बिन्दु संरचना क्या होंगे?
उत्तर:
साइक्लोपेन्टेन का सूत्र C₅H₁₀ होता है। C₅H₁₀ की इलेक्ट्रॉन बिन्दु संरचना निम्न प्रकार से है-

प्रश्न 4.
निम्न यौगिकों की संरचनाएँ चित्रित कीजिए-
(i) एथेनॉइक अम्ल
(ii) ब्रोमोपेन्टेन
(iii) ब्यूटेनोन
(iv) हेक्सेनैल
क्या ब्रोमोपेन्टेन के संरचनात्मक समावयव संभव हैं?
उत्तर:
(i) एथेनॉइक अम्ल (Ethanoic acid) CH₃COOH

हाँ, ब्रोमोपेन्टेन के संरचनात्मक समावयव संभव हैं जो इस प्रकार हैं-

प्रश्न 5.
निम्न यौगिकों का नामकरण कैसे करेंगे?

उत्तर:
(i) ब्रोमो एथेन
(ii) मेथैनल (Methanal)
(iii) 1 हेक्साइन या हेक्साइन

पाठगत प्रश्न (पृष्ठ संख्या – 79)

प्रश्न 1.
एथनॉल से एथेनॉइक अम्ल में परिवर्तन को ऑक्सीकरण अभिक्रिया क्यों कहते हैं?
उत्तर:
एथेनॉइक अम्ल में एथनॉल की अपेक्षा एक ऑक्सीजन परमाणु अधिक कमी दो हाइड्रोजन परमाणु कम होते हैं। ऑक्सीजन की वृद्धि और हाइड्रोजन की वाली रासायनिक अभिक्रियाएँ ऑक्सीकरण अभिक्रिया कहलाती हैं।

प्रश्न 2.
ऑक्सीजन और एथाइन के मिश्रण का दहन वेल्डिंग के लिए किया जाता है। क्या आप बता सकते हैं कि एथाइन तथा वायु के मिश्रण का उपयोग क्यों नहीं किया जाता?
उत्तर:
वायु में नाइट्रोजन और अन्य निष्क्रिय गैसें होती हैं जो एथाइन के दहन हेतु ऑक्सीजन की प्रचुर आपूर्ति को बाधित करती हैं। इसलिए एथाइन के दहन के लिए वायु का उपयोग नहीं कर सकते हैं।

पाठगत प्रश्न (पृष्ठ संख्या – 83)

प्रश्न 1.
प्रयोग द्वारा आप ऐल्कोहॉल एवं कार्बोक्सिलिक अम्ल में कैसे अन्तर कर सकते हैं?
उत्तर:

प्रयोग	ऐल्कोहॉल	कार्बोक्सिलिक अम्ल
1. लिटमस विलयन का उपयोग करके	लिटमस विलयन के रंग में कोई परिवर्तन नहीं होता है।	नीला लिटमस विलयन लाल रंग में बद्ल जाता है।
2. सोडियम बाइकार्बोनेट के द्वारा	तेजी से कोई बुदबुदाहट नहीं होती है।	तेजी से बुदबुदाहट होती है और साथ में कार्बन डाइऑक्साइड निकलती है।
3. सोडियम धातु का प्रयोग करके	बुदबुदाहट के साथ हाइड्रोजन गैस निकलती है।	हाइड्रोजन गैस निकलती है लेकिन शीघ्रता से नहीं निकलती।

प्रश्न 2.
ऑक्सीकारक क्या हैं?
उत्तर:
ऐसे तत्त्व एवं यौगिक जो अभिक्रिया के दौरान ऑक्सीजन देते हैं या जो इलेक्ट्रॉन को स्वीकार करते हैं, ऑक्सीकारक कहलाते हैं।

पाठगत प्रश्न (पृष्ठ संख्या – 85)

प्रश्न 1.
क्या आप डिटरजेंट का उपयोग कर बता सकते हैं कि कोई जल कठोर है अथवा नहीं?
उत्तर:
नहीं, क्योंकि अपमार्जक (डिटरजेंट) कठोर और मृदु दोनों प्रकार के जल के साथ अधिक मात्रा में झाग उत्पन्न करते हैं।

प्रश्न 2.
लोग विभिन्न प्रकार से कपड़े धोते हैं। सामान्यतः साबुन लगाने के बाद लोग कपड़े को पत्थर पर पटकते हैं, डंडे से पीटते हैं, ब्रुश से रगड़ते हैं या वाशिंग मशीन में कपड़े रगड़े जाते हैं। कपड़ा साफ करने के लिए उसे रगड़ने की क्यों आवश्यकता होती है?
उत्तर:
साबुन से कपड़े धोकर साफ करने के लिए रगड़ना या पीटना आवश्यक है क्योंकि जल में उपस्थित मैग्नीशियम और कैल्सियम के लवणों के साथ साबुन क्रिया करके अघुलनशील श्वेत दही जैसा पदार्थ बनाता है। यह पदार्थ कपड़ों पर चिपक जाता है। उसे हटाने के लिए ब्रश या हाथ से रगड़कर कपड़े को धोना आवश्यक है।

क्रिया-कलाप – 4.1

प्रश्न 1.
(i) सुबह से आपने जिन वस्तुओं का उपयोग अथवा उपभोग किया हो, उनमें से दस वस्तुओं की सूची बनाइए।
(ii) इस सूची को अपने सहपाठियों द्वारा बनाई सूची के साथ मिलाइए तथा सभी वस्तुओं को निम्नलिखित सारणी में वर्गीकृत कीजिए।
(iii) एक से अधिक सामग्रियों से बनी वस्तुओं को उपयुक्त स्तम्भों में रखिए।
उत्तर:
उपयोग तथा उपभोग की दस वस्तुओं की सूची निम्न सारणी में प्रस्तुत है।

धातु से बनी वस्तुएँ	काँच/मिट्टी से बनी वस्तुएँ	अन्य वस्तुएँ
1. साइकिल	सुराही	भोजन
2. कार	कुल्हड़	स्याही
3. बर्तन	ग्लास	कागज
4. ग्लास	प्लेट	पानी
5. प्लेट		पोलिश
6. चम्मच		साबुन
7. चाकू		तेल
8. लंच बॉक्स		क्रीम
9. पंखे		दुध
10. कूलर		चीनी

क्रिया-कलाप – 4.2

प्रश्न 1.
सूत्रों तथा आणविक द्रव्यमानों में अन्तर की गणना कीजिए-
(a) CH₃OH तथा C₂H₅OH
(b) C₂H₅OH तथा C₃H₇ OH एवं
(c) C₃H₇ OH तथा C₄H₉OH
उत्तर:

अणुसूत्र	अणुभार	अणुभार में अन्तर	अणुसूत्र में अन्तर
(a) CH3OH C2H5OH	32 U 46 U	14 U	CH2
(b) C2H5OH C3H7 OH	46 U 60 U	14 U	CH2
(c) C3H5OH C4H9OH	60 U 94 U	14 U	CH2

प्रश्न 2.
क्या इन तीनों में कोई समानता है?
उत्तर:
हाँ। सभी का प्रकार्यात्मक समूह (Functional group) ऐल्कोहॉलिक (OH) है।

प्रश्न 3.
एक परिवार तैयार करने के लिए इन ऐल्कोहॉलों को कार्बन परमाणुओं के बढ़ते हुए क्रम में व्यवस्थित कीजिए। क्या इनको एक समजातीय श्रेणी का परिवार कहा जा सकता है?
उत्तर:
CH₃OH, C₂H₅OH, C₃H₇OH, C₄H₉OH हाँ, ये एल्केन ऐल्कोहॉल के समजातीय श्रेणी हैं।

प्रश्न 4.
सारणी 4.3 में दिए गए अन्य प्रकार्यात्मक समूहों के लिए चार कार्बनों तक के यौगिकों वाली समजातीय श्रेणी तैयार कीजिए।
उत्तर:
समजातीय श्रेणी (Homologous Series):

क्रिया-कलाप – 4.3

सावधानी – इस क्रिया-कलाप के लिए शिक्षक का पर्यवेक्षण अनिवार्य है।
(i) एक स्पैचुला में एक-एक करके कुछ कार्बन यौगिकों (नैफ्थलीन, कैम्फर, ऐल्कोहॉल) को लेकर जलाइए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
ज्वाला की प्रकृति का प्रेक्षण कीजिए तथा लिखिए कि धुआँ हुआ या नहीं।
उत्तर:
वायु की प्रचुर उपस्थिति में संतृप्त हाइड्रोकार्बन नीली धुआँ रहित लौ के साथ जलते हैं। असंतृप्त हाइड्रोकार्बन वायु में पीली लौ की ज्वाला एवं अधिक धुएँ के साथ जलती हैं।

प्रश्न 2.
ज्वाला के ऊपर धातु की एक तश्तरी रखिए। इनमें से किसी भी यौगिक के कारण क्या तश्तरी पर कोई निक्षेपण हुआ?
उत्तर:
नैफ्थलीन और कैम्फर को जलाने पर तश्तरी पर निक्षेपण हुआ।

क्रिया-कलाप – 4.4
(i) एक बुन्सेन बर्नर जलाइए तथा विभिन्न प्रकार की ज्वालाओं / धुएँ की उपस्थिति को प्राप्त करने के लिए उसके आधार पर वायु छिद्र को व्यवस्थित कीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
पीली, कज्जली ज्वाला कब प्राप्त हुई?
उत्तर:
वायु की नियन्त्रित आपूर्ति से अपूर्ण दहन होता है जिसके कारण पीली चमकदार ज्वाला प्राप्त होती है।

प्रश्न 2.
नीली ज्वाला कब प्राप्त हुई?
उत्तर:
जब ऑक्सीजन की समुचित मात्रा उपलब्ध कराई जाती है तो पूर्ण दहन होता है तथा नीली ज्वाला प्राप्त होती है।

क्रिया-कलाप – 4.5

• एक परखनली में लगभग 3 mL एथेनॉल लीजिए तथा इसे जल ऊष्मक में सावधानी से गर्म कीजिए।
• इस विलयन में क्षारीय पोटैशियम परमैंगनेट का 5% एक-एक बूँद करके डालिए

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
डालने पर आरंभ में क्या पोटैशियम परमँगनेट का रंग बना रहता है?
उत्तर:
नहीं, पोटैशियम परमैंगनेट का पर्पल रंग, रंगहीन हो जाता है।

प्रश्न 2.
अधिक मात्रा में डालने पर पोटैशियम परमैंगनेट का रंग लुप्त क्यों नहीं होता है।
उत्तर:
अभिक्रिया पूर्ण हो जाती है तो पर्पल रंग बना रहता है।

क्रिया-कलाप – 4.6

शिक्षक के द्वारा प्रदर्शन- (i) लगभग दो चावल के आकार के बराबर सोडियम के एक छोटे टुकड़े को एथनॉल (परिशुद्ध ऐल्कोहॉल) में डालिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
आप क्या प्रेक्षित करते हैं?
उत्तर:
सोडियम और एथनॉल की तीव्र अभिक्रिया के फलस्वरूप सोडियम इथॉक्साइड व H₂ गैस बनाते हैं।

प्रश्न 2.
उत्सर्जित गैस की आप कैसे जाँच करेंगे?
उत्तर:
परखनली के मुँह के पास जलती हुई माचिस की तीलियाँ / मोमबत्ती लाने पर यह पॉप की आवाज के साथ जलती है जो यह बताती है कि हाइड्रोजन गैस उत्सर्जित हुई है।

क्रिया-कलाप – 4.7.

प्रश्न 1.
लिटमस पत्र एवं सार्वत्रिक सूचक का उपयोग कर तनु ऐसीटिक अम्ल तथा हाइड्रोक्लोरिक अम्ल के pH मान की तुलना कीजिए।
उत्तर:
तनु ऐसीटिक अम्ल का pH मान ज्यादा है।

प्रश्न 2.
क्या लिटमस परीक्षण में दोनों अम्ल सूचित होते हैं?
उत्तर:
हाँ।

प्रश्न 3.
सार्वत्रिक सूचक से क्या दोनों अम्लों के प्रबल होने का पता चलता है?
उत्तर:
HCl प्रबल अम्ल है।

क्रिया-कलाप – 4.8

• एक परखनली में सांद्र सल्फ्यूरिक अम्ल की कुछ बूँदें, एक-एक mL एथनॉल (परिशुद्ध ऐल्कोहॉल) एवं ग्लैशल ऐसीटिक अम्ल लीजिए।
• कम-से-कम पाँच मिनट तक जल ऊष्मक में उसे गर्म करें जैसा चित्र में दिखाया गया है।
  

प्रश्न 1.
अब इसे उस बीकर में उडेल दीजिए जिसमें 20-50 mL जल हो तथा उस मिश्रण को सूँधिए।
उत्तर:
फलों जैसी मीठी गंध निकलती है।

क्रिया-कलाप – 4.9

• अध्याय 2 के क्रिया-कलाप 2.5 के अनुसार उपकरण तैयार कीजिए।
• एक परखनली में एक स्पैचुला भरकर सोडियम कार्बोनेट लीजिए तथा उसमें 2 mL तनु इथेनॉइक अम्ल मिलाएँ।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
आप प्रेक्षित करते हैं?
उत्तर:
सोडियम कार्बोनेट से एथेनॉइक अम्ल अभिक्रिया करके सोडियम लवण, CO₂ और पानी बनाता है।

प्रश्न 2.
ताजे चूने के जल में इस गैस को प्रवाहित कीजिए। आप क्या देखते हैं?
उत्तर:
सनसनाहट के साथ CO₂ गैस उत्पन्न होती है। इसे ताजे चुने के पानी में प्रवाहित करने पर उसे दूधिया कर देती है।

प्रश्न 3.
क्या इस परीक्षण से एथेनॉइक अम्ल एवं सोडियम कार्बोनेट की अभिक्रिया से उत्पन्न गैस का पता चल सकता है?
उत्तर:
CH₃COOH और Na₂CO₃ की अभिक्रिया से सनसनाहट के साथ CO₂ गैस के बुलबुले निकलते हैं जो के पानी में प्रवाहित करने पर उसे दूधिया कर देते हैं।

प्रश्न 4.
अब सोडियम कार्बोनेट के स्थान पर सोडियम हाइड्रोजन कार्बोनेट के साथ यह क्रिया-कलाप दोहराइये।
उत्तर:

क्रिया-कलाप – 4.10

• दोनों में एक-एक बूँद तेल (पाक तेल) डालिए एवं उन्हें ‘A’ तथा ‘B’ नाम दीजिए।
• परखनली ‘B’ में साबुन के घोल की कुछ बूँदें डालिए।
• दोनों परखनलियों को समान समय तक जोर-जोर से हिलाइए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
क्या हिलाना बंद करने के बाद दोनों परखनलियों में आप तेल एवं जल की परतों को अलग-अलग देख सकते हैं?
उत्तर:
नहीं, यह स्पष्ट नहीं है।

प्रश्न 2.
कुछ देर तक दोनों परखनलियों को स्थिर रखिए एवं फिर अलग हो जाती है? ऐसा किस परखनली में पहले होता है?
उत्तर:
दोनों परखनलियों में तेल की परत अलग हो जाती है। लेकिन ऐसा पहली परखनली में होता है।

क्रिया-कलाप – 4.11

• अलग-अलग परखनलियों में 10-10 mL आसुत जल (अथवा वर्षा जल) एवं कठोर जल (हैंडपंप या कुएँ का जल) लीजिए।
• दोनों में साबुन के घोल की कुछ बूँदें मिलाइए।
• दोनों परखनलियों को एक ही समय तक हिलाइए एवं उससे बनने वाले झाग पर ध्यान दीजिए।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
किस परखनली में अधिक झाग बनता है?
उत्तर:
जिस परखनली में आसुत जल है उसमें अधिक झाग बनता है।

प्रश्न 2.
किस परखनली में श्वेत दही जैसा अवक्षेप प्राप्त होता है?
उत्तर:
जिस परखनली में कठोर जल है।

क्रिया-कलाप – 4.12

• दो परखनलियाँ लीजिए और प्रत्येक में 10-10 mL कठोर जल डालिए।
• एक में साबुन के घोल की पाँच बूँदें तथा दूसरे में अपमार्जक के घोल की पाँच बूँदें डालिए।
• दोनों परखनलियों को एक ही समय तक हिलाएँ।

क्रिया-कलाप के प्रश्नोत्तर

प्रश्न 1.
क्या दोनों में झाग की मात्रा समान है?
उत्तर:
नहीं, जिस परखनली में अपमार्जक मिलाया गया है उसमें झाग अधिक है।

प्रश्न 2.
किस परखनली में दही जैसा ठोस पदार्थ बनता है?
उत्तर:
जिस परखनली में साबुन मिलाया गया है।

Students must go through these JAC Class 10 Science Notes Chapter 15 हमारा पर्यावरण to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 15 हमारा पर्यावरण

→ पारिस्थितिक तंत्र-जीवित तथा अजीवित वातावरण की इस परस्पर निर्भरता को ही पारिस्थितिक तंत्र कहते हैं।

→ बायोम-कई पारिस्थितिक तंत्र मिलकर बायोम बनाते है।

→ जीवमण्डल-कई बायोम मिलकर जीवमण्डल बनाते है।

→ जलमण्डल-पृथ्वी का जो भाग जल से बना है।

→ स्थलमण्डल-पृथ्वी के स्थलीय सतह पर तथा सागर जल के अंदर भी मृदा एवं चट्टानें हैं। इस भाग को स्थलमण्डल कहते हैं।

→ पारिस्थितिक तंत्र के घटक-सभी पारिस्थितिक तंत्र दो घटकों से बने होते है-

• अजैविक एवं
• जैविक घटक।

→ अजैविक घटक-निर्जीव पदार्थों जैसे कार्बनिक पदार्थ, अकार्बनिक पदार्थ एवं जलवायुवीय से मिलकर बने हैं।

→ जैविक घटक-जैविक घटक के अन्तर्गत पौधे तथा जन्तु होते हैं।

→ उत्पादक-हरे पौधे (जो प्रकाश संश्लेषण करके अपना भोजन स्वयं बनाते हैं) को उत्पादक कहते हैं।

→ उपभोक्ता-ये वे जीव होते हैं जो हरे पौधों (उत्पादक) द्वारा एकत्रित भोजन का उपयोग करते हैं।

→ अपघटक-वे जीव जो मरे हुए उत्पादक्रों तथा उपभोक्ता को सड़ाकर उपयोग करते हुए साधारण भौतिक तत्त्वों में बदल देते हैं।

→ खाद्य-श्रृंखला-जीवों की वह शृंखला जो भोजन के आधार पर एक-दूसरे से सम्बन्धित रहते हैं खाद्य श्रृंखला कहलाती है।

→ खाद्य-जाल-विभिन्न खाद्य भृंखलाएँ आड़े-तिरछे जुड़कर खाद्य-जाल बनाते हैं।

→ जीवमण्डल में ऊर्जा स्थानान्तरण-

• ऊर्जा एक रूप से दूसरे रूप में रूपांतरित हो जाती है।
• आहार शृंखला में किसी पोषण रीति से अगली पोषण रीति तक ऊर्जा का निरंतर स्थानान्तरण होता रहता है।
• प्रत्येक स्थानांतरण में ऊर्जा की हानि होती है।

→ भू-रसायन चक्र-पदार्थों के चक्रीकरण को भू-रसायन चक्र कहते हैं।

→ विभिन्न चक्र-

• जल चक्र
• नाइट्रोजन चक्र
• कार्बन चक्र
• ऑक्सीजन चक्र।

→ जीवमण्डल में ऊर्जा प्रवाह-जीवमण्डल में ऊर्जा का प्रवाह सदैव एक दिशा में होता है।

→ ऊर्जा स्थानान्तरण का नियम-खाद्य- शृंखला में पोषण स्तरों पर ऊर्जा स्थानान्तरण 10% होता है। इसे 10% नियम कहते हैं।

→ आदर्श चक्र-नाइट्रोजन चक्र को आदर्श चक्र माना गया।

→ असूक्ष्म पोषक तत्त्व- H, N, O, C, P तथा K जैसे पोषक तत्त्वों की जैव जीवों को अधिक मात्रा में आवश्यकता होती है, इन्हें असूक्ष्म तत्च कहते हैं।

→ ओजोन परत-

• वायुमण्डल की ऊपरी सतह पर उपस्थित ओजोन, सूर्य से आने वाले पराबैंगनी विकिरण से पृथ्वी को सुरक्षा प्रदान करती है।
• 1980 से ओजोन परत का तीव्रता से क्षय हो रहा है।
• क्लोरोफ्लोरो कार्बन (CFCs) जैसे रसायनों को इसका मुख्य कारक माना जाता है।

→ हमारे द्वारा उत्पादित कचरे का निपटान एक गंभीर पर्यावरणीय समस्या है।

Students must go through these JAC Class 10 Science Notes Chapter 14 उर्जा के स्रोत to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 14 उर्जा के स्रोत

→ सूर्य – पृथ्वी के लिए ऊर्जा का सबसे अधिक प्रत्यक्ष एवं विशाल स्रोत सूर्य है। सूर्य ऊर्जा के सभी रूपों का आदि स्रोत है। इसका भार 10²⁹ टन है तथा यह पृथ्वी से लगभग 15 करोड़ किलोमीटर दूर हैं।

→ सौर ऊर्जा सूर्य द्वारा विमोचित प्रकाश और ऊष्मीय ऊर्जा को सौर ऊर्जा कहते हैं। यह विद्युत चुम्बकीय तरंगें हैं।

→ सौर ऊर्जा का स्त्रोत- सूर्य की ऊर्जा का स्रोत इसके नाभिक में उपस्थित हाइड्रोजन नाभिकों का उच्च दाब व ताप (लगभग 10⁷K) पर संलयित होकर हीलियम नाभिक का बनना है।

→ सूर्य प्रकाश का संघटन सूर्य का प्रकाश तीन प्रकार की विद्युत चुम्बकीय तरंगों से मिलकर बना है –

• पराबैंगनी तरंगें
• दृश्य प्रकाश तरंगें (बैंगनी, जामुनी, नीला, हरा, पीला, नारंगी तथा लाल)
• अवरक्त तरंगें।

→ सौर ऊर्जा का पृथ्वी द्वारा अवशोषण – पृथ्वी के वायुमण्डल की ऊपरी सतह का प्रत्येक वर्ग मीटर लगभग 136 जूल ऊर्जा प्रति सेकण्ड प्राप्त करता है, परन्तु इसका केवल 47% भाग ही पृथ्वी के धरातल पर पहुँचता है।

→ प्रकाश संश्लेषण- हरे पौधों द्वारा सौर ऊर्जा को ग्रहण कर संग्रह करने की यान्त्रिक प्रक्रिया प्रकाश संश्लेषण कहलाती है।

→ सौर तापन युक्तियाँ- सौर ऊर्जा का दोहन करने वाली युक्तियों को सौर ऊर्जा युक्तियाँ कहते हैं।

→ सोलर कुकर सौर ऊर्जा द्वारा खाना पकाने की युक्ति है।

→ सौर ऊष्मक-सौर ऊर्जा द्वारा पानी गर्म करने की युक्ति है।

→ परावर्तक- परावर्तक सौर ऊर्जा को इकट्ठा करके बक्से के अन्दर संकेन्द्रित करता है।

→ सोलर सेल – सौर ऊर्जा को विद्युत ऊर्जा में रूपान्तरित करने वाली युक्ति है।

→ पवन ऊर्जा बहती पवन की गतिज ऊर्जा को पवन ऊर्जा कहते हैं। इससे पवन चक्की चलाकर पवन ऊर्जा का उपयोग अनाज पीसने तथा जमीन से पानी निकालने में किया जाता है। इससे पाल नाव को भी जलाया जाता है।

→ जल ऊर्जा नदियों में बहते हुए जल की गतिज ऊर्जा एवं बाँधों में भण्डारित जल की स्थितिज ऊर्जा को जल ऊर्जा कहते हैं।

→ जल विद्युत बाँध बनाकर जल एकत्रित करके जल को ऊँचाई से टरबाइन पर गिराया जाता है जिससे टरबाइन जनरेटर को चलाकर विद्युत उत्पन्न की जाती है।

→ सागरीय तापीय ऊर्जा-म – महासागर की सतह के जल तथा गहराई के जल के ताप में अन्तर के कारण उपलब्ध ऊर्जा को ‘सागरीय तापीय ऊर्जा’ कहते हैं।

→ जैव द्रव्यमान ऊर्जा वनस्पतियों तथा जन्तुओं के शरीर में स्थित पदार्थों को जैव द्रव्यमान कहते हैं। यह ईंधन की तरह कार्य करता है।

→ ऊर्जा स्त्रोत- नवीकरणीय व अनवीकरणीय।

• ऊर्जा के वे स्रोत जिन्हें हम बार-बार उपयोग में ला सकते हैं, जैसे- जल, पवन और सूर्य का प्रकाश आदि नवीकरणीय ऊर्जा स्त्रोत कहलाते हैं।
• ऊर्जा के वे स्रोत जिनका उपयोग बार-बार नहीं हो सकता, जैसे- कोयला, पेट्रोल और प्राकृतिक गैस आदि अनवीकरणीय स्रोत कहलाते हैं।

→ ऊर्जा को न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है। इसको केवल एक रूप से दूसरे रूप में परिवर्तित किया जा सकता है।

→ ऊर्जा स्रोतों का खत्म होना ऊर्जा संकट कहलाता है। जैसे – तेल और गैस के स्रोत कुछ ही वर्षों के लिए उपलब्ध हैं।

→ बायोगैस — बायोगैस का मुख्य अवयव मेथेन गैस (CH₄) है।

→ बायोमास – सजीव वस्तुओं के मृत भाग व अपशिष्ट पदार्थ इसमें कूड़ा करकट, औद्योगिक अपशिष्ट, फसलों के अपशिष्ट व मल आदि सभी बायोमास के अवयव हैं।

→ सौर कुकर व सौर ऊष्मक – (Solar Cell and Solar Heater) – सौर कुकर व सौर ऊष्मक (Heater) ऐसी साधारण युक्तियाँ होती हैं जिनका उपयोग धूप में 5 से 7 घंटे की अवधि तक, सौर ऊर्जा को ऊष्मा के रूप में एकत्र करने के लिए किया जाता है। यह प्रयोगों द्वारा ज्ञात हो चुका है कि काला पृष्ठ, किसी श्वेत या चमकीले पृष्ठ की तुलना में अधिक ऊष्मा का अवशोषण करता है। काली सतहों का यह गुण सौर कुकर और सौर- ऊष्मक बनाने में प्रयुक्त किया जाता है।

→ ग्रीन हाउस प्रभाव – ग्रीन हाउस काँच से बना एक छोटा घर होता है, इसकी काँच की छत व दीवारें प्रकाश व ऊष्मा को भीतर तो जाने देती हैं लेकिन बाहर नहीं निकलने देती हैं। अतः ग्रीन हाउस के भीतर रखे पौधे बाहर की ठंड (सामान्यत: ठंडी जलवायु वाले स्थानों में) से बचे रहते हैं।

इसी प्रकार इस प्रभाव को ग्रीन हाउस प्रभाव कहते हैं। धूप में खड़ी बंद खिड़की वाली कार भी ग्रीन हाउस प्रभाव के कारण अंदर से गर्म हो जाती है। वातावरण में वाहनों के धुएँ में निकली CO₂ गैस (कार्बन डाइऑक्साइड) भी पृथ्वी से परावर्तित सूर्य के प्रकाश को ग्रहण करके (ग्रीन हाउस प्रभाव के कारण) वातावरण का तापक्रम बढ़ा देती है।

→ नाभिकीय संलयन द्वारा सूर्य में ऊर्जा उत्पन्न होती है। 25. गामा किरणें उच्चभेदन क्षमता वाली विद्युत चुम्बकीय तरंगें हैं।

→ नाभिकीय रिएक्टर एक ऐसी युक्ति है, जिसमें नाभिकीय विखण्डन क्रिया करायी जाती है।

→ नाभिकीय विखण्डन क्रिया में ईंधन के रूप में यूरेनियम अथवा थोरियम तथा मंदक के रूप में भारी जल (D₂O) प्रयोग होता है।

→ यूरेनियम के एक नाभिक के टूटने पर अन्य यूरेनियम के नाभिकों का श्रृंखलाबद्ध टूटना, श्रृंखला अभिक्रिया कहलाती है।

→ प्रकृति से प्राप्त होने वाले यूरेनियम के दो समस्थानिक \({ }_{92} \mathrm{U}^{235}\) तथा \({ }_{92} \mathrm{U}^{238}\) हैं।