Jharkhand Board JAC Class 10 Science Important Questions Chapter 10 Light Reflection and Refraction Important Questions and Answers.
JAC Board Class 10 Science Important Questions Chapter 10 Light Reflection and Refraction
Additional Questions and Answers
Question 1.
Solve the following examples :
1. An object is placed at a distance of 20 cm in front of a convex mirror having focal length 0.3 m. Find the position, nature and magni-fication of the image formed by the mirror.
Answer:
a = 12 cm, virtual, erect and diminished, m = 0.6
2. The radius of curvature of a concave mirror is 12 cm. The image obtained by it is real and has magnification \(\frac { 3 }{ 2 }\). Find the object distance and image distance.
Answer:
u = – 10cm, v = – 15cm
3. A convex mirror having radius of curvature 3 m is fitted as a rear view mirror in a bus. Find the position, nature and magnification of the image of a car standing behind the bus at 6 m from the mirror.
Answer:
u = 1.2m, virtual, erect and diminished, m = 0.2
4. An object of height 2 cm is placed at 32 cm from a concave mirror. If the image formed by the mirror is real, inverted and 1.5 times the object in size, find the focal length of the mirror and the image distance.
Answer:
f = 19.2 cm, u = – 48cm
5. The refractive index of diamond relative to glass is 1.61. If the refractive index of glass is 1.5, find the absolute refractive index of diamond.
Answer:
nda = 2.415
6. The absolute refractive index of ice is 1.31. The speed of light in vacuum is 3 x 108ms-1. Then find the speed of light in ice.
Answer:
v = 2.29 x 108 ms-1
7. The speed of light is 2 x 108ms-1 in a glass having refractive index 1.5. In a liquid the ; speed of light is 2.5 x 108ms-1. Find the absolute refractive index of the liquid.
Answer:
n1a = 1.2
8. A ray of light incident at an angle of 45° on a rectangular glass slab having refractive index \(\sqrt{2}\) from air. Find the angle of refraction, Take the refractive index of air as 1.
Answer:
r = 30°
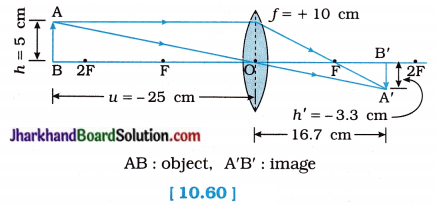
9. The image of a candle is formed at 10 cm from a concave lens having focal length 15 cm. At what distance is the candle placed from the mirror?
Answer:
u = – 30 cm
![]()
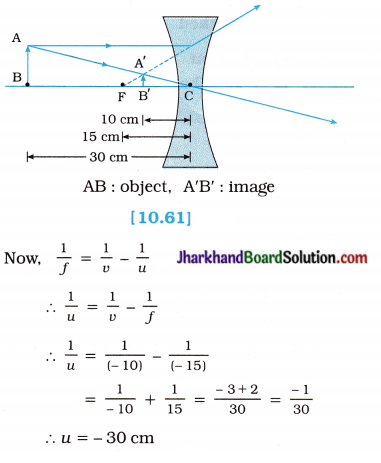
10. A virtual Image is obtained, at 20 cm in front of a lens, when an object is placed at 60 cm in front of the lens. Calculate the focal length s of the lens. State the type of the lens.
Answer:
f = – 30 cm, concave lens
11. The focal length of a lens is – 25 cm. Calculate the power of the lens. Mention the type of the lens.
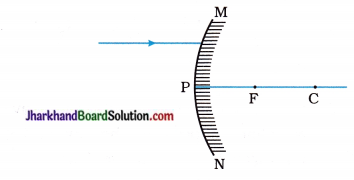
Answer:
P = – 4 D, concave lens
12. The power of a lens is +5 D. An object is placed at a distance equal to twice the focal length of the lens. (1) Calculate the focal length of the lens. (2) Find the position of the image.
Answer:
- f = 20cm
- on the opposite side of the object at a distance of 40 cm from the lens
13. The focal length of a convex lens is 25 cm. The image is obtained at a distance of 75 cm on the other side of the lens. Find the position of the object. What is the nature of the image?
Answer:
u = – 37.5cm; real, inverted and magnified
14. The power of a lens is -4D. A virtual and erect image is obtained at 5 cm from it. Find the position of the object.
Answer:
u = – 6.25 cm
15. A ray of light covers 100 m in vacuum in a certain time. How much distance will it cover in glass of refractive index 1.5 in the same time?
Answer:
\(\frac { 100 m }{ 1.5 }\) = 66.67 m
16. An object is placed at a distance of 25 cm from a concave mirror of focal length 20 cm. Find the image distance and nature of the image.
Answer:
– 100 cm; real, inverted and enlarged
17. An object, 4 cm in height, is placed at 25 cm from a concave mirror of focal length 15 cm. At what distance from the mirror should a screen be kept, so that a sharp image of the object can be obtained on the screen? Find the nature and height of the image.
Answer:
v = – 37.5 cm; size/height = 6 cm; Image is real, inverted and enlarged.
18. A doctor has prescribed a corrective lens of power +1.5 D to a patient. Find the focal length of the lens in centimetre. Is the prescribed lens diverging or converging?
Answer:
f = 67 cm, converging
19. The Sun rays are incident on a concave mirror, parallel to its principal axis. If the image of the Sun is formed at 12 cm distance from the pole of the mirror, find its radius of curvature.
Answer:
24 cm
20. An object is placed at 12 cm in front of a concave mirror. It forms a real and inverted image. Where is the image formed, if the image height is double the object height?
Answer:
In front of the concave mirror at a distance of 24 cm from it.
21. What is the position of the image when an object is placed at 10 cm in front of a concave mirror? The image is virtual and double in size as
compared to the object.
Answer:
Behind the mirror at a distance of 20 cm from it.
22. Find the size of the image formed by a concave lens of focal length 20 cm, when an object having 4 cm height is placed at 60 cm from it.
Answer:
Image size/height = 1.0 cm
23. Determine the nature and size of the image, and the type of mirror for the image formed by mirrors corresponding to magnifications + 1, -1, +0.5, -0.5, +5.0 and -5.0.
Answer:
| No. | Magni-fication (m) | Nature and size of Image | Type of Mirror |
| 1. | + 1 | Virtual, erect and of the same size as the object | Plane |
| 2. | – 1 | Real, inverted and of the same size as the object | Concave |
| 3. | + 0.5 | Virtual, erect and diminished | Convex |
| 4. | – 0.5 | Real, inverted and diminished | Concave |
| 5. | + 5.0 | Virtual, erect and magnified | Concave |
| 6. | – 5.0 | Real, inverted and magnified | Concave |
24. An object of height 4 cm is placed at 18 cm from a concave mirror having focal length 12cm. Find the position, nature and height of the image.
Answer:
v = – 36 cm, h’ = – 8 cm. Real, inverted and enlarged
25. A convex lens forms a real and inverted image of an object at a distance of 40 cm from it. What is the distance of the object from the lens if the size of the image is the same as that of the object? Determine the power of the lens.
Answer:
u = – 40 cm, P = + 5.0 D
26. An object of height 5 cm is placed at 10 cm from a convex mirror of focal length 15 cm. Find the position, nature and size of the image.
Answer:
v = 6 cm, h’ = 3 cm. Virtual, erect and diminished
27. The refractive index of glass with respect to water is 1.12. Find the absolute refractive index of water if the absolute refractive index of glass is 1.5.
Answer:
1.34
![]()
28. Light propagating in a rectangular glass slab enters into water. The refractive index of water with respect to glass is 0.9. The angle of incidence at the surface separating the two media is 26° 48′. Find the angle of refraction. Take sin 26° 48′ = 0.45 approximately.
Answer:
30°
29. An object is placed perpendicular to the principal axis of a concave lens of focal length 30 cm. Find the position of the image when the object is at a distance of 20 cm from the lens.
Answer:
v = – 12 cm
30. The power of a convex lens is +4.0 D. At what distance from the lens should the object be placed to obtain its real and inverted image of the same size as the object on the screen?
Answer:
u = – 50 cm
Question 2.
Give four points of difference between the following terms/quantities:
(1) Concave mirror and Convex mirror
Answer:
| Concave mirror | Convex mirror |
| 1. Its inner surface is reflecting. | 1. Its outer surface is reflecting. |
| 2. It forms a real or virtual image of an object depending on the position of the object. | 2. It always forms a virtual image. |
| 3. The real image can be smaller or of the same size as the size of the object or bigger than the object. The virtual image is always bigger than the object. | 3. The image is always smaller than the object. |
| 4. This mirror is used in a torch, headlight of vehicles, search-light, solar cooker, etc. | 4. This mirror is used as a rear-view (wing) mirror in vehicles. |
(2) Real Image and Virtual Image
Answer:
| Real Image | Virtual Image |
| 1. In this case, the rays of light emanating from an object meet after reflection or refraction and hence, an image is formed. | 1. In this case, the rays of light emanating from an object (when extended backwards) appear to meet after reflection or refraction. |
| 2. It can be obtained on a screen. | 2. It cannot be obtained on a screen. |
| 3. It is inverted compared to an object. | 3. It is erect compared to an object. |
| 4. In case of a spherical mirror it is formed towards the reflecting surface in front of the mirror. | 4. In case of a spherical mirror it is formed behind the reflecting surface of the mirror i.e., in the mirror itself. |
(3) Convex lens and Concave lens
Answer:
| Convex lens | Concave lens |
| 1. It is thick at the centre and thin at the edges. | 1. It is thin at the centre and thick at the edges. |
| 2. It converges parallel rays incident on it. | 2. It diverges parallel rays incident on it. |
| 3. It forms a real or virtual image of an object depending on the position of the object. | 3. It always forms a virtual image. |
| 4. The virtual image obtained with it is always enlarged. | 4. The virtual image obtained with it is always diminished. |
Question 3.
Give scientific reasons for the following statements:
(1) In a headlight, torch and search-light, a concave mirror (of small aperture) is used.
Answer:
In a headlight, torch and search-light, the light source is placed at the principal focus of a concave mirror. As a result, an intense parallel beam of light comes out from a headlight, torch, search-light.
[Note: Actually a parabolic mirror = reflector is used in a headlight, torch and search-light.]
(2) The rear-view mirror (back-view mirror) of the vehicles is a convex mirror.
Answer:
The field view of a convex mirror is very large, i.e., it gives over-all view of vast area of the backside of a vehicle and it forms a virtual, erect and diminished image of a backside object. Hence, the vehicle can be driven safely by viewing backside fully.
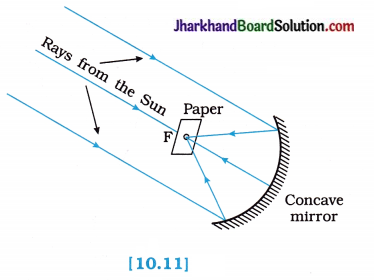
(3) A big concave mirror is used in a solar furnace and solar cooker.
Answer:
Parallel rays of light coming from the Sun fall on the concave mirror fitted in a solar s furnace and solar cooker and after reflection, these rays meet at the principal focus F of the concave i mirror. The greater the aperture of the mirror, the greater is its power to collect light. As a result, abundant amount of heat energy is produced.
(4) For shaving as well as for make-up a concave mirror is used.
Answer:
If a concave mirror is held such that the face is between the pole and principal focus of the concave mirror, a virtual, erect and magnified image of the face is obtained behind the mirror. This is of great help in shaving as well as make-up.
[A dentist also uses a concave mirror to obtain an enlarged (magnified) image of teeth.]
(5) It is difficult to pierce a fish swimming in a river.
Answer:
The rays of light from a swimming fish emerge from river – water and enter into air. Thus, they travel from a denser medium to a rarer medium. Therefore they bend away from the normal at the interface.
Hence, the correct/true position of the fish cannot be determined by the observer from air. That is why it is difficult to pierce a fish swimming in a river.
(6) A watch repairer uses a convex lens.
Answer:
If an object is kept between optical centre O and principal focus F of a convex lens, we get a virtual, erect and enlarged image of the object on the same side of the object, beyond the distance 2f from the lens. Thus, by keeping a watch between the lens and its principal focus, the watch repairer can see minute parts of the watch clearly, so that repairing becomes easy.
Objective Questions and Answers
Question 1.
Answer the following questions in one word / sentence :
(1) Can a magnified image be formed by a convex mirror? State Yes or No.
Answer:
No
(2) What is the angle of reflection when a ray c of light falls normally on a mirror?
Answer:
0°
(3) In a ray diagram, how do you draw the normal at point A on a spherical mirror?
Answer:
By drawing a line joining point A on the spherical mirror with the centre of curvature of the mirror.
(4) State the mirror formula to find the focal length of a spherical mirror.
Answer:
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ u }\) + \(\frac { 1 }{ v }\)
(5) The focal length of a convex mirror is 15cm. What is its radius of curvature?
Answer:
R = 2f = 30 cm
(6) Which two quantities change when a ray of light
Answer:
wavelength and velocity
(7) The magnification produced by concave lens is always less than 1. Why?
Answer:
The image formed by a concave lens (for any position of an object) is always diminished.
(8) Does the refractive index of a medium depend on the frequency of light passing S through it?
Answer:
No. [From n = \(\frac{c}{v}=\frac{f \lambda}{v \lambda^{\prime}}=\frac{\lambda}{\lambda^{\prime}}\) (∵frequency f = constant)]
![]()
(9) Which mirror has large vision area?
Answer:
Convex mirror
(10) Absolute refractive index of carbon disulphide is 1.63. Then, explain this statement in context to speed of light.
Answer:
From n = \(\frac { c }{ v }\), v = \(\frac { c }{ n }\) = \(\frac{3 \times 10^8}{1.68}\)
= 1.84 x 108 m s-1
Hence speed of light in carbon disulphide would be 1.84 x 108 m s-1.
(11) Between which two points on the principal axis of a concave mirror should an object be placed so that the magnification produced by the mirror is m = – 3?
Answer:
Here, m = – 3. So, the image would be real, inverted and magnified. So, the object should be placed between F and C.
(12) What is mirror?
Answer:
Mirror means smooth and polished surface which reflects (approximate 95 %) most of the light incident on it.
(13) Which lens is used as a magnifying lens?
Answer:
Convex lens
Question 2.
Fill in the blanks :
- The centre of a spherical mirror is called the ………………… and the centre of a lens is called the …………………
- The power of a convex lens having focal length 10 cm is ………………… D.
- When a ray of light travels from water to air, its speed …………………
- Focal length of a convex lens is …………………
- ………………… image can be obtained on a screen.
- Magnification produced by a spherical mirror is positive. So, the type of image is …………………
- Magnification produced by a lens is negative. So, the type of image is ………………… and …………………
- A ray of light is incident at an angle of 30° to the surface of a plane mirror. Then the angle between the incident ray and reflected ray must be …………………
- If a virtual, erect and magnified image of i an object is formed by a convex lens; the object must be at a distance …………………
- In case of a mirror or lens, the ratio of the image height to object height is called …………………
- A ………………… lens is thicker at its edges than at its centre.
- ENT specialist doctor uses a ………………… of small aperture.
- A ………………… is used as a magnifying glass.
- If the power of the correcting lens used in spectacles is – 0.4 D, then the type of lens must be …………………
- ………………… is the instrument used to measure the power of a lens.
Answer:
- Pole, Optical centre
- 10
- increases
- positive
- Real
- erect and virtual
- inverted and real
- 120°
- less than the focal length of the lens
- magnification
- concave
- concave mirror
- convex lens
- concave
- Dioptre meter
Question 3.
State whether the following statements are true or false:
- A virtual image can be obtained on a screen.
- In case of irregular reflection, the beam of reflected light remains parallel in a specific direction.
- Laws of reflection are applicable to any type of mirror.
- Laws of reflection are not applicable to a rough and irregular surface.
- The diameter of the reflecting surface of a spherical mirror is known as the aperture of the mirror.
- At least, four rays are required to obtain the position of an image formed by a mirror.
- If an object is kept at infinite distance from concave mirror, the image is formed at the centre of curvature of the mirror.
- Air is optically denser than water.
- When a ray of light enters from an optically denser medium to an optically rarer medium, its speed decreases.
- The central part of a thin lens made of glass works as a rectangular glass slab.
- According to the New Cartesian sign convention for every mirror and lens, Object distance is taken as negative.
- For a mirror, m = \(\frac { v }{ u }\) and for a lens m = – \(\frac { v }{ u }\)
- A lens has power P = 5 D. So, its focal length is f = 0.2 cm.
Answer:
- False
- False
- True
- False
- True
- False
- False
- False
- False
- True
- True
- False
- False
Question 4.
Match the following :
(1)
| Column ‘A’ | Column ‘B’ |
| 1. Concave mirror | p. Negative power |
| 2. Convex lens | q. Always m = positive |
| 3. Convex mirror | r. Always m = negative |
| 4. Concave lens | s. Used for shaving |
| t. Simple microscope |
Answer:
(1 – s), (2 – t), (3 – q), (4 – p).
(2)
| Column ‘A’ | Column ‘B’ |
| 1. Concave mirror | p. It is used by doctors |
| 2. Convex lens | q. It is used as a rear-view mirror in vehicles |
| 3. Convex mirror | r. Power is negative |
| 4. Concave lens | s. It is used in a compound microscope |
Answer:
(1 – p), (2 – s), (3 – q), (4 – r).
Question 5.
Choose the correct option from those given below each question:
1. What is the wavelength range of visible light?
A. 4 x 10-7 m to 8 x 10-7 m
B. 4 x 10-9 m to 8 x 10-9 m
C. 4 x 10-5 m to 8 x 10-5 m
D. 4 x 10-6 m to 8 x 10-6 m
Answer:
A. 4 x 10-7 m to 8 x 10-7 m
2. What is the relation between the radius of curvature (K) and the focal length (f) of a spherical mirror?
A. R = f/ 2
B. R = f
C. R = 2f
D. R = 3f
Answer:
C. R = 2f
3. Through which of the following points, will a ray passing through the centre of curvature (C) and reflected by a concave mirror pass?
A. Focus
B. Centre of curvature
C. Pole
D. All
Answer:
B. Centre of curvature
4. Where, in front of a concave mirror, should an object be placed to get its virtual and erect image?
A. At principal focus F
B. At centre of curvature C
C. Between the principal focus and the pole
D. Beyond the centre of curvature
Answer:
C. Between the principal focus and the pole
5. The magnification produced by a plane mirror is always
A. more than 1
B. 1
C. less than 1
D. zero
Answer:
B. 1
Hint: m = \(\frac { h’ }{ h }\) = 1 (∵ Here, h’ = h)
or
m = – \(\frac { v }{ u }\)
Here, | v | = | u | and u is negative
while v is positive.
∴ We get, m = 1
![]()
6. The focal length of a plane mirror is ……………
A. zero
B. infinity
C. equal to half the object distance f
D. equal to the object distance
Answer:
B. infinity
Hint: In case of plane mirror | v | = | u |, also according to the New Cartesian sign convention, v is positive and u is negative.
Now, from the mirror formula \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\), for a plane mirror, as |u| = [u| and u is negative while v is positive, we get \(\frac { 1 }{ f }\) = 0 ∴ f = ∞ (infinity)
7. The distance between the object at 2 m from a plane mirror and its image is ………………..
A. 4 m
B. 1 m
C. 2 m
D. 3 m
Answer:
A. 4 m
Hint: The distance between the object and its image = | u | + | v |
= 2 + 2 (∵ Here, | u | = | v |)
= 4 m
8. Where should an object be placed to obtain its image as real, inverted and of the same height as the object by a convex lens?
A. At the principal focus
B. Between the principal focus and centre of curvature
C. At the centre of curvature
D. Between the optical centre and principal focus
Answer:
C. At the centre of curvature
9. Which of the following materials has maximum optical density?
A. Glass
B. Water
C. Carbon disulphide
D. Diamond
Answer:
D. Diamond
Hint: From the given substances, diamond has highest refractive index.
Question 10.
The absolute refractive index of any medium is …………………
A. 1
B. > 1
C. < 1
D. zero
Answer:
B. > 1
11. Which of the lenses with focal length 10 cm, 20cm, 25cm and 50cm has maximum power?
A. 50 cm
B. 25 cm
C. 20 cm
D. 10 cm
Answer:
D. 10 cm
Hint: From power P = \(\frac { 1 }{ f }\), the lens with less focal length f has more power P. So, the lens with focal length 10 cm has maximum power.
12. What is the focal length of a convex lens having power + 5.0 D?
A. – 10 cm
B. – 20 cm
C. + 10 cm
D. + 20 cm
Answer:
D. + 20 cm
Hint : P = \(\frac { 1 }{ f }\)
∴ f = \(\frac { 1 }{ p }\) = \(\frac { 1 }{ 5 }\) = 0.2 m = + 20 cm
13. If the absolute refractive indices of water, benzene and sapphire are 1.33, 1.50 and 1.77 respectively, then which medium has maximum relative refractive index?
A. Sapphire relative to water
B. Sapphire relative to benzene
C. Benzene relative to water
D. Water relative to benzene
Answer:
A. Sapphire relative to water
Hint:
\(n_{21}=\frac{n_2}{n_1}\)
∴ n21 is maximum, when n2 is maximum and n1 is minimum.
Hence, it is obvious that in the present case, medium 1 must be water and medium 2 must be sapphire.
∴ Refractive index of sapphire with respect to water would be maximum.
14. Which type of image is formed by a plane mirror?
A. Real and inverted
B. Real and erect
C. Virtual and erect
D. Virtual and inverted
Answer:
C. Virtual and erect
15. If the absolute refractive indices of water and glass are \(\frac { 4 }{ 3 }\) and \(\frac { 3 }{ 2 }\) respectively, then what is the ratio of the speed of light in water to that in glass?
A. 2
B. \(\frac { 8 }{ 9 }\)
C. \(\frac { 9 }{ 8 }\)
D. \(\frac { 1 }{ 2 }\)
Answer:
C. \(\frac { 9 }{ 8 }\)
Hint: Taking water as medium 1 and glass as medium 2, speed of light in water would be v1 and speed of light in glass would be v2.
Here, n1 = \(\frac { 4 }{ 3 }\) and n2 = \(\frac { 3 }{ 2 }\)
Now, n21 = \(\frac{n_2}{n_1}=\frac{v_1}{v_2}\)
∴ \(\frac{3 / 2}{4 / 3}=\frac{v_1}{v_2}\)
∴ \(\frac{v_1}{v_2}=\frac{9}{8}\)
16. The absolute refractive indices of water, glass and diamond are 1.33, 1.50 and 2.42 respectively. Which medium has maximum optical density ?
A. Water
B. Glass
C. Diamond
D. Data not enough to draw any conclusion
Answer:
C. Diamond
Hint: The greater the absolute refractive index, the greater is the optical density.
17. Which of the following always form virtual image ?
A. Concave mirror and convex lens
B. Convex mirror and concave lens
C. Convex mirror and convex lens
D. Concave mirror and concave lens
Answer:
B. Convex mirror and concave lens
18. What is the angle of refraction for a light ray incident normal to the surface of a medium?
A. 90°
B. 60°
C. 30°
D. 0°
Answer:
D. 0°
Hint: According to general form of Snell’s law n1 sin i = n2 sin r. As i = 0°, then r = 0° because value of n1 and n2 are never zero.
19. No matter how far you stand from a mirror, your image appears always erect. The mirror is likely to be ………..
A. plane only.
B. concave only.
C. convex only.
D. either plane or convex.
Answer:
D. either plane or convex.
Hint: In case of both plane and convex mirror for every position of an object its image would be always erect.
20. A virtual image of an object is formed by a mirror, then …………….
A. it would be a convex mirror.
B. it would be a concave mirror.
C. it would be a plane mirror.
D. it would be any one of the mirrors given above.
Answer:
D. it would be any one of the mirrors given above.
21. An object is kept at the centre of curvature of a concave mirror. The distance between the image of the object and pole of the mirror ……………..
A. would be equal to f.
B. would be less than 2f but more than f.
C. would be equal to 2f.
D. would be more than 2f.
Answer:
C. would be equal to 2f.
22. A ray of light travelling in air is obliquely incident on undisturbed horizontal surface of pond water. Inside the water, it…
A. will travel without deviation.
B. will bend away from the normal drawn at the point of incidence.
C. will bend towards the normal drawn at the point of incidence.
D. will turn back following the original path.
Answer:
C. will bend towards the normal drawn at the point of incidence.
23. As shown in the following figure, a light ; ray travels from medium A to medium B. Then refractive index of medium B relative? to medium A would be ……………

A. \(\frac{\sqrt{3}}{\sqrt{2}}\)
B. \(\frac{\sqrt{2}}{\sqrt{3}}\)
C. \(\frac{1}{\sqrt{2}}\)
D. \(\sqrt{2}\)
Answer:
A. \(\frac{\sqrt{3}}{\sqrt{2}}\)
Hint: From Snell’s law, refractive index of medium B relative to medium A.
nBA = \(\frac{\sin 60^{\circ}}{\sin 45^{\circ}}=\frac{\sqrt{3} / 2}{1 / \sqrt{2}}=\frac{\sqrt{3}}{\sqrt{2}}\)
24. As shown in the following figure, a light ray travels from medium A to medium B. Then refractive index of medium A relative to medium B would be
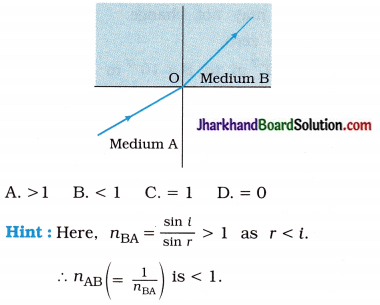
Answer:
B. < 1
25. Magnification produced by a rear-view mirror fitted in vehicles ………….
A. is always less than 1.
B. is always equal to 1.
C. is always more than 1.
D. can be more than or less than 1 depending upon the position of the object in front of the mirror.
Answer:
B. is always equal to 1.
Hint: Convex mirror is used as rear-view mirror in vehicles. Image formed by it is always virtual, erect and diminished in size compared to the
26. The absolute refractive indices of three substances A, B and C are 1.33, 1.65 and 1.46 respectively. In which substance is the speed of light maximum?
A. A
B. B
C. C
D. Would be the same in A, B and C
Answer:
A. A
Hint: nm = \(\frac { c }{ v }\)
![]()
27. An object placed in front of a convex mirror is moved from far-off distance towards the pole of the mirror. Then size of the image …
A. increases.
B. decreases.
C. remains constant.
D. first increases and then decreases.
Answer:
A. increases.
28. An object placed in front of a convex mirror is moved from far-off distance towards the pole of the mirror. Then the image ……………..
A. moves towards the pole.
B. moves away from the pole.
C. first moves away from the pole and then towards the pole.
D. first moves towards the pole and then away from the pole.
Answer:
A. moves towards the pole.
29. What is the centre of a spherical mirror called?
A. Principal focus
B. Centre of curvature
C. Principal axis
D. Pole
Answer:
D. Pole
30. What is the diameter of the reflecting circular surface of a spherical mirror called?
A. Aperture
B. Radius of curvature
C. Focal length
D. Principal axis
Answer:
A. Aperture
31. Where should the object be placed to obtain its real image of the same size as the object using a concave mirror?
A. At infinite distance from the mirror
B. At the centre of curvature of the mirror
C. At the principal focus of the mirror
D. Between the principal focus and the centre of curvature of the mirror
Answer:
B. At the centre of curvature of the mirror
32. Where should the object be placed to obtain a real and diminished image using a concave mirror?
A. Between the principal focus and the pole of the mirror
B. At the centre of curvature of the mirror
C. Between the principal focus and the centre of curvature of the mirror
D. Beyond the centre of curvature of the mirror
Answer:
D. Beyond the centre of curvature of the mirror
33. Where should the object be placed to obtain a real and magnified image using a concave mirror?
A. Between the pole and the principal focus of the mirror
B. At the principal focus of the mirror
C. Between the principal focus and the centre of curvature of the mirror
D. At the centre of curvature of the mirror
Answer:
C. Between the principal focus and the centre of curvature of the mirror
34. Which type of image cannot be obtained by a concave mirror?
A. Real and enlarged
B. Real and diminished
C. Virtual and enlarged
D. Virtual and diminished
Answer:
D. Virtual and diminished
35. Which type of image is formed by a convex mirror?
A. Real, inverted and diminished
B. Virtual, erect and diminished
C. Real, inverted and enlarged
D. Virtual, erect and enlarged
Answer:
B. Virtual, erect and diminished
36. What happens to an obliquely incident ray travelling from glass to air?
A. It bends towards the normal.
B. It bends away from the normal.
C. It does not undergo refraction.
D. It turns back following the original path.
Answer:
B. It bends away from the normal.
37. A point object emits rays in all directions. Consider one ray that the object emits which is parallel to the principal axis of a concave mirror as shown in the following figure.

Select the point in the figure given here, through which the reflected ray passes.
A. C
B. F
C. A
D. P
Answer:
B. F
38. Which type of image of an object cannot be obtained by a convex lens?
A. Real and diminished
B. Real and enlarged
C. Virtual and diminished
D. Virtual and enlarged
Answer:
C. Virtual and diminished
39. From which of the following letters, we cannot obtain its laterally inverted image?
A. N
B. O
C. P
D. Q
Answer:
B. O
40. From which of the following letters, can we obtain its laterally inverted image?
A. W
B. X
C. Y
D. Z
Answer:
D. Z
41. A boy is running with speed u towards a plane mirror, then at what speed, his image will be running towards him?
A. 2v
B. > v
C. v
D. < v
Answer:
A. 2v
42. If a spherical mirror is immersed in water, then its focal length…
A. changes.
B. does not change.
C. may or may not change
D. becomes zero.
Answer:
B. does not change.
Question 6.
Answer the following questions in very short as directed (Miscellaneous) :
(1) Write Snell’s law in mathematical form.
Answer:
If i is the angle of incidence and r is the angle of refraction, then
\(\frac { sin i }{ sin r }\) = constant
This constant is called the refractive index of the second medium with respect to the first medium.
(2) There are five different transparent media, which are in physical contact with one another. Then, write the formula for the refractive index of the fifth medium with respect to the first medium.
Answer:
n51 = \(\frac{n_5}{n_1}\)
(3) If the radius of curvature of a spherical mirror is 40 cm, what is its focal length in metre?
Answer:
f = \(\frac{R}{2}=\frac{40 \mathrm{~cm}}{2}\) = 20 cm = 0.2 m
(4) A concave mirror produces a real image of an object, placed at 10 cm from the mirror. If the image is enlarged by a factor of four relative to object, find the focal length of the mirror.
Answer:
Here, u = – 10 cm
As image formed is real and four times larger than object m = – 4
Now, m = – \(\frac { v }{ u }\)
∴ – 4 = – \(\frac { v }{ (-10) }\) ∴ v = – 40 cm
Using the mirror formula
\(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
We get
\(\frac{1}{f}=\frac{1}{(-10)}+\frac{1}{(-40)}\)
∴ f = \(\frac{-40 \times-10}{-40-10}=\frac{400}{-50}\)
∴ f = – 8 cm
(5) The magnification of an image formed by a convex lens is – 1. Find the object distance in terms of its focal length.
Answer:
Here, m = – 1 and u = – u
So, from m = \(\frac { v }{ u }\)
– 1 = \(\frac { v }{ (-u) }\)
∴ v = + u
Now, \(\frac{1}{f}=\frac{-1}{u}+\frac{1}{v}\)
∴ \(\frac{1}{f}=\frac{-1}{(-u)}+\frac{1}{(+u)}\)
∴ \(\frac{1}{f}=\frac{2}{u}\)
∴ u = 2 f
(6) An object is kept at 40 cm from a concave lens of focal length 60 cm. Find the image distance.
Answer:
Here, u = – 40 cm; f = – 60 cm
Using the lens formula,
\(\frac{1}{f}=\frac{-1}{u}+\frac{1}{v}\)
We get
∴ \(\frac{1}{-60}=\frac{-1}{-40}+\frac{1}{v}\)
∴ \(\frac{1}{v}=\frac{-1}{40}-\frac{1}{60}\)
∴ \(\frac{1}{v}=-\left(\frac{1}{40}+\frac{1}{60}\right)\)
∴ v = \(-\left(\frac{60 \times 40}{40+60}\right)=-\frac{2400}{100}\) = – 24 cm
(7) What is diffused reflection ?
Answer:
When a parallel beam of light falls on a rough surface, the light is reflected in different directions. This type of reflection is known as diffused reflection.
(8) The magnifying power of convex lens is ……………….
A. > 1
B. < 1
C. = 1
D. cannot be determined
Answer:
A, B and C
(9) A pencil, when dipped obliquely in water in a transparent glass tumbler, appears to be bent at the interface of air and water. Will the pencil appear to be bent to the same extent, if instead of water we use some other liquid like kerosene or turpentine? Support your answer with reason.
Answer:
Yes.
The angle of refraction depends on the refractive index of the medium. So, bending will vary in different liquids. It will be less for a liquid with low refractive index and more for a liquid with high refractive index.
The refractive index of kerosene as well as that of turpentine oil is more than that of water. Hence, the bending will be more for both the oils than in case of water.
(10) Draw a ray diagram showing the path of a ray of light when it enters at oblique incidence from air into water.
Answer:
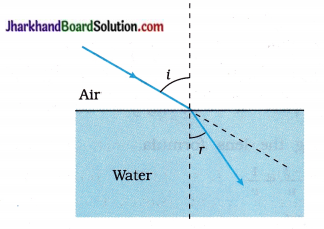
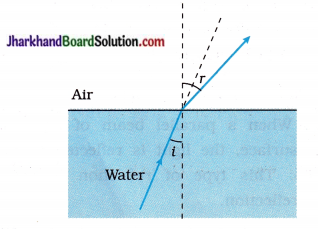
(11) Draw a ray diagram showing the path of a ray of light when it enters at oblique incidence from water into air.
Answer:
(12) A student traces the path of a ray of light passing through a rectangular glass slab and marks the angle of incidence i, angle of refraction r and angle of emergence e, as shown in the figure :
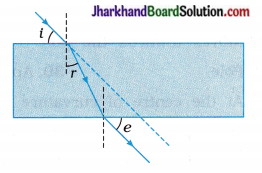
Which angle is correctly marked?
Answer:
r.
(13) What is the angle of reflection, when a ray of light falls normally on the surface of a plane mirror?
Answer:
r = 0°
(14) A ray of light strikes a plane mirror at an angle of 50° to the mirror surface. What will be the angle of reflection?
Answer:
40°
(15) Name the spherical mirror which has virtual principal focus.
Answer:
Convex mirror
(16) What is the angle of incidence for a ray of light passing through the centre of curvature of a concave mirror?
Answer:
0°
(17) What sign [+ve (plus) or -ve (minus)] has been given to the following on the basis of the New Cartesian sign convention?
(a) Height of a real image and
(b) Height of a virtual image?
Answer:
(a) -ve (minus)
(b) +ve (plus)
(18) What is the nature of the image formed by a concave mirror if the magnification produced by the mirror is (a) + 3 (b) – 2 ?
Answer:
(a) Virtual
(b) Erect
![]()
(19) An object is placed at a very long distance in front of a convex mirror of radius of curvature 30 cm. State the position of its image.
Answer:
At the principlal focus; 15 cm behind the convex mirror.
(20) The refractive index of glass with respect to air is 3/2. The refractive index of air with respect to the glass is 4/6. Do you agree with this statement?
Answer:
Yes
(21) Name the following:
A point inside a lens through which the light passes undeviated.
Answer:
Optical centre.
(22) A 2 cm high object is placed at a distance of 2f from a convex lens. What is the height of the image formed?
Answer:
m = \(\frac { v }{ u }\) = \(\frac { h’ }{ h }\)
∴ h’ = h(\(\frac { v }{ u }\))
Here, u = – 2f and also v = – 2f
∴ The height of the image formed,
h’ = 2 cm\(\left(\frac{-2 f}{-2 f}\right)\) (∵ h = 2 cm)
= 2 cm
(23) Where should an object be placed in order to use a convex lens as a magnifying glass?
Answer:
At a distance less than the focal length of the convex lens.
(24) Draw the given diagram in your answer book and complete the path of the ray of light on refraction by the lens.
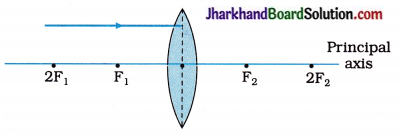
Answer:

(25) Copy and complete the diagram given below to show what happens to the ray of light when it passes through the concave lens :
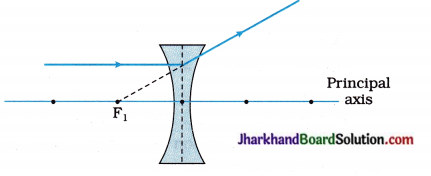
Answer:

(26) A concave lens produces an image at 20 cm from the lens of an object placed at 30 cm from the lens. Find the focal length of the lens.
Answer:
Using the lens formula,
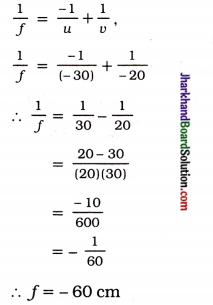
(27) Which causes more bending (or more refraction) of light rays passing through it: a convex lens of long focal length or a convex lens of short focal length?
Answer:
A convex lens of short focal length
(28) Which has more power : a thick convex lens or a thin convex lens made of the same material (glass)? Give reason for your choice.
Answer:
Thick convex lens because it has shorter focal length and hence more power.
(29) For a converging lens, the power is positive while for a diverging lens, the power is negative. Agree / Disagree?
Answer:
Agree
(30) The optician’s prescription for a pair of spectacles is :
Right eye : – 3.50 D, Left eye : – 4.00 D
(a) Are these lenses thinner at the middle or at the edges?
(b) Which is the weaker eye?
Answer:
(a) Thinner at the middle
(b) Left eye
(31) A person got his eyes tested by an optician. The prescription for the spectadle lenses to be made reads :
Right eye : + 2.00 D, Left eye : + 2.50 D
(a) State whether these lenses are thicker in the middle or at the edges.
(b) State whether these spectacle lenses will converge light rays or diverge light rays.
Answer:
(a) Thicker in the middle
(b) Converge light rays
(32) Match the following columns correctly:
| Column I | Column II |
| 1. Converging mirror | p. It is used as rear view mirror in vehicles |
| 2. Diverging mirror | q. It is used in the design of solar furnaces |
| r. It is used in a dressing-table |
Answer:
(1 – q), (2 – p).
(33) Match the following columns correctly:
| Column I | Column II |
| 1. Converging lens | p. It Is a concave lens |
| 2. Diverging lens | q. It acts as a magnifier |
| r. It is used as a reflector |
Answer:
(1 – q), (2 – p).
(34) State any two factors on which the lateral displacement of an emergent ray from a rectangular glass slab depend.
Answer:
- Angle of incidence
- Thickness of the slab
(35) What is the minimum distance between an object and its real image in case of a concave mirror?
Answer:
0 (zero). [When the object is at centre of curvature C of the mirror.]
(36) When a light ray passes obliquely through the atmosphere in the upward direction, how does its path generally change?
Answer:
Light will bend away from its normal direction.
(37) Explain briefly, why a ray of light passing through the centre of curvature of a concave mirror, gets reflected along the same path.
Answer:
The ray of light passing through the centre of curvature of a concave mirror is incident on the mirror along its normal. So, i = r = 0. Therefore, the ray retraces its path.
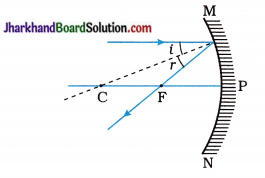
(38) A ray of light is incident on a concave mirror as shown in the adjoining figure. Redraw the diagram and complete the path of the ray after reflection from the mirror.
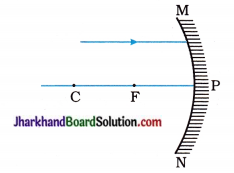
Answer:
(39) A ray of light is incident on a convex mirror as shown in the adjoining figure. Redraw the diagram and complete the path of the ray after reflection from the mirror.
Answer:
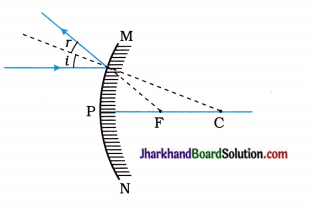
(40) What is the unit of refractive index?
Answer:
Refractive index as no unit as it is the ratio of two similar quantities.
(41) State the conditions for no bending of light travelling from one medium to another.
Answer:
- Light incident normally.
- Equal refractive index of the two different media.
(42) Why is the refractive index of atmosphere different at different altitudes?
Answer:
The refractive index of atmosphere is different at different altitudes because the air density changes with altitude.
(43) For the same angle of incidence in media P Q and R, the angles of refraction are 45°, 35° and 30° respectively. In which medium is the speed of light minimum? Give reason for your answer.
Answer:
In medium R, the speed of light is minimum.
In the usual notation, as n = \(\frac { c }{ v }\) = \(\frac { sin i }{ sin r }\).
For medium R, r is minimum and hence the speed v is minimum.
(44) Observe the following incomplete ray diagram, where the image A’B’ is formed after refraction from a convex lens :
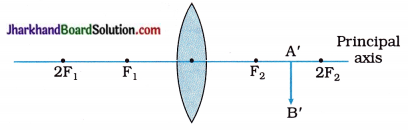
On the basis of the above information, fill in the blanks :
(1) The position of object AB (not shown in the figure) must be
(2) The size of the object must be than the size of the image.
Answer:
(1) beyond 2F1
(2) greater.
(45) Raju focussed the image of a candle flame on a white screen using a convex lens. He noted the position of the candle as 26.0 cm, the position of the convex lens as 50.0 cm and the position of the screen as 74.0 cm. What is the focal length of the convex lens?
Answer:
Here, u = the distance of the candle from the convex lens = – (50.0 – 26.0) = – 24.0 cm
v = the distance of the screen from the convex lens = (74.0 – 50.0) = 24.0 cm
From the lens formula,
∴ \(\frac{1}{f}=\frac{-1}{u}+\frac{1}{v}\)
∴ \(\frac{1}{f}=\frac{-1}{(-24)}+\frac{1}{24}=\frac{2}{24}\)
∴ f = 12 cm
(46) Study the given ray diagram. Name the device Y.
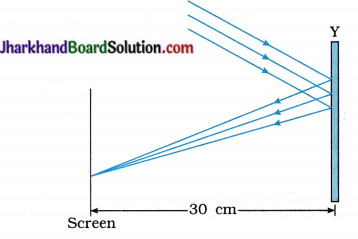
Answer:
Device Y is a concave mirror.
(47) Which property of a concave mirror is utilized for using it as a shaving mirror ?
Answer:
When an object is held between the pole and the principal focus of a concave mirror, a virtual, erect and magnified image of the object is formed. This property of a concave mirror is utilized for using it as a shaving mirror.
(48) How do you draw a normal to a spherical mirror at a particular point on the mirror?
Answer:
Join that point on the mirror to the centre of curvature of the mirror and extend the line if required.
(49) The magnification produced by a concave mirror is -1. What is the position of the object?
Answer:
The object must be at the centre of curvature of the concave mirror.
(The image formed is real, inverted and of the same size as the object. That is why magnification = -1).
(50) The magnification produced a spherical mirror is ±2. What kind of mirror can it be?
Answer:
The mirror must be a concave mirror. (Only then magnification can be positive or negative).
(51) Bharat claims to have obtained an image twice the size of the object with a concave lens. Is he correct? Give reason for your answer.
Answer:
Bharat’s claim is not correct.
This is because the image formed by a concave lens is always smaller in size than the object.
(52) Out of alcohol with n= 1.36 and carbon disulphide with n = 1.63 which is denser optically?
Answer:
Carbon disulphide with greater refractive index is optically denser than alcohol.
(53) What is the nature of the image formed by a concave mirror if the magnification produced by the mirror is +3?
Answer:
The image must be virtual, erect, enlarged (three times in size relative to the object) and formed behind the mirror.
(54) With respect to air, the refractive index of ice is 1.31 and that of rock salt is 1.54. Calculate the refractive index of rock salt with respect to ice.
Answer:
nia = 1.31 and nra = 1.54, nri = ?
Now, nri = \(\frac{n_{\mathrm{ra}}}{n_{\mathrm{ia}}}=\frac{1.54}{1.31}\) = 1.17
![]()
(55) What is the minimum number of rays required for locating the image formed by a concave mirror?
Answer:
At least two rays are required for locating the image formed by a concave mirror.
(56) By changing the object distance the focal length of a given spherical mirror cannot be changed but the linear magnification produced by the mirror can be changed. Agree / Disagree?
Answer:
Agree
(57) Write the correct sequence of angle of incidence, angle of emergence, angle of refraction and lateral displacement shown in the following diagram by numbers 1, 2, 3 and 4.
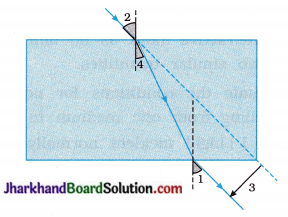
Answer:
2, 1, 4, 3.
(58) What is the relation between n1 and n2 in the following three ray diagrams (figures)?
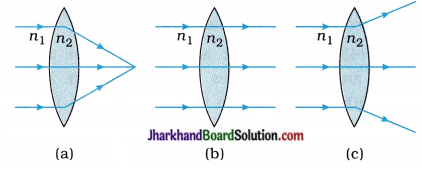
Answer:
(a) n1 < n2
(b) n1 = n2
(c) n1 > n2
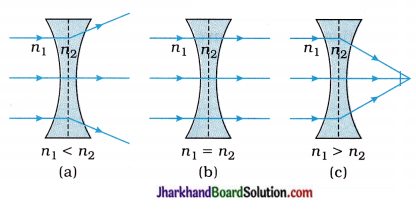
Important note: In case of a concave lens the corresponding relation between n1 and n2 along with, the ray diagrams (figures) is shown below:
(59) Which factors determine the focal length of a lens?
Answer:
The focal length of a lens depends on:
- the radii of curvature of the surfaces of the lens.
- the nature of the material of the lens.
- the nature of the medium in which the lens is placed.
[Note : It also depends upon the frequency of the incident light.]
Value Based Questions With Answers
Question 1.
Two fast friends named Anjalee and Shweta spend most of the time with each other. One S day, Anjalee observed that Shweta has pain in gums while eating her school-lunch. Anjalee’s S father is a dentist. So she advised Shweta to come with her to her father’s clinic.
Anjalee’s father examined Shweta’s mouth and teeth with a mirror and light and advised her not to eat too many chocolates and drink soft drinks, Then she started taking care of her mouth as she washed her mouth properly every time after having food and also started taking calcium-rich diet.
- Which type of mirror is used by the dentist?
- Name the phenomenon of light by which the doctor is able to examine Shweta.
- What values are shown by Anjalee?
Answer:
- Concave mirror
- Reflection of light
- Friendship
- Concern for other
- Helping nature
Question 2.
In a small town-fair, Amey took his friend and showed him a mirror in which his image showed the upper half of the body very fat and lower half of the body very thin. Amey’s friend got upset but Amey explained him by showing his similar image in the mirror.
- Name the two mirrors used in this fair shop.
- Name the mirror in which the size of image is small.
- What values are displayed by Amey?
Answer:
- Concave and convex mirror
- Convex mirror
- Compassion and empathy.
Question 3.
Prashant was going to his office in his car. While driving his car, Prashant saw a man behind him on a motorcycle through his rear-view mirror. A woman was also sitting behind the man on the motercycle. Through his rear-view mirror, Prashant noticed that the saree of the woman was almost touching the spokes of the motorcycle wheel. He signalled the motorcyclist to stop and alerted the woman. She tied her saree properly and thanked Prashant for the s alert.
(1) What type of mirror is used as a rear-view mirror?
(2) State two characteristics of the image formed by such a mirror.
(3) What values are displayed by Prashant in this incident?
Answer:
(1) Convex mirror
(2)
- Virtual and erect
- diminished (smaller than the object)
(3) The values displayed by Prashant in this incident are …
- Vigilant (because he kept careful watch for a likely mishap around him)
- Concern about others (here, he was concerned about the safety of the woman)
- Responsible citizen (because, he stopped the motorcycle and alerted the woman about an impending danger to her life).
Question 4.
On the way from Ahmedabad to Vadodara there were four friends in a car. Sanjay was driving the car. He saw from his side mirror that the car which was behind their car had met with an accident.
He suddenly applied the brakes, even after his friends asked him to leave the situation as it is. But still Sanjay did not agree and got down from the car and persuaded his friends to help the injured. All of them took the injured person to the nearest hospital. After taking first-aid from the hospital, the victim thanked them for saving his life.
(1) Name the type of mirror from which Sanjay saw the accident.
(2) Why is this type of mirror used as a side mirror in vehicles?
(3) What can you learn from Sanjay’s character?
Answer:
(1) A convex mirror
(2) Convex mirrors have a wider field of view, as they are curved outwards. Therefore, a convex mirror enables the driver to view much larger area.
(3) Sanjay is of helping nature.
We learn to help needy people.
Question 5.
At one of the blind ends of a road in a colony, lot of accidents used to take place. One day, Shalini moved into a house near ; the blind end. On a certain day, she saw an accident taking place at the blind end.
She, at once rushed to the spot and helped the victims with the first-aid. She then telephoned for an ambulance. Later on she met the president of the welfare committee of the colony and requested him to install huge convex mirrors at both the ends of the blind end. After the installation of the mirrors the accident rate suddenly dropped.
- Why did Shalini advise the installation of huge convex mirrors at both ends of the blind end?
- What according to you are the values displayed by Shalini?
- What according to you are the values displayed by president of the welfare committee of the colony?
Answer:
- A convex mirror has a wide range of view. As a result, it is capable of showing the traffic on the other side or the blind end. Since, she was aware of this fact, Shalini advised for their installation.
- The values displayed by Shalini are concern for others and right use of knowledge.
- The values displayed by the president of the welfare committee of the colony are understanding nature, sense of duty and concern for the safety of others.
Practical Skill Based Questions With Answers
Question 1.
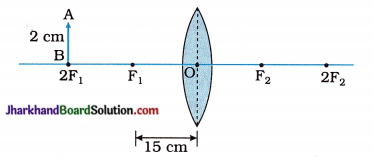
(1) In the figure, u = ……………. and f = ……………..
(2) For the image of the object AB, v = ……………. and h’ = …………….
(3) Find magnification m.
Answer:
(1) – 30 cm, +15 cm
because from the given figure,
u = 2f1 = – 2 x 15 = – 30 cm and
f = + 15 cm as the given lens is convex.

Question 2.
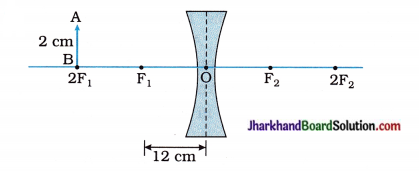
(1) In the figure, f = …………….. and u = ………………
(2) State the type of image.
(3) Will the value (modulus) of magnification be 1 or less than 1 or more than 1?
Answer:
(1) – 12 cm, – 24 cm
From the given figure, f = – 12cm.
(∵ the given lens is concave) and u = – 2f1 = – 2 x 12 = – 24 cm
(∵ (Real) object distance is always negative.)
(2) Type of image : virtual, erect and diminished
(3) Less than 1

Question 3.
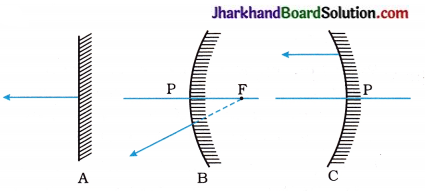
As shown in the figure, three different reflected rays are obtained from three different mirrors. Carefully study the given diagrams and answer the following questions:
- Which one of the given mirrors is convex?
- Which of the mirrors will (i) reflect light as a parallel beam of light (ii) converge the parallel beam when a parallel beam of light is incident on it?
- Which one of the given mirrors will always produce an image equal in size to that of the object?
- Which mirror will form an image smaller than object size?
- Which mirror will form an image smaller or bigger than the object depending on the object distance?
- Which mirror is used (i) in a dressing table, (ii) as a rear-view mirror in vehicles (iii) by a dentist?
Answer:
- Mirror B
- Mirror A will reflect light as a parallel beam of light and mirror C will converge a parallel beam of light.
- Mirror A
- Mirror B
- Mirror C
- Mirror A is used in a dressing table, mirror B is used as a rear-view mirror in vehicles and mirror C is used by a dentist.
Question 4.
For a spherical mirror, obtain the equation for magnification m in terms of (1) f and u only (2) f and v only.
Answer:
(1) Mirror formula : = \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
Multiply both the sides by – u
∴ \(\frac{-u}{f}=\frac{-u}{v}+\frac{-u}{u}\)
∴ \(\frac{-u}{f}=\frac{-u}{v}\) – 1
∴ \(\frac{-u}{v}=1-\frac{u}{f}\)
∴ \(\frac{-u}{v}=\frac{f-u}{f}\)
∴ \(\frac{-v}{u}=\frac{f}{f-u}\)
∴ m = \(\frac{f}{f-u}\) (∵ m = – \(\frac{v}{u}\))
(2) Mirror formula : \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Multiply both the sides by – v
∴ \(\frac{-v}{f}=\frac{-v}{v}+\frac{-v}{u}\)
∴ \(\frac{-v}{f}=-1-\frac{v}{u}\)
∴ \(\frac{-v}{u}=1-\frac{v}{f}\)
∴ \(\frac{-v}{u}=\frac{f-v}{f}\)
∴ \(\frac{-v}{u}=\frac{f-v}{f}\)
∴ m = \(\frac{f-v}{f}\) (∵ m = – \(\frac{v}{u}\))
Question 5.
For a lens, obtain the equation for magnification m in terms of (1) f and u only (2) f and v only.
Answer:
(1) Lens formula : \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
Multiply by u on both the sides,
∴ \(\frac{u}{f}=\frac{u}{v}-\frac{-u}{u}\)
∴ \(\frac{u}{f}=\frac{u}{f}\) + 1
∴ \(\frac{u}{v}=\frac{u+f}{f}\)
∴ \(\frac{v}{v}=\frac{f}{f+u}\)
∴ m = \(\frac{f}{f+u}\) (∵ m = \(\frac{v}{u}\))
(2) Lens formula : \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
Multiply by v on both the sides,
∴ \(\frac{v}{f}=\frac{v}{v}-\frac{v}{u}\)
∴ \(\frac{v}{f}= 1-\frac{v}{u}\)
∴ \(\frac{v}{u}=1-\frac{v}{f}\)
∴ \(\frac{v}{u}=\frac{f-v}{f}\)
∴ m = \(\frac{f-v}{f}\) (∵ m = \(\frac{v}{u}\))
![]()
Question 6.
In case of a convex mirror, if an object is kept at a distance equal to its focal length, then the height of the image is half the height of the object. Prove this result from the formula for magnification only.
Answer:
Here u = – f
Now, m = \(\frac { f }{ f-u }\)
∴ m = \(\frac { f }{ f-(-f)}\)
m = \(\frac { f }{ 2f }\)
= \(\frac { 1 }{ 2 }\)
Now, m = \(\frac { h’ }{ h }\)
∴ \(\frac { h’ }{ h }\) = \(\frac { 1 }{ 2 }\)
∴ h’ = \(\frac { h }{ 2 }\)
Question 7.
The focal length of a convex lens is +10 cm and the focal length of a concave lens is -10 cm. If two objects of equal height are kept on the principal focus of both the lenses, then find the position of the image formed in each case.
Answer:
In case of a convex lens, f = + 10 cm,
u = – 10 cm
Now, \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
∴ \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\)
\(\frac{1}{+10}+\frac{1}{-10}\)
= 0
∴ v = ∞
Hence, the image formed by the convex lens would be at infinite distance from the lens.
In case of concave lens, f = – 10cm, u = – 10 cm
Now, \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
∴ \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\)
= \(\frac{1}{-10}+\frac{1}{-10}\)
= \(\frac{(-10)+(-10)}{-10 \times-10}\)
= \(\frac { -20 }{ 100 }\)
= – \(\frac { 1 }{ 5 }\)
Hence, the image formed by the concave lens would be exactly between principal focus F and optical centre O of the concave lens on the same side as that of the object.
Question 8.
If p, q and r denote the object distance, image-distance and the radius of curvature of a spherical mirror, then prove, r = \(\frac{2 p q}{p+q}\).
Answer:

Question 9.
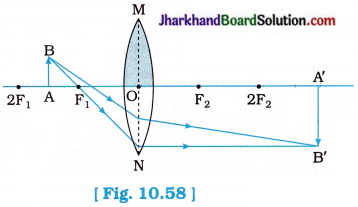
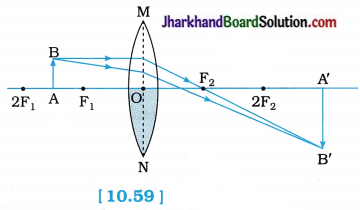
A real, inverted image of the size of the object is to be formed by holding the object at 1 metre from a convex lens. What should be the focal length of the lens? Draw the ray diagram.
Answer:
When the size of the image = the size of the object, the distance of the object from a convex lens, u = 2f where f is focal length of a convex lens.
Here, u = 2f = 1 metre (given).
∴ f = \(\frac { 1 }{ 2 }\) m = 0.5 m = 50 cm
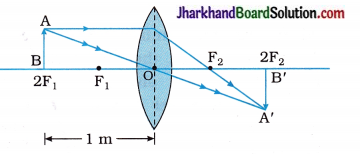
The course of rays in this case is as shown in the figure above.
Question 10.
AB and CD, two spherical mirrors, form parts of a hollow spherical ball with its centre at O, as shown in the diagram. If arc AB = \(\frac { 1 }{ 2 }\) arc CD,
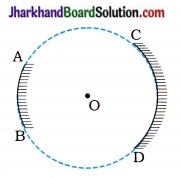
(1) What is the ratio of their focal lengths?
(2) State which of the two mirrors will always form a virtual image of an object placed in front of it and why?
Answer:
(1) f = \(\frac { R }{ 2 }\) The radius of curvature is the same in two cases. Hence, numerically, the focal length |f| will be the same. But the focal length of a convex mirror (AB) is positive while that of a concave mirror (CD) is negative. Hence the ratio of the focal lengths will be – 1.
[Note: Ratio of numerical value of the focal lengths will be 1.]
(2) Mirror AB will always form a virtual image as mirror AB is a diverging / convex mirror.
Question 11.
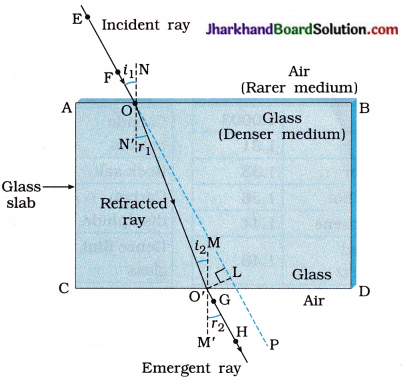
What is lateral displacement? Show that a ray incident obliquely on a rectangular glass slab, emerges parallel to the incident ray.
Answer:
- Place a glass slab on a plane sheet of paper fixed on a drawing board.
- Draw its boundary.
- Fix two pins A and B on one side of the slab.
- Look through the opposite side of the slab and fix two pins C and D in such a way that all the four pins
- A, B, C and D appear to be in a straight line.
- CD is the emergent ray. Let it subtend an angle e with the normal.
- In the first refraction from medium a (air) to medium b (glass), i is the angle of incidence and r is the angle of refraction.
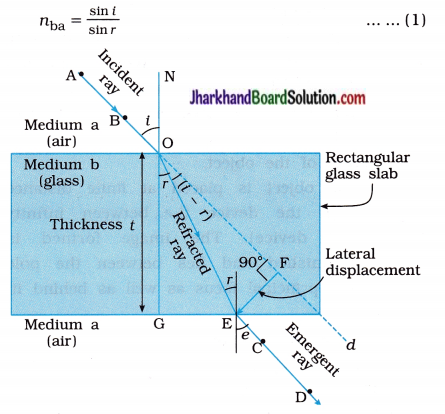
Refraction through a rectangular glass slab of thickness: A lateral displacement In the second refraction at E, the angle of incidence in medium b is r and the angle of refraction in medium a is e.
nab = \(\frac{\sin r}{\sin e}\) … (2)
From (1) and (2), we have
nba x nab = \(\frac{\sin i}{\sin r} \times \frac{\sin r}{\sin e}\)
Butnba x nab = 1, according to the principle of reversibility.
Hence, 1 = \(\frac{\sin i}{\sin e}\)
∴ sin i = sin e
∴ i = e
Thus, the angle of emergence is equal to the angle of incidence. Therefore, incident ray produced (or extended) i.e., AOd is parallel to emergent ray CD.
Thus, the emergent ray is parallel to the incident ray, but displaced sideways as shown in the figure. This sideways displacement FE is known as lateral displacement.
Question 12.
Identify the device used as a spherical mirror or lens in the following cases, when the image formed is virtual and erect in each case.
- An object is placed between the device and its principal focus. The image formed is enlarged and behind the device.
- The object is placed between the principal focus and device. The image formed is enlarged and on the same side as that of the object.
- The object is placed at finite distance from the device (i.e., between infinity and device). The image formed is diminished and lies between the principal focus and optical centre and on the same side as that of the object.
- The object is placed at finite distance from the device (i.e., between infinity and device). The image formed is diminished and lies between the pole and principal focus as well as behind it.
Answer:
- A concave mirror.
- A convex lens.
- A concave lens.
- A convex mirror.
Question 13.
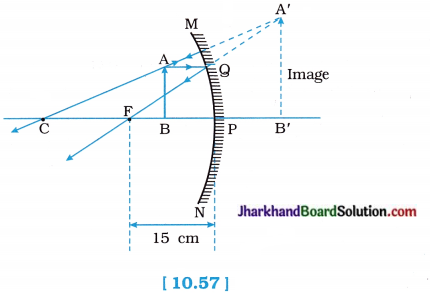
Sudha finds that a sharp image of the s windowpane of her science laboratory is formed at 15 cm from the lens. She now tries to focus the building visible to her outside the? window instead of the windowpane without disturbing the lens. In which direction will she move the screen to obtain a sharp image of s the building? What is the approximate focal length of this lens?
Answer:
To obtain a sharp image of the building instead of the windowpane, Sudha will have to move the screen slightly towards the lens. The approximate focal length of this lens is 15 cm.
Question 14.
Under what condition in an arrangement of two plane mirrors, will an incident ray and the reflected ray be always parallel to each other? (whatever may be the angle of incidence) Show the same with a diagram.
Answer:
When two plane mirrors are placed at 90° to each other, then the incident and reflected rays will always be parallel to each other, whatever may be the angle of incidence. The course of rays is shown in Fig. for i = 45°.
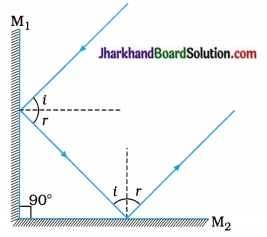
[Note: Students can repeat this activity for different angles of incidence to verify the answer given above.]
Question 15.
Study the diagram given below carefully and answer the following questions :
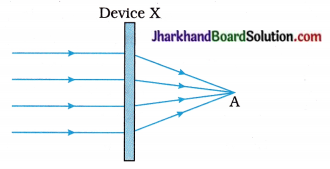
- Due to which phenomenon does the path of a ray of light get deviated?
- Name the device X.
- What is point A called ?
- Which quantity is the inverse of the distance between device X and point A?
- State the SI unit of the physical quantity mentioned as the answer to question (4).
Answer:
- Refraction
- Convex lens
- Principal Focus
- Power of a lens
- D (dioptre)
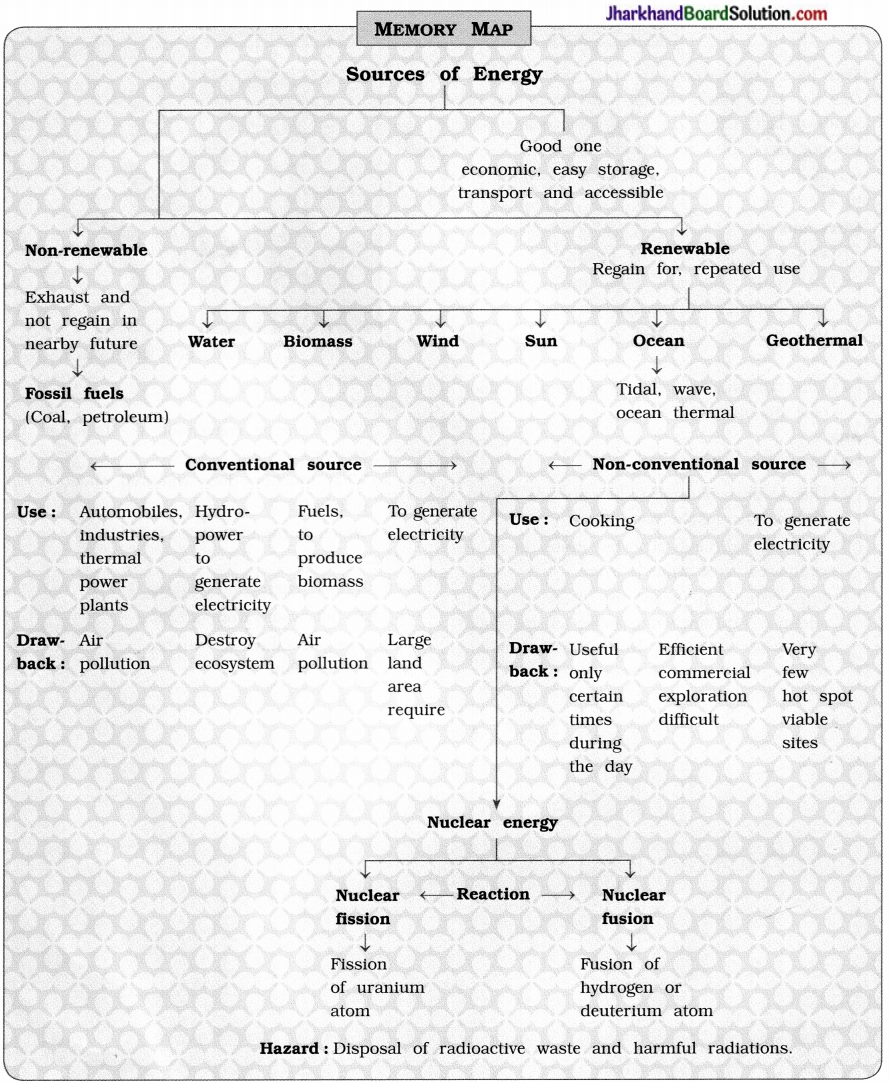
Memory Map:


















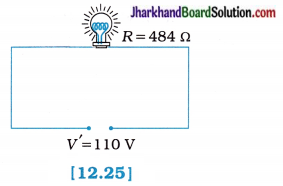

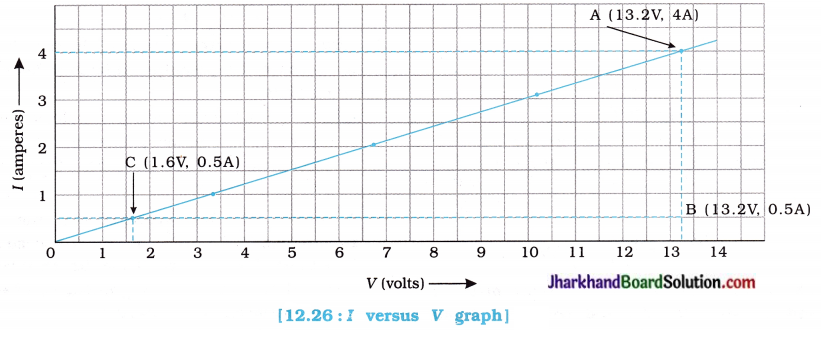
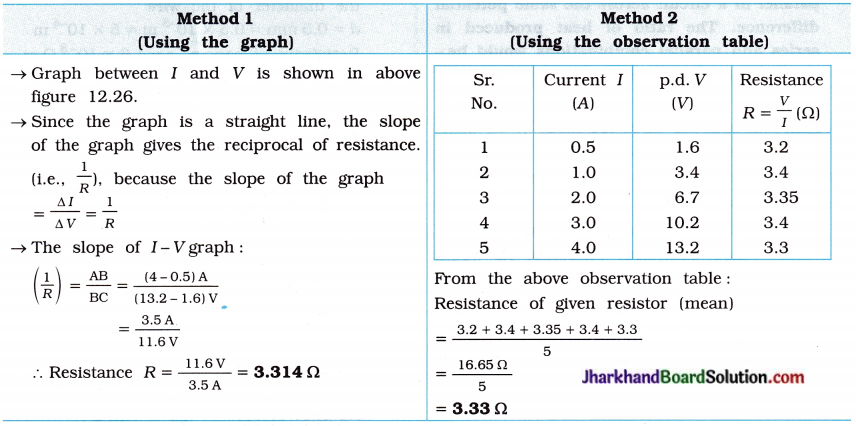
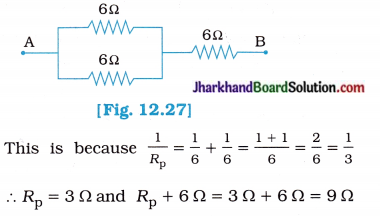






 fins cut out of a metal sheet into these slits.
fins cut out of a metal sheet into these slits.