JAC Class 10 Science Solutions Chapter 11 Human Eye and Colourful World

Jharkhand Board JAC Class 10 Science Solutions Chapter 11 Human Eye and Colourful Worlds Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 11 Human Eye and Colourful World

Jharkhand Board Class 10 Science Human Eye and Colourful World Textbook Questions and Answers

Question 1.
The human eye can focus on objects at different distances by adjusting the focal length of the eye lens. This is due to ……………
(a) presbyopia.
(b) accommodation.
(c) near-sightedness.
(d) far-sightedness.
Answer:
(b) accommodation.
[Hint : Accommodation is the ability of the eye lens to focus both nearby and distant objects by adjusting its focal length.]

Question 2.
The human eye forms the image of an object at its ……………..
(a) cornea.
(b) iris.
(c) pupil.
(d) retina.
Answer:
(d) retina.
The retina is the light sensitive surface of the eye on which the image is formed.

Question 3.
The least distance of distinct vision for a young adult with normal vision is about ……………..
(a) 25 m
(b) 2.5 m
(c) 25 m
(d) 2.5 m
Answer:
(c) 25 cm.
The minimum distance at which an object can be seen most distinctly without any strain (i.e., comfortably) is 25 cm.

Question 4.
The change in focal length of an eye lens is caused by the action of the…
(a) pupil.
(b) retina.
(c) ciliary muscles.
(d) iris.
Answer:
(c) ciliary muscles.
The ciliary muscles contract and expand, in order to change the curvature of the eye lens for focussing the image of an object at varying distances at the retina.

Question 5.
A person needs a lens of power – 5.5 dioptres for correcting his distant vision. For correcting his near vision he needs a lens of power +1.5 dioptres. What is the focal length of the lens required for correcting (1) distant vision and (2) near vision?
Solution :
(1) For distant vision, f = ?
P = – 5.5, D = – 5.5 m^-1
Now, f = \(\frac { 1 }{ p }\)
∴ f = \(\frac{1}{-5.5 m^{-1}}\)
= – 0.182m
= – 18.2 cm (concave lens)

(2) For near vision, f = ?
P = + 1.5, D = + 1.5 m^-1
Now, f = \(\frac { 1 }{ p }\)
∴ f = \(\frac{1}{+1.5 m^{-1}}\)
= 0.667 m
= 66.7 cm (Convex lens)

Question 6.
The far point of a myopic person is 80 cm in front of the eye. What is the nature and power of the lens required to correct the problem?
Solution:
1. The defect of an eye called myopia (short-sightedness or near-sightedness) is corrected by using spectacles containing concave lens of appropriate focal length.

2. Here the far point of myopic person is 80 cm. (while far point of normal person is infinity oo)

3. This means that this person can see the distant object (kept at infinity) clearly if the image of this distant object is formed at his own far point (which is 80 cm here).
So, in this case:
Object distance u = – ∞ (Normal far point)
Image distance v = – 80 cm (Far point of this defective eye in front of lens)
Focal length f = ?
Now,
By the lens formula, \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
∴ \(\frac{1}{f}=\frac{1}{-80}-\frac{1}{-\infty}\)
∴ \(\frac{1}{f}=-\frac{1}{80}\)
∴ f = – 80 cm
= – 0.8 m (Concave lens)
Now,
Power of the lens,
P = \(\frac { 1 }{ f }\)
∴ P = \(\frac { 1 }{ -0.8m }\)
= – \(\frac { 10 }{ 8 }\)m^-1
= – 1.25 D
A concave lens of power -1.25D is required to correct the problem.

Question 7.
Make a diagram to show how hypermetropia is corrected. The near point of a hypermetropic eye is 1 m. What is the power of the lens required to correct this defect? Assume that the near point of the normal eye is 25 cm.
Solution:
1. The defect of an eye called hypermetropia (long-sightedness or far-sightedness) is corrected by using spectacles containing convex lenses of appropriate focal length.

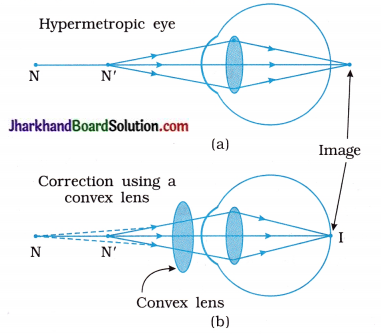
[N = Near point of a hypermetropic eye and
N’ = Near point of a normal eye]
[11.16 : (a) Hypermetropic eye (b) corrected eye]

2. Here the near point of the hypermetropic eye is 1 m = 100 cm
(while near point of normal eye is 25 cm)

3. This means that this person can see the nearby object (kept at 25 cm) clearly if the image of this nearby object is formed at his own near point (which is lm = 100 cm here).
So, in this case :
Object distance u = – 25 cm (Normal near point)
Image distance u = – 1 m = – 100 cm
(Near point of this defective eye in front of lens)
Focal length f = ?
Now,

Now,
Power of the lens,
P = \(\frac { 1 }{ f }\)
= \(\frac{1}{\left(\frac{1}{3} \mathrm{~m}\right)}\)
= 3D

Question 8.
Why is a normal eye not able to see clearly the objects placed closer than 25 cm?
Answer:
For seeing nearby objects, the ciliary muscles contract to make the eye lens thicker near the middle, so as to reduce the focal length of the eye lens.

But ciliary muscles cannot be contracted beyond a certain limit and hence we cannot see clearly the objects closer than 25 cm from the eye.

In other words, a normal eye is not able to see clearly the objects placed closer than 25 cm because all its power of accommodation has already been exhausted.

Question 9.
What happens to the image distance in the eye when we increase the distance of an object from the eye ?
Answer:
For a normal eye, the image distance (u) in the eye is fixed = distance of the retina from the eye lens ≈ 2.3 cm
When we increase the distance of the object (u) from the eye, the focal length of eye lens is changed on account of the accommodating power of the eye so as to keep the image distance (u) constant according to the relation \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\).

Question 10.
Why do stars twinkle?
Answer:
Twinkling of stars is due to atmospheric refraction of starlight.

• Starlight, on entering the earth’s atmosphere, undergoes refraction continuously before it reaches the earth.
• As the optical density of air increases towards surface of the earth, light from the star travels from rarer to denser layers, bending every time towards the normal.
• On producing the final refracted ray backwards as shown in the following figure, we find that the apparent position (B) of a star is higher than the actual position (A) of the star as shown in figure 11.11.
  
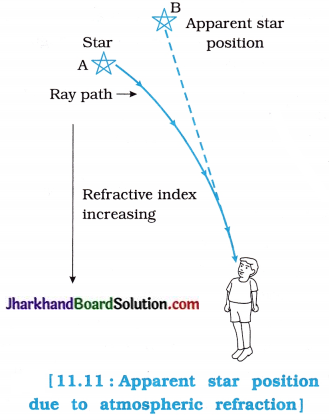
• The star appears somewhat higher (above) than its actual position when viewed near the horizon.
  Further, this apparent position of the star is not stationary, but keeps on changing slightly, since physical conditions of the earth’s atmosphere are not stationary.
• Since the stars are very distant, they appear as point-sized sources of light.
• Due to a continuous change in the direction of propagation of light, the apparent position of the star fluctuates all the time and the amount of starlight entering the eye flickers, i.e., the brightness of the star changes continuously (the star sometimes appears brighter and at some other time fainter). This is called the twinkling s of a star.

Question 11.
Explain why the planets do not twinkle.
Answer:
Planets are much closer to the earth relative to stars. Therefore, planets appear bigger > than stars. Stars are far away from the earth. Therefore they appear smaller.

• So, stars can be considered as point-sized sources and planets can be considered as a ? collection of a large number of point-sized sources of light, i.e., extended sources of light.
• As planet is a collection of a large number of point-sized sources of light, the total variation in amount of light entering our eye from all the individual point-sized sources averages out to zero, thereby nullifying the twinkling effect. That is why planets do not twinkle.

Question 12.
Why does the Sun appear reddish early in the morning?
Answer:

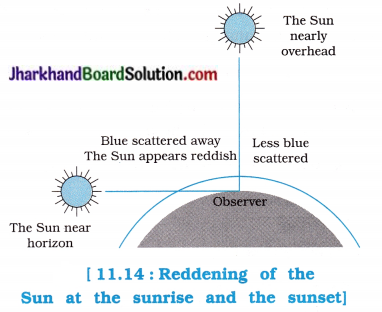
• In figure 11.14, the situation at the sunrise is shown.
• Here, the white light coming from the Sun near the horizon, passes through thick layers of air and covers larger distance in the earth’s atmosphere before reaching the observer. During this, more scattering of blue light and shorter wavelengths take place. Hence, the reddish light reaches the observer and the Sun appears reddish.
• The same thing occurs at the sunset.

[Note : Rising and setting of the full moon from the horizon appears reddish due to this reason.]

Question 13.
Why does the sky appear dark instead of blue to an astronaut?
Answer:
The sky appears dark to the astronaut because in outer space, there is no atmosphere to scatter the sunlight. Since there is no scattering of the blue component of the white sunlight which can reach the eye of an astronaut in outer space, the sky appears dark to the astrounaut, instead of blue.

Jharkhand Board Class 10 Science Human Eye and Colourful World InText Questions and Answers

Question 1.
What is meant by power of accommodation of the eye?
Answer:
The ability of the eye lens to adjust its focal length, so that nearby as well as distant objects can be focussed on the retina and hence seen comfortably and distinctly is called the power of accommodation of the eye.

Question 2.
A person with a myopic eye cannot see objects beyond 1.2 m distinctly. What should be the type of the corrective lens used to restore proper vision?
Answer:
A person with a myopic eye should use a concave lens of suitable focal length or power to restore proper vision.
[Here, the person with defect of myopia has the far point nearer than infinity at a distance of 1.2 m from the eye.
So, v = – 1.2m; u = – ∞; f = ?
So, from the lens formula
\(\frac{1}{f}=\frac{1}{-u}-\frac{1}{v}\)
∴ \(\frac{1}{f}=\frac{1}{-(-\infty)}+\frac{1}{-1.2}\)
∴ f = – 1.2 m
∴ P = \(\frac { 1 }{ – 1.2 }\) = – 0.83 D
∴ A concave lens of focal length 1.2 m should be used to restore proper vision.]

Question 3.
What is the far point and near point of the human eye with normal vision?
Answer:
For the human eye with normal vision, f the far point is at infinity and the near point is at 25 cm from the eye.

Question 4.
A student has difficulty in reading the blackboard while sitting in the last row. What could be the defect the child is suffering from? How can it be corrected?
Answer:
As the child cannot see distant objects 5 clearly it means that he is suffering from myopia or near-sightedness. In this case the child can S see nearby objects clearly but cannot see far off objects distinctiy as their images are formed s before the retina.

To correct this defect, the child has to use spectacles with concave lens of suitable focal length.

Activity 11.1 [T. B. Pg. 192]

To study the refraction of light through a s triangular glass prism.

Procedure:
1. Fix a sheet of white paper on a drawing board ; using drawing pins.

2. Place a glass prism on it in such a way that ; it rests on its triangular base. Trace the outline of the prism using a pencil.

3. Fix two pins, say at points P and Q, on the line PE as shown in the following figure :

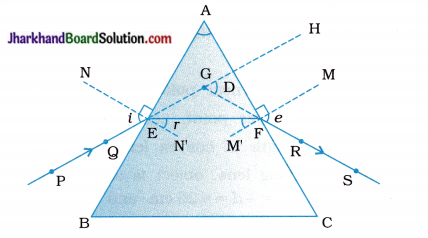
Refraction of light through a triangular glass prism
PE – Incident ray
EE – Refracted ray
FS – Emergent ray
∠A – Angle of the prism
∠i – Angle of incidence
∠r – Angle of refraction
∠e – Angle of emergence
∠D – Angle of deviation

4. Look for the images of the pins, fixed at P and Q, through the other face AC.

5. Fix two more pins, at points R and S, such that the pins at R and S and the images of the pins at P and Q lie on the same straight line.

6. Remove the pins and the glass prism.

7. Join the points P and Q and extend the line till it meets the nearest boundary of the prism. Similarly, join and produce the points R and S. Let these lines meet the boundary of the prism at E and F respectively. Join E and E

8. Extend PE and RS such that they meet at point G. Mark the angle of deviation (∠D) as shown in figure.

9. Draw perpendiculars to the refracting surfaces AB and AC of the prism at points E and F respectively.

10. Mark the angle of incidence (∠i), the angle of refraction (∠r) and the angle of emergence (∠e) as shown in the figure.

Compare the angle of incidence and the angle of refraction at each refracting surface of the prism.
Bending of rays PE, EF and FS are similar to the kind of bending that occurs in a glass slab.

Observation:
1. A ray of light suffers two refractions while passing through a prism.

2. The first refraction occurs at E on the surface AB. The incident ray PE, enters from air into glass E. It is refracted along EF bending towards normal NN’ on face AB at E.

3. The second refraction occurs at F on the surface AC. The initial refracted ray EF travelling in glass emerges in air at F It emerges along FS, bending away from normal MM’ on face AC at F.

4. At the first refracting surface AB, angle of refraction (r) is smaller than the angle of incidence (i).

But at the second refracting surface AC, angle of refraction (e) is larger than angle of incidence (∠EFM’).

5. Bending of rays PE, EF and FS is of the same kind of bending that occurs in a glass slab. The net deviation in a rectangular glass slab is zero and there is lateral shift. However, due to the peculiar shape of the prism, net diviation in passing through a prism is not zero and the prism makes the emergent ray bend at an angle to the direction of the incident ray. This angle is called the angle of deviation, i.e., D = ∠HGS, It is the angle through which the incident ray is deviated as it passes through the prism.

6. The angle of deviation depends on the angle of incidence, the angle of the prism and the nature of the material of the prism as it depends on the refractive index of the material.

Conclusion :
While passing through a prism, a ray of light undergoes two refractions as it does in case of rectangular glass slab.

However due to peculiar shape of the prism, net deviation through prism is never zero, though the net deviation is zero in case of rectangular glass slab.

In short, deviation suffered by a ray of light on passing through a prism is non-zero.

Activity 11.2 [T. B. Pg. 193]

To show that white light is made up of seven colours and different colours suffer different deviations on passing through a prism.

Procedure:
1. Take a thick sheet of cardboard and make a small hole or narrow slit in its middle.

2. Allow sunlight to fall on the narrow slit. This gives a narrow beam of white light.

3. Now, take a glass prism and allow the light from the slit to fall on one of its faces as shown in the following figure:

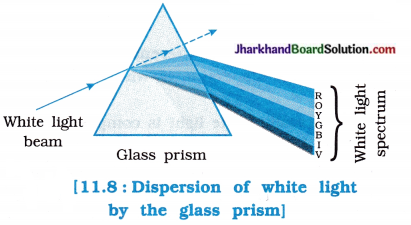
4. Turn the prism slowly until the light that comes out of it appears on a nearby screen.

• What do you observe?
• Why does this happen? OR How could white light of the Sun give us various colours of the rainbow?
• What is the sequence of colours that you observe on the screen?

Observations:

• We observe beautiful band of seven colours (VIBGYOR) on the screen. The deviation suffered by the violet light is maximum and that by the red light is minimum. Hence, the violet colour is at the lower end and the red colour is at the upper end of the screen.
• This happens because prism itself splits the incident white light into a band of colours.
• The sequence of colours seen from the lower end of the screen is violet (V), indigo (I), blue (B), green (G), yellow (Y), orange (O) and red (R).

Conclusion :
White light is made up of seven colours and different colours suffer different deviations.

Activity 11.3 [T. B. Pg. 196]

To observe scattering of light by colloidal particles.

Procedure:
1. Place a strong source (S) of white light at the focus of a convex (converging) lens (L₁) as shown in the figure 11.15 to produce a parallel beam of light.

2. Allow the light beam to pass through a transparent glass tank vessel (T) containing clean water.

3. Now, allow the beam of light to pass through the circular hole (C) made in a cardboard and obtain a sharp image of the circular hole on screen (MN) using a second convex (converging) lens (L₂) as shown in figure.

4. Dissolve 200g of sodium thiosulphate (hypo) – (Na₂S₂O₃) in about 2 L of clean water taken in the tank. Add 1 to 2 mL of concentrated sulphuric acid (H₂SO₄) in the water.
What do you observe?

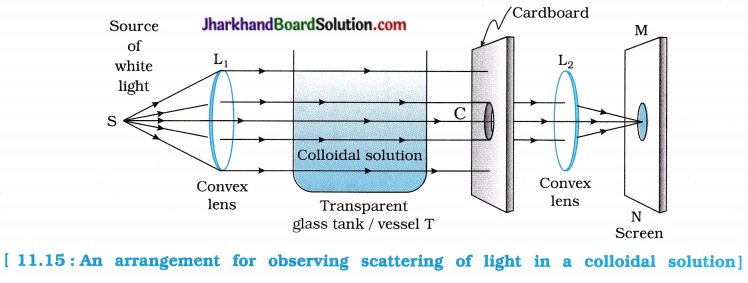
Observation:
In the arrangement shown in the figure, we find that fine microscopic sulphur particles precipitate in water (from solidum thiosulphate) in a couple of minutes.

Blue colour is seen from three sides of the tank due to scattering of short wavelengths by minute sulphur particles. We see transmitted light from the fourth side of the tank facing the hole (C) of the cardboard.

We first observe orange-red colour and then bright crimson red colour on the screen (MN) because the transmitted light contains mainly longer wavelengths only.

Conclusion:
Very fine particles of liquid, mainly scatter blue light of smaller wavelength and the red light containing longer wavelength passes straight (without scattering) from the vessel.